Attualizzazione. Attualizzazione
|
|
|
- Aurora Pandolfi
- 10 anni fa
- Visualizzazioni
Transcript
1 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe ersa della captalzzazoe; se dchamo co f( l fattore d motate abbamo C M f ( t ) La quattà ( t ) ( f prede l ome d fattore d attualzzazoe corrspodete al fattore d motate f( Fabo Bell 3 Attualzzazoe I fattor d attualzzazoe godoo delle seguet propretà: ) ( è defta per t [ T ) oppure per t [ ) ) () ) ( è ua fuzoe ocrescete del tempo t Il fattore d attualzzazoe ( esprme qud l alore attuale (al tempo coè ogg) d Euro dspoble al tempo t E' qud decrescete t e sempre more o uguale a A cascu regme d captalzzazoe assocamo u corrspodete regme d captalzzazoe: ( (regme dello scoto semplce o razoale) t ( ( ) t e δt (regme dello scoto composto) ( dt (regme dello scoto commercale) Fabo Bell 3
2 Fluss fazar L'oggetto fodametale d studo della matematca fazara tradzoale soo fluss fazar U flusso fazaro è u seme d mport ( geerale d sego posto oppure egato) che egoo rceut (oppure pagat se d sego egato) u seme prefssato d stat d tempo Matematcamete u flusso fazaro è ua coppa d ettor: l ettore degl mport R e l ettore delle scadeze t Scramo S { R ; t } U flusso fazaro cu tutt gl mport soo post prede l ome d redta fazara o semplcemete redta La caratterstca fodametale de fluss che cosderamo questo cotesto è quella d essere cert; l terme R prede l ome d rata - esma e l terme t prede l ome d scadeza -esma Grafcamete: Fabo Bell 3 Alcu tp fodametal d redte: Tp d redte a rata costate / a rata arable; utara se R temporaee (coè co u umero fto d rate) / perpetue (fte rate) perodche (le rate soo equterallate) / o perodche atcpate / postcpate (l pagameto aee all'zo/fe del perodo d competeza) mmedate (le rate zao subto) /dfferte Fabo Bell 3
3 Esemp Ua redta aua mmedata atcpata d 3 rate: ua redta aua mmedata postcpata d 3 rate: ua redta aua dfferta d perod postcpata d 3 rate: Fabo Bell 3 Il alore attuale Itroducamo ora l fodametale cocetto d alore attuale d ua redta Il alore attuale d ua redta è la somma de alor attual de sgol fluss calcolat utlzzado u regme d attualzzazoe prefssato che usualmete è quello dello scoto composto I formule se abbamo ua redta S l suo alore attuale è dato da { R ; t } V ( S) R ( t doe rappreseta l umero d rate e (t ) l fattore d attualzzazoe relato alla scadeza t Osseramo che el caso d ua redta perpetua la sommatora deta ua sere composta da ft added ) Fabo Bell 3 3
4 Propretà del alore attuale Il alore attuale gode d due propretà fodametal: addttà e omogeetà Cosderamo due redte S e S Defamo aztutto la redta "somma" S S come la redta che s ottee sommado cascua scadeza le rate delle redte S e S L'seme delle scadeze della redta S S sarà oamete l'uoe dell'seme delle scadeze delle redte S e S La propretà d addttà dce che l alore attuale della somma d due redte è la somma de alor attual delle due redte; smbol V ( S S ) V ( S) V ( S ) La dmostrazoe d questa propretà è oa: Fabo Bell 3 S ha edetemete Propretà del alore attuale V ( S S ) ( R R ) ( t ) R ( t ) R( t ) V ( S) V ( S) doe R dca la rata -esma della prma redta metre R è la rata - esma della secoda redta Per calcolare l alore attuale d ua redta complcata posso qud decomporla ella somma d redte pù semplc e po sommare l loro alor attual La propretà d omogeetà dce ece che V ( α S) ( αr ) ( t ) α R ( t ) αv ( S) coè se moltplco tutte le rate per ua costate ache l alore attuale s moltplca per la stessa costate Il alore attuale è pertato ua fuzoe leare Fabo Bell 3 4
5 Valore d ua redta u state t Fora abbamo calcolato l alore d ua redta S ell'state d tempo zale per coezoe t I modo del tutto aalogo possamo defre l cocetto d alore attuale d ua redta u state t geerco: V ( S R ( t t doe l fattore d attualzzazoe due arabl (tt ) rappreseta l alore al tempo t d Euro dspoble al tempo t Se utlzzamo l regme d attualzzazoe dello scoto composto come cosegueza della propretà d scdbltà che abbamo sto la olta scorsa l alore attuale al tempo t s ottee captalzzado l alore attuale al tempo : Negl altr regm d attualzzazoe questa propretà o è erfcata ) V ( S V ( S) ( ) t Fabo Bell 3 Calcol d alor attual Cosderamo ora ders cas che c coducoo a formule molto mportat Izamo da ua redta aua mmedata postcpata composta da rate d mporto utaro el regme dello scoto composto al tasso auo : Le crocette dcao le rate l pallo l'state d alutazoe Itroducamo aztutto la otazoe per l fattore d attualzzazoe relato ad u perodo Dato che l alore attuale è la somma de alor attual de sgol fluss abbamo Fabo Bell 3 5
6 6 Calcol d alor attual Fabo Bell 3 ha s Dato che ) ( otteamo ha s Rcordado che se 3 3 V V V Calcol d alor attual Fabo Bell 3 La quattà (- )/ è fodametale ella matematca fazara e prede l ome d "a fgurato al tasso " S dca co: Se ece (coè ) la formula precedete o è alda Possamo ragoare due mod; dal puto d sta fazaro ua tasso d teresse par a corrspode a u fattore d attualzzazoe par a per qualsas scadeza; l alore attuale d qualsas rata cocde co l suo ammotare Pertato se l alore attuale è semplcemete la somma delle rate el caso d ua redta mmedata postcpata d rate utare è par semplcemete a Dal puto d sta matematco possamo cofermare l rsultato osserado che a ) ( lm ) ( lm lm a
7 Calcol d alor attual Se la rata fosse par a R ece che a dalla propretà d omogeetà aremmo edetemete V Ra Cosderamo ora ua redta aua mmedata atcpata composta da rate d mporto utaro el regme dello scoto composto al tasso auo : Possamo rpetere l ragoameto d prma: V ( ) a& che s legge "a atcpato fgurato al tasso " Fabo Bell 3 Calcol d alor attual Ache qu se l alore attuale è par a e se la rata è R ece d l alore attuale è par a V Ra& Cofrotado la redta postcpata co quella atcpata possamo osserare mmedatamete che a&& a&& ( ) a a (dalla propretà d scdbl tà) (dalla propretà d addttà ) Fabo Bell 3 7
8 Calcol d alor attual Cosderamo ora ua redta aua mmedata postcpata dfferta d p a composta da rate d mporto utaro el regme dello scoto composto al tasso auo : S ha p p p V ( ) a Fazaramete per questa redta a p rappreseta l alore attuale ell'state tp; dalla propretà d scdbltà l alore attuale t s ottee moltplcado l alore attuale tp per p p p Fabo Bell 3 Calcol d alor attual Cosderamo ora ua redta aua mmedata postcpata composta da p rate La posso edere come somma d ua redta mmedata postcpata composta da p rate e d ua redta postcpata d rate dfferta d p perod: E pertato edete dal puto d sta fazaro che dee alere a a a p p p Fabo Bell 3 8
9 Calcol d alor attual Cosderamo ora ua redta perpetua mmedata postcpata composta da fte rate aue utare el regme dello scoto composto al tasso auo : S ha edetemete 3 V ( ) doe abbamo utlzzato la espressoe della somma d ua sere geometrca Osseramo che < se e solo se >; se la sere derge; l alore attuale derge a pù fto Fabo Bell 3 Calcol d alor attual Lo stesso rsultato s ottee facedo tedere a fto ella espressoe del alore attuale della corrspodete redta fta: lm a lm se < Se ece la redta perpetua fosse atcpata: allora l alore attuale sarebbe dato da V Fabo Bell 3 9
10 Valore attuale fuzoe del tasso I tutt cas fora cotrat la fuzoe V() che esprme l alore attuale d ua redta fuzoe del tasso d teresse gode delle seguet propretà: - V è ua fuzoe decrescete d - V() è par alla somma delle rate (che è pù fto el caso delle redte perpetue - lm V ( ) R coè quado tass detao molto grad l alore attuale tede alla rata percepta al tempo t (che può ache essere ulla) Vedremo pù aat che la derata prma della fuzoe V() è legata alla durato della redta metre la derata secoda alla sua coesstà Fabo Bell 3 Valore fale o motate d ua redta Cosderazo del tutto aaloghe a quelle fora solte s applcao al alore fale o motate d ua redta Izamo dal caso base d ua redta aua utara mmedata postcpata d cu calcolamo l alore ell state fale t: poamo u (fattore d captalzzazoe relato a u perodo) otteedo u u M u u u u s u Equaletemete posso prma calcolare l alore attuale t e po captalzzarlo per perod otteedo l dettà s a u Fabo Bell 3
11 Valore fale o motate d ua redta Se la redta fosse atcpata: aremmo semplcemete M ( ) s us & s Fabo Bell 3
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Valore attuale di una rendita. Valore attuale in Excel: funzione VA
Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
Avvertenza. Rendite frazionate
Avverteza Quest lucd soo pesat solo come u auslo per l ascolto della lezoe. No sosttuscoo l lbro d testo Possoo coteere error e svste, che gl studet soo vtat a segalare Redte frazoate L tervallo tra ua
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Lezione 1. I numeri complessi
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Ammortamento americano. Ammortamento americano
mmortameto amercao La cora lezoe abbamo vto che ell'ammortameto amercao l rmboro del debto zale avvee medate u uco verameto a cadeza, otteuto attravero ua operazoe d cottuzoe d u captale al tao attvo j;
Rendita perpetua con rate crescenti in progressione aritmetica
edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
frazione 1 n dell ammontare complessivo del carattere A x
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
MATEMATICA FINANZIARIA 1 ECONOMIA AZIENDALE. Cognome... Nome Matricola..
MATEMATICA FINANZIARIA PROVA SCRITTA DEL 0 FEBBRAIO 009 ECONOMIA AZIENDALE Cognome... Nome Matrcola.. ESERCIZIO Un ndduo ha ogg a dsposzone una somma S0.000 che ha accumulato negl ultm ann tramte l ersamento
Successioni. Grafico di una successione
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Matematica elementare art.1 di Raimondo Valeri
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Anno 5 Successioni numeriche
Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
V Tutorato 6 Novembre 2014
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
SUCCESSIONI E SERIE NUMERICHE
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
La matematica finanziaria
La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
1 Limiti di successioni
Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Appunti sulla MATEMATICA FINANZIARIA
INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
Interesse e formule relative.
Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Design of experiments (DOE) e Analisi statistica
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Manuale di Estimo Vittorio Gallerani, Giacomo Zanni, Davide Viaggi Copyright 2004 The McGraw-Hill Companies srl
Mauale d Estmo ttoro Gallera, Gacomo Za, Davde agg Copyrght 24 The McGraw-Hll Compaes srl Caso 5 Stma d u agrumeto d 3 ha ubcato ella paa d Cataa. 1. Cofermeto dell carco e uesto d stma... 2 2. Descrzoe
ESERCIZI SULLE SERIE
ESERCIZI SULLE SERIE Studiare la atura delle segueti serie. ) cos 4 + ; ) + si ; ) + ()! 4) ( ) 5) ( ) + + 6) ( ) + + + 7) ( log ) 8) ( ) + 9) log! 0)! Studiare al variare di x i R la atura delle segueti
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
L assorbimento e lo strippaggio
assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
Prova di verifica n.0 Elettronica I (26/2/2015)
Proa d erfca n.0 lettronca I (26/2/2015) OUT he hfe + L OUT - Fgura 1 Con rfermento alla rete elettrca d Fg.1, determnare: OUT / OUT / la resstenza sta dal generatore ( V ) la resstenza sta dall uscta
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Elementi di matematica finanziaria
Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Serie numeriche: esercizi svolti
Serie umeriche: esercizi svolti Gli esercizi cotrassegati co il simbolo * presetao u grado di difficoltà maggiore. Esercizio. Dopo aver verificato la covergeza, calcolare la somma delle segueti serie:
FUNZIONI LOGICHE FORME CANONICHE SP E PS
FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
Lezione 3. Funzione di trasferimento
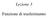Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Lezione 4. La Variabilità. Lezione 4 1
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Soluzione La media aritmetica dei due numeri positivi a e b è data da M
Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Modelli di Schedulazione
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
SUCCESSIONI NUMERICHE
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
5 ln n + ln. 4 ln n + ln. 6 ln n + ln
DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
Statistica degli estremi
Statstca degl estrem Rcham d probabltà e statstca Il calcolo della probabltà d u eveto è drettamete coesso co: - la COOSCEZA ICOMPLETA dell eveto stesso; - l assuzoe d u RISCHIO, calcolato come la probabltà
Una funzione è una relazione che ad ogni elemento del dominio associa uno e un solo elemento del codominio
Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 3 Drettore Beatrce VENTURI Uverstà degl Stud d Caglar Comtato scetfco Umberto NERI Uversty of Marylad Russel Alla
CONCETTI BASE DI STATISTICA
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
Sistemi e Tecnologie della Comunicazione
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Approssimazioni di curve
Approssmazo d curve e superfc Approssmazo d curve Il terme Computer Grafca comprede ua larga varetà d applcazo che rguardao umerevol aspett della ostra vta. U eleco esemplfcatvo d alcu de camp cu essa
Formula per la determinazione della Successione generalizzata di Fibonacci.
Formula per la determiazioe della uccessioe geeralizzata di Fiboacci. A cura di Eugeio Amitrao Coteuto dell articolo:. Itroduzioe......... uccessioe di Fiboacci....... 3. Formula di Biet per la successioe
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 15/16 Successioni cap3b.pdf 1
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 15/16 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X = N:
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Problema della Ricerca
Problema della Rcerca Pag. /59 Problema della Rcerca U dzoaro rappreseta u seme d formazo suddvso per elemet ad oguo de qual è assocata ua chave. Esempo d dzoaro è l eleco telefoco dove la chave è costtuta
EQUAZIONI ALLE RICORRENZE
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
L ammortamento dei prestiti. S. Corsaro Matematica Finanziaria a.a. 2007/08
L ammortameto dei prestiti. Corsaro Matematica Fiaziaria a.a. 27/8 Prestiti idivisi Operazioi fiaziarie co due cotraeti mutuate o creditore: presta u capitale mutuatario o debitore: si impega a restituire
Capitolo 27. Elementi di calcolo finanziario EEE 2015-2016
Capitolo 27 Elemeti di calcolo fiaziario EEE 205-206 27. Le diverse forme dell iteresse Si defiisce capitale (C) uo stock di moeta dispoibile i u determiato mometo. Si defiisce iteresse (I) il prezzo d
Terzo appello del. primo modulo. di ANALISI 18.07.2006
Terzo appello del primo modulo di ANALISI 18.7.26 1. Si voglioo ifilare su u filo delle perle distiguibili tra loro solo i base alla dimesioe: si hao a disposizioe perle gradi di diametro di 2 cetimetri
8. Quale pesa di più?
8. Quale pesa di più? Negli ultimi ai hao suscitato particolare iteresse alcui problemi sulla pesatura di moete o di pallie. Il primo problema di questo tipo sembra proposto da Tartaglia el 1556. Da allora
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
5. Le serie numeriche
5. Le serie umeriche Ricordiamo che ua successioe reale è ua fuzioe defiita da N, evetualmete privato di u umero fiito di elemeti, a R. Solitamete si idica ua successioe co la lista dei suoi valori: (a
Campi vettoriali conservativi e solenoidali
Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile