Statistica multivariata Donata Rodi 21/11/2016
|
|
|
- Orlando Stella
- 8 anni fa
- Просмотров:
Транскрипт
1 Statistica multivariata Donata Rodi 21/11/2016
2 PCA Tecnica di riduzione delle dimensioni che descrive la struttura multivariata dei dati per analisi descrittive e inferenziali Descrive la variazione di un gruppo di dati multivariati correlati (X) in funzione di variabili latenti non correlate (Y), le Componenti Principali (o Scores) Per variabili quantitative Es. 10 variabili, 100 persone: dati!!!
3 PCA vs Analisi Fattoriale Tecniche strettamente correlate PCA: scinde i dati in componenti principali Analisi Fattoriale: identificazione di fattori di fondo (dimensioni sottese) che spieghino i dati, riduzione della dimensione dello spazio di rappresentazione PCA: unico risultato FA: più modelli per un unico data set
4 PCA
5 PCA Ipotesi: i valori di p variabili originarie sono determinate da un più piccolo numero di variabili indipendenti tra loro Y: combinazione lineare delle variabili X Y1: a11x1 + a12x2+ + a1pxp Y2: a21x1 + a22x2+ + a2pxp Yk: ak1x1 + ak2x2+ + akpxp Yn: an1x1 + an2x2+ + anpxp
6 PCA Ogni componente viene derivata in ordine di importanza decrescente La prima componente Y1 spiega la quota più alta di variazione nei dati originali Scopo: ottenere un piccolo gruppo di variabili per riassumere i dati (le prime PC), con la minor perdita di informazioni possibile Controllo del trade off tra perdita di informazioni e semplificazione del problema
7 Matrice di Correlazione Se la quota di varianza in comune è sufficiente, occorrono poche PC Occorre costruire una Matrice di Correlazione tra tutte le coppie di variabili R di Pearson tra le variabili Range: -1.0 a +1.0 Question 1 - ARI Question 2 - VI Question 3 - SL Question 4 - ARI Question 5 - VI Question 1 - ARI Question 2 - VI Question 3 - SL Question 4 - ARI Question 5 - VI
8 Verifica della validità del dataset KMO Indice di adeguatezza del campionamento Confronta I valori di correlazione tra le variabili e quelli delle correlazioni parziali Più sono vicini a 1, meglio lavora la PCA 0.70: adeguato Bartlett s test Test di Sfericità basato sul chi quadro Rifiuto di H0: mancanza di sufficiente correlazione tra le variabili Testa se la matrice di correlazione differisce dalla matrice identità ovvero se c è ridondanza tra le variabili che vengono sintetizzate nei pochi fattori Perfetta correlazione: basta un fattore Kaiser-Meyer-Olkin Measure of Sampling Adequacy..861 Bartlett's Test of Sphericity Approx. Chi-Square df 990 Sig..000
9 PCA: autovalori e autovettori Ogni componente principale è rappresentata da un autovalore λ Si hanno tanti autovalori quante sono le variabili X Ognuno degli autovalori p rappresenta la quantità di varianza standardizzata catturata da una componente
10 PCA: autovalori e autovettori A ogni autovalore è associato un autovettore in cui sono riportati i pesi componenziali (component loadings): esprimono il peso di ogni variabile rispetto alle PC Equivalenti ai coefficienti bivariati di correlazione lineare tra variabili e componenti L autovettore principale dalla scomposizione dei vettori della matrice di correlazione o della covarianza descrive una serie di combinazioni lineari non correlate delle variabili che contengono la maggior parte della varianza
11 Estrazione delle Componenti principali Da p variabili: p component (non correlate) La prima PC spiega la quantità di varianza maggiore possibile La seconda cattura il più possibile di quanto rimasto, e cosi via La prima componente viene estratta dalla matrice di correlazioni originale, la seconda da quella delle correlazioni ottenuta depurando la quota di varianze e covarianze riprodotta dalla prima componente principale Segue che le PC sono ortogonali e riproducono in ordine decrescente la massima quota di varianza ottenibile
12 Estrazione delle Componenti principali
13 Estrazione della Componente principale 2 Ogni variabile ha una varianza standardizzata a 1 La varianza standardizzata totale nelle p variabili = p Tutta la varianza dei dati viene estratta Per ogni componente, la proporzione di varianza estratta = autovalore / p Sommando gli autovalori (dalla matrice delle correlazioni) si ottiene la varianza totale della matrice di correlazioni originaria Rapporto autovalore/varianza totale * 100: percentuale di varianza riprodotta da ogni componente principale
14 Quante componenti tenere? Spesso si mantiene un set più piccolo di PC in una regressione lineare o logistica per evitare problemi di multicollinearità Vari approcci: Componenti con autovalori 1 (contributo significativo ai dati) Regola dell 80%: componenti che spiegano almeno l 80% della varianza totale Scree test: in grafico autovalori con il rispettivo numero di componenti, si mantiene il numero di PC prima del break in the plot (es. al cambio di pendenza)
15 PCA: requisiti Non devono essere correlate Cov(Yk, Yk) = 0 Devono essere ordinate in base alla quantità di variabilità complessiva che ciascuna può sintetizzare V(Y1) V(Y2) V(Yp) La variabilità dei due sistemi di riferimento deve coincidere Le variabili X sono tra loro correlate: sistema ridondante, è sufficiente considerare le prime m PC (m<p)
16 PCA: requisiti Ogni asse rappresenta una componente Asse x: prima componente Asse y: componente successiva Assi da -1 a +1 (campo di variazione dei pesi componenziali): semiasse positivo (da 0 a +1) e negativo (da -1 a 0) Il punto di intersezione (0,0) è il baricentro
17 Steps in PCA 1. Preparazione della matrice dati 2. Matrice di correlazione dati osservati 3. Verifica statistica per la validità del dataset per PCA (KMO, Bartlett s) 4. Estrazione dei fattori 5. Rotazione dei fattori 6. Assegnazione dei nomi ai fattori 7. Interpretazione dei punteggi dei fattori
18 Esempio 2
19 Variabile latente Variabile latente: non misurabile direttamente ma in modo indiretto attraverso alcune variabili osservate Es. Intelligenza: memoria a breve termine, capacità di parola, scrittura, lettura, abilità di comprensione etc. Soddisfazione del paziente: variabile latente Risposte su scala Likert, punteggio da 1 a 5 Sottogruppo di variabili latenti per aspetti specifici di quella generale
20 Esempio N = 10 Score da 0 a 100
21 Matrice dati
22 Esempio 3: scatter plot
23 Esempio 3: matrice di correlazione La varianza totale è pari al numero delle variabili (ogni variabile ha varianza = 1), essendo queste standardizzate Le covarianze sono date dalla matrice di correlazione bivariata tra le stesse Regola pratica: covarianza > 0.3
24 SPSS
25
26 Output
27 Communalities coefficients Quantità di varianza nella variabile influenzata da tutti i fattori Coefficiente maggiore: variabile definite dai fattori Coefficiente minore: variabile non predetta dai fattori Percentuale di variabilità attribuita al modello
28 Varianza spiegata Elenco delle singole componenti (n = numero di variabili) con autovalori e varianza spiegata Criterio di Kaiser: si mantengono solo le componenti con autovalori maggiori di 1
29 Scree plot Pesi delle PC senza rotazione
30 Output Piccoli residui: poca differenza tra le correlazioni riprodotte e la correlazione realmente osservate tra le variabili Fino a che punto le componenti importanti riescono a spiegare le correlazioni osservate tra le variabili?
31 Output
32 Output La rotazione distribuisce l importanza dei due fattori in modo simile Dipende dall estrazione di un appropriato numero di fattori
33 Output Quantità di rotazione dei fattori Cos 45 = 0,707
34 Output: plot variabili/pc PC 1: outgoingness (estroversione, avventura, socializzazione PC2: Neuroticism (ansia, agorafobia, aracnofobia)
35 Output Es. n8: sul primo fattore, basso in ogutgoingness sul secondo fattore, basso in neuroticism
36 Esempio Studio sul fitness: 9 componenti principali X1: Weight X2 Height X3: Age X4: Waist X5: cigerettes/day X6: Systolic Blood Pressure X7: Daistolic Blood Pressure X8: Pulse rate X9: Respiratory rate
37 Esempio Extraction folder Principal Componentes Unrotated factor solution
38 Estrazione: ogni variabile ha lo stesso peso
39 Varianza Totale Spiegata: quota di variabilità spiegata dalle singole componenti
40 Contributo di ogni variabile a ogni componente (da 7 a 9, escluse) La componente 1 ha un contributo simile da tutte le variabili: descrive il punteggio unfitness PCA 2: peso negativo su alcune variabili (caratteristiche fisiche) La prima componente fornisce la media pesata dei dati
41 Template I, score folders, template III Save the variables, regression Vengono generate 9 variabili nuove
42 Scatter Plot delle due componenti principali
43 Scree plot
ANALISI MULTIVARIATA
 ANALISI MULTIVARIATA Marcella Montico Servizio di epidemiologia e biostatistica... ancora sulla relazione tra due variabili: la regressione lineare semplice VD: quantitativa VI: quantitativa Misura la
ANALISI MULTIVARIATA Marcella Montico Servizio di epidemiologia e biostatistica... ancora sulla relazione tra due variabili: la regressione lineare semplice VD: quantitativa VI: quantitativa Misura la
Tecniche statistiche di analisi del cambiamento
 Tecniche statistiche di analisi del cambiamento 07-Anova con covariata (vers. 1.0, 3 dicembre 2015) Germano Rossi 1 [email protected] 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2015-16
Tecniche statistiche di analisi del cambiamento 07-Anova con covariata (vers. 1.0, 3 dicembre 2015) Germano Rossi 1 [email protected] 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2015-16
L analisi fattoriale
 L analisi fattoriale Scopo dell analisi fattoriale e quello di identificare alcune variabili latenti (fattori) in grado di spiegare i legami, le interrelazioni e le dipendenze tra le variabili statistiche
L analisi fattoriale Scopo dell analisi fattoriale e quello di identificare alcune variabili latenti (fattori) in grado di spiegare i legami, le interrelazioni e le dipendenze tra le variabili statistiche
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
L analisi fattoriale viene effettuata per studiare, riassumere e semplificare le relazioni in un insieme di variabili
 Analisi fattoriale L analisi fattoriale viene effettuata per studiare, riassumere e semplificare le relazioni in un insieme di variabili Ciò permette di individuare uno o più fattori o dimensioni latenti
Analisi fattoriale L analisi fattoriale viene effettuata per studiare, riassumere e semplificare le relazioni in un insieme di variabili Ciò permette di individuare uno o più fattori o dimensioni latenti
STATISTICA DESCRITTIVA. Elementi di statistica medica GLI INDICI INDICI DI DISPERSIONE STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
Generazione di Numeri Casuali- Parte 2
 Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
Principal. component analysis. Dai volti agli spettri di galassie
 Principal component analysis Dai volti agli spettri di galassie SCOPO: PCA for beginners Ridurre il numero di variabili all interno di una collezione di oggetti per descriverli piu facilmente, sulla base
Principal component analysis Dai volti agli spettri di galassie SCOPO: PCA for beginners Ridurre il numero di variabili all interno di una collezione di oggetti per descriverli piu facilmente, sulla base
ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo
 ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo 1 La seguente tabella riporta le frequenze relative riguardanti gli studenti di un università e gli esiti dell esame da essi sostenuto. Qual è la percentuale
ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo 1 La seguente tabella riporta le frequenze relative riguardanti gli studenti di un università e gli esiti dell esame da essi sostenuto. Qual è la percentuale
Procedura operativa per la gestione della funzione di formazione classi prime
 Procedura operativa per la gestione della funzione di formazione classi prime Questa funzione viene fornita allo scopo di effettuare la formazione delle classi prime nel rispetto dei parametri indicati
Procedura operativa per la gestione della funzione di formazione classi prime Questa funzione viene fornita allo scopo di effettuare la formazione delle classi prime nel rispetto dei parametri indicati
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
Analisi della varianza
 1. 2. univariata ad un solo fattore tra i soggetti (between subjects) 3. univariata: disegni fattoriali 4. univariata entro i soggetti (within subjects) 5. : disegni fattoriali «misti» L analisi della
1. 2. univariata ad un solo fattore tra i soggetti (between subjects) 3. univariata: disegni fattoriali 4. univariata entro i soggetti (within subjects) 5. : disegni fattoriali «misti» L analisi della
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II [email protected] 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II [email protected] 22 ottobre 2014 Stefania Spina Esercitazioni
Capitolo 11 Test chi-quadro
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
RICERCHE DI MERCATO. 5.6 Analisi Fattoriale (Componenti Principali)
 RICERCHE DI MERCATO 5.6 Analisi Fattoriale (Componenti Principali) Prof. L. Neri Dip. di Economia Politica Premessa Come evidenziato in precedenza l approccio di segmentazione per omogeneità prevede la
RICERCHE DI MERCATO 5.6 Analisi Fattoriale (Componenti Principali) Prof. L. Neri Dip. di Economia Politica Premessa Come evidenziato in precedenza l approccio di segmentazione per omogeneità prevede la
ANALISI DEI DATI PER IL MARKETING 2014
 ANALISI DEI DATI PER IL MARKETING 2014 Marco Riani [email protected] http://www.riani.it RIPASSO SULLE MATRICI 1 Addizione tra matrici Moltiplicazione Matrice diagonale Matrice identità Matrice trasposta
ANALISI DEI DATI PER IL MARKETING 2014 Marco Riani [email protected] http://www.riani.it RIPASSO SULLE MATRICI 1 Addizione tra matrici Moltiplicazione Matrice diagonale Matrice identità Matrice trasposta
ANALISI DEI DATI PER IL MARKETING 2014
 ANALISI DEI DATI PER IL MARKETING 2014 Marco Riani [email protected] http://www.riani.it RIPASSO SULLE MATRICI 1 Addizione tra matrici Moltiplicazione Matrice diagonale Matrice identità Matrice trasposta
ANALISI DEI DATI PER IL MARKETING 2014 Marco Riani [email protected] http://www.riani.it RIPASSO SULLE MATRICI 1 Addizione tra matrici Moltiplicazione Matrice diagonale Matrice identità Matrice trasposta
QUOTATURA. Affinché un qualsiasi oggetto disegnato possa essere esattamente realizzato deve essere perfettamente individuato in forma e dimensioni
 QUOTATURA Affinché un qualsiasi oggetto disegnato possa essere esattamente realizzato deve essere perfettamente individuato in forma e dimensioni Il disegno di un oggetto è quindi completo se descrive
QUOTATURA Affinché un qualsiasi oggetto disegnato possa essere esattamente realizzato deve essere perfettamente individuato in forma e dimensioni Il disegno di un oggetto è quindi completo se descrive
Carta di credito standard. Carta di credito business. Esercitazione 12 maggio 2016
 Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
valore di a: verso l alto (ordinate crescenti) se a>0, verso il basso (ordinate decrescenti) se a<0;
 La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
I costi d impresa (R. Frank, Capitolo 10)
 I costi d impresa (R. Frank, Capitolo 10) COSTI Per poter realizzare la produzione l impresa sostiene dei costi Si tratta di scegliere la combinazione ottimale dei fattori produttivi per l impresa È bene
I costi d impresa (R. Frank, Capitolo 10) COSTI Per poter realizzare la produzione l impresa sostiene dei costi Si tratta di scegliere la combinazione ottimale dei fattori produttivi per l impresa È bene
Il test (o i test) del Chi-quadrato ( 2 )
 Il test (o i test) del Chi-quadrato ( ) I dati: numerosità di osservazioni che cadono all interno di determinate categorie Prima di tutto, è un test per confrontare proporzioni Esempio: confronto tra numero
Il test (o i test) del Chi-quadrato ( ) I dati: numerosità di osservazioni che cadono all interno di determinate categorie Prima di tutto, è un test per confrontare proporzioni Esempio: confronto tra numero
7 Disegni sperimentali ad un solo fattore. Giulio Vidotto Raffaele Cioffi
 7 Disegni sperimentali ad un solo fattore Giulio Vidotto Raffaele Cioffi Indice: 7.1 Veri esperimenti 7.2 Fattori livelli condizioni e trattamenti 7.3 Alcuni disegni sperimentali da evitare 7.4 Elementi
7 Disegni sperimentali ad un solo fattore Giulio Vidotto Raffaele Cioffi Indice: 7.1 Veri esperimenti 7.2 Fattori livelli condizioni e trattamenti 7.3 Alcuni disegni sperimentali da evitare 7.4 Elementi
Calcolo di una Regressione lineare semplice con Excel
 Calcolo di una Regressione lineare semplice con Excel Inserire i dati In un tabellone vuoto di Excel, inserire i dati di X e di Y. Ad esempio i dati della Tabella 0.1 dovrebbero essere inseriti in Excel
Calcolo di una Regressione lineare semplice con Excel Inserire i dati In un tabellone vuoto di Excel, inserire i dati di X e di Y. Ad esempio i dati della Tabella 0.1 dovrebbero essere inseriti in Excel
Quantificare la variabilità dei processi ecologici
 Scopo ecologia Quantificare la variabilità dei processi ecologici Comprensione dei meccanismi fondamentale per identificare gli effetti del disturbo antropico e per prevenire alterazioni su scala globale
Scopo ecologia Quantificare la variabilità dei processi ecologici Comprensione dei meccanismi fondamentale per identificare gli effetti del disturbo antropico e per prevenire alterazioni su scala globale
Analisi Univariata e Multivariata dei Dati Economici Bruno Ricca (Dipartimento di studi su risorse, impresa, ambiente e metodologie quantitative)
 Programma di studio AA 2008-2009 Analisi Univariata e Multivariata dei Dati Economici Bruno Ricca (Dipartimento di studi su risorse, impresa, ambiente e metodologie quantitative) Modulo unico 10 cfu corso
Programma di studio AA 2008-2009 Analisi Univariata e Multivariata dei Dati Economici Bruno Ricca (Dipartimento di studi su risorse, impresa, ambiente e metodologie quantitative) Modulo unico 10 cfu corso
Metodologia di applicazione dei modelli di massima verosimiglianza per il trattamento dei dati missing
 Metodologia di applicazione dei modelli di massima verosimiglianza per il trattamento dei dati missing Erminio A. Bonizzoni Congresso nazionale BIAS 9/3 aprile 9 Sesto Fiorentino Firenze Stimatori di Massima
Metodologia di applicazione dei modelli di massima verosimiglianza per il trattamento dei dati missing Erminio A. Bonizzoni Congresso nazionale BIAS 9/3 aprile 9 Sesto Fiorentino Firenze Stimatori di Massima
Statistica - metodologie per le scienze economiche e sociali S. Borra, A. Di Ciaccio - McGraw Hill
 - metodologie per le scienze economiche e sociali S. Borra, A. Di Ciaccio - McGraw Hill Es. Soluzione degli esercizi del capitolo 8 home - indice In base agli arrotondamenti effettuati nei calcoli, si
- metodologie per le scienze economiche e sociali S. Borra, A. Di Ciaccio - McGraw Hill Es. Soluzione degli esercizi del capitolo 8 home - indice In base agli arrotondamenti effettuati nei calcoli, si
Avviso Test TOLC-I Facoltà di Scienze Revisione del 09/02/2016
 1 Corsi di Laurea della Facoltà di Scienze (Anno Accademico 2016/2017) - Corsi di Laurea ad accesso libero Classe Corso di Laurea L-27 Chimica L-30 Fisica L-35 Matematica L-34 Scienze Geologiche Requisiti
1 Corsi di Laurea della Facoltà di Scienze (Anno Accademico 2016/2017) - Corsi di Laurea ad accesso libero Classe Corso di Laurea L-27 Chimica L-30 Fisica L-35 Matematica L-34 Scienze Geologiche Requisiti
Statistica. Esercitazione 16. Alfonso Iodice D Enza [email protected]. Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazione 16 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 24 Studio della relazione tra due variabili Commonly Asked Questions Qual è la relazione tra la spesa
Esercitazione 16 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 24 Studio della relazione tra due variabili Commonly Asked Questions Qual è la relazione tra la spesa
Scala dei bisogni lavorativi F. Avallone, M. L. Farnese, R. Porcelli
 NOTE METODOLOGICHE PER LA SOMMINISTRAZIONE DELLE SCALE In collaborazione con la Facoltà di Psicologia 2 Università degli Studi di Roma Sapienza F. Avallone, M. L. Farnese, R. Porcelli FOTOCOPIABILE Istruzioni
NOTE METODOLOGICHE PER LA SOMMINISTRAZIONE DELLE SCALE In collaborazione con la Facoltà di Psicologia 2 Università degli Studi di Roma Sapienza F. Avallone, M. L. Farnese, R. Porcelli FOTOCOPIABILE Istruzioni
La valutazione del grado di soddisfazione del servizio scolastico: redazione ed elaborazione di un questionario-tipo *
 Annali del Dipartimento di Scienze Statistiche Carlo Cecchi Università degli Studi di Bari Aldo Moro - Vol. X (2011): 227-240 Cleup, Padova - ISBN: 978-88-6129-833-0 La valutazione del grado di soddisfazione
Annali del Dipartimento di Scienze Statistiche Carlo Cecchi Università degli Studi di Bari Aldo Moro - Vol. X (2011): 227-240 Cleup, Padova - ISBN: 978-88-6129-833-0 La valutazione del grado di soddisfazione
Esercizi su Autovalori e Autovettori
 Esercizi su Autovalori e Autovettori Esercizio n.1 5 A = 5, 5 5 5 Esercizio n.6 A =, Esercizio n.2 4 2 9 A = 2 1 8, 4 2 9 Esercizio n.7 6 3 3 A = 6 3 6, 3 3 6 Esercizio n.3 A = 4 6 6 2 2, 6 6 2 Esercizio
Esercizi su Autovalori e Autovettori Esercizio n.1 5 A = 5, 5 5 5 Esercizio n.6 A =, Esercizio n.2 4 2 9 A = 2 1 8, 4 2 9 Esercizio n.7 6 3 3 A = 6 3 6, 3 3 6 Esercizio n.3 A = 4 6 6 2 2, 6 6 2 Esercizio
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
La in verifica forma teoria normale della normalizzazione fornisce comunque uno strumento di già
 Le dati Presenza Complicazioni forme relazionale normaliverificano di ridondanze la qualitàdi uno schema di una base di Forme La forma normalizzazionepermette nella gestione di degli ottenere aggiornamenti
Le dati Presenza Complicazioni forme relazionale normaliverificano di ridondanze la qualitàdi uno schema di una base di Forme La forma normalizzazionepermette nella gestione di degli ottenere aggiornamenti
Correlazione. Daniela Valenti, Treccani Scuola 1
 Correlazione 1 I dati di un indagine per riflettere Cominciamo con i dati di un indagine svolta in una quinta classe di scuola superiore. Dopo l Esame di Stato 12 studenti si sono iscritti a corsi di laurea
Correlazione 1 I dati di un indagine per riflettere Cominciamo con i dati di un indagine svolta in una quinta classe di scuola superiore. Dopo l Esame di Stato 12 studenti si sono iscritti a corsi di laurea
Problemi di scelta ESEMPI
 ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
ESEMPI Risolvere i seguenti problemi 1. Una ditta deve effettuare delle spedizioni di un certo tipo di merce. Ha la possibilità di scegliere una o l altra delle due tariffe seguenti: a) 2.500 lire al quintale
Sistemi di equazioni lineari
 Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
12 Il mercato del lavoro dei politici
 INTroDUzIoNE La figura del politico e quella dell elettore sono alla base del concetto di democrazia rappresentativa. Ma chi è il politico? Ed è giusto considerare quella del politico una professione come
INTroDUzIoNE La figura del politico e quella dell elettore sono alla base del concetto di democrazia rappresentativa. Ma chi è il politico? Ed è giusto considerare quella del politico una professione come
Analisi fattoriale. esplorativa vers. 1.0. Germano Rossi 1 [email protected]. 1 Dipartimento di Psicologia, Università di Milano-Bicocca
 Analisi fattoriale esplorativa vers. 1.0 Germano Rossi 1 [email protected] 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2009 Rossi (Dip. Psicologia) Analisi fattoriale 2009 1 / 47 Prima
Analisi fattoriale esplorativa vers. 1.0 Germano Rossi 1 [email protected] 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2009 Rossi (Dip. Psicologia) Analisi fattoriale 2009 1 / 47 Prima
Il Bollino GRIN: coordinamento nazionale per le lauree di informatica
 Il Bollino GRIN: coordinamento nazionale per le lauree di informatica Prof. Enrico Nardelli Presidente GRIN (Associazione Italiana Docenti Universitari di Informatica) http://www.di.unipi.it/grin Verona,
Il Bollino GRIN: coordinamento nazionale per le lauree di informatica Prof. Enrico Nardelli Presidente GRIN (Associazione Italiana Docenti Universitari di Informatica) http://www.di.unipi.it/grin Verona,
B2B. Manuale per l utilizzatore.
 B2B Manuale per l utilizzatore. Pag.1 di 9 Accesso al portale Dal sito istituzionale di (www.safesafety.com) si accede alla sezione e-commerce B2B cliccando sull omonima icona. E anche possibile accedere
B2B Manuale per l utilizzatore. Pag.1 di 9 Accesso al portale Dal sito istituzionale di (www.safesafety.com) si accede alla sezione e-commerce B2B cliccando sull omonima icona. E anche possibile accedere
La codifica. dell informazione
 La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
La codifica dell informazione (continua) Codifica dei numeri Il codice ASCII consente di codificare le cifre decimali da 0 a 9 fornendo in questo modo un metodo per la rappresentazione dei numeri Il numero
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE
 PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
REGIONE CALABRIA REPUBBLICA ITALIANA FINCALABRA S.P.A. REGIONE CALABRIA DIPARTIMENTO 6 SVILUPPO ECONOMICO, LAVORO, FORMAZIONE E POLITICHE SOCIALI
 REGIONE CALABRIA DIPARTIMENTO 6 SVILUPPO ECONOMICO, LAVORO, FORMAZIONE E POLITICHE SOCIALI FONDO UNICO PER L OCCUPAZIONE E LA CRESCITA (FUOC) FONDO PER L OCCUPAZIONE Avviso Pubblico per il finanziamento
REGIONE CALABRIA DIPARTIMENTO 6 SVILUPPO ECONOMICO, LAVORO, FORMAZIONE E POLITICHE SOCIALI FONDO UNICO PER L OCCUPAZIONE E LA CRESCITA (FUOC) FONDO PER L OCCUPAZIONE Avviso Pubblico per il finanziamento
Lezione 4. Sommario. L artimetica binaria: I numeri relativi e frazionari. I numeri relativi I numeri frazionari
 Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
Esercitazione n o 3 per il corso di Ricerca Operativa
 Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
SNADIR. Corso di formazione Sviluppo sociale
 SNADIR Corso di formazione Sviluppo sociale SVILUPPO SOCIALE by Donatello Barone Piergiorgio Barone E un ambito estremamente variegato e ampio per cui non esiste una definizione onnicomprensiva ma possiamo
SNADIR Corso di formazione Sviluppo sociale SVILUPPO SOCIALE by Donatello Barone Piergiorgio Barone E un ambito estremamente variegato e ampio per cui non esiste una definizione onnicomprensiva ma possiamo
Corso di Psicometria Progredito
 Corso di Psicometria Progredito 4. Esercizi di Inferenza Statistica Gianmarco Altoè Dipartimento di Psicologia Università di Cagliari, Anno Accademico 2011-2012 Esercizio 4.1 - I due esami Nella seguente
Corso di Psicometria Progredito 4. Esercizi di Inferenza Statistica Gianmarco Altoè Dipartimento di Psicologia Università di Cagliari, Anno Accademico 2011-2012 Esercizio 4.1 - I due esami Nella seguente
ˆp(1 ˆp) n 1 +n 2 totale di successi considerando i due gruppi come fossero uno solo e si costruisce z come segue ˆp 1 ˆp 2. n 1
 . Verifica di ipotesi: parte seconda.. Verifica di ipotesi per due campioni. Quando abbiamo due insiemi di dati possiamo chiederci, a seconda della loro natura, se i campioni sono simili oppure no. Ci
. Verifica di ipotesi: parte seconda.. Verifica di ipotesi per due campioni. Quando abbiamo due insiemi di dati possiamo chiederci, a seconda della loro natura, se i campioni sono simili oppure no. Ci
Statistica. Esercitazione 10. Alfonso Iodice D Enza [email protected]. Università degli studi di Cassino. Statistica. A. Iodice. V.C.
 uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
Esercitazioni di Reti Logiche. Lezione 1 Rappresentazione dell'informazione. Zeynep KIZILTAN [email protected]
 Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN [email protected] Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN [email protected] Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
INFORMAZIONI RELATIVE AL CALCOLO DELLA DIMENSIONE DI IMPRESA 1
 In conformità al D.M. 3245/Ric. del 6 dicembre 2005 - All. n. 1 INFORMAZIONI RELATIVE AL CALCOLO DELLA DIMENSIONE DI IMPRESA 1 1. Dati identificativi dell impresa Denominazione o ragione sociale Indirizzo
In conformità al D.M. 3245/Ric. del 6 dicembre 2005 - All. n. 1 INFORMAZIONI RELATIVE AL CALCOLO DELLA DIMENSIONE DI IMPRESA 1 1. Dati identificativi dell impresa Denominazione o ragione sociale Indirizzo
qwertyuiopasdfghjklzxcvbnmqwerty AppuntiBicoccaAppuntiBicoccaAppu ntibicoccaappuntibicoccaappuntibic occaappuntibicoccaappuntibicoccaa
 qwertyuiopasdfghjklzxcvbnmqwerty AppuntiBicoccaAppuntiBicoccaAppu ntibicoccaappuntibicoccaappuntibic occaappuntibicoccaappuntibicoccaa Analisi multivariata dei dati Teoria e procedimento con SPSS ppuntibicoccaappuntibicoccaappunt
qwertyuiopasdfghjklzxcvbnmqwerty AppuntiBicoccaAppuntiBicoccaAppu ntibicoccaappuntibicoccaappuntibic occaappuntibicoccaappuntibicoccaa Analisi multivariata dei dati Teoria e procedimento con SPSS ppuntibicoccaappuntibicoccaappunt
Lavoro Quantità. si determinino prodotto marginale e medio del fattore lavoro.
 Microeconomia, Esercitazione 3. A cura di Giuseppe Gori ([email protected]) 1 Esercizi. 1.1 Produzione/1 Data una certa tecnologia di produzione definita solo nell input lavoro (o, in alternativa,
Microeconomia, Esercitazione 3. A cura di Giuseppe Gori ([email protected]) 1 Esercizi. 1.1 Produzione/1 Data una certa tecnologia di produzione definita solo nell input lavoro (o, in alternativa,
ESERCITAZIONE MICROECONOMIA (CORSO B) 21-12-2009 ESEMPI DI ESERCIZI DI TEORIA DEI GIOCHI
 ESERCITZIONE MICROECONOMI (CORSO ) --009 ESEMPI DI ESERCIZI DI TEORI DEI GIOCHI Questo documento contiene alcuni esempi di esercizi di teoria dei giochi. Gli esercizi presentati non corrispondono esattamente
ESERCITZIONE MICROECONOMI (CORSO ) --009 ESEMPI DI ESERCIZI DI TEORI DEI GIOCHI Questo documento contiene alcuni esempi di esercizi di teoria dei giochi. Gli esercizi presentati non corrispondono esattamente
INSTALLAZIONE HARDWARE IDP106C Ver. 1.3 BLUE DIMMER INSTALLAZIONE HARDWARE
 INSTALLAZIONE HARDWARE IDP106C Ver. 1.3 BLUE DIMMER INSTALLAZIONE HARDWARE Di seguito vengono forniti gli elementi di base per l installazione e l utilizzo del modulo BLUE DIMMER (modello IDP106C). Il
INSTALLAZIONE HARDWARE IDP106C Ver. 1.3 BLUE DIMMER INSTALLAZIONE HARDWARE Di seguito vengono forniti gli elementi di base per l installazione e l utilizzo del modulo BLUE DIMMER (modello IDP106C). Il
Re = f (A) f. 2 ),,, f (af. n )}
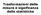 Trasformazioni delle misure e significanza delle statistiche Trasformazione e Significanza delle Statistiche: *) Invarianza assoluta. *) Invarianza di riferimento. *) Invarianza di confronto. *) Schemi
Trasformazioni delle misure e significanza delle statistiche Trasformazione e Significanza delle Statistiche: *) Invarianza assoluta. *) Invarianza di riferimento. *) Invarianza di confronto. *) Schemi
Esercitazioni di Statistica
 Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
BOLLETTINO dei controlli della produttività del latte 2015
 ASSOCIAZIONE ITALIANA ALLEVATORI ENTE MORALE D.P.R. N. 1051 DEL 27-10-1950 UFFICIO CENTRALE DEI CONTROLLI DELLA PRODUTTIVITÁ ANIMALE SOTTOPOSTO ALLA VIGILANZA DEL MINISTERO DELLE POLITICHE AGRICOLE E FORESTALI
ASSOCIAZIONE ITALIANA ALLEVATORI ENTE MORALE D.P.R. N. 1051 DEL 27-10-1950 UFFICIO CENTRALE DEI CONTROLLI DELLA PRODUTTIVITÁ ANIMALE SOTTOPOSTO ALLA VIGILANZA DEL MINISTERO DELLE POLITICHE AGRICOLE E FORESTALI
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
CAPITOLO V. DATABASE: Il modello relazionale
 CAPITOLO V DATABASE: Il modello relazionale Il modello relazionale offre una rappresentazione matematica dei dati basata sul concetto di relazione normalizzata. I principi del modello relazionale furono
CAPITOLO V DATABASE: Il modello relazionale Il modello relazionale offre una rappresentazione matematica dei dati basata sul concetto di relazione normalizzata. I principi del modello relazionale furono
Aspettative e soddisfazione degli studenti universitari. Un indagine empirica esplorativa Bruno Busacca, Giuseppe Bertoli e Ottavia Pelloni
 Copyright SDA Copyright Bocconi 2005 SDA Bocconi 2005 Bruno Busacca, Maria Carmela Ostillio 1 Aspettative e soddisfazione degli studenti universitari. Un indagine empirica esplorativa Bruno Busacca, Giuseppe
Copyright SDA Copyright Bocconi 2005 SDA Bocconi 2005 Bruno Busacca, Maria Carmela Ostillio 1 Aspettative e soddisfazione degli studenti universitari. Un indagine empirica esplorativa Bruno Busacca, Giuseppe
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Il metodo delle proporzioni crescenti
 Il metodo delle proporzioni crescenti Ulisse Di Corpo Abstract I modelli predittivi, che utilizzano le regressioni multiple, partono dall assunto che le relazioni tra le variabili sono lineari o traducibili
Il metodo delle proporzioni crescenti Ulisse Di Corpo Abstract I modelli predittivi, che utilizzano le regressioni multiple, partono dall assunto che le relazioni tra le variabili sono lineari o traducibili
SaWork ha un modulo specifico per il consulente che ha la visibilità su tutte le aziende sue clienti da dove può:
 SaWork è una soluzione software, dedicato alla gestione della sicurezza in azienda secondo quanto previsto dal Decreto Legge81/08 e dal successivo decreto 106/09 SaWork è una soluzione software pensata
SaWork è una soluzione software, dedicato alla gestione della sicurezza in azienda secondo quanto previsto dal Decreto Legge81/08 e dal successivo decreto 106/09 SaWork è una soluzione software pensata
Macroeconomia. Equilibrio in Economia Aperta. Esercitazione del 27.04.2016 (+ soluzioni) (a cura della dott.ssa Gessica Vella)
 Dipartimento di Economia, Statistica e Finanza Corso di Laurea in ECONOMIA Esercizio 1 Macroeconomia Equilibrio in Economia Aperta Esercitazione del 27.04.2016 (+ soluzioni) (a cura della dott.ssa Gessica
Dipartimento di Economia, Statistica e Finanza Corso di Laurea in ECONOMIA Esercizio 1 Macroeconomia Equilibrio in Economia Aperta Esercitazione del 27.04.2016 (+ soluzioni) (a cura della dott.ssa Gessica
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Normalizzazione. Definizione
 Normalizzazione Definizione Le forme normali 2 Una forma normale è una proprietà di una base di dati relazionale che ne garantisce la qualità, cioè l'assenza di determinati difetti Quando una relazione
Normalizzazione Definizione Le forme normali 2 Una forma normale è una proprietà di una base di dati relazionale che ne garantisce la qualità, cioè l'assenza di determinati difetti Quando una relazione
LA CIRCONFERENZA La circonferenza è il luogo geometrico dei punti equidistanti da un punto C, detto centro.
 Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
PENSIONI MINIME E MAGGIORAZIONI 2013: ATTENZIONE AI REDDITI
 PENSIONI MINIME E MAGGIORAZIONI 2013: ATTENZIONE AI REDDITI Già da qualche anno sono stati cambiati i parametri con i quali i pensionati possono ottenere le prestazioni pensionistiche legate al reddito.
PENSIONI MINIME E MAGGIORAZIONI 2013: ATTENZIONE AI REDDITI Già da qualche anno sono stati cambiati i parametri con i quali i pensionati possono ottenere le prestazioni pensionistiche legate al reddito.
VALUTAZIONE D IMPATTO DELLE POLITICHE REGIONALI PER LA PROMOZIONE DELL APPROPRIATEZZA ORGANIZZATIVA
 Mattone Misura dell appropriatezza GdLA 26 Settembre 2006 VALUTAZIONE D IMPATTO DELLE POLITICHE REGIONALI PER LA PROMOZIONE DELL APPROPRIATEZZA ORGANIZZATIVA QUESITI DELLA RICERCA Qual è stato l impatto
Mattone Misura dell appropriatezza GdLA 26 Settembre 2006 VALUTAZIONE D IMPATTO DELLE POLITICHE REGIONALI PER LA PROMOZIONE DELL APPROPRIATEZZA ORGANIZZATIVA QUESITI DELLA RICERCA Qual è stato l impatto
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
PROTEZIONE CONTRO I FULMINI (CEI 81-10) RELATORE: Dr. Nicola CARRIERO Dr. Carmineraffaele ROSELLI
 PROTEZIONE CONTRO I FULMINI (CEI 81-10) RELATORE: Dr. Nicola CARRIERO Dr. Carmineraffaele ROSELLI LE MODIFICHE INTRODOTTE DALLA VARIANTE V1 ALLA NORMA CEI 8I-10 Come noto, 81-10 è la classificazione CEI
PROTEZIONE CONTRO I FULMINI (CEI 81-10) RELATORE: Dr. Nicola CARRIERO Dr. Carmineraffaele ROSELLI LE MODIFICHE INTRODOTTE DALLA VARIANTE V1 ALLA NORMA CEI 8I-10 Come noto, 81-10 è la classificazione CEI
Lezione 12 Argomenti
 Lezione 12 Argomenti Costi di produzione: differenza tra costo economico e costo contabile I costi nel breve periodo Relazione di breve periodo tra funzione di produzione, produttività del lavoro e costi
Lezione 12 Argomenti Costi di produzione: differenza tra costo economico e costo contabile I costi nel breve periodo Relazione di breve periodo tra funzione di produzione, produttività del lavoro e costi
BOLLETTINO dei controlli della produttività del latte 2015
 ASSOCIAZIONE ITALIANA ALLEVATORI ENTE MORALE D.P.R. N. 1051 DEL 27-10-1950 UFFICIO CENTRALE DEI CONTROLLI DELLA PRODUTTIVITÁ ANIMALE SOTTOPOSTO ALLA VIGILANZA DEL MINISTERO DELLE POLITICHE AGRICOLE E FORESTALI
ASSOCIAZIONE ITALIANA ALLEVATORI ENTE MORALE D.P.R. N. 1051 DEL 27-10-1950 UFFICIO CENTRALE DEI CONTROLLI DELLA PRODUTTIVITÁ ANIMALE SOTTOPOSTO ALLA VIGILANZA DEL MINISTERO DELLE POLITICHE AGRICOLE E FORESTALI
Il Sistema LURTO LURTO
 Il Sistema LURTO Il sistema LURTO nasce dall esigenza di poter gestire, con un unico strumento software, l insieme dei pazienti in lista d attesa per un trapianto d organo e la conseguente attribuzione
Il Sistema LURTO Il sistema LURTO nasce dall esigenza di poter gestire, con un unico strumento software, l insieme dei pazienti in lista d attesa per un trapianto d organo e la conseguente attribuzione
IM-6145. Un sistema di misurazione completamente nuovo. p osi z iona re e. Sistema di misurazione dimensionale tramite immagini. Esempi di misurazione
 IM-6145 Un sistema di completamente nuovo È su ffi c iente p osi z iona re e preme re Sistema di dimensionale tramite immagini Esempi di Panoramica del sistema di dimensionale tramite immagini Obiettivo
IM-6145 Un sistema di completamente nuovo È su ffi c iente p osi z iona re e preme re Sistema di dimensionale tramite immagini Esempi di Panoramica del sistema di dimensionale tramite immagini Obiettivo
CONICHE. Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oxy sia data la conica C di equazione
 CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
Pro memoria per la ripartizione delle spese
 Pro memoria per la ripartizione delle spese Documento di lavoro post incontro del 23 e 24 novembre 2009, Roma, ad uso interno del Gruppo di lavoro Istat-Upi per la sperimentazione della contabilità ambientale
Pro memoria per la ripartizione delle spese Documento di lavoro post incontro del 23 e 24 novembre 2009, Roma, ad uso interno del Gruppo di lavoro Istat-Upi per la sperimentazione della contabilità ambientale
L indagine statistica
 1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
Cluster Analysis. La Cluster Analysis è il processo attraverso il quale vengono individuati raggruppamenti dei dati. per modellare!
 La Cluster Analysis è il processo attraverso il quale vengono individuati raggruppamenti dei dati. Le tecniche di cluster analysis vengono usate per esplorare i dati e non per modellare! La cluster analysis
La Cluster Analysis è il processo attraverso il quale vengono individuati raggruppamenti dei dati. Le tecniche di cluster analysis vengono usate per esplorare i dati e non per modellare! La cluster analysis
PROBLEMI DI SCELTA dipendenti da due variabili d azione
 prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
prof. Guida PROBLEMI DI SCELTA dipendenti da due variabili d azione in un problema di programmazione lineare, si ricorda che la funzione obiettivo z=f(x,y)=ax+by+c assume il suo valore massimo (o minimo)
PowerDIP Software gestione presenze del personale aziendale. - Guida all inserimento e gestione dei turni di lavoro -
 PowerDIP Software gestione presenze del personale aziendale - Guida all inserimento e gestione dei turni di lavoro - Informazioni preliminari. E necessario innanzitutto scaricare e installare l ultima
PowerDIP Software gestione presenze del personale aziendale - Guida all inserimento e gestione dei turni di lavoro - Informazioni preliminari. E necessario innanzitutto scaricare e installare l ultima
La traccia assegnata come seconda prova di Economia aziendale, nell Indirizzo Amministrazione, Finanza e Marketing è strutturata in due parti.
 Istituto Tecnico - Settore economico Indirizzo: Amministrazione, Finanza e Marketing Esame di Stato anno scolastico 2015/2016 Svolgimento seconda prova di Economia aziendale La traccia assegnata come seconda
Istituto Tecnico - Settore economico Indirizzo: Amministrazione, Finanza e Marketing Esame di Stato anno scolastico 2015/2016 Svolgimento seconda prova di Economia aziendale La traccia assegnata come seconda
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica
 Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
La soluzione di sicurezza flessibile
 La soluzione di sicurezza flessibile Xesar Il sistema di chiusura per situazioni complesse La soluzione di sicurezza flessibile per l uso professionale Xesar è l ultima innovazione di EVVA. Sviluppato
La soluzione di sicurezza flessibile Xesar Il sistema di chiusura per situazioni complesse La soluzione di sicurezza flessibile per l uso professionale Xesar è l ultima innovazione di EVVA. Sviluppato
Statistica - metodologie per le scienze economiche e sociali /2e S. Borra, A. Di Ciaccio - McGraw Hill
 Statistica - metodologie per le scienze economiche e sociali /e S. Borra A. Di Ciaccio - McGraw Hill s. 9. Soluzione degli esercizi del capitolo 9 In base agli arrotondamenti effettuati nei calcoli si
Statistica - metodologie per le scienze economiche e sociali /e S. Borra A. Di Ciaccio - McGraw Hill s. 9. Soluzione degli esercizi del capitolo 9 In base agli arrotondamenti effettuati nei calcoli si
Progettazione logica
 Progettazione logica Progettazione Logica Il prodotto della progettazione logica è uno schema logico che rappresenta le informazioni contenute nello schema E- R in modo corretto ed efficiente. Richiede
Progettazione logica Progettazione Logica Il prodotto della progettazione logica è uno schema logico che rappresenta le informazioni contenute nello schema E- R in modo corretto ed efficiente. Richiede
JOE ROSS - TRADING EDUCATORS www.tradingeducators.education Esempi di trade con la tecniche DAYTRADING in diversi mercati e intervalli temporali
 JOE ROSS - TRADING EDUCATORS www.tradingeducators.education Esempi di trade con la tecniche DAYTRADING in diversi mercati e intervalli temporali Esempio 1: Future Crude Oil con grafico a 5 minuti! Data
JOE ROSS - TRADING EDUCATORS www.tradingeducators.education Esempi di trade con la tecniche DAYTRADING in diversi mercati e intervalli temporali Esempio 1: Future Crude Oil con grafico a 5 minuti! Data
QUOTAZIONI USATO DEALER
 QUOTAZIONI USATO DEALER Guida all uso Ricerca... 2 Elenco dei risultati... 3 Scheda di dettaglio... 5 Icone... 6 Ricerca Inserisci la targa 1 nel campo di ricerca 2 Seleziona il mese di quotazione 3 Clicca
QUOTAZIONI USATO DEALER Guida all uso Ricerca... 2 Elenco dei risultati... 3 Scheda di dettaglio... 5 Icone... 6 Ricerca Inserisci la targa 1 nel campo di ricerca 2 Seleziona il mese di quotazione 3 Clicca
