Corso di Istituzioni di Matematiche
|
|
|
- Eva Grasso
- 5 anni fa
- Visualizzazioni
Transcript
1 Corso di Istituzioni di Matematiche Università degli Studi della Basilicata Facoltà di Scienze MM. FF. NN. Corso di laurea in Biotecnologie A.A. 2010/11 dott.ssa Vita Leonessa Elementi di calcolo combinatorio 23 dicembre 2010
2 Si vedranno alcune tecniche per determinare, senza contarli direttamente, il numero degli elementi di un insieme finito o il numero possibile degli esiti di un esperimento.
3 Esempio: il lancio di due dadi D 2 = D 2 = 6 2 = 36 (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6) (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6) (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
4 Esempio: il lancio di due dadi contare gli elementi di una tabella (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) 6 (numero righe) 6 (numero colonne) = 36 elementi
5 Più in generale... Il conto precedente è un caso particolare del problema seguente: Dato un insieme di n oggetti, contare le sequenze ordinate di k elementi (con k n) in cui un elemento può comparire più volte. Definizione Tali sequenze si dicono disposizioni con ripetizione di n oggetti presi k alla volta. Il loro numero è n k.
6 Più in generale... Il conto precedente è un caso particolare del problema seguente: Dato un insieme di n oggetti, contare le sequenze ordinate di k elementi (con k n) in cui un elemento può comparire più volte. Definizione Tali sequenze si dicono disposizioni con ripetizione di n oggetti presi k alla volta. Il loro numero è n k.
7 Più in generale... L insieme S k = {(s 1, s 2,..., s k ) : s j S, j = 1,..., k} costituito dalle k-uple ordinate di elementi di S ha S k elementi. Se S = n, da cui S k = n k. ( s 1, s 2,..., s k ) n scelte n scelte n scelte }{{} k volte
8 Più in generale... L insieme S k = {(s 1, s 2,..., s k ) : s j S, j = 1,..., k} costituito dalle k-uple ordinate di elementi di S ha S k elementi. Se S = n, da cui S k = n k. ( s 1, s 2,..., s k ) n scelte n scelte n scelte }{{} k volte - Un elemento di S si può ripetere anche più di una volta. - Le n-uple (s 1, s 2,..., s i, s j,..., s k ) e (s 1, s 2,..., s j, s i,..., s k ) sono distinte per ogni i, j = 1,..., k.
9 Altri modi di contare Esempi 1 Quante partite diverse si possono giocare con un mazzo di carte napoletane? Ovvero in quanti modi possibili possiamo mettere in sequenza le carte napoletane? 2 Quante sono le possibili classifiche finali di un torneo a 5 squadre escludendo l eventualità che ci sia pari merito?
10 Altri modi di contare Esempi 1 Quante partite diverse si possono giocare con un mazzo di carte napoletane? Ovvero in quanti modi possibili possiamo mettere in sequenza le carte napoletane? 2 Quante sono le possibili classifiche finali di un torneo a 5 squadre escludendo l eventualità che ci sia pari merito?
11 Altri modi di contare A = {a 1, a 2, a 3,..., a n } n = 1 A = {a 1 } un solo ordinamento possibile; n = 2 A = {a 1, a 2 } 2 possibili ordinamenti a 1 a 2 oppure a 2 a 1 ; n = 3 A = {a 1, a 2, a 3 } 6 possibili ordinamenti: a 1 a 2 a 3, a 1 a 3 a }{{} 2, a 2 a 1 a 3, a 2 a 3 a 1, a }{{} 3 a 1 a 2, a 3 a 2 a 1 3 2; }{{} n = 4 A = {a 1, a 2, a 3, a 4 } 24 possibili ordinamenti: per il primo elemento ho 4 scelte possibili per il secondo elemento ho 3 scelte possibili per per il terzo elemento ho 2 scelte possibili per il quarto ed ultimo elemento ho 1 sola scelta =
12 Altri modi di contare A = {a 1, a 2, a 3,..., a n } n = 1 A = {a 1 } un solo ordinamento possibile; n = 2 A = {a 1, a 2 } 2 possibili ordinamenti a 1 a 2 oppure a 2 a 1 ; n = 3 A = {a 1, a 2, a 3 } 6 possibili ordinamenti: a 1 a 2 a 3, a 1 a 3 a }{{} 2, a 2 a 1 a 3, a 2 a 3 a 1, a }{{} 3 a 1 a 2, a 3 a 2 a 1 3 2; }{{} n = 4 A = {a 1, a 2, a 3, a 4 } 24 possibili ordinamenti: per il primo elemento ho 4 scelte possibili per il secondo elemento ho 3 scelte possibili per per il terzo elemento ho 2 scelte possibili per il quarto ed ultimo elemento ho 1 sola scelta =
13 Altri modi di contare A = {a 1, a 2, a 3,..., a n } n = 1 A = {a 1 } un solo ordinamento possibile; n = 2 A = {a 1, a 2 } 2 possibili ordinamenti a 1 a 2 oppure a 2 a 1 ; n = 3 A = {a 1, a 2, a 3 } 6 possibili ordinamenti: a 1 a 2 a 3, a 1 a 3 a }{{} 2, a 2 a 1 a 3, a 2 a 3 a 1, a }{{} 3 a 1 a 2, a 3 a 2 a 1 3 2; }{{} n = 4 A = {a 1, a 2, a 3, a 4 } 24 possibili ordinamenti: per il primo elemento ho 4 scelte possibili per il secondo elemento ho 3 scelte possibili per per il terzo elemento ho 2 scelte possibili per il quarto ed ultimo elemento ho 1 sola scelta =
14 Altri modi di contare A = {a 1, a 2, a 3,..., a n } n = 1 A = {a 1 } un solo ordinamento possibile; n = 2 A = {a 1, a 2 } 2 possibili ordinamenti a 1 a 2 oppure a 2 a 1 ; n = 3 A = {a 1, a 2, a 3 } 6 possibili ordinamenti: a 1 a 2 a 3, a 1 a 3 a }{{} 2, a 2 a 1 a 3, a 2 a 3 a 1, a }{{} 3 a 1 a 2, a 3 a 2 a 1 3 2; }{{} n = 4 A = {a 1, a 2, a 3, a 4 } 24 possibili ordinamenti: per il primo elemento ho 4 scelte possibili per il secondo elemento ho 3 scelte possibili per per il terzo elemento ho 2 scelte possibili per il quarto ed ultimo elemento ho 1 sola scelta =
15 Altri modi di contare A = {a 1, a 2, a 3,..., a n } n = 1 A = {a 1 } un solo ordinamento possibile; n = 2 A = {a 1, a 2 } 2 possibili ordinamenti a 1 a 2 oppure a 2 a 1 ; n = 3 A = {a 1, a 2, a 3 } 6 possibili ordinamenti: a 1 a 2 a 3, a 1 a 3 a }{{} 2, a 2 a 1 a 3, a 2 a 3 a 1, a }{{} 3 a 1 a 2, a 3 a 2 a 1 3 2; }{{} n = 4 A = {a 1, a 2, a 3, a 4 } 24 possibili ordinamenti: per il primo elemento ho 4 scelte possibili per il secondo elemento ho 3 scelte possibili per per il terzo elemento ho 2 scelte possibili per il quarto ed ultimo elemento ho 1 sola scelta =
16 Il fattoriale Definizione Sia n N. Si definisce fattoriale di n, e si indica con il simbolo n!, il numero che si ottiene moltiplicando tutti i numeri compresi tra 1 ed n: n! = n (n 1) (n 2) Per definizione si pone 0! = 1. 1! = 1 2! = 2 3! = 3 2 = 6 4! = = 24 5! = = 5 4! = 120 n! = n(n 1)!
17 Il fattoriale Definizione Sia n N. Si definisce fattoriale di n, e si indica con il simbolo n!, il numero che si ottiene moltiplicando tutti i numeri compresi tra 1 ed n: n! = n (n 1) (n 2) Per definizione si pone 0! = 1. 1! = 1 2! = 2 3! = 3 2 = 6 4! = = 24 5! = = 5 4! = 120 n! = n(n 1)!
18 Permutazioni Definizione Si dice permutazione un qualsiasi ordinamento di n oggetti distinti. Proposizione Il numero delle permutazioni di n oggetti distinti, in simboli P n, è pari a n! Infatti: base di induzione: P 1 = 1 = 1! passo induttivo: P n 1 = (n 1)! P n = n! P n = n P n 1 = n(n 1)! = n!.
19 Permutazioni Definizione Si dice permutazione un qualsiasi ordinamento di n oggetti distinti. Proposizione Il numero delle permutazioni di n oggetti distinti, in simboli P n, è pari a n! Infatti: base di induzione: P 1 = 1 = 1! passo induttivo: P n 1 = (n 1)! P n = n! P n = n P n 1 = n(n 1)! = n!.
20 Permutazioni Definizione Si dice permutazione un qualsiasi ordinamento di n oggetti distinti. Proposizione Il numero delle permutazioni di n oggetti distinti, in simboli P n, è pari a n! Infatti: base di induzione: P 1 = 1 = 1! passo induttivo: P n 1 = (n 1)! P n = n! P n = n P n 1 = n(n 1)! = n!.
21 Permutazioni Esempio Quante partite diverse si possono giocare con un mazzo di carte napoletane? Ovvero in quanti modi possibili possiamo mettere in sequenza le carte napoletane? 40! =
22 Permutazioni Esempio Quante partite diverse si possono giocare con un mazzo di carte napoletane? Ovvero in quanti modi possibili possiamo mettere in sequenza le carte napoletane? 40! = Esempio Quante sono le possibili classifiche finali di un torneo a 5 squadre escludendo l eventualità che ci sia pari merito? 5! = 120
23 Altri modi di contare Esempi 1 5 atleti si contendono 3 medaglie (oro, argento, bronzo), quante situazioni diverse si possono verificare? 2 Se A = {lettere dell alfabeto latino}, sappiamo che A 4 = 21 4 = (insieme di tutte le parole di 4 lettere anche se prive di senso). Quante parole (anche se prive di senso) possiamo scrivere usando sempre 4 lettere diverse?
24 Altri modi di contare Esempi 1 5 atleti si contendono 3 medaglie (oro, argento, bronzo), quante situazioni diverse si possono verificare? 2 Se A = {lettere dell alfabeto latino}, sappiamo che A 4 = 21 4 = (insieme di tutte le parole di 4 lettere anche se prive di senso). Quante parole (anche se prive di senso) possiamo scrivere usando sempre 4 lettere diverse? Insieme atleti {A, B, C, D, E} per il 1 o posto ci sono 5 scelte possibili per il 2 o posto ci sono 4 scelte possibili per il 3 o posto ci sono 3 scelte possibili in totale sono = 60.
25 Altri modi di contare Esempi 1 5 atleti si contendono 3 medaglie (oro, argento, bronzo), quante situazioni diverse si possono verificare? 2 Se A = {lettere dell alfabeto latino}, sappiamo che A 4 = 21 4 = (insieme di tutte le parole di 4 lettere anche se prive di senso). Quante parole (anche se prive di senso) possiamo scrivere usando sempre 4 lettere diverse? A = {lettere dell alfabeto latino} per la prima lettera ho 21 scelte per la seconda lettera ho 20 scelte per la terza lettera ho 19 scelte per la quarta lettera ho 18 scelte in totale ho =
26 Disposizioni semplici Definizione Dato un insieme di n elementi, si chiamano disposizioni semplici D n,k degli n oggetti presi k alla volta (k n) le scelte ordinate di k di essi in modo tale che ogni elemento compaia al massimo una volta. Se k = n le disposizioni semplici non sono altro che le permutazioni e se ne contano n! D n,n = P n
27 Disposizioni semplici Definizione Dato un insieme di n elementi, si chiamano disposizioni semplici D n,k degli n oggetti presi k alla volta (k n) le scelte ordinate di k di essi in modo tale che ogni elemento compaia al massimo una volta. Se k < n, come nell esempio Insieme atleti {A, B, C, D, E} per il 1 o posto ci sono 5 scelte possibili per il 2 o posto ci sono 4 scelte possibili per il 3 o posto ci sono 3 scelte possibili in totale sono = 60. dove n = 5 e k = 3, 60 = n(n 1)(n 2) = n(n 1)(n (k 1)) = n(n 1)(n k +1)
28 Disposizioni semplici Proposizione Il numero delle disposizioni semplici di n oggetti presi k alla volta è pari a Visto che D n,k = n(n 1) (n k + 1). n(n 1) (n k +1) = si ha anche che n(n 1)(n k + 1)(n k)! (n k)! D n,k = n! (n k)! = n! (n k)!
29 Disposizioni senza ordine Esempio Ad un colloquio si presentano 8 persone. Tutte risultano valide ma possiamo sceglierne solo 3. Quante possibili scelte abbiamo sapendo che non è importante l ordine con cui scegliamo? n = 8 e k = 3 Se scegliessimo le 3 persone dando importanza all ordine, avremmo costruito una disposizione semplice, ovvero avremmo 8!/5! = 336 possibili scelte. Visto che non siamo interessati all ordine, per ogni terna di persone ce ne saranno altre 5 ad essa equivalenti (perché 6=3! sono le permutazioni possibili di 3 elementi). Allora il numero di combinazioni possibili è dato da = 56 = 8! 3!5! = n! k!(n k)!.
30 Disposizioni senza ordine Esempio Ad un colloquio si presentano 8 persone. Tutte risultano valide ma possiamo sceglierne solo 3. Quante possibili scelte abbiamo sapendo che non è importante l ordine con cui scegliamo? n = 8 e k = 3 Se scegliessimo le 3 persone dando importanza all ordine, avremmo costruito una disposizione semplice, ovvero avremmo 8!/5! = 336 possibili scelte. Visto che non siamo interessati all ordine, per ogni terna di persone ce ne saranno altre 5 ad essa equivalenti (perché 6=3! sono le permutazioni possibili di 3 elementi). Allora il numero di combinazioni possibili è dato da = 56 = 8! 3!5! = n! k!(n k)!.
31 Combinazioni Definizione Si chiama combinazione semplice ogni scelta, indipendente dall ordine, di k elementi in un insieme di n elementi e si indica con il simbolo C n,k. Proposizione Il numero di combinazioni di n oggetti in gruppi di k è ( ) n! n C n,k = k!(n k)! = k ( ) n dove il numero si chiama coefficiente binomiale e si legge k n su k.
32 Calcolo del coefficiente binomiale
33 Calcolo del coefficiente binomiale
34 Calcolo del coefficiente binomiale ( ) n k = 1 n! k! (n k)! = n(n 1) (n k + 1) k!
35 Calcolo del coefficiente binomiale C n,k = ( ) n k = 1 n! k! (n k)! = n(n 1) (n k + 1) k! = D n,k P k
36 Calcolo del coefficiente binomiale ( ) n k C n,k = = 1 n! k! (n k)! ( ) 5 = = 10 ( ) 10 = = = n(n 1) (n k + 1) k! = D n,k P k
37 Calcolo del coefficiente binomiale ( ) n = n k n! (n k)!(n (n k))! = n! (n k)!k! = ( ) n k
38 Calcolo del coefficiente binomiale ( ) n n! = n k (n k)!(n (n k))! = n! (n k)!k! = ( ) ( ) 5 5 = 10 = 2 3 ( ) ( ) = 210 = 6 4 ( ) n k
39 Combinazioni Nel campionato italiano 20 squadre si incontrano l una contro l altra. Nel girone di andata quante partite vengono giocate? ( ) 20 = 20! ! = = !18! 2!18! 190 : 10 = 19 settimane
40 Combinazioni Nel campionato italiano 20 squadre si incontrano l una contro l altra. Nel girone di andata quante partite vengono giocate? ( ) 20 = 20! ! = = !18! 2!18! 190 : 10 = 19 settimane
41 Interpretazione insiemistica delle combinazioni Dato un insieme di n elementi, scegliere una combinazione di k di essi equivale a scgliere un sottoinsieme di k elementi. Il numero di sottoinsiemi di k elementi è ( ) n k Lanci ripetuti In 4 lanci di una moneta, in quanti modi distinti si realizza l esito 3 volte testa e 1 volta croce?
42 Interpretazione insiemistica delle combinazioni Dato un insieme di n elementi, scegliere una combinazione di k di essi equivale a scgliere un sottoinsieme di k elementi. Il numero di sottoinsiemi di k elementi è ( ) n k Lanci ripetuti - Lanciare una moneta 4 volte equivale a lanciare una volta 4 monete - S = {M 1, M 2, M 3, M 4 } insieme di 4 monete - Se T esce 3 volte, questo risultato si descrive come un sottoinsieme di S in cui su 3 delle 4 monete c è T - ( 4 3) = 4 sottoinsiemi di cardinalità 3 di S: {M 1, M 2, M 3 }, {M 1, M 2, M 4 }, {M 1, M 3, M 4 }, {M 2, M 3, M 4 } - ( 4 3) è anche il numero delle sequenze ordinate di T e C in cui T compare 3 volte: T T T C, T T CT, T CT T, CT T T
43 Coefficienti binomiali e binomio di Newton La potenza n-sima del binomio (x + y) n = (x + y)(x + y) (x + y) si ottiene moltiplicando ogni fattore del binomio per tutti gli altri (compreso se stesso) in tutti i modi possibili.
44 Coefficienti binomiali e binomio di Newton La potenza n-sima del binomio (x + y) n = (x + y)(x + y) (x + y) si ottiene moltiplicando ogni fattore del binomio per tutti gli altri (compreso se stesso) in tutti i modi possibili. n = 2 (x + y) 2 = (x + y)(x + y) = xx + xy + yx + yy = x 2 + 2xy + y 2
45 Coefficienti binomiali e binomio di Newton La potenza n-sima del binomio (x + y) n = (x + y)(x + y) (x + y) si ottiene moltiplicando ogni fattore del binomio per tutti gli altri (compreso se stesso) in tutti i modi possibili. n = 3 (x + y) 3 = (x + y)(x + y)(x + y) = xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy = x 3 + 3x 2 y + 3xy 2 + y 3
46 Coefficienti binomiali e binomio di Newton La potenza n-sima del binomio (x + y) n = (x + y)(x + y) (x + y) si ottiene moltiplicando ogni fattore del binomio per tutti gli altri (compreso se stesso) in tutti i modi possibili. n qualsiasi... x n compare una sola volta x n 1 y compare n volte ( ) n x n 2 y 2 compare volte 2 x n k y k compare ( ) n volte k
47 Binomio di Newton (x + y) n = ( n + 3 n = k=0 ( ) n x n + 0 ) x n 3 y ( ) n x n k y k k Osserviamo che ( ) n = 0 ( ) ( ) n n x n 1 y + x n 2 y ( ) n x 2 y n 2 + n 2 ( ) n = 1. n ( ) n xy n 1 + n 1 ( ) n y n n
48 Triangolo di Tartaglia Permette di determinare i coefficienti binomiali, ovvero i coefficienti dello sviluppo del binomio (x + y) n. Ogni numero (tranne l 1 al vertice) è la somma dei due sovrastanti. In particolare per x = y = 1 2 n = n k=0 ( ) n k
49 Triangolo di Tartaglia Permette di determinare i coefficienti binomiali, ovvero i coefficienti dello sviluppo del binomio (x + y) n. Ogni numero (tranne l 1 al vertice) è la somma dei due sovrastanti. In particolare per x = y = 1 2 n = n k=0 ( ) n k
50 Sushruta Samhita 6 gusti fondamentali: amaro, aspro, salato, dolce, piccante e astringente Figure: Trattato medico indiano del VI sec a.c. si possono ottenere 63 sensazioni differenti combinando i gusti fondamentali
51 Sushruta Samhita Combinazioni di 6 gusti: 1 = ( 6 6) (tutto l insieme) Combinazioni di 5 gusti: ( 6 5) (sottoinsiemi di 5 elementi) Combinazione di 4 gusti: ( 6 4) (sottoinsiemi di 4 elementi) Combinazione di 3 gusti: ( 6 3) (sottoinsiemi di 3 elementi) Combinazione di 2 gusti: ( 6 2) (sottoinsiemi di 2 elementi) Combinazione di 1 gusti: ( 6 1) (sottoinsiemi di 1 elemento) Combinazione di 0 gusti: 1 = ( 6 0) (l insieme vuoto) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = 2 6 = Il numero dei sottoinsiemi (o numero delle parti) di un insieme di n elementi è pari a 2 n.
52 Sushruta Samhita Combinazioni di 6 gusti: 1 = ( 6 6) (tutto l insieme) Combinazioni di 5 gusti: ( 6 5) (sottoinsiemi di 5 elementi) Combinazione di 4 gusti: ( 6 4) (sottoinsiemi di 4 elementi) Combinazione di 3 gusti: ( 6 3) (sottoinsiemi di 3 elementi) Combinazione di 2 gusti: ( 6 2) (sottoinsiemi di 2 elementi) Combinazione di 1 gusti: ( 6 1) (sottoinsiemi di 1 elemento) Combinazione di 0 gusti: 1 = ( 6 0) (l insieme vuoto) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = 2 6 = Il numero dei sottoinsiemi (o numero delle parti) di un insieme di n elementi è pari a 2 n.
53 Combinazioni con ripetizione Definizione Si chiama combinazione con ripetizione ogni scelta, indipendente dall ordine, di k elementi in un insieme di n elementi, potendo un elemento comparire più volte fino ad un massimo di k volte. Il numero di tali combinazioni corrisponde a ( ) n + k 1 C n+k 1,k = k Una combinazione con ripetizione non corrisponde più ad un sottoinsieme dell insieme di partenza.
54 Combinazioni con ripetizione Definizione Si chiama combinazione con ripetizione ogni scelta, indipendente dall ordine, di k elementi in un insieme di n elementi, potendo un elemento comparire più volte fino ad un massimo di k volte. Il numero di tali combinazioni corrisponde a ( ) n + k 1 C n+k 1,k = k Una combinazione con ripetizione non corrisponde più ad un sottoinsieme dell insieme di partenza.
55 Combinazioni con ripetizione Definizione Si chiama combinazione con ripetizione ogni scelta, indipendente dall ordine, di k elementi in un insieme di n elementi, potendo un elemento comparire più volte fino ad un massimo di k volte. Il numero di tali combinazioni corrisponde a ( ) n + k 1 C n+k 1,k = k Una combinazione con ripetizione non corrisponde più ad un sottoinsieme dell insieme di partenza.
56 Combinazioni semplici e con ripetizione Esempio Determinare il numero delle combinazioni semplici e con ripetizione di 2 oggetti dell insieme A = {,, } ed elencarle esplicitamente. - Combinazioni semplici: C 3,2 = ( 3 2) = 3 {, }, {, }, {, } - Combinazioni con ripetizione: C 3+2 1,2 = ( 4 2) = 6 {, }, {, }, {, } {, }, {, }, {, }
57 Combinazioni semplici e con ripetizione Esempio Determinare il numero delle combinazioni semplici e con ripetizione di 2 oggetti dell insieme A = {,, } ed elencarle esplicitamente. - Combinazioni semplici: C 3,2 = ( 3 2) = 3 {, }, {, }, {, } - Combinazioni con ripetizione: C 3+2 1,2 = ( 4 2) = 6 {, }, {, }, {, } {, }, {, }, {, }
58 Formula di Liebniz Siano n, k N con n = n 1 + n n k. Allora ci sono n! M = n 1!n 2! n k! modi per dividere un insieme di n elementi in k sottoinsiemi affinché ce ne siano n 1 nel primo, n 2 nel secondo e così via. Esempio In quanti modi possibili possiamo dividere 10 pecore in 4 recinti in modo tale che nel primo recinto ce ne siano 2, nel secondo ce ne siano 3, nel terzo ce ne siano 4 e nel quarto le restanti? M = 10! = !3!4!1!
59 Formula di Liebniz Siano n, k N con n = n 1 + n n k. Allora ci sono n! M = n 1!n 2! n k! modi per dividere un insieme di n elementi in k sottoinsiemi affinché ce ne siano n 1 nel primo, n 2 nel secondo e così via. Esempio In quanti modi possibili possiamo dividere 10 pecore in 4 recinti in modo tale che nel primo recinto ce ne siano 2, nel secondo ce ne siano 3, nel terzo ce ne siano 4 e nel quarto le restanti? M = 10! = !3!4!1!
60 Formula di Liebniz Siano n, k N con n = n 1 + n n k. Allora ci sono n! M = n 1!n 2! n k! modi per dividere un insieme di n elementi in k sottoinsiemi affinché ce ne siano n 1 nel primo, n 2 nel secondo e così via. Esempio In quanti modi possibili possiamo dividere 10 pecore in 4 recinti in modo tale che nel primo recinto ce ne siano 2, nel secondo ce ne siano 3, nel terzo ce ne siano 4 e nel quarto le restanti? M = 10! = !3!4!1!
Elementi di Analisi Combinatoria
Elementi di Analisi Combinatoria Angelica Malaspina Dipartimento di Matematica, Informatica ed Economia Università degli Studi della Basilicata, Italy angelica.malaspina@unibas.it Lo studio dei vari raggruppamenti
CARDINALITÀ DI IMPORTANTI FAMIGLIE DI FUNZIONI E DI INSIEMI: ANALISI COMBINATO- RIA
CARDINALITÀ DI IMPORTANTI FAMIGLIE DI FUNZIONI E DI INSIEMI: ANALISI COMBINATO- RIA Alcune definizioni e proprietà Se n è un numero naturale, si definisce per ricorsione il numero n fattoriale, e si scrive,
Salto in alto oltre le formule
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Laura Falcone Teoria della Probabilità Legge empirica del caso: in un grande numero di prove,
DOCENTE: Vincenzo Pappalardo MATERIA: Matematica IL CALCOLO COMBINATORIO
DOCENTE: Vincenzo Pappalardo MATERIA: Matematica IL CALCOLO COMBINATORIO 43 252 003 274 489 856 000 Il calcolo combinatorio studia i modi per raggruppare e/o ordinare secondo date regole gli elementi di
Primi elementi di combinatoria Federico Lastaria, Analisi e Geometria 1
Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Primi elementi di combinatoria 11 Ottobre 2016 Indice 1 Elementi di combinatoria 2 1.1
Probabilità e Statistica
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Angela D Ambrosio Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici
Salto in alto oltre le formule
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Elisa Salvati Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo
«l arte di contare senza contare»
«l arte di contare senza contare» Numero di oggetti disponibili Numero di oggetti che costituiscono una sola estrazione Regole per costruire le estrazioni: se si possono utilizzare tutti gli oggetti o
combiniamo le lettere, ciascuna presa una sola volta per formare parole di n lettere;
CALCOLO COMBINATORIO Il calcolo combinatorio si occupa di contare i raggruppamenti che si possono fare con n oggetti di un insieme finito, secondo determinate regole. Vediamo di seguito come, a seconda
Combinatoria. Lezione del 12/02/2014. Stage di Parma Progetto Olimpiadi
Combinatoria Lezione del 12/02/2014 Stage di Parma Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
Calcolo combinatorio INTRODUZIONE. Ivan Zivko
Matematica Capitolo 3 Calcolo combinatorio Ivan Zivko INTRODUZIONE Nel calcolo combinatorio vengono sviluppate delle tecniche per determinare, senza enumerazione diretta, il numero dei possibili risultati
Combinatoria. Lezione del 04/01/2010. Stage di Terni Progetto Olimpiadi
Combinatoria Lezione del 04/01/2010 Stage di Terni Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo. Calcolo Combinatorio
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo. Calcolo Combinatorio
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Analisi. Calcolo Combinatorio. Ing. Ivano Coccorullo
Analisi Ing. Ivano Coccorullo Prof. Ivano Coccorullo ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli possibili. Quando le situazioni diventano
Olimpiadi della Matematica
Corso PON Competenze per lo sviluppo Liceo Scientifico «E. Medi Ing. Ivano Coccorullo Prof.ssa Geri Cupolo Calcolo Combinatorio Molti dei problemi classici di calcolo delle probabilità si riducono
Elementi. di Calcolo Combinatorio. Paola Giacconi
Elementi di Calcolo Combinatorio di Paola Giacconi Premessa Con la Meccanica Quantistica Il concetto di probabilità è entrato a fare parte integrante della FISICA e quindi della nostra vita La visione
Statistica Inferenziale
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
FRAME 0.3. E possibile partecipare a tre appelli su 5 (esclusi i compitini). Farà fede l iscrizione alle liste elettroniche.
FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Matematica Discreta, a.a. 2005-2006, Libreria Progetto, 2005 (costo 6 euro. Compitini FRAME 0.2. 13 maggio, ore 9.30
COMBINATORIA E PROBABILITA
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO COMBINATORIA E PROBABILITA CALCOLO COMBINATORIO Il Calcolo Combinatorio è lo studio dei
PROBABILITÁ e CALCOLO COMBINATORIO
PROBABILITÁ e CALCOLO COMBINATORIO Prof. Enrico Terrone A. S: 2008/09 Probabilità e calcolo combinatorio Abbiamo visto la definizione classica di probabilità: probabilità dell evento = (casi favorevoli)
Appendice A Richiami di calcolo combinatorio
Appendice A Richiami di calcolo combinatorio A.1. Dati due insiemi finiti A e B, concarda = m, cardb = n, siha card(a B) =m n. Possiamo anche dire che il numero di scelte possibili di un elemento di A
Calcolo combinatorio
Fondamenti di Informatica per la Sicurezza a.a. 2007/08 Calcolo combinatorio Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Cenni di analisi combinatoria
Cenni di analisi combinatoria In molti problemi concreti di teoria della probabilità e, in particolare, nell ambito della interpretazione classica occorre calcolare quanti sono gli esiti che compongono
Probabilità mediante l'analisi combinatoria D n,k = Disposizioni di n oggetti a k a k (o di classe k)
Probabilità mediante l'analisi combinatoria D n,k = Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalità con cui si presenta un evento e' utile talvolta utilizzare le definizioni
RISOLUZIONE ESERCIZI SUL CALCOLO COMBINATORIO C = =10
RISOLUZIONE ESERCIZI SUL CALCOLO COMBINATORIO A) SVILUARE E CALCOLARE LE SEGUENTI ESRESSIONI : numero esercizio risoluzione 1) D 3, 2 3 2 6 2) 4 3) 6 3 4! 4 3 24 6! 6 5 4 3 120 3! 3 4) 3,3 6 6! 6 5 4 3
Calcolo combinatorio - Quesiti esame di stato
Calcolo combinatorio - Quesiti esame di stato 1. Nello sviluppo di 2 a 2 3b 3 n compare il termine 1080 a 4 b 9. Qual è il valore di n? [Q3 2014] 2. Con le cifre da 1 a 7 è possibile formare 7!=5040 numeri
Università degli Studi di Milano
Università degli Studi di Milano Laurea in Sicurezza dei sistemi e delle reti informatiche Note di Matematica STEFANO FERRARI Fondamenti di informatica per la sicurezza Note di Matematica Pagina 2 di 8
PROBABILITÀ. a) 0,04 b) 0,8 c) 0,25 d) 0,64 e) 0,96
QUESITI 1 PROBABILITÀ 1. (Da Medicina e Odontoiatria 2015) La probabilità con cui un paziente deve attendere meno di dieci minuti il proprio turno in un ambulatorio medico è 0,8. Qual è la probabilità
ESERCIZI DI CALCOLO COMBINATORIO
ESERCIZI DI CALCOLO COMBINATORIO (G.T.Bagni) Sintesi delle nozioni teoriche da utilizzare a) Dati n elementi e k n, si dicono disposizioni semplici di n elementi di classe k tutti i raggruppamenti ottenuti
Tecniche di conteggio
Tecniche di conteggio 9 Ottobre 2003 Principio della somma Il numero di elementi dell unione di una famiglia di insiemi disgiunti è la somma del numero di elementi contenuti in ogni singolo insieme F =
SOMMARIO 1 Introduzione al calcolo delle probabilità 2. 2 Cenni di calcolo combinatorio 4
SOMMARIO 1 Introduzione al calcolo delle probabilità 2 1.1 La probabilità 2 1.1.1 Legge empirica del caso: legge dei grandi numeri 2 1.1.2 Proprietà additiva della probabilità 2 1.1.3 Probabilità condizionata
{ } corrisponde all uscita della faccia i-esima del dado. La distribuzione di probabilità associata ( )
Università di Trento - Corsi di Laurea in Ingegneria Civile e in Ingegneria per l Ambiente e il Territorio - 2017/18 Analisi Matematica 1 - professore Alberto Valli 2 foglio di esercizi 25 settembre 2017
Introduzione. 1.Palline e Scatole Distinguibili
Introduzione L argomento è semplice, quasi infantile: abbiamo a disposizione un certo numero di palline da disporre in un insieme di scatole e ci chiediamo quanti modi ci sono per farlo. Affronteremo il
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Statistica Inferenziale
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riferimenti Ricevimento per appuntamento: folgieri@mtcube.com In ogni mail indicare: nome e cognome, matricola,
Qualche Esempio di Processo Markoviano
Qualche Esempio di Processo Markoviano Giugno 2002 O.Caligaris Alcuni problemi con caratteristiche comuni La Rovina del Giocatore Un Giocatore gioca contro il banco Ad ogni puntata può vincere 1 gettone
In molte applicazioni sorge il problema di sapere in quanti modi possibili si può presentare un certo fenomeno.
Calcolo Combinatorio Definizione Oggetto del calcolo combinatorio è quello di determinare il numero dei modi mediante i quali possono essere associati, secondo prefissate regole, gli elementi di uno stesso
P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =
![P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =](/thumbs/60/44901085.jpg "P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =")
Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Calcolo delle Probabilità Soluzioni 2. Calcolo combinatorio
ISTITUZIONI DI STATISTICA A. A. 2007/2008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
Cos é la probabilitá?
Sí, no, anzi: probabilmente http://www.uniba.it/docenti/taglialatela-giovanni Giovanni Taglialatela giovanni.taglialatela@uniba.it Dipartimento di Economia e Finanza 20 febbraio 2019 Cos é la probabilitá?
.. x n k. n 1 x n 2. La differenza fra i due casi precedenti sta nella possibilità di ripetere oppure no una stessa scelta.
Calcolo combinatorio Problema Quante parole di 3 lettere si possono scrivere utilizzando solo le 4 lettere a, b, c, d? Soluzione: scriviamole tutte e poi le contiamo Esercizio 2 Quante sono le parole di
22/07/2013 PRECORSO Dipartimento di Scienze Biomediche, Sperimentali e Cliniche. Numeri, frazioni, operazioni fondamentali
PRECORSO 2013 Problemi di Matematica Alessandro Passeri Dipartimento di Scienze Biomediche, Sperimentali e Cliniche PRECORSO 2013: ciclo formativo di orientamento alle prove di ammissione ai Corsi di studio
LEZIONI Dispense a cura del Docente.
LEZIONI 06-07-08 Contents 5. INTRODUZIONE ALLO STUDIO QUALITATIVO DELLE FUNZIONI. 5.. Operazioni elementari sui grafici di funzioni. 5.. Funzione composta. Monotonia della funzione composta. 5 5.. Grafico
Combinatoria. Lezione del 16/12/2009. Stage di Treviso Progetto Olimpiadi
Combinatoria Lezione del 16/12/2009 Stage di Treviso Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di
Quanti sono...? Introduzione al Calcolo Combinatorio
Prof.ssa Garagnani Elisa ISIS Archimede Quanti sono...? Introduzione al Calcolo Combinatorio Per cominciare... aiutati con un grafo ad albero Noti 3 vincitori, in quanti modi diversi possono salire sul
Funzioni e combinatoria
Funzioni e combinatoria Mauro Saita e-mail: maurosaita@tiscalinetit Versione provvisoria Maggio 206 Indice Combinatoria 2 Contare funzioni da un insieme ad un altro 2 2 Contare funzioni iniettive 3 3 Contare
Elementi di Calcolo Combinatorio. Dato un insieme I n, con P n si indica il numero di tutte le possibili permutazioni semplici di I n.
1 Elementi di Calcolo Combinatorio Def.: Dato un insieme I n, con P n si indica il numero di tutte le possibili permutazioni semplici di I n. ( n 1)... 3 2 1 P n n In quanti modi diversi si possono disporre
ESERCIZI SUL CALCOLO COMBINATORIO
ESERCIZI SUL CALCOLO COMBINATORIO A) SVILUPPARE E CALCOLARE LE SEGUENTI ESPRESSIONI : numero esercizio risoluzione 1) D 3, ) P 4 3) P 6 3 4) 3,3 P 6 5) D ' 3, 6) C 4, 7) C n, n 8) D + D' C 4, 3, 3 3, 9)
Foglio di Esercizi 10 con Risoluzione 18 dicembre 2017
Matematica per Farmacia, a.a. 07/8 Foglio di Esercizi 0 con Risoluzione 8 dicembre 07 ATTENZIONE: in alcuni degli esercizi di Probabilità puó essere utile usare il Teorema di Bayes. Esercizio (Vedere il
2 per ogni n N +. k=1 a k) ( n. k=1 b k) n
(ii) il prodotto di due irrazionali è irrazionale; (iii) la somma di un razionale e di un irrazionale è irrazionale; (iv) il prodotto di un razionale e di un irrazionale è irrazionale. 5. Siano a, b R.
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini e Leonardo Bertini. Lezione 1: Probabilità: fondamenti
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini e Leonardo Bertini Lezione 1: Probabilità: fondamenti Progettazione probabilistica: Considerazione delle incertezze
UNIVERSITÀ di ROMA TOR VERGATA
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( )( ) ( )( )
SOLUZIONI II ALLENAMENTO REGIONALE TEMATICO VENERDÌ 4 DICEMBRE 08 Quesito Siano due numeri interi primi tra loro tali che quanto vale? Sviluppando l espressione si ottiene quindi e e la soluzione è Quesito
Il principio di induzione Applicazioni
MINISTERO DELL ISTRUZIONE, DELL UNIVERSITA E DELLA RICERCA LICEO STATALE P. E. IMBRIANI Linguistico - Scientifico - Scientifico delle Scienze Applicate Via S. Pescatori, 155 83100 Avellino Tel. (2 linee)
Figura 7: Ruota della Fortuna. Quanti sono i casi possibili? G. Sanfilippo - CdP - STAD - Lezione 2 del 12 Aprile pag. 15
Figura 7: Ruota della Fortuna. Quanti sono i casi possibili? G. Sanfilippo - CdP - STAD - Lezione 2 del 12 Aprile 2012- pag. 15 Casi Possibili B= La lancetta indica il Blu V= La lancetta indica il Verde
Analisi combinatoria. 1. Disposizioni semplici di n oggetti
Analisi combinatoria 1. Disposizioni semplici di n oggetti Siano dati n oggetti distinti tra loro che verranno indicati da una stessa lettera contrassegnata da un indice, per esempio con a 1, a 2,., a
CALCOLO COMBINATORIO
Il DNA fa l RNA, l RNA fa le proteine e le proteine fanno noi (F.H.C, Crick) La fase di costruzione della proteina da parte dell RNA prende il nome di traduzione: le basi dell RNA vengono lette in triplette,
CALCOLO COMBINATORIO E DELLE PROBABILITÀ
CALCOLO COMBINATORIO E DELLE PROBABILITÀ Progetto Giochi matematici Referente: prof. Antonio Fanelli Mail: fanelli.xy@gmail.com Sito Internet:fanelliant.wordpress.com CALCOLO COMBINATORIO E DELLE PROBABILITÀ
Numero di successi su n prove
Numero di successi su n prove Risultati possibili lanciando, volte una moneta. numero di volte in cui esce croce... (,) 0. 0 0 0..... numero di volte in cui esce testa Figura : I risultati favorevoli all
Calcolo delle Probabilità e Statistica Matematica Fisciano, 10/1/2012
Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
$% #$$ + ( + + ( +67!#$% + ( + %+ 3+ ( + ( + %+ // 01 21, // 01,. // 01 21,.4+/ // 0.15 ( * + +// 0.9*,.92, ) +// 0.9*,.9$, *2: ; %1 !!
!!"!&!!"!&!! ' ''#(#))#$*+ # ( #))) $, " #$ $% #$$ # -!!" #$.!!!" #$ $ -.!!!" // 012, // 01,. // 01 21, // 01 21,.4+/ // 0.4+*1,1+1 // 0.15 // 0.15 ( #$ +!" +3+ + ( + %+ 3+ ( + ( + %+ + ( + + ( +67!#$%!%
FRAME giugno ore 9.30, 6 luglio ore settembre ore 9.30, 19 settembre ore 14.30
FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Mat D, I parte e II parte, dispense ROSSE, Libreria Progetto, 2005. Dispensina su integrali multipli, copisteria di
Rispondere in modo conciso ai seguenti quesiti nelle apposite caselle. 1
Liceo Scientifico L. Cremona TEST DI MATEMATICA. Combinatoria. Classe: Docente: M. Saita Cognome: Nome: Maggio 2015 Rispondere in modo conciso ai seguenti quesiti nelle apposite caselle. 1 Esercizio 1.
Definizione 1. Una k-colorazione dei vertici di un grafo G consiste nell assegnazione di k colori 1, 2,..., k ai vertici di G in modo tale che a due
Definizione 1. Una k-colorazione dei vertici di un grafo G consiste nell assegnazione di k colori 1, 2,..., k ai vertici di G in modo tale che a due vertici adiacenti non sia assegnato lo stesso colore.
NOTE DI CALCOLO COMBINATORIO
NOTE DI CALCOLO COMBINATORIO VINCENZO C. NARDOZZA 1. Richiami Ricordiamo molto brevemente gli strumenti di calcolo combinatorio esaminati durante le lezioni e i risultati ottenuti. Se X n, il suo insieme
In molte applicazioni sorge il problema di sapere in quanti modi possibili si può presentare un certo fenomeno.
Definizione Oggetto del calcolo combinatorio è quello di determinare il numero dei modi mediante i quali possono essere associati, secondo prefissate regole, gli elementi di uno stesso insieme o di più
Matematica e Statistica per Scienze Ambientali
per Scienze Ambientali Insiemi e Combinatoria - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 23 - Ottobre 2012 Il concetto di insieme Non tratterò la teoria assiomatica degli
Probabilità: teoremi e distribuzioni
Probabilità: teoremi e distribuzioni OBIETTIVO DIDATTICO DELLA LEZIONE Illustrare le più importanti distribuzioni di probabilità che vengono utilizzate in statistica Distribuzioni di probabilità 1. La
Combinatoria Test Senior
Test intermedi December 16, 2004 19 Tempo concesso: 120 minuti Valutazione: risposta errata 0 punti, mancante +2, esatta +5 1. Determinare quanti sono gli anagrammi (anche senza senso) della parola TATTILI.
Calcolo Combinatorio e Probabilità
Calcolo Combinatorio e Probabilità Andrea Galasso 1 Calcolo Combinatorio Definizione 1 Fissati n, k N, con k n, indicheremo con D n,k := n! (n k)! le disposizioni di n oggetti in k posti e con DR n,k :=
Analizziamo ora alcuni esempi, al fine di acquisire quel un metodo di ragionamento tipico dell intera teoria della probabilità.
1 Il calcolo delle probabilità nasce dalla necessità di prevedere l incerto. Inizialmente si sviluppò principalmente per dare risposte a quesiti riguardanti i giochi d azzardo (dadi, carte, ), ove il realizzarsi
Richiami sul calcolo delle probabilità
robabilità Richiami sul calcolo delle probabilità TEORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INFORMAZIONE Modello matematico Sommario Assiomi del calcolo delle probabilità robabilità di un evento robabilità
0.1 Esercizi calcolo combinatorio
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
Raggruppamenti. Esercizio 1
Raggruppamenti Nelle prossime lezioni ci occuperemo delle basi del calcolo combinatorio. Per semplicità partiremo da un esercizio e poi analizzeremo il caso generale con la definizione e la formula da
Calcolo combinatorio
1 Calcolo combinatorio Ricordiamo che uno spazio di probabilità (Ω, P(Ω), P) si dice uniforme se Ω è un insieme finito e si ha P(A) = A Ω, per ogni A Ω. Pertanto, il calcolo della probabilità di un evento
Binomio di Newton. Pertanto, il numero di sottoinsiemi di S, compreso il sottoinsieme vuoto ; elostessos, è dato da. = 2 n, r. (a + b) n = a r b n r,
Binomio di Newton Osserviamo che, volendo costruire un generico sottoinsieme I S, si deve eseguire una procedura di n passi, con alternative in ogni passo. Infatti, occorre decidere per ciascuno degli
3.Polinomi ed operazioni con essi
MatematicaC Algebra1 1.Lebasidelcalcololetterale1.Polinomieoperazioniconessi....Polinomi ed operazioni con essi 1. Definizioni fondamentali Un polinomio è una somma algebrica di monomi, ciascuno dei quali
UNIVERSITÀ di ROMA TOR VERGATA
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
Fondamenti di Statistica. Prof. V. Simoncini. Orario di Lezione: Mar Gio
Fondamenti di Statistica Prof. V. Simoncini Orario di Lezione: Mar 14-16 Gio 9.00-11.00 Orario di ricevimento: per appuntamento valeria@dm.unibo.it Siti del corso: www.dm.unibo.it/ simoncin/fondamenti.html
Calcolo combinatorio
Calcolo combinatorio I l. Disposizioni semplici, permutazioni semplici, combinazioni semplici In questo numero considereremooggetti in numero finito, di natura qualsiasi e di essi studieremo particolari
Laurea triennale in MATEMATICA, Corso di PROBABILITÀ 1 Compito scritto del FOGLIO RISPOSTE
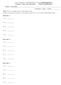NOME e COGNOME Laurea triennale in MATEMATICA, Corso di PROBABILITÀ Compito scritto del.6. - FOGLIO RISPOSTE CANALE: G. Nappo VOTO: N.B. Scrivere le risposte dei vari punti degli esercizi oppure, in mancanza
ALGEBRA DEGLI EVENTI
ALGEBRA DEGLI EVENTI Appunti introduttivi al Calcolo Combinatorio e al Calcolo delle Probabilità Classe Terza a cura di Franca Gressini Novembre 2008 1 Conosciamo tante algebre. quella letterale (gli oggetti
Prima lezione. Gilberto Bini. 16 Dicembre 2006
16 Dicembre 2006 Vediamo alcune nozioni di teoria ingenua degli insiemi. Vediamo alcune nozioni di teoria ingenua degli insiemi. Un insieme è una collezione di oggetti di cui possiamo specificare una proprietà
APPUNTI DI CALCOLO COMBINATORIO E PROBABILITA' Corso di Matematica ed Elementi di Statistica Scienze della Natura a.a. 2014/15
APPUNTI DI CALCOLO COMBINATORIO E PROBABILITA' Corso di Matematica ed Elementi di Statistica Scienze della Natura a.a. 2014/15 Elementi di calcolo combinatorio. Primi elementi di probabilita: denizioni
Calcolo combinatorio
Calcolo combinatorio Fattoriale: n! = n( n 1)( n 2)...1 1 1 n n = 0 Fattoriale discendente: n( n 1)...( n k + 1) n! (n) k = = ( n k)! 1 1 k n k = 0 Coefficiente binomiale (k n) : n (n) = k n! = k k! k!(
Matematica Esempio esame Unità 7
Matematica Esempio esame Unità 7 Giuseppe Vittucci Marzetti Dipartimento di Sociologia e Ricerca Sociale Università degli Studi di Milano-Bicocca Corso di Laurea in Scienze dell Organizzazione Novembre
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N 2 ARGOMENTO: Calcolo combinatorio (LEZIONE N 2) ATTIVITA' N 1: In quanti
Matematica con elementi di statistica ESERCIZI: probabilità
Matematica con elementi di statistica ESERCIZI: probabilità Esercizi sulla Probabilità Esercizio 1. In un corso di laurea uno studente deve scegliere un esame fra 8 di matematica e un esame fra 5 di fisica.
Capitolo 1: Concetti matematici di base
Capitolo 1: Concetti matematici di base 1 Insiemi x A x é elemento dell insieme A. B A B é un sottoinsieme di A. B A B é un sottoinsieme proprio di A. A costituito da n elementi A = n é la sua cardinalitá.
Domande di teoria. Esercizi
1 Domande di teoria 1. Vedi pp. 131-132 2. Vedi pp. 132-134 3. Vedi p. 134 4. Vedi p. 135 5. Vedi pp. 136-142 6. Vedi pp. 138-139 7. Vedi pp. 141-142 8. Vedi pp. 143-146 9. Vedi pp. 146-148 Esercizi Esercizio
Calcolo combinatorio
Probabilità e Statistica a.a. 2016/2017 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Meccanica e dei Materiali, Ingegneria Gestionale, Ingegneria Informatica C.d.L.: Ingegneria Elettronica
Esercitazioni di Statistica Dott.ssa Cristina Mollica niroma1.it. Probabilità
Esercitazioni di Statistica Dott.ssa Cristina Mollica cristina.mollica@u niroma1.it Probabilità Esercizio 1. Un esperimento casuale consiste nel lanciare tre volte una moneta. Si determini lo spazio campionario
1 Principio di Induzione
1 Principio di Induzione Per numeri naturali, nel linguaggio comune, si intendono i numeri interi non negativi 0, 1,, 3, Da un punto di vista insiemistico costruttivo, a partire dall esistenza dell insieme
Prodotti notevoli Quadrato di un binomio
Prodotti notevoli Con l espressione prodotti notevoli si indicano alcune identità che si ottengono in seguito alla moltiplicazione di polinomi aventi caratteristiche particolari facili da ricordare.. Quadrato
Esercizi settimana 5. Esercizi applicati. Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 2 3
1 Esercizi settimana 5 Esercizi applicati Esercizio 1. Si considerino tre monete truccate, ognuna con probabilità 3 di ottenere testa. Se scegliete la prima moneta vincete 10 punti se esce testa e punti
Calcolo delle Probabilità e Statistica. Test di verifica - 05/04/2005
Corso di Laurea in Informatica - a.a. 2004/05 Calcolo delle Probabilità e Statistica Test di verifica - 05/04/2005 Il candidato risolva due (e solo due) problemi tra i seguenti, motivando le proprie risposte.
INTRODUZIONE AL CORSO Una passeggiata fra i numeri.
INTRODUZIONE AL CORSO 2011-12 Una passeggiata fra i numeri. Dagli albori della civiltà: necessità di contare, di rappresentare il risultato e di eseguire operazioni. ESEMPIO: le tacche incise su una tibia
Se la base è 10, il risultato della potenza è una potenza di 10 con tanti zeri quante sono le unità dell esponente:
Definizione di potenza Si definisce potenza ennesima di A, con n intero maggiore di 1, il prodotto di A per se stesso eseguito n volte A n =(AxAxAx A) n volte 2 5 = 2 2 2 2 2=32 Se la base è 10, il risultato