Quaderni di. Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) ISSN Anno 2009_Numero 75
|
|
|
- Battistina Marchetti
- 5 anni fa
- Visualizzazioni
Transcript
1 ISSN Anno 2009_Numero 75 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Quaderni di Istituto Nazionale di Geofisica e Vulcanologia
2 Quaderni di Geofisica Direttore Enzo Boschi Editorial Board Raffaele Azzaro (CT) Sara Barsotti (PI) Mario Castellano (NA) Viviana Castelli (BO) Anna Grazia Chiodetti (AC) Rosa Anna Corsaro (CT) Luigi Cucci (RM1) Mauro Di Vito (NA) Marcello Liotta (PA) Lucia Margheriti (CNT) Simona Masina (BO) Nicola Pagliuca (RM1) Salvatore Stramondo (CNT) Andrea Tertulliani - coordinatore (RM1) Aldo Winkler (RM2) Gaetano Zonno (MI) Segreteria di Redazione Francesca Di Stefano - coordinatore Tel Fax Rossella Celi Tel Fax redazionecen@ingv.it
3 ISSN Anno 2009_Numero 75 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi 1 Umberto Sciacca 2 Alessandro Settimi 3 1 Università Sapienza (Dipartimento di Fisica) 2 INGV (Istituto Nazionale di Geofisica e Vulcanologia Sezione Roma 1) 3 INGV (Istituto Nazionale di Geofisica e Vulcanologia Sezione Roma 2) in copertina equazione 1.4 di questo volume (particolari)
4 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Nazionale di Geofisica e Vulcanologia si è occupato sin dalla sua fondazione della previsione delle condizioni in cui può aver luogo un radio collegamento che faccia uso della propagazione per onda L Istituto ionosferica. Negli ultimi tempi ha assunto importanza anche il prevedere con precisione la traiettoria percorsa da un onda radio che si propaga nell atmosfera in particolare nella ionosfera che si può considerare in prima approssimazione come un mezzo non omogeneo caratterizzato da un indice di rifrazione variabile lentamente nel tempo. Questo lavoro descrive le basi teoriche per lo studio di una traiettoria; esse fanno uso essenzialmente dei metodi dell ottica geometrica. Tali basi teoriche trovano applicazione in metodi numerici di calcolo delle traiettorie come citato in bibliografia [Bianchi 2009]. The Istituto Nazionale di Geofisica e Vulcanologia has been involved since its foundation in the forecast of the conditions in which a radio link that makes use of propagation by means of ionospheric wave takes place. In the last times it gained interest also the precise forecast of the trajectory covered by a radio wave propagating into the atmosphere specifically into the ionosphere which can be considered at first approximation as an inhomogeneous medium defined by a refraction index slowly varying in time. This work describes the theoretical bases to study a trajectory; they substantially make use of the methods of the geometrical optics. Such theoretical bases find applications in numerical methods to calculate the trajectories as quoted in references [Bianchi 2009]. Introduzione Una corretta caratterizzazione dei collegamenti radio su grandi distanze non può prescindere dallo studio degli effetti generati dalla presenza dell atmosfera terrestre in particolare della troposfera il cui indice di rifrazione diminuisce lentamente con la quota. In un radiocollegamento la propagazione avviene quindi in mezzi ad indice di rifrazione lentamente variabile. In generale si hanno i modi di propagazione di cui in fig. 1. Visto che l andamento dell indice di rifrazione varia la traiettoria del segnale non è rettilinea. È necessario prevederla per valutare l esatto puntamento delle antenne l esatta attenuazione e l esatto ritardo di propagazione. Una trattazione della propagazione in modo esatto a partire dalle equazioni di Maxwell è molto complessa ed è quindi necessario ricorrere ad una trattazione semplificata. La natura ed il comportamento della luce ci consentono di interpretare alcuni fenomeni tramite i raggi luminosi ognuno dei quali si può pensare come un segmento di retta che ha la direzione di propagazione del fronte d'onda. Tale modello noto come ottica geometrica fu introdotto da Keplero costituisce una buona approssimazione della realtà ed è di estrema utilità nello studio dei fenomeni di riflessione e rifrazione nonché degli effetti prodotti dai vari tipi di specchi (piani concavi e convessi) e dalle lenti. I fenomeni interpretati mediante l'ottica geometrica possono essere spiegati anche con la teoria ondulatoria della luce 4
5 sebbene con maggiore difficoltà nell'effettuare i calcoli. Il campo f( t) in questo caso è soluzione descritto dalla cosiddetta equazione delle onde: dove v è la velocità della luce nel mezzo considerato. La funzione d onda può poi essere associata ad una delle componenti del campo elettromagnetico ed applicare a tale componente tutte le considerazioni fatte nei corsi di Campi Elettromagnetici. È importante sottolineare che questa è una teoria scalare e che quindi fa perdere la possibilità di descrivere tutti quei fenomeni come ad esempio la polarizzazione che richiedono la conoscenza di tutte le componenti del campo. La teoria geometrica è un modello più semplice della teoria ondulatoria è in grado di descrivere la propagazione in mezzi non omogenei inizialmente supposti senza perdite a condizione che gli scostamenti dall uniformità siano piccoli su lunghezze confrontabili con la lunghezza d onda. I casi in cui si manifestano i fenomeni tipici dell ottica (riflessione rifrazione e diffrazione) che sono accomunati dal fatto che il sistema interagente con il campo è costituito da oggetti di grandi dimensioni rispetto alla lunghezza d onda sono: 1. regioni caratterizzate da costanti costitutive del mezzo lentamente variabili nello spazio (tipicamente nell atmosfera) come la permittività dielettrica ε r ( ) o l indice di rifrazione (in questo caso l ottica geometrica diviene sempre più precisa al crescere della frequenza); 2. estese superfici di materiale solido come spigoli pareti (in questo caso valgono le teorie delle riflessione l ottica fisica e la teoria geometrica delle diffrazione). Le condizioni di lenta variabilità ancorché necessarie non sono sufficienti a garantire la totale esattezza delle soluzioni ottenute con l ottica geometrica; possono infatti sussistere concentrazioni di raggi in regioni dette fuochi o caustiche in cui l ottica geometrica porta a soluzioni incomplete o erronee. L insieme dei raggi rifratti riflessi e diffratti costituisce una descrizione del campo sufficientemente approssimata in regioni complesse quali l ambito urbano o extraurbano quando si voglia tener conto del profilo verticale dell indice di rifrazione troposferica e/o delle irregolarità del terreno. Figura 1 Possibili modi di propagazione dell onda elettromagnetica da un terminale Tx a un terminale Rx. Figure 1 Possible ways of propagation of an electromagnetic wave from a Tx to an Rx terminal. Rimangono escluse le onde superficiali non configurabili come raggi ma la cui importanza decresce all aumentare della frequenza. 1. Principio di funzionamento 1.1 Equazioni di base Ricaveremo le equazioni fondamentali dell ottica geometrica nell ambito della trattazione scalare partendo dall equazione di Helmholtz scritta per un mezzo in cui l indice di rifrazione possa variare da punto a punto. Indicando con U(xyzt) la funzione caratterizzante l onda elettromagnetica e con n(xyzt) l indice di rifrazione entrambe funzioni del punto di raggio vettore e dell istante t si riscrive l equazione delle onde: essendo c la velocità della luce nel vuoto. Le proprietà spaziotemporali di un mezzo continuo sono caratterizzate da una funzione continua l indice di rifrazione n(xyzt); esso nell ipotesi che il mezzo sia invariante nel tempo non dipenderà esplicitamente da t. Inoltre se l onda e.m. è monocromatica cioè un armonica pura esprimibile come U(xyz)e -iωt con pulsazione ω si può risolvere l equazione (1.1) applicando il metodo della separazione nelle variabili spaziali (xyz) e temporale t: (1.2) 5 (1.1)
6 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 nota come equazione di Helmholtz dove il vettore d onda nel vuoto k 0 è definito tramite la pulsazione k 0 =ω/c o la lunghezza d onda k 0 =2π/λ. Si osserva che l equazione (1.2) vale nell ipotesi di cambiamenti non troppo bruschi di n(xyz) condizione che si verifica quando il mezzo è generalmente continuo. Scriviamo U(xyz) nella forma: con A(xyz) ed S(xyz) reali. Come casi particolari se l indice di rifrazione n è costante quindi per mezzo omogeneo tra le soluzioni esatte della (1.2) vi è quella che descrive l onda piana: dove ˆnil versore normale al fronte d onda e r il versore parallelo alla direzione di propagazione. Altra soluzione (valida anche per mezzo isotropo) è l onda sferica: che si propaga indipendentemente dalla direzione. Vediamo quale espressione assume la (1.2) inserendovi la (1.3). Differenziando U(xyz) rispetto a x si ottiene: dove per brevità si è omessa la dipendenza esplicita di S e A da (xyz). Differenziando ancora U/ x rispetto ad x si ottiene: (1.3) Sostituendo le equazioni (1.4) e (1.3) nella (1.2) poiché l esponenziale e non può essere uguale a zero si deduce: Separando la parte reale e la parte immaginaria si ottengono le equazioni: (1.5). (1.6) Si noti che con opportuna scelta di A(r ) ed S(r ) è sempre possibile porre U(r ) nella forma (1.3) perciò le (1.5) e (1.6) hanno validità generale. A questo punto si può introdurre l approssimazione che porta all ottica geometrica; essa consiste nell ammettere che nella (1.5) il termine 2 A sia trascurabile rispetto agli altri due:. (1.7) Poiché questi ultimi sono moltiplicati per k 2 e quindi hanno 0 un peso che cresce come ω 2 (ovvero 1/λ2) si usa dire che l ottica geometrica è il limite di quella ondulatoria nell ipotesi di frequenze relativamente alte ω (ovvero di lunghezze d onda basse λ 0). Introducendo l approssimazione detta (1.7) nella (1.5) poiché si esclude la soluzione banale in cui l ampiezza A è uguale a zero si ottiene l equazione:.. (1.8) Differenziando U(xyz) anche rispetto a y e z si ottengono espressioni del tutto analoghe alla precedente solo con le variabili y e z al posto di x riportate nella seguente espressione in cui si va a sommare membro a membro le tre derivate:.. (1.4) La funzione S(r ) si chiama iconale mentre l equazione (1.8) è nota come equazione dell iconale; essa descrive la variazione spaziale della fase e la mette in relazione con l indice di rifrazione. Risolta tale equazione ci si può servire della (1.6) nota come equazione di trasporto per trovare la funzione di ampiezza A(r ). Ci interessiamo per ora della equazione (1.8). Le superfici S(r )=cost sono le superfici equifase dell onda e.m U(r ) [vedi eq. (1.3)] mentre le linee di forza S vengono prese per definizione come raggi luminosi. In altre parole se S(xyz)=cost è una superficie equifase allora le derivate parziali S/ x S/ y S/ z sono le componenti di un vettore normale alla superficie equifase cioè il gradiente dell iconale con modulo pari all indice di rifrazione n(xyz). Il collegamento tra questa definizione di raggio luminoso ed il corrispondente concetto intuitivo sarà chiarito nel seguito. Da quanto abbiamo detto risulta dunque che i raggi 6
7 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 luminosi sono le traiettorie ortogonali alle superfici d onda. Una famiglia di curve di questo tipo viene detta congruenza normale in particolare è detta congruenza rettilinea quando i raggi sono rette. Volendo prevedere anche l andamento dell ampiezza dell onda consideriamo un generico raggio luminoso ed introduciamo su di esso un ascissa. Detto ŝ il versore della tangente al raggio dato che l equazione dell iconale può scriversi:. (1.9) (1.12) avendo posto S( ) = S 1 e S( ) = S 2. Supponiamo ora che P 1 e P 2 si trovino su uno stesso raggio luminoso (fig. 2). In questo caso è e la (1.12) diventa:. (1.13) Ammettiamo che un solo raggio luminoso passi per P 1 e P 2 ; Se riscriviamo la (1.6) dividendola per A essa si può scrivere nella forma: inserendovi l equazione dell iconale (1.9) si ottiene: ; (in questo contesto il termine ŝ [ ] assume il significato di derivata direzionale d[ ]/ds dato che il versore ŝ è tangente all ascissa curvilinea s) per cui:. (1.10) L integrazione numerica dell equazione differenziale (1.10) porta alla determinazione dell ampiezza d onda A( ) lungo il raggio luminoso s. La (1.10) insieme alla (1.9) costituisce un approssimazione migliore rispetto alla sola equazione dell iconale (1.8) in quanto tiene conto anche delle variazioni dell ampiezza A( ). 1.2 Interpretazione grafica dell equazione dell iconale L equazione dell iconale (1.9) è passibile di un interpretazione grafica per la quale ci si avvale dell ausilio della fig. 2. Vale l ipotesi di propagazione in un mezzo non omogeneo cosa che comporta un percorso del raggio curvo (riportato in fig. 2 ove è segnata la coordinata curvilinea s). Con riferimento all equazione dell iconale (1.9) il campo vettoriale nŝ è dunque il gradiente della funzione scalare iconale S e quindi è conservativo ( x( f=0) per qualunque funzione f ). Lungo qualunque linea chiusa l si ha allora: (1.11) essendo il generico elemento della linea l. L integrale curvilineo (1.11) è noto come invariante integrale di Lagrange. Presi due punti P 1 e P 2 con raggi vettori ed e scelta una qualunque linea che li congiunga in base alla eq. (1.9) si ha: Figura 2 Il percorso del raggio luminoso nel punto P intercetta la superficie equifase dell indice di rifrazione nel punto P. Il versore ŝ è tangente al raggio d onda e normale alle superficie equifase. Figure 2 The light ray path in the point P intercepts the equiphase surface of the refraction index in the point P. The unity vector ŝ is tangent to the wave ray and it is normal to the equiphase surface. presa allora una qualunque altra linea l che colleghi P 1 e P 2 lungo tale linea sarà e quindi [vedi eq. (1.12)]: La quantità. (1.14) (1.15) lungo una generica linea o in particolare lungo un raggio luminoso prende il nome di cammino ottico lungo la linea detta. Nel caso in cui la linea coincida con un raggio luminoso il cammino ottico è uguale alla variazione di iconale fra i due punti estremi considerati [vedi eq. (1.13)] mentre per un altra linea esso è maggiore di tale variazione. L equazione (1.14) giustifica il celebre principio di Fermat 7
8 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 enunciato nel 1657 (quindi ben prima della teoria elettromagnetica della luce) e noto come principio del minimo cammino ottico: Il cammino ottico lungo il raggio luminoso che congiunge due punti è minimo rispetto a tutti i percorsi che congiungono i due punti (in realtà l enunciato di Fermat era più teleologico: La natura segue sempre le vie più brevi ). Tenendo presente la definizione dell indice di rifrazione si vede che la quantità ndl è proporzionale al tempo impiegato dalla luce per compiere il tratto dl; per questa ragione il principio di Fermat va anche sotto il nome di principio del minimo tempo. Tuttavia in altri casi si può trovare addirittura che il percorso seguito dal raggio corrisponde ad un massimo locale del cammino ottico. Una formulazione del principio valida in generale asserisce che il cammino ottico lungo un raggio è stazionario nel senso del calcolo delle variazioni cioè che la cosiddetta variazione prima dell integrale (1.15) è nulla per piccole deformazioni del percorso di integrazione rispetto a quel raggio. Per quanto riguarda la rifrazione è facile stabilire la legge di Snell-Cartesio applicando il principio di Fermat con il seguente procedimento (vedi fig. 3). (1.16) dove d è la distanza fra i piedi delle perpendicolari abbassate da A e B sulla superficie di separazione. Se il percorso considerato coincide con quello del raggio il cammino corrispondente deve essere stazionario. Nel caso in esame ciò significa semplicemente che si deve annullare la derivata rispetto ad x. Imponendo questa condizione si ritrova subito la legge di Snell-Cartesio:. (1.17) Ci si rende conto inoltre che l ipotesi di superficie di separazione piana è inessenziale e che la legge vale per una superficie di separazione di forma qualsiasi (almeno nei punti in cui la superficie è dotata di piano tangente) Andamento dell intensità luminosa Tubi di flusso La funzione d onda U può essere pensata come rappresentativa del campo elettrico dell onda e.m.. Ricordiamo che per un onda piana sinusoidale l intensità luminosa media ha l espressione (potenza istantanea dell onda): (1.18) essendo E l ampiezza del campo elettrico ε 0 e µ 0 la costante dielettrica e la permeabilità magnetica del vuoto ε r e µ r le analoghe permittività relative del mezzo. Nell ultimo passaggio si è supposto µ r 1 (come è ragionevole per mezzi otticamente trasparenti) e si è indicata con la cosiddetta impedenza caratteristica del vuoto. In analogia con la eq. (1.18) e trascurando le costanti di proporzionalità poniamo: Figura 3 Semplice schema che mostra la minimizzazione del tempo di propagazione. Figure 3 A simple scheme that shows the minimization of the propagation time. Dati due punti A e B in due mezzi omogenei con indici di rifrazione n 1 e n 2 separati da una superficie che per il momento supponiamo piana consideriamo il piano passante per i due punti e ortogonale alla superficie di separazione (tale piano costituisce il piano del disegno nella figura). Il cammino ottico da A a B lungo un percorso formato dai due segmenti AP e PB è funzione della posizione di P sulla superficie di separazione. Con le notazioni di figura 3 tale cammino diciamo L AB (x) può esprimersi come: I = na 2. (1.19) L andamento dell intensità luminosa in ottica geometrica può essere studiato a partire dall equazione di trasporto (1.6) che regola il comportamento dell ampiezza A. Inserendovi l equazione (1.19) riscriviamo l equazione di trasporto (1.10) nella forma:. (1.20) Integrando l equazione (1.20) fra due punti generici di ascisse curvilinee s 1 e s 2 otteniamo:. (1.21) 8
9 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 L equazione (1.21) permette il calcolo dell intensità lungo un generico raggio se è stata risolta l equazione dell iconale (1.9) in modo che 2 S sia una funzione nota. Osservando la (1.21) si nota che se l intensità si annulla in un punto di un raggio allora si annulla lungo tutto il raggio; ciò suggerisce l idea che l energia luminosa si propaghi lungo i raggi. Se si moltiplica l equazione (1.6) per A si può scrivere: A 2 2 S+2A A S= (A 2 S)=0 (1.22) che utilizzando le (1.9) e (1.19) diventa: (Iŝ) = 0 (1.23) Dunque il campo Iŝ è solenoidale. Ora si può ricavare la legge di intensità dell ottica geometrica che è un evoluzione dell espressione dell intensità in termini di tubi di flusso. Si definisce tubo di flusso dell energia una superficie chiusa costituita lateralmente da una famiglia di raggi ed ortogonalmente da due porzioni di superficie d onda (vedi fig. 4). L energia luminosa viaggia all interno del tubo di flusso e l intensità varia in modo inversamente proporzionale alla sezione del tubo. Si definisce il fattore di divergenza u come:. (1.26) Tale grandezza tiene conto dell eventuale attenuazione dovuta all allargamento del fronte d onda con la propagazione. L intensità portata da ogni raggio può diminuire con la distanza anche se il mezzo é privo di perdite poiché man mano che l onda avanza l energia viene distribuita su una superficie sempre più ampia. Si faccia ora riferimento alla figura 5 ove C 1 C 2 e C 3 C 4 sono le cosiddette caustiche dell onda. In generale la superficie costituita dall insieme dei punti in cui i raggi convergono si chiama caustica e nel caso tale superficie si riduca ad un punto i raggi convergono su di esso che viene detto fuoco. Nell ipotesi di mezzo omogeneo quando un onda generica si propaga per raggi rettilinei si può dimostrare che il fattore di divergenza assume l espressione (ρ 1 e ρ 2 sono i raggi di curvatura principali dell onda):. (1.27) Si possono distinguere i tre casi usuali di riferimento: 1. onda sferica 2. onda cilindrica ; (1.28) ; (1.29) Figura 4 Tubo di flusso. Figure 4 Flux tube. 3. onda piana. (1.30) Nell ipotesi di mezzo privo di perdite applichiamo il teorema di Poynting ad un tubo di flusso di sezioni sufficientemente piccole d 1 e d 2 tali da poter considerare su di esse il vettore di Poynting quasi costante (Iŝ cost.); per la conservazione dell energia si ha: Il fattore di divergenza permette di capire come evolve l ampiezza e quindi l intensità del campo lungo il raggio ottico. Infatti se il mezzo è omogeneo si può risolvere l equazione differenziale (1.20) ottenendo che la propagazione dell onda e.m. lungo un raggio è descritta dalla seguente relazione:. (1.31) (1.24) da cui si deduce la legge di intensità dell ottica geometrica: I 1 d 1 = I 2 d 2. (1.25) La (1.31) permette quindi di calcolare il campo in un punto P 2 partendo dal valore del campo nel punto P 1 da cui esce il raggio passante per P 2. Il suo uso non è ammissibile in prossimità dei punti in cui la sezione del fascio infinitesimo preso intorno al raggio considerato si annulla cioè per un fascio omocentrico (tutti i raggi passano per un punto); in 9
10 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 questo caso infatti il fattore di divergenza tende all infinito e il campo calcolato diverge. Questo risultato privo di senso fisico è dovuto al fatto che in prossimità del centro del tubo di flusso dove l ampiezza A varia molto rapidamente non è più lecita l approssimazione (1.7) di trascurare 2 A fatta nel passaggio dalla equazione (1.5) alla (1.8). In tali regioni quindi in prossimità delle caustiche e dei fuochi i risultati dell ottica geometrica sono inaccettabili perciò si dovrà usare l ottica ondulatoria. f d. Anche per la derivata parziale di S(xyz) rispetto ad x cioè S/ x si può calcolare il suo differenziale che è d( S/ x)= ( S/ x) d ; ne segue:. Se ŝ è il versore della tangente al raggio luminoso allora per definizione ŝ = d /ds; segue che applicando la (1.9) si può riscrivere la precedente come: Applicando ancora la (1.9) e svolgendo dei passaggi intermedi:. si trova la proiezione dell equazione dei raggi lungo la direzione x:. (2.2) Si procede analogamente per trovare la proiezione dell equazione dei raggi lungo le direzioni y e z: Figura 5 Caustiche di un onda. Figure 5 Caustics of a wave. (2.3) 2. Equazione dei raggi 2.1 Caso generale Riscriviamo l eq. dell iconale (1.8): S S = S 2 = n 2 ossia l equazione (1.9): S= nŝ dove n( ) è l indice di rifrazione S( ) è l iconale e ŝ è il versore tangente al raggio luminoso con ascissa curvilinea s normale alla superficie equifase S( )= cost. Derivando la (1.9) rispetto a s otteniamo (2.1) dove x ŷ ẑ sono i versori che generano lo spazio cartesiano. Per ora si prende in considerazione solo la componente lungo la direzione x per cui si opera sul primo termine del secondo membro della (2.1). Assegnata una generica funzione f(xyz) il suo differenziale totale è definito come df=( f/ x)dx+( f/ y)dy+( f/ z)dz=. (2.4) Inserendo le ultime tre espressioni nella (2.1) si ricava l equazione dei raggi in una forma indipendente dal sistema di riferimento cartesiano:. (2.5) L equazione differenziale (2.5) è molto importante in ottica geometrica classica poiché tiene conto della variazione del versore del raggio luminoso ŝ al variare dell indice di rifrazione n. La (2.5) può essere integrata numericamente tramite il metodo di Runge-Kutta; caso per caso si dovrà poi individuare la congruenza di raggi che soddisfa le condizioni iniziali del particolare problema in esame. Ad esempio per un mezzo omogeneo in cui si ha una congruenza rettilinea a seconda del problema la soluzione può essere un fascio di raggi paralleli un insieme di rette divergenti da un punto o una famiglia di rette senza un punto in comune né al finito né all infinito come accade per i raggi uscenti da uno stru- 10
11 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 mento che non formi immagini stigmatiche. Generalmente se il mezzo non è omogeneo allora il raggio luminoso procede su linee curve. In particolare se n=0 cioè l indice di rifrazione n è costante ed il mezzo è omogeneo allora d(nŝ)/ds=0 cioè il versore ŝ mantiene direzione e verso costanti quindi il raggio procede su una linea retta. Consideriamo ora il caso di un mezzo con indice di rifrazione a simmetria sferica cioè in cui l indice di rifrazione dipenda solo dalla distanza r da un punto O (centro di simmetria del mezzo): n = n(r) (2.6) per cui il n avrà sempre la direzione di r. Prendiamo O come origine dei vettori di posizione e deriviamo rispetto ad s la quantità x nŝ:. (2.7) Essendo d /ds = ŝ il primo termine a secondo membro è nullo mentre il secondo termine può scriversi in base alla (2.5): (2.8) quindi risulta anch esso nullo in base all ipotesi (2.6). Pertanto si ha: (2.9) dove è un vettore costante. Secondo la (2.9) i raggi luminosi sono curve giacenti in piani che passano per il centro di simmetria. Inoltre detto ϕ l angolo tra e ŝ nel generico punto di un raggio si ha lungo tutto il raggio: Fissiamo un asse x ortogonale a z nel piano di un generico raggio che passi per un dato punto (x 0 z 0 ) formando un angolo ϕ 0. Lungo il percorso del raggio l angolo ϕ che esso forma con l asse z cambierà. Tale angolo dipende quindi da x z e dalle condizioni iniziali. Per la legge di Bouguer avremo (fig.6): n(z)sinϕ=n(z 0 )sinϕ 0 =C ; (2.11) essa generalizza la legge di Snell-Cartesio e può pensarsi ottenuta da questa nel caso di una successione di strati piani paralleli di spessore infinitesimo. Dalle (2.11) si può ricavare l equazione z=z(x) della traiettoria seguita da un generico raggio. Notiamo infatti che è: (2.12) e che limitandoci a considerare raggi con angolo ϕ compreso fra zero e π possiamo ricavare dalla (2.11):. (2.13) Inserendo le equazioni (2.11) e (2.13) nella (2.12) otteniamo l equazione differenziale:. (2.14) Essa una volta assegnata la funzione n(z) si risolve per separazione di variabili nel seguente modo: (2.15) nr sin ϕ = cost. (2.10) Le equazioni (2.9) e (2.10) vanno sotto il nome di legge di Bouguer. Tale legge è analoga a quella della conservazione del momento della quantità di moto per una particella in moto sotto l azione di una forza centrale. Infatti tale relazione (legge di Snell per mezzi a simmetria sferica) è alla base della propagazione ionosferica o per onda di cielo che sfrutta cioè la possibilità di avere rientro a terra oltre l orizzonte geometrico di onde lanciate con elevazione maggiore di zero. 2.2 Mezzo stratificato Come caso limite di mezzi con indice di rifrazione a simmetria sferica si può considerare quello di mezzi con indice di rifrazione dipendente da una sola variabile cartesiana diciamo z (è il caso in cui il centro di simmetria si allontana indefinitivamente). Figura 6 Mezzo a stratificazione piana. Figure 6 Medium with plane stratification. 11
12 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 dove l integrale è indefinito e quindi contiene una costante di integrazione da determinare imponendo le condizioni iniziali cioè che il raggio passi per il punto assegnato (x 0 z 0 ) formando con z l angolo assegnato ϕ Derivazione della legge di Snell in termini differenziali L equazione dei raggi (2.5) può essere usata per derivare la legge di Snell-Cartesio in termini differenziali. Essa si enuncia nel modo seguente: in un mezzo disomogeneo quando il raggio luminoso compie un percorso infinitesimo da un punto con indice di rifrazione n( ) a un punto +d con indice di rifrazione n( +d )=n( )+dn( ) (fig.7) il raggio viene rifratto in accordo con la seguente legge: Con riferimento alla figura 7 se si risolve la (2.5) lungo un percorso infinitesimo tra i punti e +d : (2.17) dove ŝ è il versore normale alla superficie equifase dell indice di rifrazione S( )=cost. Si definisce il versore ˆτ tangente alla superficie equifase dell indice di rifrazione che risulta normale al raggio luminoso nel punto dove superficie equifase e raggio si intercettano. Il versore ˆτ è normale al versore ŝ che forma gli angoli ϕ( ) e ϕ( )+dϕ( ) rispettivamente con i versori ŝ ϕ e ŝ ϕ+dϕ. Se si proietta la (2.17) lungo la direzione del versore τ dato che il contributo del secondo membro è nullo: n( ) sinϕ( )=[n( )+dn( )] sin[ϕ( )+dϕ( )] (2.16) dove ϕ( ) e ϕ( )+dϕ( ) sono gli angoli di rifrazione rispettivamente definiti nei punti e ( )+d( ). si ottiene la (2.16). (2.18) Figura 7 Percorso del raggio luminoso tra i punti e ( )+d( ). Figure 7 Path of the light ray between points and ( )+d( ). In fig. 7 i versori ŝ ϕ e ŝ ϕ+dϕ formano rispettivamente gli angoli ϕ e ϕ+dϕ con il versore ŝ normale alla superficie equifase dell indice di rifrazione S( )=cost (In figura le superfici equifase dell indice di rifrazione sono state disegnate come dei piani ma in generale si possono immaginare come superfici curve). In bibliografia esiste una dimostrazione rigorosa per l enunciato appena esposto. Qui se ne riportano sommariamente le linee guida. In accordo con l equazione dei raggi (2.5) il versore ŝ tangente al raggio luminoso risulta normale alla superficie equifase dell indice di rifrazione nel punto dove raggio e superficie equifase si intercettano. 2.4 Esempio Come esempio di applicazione di quanto detto studiamo il fenomeno del miraggio ben noto perché si osserva frequentemente per esempio sulle strade d estate. Le zone dell asfalto più lontane dall osservatore sembrano bagnate salvo risultare perfettamente asciutte quando l osservatore si avvicina ad esse. In realtà tali zone si comportano come riflettenti; l attribuire questa riflessione alla presenza di acqua è un interpretazione legata a due fattori: a) la nostra radicata ma errata convinzione che i raggi luminosi debbano per forza procedere in linea retta e che possano deviare solo se riflessi; b) l identificazione fra quello che osserviamo e ciò che abbiamo altre volte osservato in presenza di chiazze d acqua sul terreno. Fisicamente ciò che accade è che gli strati d aria prossimi all asfalto sono più caldi e quindi meno densi di quelli sovrastanti di conseguenza si ha un gradiente verticale dell indice di rifrazione. I raggi luminosi si incurvano cosicché un raggio inizialmente diretto verso il basso può arrivare a incurvarsi verso l alto prima di incontrare il terreno raggiungendo l osservatore come se fosse stato riflesso. Dato che i gradienti in gioco sono piccoli solo i raggi con un angolo ϕ 0 prossimo a π/2 subiscono il fenomeno; è per questo che avvicinandosi si ha la sensazione che l acqua sparisca. Per trovare la forma dei raggi adottiamo un modello semplice per n(z): n(z)=n min +βz (2.19) in cui n min è il valore minimo dell indice di rifrazione e β una costante opportuna. Naturalmente penseremo che la (2.19) valga in un certo intervallo 0 z z max. Introduciamo la 12
13 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 (2.19) nella (2.15) operando il seguente cambiamento di variabile: La (2.15) diventa allora: la cui soluzione è:. (2.20) (2.21) (2.22) Bibliografia Balanis C. A. (1989). Advanced Engineering Electromagnetics Wiley. Bertoni H. L. (2000). Radio Propagation for Modern Wireless Systems Prentice Hall. Bianchi C. e Bianchi S. (2009). Problema generale del ray tracing nella propagazione ionosferica Rapporti Tecnici INGV n 104. Born M. e Wolf E. (1993). Principles of Optics Cambridge University Press. Felsen L. e Marcuvitz N. (1994). Radiation and scattering of waves IEEE. Kline M. e Kay I. (1965). Electromagnetic Theory and Geometrical Optics Interscience. Sommerfeld A. J. W. (1954). Optics Academic Press. ovvero: (2.23) dove la costante A è da determinare per ogni particolare raggio conoscendo le coordinate (x 0 z 0 ) di un suo punto P e il corrispondente valore di ϕ 0. Con la (2.11) si determina C e con la (2.20) il valore di Z in P 0. La (2.23) scritta nel punto P 0 consente di ricavare A. Nelle nostre ipotesi (0<ϕ<π) è facile controllare che risulta A>0 perciò potremo porre: (2.24) dando a x un opportuno valore (positivo nullo o negativo). Risolvendo la (2.23) rispetto a Z otteniamo: (2.25) da cui tenendo presente la (2.20) segue:. (2.26) Dunque i raggi hanno a meno di traslazioni verticali la forma di coseni iperbolici o come anche si dice di catenarie. Naturalmente la (2.26) è valida nell intervallo 0 z z max. 13
14 Teoria della propagazione radio nei mezzi disomogenei (Metodo dell iconale) Silvio Bianchi et al Quaderni di Geosifica No. 75 Ottobre 2009 Indice Introduzione 4 1. Richiami di ottica geometrica Equazioni di base Interpretazione grafica dell equazione dell iconale Andamento dell intensità luminosa Tubi di flusso 8 2. Equazione dei raggi Caso generale Mezzo stratificato Derivazione della legge di Snell in termini differenziali Esempio 12 Bibliografia 13 14
15 Coordinamento editoriale e impaginazione Centro Editoriale Nazionale INGV Progetto grafico e redazionale Daniela Riposati Laboratorio Grafica e Immagini INGV 2009 INGV Istituto Nazionale di Geofisica e Vulcanologia Via di Vigna Murata Roma Tel Fax
16 Istituto Nazionale di Geofisica e Vulcanologia
OTTICA GEOMETRICA CLASSICA: PROPAGAZIONE NEI MEZZI DISOMOGENEI.
 P P Istituto P P Università OTTICA GEOMETRICA CLASSICA: PROPAGAZIONE NEI MEZZI DISOMOGENEI. (Metodo dell iconale) (1) () () Silvio BianchiP P, Umberto SciaccaP P, Alessandro SettimiP P () (1) Sapienza
P P Istituto P P Università OTTICA GEOMETRICA CLASSICA: PROPAGAZIONE NEI MEZZI DISOMOGENEI. (Metodo dell iconale) (1) () () Silvio BianchiP P, Umberto SciaccaP P, Alessandro SettimiP P () (1) Sapienza
Teoria geometrica della propagazione
 Teoria geometrica della propagazione Valeria Petrini - Propagazione M Introduzione Le onde elettromagnetiche, una volta irradiate dall antenna trasmittente possono raggiungere l antenna ricevente in quattro
Teoria geometrica della propagazione Valeria Petrini - Propagazione M Introduzione Le onde elettromagnetiche, una volta irradiate dall antenna trasmittente possono raggiungere l antenna ricevente in quattro
Ottica geometrica. H = η 1 u E. S = 1 2 η 1 E 2 u = 1 2 η H 2 u
 Ottica geometrica L ottica geometrica assume che il campo elettromagnetico in un mezzo senza perdite possa essere rappresentato in ogni punto di regolarità come somma di onde localmente piane uniformi.
Ottica geometrica L ottica geometrica assume che il campo elettromagnetico in un mezzo senza perdite possa essere rappresentato in ogni punto di regolarità come somma di onde localmente piane uniformi.
PRINCIPI TEORICI DI OTTICA GEOMETRICA
 paolo carlizza (paolo.carlizza) PRINCIPI TEORICI DI OTTICA GEOMETRICA 21 July 2017 La gamma delle onde elettromagnetica è talmente vasta, che nel variare la loro frequenza cambiano i comportamenti d'interazione
paolo carlizza (paolo.carlizza) PRINCIPI TEORICI DI OTTICA GEOMETRICA 21 July 2017 La gamma delle onde elettromagnetica è talmente vasta, che nel variare la loro frequenza cambiano i comportamenti d'interazione
E = E 2 E =(jωɛ)( jωµ 0 )E = k 2 E E = Propagazione in mezzi non dissipativi. Mezzo privo di dissipazioni (g = ɛ =0)
 Propagazione in mezzi non dissipativi Mezzo privo di dissipazioni (g = ɛ =0) Si ricava H dalla prima equazione di Maxwell e si sostituisce nella seconda E = E 2 E =(jωɛ)( jωµ 0 )E = k 2 E dove si è posto
Propagazione in mezzi non dissipativi Mezzo privo di dissipazioni (g = ɛ =0) Si ricava H dalla prima equazione di Maxwell e si sostituisce nella seconda E = E 2 E =(jωɛ)( jωµ 0 )E = k 2 E dove si è posto
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1
 FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
Corso di Laurea in Astronomia. Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA 2
 Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
Teoria geometrica della propagazione
 Teoria geometrica della propagazione 1 Valeria Petrini, Ph.D. Student DEIS/ARCES - Fondazione Ugo Bordoni valeria.petrini@unibo.it Introduzione (1) 2 Una corretta caratterizzazione dei collegamenti radio
Teoria geometrica della propagazione 1 Valeria Petrini, Ph.D. Student DEIS/ARCES - Fondazione Ugo Bordoni valeria.petrini@unibo.it Introduzione (1) 2 Una corretta caratterizzazione dei collegamenti radio
Indice. Presentazione 1
 Presentazione 1 1 Perchè e come studiare i fenomeni elettromagnetici 3 1.1 Introduzione............................ 3 1.2 Approccio induttivo e deduttivo................. 6 1.3 Teorie per descrivere i
Presentazione 1 1 Perchè e come studiare i fenomeni elettromagnetici 3 1.1 Introduzione............................ 3 1.2 Approccio induttivo e deduttivo................. 6 1.3 Teorie per descrivere i
1 FORMA GENERALE DELLE ONDE PIANE
 1 FORMA GENERALE DELLE ONDE PIANE Quando abbiamo ricavato le equazioni delle onde piane, abbiamo scelto il sistema di riferimento in direzione z, e questo ha condotto, per una onda che si propaga in direzione
1 FORMA GENERALE DELLE ONDE PIANE Quando abbiamo ricavato le equazioni delle onde piane, abbiamo scelto il sistema di riferimento in direzione z, e questo ha condotto, per una onda che si propaga in direzione
S.Barbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie. Cap. 2. Cinematica del punto
 SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
A - TEORIA DELLA PROPAGAZIONE RADIO IN AMBIENTE REALE
 A - TEORIA DELLA PROPAGAZIONE RADIO IN AMBIENTE REALE Effetto di gas atmosferici e idrometeore Attenuazione supplementare da gas atmosferici Attenuazione supplementare da pioggia Propagazione ionosferica,
A - TEORIA DELLA PROPAGAZIONE RADIO IN AMBIENTE REALE Effetto di gas atmosferici e idrometeore Attenuazione supplementare da gas atmosferici Attenuazione supplementare da pioggia Propagazione ionosferica,
Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi)
 Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi) Corso di Ottica - Massimo Santarsiero Consideriamo un onda e.m. piana armonica, di pulsazione ω i, che incide con
Trasmissione e riflessione di onde piane su interfacce dielettriche (incidenza qualsiasi) Corso di Ottica - Massimo Santarsiero Consideriamo un onda e.m. piana armonica, di pulsazione ω i, che incide con
ONDE ELETTROMAGNETICHE
 Fisica generale II, a.a. 01/014 OND LTTROMAGNTICH 10.1. Si consideri un onda elettromagnetica piana sinusoidale che si propaga nel vuoto nella direzione positiva dell asse x. La lunghezza d onda è = 50.0
Fisica generale II, a.a. 01/014 OND LTTROMAGNTICH 10.1. Si consideri un onda elettromagnetica piana sinusoidale che si propaga nel vuoto nella direzione positiva dell asse x. La lunghezza d onda è = 50.0
Gradiente, divergenza e rotore
 Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33
 ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
CINEMATICA DEL PUNTO MATERIALE: MOTI RETTILINEI E INTRODUZIONE AL MOTO IN PIÙ DIMENSIONI PROF. FRANCESCO DE PALMA
 CINEMATICA DEL PUNTO MATERIALE: MOTI RETTILINEI E INTRODUZIONE AL MOTO IN PIÙ DIMENSIONI PROF. FRANCESCO DE PALMA Sommario INTRODUZIONE ALLA CINEMATICA... 3 MOTO RETTILINEO UNIFORMEMENTE ACCELERATO...
CINEMATICA DEL PUNTO MATERIALE: MOTI RETTILINEI E INTRODUZIONE AL MOTO IN PIÙ DIMENSIONI PROF. FRANCESCO DE PALMA Sommario INTRODUZIONE ALLA CINEMATICA... 3 MOTO RETTILINEO UNIFORMEMENTE ACCELERATO...
Equazione d onda per il campo elettromagnetico
 Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
RICHIAMI DI ELETTROMAGNETISMO
 RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
Prova Scritta di Elettricità e Magnetismo e di Elettromagnetismo A. A Febbraio 2008 (Proff. F.Lacava, C.Mariani, F.Ricci, D.
 Prova Scritta di Elettricità e Magnetismo e di Elettromagnetismo A. A. 2006-07 - 1 Febbraio 2008 (Proff. F.Lacava, C.Mariani, F.Ricci, D.Trevese) Modalità: - Prova scritta di Elettricità e Magnetismo:
Prova Scritta di Elettricità e Magnetismo e di Elettromagnetismo A. A. 2006-07 - 1 Febbraio 2008 (Proff. F.Lacava, C.Mariani, F.Ricci, D.Trevese) Modalità: - Prova scritta di Elettricità e Magnetismo:
R. Capone Analisi Matematica Integrali multipli
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
I raggi luminosi. Per secoli si sono contrapposti due modelli della luce. il modello ondulatorio (Christiaan Huygens)
 I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Onde ele'romagne-che. Propagazione delle onde Riflessione e rifrazione
 Onde ele'romagne-che Propagazione delle onde Riflessione e rifrazione Propagazione delle onde EM L antenna si comporta come il binario su cui si muovono le cariche di un dipolo elettrico che generano un
Onde ele'romagne-che Propagazione delle onde Riflessione e rifrazione Propagazione delle onde EM L antenna si comporta come il binario su cui si muovono le cariche di un dipolo elettrico che generano un
Lezione 04. Costruzione grafica dei cammini ottici
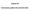 Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
Propagazione in presenza di discontinuità: Riflessione e Rifrazione
 Propagazione in presenza di discontinuità: Riflessione e Rifrazione 1 Valeria Petrini, Ph.D. Student DEIS/ARCES - Fondazione Ugo Bordoni valeria.petrini@unibo.it Introduzione 2 Una corretta caratterizzazione
Propagazione in presenza di discontinuità: Riflessione e Rifrazione 1 Valeria Petrini, Ph.D. Student DEIS/ARCES - Fondazione Ugo Bordoni valeria.petrini@unibo.it Introduzione 2 Una corretta caratterizzazione
Algebra dei vettori OPERAZIONI FRA VETTORI SOMMA DI VETTORI
 Algebra dei vettori Il vettore è un oggetto matematico che è caratterizzato da modulo, direzione e verso. Si indica graficamente con una freccia. Un vettore è individuato da una lettera minuscola con sopra
Algebra dei vettori Il vettore è un oggetto matematico che è caratterizzato da modulo, direzione e verso. Si indica graficamente con una freccia. Un vettore è individuato da una lettera minuscola con sopra
Onde elettromagnetiche. Propagazione delle onde Riflessione e rifrazione
 Onde elettromagnetiche Propagazione delle onde Riflessione e rifrazione Arcobaleno di Maxwell La luce visibile è solo una piccola regione dello spettro elettromagnetico. Alcune radiazioni si producono
Onde elettromagnetiche Propagazione delle onde Riflessione e rifrazione Arcobaleno di Maxwell La luce visibile è solo una piccola regione dello spettro elettromagnetico. Alcune radiazioni si producono
Premesse matematiche. 2.1 Gradiente
 Premesse matematiche 2.1 Gradiente ia f(x, y, z) : R 3 una funzione scalare delle coordinate spaziali (x, y, z). L ampiezza della funzione f(x, y, z) dipende dal punto di osservazione e risulta in genere
Premesse matematiche 2.1 Gradiente ia f(x, y, z) : R 3 una funzione scalare delle coordinate spaziali (x, y, z). L ampiezza della funzione f(x, y, z) dipende dal punto di osservazione e risulta in genere
Le equazioni di Maxwell danno una descrizione completa delle relazioni tra i campi elettromagnetici, le cariche e le distribuzioni di correnti e
 Le equazioni di Maxwell danno una descrizione completa delle relazioni tra i campi elettromagnetici, le cariche e le distribuzioni di correnti e costituiscono il modello matematico della teoria elettromagnetica.
Le equazioni di Maxwell danno una descrizione completa delle relazioni tra i campi elettromagnetici, le cariche e le distribuzioni di correnti e costituiscono il modello matematico della teoria elettromagnetica.
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Fili, finiti e infiniti, uniformemente carichi
 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca, Aprile 003 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca DIIMA - Università degli Studi di Salerno 84084 Fisciano (SA).
Fili, finiti e infiniti, uniformemente carichi Roberto De Luca, Aprile 003 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca DIIMA - Università degli Studi di Salerno 84084 Fisciano (SA).
Coordinate cartesiane e coordinate omogenee
 Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Corso di fisica generale con elementi di fisica tecnica
 Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 4 Onde elettromagnetiche Sommario
Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 4 Onde elettromagnetiche Sommario
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
ELETTROMAGNETISMO APPLICATO ALL'INGEGNERIA ELETTRICA ED ENERGETICA_2b (ultima modifica 30/09/2015)
 ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC_2b (ultima modifica 30/09/2015) M. Usai ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC 27 L integrale S d s è un integrale superficiale
ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC_2b (ultima modifica 30/09/2015) M. Usai ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC 27 L integrale S d s è un integrale superficiale
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Curve e lunghezza di una curva
 Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
SOLUZIONE DELL EQUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME
 SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
CU. Proprietà differenziali delle curve
 484 A. Strumia, Meccanica razionale CU. Proprietà differenziali delle curve Richiamiamo in questa appendice alcune delle proprietà differenziali delle curve, che più frequentemente vengono utilizzate in
484 A. Strumia, Meccanica razionale CU. Proprietà differenziali delle curve Richiamiamo in questa appendice alcune delle proprietà differenziali delle curve, che più frequentemente vengono utilizzate in
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
1. Teorema di reciprocità
 . Teorema di reciprocità Consideriamo un mezzo in cui sono presenti i campi (E, H ) e (E, H ). Questi campi hanno per sorgenti rispettivamente (J, M) e (J, M), ricavabili sostituendo i campi nelle equazioni
. Teorema di reciprocità Consideriamo un mezzo in cui sono presenti i campi (E, H ) e (E, H ). Questi campi hanno per sorgenti rispettivamente (J, M) e (J, M), ricavabili sostituendo i campi nelle equazioni
Lezione 04. Costruzione grafica dei cammini ottici
 Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
Soluzione Compito di Fisica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018
 Soluzione Compito di isica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018 Esercizio 1 1) Scriviamo le equazioni del moto della sfera sul piano inclinato. Le forze agenti sono il peso
Soluzione Compito di isica Generale I Ing. Elettronica e delle Telecomunicazioni 12/01/2018 Esercizio 1 1) Scriviamo le equazioni del moto della sfera sul piano inclinato. Le forze agenti sono il peso
Appunti di geometria analitica dello spazio. di Fabio Maria Antoniali
 Appunti di geometria analitica dello spazio di Fabio Maria Antoniali versione del 23 maggio 2017 1 Un po di teoria 1.1 Vettori e punti 1.1.1 Componenti cartesiane e vettoriali Fissato nello spazio un riferimento
Appunti di geometria analitica dello spazio di Fabio Maria Antoniali versione del 23 maggio 2017 1 Un po di teoria 1.1 Vettori e punti 1.1.1 Componenti cartesiane e vettoriali Fissato nello spazio un riferimento
Esercizi geometria analitica nel piano. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Prodotto scalare e norma
 Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Un materiale si definisce un buon conduttore se la sua conducibilità σ soddisfa a
 BUON CONDUTTORE Un materiale si definisce un buon conduttore se la sua conducibilità σ soddisfa a σ ωε (137). Mentre in un materiale con conducibilità infinita il campo deve essere nullo, la presenza di
BUON CONDUTTORE Un materiale si definisce un buon conduttore se la sua conducibilità σ soddisfa a σ ωε (137). Mentre in un materiale con conducibilità infinita il campo deve essere nullo, la presenza di
Flusso di un campo vettoriale
 Flusso di un campo vettoriale Il concetto è stato originariamente introdotto nella teoria dei fluidi, dove il flusso è legato alla quantità di fluido che passa attraverso una data superficie geometrica,
Flusso di un campo vettoriale Il concetto è stato originariamente introdotto nella teoria dei fluidi, dove il flusso è legato alla quantità di fluido che passa attraverso una data superficie geometrica,
FISICA APPLICATA 2 FENOMENI ONDULATORI - 2
 FISICA APPLICATA 2 FENOMENI ONDULATORI - 2 DOWNLOAD Il pdf di questa lezione (onde2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 10/10/2017 LE ONDE NELLO SPAZIO Finora si è considerata
FISICA APPLICATA 2 FENOMENI ONDULATORI - 2 DOWNLOAD Il pdf di questa lezione (onde2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 10/10/2017 LE ONDE NELLO SPAZIO Finora si è considerata
La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli relativi.
 Corso di Laurea in Matematica Seconda prova in itinere di Fisica (Prof. E. Santovetti) 13 gennaio 016 Nome: La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli
Corso di Laurea in Matematica Seconda prova in itinere di Fisica (Prof. E. Santovetti) 13 gennaio 016 Nome: La risposta numerica deve essere scritta nell apposito riquadro e giustificata accludendo i calcoli
Riflessione e rifrazione tra due mezzi omogenei isotropi non conduttori
 Riflessione e rifrazione tra due mezzi omogenei isotropi non conduttori Vogliamo descrivere i fenomeni dovuti ad un onda elettromagnetica piana (polarizzata linearmente ) monocromatica incidente su di
Riflessione e rifrazione tra due mezzi omogenei isotropi non conduttori Vogliamo descrivere i fenomeni dovuti ad un onda elettromagnetica piana (polarizzata linearmente ) monocromatica incidente su di
CINEMATICA DEL PUNTO MATERIALE
 CINEMATICA DEL PUNTO MATERIALE Regole di derivazione per il prodotto scalare e per il prodotto vettore Sia v funzione di un parametro reale t, t.c. 5 v : R R 3 t 7 v (t). (1) Proprietà: 1. Limite. Il concetto
CINEMATICA DEL PUNTO MATERIALE Regole di derivazione per il prodotto scalare e per il prodotto vettore Sia v funzione di un parametro reale t, t.c. 5 v : R R 3 t 7 v (t). (1) Proprietà: 1. Limite. Il concetto
Analisi Matematica 2. Curve e integrali curvilinei. Curve e integrali curvilinei 1 / 29
 Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
CALCOLO INTEGRALE: L INTEGRALE DEFINITO
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA CALCOLO INTEGRALE: L INTEGRALE DEFINITO A. A. 2013-2014 1 IL PROBLEMA DELL AREA Determinare l area della regione S di piano compresa tra il grafico
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA CALCOLO INTEGRALE: L INTEGRALE DEFINITO A. A. 2013-2014 1 IL PROBLEMA DELL AREA Determinare l area della regione S di piano compresa tra il grafico
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO
 APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
Appunti della lezione sulla Equazione Differenziale delle Onde
 Appunti della lezione sulla Equazione Differenziale delle Onde ultima revisione: 21 giugno 2017 In tutti i casi analizzati precedentemente si osserva che le onde obbediscono alla stessa Equazione Differenziale
Appunti della lezione sulla Equazione Differenziale delle Onde ultima revisione: 21 giugno 2017 In tutti i casi analizzati precedentemente si osserva che le onde obbediscono alla stessa Equazione Differenziale
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria. Curve nello spazio Gennaio Lunghezza d arco
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Sezione d urto classica
 Capitolo Sezione d urto classica In meccanica classica, ogni particella del fascio incidente segue una traiettoria ben definita sotto l azione del potenziale. Se V (r) è centrale, il momento angolare è
Capitolo Sezione d urto classica In meccanica classica, ogni particella del fascio incidente segue una traiettoria ben definita sotto l azione del potenziale. Se V (r) è centrale, il momento angolare è
Corso di Radioastronomia 1
 Corso di Radioastronomia 1 Aniello (Daniele) Mennella Dipartimento di Fisica Prima parte: introduzione e concetti di base Parte 1 Lezione 3 Caratteristiche principali delle linee di trasmissione Linee
Corso di Radioastronomia 1 Aniello (Daniele) Mennella Dipartimento di Fisica Prima parte: introduzione e concetti di base Parte 1 Lezione 3 Caratteristiche principali delle linee di trasmissione Linee
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Geometria analitica del piano pag 25 Adolfo Scimone. Equazione della retta perpendicolare ad una retta data passante per un punto
 Geometria analitica del piano pag 5 Adolfo Scimone Equazione della retta perpendicolare ad una retta data passante per un punto Consideriamo una retta r di equazione r: ax by sia P ( x y), un punto del
Geometria analitica del piano pag 5 Adolfo Scimone Equazione della retta perpendicolare ad una retta data passante per un punto Consideriamo una retta r di equazione r: ax by sia P ( x y), un punto del
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
Note di ottica geometrica.
 Note di ottica geometrica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, novembre 2012. Indice 1 ttica geometrica 1 2 Riflessione. 2 2.1 La legge della riflessione..............................
Note di ottica geometrica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, novembre 2012. Indice 1 ttica geometrica 1 2 Riflessione. 2 2.1 La legge della riflessione..............................
Quick calculus Capitolo 1 Il problema della tangente
 Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
Diffusione dei raggi X da parte di un elettrone
 Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Forme differenziali lineari e loro integrazione
 Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Le caratteristiche delle onde. perturbazione che si propaga nello spazio e nel tempo
 Fenomeni ondulatori Un onda è costituita da una successione regolare di punti di massimo e di minimo, sia nello spazio che nel tempo, secondo una sequenza definita Può essere utile osservare la seguente
Fenomeni ondulatori Un onda è costituita da una successione regolare di punti di massimo e di minimo, sia nello spazio che nel tempo, secondo una sequenza definita Può essere utile osservare la seguente
La circonferenza nel piano cartesiano
 6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
Corso di Fisica tecnica e ambientale a.a. 2011/ Docente: Prof. Carlo Isetti
 CENNI DI CINEMATICA.1 GENERALITÀ La cinematica studia il moto dei corpi in relazione allo spazio ed al tempo indipendentemente dalle cause che lo producono. Un corpo si muove quando la sua posizione relativa
CENNI DI CINEMATICA.1 GENERALITÀ La cinematica studia il moto dei corpi in relazione allo spazio ed al tempo indipendentemente dalle cause che lo producono. Un corpo si muove quando la sua posizione relativa
Mauro Saita Gennaio Equazioni cartesiane di rette e equazioni parametriche di piani Esempi...
 ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
INTERFERENZA - DIFFRAZIONE
 INTERFERENZA - F. Due onde luminose in aria, di lunghezza d onda = 600 nm, sono inizialmente in fase. Si muovono poi attraverso degli strati di plastica trasparente di lunghezza L = 4 m, ma indice di rifrazione
INTERFERENZA - F. Due onde luminose in aria, di lunghezza d onda = 600 nm, sono inizialmente in fase. Si muovono poi attraverso degli strati di plastica trasparente di lunghezza L = 4 m, ma indice di rifrazione
