Geometria 1 a.a. 2016/17 Esercizi 6
|
|
|
- Adolfo Carletti
- 5 anni fa
- Visualizzazioni
Transcript
1 Geometria 1 a.a. 2016/17 Esercizi 6 (1) In (R, τ Eucl ) si consideri il sottoinsieme Y deinito da { } 1 Y = al variare di n N n Determinare parte interna, chiusura e rontiera di Y in R. (2) Sia : (X, τ X ) (Y, τ Y ) un applicazione continua e sia Z X un sottoinsieme. Dimostrare che : (Z, i τ X ) (Y, τ Y ) Z è continua. (3) Si considerino il sottospazio [0, 2π) di R ed il sottospazio S 1 = {(x, y) R 2 tali che x 2 + y 2 = 1} di R 2, entrambi con la topologia indotta dalla topologia euclidea dell ambiente. Sia : ([0, π), i τ Eucl ) (S 1, i τ Eucl ) l applicazione data da (t) = (cos(t), sen (t)). Dimostrare che è continua e biiettiva. L applicazione è anche un omeomorismo? (4) Sia X = {x, y} un insieme costituito da due elementi, e sia τ la seguente collezione di sottoinsiemi di X: ; {x}; X. dimostrare che τ è una topologia su X; (X, τ) è connesso? (X, τ) è compatto? (X, τ) è di Hausdor? (T2?) la topologia τ può essere indotta da una metrica su X? (5) Su R n si consideri la topologia euclidea τ Eucl. Consideriamo la relazione di equivalenza su R n indotta dall azione di moltiplicazione a sinistra del gruppo GL(n; R), ovvero delle matrici n n invertibili: A GL(n; R) tale che A x = y. Sull insieme quoziente R n /GL(n; R) si consideri la toplogia quoziente π τ Eucl, dove π : R n R n /GL(n; R) è la proiezione al quoziente. Dove si è già incontrato lo spazio topologico (R n /GL(n; R), π τ Eucl )? (6) Ricordiamo che, come insieme, lo spazio proiettivo P n (R) è il quoziente P n (R) = ( R n+1 \ {0} ) /R. Indichiamo con π : R n+1 \ {0} P n (R) la proiezione al quoziente, e consideriamo su P n (R) la topologia quoziente π i τ Eucl, dove i τ Eucl è la topologia di sottospazio su R n+1 \ {0} R n+1. (P n (R), π τ Eucl ) è connesso? (P n (R), π τ Eucl ) è compatto? (suggerimento: cercare un sottoinsieme compatto K di R n+1 \ {0} tale che π K : K (P n (R) sia suriettiva).
2 2 (7) Sia S n R n+1 il sottoinsieme S n = { x R n+1 tali che x 2 = 1} dove è l usuale norma euclidea. Su S n si consideri la relazione di equivalenza indotta dalla moltiplicazione per gli elementi del gruppo moltiplicativo {1, 1}, cioè x = ±y. Sia π : S n S n /{±1} la proiezione al quoziente e sia π i τ Eucl la topologia quoziente (dove i τ Eucl è la topologia di sottospazio su S n R n+1 ). Dimostrare che (S n /{±1}, π i τ Eucl ) è omeomoro a (P n (R), π i τ Eucl ). (8) Sia (X, τ) uno spazio topologico e sia π : X Y un applicazione suriettiva di insiemi. Consideriamo su Y la topologia quoziente π τ. Dimostrare che un sottoinsieme F di Y è chiuso in (Y, π τ) se e solo se π 1 (F ) è chuso in (X, τ). (9) Sia (X, τ) uno spazio topologico e sia π : X Y un applicazione suriettiva di insiemi. Consideriamo l applicazione (π, π): X X Y Y Dimostrare che, se π : (X, τ) (Y, π τ) è aperta, 1 allora la topologia quoziente (π, π) (τ τ) coincide con la topologia prodotto delle topologie quoziente π τ π τ. (suggerimento: dimostrare che la base standard della topologia prodotto è una base della topologia quoziente). (10) Diremo che un gruppo G agisce su uno spazio topologico (X, τ) mediante applicazioni continue se per ogni elemnto g di G è assegnata un applicazione continua ρ g : (X, τ) (X, τ) in modo tale che si abbia ρ e = id X, dove e è l elemento neutro di G; ρ gh = ρ g ρ h per ogni g, h G. Dimostrare che se G agisce su (X, τ) mediante applicazioni continue le applicazioni ρ g sono tutte omeomorismi. (11) Supponiamo che il gruppo Gagisca sullo spazio topologico (X, τ) mediante applicazioni continue. Sull insieme X consideriamo la relazione di equivalenza x y se e solo se esiste g G tale che y = ρ g (x), e indichiamo con X/G l insieme quoziente e con π : X X/G la proiezione al quoziente. Dimostrare che l applicazione π : (X, τ) (X/G, π τ) è aperta. (12) Sia (X, τ) lo spazio topologico dato dall insieme X = {0, 1, 2} con la topologia τ costituita dai sottoinsiemi, {0}, {0, 1}, X. Sia Y l insieme Y = {0, 1} e sia : X Y l applicazione suriettiva data da (0) = 0; (1) = 1; (2) = 0. Dimostrare che l applicazione : (X, τ) (Y, τ) non è aperta. (13) Dimostrare che (P n (R), π i τ Eucl ) è T2. (suggerimento: dimostrare che la diagonale è chiusa nel prodotto). 1 Senza questa ipotesi l enunciato è in generale also. Esibire un controesempio, tuttavia, non è aatto semplice: si veda James Munkres, Topology, Sezione 22, Esercizo 6.
3 (14) Su R dotato della topologia euclidea si consideri la relazione di equivalenza indotta dalla moltiplicazione per gli elementi del gruppo moltiplicativo {1, 1}, cioè 3 x = ±y. Sia π : R R/{±1} la proiezione al quoziente. Dimostrare che (R/{±1}, π τ Eucl ) è omeomoro a ([0, + ), i τ Eucl ). (15) Sul sottoinsieme Z R si consideri la topologia di sottospazio indotta dalla topologia euclidea di R. Dimostrare che la topologia ı τ Eucl su Z coincide con la topologia discreta. (16) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme. Supponiamo che (Y, i τ) sia uno spazio connesso (dove i τ indica la topologia di sottospazio). Dimostrare che Y (la chiusura di Y in X) è un sottospazio conesso di X. (17) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme. Inine sia Z un sottoinsieme di X con Y Z Y. Supponiamo che (Y, i τ) sia uno spazio connesso. Dimostrare che (Z, i τ) è connesso. (18) Sia (X, τ) uno spazio topologico e siano x 0 e x 1 punti di X. Un arco in X da x 0 ad x 1 è un applicazione continua α: [0, 1] X tale che α(0) = x 0 e α(1) = x 1. Dimostrare che se esistono un arco α da x 0 a x 1 ed un arco β da x 1 ad x 2 allora esiste anche un arco γ da x 0 a x 2. (19) Uno spazio topologico (X, τ) si dice connesso per archi se presi comunque x 0 e x 1 in X esiste un arco α da x 0 ad x 1. Dimostrare che (X, τ) è connesso per archi se e solo se esiste un punto x in X tale che, per ogni altro punto x di X esiste un arco da x a x. (20) Dimostrare che uno spazio connesso per archi è connesso (suggerimento: [0, 1] è connesso). (21) Dimostrare che R n è connesso per archi. (22) Dimostrare che l immagine di uno spazio connesso per archi è connessa per archi. (23) Dimostrare che il sottospazio S 1 = {(x, y) R 2 tali che x 2 + y 2 = 1} è connesso per archi. (24) Dimostrare che il sottospazio S 2 = {(x, y, z) R 3 tali che x 2 +y 2 +z 2 = 1} è connesso per archi (suggerimento: dati due punti p e q di S 2, considerare il piano per l origine contenente p e q) (25) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme, dotato della topologia di sottospazio. Supponiamo che (Y, i τ) sia connesso per archi e che per ogni punto x di X esista un arco α con α(0) = x e α(1) Y. Dimostrare che X è connesso per archi. (26) Dimostrare che R 2 \ {(0, 0)} è connesso per archi.
4 4 (27) Dimostrare che se (X, τ X ) e (Y, τ Y ) sono connessi per archi allora (X Y, τ prod ) è connesso per archi. (28) Uno spazio topologico (X, τ) si dice localmente connesso per archi se per ogni punto x di X e per ogni intorno I di x in X esiste un intorno J di x in X con x J I e J connesso per archi (nella topologia di sottospazio). Dimsotrare che un aperto di R n è localmente connesso per archi. (29) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme. Dimostrare che un punto x di X appartiene a Y (la chiusura di Y in X) se e solo se per ogni I intorno di x in X si ha I Y. (30) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme. Dimostrare che un punto x di X appartiene a Y (la rontiera di Y in X) se e solo se per ogni I intorno di x in X si ha I Y e I (X \ Y ). (31) Sia (X, τ) uno spazio topologico e sia Y X un sottoinsieme. Dimostrare che Y è chiuso se e solo se Y Y. (32) Sia (X, τ) uno spazio topologico localmente connesso per archi e sia x X. Dimostrare che il sottoinsieme U x = {y X tali che esista un arco in X da x a y} è aperto e chiuso in X. (33) Sia (X, τ) uno spazio topologico connesso e localmente connesso per archi. Dimostrare che (X, τ) è connesso per archi. (34) In (R n, τ Eucl ) si consideri il sottoinsieme B 1 (0) = { x R n tali che x 2 < 1}, dove è l usuale norma euclidea. Dimostrare che B 1 (0) = { x R n tali che x 2 1} (35) Uno spazio topologico (X, τ) si dice localmente compatto se per ogni punto x di X e per ogni intorno I di x in X esiste un intorno J di x in X con x J I e J compatto (nella topologia di sottospazio). Dimsotrare che un aperto di R n è localmente compatto. (36) Si consideri su R la topologia Euclidea τ Eucl e sia Y R un sottoinsieme limitato. Dimostrare che in(y ) e sup(y ) appartengono a Y (la rontiera di Y in R). Dedurne che se Y è anche chiuso allora in(y ) e sup(y ) appartengono ad Y. (37) Sia (X, τ) uno spazio topologico compatto e sia : (X, τ) (R, τ Eucl ) una unzione continua. Dimostrare che ha massimo e minimo. (38) Esibire un omoemorismo tra (R, τ Eucl ) e ((0, 1), τ Eucl ). (39) Esibire un omoemorismo tra ([0, + ), τ Eucl ) e ([0, 1), τ Eucl ). (40) Dimostrare che ([0, 1], τ Eucl ) e ((0, 1), τ Eucl ) non sono omeomori.
5 (41) Sia : (X, τ X ) (Y, τ Y ) un omeomorismo e sia x un punto di X. Dimostrare che la restrizione di a X \ {x}, : X \ {x} Y \ {(x)} X\{x} è ancora un omeomorismo. (42) Dimostrare che ([0, 1), τ Eucl ) e ((0, 1), τ Eucl ) non sono omeomori (suggerimento: utilizzare l esercizio precedente; dove va il punto 0?) (43) Dimostrare che (R, τ Eucl ) e (R 2, τ Eucl ) non sono omeomori. (44) Sia : (R n, τ Eucl ) (R n, τ Eucl ) un omeomorismo, e sia Y R n un sottoinsieme limitato. Dimostrare che (Y ) è limitato. (45) Sia : (R n, τ Eucl ) (R n, τ Eucl ) un omeomorismo, e sia Y R n un sottoinsieme illimitato. Dimostrare che (Y ) è illimitato. (46) Sia : (X, τ X ) (Y, τ Y ) un omeomorismo e sia Z X un sottoinsieme. Dimostrare che : (Z, i τ X ) ((Z), i τ Y ) Z è un omeomorismo. (47) Sia X R un sottoinsieme limitato. Si consideri su R la topologia euclidea. Dimostare che (X, i τ Eucl ) è connesso e compatto se e solo se X = [a, b] per opportuni a e b con a b. (48) Sia : (R, τ Eucl ) (R, τ Eucl ) un applicazione continua, e sia Z = [a, b] R un intervallo chiuso e limitato. Dimostrare che in generale ( Z) (Z). (49) Sia : (X, τ X ) (Y, τ Y ) un applicazione continua e biiettiva, e sia Z X. Dimostrare che in generale ( Z) (Z). (50) Sia : (R, τ Eucl ) (R, τ Eucl ) un applicazione continua e biiettiva, e sia Z = [a, b] R un intervallo chiuso e limitato. Dimostrare che ( Z) = (Z). (51) Sia : (R, τ Eucl ) (R, τ Eucl ) un applicazione continua e biiettiva, e sia Z = (a, b) R un intervallo aperto e limitato. Dimostrare che (Z) è aperto. (52) Sia : (X, τ X ) (Y, τ Y ) una unzione continua e sia B una base di τ X. Dimostrare che è aperta se e solo se (B) è aperto in Y per ogni B B. (53) Sia : (R, τ Eucl ) (R, τ Eucl ) un applicazione continua e biiettiva. Dimostrare che è un omeomorismo. Gli esercizi dell esonero saranno molto simili a quelli di questa lista, ma saranno ormulati in modo da avere una risposta chiusa. Ad esempio: Un applicazione continua e biiettiva : (R, τ Eucl ) (R, τ Eucl ) è necessariamente un omeomorismo? sì no 5
Corso di Laurea in Matematica Geometria 2. Esercizi di preparazione allo scritto a.a Topologia
 Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Vi prego di segnalare ogni inesattezza o errore tipografico a Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi
 ESERCIZI DI GEOMETRIA 3 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi Esercizio 1. Sia (X, d) uno spazio
ESERCIZI DI GEOMETRIA 3 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi Esercizio 1. Sia (X, d) uno spazio
Prima prova scritta di Geometria 3,
 Prima prova scritta di Geometria 3, 27. 6. 2017 1. i) Dimostrare che una successione x n in un prodotto Π α J X α converge a x se e solo se π β (x n ) converge a π β (x), per ogni β J ( convergenza puntuale
Prima prova scritta di Geometria 3, 27. 6. 2017 1. i) Dimostrare che una successione x n in un prodotto Π α J X α converge a x se e solo se π β (x n ) converge a π β (x), per ogni β J ( convergenza puntuale
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2015/2016
 Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2015/2016 Martedì 29 settembre (2 ore). Introduzione del corso. Definizione di spazio topologico. Primi esempi: 1) topologia
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2015/2016 Martedì 29 settembre (2 ore). Introduzione del corso. Definizione di spazio topologico. Primi esempi: 1) topologia
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 2 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 2 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.5, 3.6,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 2 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.5, 3.6,
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2016/2017
 Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2016/2017 Mercoled ì 29 settembre (2 ore). Introduzione del corso. Definizione di spazio topologico. Primi esempi: 1) topologia
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2016/2017 Mercoled ì 29 settembre (2 ore). Introduzione del corso. Definizione di spazio topologico. Primi esempi: 1) topologia
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 4 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 4 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 5.2, 5.3
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 4 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 5.2, 5.3
Esercizi Algebra dicembre 2016
 Esercizi Algebra 2 20 dicembre 2016 Sia a un elemento di un anello R. Consideriamo R = R[x]/(ax 1). Denotiamo con ϕ la mappa data componendo R R[x] con la proiezione R[x] R. Provare che Ker(ϕ) := {b R
Esercizi Algebra 2 20 dicembre 2016 Sia a un elemento di un anello R. Consideriamo R = R[x]/(ax 1). Denotiamo con ϕ la mappa data componendo R R[x] con la proiezione R[x] R. Provare che Ker(ϕ) := {b R
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Esame scritto di Geometria 2
 Esame scritto di Geometria 2 Università degli Studi di Trento Corso di Laurea in matematica A.A. 2012/2013 10 giugno 2013 Si svolgano i seguenti esercizi. Esercizio 1. Sia E 3 lo spazio euclideo reale
Esame scritto di Geometria 2 Università degli Studi di Trento Corso di Laurea in matematica A.A. 2012/2013 10 giugno 2013 Si svolgano i seguenti esercizi. Esercizio 1. Sia E 3 lo spazio euclideo reale
Esame scritto di Geometria 2
 Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
Geometria 3 A.A Esercizi
 Geometria 3 A.A. 2012 2013 Esercizi Omotopia di applicazioni contiue. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Siano x, y punti di uno spazio topologico X. Si dimostri che le applicazioni
Geometria 3 A.A. 2012 2013 Esercizi Omotopia di applicazioni contiue. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Siano x, y punti di uno spazio topologico X. Si dimostri che le applicazioni
Mercoledì 15 ottobre (2 ore):
 Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2014/2015 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2014/2015 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Mercoledì 15 ottobre (2 ore):
 Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2014/2015 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2014/2015 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 5 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 5 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 10.1,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 5 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 10.1,
Geometria 3 A.A Esercizi
 Geometria 3 A.A. 2014 2015 Esercizi Equivalenza omo- Omotopia di applicazioni contiue. topica. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Si dimostri che lo spazio topologico è connesso. X
Geometria 3 A.A. 2014 2015 Esercizi Equivalenza omo- Omotopia di applicazioni contiue. topica. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Si dimostri che lo spazio topologico è connesso. X
SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220
 SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220 ESERCIZIO 1 (6 punti) Sia X uno spazio topologico. Dimostrare che: (i) (3 punti) X è uno spazio T 1 se e solo se per ogni x X l intersezione di tutti
SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220 ESERCIZIO 1 (6 punti) Sia X uno spazio topologico. Dimostrare che: (i) (3 punti) X è uno spazio T 1 se e solo se per ogni x X l intersezione di tutti
Lezione 3. Martedì 8 ottobre (2 ore).
 Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2013/2014 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Geometria I- Diario delle lezioni L. Stoppino, Università dell Insubria, a.a. 2013/2014 Qui ci sono gli argomenti delle lezioni e delle esercitazioni svolte da me, non delle esercitazioni svolte dagli
Geometria Algebrica A.A Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica A.A. 2014 2015 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Geometria Algebrica A.A. 2014 2015 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
14 Spazi metrici completi
 54 2006-apr-26 Geometria e Topologia I 14 Spazi metrici completi (14.1) Definizione. Una successione {x n } n in uno spazio metrico si dice di Cauchy se per ogni ɛ > 0 esiste un intero N = N(ɛ) per cui
54 2006-apr-26 Geometria e Topologia I 14 Spazi metrici completi (14.1) Definizione. Una successione {x n } n in uno spazio metrico si dice di Cauchy se per ogni ɛ > 0 esiste un intero N = N(ɛ) per cui
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 1 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Geometria 2. Università degli Studi di Trento Corso di Laurea in Matematica A.A. 2011/ settembre 2012
 Geometria 2 Università degli Studi di Trento Corso di Laurea in Matematica A.A. 2011/2012 06 settembre 2012 Si svolgano i seguenti esercizi. Esercizio 1. Sia P 3 R il 3-spazio proiettivo reale dotato del
Geometria 2 Università degli Studi di Trento Corso di Laurea in Matematica A.A. 2011/2012 06 settembre 2012 Si svolgano i seguenti esercizi. Esercizio 1. Sia P 3 R il 3-spazio proiettivo reale dotato del
4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].
![4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1]. 4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].](/thumbs/96/128120172.jpg) Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
10. Il gruppo Speciale Lineare SL(V )
 1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
Geometria e Topologia I - 15 lug 2008 (14:30 - U1-02) 1/10. Cognome:... Nome:... Matricola:...
 Geometria e Topologia I - 5 lug 2008 (4:0 - U-02) /0 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le risposte.) () Si determinino
Geometria e Topologia I - 5 lug 2008 (4:0 - U-02) /0 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le risposte.) () Si determinino
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220 A.A. 2010-2011 - Docente: Prof. Edoardo Sernesi Tutori: Filippo Maria Bonci, Annamaria Iezzi e Maria Chiara Timpone Tutorato
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220 A.A. 2010-2011 - Docente: Prof. Edoardo Sernesi Tutori: Filippo Maria Bonci, Annamaria Iezzi e Maria Chiara Timpone Tutorato
Ψ(U i ). Dalla proposizione 0.3 segue che per ogni i R h esiste c i ( δ, δ) n k tale che ϕ 2 Ψ(U i ) c i, quindi ϕ 2 (L h ) = i R h
 Foliazioni Definition 0.1 Siano date una varieta M, C, una distribuzione involutiva di dimensione k ed una immersione iniettiva Ψ : N M con N varieta connessa di dimensione k. Diremo che N e una sottovarieta
Foliazioni Definition 0.1 Siano date una varieta M, C, una distribuzione involutiva di dimensione k ed una immersione iniettiva Ψ : N M con N varieta connessa di dimensione k. Diremo che N e una sottovarieta
CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI
 CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI ). Siano A, B, C insiemi. Provare che (A B) C = A (B C) A (B C) =(A B) (A C) C(A B) =C(A) C(B). 2). Definiamo la differenza simmetrica
CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI ). Siano A, B, C insiemi. Provare che (A B) C = A (B C) A (B C) =(A B) (A C) C(A B) =C(A) C(B). 2). Definiamo la differenza simmetrica
A.A CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 4.
 A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 4. Esercizio 4. 1. Data una coppia a, b N, consideriamo la loro fattorizzazione in primi. Esprimere in termini
A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 4. Esercizio 4. 1. Data una coppia a, b N, consideriamo la loro fattorizzazione in primi. Esprimere in termini
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Esonero 30 marzo 2015.
 Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Esonero 30 marzo 2015 Nome e Cognome: Esercizio 1 6 punti Esercizio 2 4 punti Esercizio 3 6 punti Esercizio
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Esonero 30 marzo 2015 Nome e Cognome: Esercizio 1 6 punti Esercizio 2 4 punti Esercizio 3 6 punti Esercizio
Data le funzioni e con, e tre generici insiemi, non. x A X. , a sua volta a questo elemento corrisponde, tramite la funzione, l elemento
 Funzione composta Chiariamo prima di tutto il concetto di unzione composta: Data le unzioni e con, e tre generici insiemi, non necessariamente numerici, si ha che tramite ad ogni (x) Y l elemento : A X
Funzione composta Chiariamo prima di tutto il concetto di unzione composta: Data le unzioni e con, e tre generici insiemi, non necessariamente numerici, si ha che tramite ad ogni (x) Y l elemento : A X
Foglio di esercizi di Istituzioni di Geometria
 Foglio di esercizi di Istituzioni di Geometria 11 ottobre 2017 Esercizio 1 Sia M varietà differenziabile, p M e si consideri un funzionale lineare D : C (M) R tale che D(fg) = f(p)d(g) + g(p)d(f). 1. Si
Foglio di esercizi di Istituzioni di Geometria 11 ottobre 2017 Esercizio 1 Sia M varietà differenziabile, p M e si consideri un funzionale lineare D : C (M) R tale che D(fg) = f(p)d(g) + g(p)d(f). 1. Si
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
4 Sottoinsiemi chiusi di uno spazio metrico
 Geometria I 2009-mar-18 15 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto limite) per
Geometria I 2009-mar-18 15 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto limite) per
Esercitazioni di Geometria II
 Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 8 maggio 202 Esercizio. [Metrica del riccio] Si considieri R 2 munito della metrica del riccio, la quale è definita da y x
Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 8 maggio 202 Esercizio. [Metrica del riccio] Si considieri R 2 munito della metrica del riccio, la quale è definita da y x
AL210 - Appunti integrativi - 3
 AL210 - Appunti integrativi - 3 Prof. Stefania Gabelli - a.a. 2016-2017 Nello studio delle strutture algebriche, sono interessanti le relazioni che sono compatibili con le operazioni. Vogliamo dimostrare
AL210 - Appunti integrativi - 3 Prof. Stefania Gabelli - a.a. 2016-2017 Nello studio delle strutture algebriche, sono interessanti le relazioni che sono compatibili con le operazioni. Vogliamo dimostrare
4 Sottoinsiemi chiusi di uno spazio metrico
 Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova II prova parziale TEMA n.1
 CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
Insiemi con una operazione
 CAPITOLO 3 Insiemi con una operazione Lo studio dell algebra è cominciato con la manipolazione di espressioni dapprima numeriche e via via sempre più simboliche; si pensa infatti che la stessa parola algebra
CAPITOLO 3 Insiemi con una operazione Lo studio dell algebra è cominciato con la manipolazione di espressioni dapprima numeriche e via via sempre più simboliche; si pensa infatti che la stessa parola algebra
Capitolo 1. Spazi quoziente. 1.1 Spazi quoziente
 Capitolo 1 Spazi quoziente 1.1 Spazi quoziente Siano (S, A ) uno spazio topologico, Σ una relazione di equivalenza definita in S e p la proiezione canonica di S su S/Σ. Posto S = S/Σ definiamo topologia
Capitolo 1 Spazi quoziente 1.1 Spazi quoziente Siano (S, A ) uno spazio topologico, Σ una relazione di equivalenza definita in S e p la proiezione canonica di S su S/Σ. Posto S = S/Σ definiamo topologia
Esercizi tratti da temi d esame
 Gianluca Occhetta Esercizi tratti da temi d esame Geometria IV e V unità didattica 00 11 0 1 0 1111111111 Università di Trento Dipartimento di Matematica Via Sommarive 14 38050 - ovo (TN) 1 Topologia
Gianluca Occhetta Esercizi tratti da temi d esame Geometria IV e V unità didattica 00 11 0 1 0 1111111111 Università di Trento Dipartimento di Matematica Via Sommarive 14 38050 - ovo (TN) 1 Topologia
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Topologia generale. Geometria course outline and diary of notes day by day
 Topologia generale Geometria course outline and diary of notes day by day Warning: there will be typos! Please let me know if you find them so I can make changes. March 24, 2015 Contents 1 Point set topology
Topologia generale Geometria course outline and diary of notes day by day Warning: there will be typos! Please let me know if you find them so I can make changes. March 24, 2015 Contents 1 Point set topology
Geometria Algebrica Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica 2009 2010 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non detto al contrario, che il campo k è algebraicamente chiuso. Sia V A n
Geometria Algebrica 2009 2010 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non detto al contrario, che il campo k è algebraicamente chiuso. Sia V A n
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
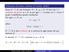 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 3/9/2015 Appello X
 Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 3/9/2015 Appello X Nome e Cognome: Esercizio 1 6 punti Esercizio 2 6 punti Esercizio 3 8 punti
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 3/9/2015 Appello X Nome e Cognome: Esercizio 1 6 punti Esercizio 2 6 punti Esercizio 3 8 punti
Esame di GEOMETRIA 27 giugno ore 11
 Esame di GEOMETRIA 27 giugno 2011 - ore 11 Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta
Esame di GEOMETRIA 27 giugno 2011 - ore 11 Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta
CORSO DI TOPOLOGIA 2006
 CORSO DI TOPOLOGIA 2006 BRUNO MARTELLI Si consiglia di svolgere gli esercizi nel momento in cui si presentano durante la lettura. Le parti (di teoria o esercizi) contrassegnate con ( ) sono invece facoltative
CORSO DI TOPOLOGIA 2006 BRUNO MARTELLI Si consiglia di svolgere gli esercizi nel momento in cui si presentano durante la lettura. Le parti (di teoria o esercizi) contrassegnate con ( ) sono invece facoltative
Indice. 1 Cenni di logica. 2 Elementi di teoria degli insiemi. 3 Relazioni e funzioni. 4 Strutture algebriche
 Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Silvia Pianta - Laura Montagnoli Geometria I - Prerequisiti - UCSC A.A. 2015/2016 1 / 36 1. Cenni
Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Silvia Pianta - Laura Montagnoli Geometria I - Prerequisiti - UCSC A.A. 2015/2016 1 / 36 1. Cenni
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
Insiemi con una operazione
 CAPITOLO 3 Insiemi con una operazione Lo studio dell algebra è cominciato con la manipolazione di espressioni dapprima numeriche e via via sempre più simboliche; si pensa infatti che la stessa parola algebra
CAPITOLO 3 Insiemi con una operazione Lo studio dell algebra è cominciato con la manipolazione di espressioni dapprima numeriche e via via sempre più simboliche; si pensa infatti che la stessa parola algebra
Esame scritto di Geometria 2
 Esame scritto di Geometria 2 UNIVERSITÀ DEGLI STUDI DI TRENTO CORSO DI LAUREA IN MATEMATICA A.A. 2014/2015 Settembre 2015 Esercizio 1 Sia E 4 lo spazio euclideo a quattro dimensioni con un sistema di coordinate
Esame scritto di Geometria 2 UNIVERSITÀ DEGLI STUDI DI TRENTO CORSO DI LAUREA IN MATEMATICA A.A. 2014/2015 Settembre 2015 Esercizio 1 Sia E 4 lo spazio euclideo a quattro dimensioni con un sistema di coordinate
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA AMBIENTE-TERRITORIO Padova I Appello TEMA n.1
 CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA AMBIENTE-TERRITORIO Padova 16-06-2012 I Appello TEMA n.1 Esercizio 1. (a) In R 3 dotato del prodotto scalare usuale, si consideri
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA AMBIENTE-TERRITORIO Padova 16-06-2012 I Appello TEMA n.1 Esercizio 1. (a) In R 3 dotato del prodotto scalare usuale, si consideri
Geometria Algebrica A.A Esercizi. Insiemi algebrici affini, Insiemi algebrici irriducibili.
 Geometria Algebrica A.A. 2017 2018 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Geometria Algebrica A.A. 2017 2018 Esercizi Insiemi algebrici affini, Insiemi algebrici irriducibili. Negli esercizi si suppone, se non scritto al contrario, che il campo k sia algebricamente chiuso di
Geometria 2. Università degli Studi di Trento Corso di Laurea in Matematica A.A. 2011/ febbraio 2013
 Geometria Università degli Studi di Trento Corso di Laurea in Matematica A.A. 0/0 4 febbraio 03 Si svolgano i seguenti esercizi. Esercizio. Sia E 3 il 3-spazio euclideo dotato del riferimento cartesiano
Geometria Università degli Studi di Trento Corso di Laurea in Matematica A.A. 0/0 4 febbraio 03 Si svolgano i seguenti esercizi. Esercizio. Sia E 3 il 3-spazio euclideo dotato del riferimento cartesiano
Primi elementi di topologia dell asse reale. Intorni
 Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
XI Settimana. 2. Elementi basilari della teoria degli anelli (II parte)
 XI Settimana 2. Elementi basilari della teoria degli anelli (II parte) Dati due anelli (, +, ) e (, +, ), un applicazione f : si dice un omomorfismo di anelli se: f(x + y) = f(x) + f(y) e f(x y) = f(x)
XI Settimana 2. Elementi basilari della teoria degli anelli (II parte) Dati due anelli (, +, ) e (, +, ), un applicazione f : si dice un omomorfismo di anelli se: f(x + y) = f(x) + f(y) e f(x y) = f(x)
Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento)
 Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17
Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17
Grafi e gruppo fondamentale di un grafo
 Grafi e gruppo fondamentale di un grafo Note per il corso di Geometria IV (relative alla parte dei 6 crediti) Milano, 2010-2011, M.Dedò Come trovare un grafo omotopicamente equivalente all'oggetto 3d raffigurato
Grafi e gruppo fondamentale di un grafo Note per il corso di Geometria IV (relative alla parte dei 6 crediti) Milano, 2010-2011, M.Dedò Come trovare un grafo omotopicamente equivalente all'oggetto 3d raffigurato
MINITOPOLOGIA M.M. Sommario. Un minicorso base di topologia generale orientato allo studio delle varietà differenziabili.
 MINITOPOLOGIA M.M. Sommario. Un minicorso base di topologia generale orientato allo studio delle varietà differenziabili. Indice 1. Notazioni e riscaldamento 1 2. Relazioni di equivalenza e di ordine 3
MINITOPOLOGIA M.M. Sommario. Un minicorso base di topologia generale orientato allo studio delle varietà differenziabili. Indice 1. Notazioni e riscaldamento 1 2. Relazioni di equivalenza e di ordine 3
LAUREA IN INGEGNERIA CIVILE Corso di Matematica 2 II a prova di accertamento Padova Docenti: Chiarellotto - Cantarini TEMA n.
 LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
LAUREA IN INGEGNERIA CIVILE Corso di Matematica II a prova di accertamento Padova 10-1-07 Docenti: Chiarellotto - Cantarini TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Terza lezione - 15/03/2018
 Università degli Studi di Trento CORSO DI ANALISI MATEMATICA II DIPARTIMENTO DI FISICA ANNO ACCADEMICO 2017/2018 ALBERTO MAIONE Terza lezione - 15/03/2018 1. Richiami teorici 1.1. Spazi Topologici. Definizione
Università degli Studi di Trento CORSO DI ANALISI MATEMATICA II DIPARTIMENTO DI FISICA ANNO ACCADEMICO 2017/2018 ALBERTO MAIONE Terza lezione - 15/03/2018 1. Richiami teorici 1.1. Spazi Topologici. Definizione
Matematica Discreta Classe 1 Dott. C. Delizia 31 Gennaio 2008
 Matematica Discreta Classe 1 Dott. C. Delizia 31 Gennaio 2008 Cognome Matricola Nome Esercizio 1. Per ogni n Z sia nz = {na : a Z}. Sia inoltre A = {a Z : 6 a 6}. Elencandone gli elementi, si descrivano
Matematica Discreta Classe 1 Dott. C. Delizia 31 Gennaio 2008 Cognome Matricola Nome Esercizio 1. Per ogni n Z sia nz = {na : a Z}. Sia inoltre A = {a Z : 6 a 6}. Elencandone gli elementi, si descrivano
Topologia generale. Geometria course outline and diary of notes day by day. Warning: notes very likely contain typos! March 31, 2014.
 Topologia generale Geometria course outline and diary of notes day by day Warning: notes very likely contain typos! March 31, 2014 Contents I Topologia 2 1 Lesson 1 2 1.1 Definizione di una topologia.......................................
Topologia generale Geometria course outline and diary of notes day by day Warning: notes very likely contain typos! March 31, 2014 Contents I Topologia 2 1 Lesson 1 2 1.1 Definizione di una topologia.......................................
Esercizi complementari
 Esercizi complementari (tratti dagli esercizi del prof. Alberto Del Fra) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y
Esercizi complementari (tratti dagli esercizi del prof. Alberto Del Fra) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y
I Esonero di Matematica Discreta - a.a. 06/07 Versione C
 I Esonero di Matematica Discreta - a.a. 06/07 Versione C 1. a. Sono dati gli insiemi A = 1, 2, 3,, 5, 6} e B = numeri naturali dispari}. Determinare A B, A B, B C N (A), C N (A B), P(A B), P(A) P(B). b.
I Esonero di Matematica Discreta - a.a. 06/07 Versione C 1. a. Sono dati gli insiemi A = 1, 2, 3,, 5, 6} e B = numeri naturali dispari}. Determinare A B, A B, B C N (A), C N (A B), P(A B), P(A) P(B). b.
GEOMETRIA 4 PROVE D ESAME
 GEOMETRIA 4 PROVE D ESAME 1. (09/06/2008) Esercizio 1.1. Sia G un gruppo topologico connesso e sia H un suo sottogruppo normale discreto. Si dimostri che H è contenuto nel centro di G. Soluzione. Per ogni
GEOMETRIA 4 PROVE D ESAME 1. (09/06/2008) Esercizio 1.1. Sia G un gruppo topologico connesso e sia H un suo sottogruppo normale discreto. Si dimostri che H è contenuto nel centro di G. Soluzione. Per ogni
A.A CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO SPECIALE 1.
 A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO SPECIALE 1. Nota preliminare. Nell esercizio S. 1. 5. non vi è alcuna ragione per restringersi ai campi finiti
A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO SPECIALE 1. Nota preliminare. Nell esercizio S. 1. 5. non vi è alcuna ragione per restringersi ai campi finiti
MATEMATICA DISCRETA E LOGICA MATEMATICA
 Cognome Nome Matricola MATEMATICA DISCRETA E LOGICA MATEMATICA Proff. F. Bottacin, C. Delizia Quinto Appello 21 luglio 2009 IMPORTANTE: indicare l esame che si intende sostenere e fare solo gli esercizi
Cognome Nome Matricola MATEMATICA DISCRETA E LOGICA MATEMATICA Proff. F. Bottacin, C. Delizia Quinto Appello 21 luglio 2009 IMPORTANTE: indicare l esame che si intende sostenere e fare solo gli esercizi
Prove d esame di Algebra I
 Prove d esame di Algebra I aa 2015/2016 Prova scritta 15 gennaio 2016 Esercizio 1 Dimostrare che, per ogni z Z, vale mcd(z 2 + 3, z 2) {1, 7} Determinare gli interi z tali che mcd(z 2 + 3, z 2) = 7 Esercizio
Prove d esame di Algebra I aa 2015/2016 Prova scritta 15 gennaio 2016 Esercizio 1 Dimostrare che, per ogni z Z, vale mcd(z 2 + 3, z 2) {1, 7} Determinare gli interi z tali che mcd(z 2 + 3, z 2) = 7 Esercizio
Geometria 2. Università degli Studi di Trento Corso di Laurea in Matematica A.A. 2011/ giugno 2012
 Geometria Università degli Studi di Trento Corso di Laurea in Matematica A.A. 011/01 11 giugno 01 Si svolgano i seguenti esercizi. Esercizio 1. Sia E 3 il 3-spazio euclideo dotato del riferimento cartesiano
Geometria Università degli Studi di Trento Corso di Laurea in Matematica A.A. 011/01 11 giugno 01 Si svolgano i seguenti esercizi. Esercizio 1. Sia E 3 il 3-spazio euclideo dotato del riferimento cartesiano
MATEMATICA DISCRETA E LOGICA MATEMATICA
 Cognome Nome Matricola MATEMATICA DISCRETA E LOGICA MATEMATICA Docenti: C. Delizia, M. Tota Terzo Appello 19 giugno 2012 IMPORTANTE: indicare l esame che si intende sostenere e svolgere solo gli esercizi
Cognome Nome Matricola MATEMATICA DISCRETA E LOGICA MATEMATICA Docenti: C. Delizia, M. Tota Terzo Appello 19 giugno 2012 IMPORTANTE: indicare l esame che si intende sostenere e svolgere solo gli esercizi
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento)
 Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile
Soluzioni agli Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile
Indice. 1. Cenni di logica 2. Elementi di teoria degli insiemi 3. Relazioni e funzioni 4. Strutture algebriche. 1 Cenni di logica
 Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Cenni di logica Dispongo queste quattro carte da gioco davanti a voi, due coperte e due scoperte
Indice 1 Cenni di logica 2 Elementi di teoria degli insiemi 3 Relazioni e funzioni 4 Strutture algebriche Cenni di logica Dispongo queste quattro carte da gioco davanti a voi, due coperte e due scoperte
QUADERNI DIDATTICI. Dipartimento di Matematica
 Università ditorino QUADERNI DIDATTICI del Dipartimento di Matematica P. M. Gandini, S. Garbiero Appunti di Geometria III Quaderno # 30 - Novembre 2004........... Indice Prefazione v Parte 1. Topologia
Università ditorino QUADERNI DIDATTICI del Dipartimento di Matematica P. M. Gandini, S. Garbiero Appunti di Geometria III Quaderno # 30 - Novembre 2004........... Indice Prefazione v Parte 1. Topologia
Geometria iperbolica - Primo foglio Andrea Petracci
 Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
10 Spazi connessi. Geometria I 67. Cfr: Sernesi Vol II, Cap III, 11 [1]. Il teorema del valore intermedio si può esprimere in termini di connessione:
![10 Spazi connessi. Geometria I 67. Cfr: Sernesi Vol II, Cap III, 11 [1]. Il teorema del valore intermedio si può esprimere in termini di connessione: 10 Spazi connessi. Geometria I 67. Cfr: Sernesi Vol II, Cap III, 11 [1]. Il teorema del valore intermedio si può esprimere in termini di connessione:](/thumbs/70/62816521.jpg) Geometria I 67 10 Spazi connessi Cfr: Sernesi Vol II, Cap III, 11 [1]. Il teorema del valore intermedio si può esprimere in termini di connessione: (10.1) Definizione. Uno spazio topologico X è detto connesso
Geometria I 67 10 Spazi connessi Cfr: Sernesi Vol II, Cap III, 11 [1]. Il teorema del valore intermedio si può esprimere in termini di connessione: (10.1) Definizione. Uno spazio topologico X è detto connesso
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
LEZIONE 37. x 2 a 2 + y2. b 2 = 2z, x 2. a 2 y2. b 2 = 2z. Esempio Sia S il cilindro luogo dei punti P = (x, y, z) soddisfacenti l equazione
 LEZIONE 37 37.1. Altri esempi di superfici. In questo paragrafo daremo altri esempi di superfici. Esempio 37.1.1. Sia D R 2 un aperto. Allora il grafico Γ ϕ di una funzione ϕ: D R 3 di classe C 1 è una
LEZIONE 37 37.1. Altri esempi di superfici. In questo paragrafo daremo altri esempi di superfici. Esempio 37.1.1. Sia D R 2 un aperto. Allora il grafico Γ ϕ di una funzione ϕ: D R 3 di classe C 1 è una
Esercizi Analisi Matematica II Anno accademico
 Esercizi Analisi Matematica II Anno accademico 2017-2018 Foglio 3 1. T Sia (X, d) uno spazio metrico. Determinare la frontiera di X e dell insieme vuoto. 2. T Sia (X, d) uno spazio metrico. Dimostrare
Esercizi Analisi Matematica II Anno accademico 2017-2018 Foglio 3 1. T Sia (X, d) uno spazio metrico. Determinare la frontiera di X e dell insieme vuoto. 2. T Sia (X, d) uno spazio metrico. Dimostrare
ALGEBRA 1 PB-Z X. 25 V 2012
 ALGEBRA 1 PB-Z X. 25 V 2012 Esercizio 1. Sia A un dominio d integrità unitario e a ideali principali. Si mostri che, per un ideale di A, esser massimale è equivalente a esser primo ( 1 ). Soluzione. La
ALGEBRA 1 PB-Z X. 25 V 2012 Esercizio 1. Sia A un dominio d integrità unitario e a ideali principali. Si mostri che, per un ideale di A, esser massimale è equivalente a esser primo ( 1 ). Soluzione. La
Soluzioni esercizi complementari
 Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Esercizi 0 Strutture algebriche
 Esercizi 0 Strutture algebriche e Esercizio. Siano f : Q[x] Q[x] : p(x) p(x 2 2x + 1), g : Q[x] Q[x] : p(x) p(x) 2 h : Q[x] Q[x] : p(x) p(x 3). Si determini (g f)(x 3 x 2 ) e (f g h)(x + 3). Esercizio.
Esercizi 0 Strutture algebriche e Esercizio. Siano f : Q[x] Q[x] : p(x) p(x 2 2x + 1), g : Q[x] Q[x] : p(x) p(x) 2 h : Q[x] Q[x] : p(x) p(x 3). Si determini (g f)(x 3 x 2 ) e (f g h)(x + 3). Esercizio.
Esercizi di Algebra commutativa e omologica
 Esercizi di Algebra commutativa e omologica Esercizio 1. Sia A un anello non nullo. Dimostrare che A è un campo se e solo se ogni omomorfismo di A in un anello non nullo B è iniettivo. Esercizio 2. Sia
Esercizi di Algebra commutativa e omologica Esercizio 1. Sia A un anello non nullo. Dimostrare che A è un campo se e solo se ogni omomorfismo di A in un anello non nullo B è iniettivo. Esercizio 2. Sia
MINITOPOLOGIA MARCO MANETTI
 MINITOPOLOGIA MARCO MANETTI Sommario. Minicorso di topologia generale orientato allo studio delle varietà differenziabili. Per approfondimenti e maggiori dettagli rimandiamo alla monografia [1]. Indice
MINITOPOLOGIA MARCO MANETTI Sommario. Minicorso di topologia generale orientato allo studio delle varietà differenziabili. Per approfondimenti e maggiori dettagli rimandiamo alla monografia [1]. Indice
Matematica Discreta e Logica Matematica ESERCIZI
 Matematica Discreta e Logica Matematica ESERCIZI Proff. F. Bottacin e C. Delizia Esercizio 1. Scrivere la tavola di verità della seguente formula ben formata e determinare se essa è una tautologia: A ((A
Matematica Discreta e Logica Matematica ESERCIZI Proff. F. Bottacin e C. Delizia Esercizio 1. Scrivere la tavola di verità della seguente formula ben formata e determinare se essa è una tautologia: A ((A
Il teorema di Lusin (versione )
 G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
Analisi funzionale. Riccarda Rossi Lezione 2. Spazi normati Definizioni topologiche Continuità Convergenza di successioni Compattezza
 Riccarda Rossi Lezione 2 Programma 1. Spazi normati; 2. Definizioni topologiche 3. Continuità di funzioni in spazi topologici in spazi metrici in spazi normati 4. Convergenza di successioni in spazi topologici
Riccarda Rossi Lezione 2 Programma 1. Spazi normati; 2. Definizioni topologiche 3. Continuità di funzioni in spazi topologici in spazi metrici in spazi normati 4. Convergenza di successioni in spazi topologici
LEZIONE 30. Se x = 1 si dice che x è un versore. Se poi y = (y 1,..., y n ) R n poniamo. Ricordiamo che vale la cosiddetta disuguaglianza triangolare
 LEZIONE 30 30.1. Insiemi aperti e chiusi in R n. Nel corso di Analisi sono state introdotte alcune nozioni di topologia di R, come la nozione di aperto, di chiuso, di punto d accumulazione. Lo scopo di
LEZIONE 30 30.1. Insiemi aperti e chiusi in R n. Nel corso di Analisi sono state introdotte alcune nozioni di topologia di R, come la nozione di aperto, di chiuso, di punto d accumulazione. Lo scopo di
Università degli Studi di Firenze Facoltà di Scienze
 Università degli Studi di Firenze Facoltà di Scienze C.d.L. in Matematica Tesi di Laurea Triennale Anno Accademico 2008-2009 Spazi completamente regolari e compattificazione di Stone - ƒech Candidato:
Università degli Studi di Firenze Facoltà di Scienze C.d.L. in Matematica Tesi di Laurea Triennale Anno Accademico 2008-2009 Spazi completamente regolari e compattificazione di Stone - ƒech Candidato:
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 25/6/2015 Appello A
 Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 25/6/2015 Appello A Nome e Cognome: Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio
Università degli Studi di Roma Tre Corso di Laurea in Matematica a.a. 2014/2015 GE220 Topologia Prova scritta 25/6/2015 Appello A Nome e Cognome: Esercizio 1 Esercizio 2 Esercizio 3 Esercizio 4 Esercizio
6. Boreliani di uno spazio topologico.
 6. Boreliani di uno spazio topologico. 6.1. La σ-algebra degli insiemi di Borel di uno spazio topologico. Definizione 6.1.1. (σ-algebra di Borel di uno spazio topologico). Sia S uno spazio topologico.
6. Boreliani di uno spazio topologico. 6.1. La σ-algebra degli insiemi di Borel di uno spazio topologico. Definizione 6.1.1. (σ-algebra di Borel di uno spazio topologico). Sia S uno spazio topologico.
Fondamenti di Algebra Lineare e Geometria
 Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale ed Ingegneria dell Energia - Canale B Primo Appello - 6 giugno 24 TEMA A Risolvere i seguenti esercizi motivando adeguatamente ogni risposta.
Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale ed Ingegneria dell Energia - Canale B Primo Appello - 6 giugno 24 TEMA A Risolvere i seguenti esercizi motivando adeguatamente ogni risposta.
Esame di Geometria - 9 CFU (Appello del 26 gennaio A)
 Esame di Geometria - 9 CFU (Appello del 26 gennaio 25 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. In R 3, siano dati il punto P = (, 2, 3) e la retta r : (,, ) + t(, 2), t R.. Determinare
Esame di Geometria - 9 CFU (Appello del 26 gennaio 25 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. In R 3, siano dati il punto P = (, 2, 3) e la retta r : (,, ) + t(, 2), t R.. Determinare
