VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI
|
|
|
- Filippa Massaro
- 5 anni fa
- Visualizzazioni
Transcript
1 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI ANTONIO CARRIERO. Introduzione Il principio d esclusione competitiva (Gause 935) afferma che piú popolazioni in disputa per una stessa risorsa limitante (nutrimento o spazio vitale) in un dato habitat a lunga scadenza non possono convivere, ma che tutte salvo una si estingueranno. D altra parte, in numerose situazioni, la natura non sembra tenere conto di tale principio d esclusione o almeno ha trovato mezzo d aggirarlo. Un esempio su tutti è il cosiddetto Paradosso del Plancton (Hutchinson 96), e cioè la convivenza su di una stessa risorsa nutrizionale limitante di alcune specie di plancton dalle caratteristiche biologiche simili. In due serie d articoli, Sommer [3-4-5] e Grover [6-7-8], è stato dimostrato che la paradossale convivenza, è una conseguenza diretta delle fluttuazioni temporali della concentrazione della risorsa nutrizionale limitante. Queste fluttuazioni sono causate sia da fenomeni esterni, cioè non dipendenti dalla natura delle specie studiate, ad esempio l alternarsi delle stagioni o del giorno e della notte, sia da specifici comportamenti del plancton, un esempio sono le periodiche migrazioni verticali: da acque relativamente profonde alla superficie e viceversa; da queste migrazioni verticali il plancton trae ulteriori vantaggi: una forte riduzione della mortalità per predazione, e l aumento del tasso di crescita. Le tradizionali formulazioni e risoluzioni matematiche di questo ed altri presunti fenomeni paradossali, sono nella maggior parte dei casi troppo sofisticate, e quindi di non facile divulgazione. Lo scopo di questo breve scritto è di sviluppare e giustificare alcuni aspetti di un metodo d analisi qualitativa semplice, proposto da un gruppo di ricercatori francesi [], che permette di spiegare fenomeni paradossali 69
2 70 ANTONIO CARRIERO di questo tipo, attraverso lo studio degli effetti che hanno le fluttuazioni temporali della concentrazione di risorse limitanti sulla crescita delle popolazioni (in competizione e no). 2. Modello d ambiente variabile Consideriamo l insieme biologico formato da due popolazioni X e Y (due specie in competizione o due stadi evolutivi della stessa specie) le cui concentrazioni sono rappresentate dalle variabili x e y. Le variazioni temporali della concentrazione di risorse limitanti si riflettono nell evoluzione dei parametri caratterizzanti l insieme biologico studiato. Chiameremo tali parametri ambiente. Sia U(t) il vettore (o funzione) che rappresenta l evoluzione dell ambiente (ogni componente di U(t) rappresenta l evoluzione di un unico parametro), e supponiamo che l evoluzione dell insieme biologico studiato sia rappresentabile attraverso il seguente sistema d equazioni differenziali: { ẋ(t) = f(x(t), y(t), U(t)) ẏ(t) = g(x(t), y(t), U(t)) Il Principio Bang-Bang proprio della teoria del controllo [2], ci assicura che ogni evoluzione dell insieme biologico causata dalla variazione della funzione U(t), può essere realizzata utilizzando unicamente i valori estremi che essa assume. Siano U e U2 i vettori rappresentanti due ambienti estremi (cioè i valori estremi della funzione U(t)), ad esempio l inverno e l estate, o il giorno e la notte, o ancora due diverse profondità marine. Grazie al Principio Bang-Bang, ci possiamo quindi limitare, senza perdita d informazione, a funzioni U(t) che saltano in modo discontinuo tra i valori U e U2. 3. Fiumi e affluenti Le traiettorie nel piano di fase di numerosi sistemi d equazioni differenziali di dimensione 2 sono paragonabili a quelle presentate nella figura, dove ogni singola traiettoria, caratterizzata da precise condizioni iniziali, sembra convergere verso una traiettoria privilegiata, come affluenti che confluiscono in un unico fiume; per questa ragione le traiettorie che presentano tale caratteristica saranno chiamate traiettorie-fiume.
3 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 7 Figura
4 72 ANTONIO CARRIERO Occupiamoci ora di un sistema d equazioni differenziali del tipo presentato nel secondo paragrafo che produce traiettorie-fiume nei due ambienti U e U2 (figg. 2a e 2b). Se il valore della funzione U(t) passa rapidamente da U a U2 e viceversa, la traiettoria del sistema si situa unicamente negli affluenti, e la direzione del movimento risultante, cioè l evoluzione dell insieme biologico sarà probabilmente diversa da quella dei due fiumi iniziali (fig. 2c). Questa idea geometrica guida la costruzione degli esempi che seguono. Il nostro principale obiettivo è mettere in evidenza un modello nel quale il comportamento in ambiente costante (U(t) = U oppure U(t) = U 2) è qualitativamente diverso dal comportamento in ambiente variabile (nel caso d una commutazione periodica della funzione U(t) tra i suoi estremi U e U2). 4. Crescita in condizioni difficili 4.. Presentazione del modello. Consideriamo un modello di crescita lineare di una popolazione strutturata in due stadi evolutivi: larve e adulti, le cui concentrazioni sono rappresentate dalle funzioni x(t) e y(t). { ẋ(t) = x(t) + n y(t) ẏ(t) = p x(t) m y(t) La scelta dell unità di tempo ci permette di fissare a il coefficiente davanti a x(t) nella prima equazione. I coefficienti n e m sono i tassi di natalità e di mortalità, il parametro p rappresenta la proporzione di larve che diventa adulta (0 p ). Per ottenere a lunga scadenza l estinzione della popolazione, e cioè una soluzione asintoticamente stabile, è essenziale far si che i valori propri del sistema siano entrambi negativi. Essi sono le soluzioni dell equazione caratteristica λ 2 + (m + )λ + (m np) = 0 basterà quindi supporre np < m. Siano U = (n, p, m ) e U2 = (n 2, p 2, m 2 ) due ambienti dove n p < m e n 2 p 2 < m 2, in entrambi i casi le condizioni poste implicano l estinzione della popolazione. E in ambiente variabile cosa succede? Se l ambiente commuta rapidamente tra i suoi estremi U e U2, cioè se i coefficienti n e m e
5 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 73 Figura 2
6 74 ANTONIO CARRIERO il parametro p assumono alternativamente i valori n, m, p e n 2, m 2, p 2, a quali condizioni è possibile evitare l estinzione della popolazione? Per facilitare le risposte a queste domande, in un primo tempo, ci limiteremo allo studio del sistema nel caso particolare definito dagli ambienti U = (0, p, m ) e U2 = (n 2, 0, m 2 ) I calcoli Il modello in ambiente costante U. { ẋ = x ẏ = p x m y Scegliendo un valore relativamente grande per il parametro p (p >.5) e uno sufficientemente piccolo per il coefficiente m (vedi più sotto), l ambiente U cosí caratterizzato, corrisponde ad una situazione di debole attività biologica. L equazione caratteristica del sistema diventa λ 2 + (m + )λ + m = 0 e i valori propri sono, m. Si ottiene cosí la soluzione: x = A (m ) e t y = A p e t + B p e mt dove le costanti sono determinate dalle condizioni iniziali C.I. x(0) = x 0 > 0, y(0) = 0. Tenendo conto di quest ultima relazione la soluzione diventa x = x 0 e t y = x 0 p m e t x 0 p m e mt e grazie alla semplicità della stessa possiamo scrivere l equazione della traiettoria Γ nella sua forma esplicita Γ : y(x) = p (x x m 0 x m ). m
7 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 75 Affinché la traiettoria sia a fiume-verticale (fig.3), la sua derivata deve tendere a + per x 0: dy lim x 0 dx = lim x 0 y (x) = + ossia lim x 0 p m ( m x m 0 x m ) = +, cioè se e solamente se m <. Analizziamo in modo più preciso la funzione y(x): partendo dal punto di coordinate (x 0, 0), nel quale la derivata della funzione è negativa e vale p, il valore della funzione aumenta sino a raggiungere il suo massimo nel punto di coordinate ( m x 0 m, p x 0 m m m per poi diminuire sempre più velocemente (il valore della sua derivata è positivo e sempre più grande) raggiungendo asintoticamente il valore 0. Per ogni scelta del valore iniziale di x 0 (> 0), il punto di massimo della traiettoria corrispondente si trova sulla retta ρ d equazione ρ : y = p m x che chiameremo 0-isocline dei massimi verticali. Riassumendo: Sia il punto P = ( x, ỹ) dove 0 < x e 0 < ỹ < p m x allora esiste un unico valore x 0 ed un unica traiettoria a fiume-verticale Γ d equazione ) y(x) = p (x x m 0 x m ) m
8 76 ANTONIO CARRIERO Figura 3. Traiettorie a fiume verticale passante da P tale che p < ẏ(x = x) < Il modello in ambiente costante U 2. { ẋ = x + n2 y ẏ = m 2 y Scegliendo valori relativamente grandi per i coefficienti n 2 e m 2 (vedi più sotto) possiamo associare all ambiente U 2 una situazione di forte attività biologica.
9 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 77 Analogamente al paragrafo precedente, la soluzione del sistema, poste le condizioni iniziali è data da C.I. x(0) = 0, y(0) = y 0 > 0. x = y 0 m 2 n 2 e t + y 0 m 2 n 2 e m2t y = y 0 e m2t anche in questo caso possiamo facilmente dedurre l equazione della traiettoria Γ 2 nella sua forma esplicita Γ 2 : x(y) = n 2 m 2 ( y y m 2 0 y m 2 ). Affinché la traiettoria sia a fiume-orizzontale (fig.5), la sua derivata deve tendere a + per y 0: dx lim y 0 dy = lim y 0 x (y) = + ossia lim y 0 n ( 2 m 2 m 2 y m 2 0 y m 2 ) = +, cioè se e solamente se m 2 >. Partendo dal punto di coordinate (0, y 0 ), nel quale ẋ(y = y 0 ) = n 2 m 2, il valore della funzione x(y) aumenta sino a raggiungere il suo massimo nel punto di coordinate ( m 2 m y 0 m 2 2, n 2 y 0 m m 2 m 2 2 per poi diminuire sempre più velocemente (il valore di ẋ(y) è positivo e sempre più grande) raggiungendo asintoticamente il valore 0. )
10 78 ANTONIO CARRIERO Come nella situazione precedente, per ogni scelta del valore iniziale di y 0, il punto di massimo della traiettoria Γ 2 corrispondente si trova sulla retta ρ 2 d equazione ρ 2 : x = n 2 y cioè y = n 2 x che chiameremo 0-isocline dei massimi orizzontali. Riassumendo: SAia il punto P = ( x, ỹ) dove 0 < x e x < ỹ n 2 allora esiste unico valore y 0 e un unica traiettoria Γ 2 d equazione x(y) = n ( 2 m 2 passante da P tale che y y m 2 ) 0 y m 2 n 2 m 2 < ẋ(y = ỹ) < Effetti della commutazione tra gli ambienti estremi U e U2. Occupiamoci del sistema non autonomo { ẋ(t) = x(t) + n(t) y(t) ẏ(t) = p(t) x(t) m(t) y(t) nel quale poniamo { 0 se t [2kT, (2k + )T [ n(t) = n 2 se t [(2k + )T, 2(k + )T [ { m se t [2kT, (2k + )T [ m(t) = m 2 se t [(2k + )T, 2(k + )T [ { p se t [2kT, (2k + )T [ p(t) = 0 se t [(2k + )T, 2(k + )T [ con k = 0,, 2,... e dove T è il semi-periodo di commutazione. Se la frequenza di commutazione ν (ν = /T ), è sufficientemente grande, la traiettoria risultante si situa unicamente negli affluenti dei due fiumi.
11 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 79 Figura 4. Traiettorie a fiume verticale
12 80 ANTONIO CARRIERO Sia P = ( x, ỹ) un punto nel piano di fase dove x < ỹ < p x n 2 m P si trova tra la 0-isocline dei massimi verticali e la 0-isocline dei massimi orizzontali, cioè tra il fiume verticale generato dal sistema in ambiente costante U e quello orizzontale generato dal sistema in ambiente costante U2. Inoltre, da P passa un unica traiettoria Γ ed un unica traiettoria Γ 2 (cf e 4.2.2). Se in P voglio cambiare affluente, passando da uno verticale ad un orizzontale o viceversa, e in tale modo assicurarmi che la direzione del movimento risultante sia diversa da quella dei fiumi corrispondenti ai sistemi in ambiente costante, allora la seguente condizione (fig. 5) deve essere soddisfatta: dy dx (Γ, x = x) < dy dx (Γ 2, x = x) = semplificandone la forma essa diventa: y ( x) < x (ỹ). dx dy (Γ 2, y = ỹ) Quindi in ogni punto P = (x, y) nel quale voglio cambiare affluente, la condizione è data da: y (x) < x (y). cioè ( y )( p + m n 2 + x m 2 x ) m 2 y x 2 + m n 2 y 2 + m 2 p n 2 m xy p p }{{ } > < 0
13 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 8 Figura 5 è della forma (x + ay)(x + by), con a,b R, soluzioni del sistema d equazioni: ab = m n 2 p a + b = m 2 p n 2 m p. Tenendo conto di tutte le condizioni poste, (4.3) è verificata se e solamente se x + a y < 0 dove x + b y > 0 a = m 2 p n 2 m (m 2 p n 2 m ) 2 4p m n 2 2 p b = m 2 p n 2 m + (m 2 p n 2 m ) 2 4p m n 2 2 p
14 82 ANTONIO CARRIERO Figura 6 con (m 2 p n 2 m ) < 4p m n 2. Quindi se vogliamo che l evoluzione del sistema biologico studiato, generata dalla commutazione periodica della funzione U(t) tra i valori estremi U e U2, sia diversa da quella dei fiumi caratterizzanti gli ambienti estremi, allora il passaggio da un affluente all altro deve avvenire in un punto P = (x, y) del piano di fase, le cui componenti soddisfano la relazione (fig. 6) a x < y < b x. Questo modello rappresenta la situazione paradossale di due ambienti entrambi sfavorevoli a lungo termine (estinzione della popolazione), ma che in successione sufficientemente rapida diventano favorevoli
15 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 83 (crescita della popolazione). La figura 7 è una simulazione numerica di questa situazione paradossale Generalizzazione dei risultati ottenuti nel caso fiume verticale-fiume orizzontale. Consideriamo ora gli ambienti estremi U = (n, p, m ) e U2 = (n 2, p 2, m 2 ), dove n p < m e n 2 p 2 < m 2. Contrariamente alla situazione precedente (verticale- orizzontale), non è possibile esprimere esplicitamente le equazioni delle traiettorie Γ e Γ 2, ciononostante le derivate corrispondenti sono facilmente calcolabili: y (x, Γ ) = dy dx = p x m y x + n y x (y, Γ 2 ) = dx dy = x + n 2 y p 2 x m 2 y. Le traiettorie Γ e Γ 2, hanno i loro massimi sulle rette ρ, rispettivamente ρ 2 d equazione ρ : y = p m x ρ 2 : x = n 2 y cioè y = n 2 x. Tralasciando i calcoli, ecco le equazioni dei fiumi f e f 2 relativi alle traiettorie Γ rispettivamente Γ 2 : 2p f : y = (m ) + x (m ) 2 + 4n p f 2 : y = ( m 2) + ( m 2 ) 2 + 4n 2 p 2 x 2n 2 I ruoli degli ambienti estremi sono interscambiabili; possiamo quindi limitarci allo studio del caso in cui la pendenza del fiume corrispondente all ambiente costante U, è maggiore di quella del fiume corrispondente all ambiente costante U 2, ovvero
16 84 ANTONIO CARRIERO Figura 7
17 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 85 2p (m ) + (m ) 2 + 4n p > p m > > n 2 > ( m 2) + ( m 2 ) 2 + 4n 2 p 2 2n 2 Sia P = ( x, ỹ) un punto del piano di fase, dove x < ỹ < p x n 2 m cioè un punto appartenente al semi-cono positivo generato dalle 0- isocline dei massimi delle due traiettorie, allora y ( x, Γ ) < 0 e x (ỹ, Γ 2 ) < 0 cioè y ( x, Γ 2 ) = x (ỹ, Γ 2 ) < 0. Le situazioni possibili (fig.8) sono due:. y ( x, Γ ) < y ( x, Γ 2 ) 2. y ( x, Γ 2 ) < y ( x, Γ ) Se in P vogliamo passare da un affluente d ambiente U, a uno d ambiente U2 o viceversa, e in tal modo far si che la direzione d evoluzione del sistema biologico sia differente da quella corrispondente agli ambienti estremi (estinzione della popolazione), allora la seconda situazione è da escludere. Quindi in ogni punto P = (x, y) (appartenente al semi-cono positivo generato dalle 0-isocline dei massimi delle due traiettorie) nel quale avviene il passaggio da un affluente all altro la seguente condizione deve essere soddisfatta cioè p x m y x + n y < p 2 x m 2 y x + n 2 y che diventa y (x, Γ ) < y (x, Γ 2 ) (p p 2 ) x 2 + (p 2 n + m 2 m p n 2 ) xy + (m n 2 m 2 n ) y 2 < 0 dunque
18 86 ANTONIO CARRIERO Figura 8
19 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 87 se p p 2 > 0 la condizione diventa x 2 + p 2 n + m 2 m p n 2 xy + m n 2 m 2 n y 2 < 0 p p 2 p p }{{ 2 } è della forma (x+c y)(x+c 2 y), con c,c 2 R, soluzioni del sistema d equazioni: c c 2 = m n 2 m 2 n p p 2 c + c 2 = p 2 n + m 2 m p n 2 p p 2. Assumendo tutte le condizioni poste, (4.4) è verificata se e solamente se x + c y < 0 dove x + c 2 y > 0 p 2 n + m 2 m p n 2 < 4(p p 2 )(m n 2 m 2 n ). Osservazione: < n 2 c < c 2 < p m se p p 2 < 0 la condizione diventa x 2 + p 2 n + m 2 m p n 2 xy + m n 2 m 2 n y 2 > 0 p p 2 p p }{{ 2 } è della forma (x + d y)(x + d 2 y),dove d,d 2 R sono le radici dell equazione: d 2 p 2 n + m 2 m p n 2 p p 2 d + m n 2 m 2 n p p 2 = 0. La condizione (4.4) è verificata se n 2 x < y < d 2 x oppure se d x < y < p m x
20 88 ANTONIO CARRIERO dove p 2 n + m 2 m p n 2 > 4(p p 2 )(m n 2 m 2 n ). Osservazione: se p p 2 = 0 la condizione diventa < n 2 d < d 2 < p m (p 2 n + m 2 m p n 2 ) xy + (m n 2 m 2 n ) y 2 < 0 ovvero y < m m 2 p (n n 2 ) m n 2 m 2 n x, se m n 2 m 2 n > 0 y > m m 2 p (n n 2 ) m n 2 m 2 n x, se m n 2 m 2 n < 0. La condizione (4.4) è dunque verificata se dove x < y < m m 2 p (n n 2 ) x n 2 m n 2 m 2 n m n 2 m 2 n > 0 m m 2 n n 2 < p oppure se dove < m m 2 p (n n 2 ) n 2 m n 2 m 2 n m m 2 p (n n 2 ) m n 2 m 2 n x < y < p m x m n 2 m 2 n < 0 m m 2 > p n n 2 m m 2 p (n n 2 ) < p m n 2 m 2 n m
21 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 89 Riassumendo: Relativamente ai parametri caratterizzanti il sistema, la condizione (4.4) delimita un semi-cono positivo del piano di fase compreso tra le 0-isocline dei massimi corrispondenti ai sistemi in ambiente costante (U e U 2). Se vogliamo sconvolgere l evoluzione della popolazione studiata, cioè se vogliamo che il comportamento in ambiente variabile sia diverso da quello in ambiente costante, allora dobbiamo assicurarci che la traiettoria relativa al sistema in ambiente variabile resti all interno del semi-cono positivo, una volta penetrata in esso. Il presunto paradosso, cioè la sopravvivenza, è cosí conseguenza diretta delle periodiche variazioni dei parametri ambientali; variazioni che sono causate dalle fluttuazioni delle risorse limitanti Il problema della frequenza di commutazione. Occupiamoci inizialmente del sistema in ambiente variabile tra gli estremi verticale ed orizzontale. Nella sezione abbiamo stabilito in un primo tempo la condizione sufficiente (4.3), grazie alla quale, se l ambiente varia rapidamente tra i suoi estremi, la popolazione non si estingue. Successivamente abbiamo visto che la regione del piano di fase nella quale la condizione (4.3) è soddisfatta, corrisponde al semi-cono positivo delimitato dalle rette d equazione y = a x e y = b x È bene, a questo punto, chiarire il significato di variazione periodica e rapida. Ovvero, a partire dall istante nel quale la traiettoria del sistema in ambiente variabile entra nel semi-cono, quale frequenza di commutazione della funzione U(t) ci assicura che essa non ne esce, cioè che la condizione (4.3) è sempre soddisfatta? Rispondiamo alla domanda. Sia P 0 = (x 0, y 0 ) un punto del piano di fase dove x 0 > 0 e y 0 = a x 0
22 90 ANTONIO CARRIERO e sia x(t) = x 0 e t ( y 0 + x 0 p m ) e mt x 0 p y(t) = m e t + l equazione parametrica dell unica traiettoria a fiume verticale Γ 0 passante da P 0. La traiettoria Γ 0 incontra la retta d equazione y = b x nel punto P = (x, y ). Un veloce calcolo ci permette di stabilire il tempo (t 0 ) necessario per raggiungere P partendo da P 0 seguendo l affluente Γ 0 : Sia adesso { x(t) = t 0 = y(t) = y e m2t log a ( m + p b ) m b ( m + p a ). ( x + y m 2 n 2 ) e t + y m 2 n 2 e m2t l equazione parametrica dell unica traiettoria a fiume orizzontale Γ 2 2 passante da P ; essa incontra la retta d equazione y = x nel punto a P 2 = (x 2, y 2 ). Calcoliamo anche in questo caso il tempo (t 2 ) necessario per raggiungere P 2 partendo da P seguendo l affluente Γ 2 t 2 = m 2 log a (m 2 ) + n 2 b (m 2 ) + n 2. 2 : Osservazioni:. t 0 e t 2 > 0 ; 2. t 0 e t 2 dipendono unicamente dai parametri p, m, n 2, m 2, cioè non dipendono dalle coordinate dei punti P 0, P e P 2 ; Quindi t 0 e t 2 sono i tempi necessari per andare da un bordo all altro del semi-cono positivo, seguendo alternativamente un affluente del fiume verticale e uno di quello orizzontale.
23 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 9 Figura 9 Consideriamo allora il semi-cono positivo (fig. 9) generato dalle rette r α e r β d equazione r α : y = α x e r β : y = β x, α > β > 0 dove b β > α a. Senza esplicitarne i calcoli, ecco i tempi necessari per andare da un estremo all altro del nuovo semi-cono (incluso nel precedente), sempre seguendo alternativamente un affluente del fiume verticale ed uno di
24 92 ANTONIO CARRIERO quello orizzontale: T 0 = T 2 = log α ( m + p β) m β ( m + p α) m 2 log α (m 2 ) + n 2. β (m 2 ) + n 2 Chiaramente i valori di T 0 e T 2 non dipendono dalla scelta degli affluenti; in altre parole, il tempo necessario per andare da un punto sulla retta r α (risp. r β ) alla retta r β (risp. r α ) seguendo un affluente verticale (risp. orizzontale) non dipende dalla scelta del punto di partenza. Concludendo, siano α, β R + tali che a α > β b allora la condizione (4.3) è sicuramente soddisfatta, se i punti nei quali la traiettoria del sistema in ambiente variabile cambia direzione passando da un affluente verticale ad uno orizzontale e viceversa, si trovano sulle rette r α rispettivamente r β. Abbiamo finalmente stabilito tutti i parametri che ci permettono di controllare e dirigere l evoluzione della popolazione. Consideriamo quindi il seguente sistema in ambiente variabile: { ẋ(t) = x(t) + n(t) y(t) ẏ(t) = p(t) x(t) m(t) y(t) nel quale poniamo { 0 se t [k(t0 + T n(t) = 2 ), (k + )T 0 + kt 2 [ n 2 se t [(k + )T 0 + kt 2, (k + )(T 0 + T 2 )[ { m se t [k(t m(t) = 0 + T 2 ), (k + )T 0 + kt 2 [ m 2 se t [(k + )T 0 + kt 2, (k + )(T 0 + T 2 )[ { p se t [k(t p(t) = 0 + T 2 ), (k + )T 0 + kt 2 [ 0 se t [(k + )T 0 + kt 2, (k + )(T 0 + T 2 )[ con k = 0,, 2,... le cui condizioni iniziali sono: x(0) = x 0 > 0, y(0) = α x 0. Imponendo i cambiamenti d affluente sulle rette r α e r β, ovvero, costringendo la traiettoria del sistema all interno del semi-cono da esse generato, provochiamo l esplosione demografica della popolazione modellizzata.
25 VARIAZIONI AMBIENTALI ED EFFETTI PARADOSSALI 93 Osservazione: I valori T 0 e T 2 rappresentano le durate rispettive del giorno e della notte. In ambiente variabile tra estremi qualsiasi (cf. sezione 4.3), abbiamo stabilito che, relativamente ai parametri caratterizzanti U e U2, la condizione di crescita della popolazione (4.4) delimita uno o più semi-coni positivi nel piano di fase. Se vogliamo determinare la frequenza di commutazione della funzione U(t), affinché la traiettoria del sistema sia costretta all interno del semi-cono corrispondente ai parametri in gioco, allora basterà applicare le operazioni di calcolo che abbiamo sviluppato nel caso verticale-orizzontale alla specifica situazione. 5. Conclusioni Abbiamo esposto e sviluppato un metodo analiticogeometrico semplice, che ci permette di studiare l effetto che hanno le fluttuazioni ambientali sull evoluzione di una popolazione. Applicando questo metodo all esempio particolare di una popolazione strutturata in due stadi evolutivi: larve e adulti, la cui evoluzione è modellizzata da un sistema lineare d equazioni differenziali, abbiamo messo in evidenza la situazione paradossale seguente: il rapido alternarsi di due ambienti, entrambi sfavorevoli alla crescita della popolazione, favorisce la crescita della popolazione studiata! Questo stesso metodo può essere applicato ad altri sistemi d equazioni differenziali rappresentanti la dinamica di una o più popolazioni; ad esempio al modello di concorrenza tra specie (Lotka-Volterra): l alternanza ambientale tra due estremi sfavorevoli ad una specie, permette di modificare il risultato della competizione a favore della specie minacciata d estinzione negli ambienti estremi. Questo studio è semplice ed efficace nel caso di sistemi d equazioni differenziali di dimensione due, in effetti di fronte a sistemi di dimensione superiore siamo limitati dall impossibilità di rappresentare geometricamente le condizioni di crescita della popolazione studiata. Infine è necessario studiare la stabilità del metodo proposto, ovvero la robustezza degli effetti delle fluttuazioni ambientali, ad ulteriori perturbazioni del modello.
26 94 ANTONIO CARRIERO Riferimenti bibliografici [] Lobry C., Sciandra A., Nival P. (993), Effets paradoxaux des fluctuations de l environnement sur la croissance des populations et la compétition entre espèces. di prossima pubblicazione [2] Brunovsky P., Lobry C. (975), Contrôlabilité Bang-Bang, Contrôlabilité différentiable et perturbation des systèmes non linéaires. Annali di matematica Pura ed Applicata (IV), Vol CV [3] Sommer U. (983), Nutrient competition between phytoplancton species in multispecies chemostat experiments. Arch. Hydrobiol 96(4) [4] Sommer U. (984), The paradox of the plancton: Fluctuations of phosphorus availability maintain diversity of phytoplancton in flow-through cultures. Limnol. Oceanogr. 29(3) [5] Sommer U. (985), Comparaison between steady state and non-steady state competition: Experiments with natural phytoplancton. Limnol. Oceanogr. 30(2) [6] Grover J.P. (990), Resource competition in a variable environment: phytoplancton growing according to Monod s model. The American Naturalist 36(6) [7] Grover J.P. (99), Resource competition in a variable environment: phytoplancton growing according to variable-internal-store model. The American Naturalist 38(4) [8] Grover J.P. (99), Non-steady state dynamics of algal population growth: Experiments with two cholrophytes J. Phycol Antonio Carriero, École Polytechnique Fédérale, Département de mathématiques, CH-05 Lausanne
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori.
 ËÁËÌ ÅÁ ÈÁ ÆÁ ½ Queste note attualmente e probabilmente per un bel po ) sono altamente provvisorie e molto probabilmente) non prive di errori 41 Sistemi 2D Come abbiamo già detto tipicamente è impossibile
ËÁËÌ ÅÁ ÈÁ ÆÁ ½ Queste note attualmente e probabilmente per un bel po ) sono altamente provvisorie e molto probabilmente) non prive di errori 41 Sistemi 2D Come abbiamo già detto tipicamente è impossibile
Il modello preda predatore. Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita:
 Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Modelli Matematici Ambientali, 2015/16 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Note sul sistema di Lotka-Volterra. Prima versione. Commenti e correzioni sono benvenuti.
 Ottobre 2016 Note sul sistema di Lotka-Volterra Prima versione. Commenti e correzioni sono benvenuti. 1 Introduzione Il sistema di Lotka Volterra (LV), o sistema preda predatore è probabilmente il primo
Ottobre 2016 Note sul sistema di Lotka-Volterra Prima versione. Commenti e correzioni sono benvenuti. 1 Introduzione Il sistema di Lotka Volterra (LV), o sistema preda predatore è probabilmente il primo
Il modello preda predatore. Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popo
 Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
Modellistica Ambientale, 2013/14 Dinamiche di Crescita: 2 popolazioni Il modello preda predatore Interazione di due popolazioni: il modello Preda-Predatore Il modello Preda-Predatore è stato sviluppato
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
Esercizi di modellistica, linearizzazione, punti di equilibrio e calcolo funzione di trasferimento
 Esercizi di modellistica, linearizzazione, punti di equilibrio e calcolo funzione di trasferimento Esercizio Si considerino 3 popolazioni P, P, P 3 che vivono nelle regioni A, B, C le cui numerosità sono
Esercizi di modellistica, linearizzazione, punti di equilibrio e calcolo funzione di trasferimento Esercizio Si considerino 3 popolazioni P, P, P 3 che vivono nelle regioni A, B, C le cui numerosità sono
1.1 Sistemi dinamici monodimensionali
 ½ ½½º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 1.1 Sistemi dinamici monodimensionali Esercizio 1.1: Consideriamo
½ ½½º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 1.1 Sistemi dinamici monodimensionali Esercizio 1.1: Consideriamo
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Matematica con elementi di Informatica
 Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Modelli discreti di due popolazioni
 Capitolo 7 Modelli discreti di due popolazioni Analogo del caso di un sistema di equazioni differenziali è un sistema di più successioni. Tale sistema descrive un sistema ecologico di due o più popolazioni
Capitolo 7 Modelli discreti di due popolazioni Analogo del caso di un sistema di equazioni differenziali è un sistema di più successioni. Tale sistema descrive un sistema ecologico di due o più popolazioni
Geometria analitica del piano pag 12 Adolfo Scimone
 Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
di 4, che è l area dell intera mattonella, imponiamo che 5 e quindi a = 7 5
 Problemi Problema 1) 1) Siccome la funzione f(x) è una retta, l espressione cercata è f(x) = 1 x che soddisfa le condizioni a), b) e c) richieste. Per riflessione rispetto all asse y, all asse x e all
Problemi Problema 1) 1) Siccome la funzione f(x) è una retta, l espressione cercata è f(x) = 1 x che soddisfa le condizioni a), b) e c) richieste. Per riflessione rispetto all asse y, all asse x e all
Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali
 Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali Argomenti trattati Introduzione ai modelli Equazioni differenziali del primo ordine Metodi risolutivi:integrazione diretta
Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali Argomenti trattati Introduzione ai modelli Equazioni differenziali del primo ordine Metodi risolutivi:integrazione diretta
Sistemi differenziali ordinari. Davide Manca Calcoli di Processo dell Ingegneria Chimica Politecnico di Milano
 E8 Sistemi differenziali ordinari E8 Costruzione di un modello E8. Il sistema Predatore-Preda Si desidera studiare l evoluzione dinamica di un ecosistema costituito da due specie: preda e predatore (ad
E8 Sistemi differenziali ordinari E8 Costruzione di un modello E8. Il sistema Predatore-Preda Si desidera studiare l evoluzione dinamica di un ecosistema costituito da due specie: preda e predatore (ad
GRAFICA E COMPUTER. 19 giugno () PLS-Grafica 19 giugno / 32
 GRAFICA E COMPUTER 19 giugno 2013 3 2 1 0 1 2 3 3 2 1 0 1 2 3 () PLS-Grafica 19 giugno 2013 1 / 32 Equazioni differenziali modellizzano fenomeni (fisici e non) che variano nel tempo partendo da dati noti,
GRAFICA E COMPUTER 19 giugno 2013 3 2 1 0 1 2 3 3 2 1 0 1 2 3 () PLS-Grafica 19 giugno 2013 1 / 32 Equazioni differenziali modellizzano fenomeni (fisici e non) che variano nel tempo partendo da dati noti,
x + b! y + c! Osservazione: poiché ci sono infiniti piani ai quali appartiene una retta r, le equazioni non sono univocamente determinate.
 4 La retta in R 3 4 Le equazioni cartesiane di una retta Dati due piani Γ :ax +by +cz +d = 0 e Γ!: a! x + b! y + c! z + d! = 0 non paralleli tra loro, il luogo geometrico dei punti di intersezione tra
4 La retta in R 3 4 Le equazioni cartesiane di una retta Dati due piani Γ :ax +by +cz +d = 0 e Γ!: a! x + b! y + c! z + d! = 0 non paralleli tra loro, il luogo geometrico dei punti di intersezione tra
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
3.1 Esempio 1. Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori.
 ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori 31 Esempio 1 Consideriamo il sistema ẋ = 1 3 (x y(1 x y = f 1(xy ẏ
½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori 31 Esempio 1 Consideriamo il sistema ẋ = 1 3 (x y(1 x y = f 1(xy ẏ
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo compito in itinere 3 Febbraio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004
 Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
Risoluzione del compito n. 5 (Luglio 2018/2)
 Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
Elementi di matematica - dott. I. GRASSI
 Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017
 Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = x 2 + y 3 4y. 4 1, y 2 2(1 + }
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento
 Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Francesco Zumbo
 La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del ẋ = y y 2 + 2x
 Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Es. 1 Es. 2 Es. 3 Es. 4 Totale. Cognome: Nome: Matricola: Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es Es Es Es Totale Analisi e Geometria Secondo compito in itinere 0 Gennaio 0 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es: 8 punti;
Es Es Es Es Totale Analisi e Geometria Secondo compito in itinere 0 Gennaio 0 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es: 8 punti;
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Compito A Corso del Prof.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
Prova scritta del 18/12/2008, tema A
 1 È Data la funzione: fx) e x x 3x + 3) Prova scritta del 18/1/8, tema A Determinarne: a) dominio, limiti significativi, asintoti; b) derivata prima, crescenza, punti di massimo e di minimo; c) derivata
1 È Data la funzione: fx) e x x 3x + 3) Prova scritta del 18/1/8, tema A Determinarne: a) dominio, limiti significativi, asintoti; b) derivata prima, crescenza, punti di massimo e di minimo; c) derivata
4.1 Sulla linearizzazione attorno agli equilibri
 ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori 41 Sulla linearizzazione attorno agli equilibri Come abbiamo già
½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori 41 Sulla linearizzazione attorno agli equilibri Come abbiamo già
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Sistemi di riferimento in moto relativo
 Capitolo 2 Sistemi di riferimento in moto relativo Consideriamo due sistemi di riferimento = Oê 1 ê 2 ê 3 = O ê 1ê 2ê 3 nello spazio euclideo E 3. Le terne di vettori {ê 1,ê 2,ê 3 } e {ê 1,ê 2,ê 3 } dei
Capitolo 2 Sistemi di riferimento in moto relativo Consideriamo due sistemi di riferimento = Oê 1 ê 2 ê 3 = O ê 1ê 2ê 3 nello spazio euclideo E 3. Le terne di vettori {ê 1,ê 2,ê 3 } e {ê 1,ê 2,ê 3 } dei
k 2 m 1 u 2 Figura 1 z 1 β m 1 ż 1 + β m 1 ż m 2 z 2 β m 2 ẋ = A x + B u y = C x + D u
 Esercizio Si consideri il sistema meccanico riportato in Figura, dove m e m sono le masse dei carrelli, z e z sono le rispettive posizioni, k e k sono i coefficienti elastici delle molle, e β è un coefficiente
Esercizio Si consideri il sistema meccanico riportato in Figura, dove m e m sono le masse dei carrelli, z e z sono le rispettive posizioni, k e k sono i coefficienti elastici delle molle, e β è un coefficiente
LICEO SCIENTIFICO PROBLEMA 2
 www.matefilia.it LICEO SCIENTIFICO 2018 - PROBLEMA 2 Consideriamo f k (x): R R così definita: f k (x) = x + kx + 9, con k Z 1) Detto Γ k il grafico della funzione, verifica che per qualsiasi valore del
www.matefilia.it LICEO SCIENTIFICO 2018 - PROBLEMA 2 Consideriamo f k (x): R R così definita: f k (x) = x + kx + 9, con k Z 1) Detto Γ k il grafico della funzione, verifica che per qualsiasi valore del
Matematica Lezione 5
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 5 Sonia Cannas 23/10/2018 Relazioni Dati due insiemi A e B molto spesso capita di definire una relazione (o legge) fra essi. Sia A
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 5 Sonia Cannas 23/10/2018 Relazioni Dati due insiemi A e B molto spesso capita di definire una relazione (o legge) fra essi. Sia A
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI. Lezione XI: Stabilità interna
 ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Rette e piani: eq. parametriche di rette
 In A 3 (R) fissiamo un riferimento affine [O, B], con B = ( e 1, e 2, e 3 ). Assi coordinati: asse delle ascisse: [O, < e 1 >], asse delle ordinate: [O, < e 2 >], asse delle quote: [O, < e 3 >]. Piani
In A 3 (R) fissiamo un riferimento affine [O, B], con B = ( e 1, e 2, e 3 ). Assi coordinati: asse delle ascisse: [O, < e 1 >], asse delle ordinate: [O, < e 2 >], asse delle quote: [O, < e 3 >]. Piani
Soluzioni dei problemi della maturità scientifica A.S. 2012/2013
 Soluzioni dei problemi della maturità scientifica A.S. / Nicola Gigli Sun-Ra Mosconi June, Problema. Il teorema fondamentale del calcolo integrale garantisce che Quindi f (x) = cos x +. f (π) = cos π +
Soluzioni dei problemi della maturità scientifica A.S. / Nicola Gigli Sun-Ra Mosconi June, Problema. Il teorema fondamentale del calcolo integrale garantisce che Quindi f (x) = cos x +. f (π) = cos π +
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 30 agosto 2011 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) agosto Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio di una pagina.
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI. m(x, y, z) = (2x 2 + y 2 )e x2 y 2, f(x, y) = (y x 2 )(y x2. f(x, y) = x 3 + (x y) 2,
 ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
Per rispondere al primo quesito è necessario avere una stima de volume della stanza, la cui base è la regione rappresentata in figura 1
 Problema1 Suppletiva 2016 Soluzione 1. Per rispondere al primo quesito è necessario avere una stima de volume della stanza, la cui base è la regione rappresentata in figura 1 La regione ha un contorno
Problema1 Suppletiva 2016 Soluzione 1. Per rispondere al primo quesito è necessario avere una stima de volume della stanza, la cui base è la regione rappresentata in figura 1 La regione ha un contorno
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali.
 Sistemi dinamici In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali. Le equazioni differenziali sono delle equazioni in cui le incognite rispetto
Sistemi dinamici In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali. Le equazioni differenziali sono delle equazioni in cui le incognite rispetto
LIMITI E DERIVATE DI UNA FUNZIONE
 LIMITI E DERIVATE DI UNA FUNZIONE INTRODUZIONE In generale, abbiamo un idea chiara del significato di pendenza quando viene utilizzata in contesti concernenti l esperienza quotidiana, ad esempio quando
LIMITI E DERIVATE DI UNA FUNZIONE INTRODUZIONE In generale, abbiamo un idea chiara del significato di pendenza quando viene utilizzata in contesti concernenti l esperienza quotidiana, ad esempio quando
S.Barbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie. Cap. 2. Cinematica del punto
 SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
1 Equazioni Differenziali
 Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Matematica e Statistica
 Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo Appello 8 Settembre 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Matematica - Prova d esame (09/09/2004)
 Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
F x 1 = x 1 + x 2. 2x 1 x 2 Determinare la matrice C associata a F rispetto alla base canonica (equivalentemente,
 Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Matematica e Statistica
 Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
Metodi di Iterazione Funzionale
 Appunti di Matematica Computazionale Lezione Metodi di Iterazione Funzionale Il problema di calcolare il valore per cui F() = si può sempre trasformare in quello di trovare il punto fisso di una funzione
Appunti di Matematica Computazionale Lezione Metodi di Iterazione Funzionale Il problema di calcolare il valore per cui F() = si può sempre trasformare in quello di trovare il punto fisso di una funzione
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7
![0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7 0 < x 3. A1 1 [7 punti] Determinare le eventuali soluzioni del seguente sistema di congruenze: x 2 mod 5 2x 1 mod 3. x 21 mod 7](/thumbs/96/126857371.jpg) Dipartimento di Matematica e Informatica Anno Accademico 017-018 Corso di Laurea in Informatica L-31 Prova scritta di Matematica Discreta 1 CFU 5 Settembre 018 A1 1 [7 punti] Determinare le eventuali soluzioni
Dipartimento di Matematica e Informatica Anno Accademico 017-018 Corso di Laurea in Informatica L-31 Prova scritta di Matematica Discreta 1 CFU 5 Settembre 018 A1 1 [7 punti] Determinare le eventuali soluzioni
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e strofisica Foglio 5 - Soluzioni Esercizio 1. Nello spazio R 3, si considerino i punti (1,0,0), (1,0,2), (0, 1,0), D (2, 1,2), E (2,1, 0), F (0, 1,2), G (3,2,0),
Esercizi di geometria per Fisica / Fisica e strofisica Foglio 5 - Soluzioni Esercizio 1. Nello spazio R 3, si considerino i punti (1,0,0), (1,0,2), (0, 1,0), D (2, 1,2), E (2,1, 0), F (0, 1,2), G (3,2,0),
1.9 Massimi e minimi vincolati
 .9 Massimi e minimi vincolati Sia K un compatto di R N e sia f : K R una funzione continua. Per il teorema di Weierstrass, f assume massimo e minimo su K. Come determinarli? Se K ha punti interni e f è
.9 Massimi e minimi vincolati Sia K un compatto di R N e sia f : K R una funzione continua. Per il teorema di Weierstrass, f assume massimo e minimo su K. Come determinarli? Se K ha punti interni e f è
LEZIONE 9. Figura 9.1.1
 LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
Istituzioni ed Esercitazioni di Matematica 2
 Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Istituzioni ed Esercitazioni di Matematica 2 01 Marzo 2017 Schema Prima Lezione Outline Cosa è un
Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Istituzioni ed Esercitazioni di Matematica 2 01 Marzo 2017 Schema Prima Lezione Outline Cosa è un
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
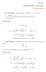 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati:
 ANALISI Soluzione esercizi 2 gennaio 212 12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati: (x, y) R 2 : x < y} (x, y) R 2 : 2 x 3} (x, y) R 2 : x 2 +
ANALISI Soluzione esercizi 2 gennaio 212 12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati: (x, y) R 2 : x < y} (x, y) R 2 : 2 x 3} (x, y) R 2 : x 2 +
SOLUZIONI COMPITO A. 3. Imponendo la condizione iniziale y(0) = 1 e, si ricava C = 0, quindi la soluzione cercata sarà. y(x) + 1 = exp(e x x2 2 1)
 SOLUZIONI COMPITO A Esercizio Utilizzando lo sviluppo di Mc Laurin al terzo ordine per il sin t, con t = x 4/, e quello al primo ordine per il log( + t), con t = x, otteniamo e quindi il ite proposto diviene
SOLUZIONI COMPITO A Esercizio Utilizzando lo sviluppo di Mc Laurin al terzo ordine per il sin t, con t = x 4/, e quello al primo ordine per il log( + t), con t = x, otteniamo e quindi il ite proposto diviene
a.a Geometria 2. Esercizi 9. Interpolazione. Curve composte. 1/2, b 3, b = 1
 aa - Geometria Esercizi 9 Interpolazione Curve composte Siano dati i punti del piano b i Determinare una curva di grado che passa per tali punti per t / / ii Quante ce ne sono? iii Col metodo dei minimi
aa - Geometria Esercizi 9 Interpolazione Curve composte Siano dati i punti del piano b i Determinare una curva di grado che passa per tali punti per t / / ii Quante ce ne sono? iii Col metodo dei minimi
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Analisi e Geometria 1 - primo Appello - 16 Febbraio 2016 Terza parte (Compito A)
 Politecnico di Milano, Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 - primo Appello - 16 Febbraio 016 Terza parte (Compito A Verificare che l equazione z 3 (1 iz +i + ] (
Politecnico di Milano, Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 - primo Appello - 16 Febbraio 016 Terza parte (Compito A Verificare che l equazione z 3 (1 iz +i + ] (
I sistemi di Lotka-Volterra.
 I sistemi di Lotka-Volterra. Il modello considerato nella sezione precedente può essere facilmente modificato per includere la competizione o l interazione fra due o più specie di individui. Consideriamo
I sistemi di Lotka-Volterra. Il modello considerato nella sezione precedente può essere facilmente modificato per includere la competizione o l interazione fra due o più specie di individui. Consideriamo
La retta nel piano. Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione.
 La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA
 ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 6-7 Settimana : Equazioni Differenziali Esempio. L esempio più familiare di equazione differenziale proviene dalla legge di Newton. Se t y(t)
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 6-7 Settimana : Equazioni Differenziali Esempio. L esempio più familiare di equazione differenziale proviene dalla legge di Newton. Se t y(t)
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Proprietà strutturali e leggi di controllo
 Proprietà strutturali e leggi di controllo Retroazione statica dallo stato La legge di controllo Esempi di calcolo di leggi di controllo Il problema della regolazione 2 Retroazione statica dallo stato
Proprietà strutturali e leggi di controllo Retroazione statica dallo stato La legge di controllo Esempi di calcolo di leggi di controllo Il problema della regolazione 2 Retroazione statica dallo stato
Esercizi geometria analitica nel piano. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
4. Sia Γ la conica che ha fuoco F (1, 1) e direttrice d : x y = 0, e che passa per il punto P (2, 1).
 Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Seconda prova in itinere 31 gennaio 2011
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Matematica Lezione 22
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 22 Sonia Cannas 14/12/2018 Indici di posizione Indici di posizione Gli indici di posizione, detti anche misure di tendenza centrale,
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 22 Sonia Cannas 14/12/2018 Indici di posizione Indici di posizione Gli indici di posizione, detti anche misure di tendenza centrale,
Analisi Matematica 2. Ottimizzazione in due variabili. Ottimizzazione in due variabili 1 / 31
 Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
1 Note ed esercizi risolti a ricevimento
 1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
Equazioni differenziali
 Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercitazione 04: Sistemi a tempo discreto
 18 marzo 2019 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state scritte e redatte dal Prof. Alessandro Papadopoulos, Mälardalen University
18 marzo 2019 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state scritte e redatte dal Prof. Alessandro Papadopoulos, Mälardalen University
2) Scrivere la soluzione generale del seguente sistema di equazioni differenziali lineari del primo ordine. y 1 = 2y 1 5y 3 y 2
 Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
