Cambi di variabile. 1 2 y ; x 2 + y 2, (x,y) :x 2 + y 2 1, (x 1) 2 + (y 1) ; y x su {(x,y) : x 2 + y 2 4, 1 x}.
|
|
|
- Dorotea Gennara Perrone
- 4 anni fa
- Visualizzazioni
Transcript
1 Analisi Matematica II, Anno Accademico Ingegneria Edile ed Architettura Vincenzo M. Tortorelli FOGLIO DI EERCIZI n. CAMBI DI VARIABILE NEGLI INTEGRALI: CALCOLO DI INTEGRALI IN COORDINATE CURVILINEE INTEGRALI U UPERFICE, OMMABILITÀ Gli esercizi contrassegnati con sono piú impegnativi Cambi di variabile Esercizio Calcolare le misure degli insiemi e gli integrali delle funzioni: f(x,y) = x y su (x,y) : x + y, 0 y } ; f(x,y,z) = x sul dominio definito da x + y + z ; f(x,y) = + (3x + y + 5), su (x,y) : x + y 3 }; (x,y) R : xy, y x y } ; f(x,y) = x su (x,y) : 4(x 3) + 3(y ) 4 } ; f(x,y) = 4x y, sul paralleogramma di vertici (±, 0), (0, ±); f(x,y,z) = (x ) z su (x,y,z) : x + y 4, z 3}; f(x,y) = y x su (x,y) : x y x }; f(x,y,z) = z sull intersezione della palla unitaria di centro l origine con il cono retto di vertice l origine, apertura π, e asse x = y = 0; 6 f(x,y) = x + y, [0; ] [0; ]; (x,y) :x + y, (x ) + (y ) (x,y) : x + y, } y ; f(x,y) = x + y su } ; y x su (x,y) : x + y 4, x}. Esercizio Calcolare le misure degli insiemi e gli integrali delle funzioni specificati: (i) x + y, (x,y) : x + y, 3 y < x} ; (ii) x + y, (x,y) : x + y, 3 y < x}; (x,y,z) : (x ) + y z x} ; (iv) (x,y,z) : x + y z x} ; (v) z + x + y, 0 z ; (vi) z + x + y, 0 z x y ; (vii) (x,y,z) : z r ( } x + y R), r < R, toro ; (viii) (x,y,z,w) : x + y R, z + w r } toro spiaccicato ; (ix) x + y + z, su (x,y,z) : 0 z x + y, x + y + z }, (xii) y x + y, (x,y) : x + y 4, x, 0 y } ; (xiii) y z, (x,y,z) :x +y +z min, z}} ( ) x 3 + y 3 Esercizio 3 Calcolare l integrale di sin, su (x,y) : x y, y x}. xy Esercizio 4 Calcolare: (i)] 3y x dxdy ; (ii) x dxdy ; B((0,0);) B((0,0);) y x } y + z dxdydz ; (iv) x + y + z dxdydz y +z e x } B((0,0,0);) x+y+z }
2 Esercizio 5 a- (Guldino.0-Pappo) i provi che nello spazio il volume di un solido di rotazione (su piani ortogonali all asse di rotazione) di un sottoinsieme di un sempiano determinato dall asse, è uguale al prodotto dell area della figura ruotante per la lunghezza dell arco di circonferenza descritta dal suo baricentro. b- (Guldino 0.-Pappo) i consideri D = x J, 0 z F(x)} con J [0; + ) intervallo e F misurabile non negativa; si denotino con (x D,z D ) le coordinate del suo baricentro. Il volume del solido di rotazione, per un angolo di α radianti, di D attorno all asse z è dato da: V z = α x F(x)dx = α Area(D) x D = Area(D) lungh. arco percorso dal baricentro = J = α Area(D) distanza media dall asse. [cfr. Foglio di Esercizi n. 0 Es.0b-0bis.-] Esercizio 6 Calcolare gli integrali, sui rispettivi domini, delle seguenti funzioni: x + y, (x,y,z) : a (x + y ) z R x y } ; x + y + z, e su (x,y,z) : a (x + y ) z R x y } ; Esercizio 7 (Coordinate sferiche geogrfiche in R N ) Per N sia G : [0, [ [ π,π] [ π, π ]N R N : G(ρ,ϑ,...,ϑ N ) = x definita induttivamente x = ρˆr N = ρ(cosϑ N ˆr N, sin ϑ N ) da ˆr = (cosϑ, sin ϑ ) x N = ρ sin ϑ N x N = ρ cos ϑ N sin ϑ N x N 3 = ρ cos ϑ N cosϑ N sin ϑ N 3 ovvero... x 3 = ρ cos ϑ N cos ϑ N cos ϑ N...cosϑ 3 sin ϑ x = ρ cos ϑ N cos ϑ N...cos ϑ 3 cos ϑ sin ϑ x = ρ cos ϑ N cos ϑ N...cos ϑ 3 cos ϑ cos ϑ i- i mostri che G è surgettiva su R N. ii- i mostri cheg è iniettiva da [0, [ ( π,π] ( π, π )N (ovvero dato x si ha che ϑ h è individuato univocamente se ϑ h+,...ϑ N ± π ), e se ne determini l immagine, e la misura N-dimensionale del suo complementare. iii- i provi che le derivate parziali di G sono tra loro ortogonali. iv- i calcoli la matrice Jacobiana di G verificando che JG(ρ,ϑ,...,ϑ N,ϑ N ) =ρ N (cos ϑ N ) N (cos ϑ N ) N 3... (cos ϑ 3 ) (cos ϑ ). v- Posto B N (R) = x R N : x N R}, si ricavi la formula m N (B N (R)) = N+ [ ] π [ N ] R N = N!! M! πm R M N = M M! (M+)! 4M π M R M+ N = M +, ove [t] denota la parte intera del numero reale t e k!! è il prodotto di tutti i naturali fra e k che hanno la stessa parità di k (convenendo che 0!! = ).
3 Area di superficie Esercizio 8 Calcolare l area delle seguenti superfici o varietà bidimensionali nello spazio: i- z = x + y 37; ii- z = x + y x + ; iii- x + y = 4, 3 z 5; iv- x + y 4, x + y + z = ; v- superficie del cono retto di altezza ; vi- s(cost, sin t,t) + ( s)(0, 0,t), 0 [ t 3π, 0 s + x = (log(x + + x ) + x ) ] + x +c ; vii- (ridursi ad un integrale di funzione razionale di una variabile) x + y + z =, 0 z, 0 y x. Esercizio 9 (i) x y ds, ove è è la frontiera della regione compresa fra il cilindro x + y =, il piano x + y + z = 8 e il piano z = 0; (ii) i calcoli l area della frontiera del sottoinsime delimitato dal paraboloide z = x + y, dal cilindro x + y =, e dal piano z = ; ( π sin (z ) x + y ) ds, ove = (x,y,z) R 3 : 0 y, z, e z = x + y }. Esercizio 0 (Guldino.0 -Pappo) a- e γ(t) = (r(t), 0,z(t)) (per semplicità r(t) 0) è una curva regolare a tratti, si dia una parametrizzazione della supericie di rotazione ottenuta ruotandola attorno all asse x = y = 0 di α radianti. b- Data una curva contenuta in un semipiano determinato dall asse di rotazione, l area della superficie di rotazione, ottenuta ruotando la curva attorno all asse di α radianti, è data da: lunghezza dell arco di circonferenza percorso dal baricentro della curva lunghezza della curva = = α distanza del baricentro della curva dall asse lunghezza della curva Esercizio 0-bis Calcolare l area delle seguenti varietà: - (x,y, arsin x + y ), x + y 4 ; - superficie ottenuta ruotando di una giro la curva (x, x a, 0), x a, a > 0, attorno a all asse x = z = 0; - superficie e ottenuta ruotando di un giro la stessa attorno all asse y = z = 0; Esercizio - i scriva l elemento d area della superficie parametrica sferica di raggio r: (ρ cos ϕ cos ϑ,ρcos ϕ sin ϑ,ρsin ϕ), 0 < ρ r, π < ϕ < π, 0 ϑ < π. - i calcoli il volume V (r) = m 3 (B(r)) della palla di raggio r. - e A(r) è l area della sfera di raggio r, (r), si mostri che d V (r) = A(r). dr - i verifichi il fatto intuitivo che il 4αr è la misura della regione di (r), compresa tra due cerchi massimi che si incontrano con un angolo di α radianti. - i mostri che l area A = A(r,α,β,γ) di un triangolo sferico, delimitato da tre cerchi massimi, con i tre angoli di incidenza eguali a α, β, γ radianti è uguale a (α + β + γ π)r [conviene un ragionamento sintetico].
4 Esercizio Calcolare i seguenti integrali di superficie: ( x + y + z)ds, = (x,y,z) : z = x + y }; (x + y + xy + yz)ds, = (x,y,z) : x + y =, z 3}; z (x + y ) + z ds, ottenuta ruotando attorno all asse x = y = 0 la curva di equazione ( ) 4 x x, 0,, 0 x 0 x ; Esercizio 3 (Area settore curvilineo, volume conoide) a- Data una curva in coordinate polari r = Γ(θ), θ [α;β] (i.e. γ(θ) = (Γ(θ) cos θ, Γ(θ) sin θ) mostrare che Γ(θ) dθ α calcola l area del settore curvilineo delimitato dalla curva e con vertice l origine: (x, y) = rγ(θ), r [0; ],θ [α;β]}. b.- ia γ(t) = (x(t),y(x)), t I una curva piana semplice regolare. Per semplicità si assuma che non passi per l origine e che γ γ sia bigettiva su di un arco della circonferenza γ unitaria. i mostri che det (γ,γ ) dt = xy x y dt calcola l area del settore con vertice l origine e delimitato da γ: (x,y) : (x,y) = rγ(t), r [0; ], t I}. b.- A livello intuitivo, non assumendo altro che la regolatà a tratti del cammino, cosa rappresentano xy x y dt e (xy x y)dt. i esprima l integrale di superficie di f(x,y,z) su (x,y) : (x,y,z) = rγ(t), r [0; ], t I} in termini di integrazione di foγ, γ. b.3-ia γ(t) = (x(t),y(x),z(t)), t I una curva semplice regolare. Per semplicità si assuma che non passi per l origine e che γ γ sia iniettiva nella sfera unitaria. γ i esprima in termini di x(t), y(x), z(t) e delle loro derivate l area della suprficie parametrica (x,y,z) : (x,y,z) = rγ(t), r [0; ], t I}. Che interpretazione dare del risultato? [cfr. formula di Cauchy-Binet, ed interpretazione geometrica del modulo del prodotto vettoriale]. c- ia σ(s,t), (s,t) T una superficie parametrica regolare. Per semplicità si assuma che non passi per l origine e che σ σ sia iniettiva. σ i mostri che σ (σ s σ t ) dsdt calcola il volume del cono con vertice l origine e 3 T delimitato da σ: (x,y,z) : (x,y,z) = rσ(s,t), r [0; ], (s,t) T }. Esercizio 3-bis - i calcoli l area della regione delimitata dal sostegno della curva γ(t) = (cost, sin t). - i calcoli il volume dell immagine della funzione (rx,ry,r(x y +)), 0 r, x +y. Esercizio 4 ia E il sottoinsieme di R descritto, in coordinate polari, dalla diseguaglianza ρ α(ϑ), ϑ [0, π], ove α è una funzione continua e non negativa su [0, π]. i calcoli m (E). Che cosa succede quando α assume anche valori negativi? β
5 ommabilità Esercizio 5 Discutere la finitezza delle misure dei seguenti insiemi e la sommabilità delle seguenti funzioni nei domini specificati: (i) (v) x + y, B((0, 0); ) ; (ii), B((0, 0); ) \ B((0, ); ) B((0, ); ) ; x + y x + y, R \ B((0, 0); ) ; (iv) (x + + x N )α, x + + x N ; (vi) (vii) (x + y + z ), x + y z α x + y, α 0 ; (viii) (x) ( xii) x + y, (x,y) : 0 y x, y yx } ; xyz, [0; ] [0; ] [0; ] ; (x + y + z ) 6 x 3 + y, [0; ] [0; ] ; (ix) 3 x 6 + y 6 + z, 6 z4 x + y ; x + y, [0; ] [0; ] ; (xi) x + y, x + y ; sin x + siny, [0; ] [0; ] ; [(xiii)] (xiv) x +y 3, x, y 0; [(xv)] x y α x +y, x + y <, α 0 ; cos sin(xy) cos x + y (xvi) x 4 +y 4 +z, x3 + y 3 + z 0, x 0, y 0 ; (xvii) (xviii), x 0, y 0; x + y4, [0; ] [0; ] ; x y z x + y 4 + z α per x + y + z, e per x + y + z al variare di α R. Esercizio 6 Discutere la finitezza delle misure dei seguenti insiemi e la sommabilità delle seguenti funzioni nei domini specificati: (i) (iv) x + y, [0; ] [0; ]; (ii) x + y 4, R \B((0, 0); ); x + y 4, 0 x 3y 3x ; (v) x + y 3 + z 4, R \B((0, 0); ); x y x + y, n N max x n ; y n } n ; Miscellanea Esercizio 7 ia data l applicazione Φ λ (x,y) = (x+λ,y +e λy ) =: (u,v), e sia B il disco determinato dalla disequazione x + y. i calcoli [ ] d D = ududv.. dλ Φ λ (B) λ=0 Esercizio 8 Calcolare i seguenti integrali: (i) x dxdy, ove A è il semicerchio di centro (r, 0) e raggio r > 0, e y > 0; A
6 (ii) (iv) (v) (vi) (vii) B E C D F y e x dxdy, ove B = (x,y) R : ρ cos ϑ}; y dxdy, ove C R è la regione definita da x + y x + 4 ; dxdy, D = trapezio di vertici (, 0), (3, 0), (, ), (3, 3); x + y x x + y dxdy, ove E = (x,y) R : y x r, x + y r } (r > 0); arctan y x dxdy, ove F è definito da 0 < x, y, x + y 4. dxdy, ove G è la regione delimitata dalla curva (lemniscata di Bernoulli) di G + x + y equazione (x + y ) (x y ) = 0. Esercizio 9 Calcolare i seguenti integrali: (i) ln( + xy)dxdy, ove A = (x,y) R : 0 xy, y x, y x}; (ii) A B x + y dxdy, ove B è delimitato dalla retta y +x = e dalla parabola passante per i punti (, 0), (0, ) con vertice in (0, 0); C xy dxdy, ove C = (x,y) R : x }; y x, x y 4 x (iv) (x + y) x y dxdy, ove D = (x,y) R : x + y, x + y 0}; (v) (vi) (vii) (viii) (ix) (x) E D F J I y(x y) sin(x + y )dxdy, ove E = (x,y) R : 4 x + y 6, y x 3y}; G x y dxdy, ove F = (x,y) R : x y x, x y x}; x y (y x )dxdy, ove G = (x,y) R : x,y 0, x + y x +, H sin 3 (x + y )dxdy, ove H R è definito da π x + y π, y x. x y } ; x y dxdy, ove I R è definito da x 0, y 0, y(x ), xy. x + y dxdy, ove J è la regione interna alle due circonferenze (x ) + y =, x + (y ) =. (xi) xdxdy, ove K è il dominio del primo quadrante interno alla circonferenza di centro K (0, ) e raggio ed esterno alla circonferenza di centro (0, /) e raggio /.
; y x su {(x, y) : x 2 + y 2 4, 1 x}.
 Analisi Matematica II, Anno Accademico 07-08. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMBI DI VARIABILE NEGLI INTEGRALI: CALCOLO DI INTEGRALI IN COORDINATE CURVILINEE
Analisi Matematica II, Anno Accademico 07-08. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMBI DI VARIABILE NEGLI INTEGRALI: CALCOLO DI INTEGRALI IN COORDINATE CURVILINEE
Analisi Matematica II, Anno Accademico Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n.
 Analisi Matematica II, Anno Accademico 17-18. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMMINI ESERCIZIO 1 Un cammino soddisfa le relazioni y = x z, z = y + x 3, essendo
Analisi Matematica II, Anno Accademico 17-18. Ingegneria Edile e Architettura Vincenzo M. Tortorelli FOGLIO DI ESERCIZI n. CAMMINI ESERCIZIO 1 Un cammino soddisfa le relazioni y = x z, z = y + x 3, essendo
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Analisi Matematica 2. Superfici e integrali superficiali. Superfici e integrali superficiali 1 / 27
 Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Esercizi sull integrazione
 ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Provadiprova 2 - aggiornamento 7 giugno 2013
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica 2 - a.a. 2012-13 - Prof. Gabriele Anzellotti Provadiprova 2 - aggiornamento 7 giugno 2013 La seconda provetta
Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica 2 - a.a. 2012-13 - Prof. Gabriele Anzellotti Provadiprova 2 - aggiornamento 7 giugno 2013 La seconda provetta
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Esercizi sull integrazione I
 ANALII MAEMAICA -2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. I ANALII MAEMAICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione I (Grazie agli studenti del corso
ANALII MAEMAICA -2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. I ANALII MAEMAICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione I (Grazie agli studenti del corso
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Integrali multipli - Esercizi svolti
 Integrali multipli - Esercizi svolti Integrali di superficie. Si calcoli l integrale di superficie Σ z +y +4(x +y ) dσ, dove Σ è la parte di superficie di equazione z = x y che si proietta in = {(x,y)
Integrali multipli - Esercizi svolti Integrali di superficie. Si calcoli l integrale di superficie Σ z +y +4(x +y ) dσ, dove Σ è la parte di superficie di equazione z = x y che si proietta in = {(x,y)
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
Syllabus per la seconda prova intermedia e per le prove scritte di esame. Esercizi di preparazione.
 Università di Trento - Corsi di Laurea in Ingegneria Civile e in Ingegneria Ambientale Analisi matematica 2 - a.a. 2013-14 - Prof. Gabriele Anzellotti Syllabus per la seconda prova intermedia e per le
Università di Trento - Corsi di Laurea in Ingegneria Civile e in Ingegneria Ambientale Analisi matematica 2 - a.a. 2013-14 - Prof. Gabriele Anzellotti Syllabus per la seconda prova intermedia e per le
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
6. Integrali curvilinei
 6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. ott. Franco Obersnel Esercizio 1 Sia R = [a 1, b 1 ] [a, b ] [a 3, b 3 ] IR 3 un parallelepipedo di IR 3. Si diano le
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. ott. Franco Obersnel Esercizio 1 Sia R = [a 1, b 1 ] [a, b ] [a 3, b 3 ] IR 3 un parallelepipedo di IR 3. Si diano le
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
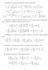 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Curve e integrali curvilinei
 6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
Esercizi di riepilogo sulle curve. 1. Si fornisca una parametrizzazione per le seguenti curve:
 Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Analisi Matematica II, Anno Accademico Ingegneria Edile e Architettura Vincenzo M. Tortorelli 16 Gennaio 2018: primo appello.
 Analisi Matematica II Anno Accademico 7-8 Ingegneria Edile e Architettura Vincenzo M Tortorelli 6 Gennaio 8: primo appello ESERCIZIO Si consideri l intersezione dei sottoinsiemi di R definiti da z = x
Analisi Matematica II Anno Accademico 7-8 Ingegneria Edile e Architettura Vincenzo M Tortorelli 6 Gennaio 8: primo appello ESERCIZIO Si consideri l intersezione dei sottoinsiemi di R definiti da z = x
Esercizi su curve e integrali di linea. 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza
 Esercizi su curve e integrali di linea 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza : {(x, y) R, x + y 4, y } Soluzione: possibili parametrizzazioni per la curva sono: α 1 (t)
Esercizi su curve e integrali di linea 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza : {(x, y) R, x + y 4, y } Soluzione: possibili parametrizzazioni per la curva sono: α 1 (t)
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL 2/9/2011
 TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Secondo Parziale, , Versione A Cognome e nome:...matricola:...
 es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
ESERCIZI SULLE CURVE
 ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 2. Giugno Docenti: F. Lastaria, M. Citterio, M.
 POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
Preparazione al primo foglio di esercizi di Analisi 2
 Preparazione al primo foglio di esercizi di Analisi 2 Verona, 2 ottobre 2017 Esercizio 1. Si tracci il graco delle seguenti regioni del piano cartesiano: (1.1 D 1 := {(x, y R 2 : x 2 + y 2 1, x + 3y 2
Preparazione al primo foglio di esercizi di Analisi 2 Verona, 2 ottobre 2017 Esercizio 1. Si tracci il graco delle seguenti regioni del piano cartesiano: (1.1 D 1 := {(x, y R 2 : x 2 + y 2 1, x + 3y 2
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Analisi Matematica 2. Curve e integrali curvilinei. Curve e integrali curvilinei 1 / 29
 Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Integrale curvilinei (o di densità) 19 Novembre 2018
 Integrale curvilinei (o di densità) 19 Novembre 2018 Indice: urve parametrizzate nello spazio. Lunghezza di una curva. Integrali curvilinei. Applicazioni geometriche e fisiche. Federico Lastaria. Analisi
Integrale curvilinei (o di densità) 19 Novembre 2018 Indice: urve parametrizzate nello spazio. Lunghezza di una curva. Integrali curvilinei. Applicazioni geometriche e fisiche. Federico Lastaria. Analisi
Integrali di superficie
 Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.
 ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
ESERCIZI DI ANALISI MATEMATICA Università di Firenze - Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica M Z Prof. M.Patrizia Pera Parte 2 Funzioni reali di più variabili 1. Stabilire se i
Fondamenti di Analisi Matematica 2 per IPIM-IEN-ICM, 17/02/14. Tema 1 (parte di esercizi)
 Fondamenti di Analisi Matematica 2 per IPIM-IEN-ICM, 17/02/14 Cognome e Nome... Matr.... Scrivere le risposte richieste su questo foglio senza giustificazione. Il candidato deve riconsegnare questo foglio,
Fondamenti di Analisi Matematica 2 per IPIM-IEN-ICM, 17/02/14 Cognome e Nome... Matr.... Scrivere le risposte richieste su questo foglio senza giustificazione. Il candidato deve riconsegnare questo foglio,
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Analisi Matematica II, Anno Accademico Ingegneria Edile e Architettura Vincenzo M. Tortorelli 17 Gennaio primo appello SOLUZIONI
 Analisi Matematica II, Anno Accademico 6-7 Ingegneria Edile e Architettura Vincenzo M Tortorelli 7 Gennaio 7 - primo appello SOLUZIONI ESERCIZIO Si fissi c > e sia fx,y,z = c x y z e xy + yz + xz, x,y,z
Analisi Matematica II, Anno Accademico 6-7 Ingegneria Edile e Architettura Vincenzo M Tortorelli 7 Gennaio 7 - primo appello SOLUZIONI ESERCIZIO Si fissi c > e sia fx,y,z = c x y z e xy + yz + xz, x,y,z
Superfici e integrali di superficie. 1. Scrivere una parametrizzazione per le seguenti superfici
 Superfici e integrali di superficie 1. Scrivere una parametrizzazione per le seguenti superfici (a) Il grafico della funzione f(x, y) = x 2 y 3 (b) La superficie laterale di un cilindro di raggio R e altezza
Superfici e integrali di superficie 1. Scrivere una parametrizzazione per le seguenti superfici (a) Il grafico della funzione f(x, y) = x 2 y 3 (b) La superficie laterale di un cilindro di raggio R e altezza
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Analisi Matematica 2
 Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2
![Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2 Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2](/thumbs/99/141851732.jpg) urve parametrizzate Definizione Una curva parametrizzata nello spazio R 3 è una funzione [a, b] R 3 t (t) = (x(t), (t), z(t)) t [a, b] Il sostegno di una curva è l immagine Im della funzione, cioè l insieme
urve parametrizzate Definizione Una curva parametrizzata nello spazio R 3 è una funzione [a, b] R 3 t (t) = (x(t), (t), z(t)) t [a, b] Il sostegno di una curva è l immagine Im della funzione, cioè l insieme
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
( ) 3 ESERCIZI. Calcolare il valore dei seguenti integrali curvilinei: 1) xyds. dove γ è il contorno del quadrato x y a.
 ESERCIZI Calcolare il valore dei seguenti integrali curvilinei: ) ds ) 3) dove è il contorno del quadrato a + + + = con a > 0 [0] 4 ds dove è il segmento della retta che congiunge i punti O(0,0) ed A(,)
ESERCIZI Calcolare il valore dei seguenti integrali curvilinei: ) ds ) 3) dove è il contorno del quadrato a + + + = con a > 0 [0] 4 ds dove è il segmento della retta che congiunge i punti O(0,0) ed A(,)
Analisi Matematica II, Anno Accademico Ingegneria Cvile Ambientale Edile
 Analisi Matematica II, Anno Accademico 2015-2016. Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 10, dal 3 al 18 Dicembre 2015 Calcolo Differenziale 4: massimi e minimi. Altri esercizi ed esempi
Analisi Matematica II, Anno Accademico 2015-2016. Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 10, dal 3 al 18 Dicembre 2015 Calcolo Differenziale 4: massimi e minimi. Altri esercizi ed esempi
Integrali doppi. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Esercizi svolti e assegnati su integrali doppi e tripli
 Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
3 ) (5) Determinare la proiezione ortogonale del punto (2, 1, 2) sul piano x + 2y + 3z + 4 = 0.
 1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
Funzioni di due variabili: Limiti, Continuità, Differenziabilità
 Funzioni di due variabili: Limiti, Continuità, Differenziabilità 1 arctan( x y), (x, y) (0, 0) f(x, y) = x2 + y2 0, (x, y) = (0, 0) A 3 Stabilire se f è continua e differenziabile in (0, 0) B 2 Stabilire
Funzioni di due variabili: Limiti, Continuità, Differenziabilità 1 arctan( x y), (x, y) (0, 0) f(x, y) = x2 + y2 0, (x, y) = (0, 0) A 3 Stabilire se f è continua e differenziabile in (0, 0) B 2 Stabilire
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Esercizi di Analisi 2. Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni
 Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
Esercizi di Analisi 2 Nicola Fusco (Dipartimento di Matematica e Applicazioni, Università Federico II, Napoli) 1. Successioni e Serie di Funzioni 1.1 Al variare di α IR studiare la convergenza della serie
Integrali superficiali eteoremi digaussestokes/ Esercizi proposti
 SRolando, 4 Integrali superficiali eteoremi digaussestokes/ Esercizi proposti L asterisco contrassegna gli esercizi più difficili Data la parametrizzazione σ (u, v) =(u + v, log u, log v), (u, v) [, ]
SRolando, 4 Integrali superficiali eteoremi digaussestokes/ Esercizi proposti L asterisco contrassegna gli esercizi più difficili Data la parametrizzazione σ (u, v) =(u + v, log u, log v), (u, v) [, ]
Analisi Matematica II (Prof. Paolo Marcellini) 1 Esercizi tratti da temi d esame di anni precedenti
 Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Provadiprova 1 - aggiornamento del 23 Ottobre 2013
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica - a.a. 03-4 - Prof. Gabriele Anzellotti Provadiprova - aggiornamento del 3 Ottobre 03 a) Curve: rappresentazione
Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica - a.a. 03-4 - Prof. Gabriele Anzellotti Provadiprova - aggiornamento del 3 Ottobre 03 a) Curve: rappresentazione
Raccolta esami di Analisi II
 Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
Analisi Matematica 2 3 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 3 febbraio 204 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = ) Esercizio. Se il raggio di convergenza della serie di potenze a n (x
Analisi Matematica 2 3 febbraio 204 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = ) Esercizio. Se il raggio di convergenza della serie di potenze a n (x
12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati:
 ANALISI Soluzione esercizi 2 gennaio 212 12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati: (x, y) R 2 : x < y} (x, y) R 2 : 2 x 3} (x, y) R 2 : x 2 +
ANALISI Soluzione esercizi 2 gennaio 212 12.1. Esercizio. Disegnare i seguenti insiemi di R 2 e dire se sono o meno aperti, chiusi, limitati: (x, y) R 2 : x < y} (x, y) R 2 : 2 x 3} (x, y) R 2 : x 2 +
I = 1 2. dtdx. (x 2 + t) 7/2 t=x 2 = 1 2 = 27/2 1. x 7 dx = 27/ b) Il segmento OP in figura. t=0. x=0
 X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ANALISI VETTORIALE COMPITO PER CASA DEL 6/12/ y x 2 + y 2 dxdy =
 ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
Simmetrie e quadriche
 Appendice A Simmetrie e quadriche A.1 Rappresentazione e proprietà degli insiemi nel piano Una delle prime difficoltà che si incontrano nell impostare il calcolo di un integrale doppio consiste nel rappresentare
Appendice A Simmetrie e quadriche A.1 Rappresentazione e proprietà degli insiemi nel piano Una delle prime difficoltà che si incontrano nell impostare il calcolo di un integrale doppio consiste nel rappresentare
(a) E è convesso; (b) (1, 0) non è punto interno; (c) E non è misurabile.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 3 4 5 6 A Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni A.A.
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 3 4 5 6 A Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni A.A.
GEOMETRIA B Esercizi
 GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
7. Integrazione delle funzioni di più variabili (II)
 7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
Π 1 (P) Π 2 (H) Π 3 (H) Π 1
 Prova scritta di Matematica II 4 settembre 8 COEZIONE Fila B c.d.l. Scienze dell Architettura Prof.. izzi 1.a. Determinare le equazioni dei seguenti piani: 1.a.a. piano Π 1 passante per i punti (5,1 π,5),
Prova scritta di Matematica II 4 settembre 8 COEZIONE Fila B c.d.l. Scienze dell Architettura Prof.. izzi 1.a. Determinare le equazioni dei seguenti piani: 1.a.a. piano Π 1 passante per i punti (5,1 π,5),
ELIO CABIB. Esami di Analisi 2
 ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
COGNOME: NOME: MATR.: 1. Si consideri la serie di Fourier data da n 2
 COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
 Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica Dott. Franco Obersnel Lezione : superficie nello spazio; area e integrali superficiali; teorema
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica Dott. Franco Obersnel Lezione : superficie nello spazio; area e integrali superficiali; teorema
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
