Lezioni di Aerodinamica

Transcript

1 Università di Napoli Federico II Dipartimento di Ingegneria Aerospaziale 1/293 Lezioni di Aerodinamica A.A Renato Tognaccini Dipartimento di Ingegneria Aerospaziale Università di Napoli Federico II Piazzale V. Tecchio 80, Napoli

2 Introduzione Aerodinamica: ramo della Meccanica dei fluidi (Fluidodinamica) che si concentra sull analisi dell interazione tra una corrente fluida ed un corpo immerso in essa. Fluido: materia senza una forma propria; caratterizzato da un proprio volume (liquido), o senza volume proprio (gas), assume cioè il volume del suo contenitore. Ipotesi del continuo: il fluido è un mezzo continuo, cioè si assume che una qualsiasi parte di esso, comunque piccola, contenga un numero molto grande di molecole. Particella di fluido: un elemento di volume infinitamente piccolo nella scala di lunghezze (macroscopica) di nostro interesse, ma comunque grande nella scala di lunghezza delle molecole (microscopica). 2/293

3 Le forze aerodinamiche Si sceglie un sistema di riferimento (inerziale) O(x, y, z) solidale con l aeromobile, che è quindi investito da una corrente uniforme di velocità V, alla quota h, caratterizzata dalla pressione p e densità ρ. 3/293 Equilibrio dell aeromobile in volo livellato uniforme: L = W (1) T = D (2) F = [L, D]: forza aerodinamica L: portanza (Lift) V D: resistenza (Drag) V W : peso (Weight) a T : spinta (Thrust) a G è il baricentro

4 I coefficienti delle forze aerodinamiche Forza aerodinamica di riferimento: 1 2 ρ V 2 S. S: superficie di riferimento (in genere la superficie alare S W ). 4/293 Coefficiente di portanza C L = L 1 ρ 2 V S 2 (3) Coefficiente di resistenza Efficienza aerodinamica C D = D 1 ρ 2 V S 2 (4) E = L D = C L C D (5)

5 ATR /293

6 Alcune prestazioni dell ATR W T Omax = Kgp W OEmax = Kgp Payload= 5450 Kgp V max = 556 Km/h TO-length= 1165 m P = KW Ceiling= 5485 m Max Range= 2963 Km S W = m 2 6/293 Alcuni dati geometrici e aerodinamici S W = m 2 b = m W/S = Kgp/m 2 AR = 11.1 C Lmax = 1.75 (δ f = 0 0 ) C Lmax = 2.61 (δ f = 15 0 ) C Lmax = 3.15 (δ f = 27 0 )

7 Prob. n. 1: determinazione del C L di un aeromobile in volo livellato 1 W C L = 1 ρ (6) 2 V 2 S Occorre: quota, velocità di volo, peso e superficie di riferimento del velivolo. 7/293 Prob. n. 2: determinazione della velocità minima di sostentamento (velocità di stallo) 1 W 2 V s = (7) S ρ C Lmax Occorre: quota, peso e superficie di riferimento del velivolo, portanza massimo del velivolo (C Lmax ). coefficiente di

8 I parametri fondamentali della corrente Il numero di Mach 8/293 V : velocità della particella; a: velocità del suono locale. M = V a, (8) Un flusso a densità costante in tutto il campo si dice incomprimibile o incompressibile. In un flusso incomprimibile: M = 0 (9) in tutto il campo di moto. In certe condizioni anche i fluidi comprimibili (gas) si comportano come incomprimibili (liquidi): per M 0 il flusso tende a diventare incomprimibile.

9 La viscosità 9/293 Un fluido si dice newtoniano quando la forza df (di attrito) è data da df = µ V da (10) z µ: viscosità dinamica del fluido, si misura in Kg/(m s); ν = µ/ρ: viscosità cinematica del fluido, si misura in m 2 /s.

10 Il numero di Reynolds Re = ρ V L µ (11) L: lunghezza di riferimento caratteristica del problema in studio, 10/293 Il numero di Reynolds misura l importanza relativa delle forze di natura dinamica (convettive), associate alla quantità di moto delle particelle, e le forze di natura viscosa. Un fluido o un flusso non dissipativo si dice ideale. Vedremo che un un fluido o un flusso caratterizzato da viscosità nulla (Re ) è ideale. Nei flussi ideali la viscosità è trascurabile.

11 Regimi di moto Classificazione in base al numero di Mach M = 0: flusso incomprimibile M 1 ovunque: flusso iposonico M < 1 ovunque: flusso subsonico M < 1 e M > 1: flusso transonico M > 1 ovunque: flusso supersonico M 1: flusso ipersonico 11/293 Classificazione in base al numero di Reynolds Re 0: flusso alla Stokes (creeping flow) Re : flusso ideale

12 Numero di Mach critico inferiore (M,cr): numero di Mach subsonico minimo della corrente asintotica per il quale esiste almeno un punto nel campo di moto in cui M = 1 (limite del regime subsonico). Numero di Mach critico superiore (M,cr): numero di Mach supersonico minimo della corrente asintotica per il quale tutti i punti nel campo di moto sono supersonici (limite del regime transonico). 12/293 Per un dato fluido, le equazioni adimensionali della dinamica del flusso dipendono solo da M e Re.

13 Prob. n. 3: determinazione di M M = V a Per un gas perfetto a = γrt. γ è il rapporto dei calori specifici a pressione e volume costanti (per l aria γ = 1.4). R = 287 J Kg K è la costante del gas aria nel modello di gas perfetto. T è la temperatura assoluta della corrente asintotica (espressa in gradi Kelvin) che dipende dalla quota. 13/293 Prob. n. 4: determinazione di Re Re = ρ V L µ Occorre: La quota, la velocità di volo e la lunghezza caratteristica dell aeromobile.

14 Genesi di portanza e resistenza Teoria globale 14/293 Principio di azione e reazione: la forza aerodinamica agente sull aeromobile è pari all azione dell aeromobile sulla portata d aria ṁ interagente; in virtù della II legge della dinamica: V: variazione media della quantità di moto; F = ṁ V (12) ṁ = eρ V πb 2 /4 (b è l apertura alare, e 1). La portanza è data dalla componente perpendicolare a V di V: Dalla definizione di C L : L = ṁ V v (13) V v V AR = b 2 /S è l allungamento alare. = 2C L πear (14)

15 La resistenza indotta (dalla portanza) L energia cinetica della portata d aria ṁ è aumentata dopo l interazione con l aeromobile: E = 1 [ ] V 2 + V 2 v V 2 1 = 2 2ṁ 2ṁ V v. (15) Per il principio di conservazione dell energia deve esserci una forza che compie un lavoro equivalente che non può che essere T = D: E = DV, (16) per cui, ricordando l espressione del C D e di V v /V si ottiene: C Di = C2 L πear, (17) espressione del coefficiente di resistenza indotta. e è il fattore di Oswald; in genere e < 1. e = 1 nel caso di ala con distribuzione di carico ellittica. Un caso particolare di distribuzione di carico ellittica: distribuzione di corde ellittica, svergolamento aerodinamico nullo, profilo alare costante. 15/293

16 La resistenza totale di un aeromobile D i, resistenza indotta (dalla portanza); D = D i + D p + D w (18) D p, resistenza di profilo, associata all azione diretta delle forze viscose (attrito e forma); in regime transonico e supersonico si aggiunge anche D w, la resistenza d onda, legata alla probabile presenza di onde d urto nel campo di moto. 16/293 La polare di un aeromobile Le curve C D = C D (C L ) si chiamano curve polari. Per ogni aeromobile esistono infinite polari, al variare di Re, M e della configurazione del velivolo.

17 Espressione approssimata della polare C D = C D0 + C2 L πare C D0 : coefficiente di resistenza a portanza nulla. (19) L espressione parabolica della polare costituisce una buona approssimazione della polare reale nell intorno della crociera del velivolo. Errori insiti in questa approssimazione: in generale il coefficiente di resistenza non è minimo per C L = 0; la resistenza di profilo varia al variare di C L ; in condizioni di alta portanza la polare del velivolo si discosta molto dall andamento parabolico che addirittura non prevede lo stallo dell aeromobile. 17/293

18 Prob. n. 5: determinazione del C Di di un aeromobile in volo livellato Tra l altro occorre conoscere il fattore di Oswald dell aeromobile. 18/293 Prob. n. 6: confronto delle resistenze indotte di un aeromobile in crociera ed in atterraggio Attenzione resistenza non è equivalente a coefficiente di resistenza.

19 Geometria dell ala 19/293 η = y, λ = c b/2 t/c r, c = c r [1 η(1 λ)], S = 2 b/2 0 c(y)dy Corda media aerodinamica (m.a.c.): c = 2 b/2 S 0 c 2 (y)dy

20 La curva C L = C L (α) (curva di portanza) Definizione di angolo di attacco: 20/293 Sezione dell ala alla radice Polare, curva di portanza e dei momenti per un ala di AR = 10

21 Caratteristiche della curva di portanza È presente un tratto lineare nell intorno delle basse incidenze: C L C Lα α ; (20) 21/293 si evidenzia il fenomeno dello stallo; dipende da M e Re.

22 Il profilo alare Sezione di un ala parallela a V. 22/293 c: corda; t: spessore; τ = t/c: spessore percentuale; F : fuoco, posto ad 1/4 della corda. Nel caso di un ala rettangolare dritta di allungamento infinito il campo di moto risulta bidimensionale nel piano del profilo. AR C Di = 0, quindi D = D p + D w.

23 Caratteristiche aerodinamiche di un profilo alare Portanza: Resistenza: l = C l 1 2 ρ V 2 c d = C d 1 2 ρ V 2 c; Momento di beccheggio rispetto al bordo di attacco: m le = C mle 1 2 ρ V 2 c 2. Momento di beccheggio rispetto al fuoco: m 1/4 = C m1/4 1 2 ρ V 2 c 2. I momenti sono positivi se cabranti. 23/293

24 Profilo NACA 2412 (flusso iposonico) 24/293

25 Portanza di un ala finita e di un profilo Per un profilo poco spesso e curvo a piccoli angoli di attacco: C l = C lα (α α zl ), (21) 25/293 C lα 2π, α zl : angolo di portanza nulla del profilo. AR 1 : C Lα C lα 1 + C lα πar (22) AR < 1 : C Lα π AR (23) 2

26 Idrostatica Si assume che in tutto il campo fluido V = 0. 26/293 La pressione S: superficie elementare di inclinazione generica nel fluido. F : modulo della forza che agisce sulla superficie S dovuta allo scambio di quantità di moto a livello molecolare. In un fluido in quiete F è perpendicolare a S (Principio di Pascal). F p = lim S 0 S Su una superficie infinitesima ds di normale n agisce la forza p è detta pressione idrostatica. (24) df = pnds (25)

27 Legge di Stevino Si consideri un volume infinitesimo dxdydz di un fluido in quiete. z indica la quota (asse verticale e diretto verso l alto). Forza di pressione totale: p dxdy ( p + dp dz dz Equilibrio tra forza di gravità e forza di pressione: ) dxdy = dp dxdydz (26) dz dp dxdydz ρgdxdydz = 0 (27) dz dp = ρgdz (28) Integrando tra le quote z 1 e z 2 in un fluido a densità costante: h = z 2 z 1 p = p 2 p 1 p = ρg h (29) 27/293

28 Prob. n. 7: ricavare il Principio di Archimede La forza di galleggiamento che agisce su un corpo immerso in un fluido in quiete è pari al peso del fluido spostato dal corpo. 28/293 Prob. n. 8: descrivere il funzionamento del barometro a colonna di liquido

29 Atmosfera standard (ISA) Ipotesi 1. L aria è secca e si comporta come un gas più che perfetto: p = ρrt ; 2. l aria è in quiete ed è valida la legge di Stevino: dp = ρgdz. In base alle ipotesi: dp p = g dz. (30) RT Per deteminare p = p(z) occorre un modello per la distribuzione di temperatura al variare della quota T = T (z) Km: troposfera, la temperatura decresce linearmente di 6.5 gradi per chilometro; Km: stratosfera, la temperatura rimane costante con la quota; > 20 Km: esosfera, la temperatura aumenta con la quota. Questo modello descrive bene l atmosfera nelle zone temperate. 29/293

30 Troposfera ρ SL = 1.23 Kg/m 3, T SL = 288 K, T z = K/m. Integrando la (30) si ottiene ( p T = p SL Stratosfera T SL T = T SL T z z. (31) ) g RTz Integrando la (30) si ottiene p p ST =, ρ ρ SL = ( T T SL ) g RTz 1. (32) T = T ST. (33) ρ = e g RTz (z z ST ), (34) ρ ST dove z ST = m, T ST = T (z ST ), p ST = p(z ST ) e ρ ST = ρ(z ST ). Prob. n. 9: diagrammare T, p e ρ al variare della quota 30/293

31 Elementi di calcolo tensoriale Sia f una grandezza in generale funzione (in un determinato dominio) dello spazio e del tempo f = f(x, y, z, t). f è una grandezza scalare quando è completamente individuata unicamente da un numero reale. Uno scalare viene anche denominato tensore di ordine 0. f è una grandezza vettoriale quando è completamente individuata da un numero reale e da una direzione orientata. Un vettore viene anche denominato tensore di ordine 1 (lo indicheremo con il simbolo f). f è un tensore di ordine 2 quando la sua individuazione richiede la conoscenza di due direzioni orientate (lo indicheremo con il simbolo f). In questo corso con i termini scalare, vettore e tensore ci riferiremo rispettivamente al tensore di ordine 0, 1 e 2. 31/293

32 Algebra dei vettori Sia O(x 1, x 2, x 3 ) una terna di riferimento cartesiana levogira di versori σ 1, σ 2 e σ 3. 32/293 f = (f 1, f 2, f 3 ) = σ i f i, (35) dove f i sono le componenti di f e σ i f i = 3 i=1 σ i f i (convenzione dell indice ripetuto di Einstein). Eguaglianza Vettore nullo a = b a i = b i i. (36) Prodotto scalare a = 0 a i = 0 i. (37) a b = a b cos θ = a i b i, θ : angolo tra a e b. (38)

33 In particolare: dove δ ij = 1 se i = j altrimenti δ ij = 0. σ i σ j = δ ij, (39) 33/293 f i = σ i f. (40) Intensità o modulo del vettore Versore v di V a = a = a i a i. (41) v = V V. (42)

34 Prodotto vettoriale il vettore c è dato da: a b = c ; (43) 34/293 c = ab sin θ, (a, b, c) terna ortogonale levogira ; (44) c è quindi perpendicolare sia ad a che b. Si dimostra che σ 1 σ 2 σ 3 c = a 1 a 2 a 3, (45) b 1 b 2 b 3 dove il determinante simbolico è calcolato con la regola di Laplace per la prima riga. Inoltre c = σ i c i = σ i ε ijk a j b k, (46) dove ε ijk = 0 se i = j, oppure i = k, oppure j = k; ε ijk = ±1 se la terna (i, j, k) costituisce una permutazione di classe pari (+) o dispari (-) dei numeri 1, 2, 3.

35 Si nota che Doppio prodotto vettoriale b a = a b. (47) 35/293 c (a b) = a(b c) b(a c). (48)

36 Calcolo differenziale vettoriale Il vettore nabla In un riferimento cartesiano: σ i. (49) x i In un riferimento cilindrico O(R, θ, z) di versori (a 1, a 2, a 3 ): Gradiente di uno scalare a 1 R + a 1 2 R θ + a 3 z. (50) f = σ i f x i. (51) 36/293

37 Proprietà del gradiente di uno scalare 1. n f = f ; derivata direzionale di f nella direzione n, misura la n variazione (unitaria) di f nella direzione orientata n. 2. f, modulo di f, dà la variazione (unitaria) massima di f. 3. Il versore di f dà la direzione in cui la variazione di f è massima. 4. Data la superficie f(r) = cost 1, f è perpendicolare ad essa ed è orientato nel verso delle f crescenti. 37/293 Divergenza di un vettore 1 r = σ i x i è il vettore posizione. V = V i x i (52)

38 Rotore di un vettore σ 1 σ 2 σ 3 V = x 1 x 2 x 3 V 1 V 2 V 3 = σ i ε ijk V k x j. (53) Un campo V con rotore identicamente nullo è detto irrotazionale. 38/293 Operatori differenziali di ordine superiore Il rotore del gradiente di uno scalare è identicamente nullo: ( f) = 0. (54) La divergenza del rotore di un vettore è identicamente nulla: ( V) = 0. (55) La divergenza del gradiente di uno scalare si chiama laplaciano: 2 f = f. (56)

39 Le funzioni scalari con laplaciano identicamente nullo si dicono armoniche. Vale infine la seguente identità: ( V) = ( V) 2 V. (57) 39/293 Campi potenziali Un campo vettoriale V(r) si dice potenziale se esiste una funzione scalare φ(r) tale che V = φ. (58) Se un campo V(r) è potenziale allora un qualsiasi integrale di linea P2 V dl dipende solo dagli estremi di integrazione. P 1 Condizione necessaria e sufficiente affinchè V sia a potenziale in R 3 è che V sia irrotazionale, cioè V = 0. Se V(r) è a potenziale allora V = 2 φ. (59)

40 Campi solenoidali Un campo vettoriale V(r) si dice solenoidale se esiste un altro campo vettoriale A (potenziale vettore) tale che V = A. (60) 40/293 Condizione necessaria e sufficiente affinchè V sia solenoidale è V = 0. Il potenziale di un campo solenoidale ed a potenziale è armonico; in questo caso il campo si dice laplaciano. Il teorema fondamentale dell analisi vettoriale Sia V(r) un campo vettoriale continuo con divergenza e rotore continui, tale che per r V si comporta come 1/r 1+ε mentre V e V si comportano come 1/r 2+ε dove ε > 0. Allora, a meno di un vettore costante (c 1 ), V può essere espresso come la somma di un campo potenziale e di uno solenoidale, cioè: V = φ + A + c 1. (61)

41 Calcolo tensoriale Introduzione (diadi) Si chiama diade la coppia di vettori 41/293 a b. (62) Una diade è associata a due direzioni orientate (ma non identificata da esse). La diade a b costituisce il risultato dell operazione prodotto tensoriale tra i vettori a e b. Il prodotto tensoriale non è commutativo: b a a b. Rappresentazione cartesiana della diade: a b = σ i a i b j σ j, la diade è quindi rappresentata nel riferimento cartesiano dalle 9 componenti scalari (a i b j ).

42 Tensore (di ordine 2) Il tensore A è definito in un riferimento cartesiano come A = σ i A ij σ j. (63) A è stato individuato come la somma di 9 diadi coordinate. A differenza della diade, le due direzioni orientate associate al tensore A non sono esplicite. Il tensore è rappresentato nel riferimento cartesiano dalle 9 componenti scalari A ij. Un tensore è esprimibile con la matrice quadrata (3 3): A 11 A 12 A 13 A = A 21 A 22 A 23 (64) A 31 A 32 A 33 A ii sono le componenti normali, A ij (j i) sono le componenti tangenziali. 42/293

43 Tensore trasposto (Ã) ij = A ji. (65) 43/293 Tensore simmetrico Tensore antisimmetrico à = A A ji = A ij. (66) A ji = A ij. (67) Un tensore antisimmetrico ha necessariamente nulle le componenti lungo la diagonale principale.

44 Algebra dei tensori Eguaglianza 44/293 A = B A ij = B ij. (68) Tensore nullo Prodotto di uno scalare per un tensore A = 0 A ij = 0. (69) fa = σ i fa ij σ j. (70)

45 Prodotto scalare di un vettore per un tensore a sinistra V A = V i A ij σ j. (71) 45/293 Prodotto scalare di un vettore per un tensore a destra Componente vettoriale sinistra o destra A V = σ i A ij V j. (72) σ i A = A ij σ j = d i ; (73) A σ j = σ i A ij = s j. (74) I 3 vettori d i sono le componenti vettoriali destre di A nel riferimento O(x 1, x 2, x 3 ), mentre i 3 vettori s j sono le componenti vettoriali sinistre. A = σ i d i = s i σ i. (75)

46 Prodotto scalare di due tensori A B = C = σ i A ik B kj σ j. (76) Il prodotto scalare di due tensori è equivalente al prodotto di due matrici (3 3) e non commuta. (A B) = B Ã. (77) 46/293 Doppio prodotto scalare di due tensori Prodotti vettoriali A : B = A ik B ki. (78) V A = σ i ε ilm V l A mj σ j, (79) A V = σ i ε mlj A im V l σ j. (80)

47 Traccia di un tensore Tr(A) = A ii. (81) La traccia del tensore è invariante (non dipende dal sistema di riferimento). 47/293 Tensore unitario Si nota che, ad esempio: U = (82) V U = U V = V. (83) Tensore isotropo Si dice isotropo un tensore del tipo fu con f R.

48 Applicazione: il tensore degli sforzi in un fluido in quiete τ: tensore degli sforzi; t n = n τ. (84) t n : sforzo (vettore forza per unità di superficie) agente su una superficie elementare di normale generica n, positivo se di trazione. Nel caso di un fluido in quiete 48/293 il tensore degli sforzi è isotropo. Infatti: τ = pu ; (85) df = n ( pu)ds = pnds, (86) che è appunto la definizione di pressione idrostatica in un fluido in quiete. Riformulazione del Principio di Pascal: il tensore degli sforzi in un fluido in quiete è isotropo.

49 Parte simmetrica, antisimmetrica e isotropa di un tensore È sempre possibile decomporre un tensore in una parte simmetrica ed una antisimmetrica A = A (s) + A (a) : A (s) = A + Ã 2, A (a) = A Ã 2. (87) 1Tr(A)U: parte isotropa di A. 3 1Tr(A) è la media aritmetica delle 3 componenti normali del tensore 3 ed è invariante. A = 1Tr(A)U+A, dove A è detto parte deviatorica di A (è a traccia nulla). V A = V 1 3 Tr(A)U + V A 0 = 1 3 Tr(A)V + V A 0. A = 1 Tr(A)U + A(s) + A (a) /293

50 Calcolo differenziale tensoriale Gradiente di un vettore V = σ i V j x i σ j. (88) Derivata direzionale (in n) di V: n V = n i V x i. (89) Tr( V) = V. (90) ( V 2) ( V) V =. (91) 2 Un identità particolarmente notevole: ( V 2) V V = + ( V) V. (92) 2 Dividendo la (92) per V : v V = (V ) + ( V) v. 50/293

51 Divergenza di un tensore A = A ij x i σ j. (93) 51/293 (fa) = f A + f A. (94)

52 Teoremi di Gauss 52/293 Sia V(r) un campo vettoriale continuo con le derivate delle sue componenti in V S, allora: VdV = n VdS, (95) V S VdV = n VdS, (96) V S VdV = n VdS. (97) V S

53 Sia f(r) una funzione scalare continua con le sue derivate in V S, allora: fdv = n fds. (98) V S 53/293 Una definizione di indipendente dal riferimento 1 = lim n( )ds. (99) V 0 V 1 f = lim V 0 V 1 V = lim V 0 V S S S nfds. (100) n VdS. (101)

54 Teorema di Stokes 54/293 Data la superficie S delimitata dal circuito C e dato V(r), un campo vettoriale continuo con le derivate delle sue componenti in S C, allora n VdS = V dl. (102) S dl: vettore spostamento elementare lungo il circuito C. Γ = C V dl: circolazione del vettore V lungo il circuito C. Il teorema di Stokes lega il rotore alla circolazione. C

55 Equazioni di bilancio 55/293 V: volume di controllo (per ora lo si suppone fisso rispetto al riferimento inerziale), è il volume che contiene il sistema che si intende studiare; S: superficie di controllo; n: versore localmente normale alla superficie di controllo orientato verso l esterno del volume.

56 Una grandezza G si dice estensiva quando è associata (proporzionale) alla massa. Una grandezza G si dice intensiva quando non è associata alla massa ed è funzione solo del punto. Massa, quantità di moto, energia, entropia sono esempi di grandezze estensive. Temperatura, pressione, viscosità sono esempi di grandezze intensive. Per una grandezza estensiva è possibile formulare un equazione di bilancio all interno del volume di controllo: 56/293 Variazione di G nell unità di tempo = Scambio di G con l esterno + Produzione di G nel volume di controllo

57 M: massa all interno di un volume V; G g = lim : grandezza G specifica (per unità di massa); V 0 M g + = lim : grandezza G per unità di volume. V La densità ρ è la massa per unità di volume. V 0 G g + M = lim = ρg. (103) M V Variazione nell unità di tempo di G in V: d ρgdv = dt t (ρg)dv. V V 0 G V 57/293

58 Il flusso di una grandezza Il flusso ϕ G di una grandezza G dà, in intensità e direzione, la quantità di G che attraversa una superficie elementare, per unità di tempo e di superficie. 58/293 ϕ G è un vettore se G è uno scalare; ϕ G è un tensore se G è un vettore. [ϕ G ] = [G] [L 2 ][t] = [G] [L] [L 3 ] [t] quindi è possibile esprimere il flusso come, (104) ϕ G = g + W = ρgw, (105) con W un vettore velocità opportuno. Nel caso della massa M: ϕ M ρv. (106)

59 Scambio di G con l esterno: Produzione S n ϕ G ds. ġ + = [G] : produzione di G nell unità di volume e di tempo; [L 3 ][t] ġ = [G] : produzione specifica di G; [M][t] ġ + = ρġ. Produzione di G nel volume di controllo: ρġdv. V 59/293

60 Equazione di bilancio integrale V t S (ρg)dv = n ϕ G ds + V ρġdv. (107) 60/293 Equazione di bilancio differenziale Applicando il teorema di Gauss all integrale del flusso nella (107): [ ] t (ρg) + ϕ ρġ dv = 0. (108) G V Questo integrale è nullo qualunque sia la scelta di V se e soltanto se l integrando è nullo, da cui l equazione di bilancio in forma differenziale: t (ρg) + ϕ G = ρġ. (109) La fisica del problema è racchiusa nella determinazione dell espressione del flusso e della produzione.

61 Equazione di bilancio della massa (continuità) g = 1, g + = ρ; ϕ M = ρv; ġ = 0: la massa si conserva. Forma integrale dell equazione di conservazione della massa: ρ V t S dv + n ρvds = 0. (110) Forma differenziale: ρ t + (ρv) = 0. (111) 61/293

62 Rappresentazione euleriana e lagrangiana Rappresentazione euleriana: si assumono come variabili indipendenti le coordinate dello spazio ed il tempo (x 1, x 2, x 3, t) = (r, t); il problema fluidodinamico consiste nell individuazione della generica grandezza g(r, t) in ciascun punto del campo al variare del tempo. Rappresentazione lagrangiana: Individuazione al variare tempo dell evoluzione della generica grandezza di una data particella. Indicando con R = σ i X i la posizione che la data particella assume al tempo iniziale t 0, le variabili indipendenti diventano (R, τ) con τ = t. Per passare da una rappresentazione all altra occorre conoscere la trasformazione in forma vettoriale: i = 1, 2, 3 x i = x i (X 1, X 2, X 3, τ), t = τ; (112) r = r(r, t), t = τ. (113) 62/293

63 Si assume che: 1. nessuna regione di volume finito si trasforma nel tempo in una regione di volume nullo o infinito; 2. nel tempo volumi si trasformano in volumi, superfici in superfici, curve in curve, costituiti sempre dalle stesse particelle. Nota l evoluzione di una grandezza in una rappresentazione lagrangiana g(r, τ), la rappresentazione euleriana si ottiene tramite le (112) o (113): g(r, t) = g[r(r, τ), t]. (114) 63/293

64 Derivata sostanziale Definizione di velocità di una particella: V = V(R, τ) = r ( ) r (R, τ) = τ τ Definizione di derivata sostanziale: D Dt = ( τ R=cost ) R=cost ( ) xi = σ i τ R=cost. (115). (116) Tenendo conto della (113), della regola di derivazione delle funzioni di funzioni: Dg Dt = g ( ) ( ) t g t τ + xi. (117) x i t=cost τ R=cost Essendo t/ τ = 1, è possibile ottenere la seguente rappresentazione euleriana della derivata sostanziale: D Dt = t + V. (118) 64/293

65 Flusso convettivo e diffusivo ϕ G ρgv + J G (119) 1. ρgv: flusso convettivo, associato al trasporto della grandezza g con la velocità di massa V. 2. J G : flusso diffusivo, associato al trasporto della grandezza con la velocità molecolare relativa al moto del baricentro della particella. È possibile definire il flusso diffusivo o con leggi fenomenologiche o ricorrendo alla Teoria cinetica dei gas. 65/293

66 Equazioni del bilancio in forma lagrangiana 66/293 d (ρg)dv m = n J dt G ds m + ρġdv m. (120) V m (t) S m (t) V m (t)

67 Essendo (ρdv m = dm): d m = dt V m (t)(ρg)dv d dt M g(r, τ)dm = si ha che d (ρg)dv m = dt V m (t) V m (t) allora, sempre applicando il teorema d Gauss: V m (t) [ ρ Dg Dt + J G ρġ valida comunque si sceglie V m (t), per cui: M g(r, τ) dm, (121) τ ρ Dg Dt dv m, (122) ] dv m = 0, (123) ρ Dg Dt + J G ρġ = 0, (124) equazione di bilancio differenziale in forma lagrangiana. Nell equazioni di bilancio in forma lagrangiana compare solo il flusso diffusivo. 67/293

68 Le equazioni della Fluidodinamica Conservazione della massa (continuità) Forma integrale dell equazione di conservazione della massa: ρ V t S dv + n ρvds = 0. (125) Forma differenziale: ρ + (ρv) = 0. (126) t Svolgendo la divergenza nella (126) si ottiene (v = 1/ρ, volume specifico): V = 1 Dv v Dt ; (127) la divergenza della velocità misura la variazione percentuale nell unità di tempo del volume di una particella. 68/293

69 Se il flusso è incomprimibile: V = 0 ; (128) la conservazione della massa assicura che un campo di moto incomprimibile è solenoidale. Se il flusso è stazionario: 69/293 (ρv) = 0 ; (129) la conservazione della massa assicura che in un campo di moto comprimibile e stazionario è solenoidale il vettore ρv. Prob. n. 10: dimostrare che in flusso stazionario la portata di un condotto è costante Occorre scrivere l equazione di conservazione della massa in forma integrale per un condotto con pareti laterali impermeabili (n V = 0).

70 Bilancio della quantità di moto g = V, g + = ρv; flusso diffusivo J V = τ; produzione per unità di volume f + = ρg; g = Ψ, Ψ = gz energia potenziale del campo gravitazionale. Forma integrale del bilancio di quantità di moto: d ( ) ρvdv + n ρvv τ ds = dt ρgdv. (130) Forma differenziale: V S ρv t Forma integrale lagrangiana: d ρvdv m = dt V m (t) + (ρvv τ) = ρg. (131) S m (t) n τds m + V V m (t) ρgdv m. (132) 70/293

71 Forma differenziale lagrangiana: ρ DV Dt L espressione di τ dipende dal tipo di fluido. τ = ρg. (133) 71/293 Modello di fluido newtoniano: τ = pu + µ 2 ( V)U + 2µ( V) (s) 0 (134) µ 2 : secondo coefficiente di viscosità del fluido. Per i fluidi di nostro interesse µ 2 /µ 1, per cui lo trascureremo: τ = pu + τ d, (135) τ d = 2µ( V) (s) 0. (136) Nel modello newtoniano, così come nella maggior parte dei problemi di nostro interesse, il tensore degli sforzi è simmetrico.

72 Prob. n. 11: determinare le 9 componenti del tensore degli sforzi di un fluido newtoniano Prob. n. 12: determinare l espressione della forza (aerodinamica) che agisce su un corpo immerso in una corrente fluida (Non è altro che il flusso di quantità di moto attraverso il corpo). 72/293

73 Conservazione dell energia Principio dell equilibrio evolutivo: si assume che i tempi caratteristici del problema fluidodinamico siano molto maggiori del tempo caratteristico con cui il sistema termodinamico particella raggiunge il proprio equilibrio per cui, istante per istante, la particella è in equilibrio termodinamico. g = e, g + = ρe; e = u + V 2 /2 + Ψ, u è l energia interna specifica; flusso diffusivo J e = J u + J c ; legge di Fourier: J u = λ T (flusso di energia nel modo calore); λ: conducibilità termica, si misura in J/(m s K); J c = τ V (flusso di energia nel modo lavoro); ė = 0, l energia totale si conserva. 73/293

74 Forma differenziale lagrangiana ρ D (u + V 2 ) Dt 2 + Ψ (λ T ) (τ V) = 0. (137) Identità vettoriale: 74/293 (τ V) = ( τ) V + τ : V. (138) Il flusso di energia nel modo lavoro consta di due contributi: 1. ( τ) V: lavoro compiuto sulla particella per effetto dello spostamento V; 2. τ : V: contributo dovuto alla deformazione della particella. Bilancio dell energia cinetica ρ D ( V 2) (τ V) = ρ ε c. (139) Dt 2

75 Questa equazione si può riottenere moltiplicando scalarmente per V il bilancio di quantità di moto: ρ DV Dt V ( τ) V = ρg V. (140) In base alle identità vettoriali (138) e (91): ρ D ( V 2) (τ V) = ρg V τ : V. (141) Dt 2 La produzione di energia cinetica è quindi: 75/293 ρ ε c = ρg V τ : V. (142) Il bilancio di energia cinetica non è un equazione indipendente.

76 Bilancio dell energia potenziale ρ DΨ Dt = ρ ε p. (143) Il flusso diffusivo di energia potenziale è nullo. Il potenziale (gravitazionale) dipende solo dallo spazio e non dal tempo. Ψ = g. per cui e DΨ Dt ρ DΨ Dt = V Ψ, (144) = ρg V (145) ρ ε p = ρg V, (146) da confrontare con la produzione di energia cinetica. Il bilancio di energia potenziale non è un equazione indipendente. 76/293

77 Bilancio dell energia interna Si ottiene sottraendo i bilanci di energia cinetica e potenziale a quello di energia totale: ρ Du Dt + J u = τ : V (147) e ρ ε u = τ : V, (148) da confrontare con la produzione di energia cinetica. Nulla possiamo ancora dire sul segno della produzione di energia interna. 77/293

78 Bilancio dell entropia ρ Ds Dt + J s = ρṡ. (149) Du Dt = T Ds Dt pdv Dt. (150) Il bilancio di entropia si ottiene combinando il bilancio di energia interna e di volume specifico. Si ottiene: Confrontando con la (149): ρ Ds Dt = 1 T τ : V 1 T J u + p T V. (151) T ρṡ T J s = + τ : V J u + p V, (152) T ρṡ (T J s ) = J s T + τ : V J u + p V, (153) da cui: J s = J u T ; T ρṡ = J s T + τ : V + p V. (154) 78/293

79 Per un fluido newtoniano e fourieriano si ottiene 2 τ : V = p( V) + Φ, (155) Φ = 2µ( V) (s) 0 : ( V) (s) 0. (156) 79/293 Φ: funzione di dissipazione. T ρṡ = λ T T + Φ. (157) T Affinchè sia soddisfatto il II principio della termodinamica (la produzione di entropia è positiva): λ > 0, µ > 0 ; (158) il flusso termico va da zone a temperatura maggiore a zone a temperatura minore e l energia cinetica (parte) si dissipa in energia interna, processi entrambi irreversibili. 2 Si sfruttano le seguenti identità: A 0 : U = 0, A (s) : A (a) = 0.

80 Le equazioni di Navier-Stokes Caso di fluido newtoniano e foureriano. Continuità: ρ + (ρv) = 0 ; t (159) quantità di moto: ρ DV Dt + p = 2 [µ( V)(s) 0 ] + ρg ; (160) energia: ρ D (u + V 2 ) Dt 2 + Ψ = (λ T ) (pv) + 2 [µ( V) (s) 0 V]. (161) La chiusura del sistema richiede la conoscenza delle relazioni di stato: p = p(ρ, T ), u = u(ρ, T ), (162) µ = µ(p, T ), λ = λ(p, T ). (163) 80/293

81 Condizioni iniziali e al contorno V(r, t 0 ) = V i (r), p(r, t 0 ) = p i (r), ρ(r, t 0 ) = ρ i (r). (164) 81/293 Parete impermeabile fissa: V = 0, p =?. Nel caso di proprietà costanti (ρ e µ), la temperatura non compare nell equazioni di continuità e quantità di moto. Continuità e quantità di moto possono essere integrate indipendentemente dall equazione dell energia. L equazione dell energia può essere risolta, se necessario, successivamente, con il campo di velocità già noto. Prob. n. 13: scrivere le equazioni scalari di Navier- Stokes nel caso 2D a proprietà costanti (ρ, µ, λ)

82 Alcune soluzioni esatte delle equazioni di Navier Stokes Ipotesi: flusso incomprimibile, flusso stazionario, fluido Newtoniano con proprietà costanti. 82/293 V = 0, (165) ρv V + p = µ 2 V. (166)

83 Flusso alla Couette Flusso confinato fra due pareti di lunghezza infinita distanti 2h l una dall altra, la parete superiore si muove con velocità U rispetto alla parete inferiore. pareti di lunghezza infinita u = u(y) pressione costante p = 0 Condizioni al contorno: 83/293 u( h) = 0, v( h) = 0, u(h) = U, v(h) = 0. (167)

84 Dall equazione di continuità e dalla condizione al contorno per v: v y = 0 v = 0. (168) Dall equazione della quantità di moto lungo y e dalle condizioni al contorno per u: µ d2 u dy = 0 u = U ( 1 + y ). (169) 2 2 h 84/293 C f ṁ = ρuh, 2 (170) τ = µ du dy = µu 2h, (171) τ 1 h = µ ρuh = 1. Re 2 h (172)

85 Flusso in un condotto a sezione circolare (flusso alla Hagen- Poiseuille) Si utilizza un sistema di riferimento cilindrico (per simmetria θ = 0). Si assume che il flusso nel condotto sia completamente sviluppato: u = u(r), v = v(r) Condizioni al contorno sulla parete del condotto: 85/293 u(r 0 ) = v(r 0 ) = 0. (173) Dall equazione di continuità si ottiene ancora che v = 0 per cui p = 0 r dall equazione di quantità di moto lungo z e quindi p = p(x). Equazione di quantità di moto lungo r dp dx = µ ( d2 u(r) dr r du(r) dr ). (174) Essendo p = p(x) e u = u(y), affinchè l equazione sia soddisfatta si ricava che dp/dx deve essere una costante.

86 L equazione di quantità di moto è lineare e può essere risolta: u = dp/dx (r 2 0 r 2 ) (175) 4µ risultati per il flusso alla Hagen-Poiseuille Portata: ( ṁ = πr4 0 dp ). (176) 8µ dx Velocità media e massima: u m = dp/dx r 2 0 = 1 8µ 2 u max, u max = dp/dx r 2 0. (177) 4µ Sforzo di attrito alla parete: ( τ w = µ du ) = 4µu m. (178) dr w r 0 Coefficiente d attrito fattore d attrito di Fanning : C f = τ w = 8µ. (179) 1/2ρu 2 m ρu m r 0 86/293

87 Flusso alla Poiseuille piano Si ricava in modo analogo: ( ) dp h 2 ) u = (1 y2, dx 2µ h 2 (180) ( ) dp h 2 u max = dx 2µ, (181) 87/293 ṁ = 4 3 hu max, (182) u m = Q 2h = 2 3 u max, (183) τ w = 3µu m h, C f = 6µ ρu m h. (184)

88 Equazioni di bilancio adimensionali Il problema consiste nella scelta di opportune grandezze di riferimento delle variabili indipendenti e dipendenti. ḡ = g/g r ; ḡ: grandezza adimensionale; g r : grandezza di riferimento. La scelta di g r è appropriata quando ḡ O(1). 88/293

89 Continuità Si assuma il flusso isoentropico (ds = 0) per cui ( ) Dρ ρ Dt = Dp p Dt = 1 Dp a 2 Dt, (185) s a: velocità del suono. Scegliendo t r = L r /V r e p r = ρ r Vr 2 il bilancio di volume specifico (127) diventa Mr 2 D p ρā 2 D t + V = 0. (186) M 2 r = V 2 r /a 2 r: numero di Mach di riferimento. M r 0 V = 0 flusso incomprimibile. 89/293

90 Quantità di moto L r ( ρ V) V r t r t St r = t rv r L r + ( ρ V V) + p = µ r 2 ρ r V r L (s) [ µ( V) 0 ] + L rg r ρḡ. r Vr 2 (187) Re r = ρ rv r L r µ r F r r = V r 2 L r g r convezione di V, numero di Strouhal. instazionarieta convezione di V, numero di Reynolds. effetti viscosi convezione di V, numero di Froude. gravita 1 ( ρ V) + St r t ( ρ V V) + p = 1 2 Re (s) [ µ( V) 0 ] + 1 ρḡ. (188) r F r r Scegliendo p r = ρ r a 2 r il termine di pressione diventa 1 p che implica un secondo significato a M r Mr 2 : 90/293

91 M r convezione di V diffusione reversibile di V. Combinando questi numeri caratteristici si possono misurare le importanze relative tra tutti i vari contributi. 91/293

92 Energia e r = u r = a 2 r, Ψ r = g r L r : ē = ū + M 2 r V 2 Ulteriore significato di M 2 r e F r r. T r = a 2 r/c p r, p r = ρ r a 2 r: 2 + M 2 r F r r Ψ. (189) 1 ( ρē) + St r t ( ρē V) = 1 M ( λ T ) r ( p V)+ 2 (s) 2 [ µ( V) 0 V]. P e r Re r (190) P r r = µ rc p r flusso lavoro viscoso, numero di Prandtl. λ r f lusso termico convezione di energia P e r = Re r P r r, numero di Peclet. f lusso termico M 2 r Re r flusso lavoro viscoso convezione di energia. 92/293

93 Aerodinamica dei flussi non dissipativi (ideali) Le equazioni di Eulero Ipotesi: Re r, Pr r O(1) (almeno), per cui anche P e r. 1 ρ St r t + ( ρ V) = 0 ; (191) 1 ( ρ V) + St r t ( ρ V V ) + pu = 1 ρḡ ; (192) F r [ ( r 1 ( ρē) + St r t ρ ē + p ρ ) ] V = 0. (193) Scompaiono dalle equazioni tutti i termini che portano a produzione di entropia: il fenomeno è non dissipativo; queste equazioni governano la dinamica di un fluido (o di un flusso) ideale. Si abbassa l ordine di derivazione (scompaiono tutte le derivate seconde): attenzione alle condizioni al contorno. 93/293

94 In molte applicazioni aerospaziali F r r 1, per cui può essere trascurato sia il temine di produzione nel bilancio di quantità di moto (che pure diventa un equazione di conservazione) sia l energia potenziale gravitazionale nel bilancio dell energia. 94/293

95 Cinematica della particella Traiettoria: luogo delle successive posizioni assunte da una particella durante il suo moto, al variare del tempo. Linea di corrente: curva inviluppo del vettore velocità nella rappresentazione euleriana. Linea tracciante: luogo delle posizioni assunte, al variare del tempo, dalle successive particelle che passano per uno stesso punto. In regime instazionario, in generale, traiettorie, linee di corrente e linee traccianti sono diverse. In regime stazionario traiettorie, linee di corrente e linee traccianti coincidono. 95/293

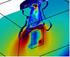
96 96/293 Visualizzazione delle linee di corrente intorno ad un profilo NACA tramite bolle d aria, M 0, Re 6000.

97 97/293 Visualizzazione (con tracciante) della formazione del vortice di distacco al bordo di uscita di un profilo alare, M 0, Re S 1000.

98 Deformazione lineare della particella 98/293 u Q = u P + u x ; x (194) u P t + x = x + u Q t ; (195) ε x = x x = u x x t, dε x dt = u x. (196) ε x : deformazione lineare (percentuale) nella direzione x; dε x : velocità di deformazione. dt

99 Velocità angolare di rotazione della particella 99/293 α 1 = v x t, Ω z = 1 (α 1 + α 2 ) 2 t α 2 = u t ; y (197) = 1 ( v 2 x u ). y (198) Ω = 1 ( V), V = ζ (vorticita ). (199) 2

100 Deformazione angolare della particella 100/293 γ xy = 1 α + β 2 t = 1 2 ( v x + u ) y = [( V) (s) 0 ] xy (200) Una particella trasla con velocità V, ruota con velocità angolare V, si dilata secondo V e si deforma secondo ( V)(s) 1 2 E newtoniano un fluido in cui sforzi tangenziali e deformazioni della particella da essi provocati sono proporzionali tra loro. 0.

101 Il teorema di Crocco Accelerazione della particella: DV Dt = V t + V V ; (201) ( V 2) V V = + ( V) V ; (202) 2 relazione di Gibbs: 1 p = h T s. (203) ρ Sostituendo queste relazioni nel bilancio di quantità di moto e definendo l entalpia totale come H = h + V 2 /2 + Ψ si ottiene il teorema di Crocco: V t + H + ( V) V = T s + f d. (204) f d è la forza dissipativa per unità di massa che agisce sulla particella. 101/293

102 Bilancio dell energia cinetica: ( V 2) + V H = T V s + V f t 2 d. (205) Ipotesi: 1. flusso ideale (Re e P e ); 2. regime stazionario. Il bilancio dell entropia diventa: Ds = V s = 0, (206) Dt in un flusso ideale e stazionario l entropia è costante lungo una linea di corrente (flusso isoentropico). Il bilancio dell energia cinetica diventa: DH = V H = 0, (207) Dt in un flusso ideale e stazionario l entalpia totale è costante lungo una linea di corrente (flusso isoentalpico). 102/293

103 Il teorema di Bernoulli (generalizzato) Se l entropia a monte è uniforme (s = s ) allora s è costante in tutto il campo (flusso omoentropico). Se l entalpia totale a monte è uniforme (H = H ) allora H è costante in tutto il campo (flusso omoentalpico). Il risultato h + V 2 + Ψ = cost (208) 2 è noto come teorema di Bernoulli (generalizzato). Il teorema di Crocco per un flusso stazionario ed ideale: H + ( V) V = T s (209) mostra che se il flusso è anche omoentalpico ed omoentropico: Cioè è verificata una delle seguenti possibilità: ( V) V = 0. (210) 1. V = 0, il campo è irrotazionale φ V = φ; 2. V V, campo alla Beltrami. 103/293

104 Il teorema di Bernoulli (incomprimibile) Sia M 0 ρ = cost. In un fluido isoentropico, incomprimibile la relazione di Gibbs diventa dh = d(p/ρ), cioè dell entalpia può variare solo la parte legata alla pressione, mentre l energia interna rimane costante: in un flusso incomprimibile isoentropico la temperatura non varia. Il teorema di Bernoulli generalizzato assume allora la forma 104/293 p ρv 2 + ρψ = cost. (211)

105 Flusso incomprimibile quasi-unidimensionale Ipotesi: 1. regime stazionario; 2. condotto orizzontale (gravità trascurabile) con deboli variazioni dell area della sezione; 3. regime incomprimibile; 4. flusso ideale (isoentropico). V 1 : velocità media alla sezione di area A 1 ; p 1 : pressione media alla sezione di area A 1. Conservazione della massa: Teorema di Bernoulli: V 1 A 1 = V 2 A 2. (212) p ρv 2 1 = p ρv 2 2. (213) 105/293

106 Prob. n. 14: determinazione della portata di un condotto tramite il tubo Venturi 106/293 Occorre collegare le sezioni 1 e 2 con un manometro per misurare la differenza di pressione p = p 1 p 2. Prob. n. 15: determinazione della velocità di un aeromobile con il tubo di Pitot (facoltativo)

107 Il teorema di Bernoulli instazionario (generalizzato) Ipotesi: 1. regime ideale omoentropico; 2. campo di moto irrotazionale. Dal teorema di Crocco si ricava: ( ) ϕ + H = 0 ; (214) t integrando: ϕ t + h + V Ψ = f(t). (215) 107/293

108 Equazione di bilancio della vorticità ζ = V Si ottiene effettuando il rotore dell equazione di bilancio della quantità di moto: 108/293 Dζ Dt = ζ V ( V)ζ + 1 ρ2 ρ p + Se ρ = ρ(p) il fluido si dice barotropico. Un flusso incomprimibile è barotropico: ρ = k. Un flusso omoentropico è barotropico: ρ = k/p 1/γ. Equazione di bilancio di vorticità per un flusso incomprimibile: ( ) τ d ρ (216) Dζ Dt = ζ V ( V)ζ + ν 2 ζ. (217) Equazione di bilancio di vorticità per un flusso omentropico (comprimibile): Dζ = ζ V ( V)ζ. (218) Dt Non compare la pressione!

109 Circuiti Un circuito C di una regione V si dice riducibile se può essere trasformato con continuità in un punto senza abbandonare la regione, altrimenti il circuito è detto irriducibile. Una regione V si dice semplicemente connessa se contiene tutti circuiti riducibili, altrimenti la regione è detta molteplicemente connessa. Teorema di Stokes: n ζ ds = V dl. (219) S La validità del teorema richiede che V sia regolare in S, cioè il circuito C deve essere riducibile. Un importante corollario del teorema di Stokes è che se V è irrotazionale in una regione semplicemente connessa V allora le circolazioni di V su qualsiasi circuito di V sono nulle. C 109/293

110 Con degli opportuni tagli una regione molteplicemente connessa può sempre essere trasformata in una regione semplicemente connessa. 110/293 In un dominio reso semplicemente connesso con dei tagli non è richiesta la continuità di una grandezza attraverso il taglio. Due circuiti sono riconducibili se è possibile trasformare con continuità l uno nell altro senza abbandonare il dominio.

111 I teoremi di Helmholtz Linea vorticosa: una curva tangente in ogni punto a ζ = V. Superficie vorticosa: una superficie con il vettore ζ tangente in ogni suo punto. Tubo vorticoso: L insieme delle linee vorticose passanti per una curva chiusa che racchiude un area finita. Filetto vorticoso: L insieme delle linee vorticose passanti per una curva chiusa che racchiude un area infinitesima. Si definisce intensità di un tubo vorticoso il flusso di ζ attraverso una sua sezione: Γ = n ζds. (220) S I teorema di Helmholtz: l intensità di un tubo vorticoso è la stessa in tutte le sue sezioni trasversali. 111/293

112 112/293 La dimostrazione del I teorema di Helmoltz è immediata applicando il teorema di Gauss al vettore vorticità nel volume indicato in figura e tenendo conto della solenoidalità di ζ e della definizione di tubo vorticoso per cui il flusso di ζ sulla superficie laterale del cilindro è nullo. Conseguenze del I teorema di Helmholtz: un tubo vorticoso o è chiuso o inizia e finisce su un confine del dominio. Tubo vorticoso isolato: quando all esterno del tubo il campo è irrotazionale.

113 II teorema di Helmholtz: la circolazione presa nello stesso senso intorno a due qualsiasi circuiti irriducibili e riconciliabili che circondino un tubo vorticoso isolato una sola volta è la stessa ed è uguale, in valore assoluto, all intensità del tubo vorticoso. 113/293 Basta collegare i due circuiti con un taglio per ottenere un unico circuito riducibile in un campo irrotazionale che avrà quindi circolazione totale nulla. Essendo il contributo del taglio alla circolazione nullo (percorso 2 volte con verso contrario) ed essendo i due circuiti percorsi in verso opposto ne risulta che la loro circolazione deve coincidere. Se si sceglie uno dei due circuiti lungo il tubo vorticoso si ottiene anche che la circolazione è pari all intensità del tubo vorticoso che non varia in base al I teorema di Helmholtz.

114 Velocità indotta da un vortice isolato 114/293 V(P ) = Γ 4π Caso di vortice infinito rettilineo: L k r r 3 dl. (221) V = Γ 2πR ; (222) R: distanza del punto P dal vortice, V giace nel piano ortogonale al vortice con verso tale che k, R, V è una terna levogira.

115 Il teorema di Kelvin Γ(t) = V dl, (223) C m C m : circuito materiale. DΓ = D ( ) D V dl = (V dl) = Dt Dt C m C m Dt DV C m Dt dl + V dv = C m ( DV V 2) C m Dt dl + d = C m 2 DV dl. (224) C m Dt Dal bilancio di quantità di moto: DV Dt = (h + Ψ) + T s + f d ; (225) 115/293

116 quindi: DΓ Dt = T s dl + f d dl. (226) C m C m Teorema di Kelvin: in un flusso ideale e omoentropico la circolazione di un circuito materiale non varia nel tempo. Corollari 1. Tubi vorticosi, superfici vorticose e filetti vorticosi sono costituiti sempre dalle stesse particelle. Si consideri un arbitrario circuito materiale giacente su una superficie vorticosa, avrà quindi circolazione nulla e per il teorema di Kelvin la circolazione rimarrà nulla al variare del tempo e data l arbitrarietà della scelta la superficie su cui giace il circuito continuerà ad essere tangente alla vorticità ne segue che essa è ancora superficie vorticosa. 2. L intensità di un tubo vorticoso non varia con il tempo. È un ovvia conseguenza del precedente corollario. 116/293

117 Flussi incomprimibili ideali L equazione di continuità ci assicura che il campo di velocità di un flusso incomprimibile è solenoidale quindi 117/293 V = 0 (227) Se il campo è anche irrotazionale in un dominio semplicemente connesso esiste il potenziale cinetico φ : φ = V. La continuità diventa: 2 φ = 0 (228) Il campo di velocità è governato dall equazione di Laplace con una sola incognita!

118 Flussi incomprimibili ideali 2D L equazione di continuità ci assicura che il campo di velocità di un flusso incomprimibile è solenoidale quindi 118/293 ed inoltre esiste il potenziale vettore A tale che V = 0 (229) V = A. (230) La funzione di corrente Per campi di moto bidimensionali (ci si concentra qui sul caso piano) deve risultare V 3 = 0, che implica in termini di A (definizione di rotore): soddisfatta per A 1 = A 2 = 0. A 2 x 1 A 1 x 2 = 0 ; (231)

119 Si definisce funzione di corrente ψ(r) l unica componente diversa da zero del potenziale vettore di un campo bidimensionale: ψ(r) = A 3. (232) In un riferimento cartesiano O(x, y) le componenti (u, v) di V sono date da u = ψ y ; v = ψ x. (233) In un riferimento polare O(r, θ) le componenti (V r, V θ ) di V sono date da V r = 1 ψ r θ ; V θ = ψ r. (234) Un campo di cui è data la funzione di corrente è certamente solenoidale ma non irrotazionale; irrotazionalità 2 ψ = 0. Un campo di cui è dato il potenziale φ è certamente irrotazionale ma non solenoidale; solenoidalità 2 φ = /293

120 Proprietà della funzione di corrente 1. L equazione di una linea di corrente è data da in termini di ψ questa relazione diventa: ψ x dy dx = v u, (235) ψ dx + dy = dψ = 0 ; (236) y la funzione di corrente è costante lungo una linea di corrente. 2. Il flusso di V attraverso una curva che congiunge due punti A e B di versore tangente t = (t 1, t 2 ) (quindi versore normale dato da n = (t 2, t 1 ) è dato da: B A V ndt = B A ψ dt = B A dψ = ψ(b) ψ(a). (237) 120/293

121 Il problema matematico 121/293 Ipotesi: 1. flusso 2D piano e stazionario f = f(x, y); 2. ρ = cost V = 0; 3. flusso ideale; 4. corrente uniforme.

122 Le ipotesi ci assicurano che il campo di velocità è solenoidale (incomprimibilità) ed irrotazionale (ideale e corrente uniforme). Il problema è governato dall equazione di continuità (equazione di Laplace): 2 φ = 0. (238) In coordinate cartesiane: In coordinate polari: 2 φ x + 2 φ 2 y = 0. (239) 2 2 φ r φ 2 r 2 θ + 1 φ 2 r r = 0. (240) 122/293

123 Condizioni al contorno 1. All infinito: lim r φ = V ; (241) 2. sul corpo di equazione nota y = y u (x), y = y l (x): 123/293 φ n = 0. (242) Problema ben posto: esiste una soluzione unica per φ continua in tutto il campo (a meno di una costante inessenziale).

124 Il problema in termini di ψ L equazione da risolvere è ancora l equazione di Laplace (con significato diverso!). Si impone l irrotazionalità del campo. 124/293 2 ψ = 0 ; (243) cambiano le condizioni al contorno. All infinito deve verificarsi ψ lim r y = V cos α, ψ lim r x = V sin α. (244) Sul corpo ψ = cost. (245) Campo di pressione Noto il campo delle velocità è possibile determinare il campo di pressione utilizzando il teorema di Bernoulli: p p = 1 2 ρ(v 2 V 2 ). (246)

125 Soluzioni elementari dell equazione di Laplace Le soluzioni dell equazione di Laplace vengono dette funzioni armoniche. Essendo quest equazione lineare la somma di due funzioni armoniche è ancora armonica. È possibile ottenere soluzioni complesse sommando più soluzioni elementari. 125/293 Corrente uniforme φ = V cos α x + V sin α y ; (247) ψ = V cos α y V sin α x. (248) Sorgente (o pozzo) In coordinate polari: φ = Q 2π ln r ; ψ = Q 2π θ. (249)

126 Doppietta Si ottiene dalla sovrapposizione al limite di una sorgente e di un pozzo di intensità uguali ed opposte mantenendo costante il prodotto k = Q l. 126/293 φ = k cos θ 2π r ; ψ = k sin θ 2π r. (250)

127 Flusso non portante intorno al cilindro Si sovrapponga una corrente uniforme parallela all asse x ad una doppietta con asse parallelo ad x: ( = V r sin θ 1. (251) ψ = V r sin θ k sin θ 2π r ) k 2πV r 2 127/293 Ponendo R = k/2πv : ψ = V r sin θ [ 1 ( ) ] R 2 r. (252) r ψ V r sin θ = ψ. (253) ψ(r, θ) = 0. (254) Abbiamo trovato la soluzione potenziale incomprimibile di una corrente uniforme che investe un cilindro di raggio R.