INTRODUZIONE A. Guido Vagliasindi Controlli Automatici A.A. 06/07 Introduzione a MATLAB
|
|
|
- Lucia Corsi
- 8 anni fa
- Visualizzazioni
Transcript
1 INTRODUZIONE A
2 Documentazione Sito web di Mathworks: seguendo i link alla voce support e possibile trovare i manuali di Matlab in formato pdf. ( oc/matlab.shtml) Un testo in italiano di introduzione a matlab e Simulink: Guida Operativa a MATLAB, SIMULINK e Control Toolbox Alberto Cavallo, Roberto Setola, & Francesco Vasca Liguori Editore, 1994
3 OUTLINE Descrizione generale di MATLAB Quadro delle funzioni predefinite Definizione di matrici e vettori Definizione di polinomi Rappresentazione di sistemi dinamici lineari Analisi di sistemi di controllo Rappresentazione grafica dei dati
4 Descrizione generale di Matlab MATrix LABoratory Software esplicitamente realizzato per manipolazione di matrici Interattivo Interprete di comandi Elemento base: matrice (che non richiede dimensionamento) Sviluppato agli inizi degli anni '80, come sottoprodotto dei progetti LINPACK ed EISPACK, da The MathWorks Inc.
5 Interfaccia MATLAB Workspace COMMAND WINDOW History
6 Help di MATLAB E disponibile un aiuto in linea accessibile direttamente dalla riga di comando. Digitando help nella riga di comando vengono restituite tutte le funzioni. Digitando invece help nome_funzione viene restituita la sintassi d uso della funzione e una descrizione della stessa. E possibile anche utilizzare l help di windows associato al programma MATLAB. Sono presenti vari esempi dimostrativi accessibili digitando demos nella riga di comando. Infine si può utilizzare la funzione lookfor per cercare all interno della descrizione delle varie funzioni una parola chiave.
7 VARIABILI MATLAB supporta nomi di variabili sino a 63 caratteri ed è case sensitive. E possibile utilizzare lettere, numeri e i caratteri speciali che non hanno un corrispondente significato come operatori in MATLAB (praticamente solo l underscore _). La variabile deve sempre cominciare con una lettera. E' opportuno non utilizzare i nomi delle funzioni predefinite da MATLAB, ciò comporta l'annullamento del significato prestabilito da MATLAB per quella funzione e di conseguenza un messaggio di errore. Per assegnare una variabile non è necessaria una precedente dichiarazione.
8 VARIABILI Posso visualizzare il contenuto di una variabile inserendone semplicemente il nome dalla riga di comando. Utilizzando la funzione who viene restituita la lista di variabili definite nel workspace. La funzione whos fornisce anche una descrizione delle stesse indicandone anche la dimensione, il numero di bytes occupati e la classe. Ans è una variabile di MATLAB dove viene memorizzato il risultato di una eventuale operazione se non viene specificata una variabile a cui assegnare il risultato. Variabili speciali: eps = 2-52 rappresenta l'accuratezza (o Inf) infinito NaN risultato di 0/0 (Not A Number) pi π
9 VARIABILI Range: da a Accuratezza: 16 cifre decimali Operatori: +, *, -, / (divisione destra), \ (divisione sinistra), ^ (elevamento a potenza) Uso "normale" delle parentesi per cambiare la priorità tra gli operatori MATLAB consente l'uso di numeri complessi: si usa il simbolo "i" o "j" per indicare la parte immaginaria. La dichiarazione di variabili complesse avviene moltiplicando la parte complessa per "i" o "j" e sommando la parte reale:» z = 3+4*i; (niente spazi tra i termini) N.B. E equivalente usare z=3+4i; Tutte le funzioni MATLAB accettano variabili complesse come ingressi
10 MATRICI Qualunque variabile è considerata in MATLAB come una matrice, anche gli scalari e i vettori. In particolare uno scalare sarà una matrice (1x1) mentre un vettore sarà una matrice con una sola colonna (nx1) o con una sola riga (1xn). Una matrice può essere inserita in MATLAB in diverse maniere: a. assegnazione di lista di elementi b. generate da funzioni built-in c. create con un programma (m-file) d. caricate da file esterni (di dati)
11 MATRICI a. Assegnazione di lista di elementi Bisogna: Separare gli elementi di una riga con spazi vuoti o virgole; Usare un punto e virgola ; o un invio per indicare la fine di ciascuna riga. Racchiudere l elenco intero di elementi tra parentesi quadre» A=[1 2 3; 4 5 6; 7 8 9]» A=[1,2,3; 4,5,6; 7,8,9]» A=[ ] A= Se alla fine di ciascuna assegnazione metto» un ; non c è echo. Una volta fornita la matrice essa sarà memorizzata nel workspace e richiamabile semplicemente digitanto A e invio nella CW.
12 MATRICI b. Generate da funzioni built-in L output di alcune funzioni MATLAB è costituito da una matrice. Alcune funzioni elementari che restituiscono una matrice come uscita sono: eye(n,n) -> matrice identita nxn; zeros(n,m) -> matrice di zeri nxm; ones(n,m) -> matrice di uni nxm; rand(n,m) -> matrice nxm con elementi distribuiti uniformemente tra 0 e 1. c. Create con un programma In MATLAB è possibile scrivere degli script definiti m-files che contengono al loro interno una sequenza di comandi elementari o chiamate a funzioni che vengono poi interpretate da MATLAB come se venisse scritta nella command window.
13 MATRICI d. Caricate da file esterni (di dati) Ciascuna variabile contenute nel workspace possono essere salvate su disco con il comando save nome_file lista_variabili <opzioni> E possibile salvare tutto il workspace nel file nome_file.mat semplicemente con il comando save nome_file E possibile richiamare le variabili salvate precedentemente con un save o contenute in file di dati ottenuti attraverso altri programmi o acquisizioni con i comandi load nome_file lista_variabili <opzioni> load nome_file <opzioni> Per un dettaglio delle opzioni, digitare help load e help save nella command window
14 MATRICI E possibile accedere ai singoli elementi della matrice specificando la riga e la colonna.»a(1,2) ans = 2 E possibile selezionare intere righe o intere colonne della matrice utilizzando la wildcard :» A(1,:)» A(:,2) ans = ans = E anche possibile selezionare porzioni di matrice con la seguente sintassi» A(1:2,2:3) ans=
15 Funzioni in MATLAB MATLAB prevede un gran numero di funzioni matematiche standard Funzioni trigonometriche (sin, cos, tan, acos, asin, atan ) Esponenziale e logaritmo (exp, log, log10, sqrt ) Numeri complessi (abs -> modulo, angle -> fase, real -> parte reale, imag -> parte immaginaria ) Per un elenco delle funzioni matematiche elementari digitare help elfun per un elenco più avanzato help specfun o help elmat Esistono anche funzioni più complesse, realizzate tramite m-file e raccolte in forma di libreria dette toolbox. Per maggiori informazioni è possibile visitare il sito e scaricare i manuali dei singoli toolbox.
16 Operazioni su matrici Sono definite le normali operazioni aritmetiche: addizione + sottrazione - moltiplicazione * divisione / elevamento a potenza ^ ADDIZIONE E SOTTRAZIONE Le operazioni si possono effettuare tra elementi della stessa dimensione ed elementi di dimensioni diverse. Esempio :» A = [1 2 ; 2 1];» B = [2 1; 1 2];»A+B ans = »A-B ans = » x = [1 2 3]';» y = x + 1 y = 2 3 4
17 Operazioni su matrici PRODOTTO Anche in questo caso ci possono essere diverse combinazioni. Matrice * Matrice Matrice * Vettore Matrice * Scalare» A = [1 2 ; 2 1];» B = [2 1; 1 2];»A*B» ans= » A = [1 2 ; 2 1];» x = [1 2];»x*A» ans 5 4» A = [1 2 ; 2 1];»a=2;»a*A» ans
18 Operazioni su matrici DIVISIONE Sia A invertibile (quadrata, non singolare): A\B equivale a: A -1 B inv(a)*b B/A equivale a: BA -1 B*inv(A) Si usa nella soluzione di sistemi di equazioni lineari: x = B/A soluzione di x*a = B x = A\B soluzione di A*x = B ELEVAMENTO A POTENZA Sia A matrice quadrata, p uno scalare (non necessariamente intero) A^p p-esima potenza di A ovvero A*A*A*...*A se p intero
19 Operazioni su matrici FUNZIONI TRASCENDENTI exp(a) e sqrt(a) eseguono rispettivamente l'esponenziale e la radice quadrata dei singoli elementi si A expm(a), logm(a) e sqrtm(a) operano invece sulle matrici nella loro globalità: expm(a) I + A + A 2 / sqrtm(a) A^(1/2) TRASPOSIZIONE L operatore di trasposizione di una matrice è l apice. Se applicato ad un vettore lo trasforma da riga a colonna e viceversa. Se applicato ad una matrice a coefficienti complessi restituisce la matrice complessa coniugata trasporta.
20 Operazioni su matrici ALTRE FUNZIONI det(a) Calcola il determinante della matrice A eig(a) Calcola gli autovalori della matrice A inv(a) Calcola l inversa della matrice A rank(a) Calcola il rango della matrice A trace(a) Calcola la traccia della matrice A poly(a) Calcola i coefficienti del polinomio caratteristico di A norm(a) Calcola la norma della matrice A size(a) Calcola le dimensioni della matrice A
21 Array o vettori I vettori hanno due funzioni fondamentali in Matlab: rappresentazione dei polinomi (un polinomio è descritto dal vettore dei suoi coefficienti); rappresentazione di segnali (un segnale è rappresentato mediante la sequenza dei valori che assume in un insieme di istanti di tempo, quindi mediante un vettore). Possono essere definiti: Con l operatore : :» v=(0:10) v = » v=(0:0.5:3) v = Come matrici riga o colonna:» v=[1 2 3] v =1 2 3
22 Operazioni su array Finora gli operatori aritmetici visti agivano sulle matrici nella loro globalità Le operazioni sugli array si riferiscono ad operazioni aritmetiche eseguite elemento per elemento. Gli operatori su array si distinguono da quelli per matrici per il simbolo "." prima dell'operatore (niente spazio tra punto e operatore) Addizione (.+) e sottrazione (.-) sono le stesse Moltiplicazione (.*) e divisione (./ oppure.\) si differenziano:» x = [1 2 3]; y = [4 5 6];»z = x.*y z= » z = x.\y z=
23 Operazioni sui polinomi Detto p un polinomio definito sotto forma di vettore pol=[1 2 5], possiamo utilizzare le seguenti funzioni roots(pol): calcola le radici del polinomio polyval(pol,0): calcola il valore del polinomio in un punto conv(p1,p2): esegue il prodotto tra polinomi [Q,R]=deconv(p1,p2): calcola la divisione tra polinomi. Restituisce in Q e R rispettivamente il quoziente e il resto. [R,P,K]=residue(p1,p2): calcola i residui, i poli e i termini diretti della espansione in fratti semplici del rapporto tra due polinomi p1 e p2.
24 Operatori relazionali Operatori relazionali: <, <=, >, >=, ==, ~= (~ alt-126) Operano una comparazione elemento per elemento. Il risultato è 1 se il test è TRUE 0 se il test è FALSE Operatori logici: & (and), (or), ~ (not) Consentono di combinare più operatori relazionali. Le variabili su cui operano vanno considerate TRUE se diverse da 0 FALSE se uguali a 0 I risultati sono 1 se TRUE 0 se FALSE >> a=(1>2) a = 0 >> a=(1<2) a = 1
25 GRAFICA 2D plot(y): produce un grafico lineare degli elementi di y in cui le ascisse sono l indice degli elementi di y plot(x,y): produce un grafico lineare di y rispetto a x plot(x,y, colore_stile_marcatore ): produce un grafico di y rispetto a x specificando il colore della linea, lo stile della linea e il marcatore per identificare gli elementi di y nel grafico plot(x1,y1,x2,y2,,xn,yn): produce un grafico multiplo. hold on: consente di aggiungere un tracciato ad un grafico preesistente xlabel( string ), ylabel( string ), title( string ): consentono di specificare una label per l asse x, l asse y e l intero grafico axis: consente di personalizzare la misurazione in scala e il rapporto di aspetto tra i tracciati
26 GRAFICA 2D subplot(m,n,p): permette di esporre grafici multipli sulla stessa finestra. Si trasforma la finestra della figura in una matrice mxn e si accede di volta in volta all elemento specificato in p. loglog(x,y): produce un grafico in scala logaritmica di y rispetto a x semilogx(x,y): produce un grafico in scala semilogaritmica, con un solo asse logaritmico (l asse x) semilogy(x,y): produce un grafico in scala semilogaritmica, con un solo asse logaritmico (l asse y) ginput: consente di risalire alle coordinate di un punto specifico
27 Controllo di flusso Cicli "for"» for i = 1:n for j = 1:n A(i,j) = i+j, end metterli a fine ciclo!!! end» for i = 1:2:n incrementi di 2 ad ogni iterazione Cicli "while"» while (condizione) istruzioni; end
28 Controllo di flusso Operazioni condizionate... "if"» if (espressione) istruzioni elseif (espressione) istruzioni else istruzioni end Si può uscire in modo immediato da un ciclo con l'istruzione "break"» while 1 n = input('scrivi un numero'); if n <= 0, break, end m = sqrt(n) end Questo programma stampa indefinitamente la radice del numero introdotto finchè non si scrive un numero minore o uguale a zero.
29 Controllo di flusso Switch case» switch variable case val1 istruzioni case val2 istruzioni case istruzioni otherwise istruzioni end
30 Control System Toolbox E un insieme di funzioni per l analisi di sistemi dinamici (tipicamente lineari tempo invarianti LTI) e per la sintesi di controllori. E possibile visionare tutte le funzioni della libreria utilizzando help control. Tra queste funzioni andremo ad analizzare quelle preposte a: Creazione di modelli LTI Conversioni tra modelli Analisi nel dominio del tempo Analisi nel dominio della frequenza
31 Creazione di modelli LTI Un generico sistema dinamico può essere rappresentato in varie forme: State-space Transfer-function Zero-Pole-Gain MODELLI STATE-SPACE (SS) Dato un sistema in forma di stato x& ( t) y( t) = Ax( t) + Bu( t) = Cx( t) + Du( t) le cui matrici sono A =,, [ 0 1], B = 1 C = D = per creare il modello in MATLAB bisogna usare la funzione ss» sys=ss(a,b,c,d);
32 Creazione di modelli LTI MODELLI TRANSFER-FUNCTION Dato un sistema in forma di stato rappresentato attraverso la relazione ingresso-uscita, cioè la sua funzione di trasferimento m N( s) bms b0 G( s) = = = n 3 D( s) a s a s per creare il modello in MATLAB bisogna usare la funzione tf» num=[1 2];» den=[ ];» sys=tf(num,den); Transfer function: s s^3 + 2 s + 4 n 0 s s + 4
33 Creazione di modelli LTI MODELLI ZERO-POLE-GAIN Dato un sistema in forma di stato rappresentato attraverso la relazione ingresso-uscita, cioè la sua funzione di trasferimento G( s) = N( s) = K D( s) per creare il modello in MATLAB bisogna usare la funzione zpk»k=3;»z=[-1];» p=[ ];» sys=zpk(z,p,k); Zero/pole/gain: 3 (s+1) (s+3) (s+5) (s+10) m i= 1 n i= 1 ( s + zi ) ( s + 1) = 3 ( s + 3)( s + 5)( s + 10) ( s + p ) i
34 Conversione tra modelli Le funzioni precedentemente introdotte (ss,tf,zpk) servono anche per convertire un sistema da una forma all altra. Dato per esempio un sistema in forma di stato memorizzato nella variabile sys, se vogliamo convertirlo in termini di funzione di trasferimento posso scrivere» sys1=tf(sys); Le funzioni ssdata, tfdata, zpkdata consentono di estrarre da un modello LTI qualsiasi i dati caratteristici di una particolare rappresentazione:» [A,B,C,D]=ssdata(sys);» [NUM. DEN]=tfdata(sys, v );» [Z,P,K]=zpkdata(sys, v ); Dove il parametro v da utilizzarsi per sistemi SISO specifica di restituire il risultato in forma vettoriale
35 Operazioni sui modelli sys=sys1+sys2 sys=sys1-sys2
36 Operazioni sui modelli sys=sys1+sys2 sys=sys1-sys2 sys=sys1*sys2
37 Operazioni sui modelli Altre funzioni utili che consentono di fornire alcune informazioni sul sistema espresso in qualunque delle rappresentazioni possibili:» P=pole(sys); Restituisce i poli del sistema memorizzato nella variabile sys» Z=zero(sys); Restituisce gli zeri del sistema memorizzato nella variabile sys» [P Z]=pzmap(sys); Calcola poli e zeri del sistema e li salva nei vettori P e Z» pzmap(sys); Disegna la mappa dei poli e zeri del sistema» dcgain(sys); Calcola il guadagno statico del sistema sys» [Wn, CSI]=damp(sys); Calcola smorzamento e pulsazione naturale dei poli del sistema
38 Interconnessione tra modelli Concatenazione Orizzontale: sys=[sys1,sys2] Verticale: sys=[sys1;sys2] Feedback sys=feedback(sys1,sys2)
39 Analisi nel dominio del tempo L analisi nel dominio del tempo comporta la valutazione della risposta del sistema agli ingressi canonici o di tipo generico Impulse risposta all impulso» impulse(sys); Traccia la risposta ad impulso del sistema» impulse(sys, Tend); Traccia la risposta all impulso fino all istante di tempo specificato in Tend» impulse(sys,t); Traccia la risposta all impulso utilizzando il vettore degli istanti di tempo specificato» impulse(sys1, sys2,,t); Traccia la risposta all impulso di più sistemi mettendole a confronto» [Y,t]=impulse(sys);» [Y]=impulse(sys,t); Calcola la risposta all impulso e salva il risultato nel vettore Y. Il vettore del tempo può essere specificato come output o parametri di ingresso
40 Analisi nel dominio del tempo step risposta al gradino» step(sys); Traccia la risposta ad un gradino del sistema» step(sys, Tend); Traccia la risposta ad un gradino fino all istante di tempo specificato in Tend» step(sys,t); Traccia la risposta ad un gradino utilizzando il vettore degli istanti di tempo specificato» step(sys1, sys2,,t); Traccia la risposta ad un gradino di più sistemi mettendole a confronto» [Y,t]=step(sys);» [Y]=step(sys,t); Calcola la risposta ad un gradino e salva il risultato nel vettore Y. Il vettore del tempo può essere specificato come output o parametri di ingresso
41 Analisi nel dominio del tempo Initial evoluzione libera di un sistema» initial(sys, X0); Traccia l'evoluzione libera del sistema a partire dalla condizione iniziale X0» initial(sys, X0, Tend); Traccia l'evoluzione libera fino all istante di tempo specificato in Tend» initial(sys,x0, t); Traccia l'evoluzione libera utilizzando il vettore degli istanti di tempo specificato» initial(sys1, sys2,,x0,t); Traccia l'evoluzione libera di più sistemi mettendole a confronto» [Y,t]=initial(sys,X0);» [Y]=initial(sys,X0,t); Calcola l'evoluzione libera e salva il risultato nel vettore Y. Il vettore del tempo può essere specificato come output o parametri di ingresso
42 Analisi nel dominio del tempo lsim risposta ad un ingresso arbitrario» lsim(sys,u,t); Traccia la risposta del sistema all ingresso descritto dai vettori u e t.» lsim(sys,u,t,x0); Traccia la risposta del sistema all ingresso u specificando le condizioni iniziali del sistema per l istante di tempo t(1). Quando non specificato le condizioni iniziali sono considerate nulle» lsim(sys1, sys2,,u,t,x0); Traccia la risposta di più sistemi all ingresso u mettendole a confronto» [Y]=lsim(sys,u,t,X0); Calcola la risposta del sistema all ingresso u e salva il risultato nel vettore Y.» [Y,T,X]=lsim(sys,u,t,X0); Quando il sistema è di tipo SS restituisce anche la traiettoria dello stato, una matrice con tante righe quanti sono gli istanti di tempi e tante colonne quanti sono gli stati del sistema
43 Analisi nel dominio del tempo Altre funzioni utili sono: ltiview Apre una interfaccia grafica per l analisi della risposta nel tempo e in frequenza gensig Funzione che genera segnali periodici per la simulazione della risposta nel tempo con lsim stepfun Consente di creare la funzione a gradino da utilizzare eventualmente con lsim
44 Analisi nel dominio della frequenza bode diagramma di Bode» bode(sys); Traccia il diagrama di Bode (modulo e fase) del sistema.» bode(sys,{wmin wmax}); Traccia il diagramma di Bode del sistema nell intervallo di frequenze specificato dai valori wmin e wmax» bode(sys,w) Traccia il diagramma di Bode alle frequenze specificate nel vettore w» bode(sys1,sys2,,w); Traccia il diagramma di Bode di più sistemi mettendoli a confronto» [MAG,PHASE]=bode(sys,w);» [MAG,PHASE,w]=bode(sys); Calcola il diagramma di Bode e salva in MAG e PHASE i vettori dei guadani e degli sfasamenti. Il vettore w può essere specificato come ingresso o richiesto come output
45 Analisi nel dominio della frequenza margin margine di fase e di guadagno» margin(sys); Traccia il diagrama di Bode (modulo e fase) del sistema indicando i margini di fase e di guadagno» [Gm,Pm,Wg,Wp]=margin(sys); Calcola il diagramma di Bode e salva il margine di guadagno e di fase in Gm e Pm salvandone anche le frequenze in Wg e Wp.
46 Analisi nel dominio della frequenza nyquist diagramma di Nyquist» nyquist(sys); Traccia il diagrama di Nyquist del sistema.» nyquist(sys,{wmin wmax}); Traccia il diagramma di Nyquist del sistema nell intervallo di frequenze specificato dai valori wmin e wmax» nyquist(sys,w) Traccia il diagramma di Nyquist alle frequenze specificate nel vettore w» nyquist(sys1,sys2,,w); Traccia il diagramma di Nyquist di più sistemi mettendoli a confronto» [RE,IMG]=nyquist(sys,w);» [RE,IMG,w]=nyquist(sys); Calcola il diagramma di Nyquist e salva in RE e IMG i vettori della parte reale e immaginaria della risposta in frequenza. Il vettore w può essere specificato come ingresso o richiesto come output
47 Analisi nel dominio della frequenza rlocus luogo delle radici» rlocus(sys); Traccia il luogo delle radici del sistema.» rlocus(sys,k); Traccia il luogo delle radici del sistema utilizzando il vettore dei guadagni specificato» rlocus(sys1,sys2,,k); Traccia il luogo delle radici di più sistemi mettendoli a confronto» [RE,IMG]=rlocus(sys,k);» [RE,IMG,w]=rlocus(sys); Calcola il luogo delle radici e salva in RE e IMG i vettori della parte reale e immaginaria dei rami del luogo. Il vettore k può essere specificato come ingresso o richiesto come output
48 Altre funzioni obsv(a,c) restituisce la matrice di osservabilità per il sistema specificato ctrb(a,b) restituisce la matrice di controllabilità per il sistema dato [Abar,Bbar,Cbar,T,K]=obsvf(A,B,C) trasforma il sistema originario in uno equivalente in forma canonica di osservabilità, restituendo anche la matrice di trasformazione T e un vettore la cui somma (sum(k)) restituisce il numero di stati osservabili [Abar,Bbar,Cbar,T,K]=ctrbf(A,B,C) trasforma il sistema originario in uno equivalente in forma canonica di controllabilità, restituendo anche la matrice di trasformazione T e un vettore la cui somma (sum(k)) restituisce il numero di stati controllabili
Control System Toolbox
 Control System Toolbox E` un insieme di funzioni per l analisi di sistemi dinamici (tipicamente lineari tempo invarianti o LTI) e per la sintesi di controllori (in particolare a retroazione). All'interno
Control System Toolbox E` un insieme di funzioni per l analisi di sistemi dinamici (tipicamente lineari tempo invarianti o LTI) e per la sintesi di controllori (in particolare a retroazione). All'interno
INTRODUZIONE A MATLAB Matrix Laboratory
 INTRODUZIONE A MATLAB Matrix Laboratory Introduzione Linguaggio di programmazione per applicazioni scientifiche e numeriche Vasto set di funzioni predefininte Interprete di comandi Possibilità di scrivere
INTRODUZIONE A MATLAB Matrix Laboratory Introduzione Linguaggio di programmazione per applicazioni scientifiche e numeriche Vasto set di funzioni predefininte Interprete di comandi Possibilità di scrivere
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari
 Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
MATLAB Analisi di Sistemi LTI
 Esercitazione 1/30 MATLAB Analisi di Sistemi LTI Vincenzo LIPPIELLO PRISMA Lab Dipartimento di Informatica e Sistemistica Università di Napoli Federico II vincenzo.lippiello@unina.it www.prisma.unina.it
Esercitazione 1/30 MATLAB Analisi di Sistemi LTI Vincenzo LIPPIELLO PRISMA Lab Dipartimento di Informatica e Sistemistica Università di Napoli Federico II vincenzo.lippiello@unina.it www.prisma.unina.it
Principali comandi MATLAB utili per il corso di Controlli Automatici
 Principali comandi MATLAB utili per il corso di Controlli Automatici In questo documento sono raccolti i principali comandi Matlab utilizzati nel corso; per maggiore comodità, sono riportati facendo riferimento
Principali comandi MATLAB utili per il corso di Controlli Automatici In questo documento sono raccolti i principali comandi Matlab utilizzati nel corso; per maggiore comodità, sono riportati facendo riferimento
MATLAB (1) Introduzione e Operazioni con array
 Laboratorio di Informatica per Ingegneria elettrica A.A. 2010/2011 Prof. Sergio Scippacercola MATLAB (1) Introduzione e Operazioni con array N.B. le slide devono essere utilizzate solo come riferimento
Laboratorio di Informatica per Ingegneria elettrica A.A. 2010/2011 Prof. Sergio Scippacercola MATLAB (1) Introduzione e Operazioni con array N.B. le slide devono essere utilizzate solo come riferimento
CONTROLLI AUTOMATICI E AZIONAMENTI ELETTRICI Ingegneria Meccatronica
 CONTROLLI AUTOMATICI E AZIONAMENTI ELETTRICI Ingegneria Meccatronica CONTROLLI AUTOMATICI e AZIONAMENTI ELETTRICI INTRODUZIONE A MATLAB Ing. Alberto Bellini Tel. 0522 522626 e-mail: alberto.bellini@unimore.it
CONTROLLI AUTOMATICI E AZIONAMENTI ELETTRICI Ingegneria Meccatronica CONTROLLI AUTOMATICI e AZIONAMENTI ELETTRICI INTRODUZIONE A MATLAB Ing. Alberto Bellini Tel. 0522 522626 e-mail: alberto.bellini@unimore.it
MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c
![MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c](/thumbs/25/4541811.jpg) Caratteristiche MATLAB Linguaggio di programmazione orientato all elaborazione di matrici (MATLAB=MATrix LABoratory) Le variabili sono matrici (una variabile scalare equivale ad una matrice di dimensione
Caratteristiche MATLAB Linguaggio di programmazione orientato all elaborazione di matrici (MATLAB=MATrix LABoratory) Le variabili sono matrici (una variabile scalare equivale ad una matrice di dimensione
Cenni sull'impiego di Matlab. Matrici
 Cenni sull'impiego di Matlab Il Matlab è un potente valutatore di espressioni matriciali con valori complessi. Lavorando in questo modo il Matlab indica una risposta ad ogni comando od operazione impartitagli.
Cenni sull'impiego di Matlab Il Matlab è un potente valutatore di espressioni matriciali con valori complessi. Lavorando in questo modo il Matlab indica una risposta ad ogni comando od operazione impartitagli.
Matlab: Strutture di Controllo. Informatica B
 Matlab: Strutture di Controllo Informatica B Tipo di dato logico È un tipo di dato che può avere solo due valori true (vero) 1 false (falso) 0 I valori di questo tipo possono essere generati direttamente
Matlab: Strutture di Controllo Informatica B Tipo di dato logico È un tipo di dato che può avere solo due valori true (vero) 1 false (falso) 0 I valori di questo tipo possono essere generati direttamente
Richiesta pagina PHP (es: index.php)
 PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
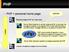
PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
Finestre grafiche. >> figure >> figure(n)
 Finestre grafiche MATLAB ha anche la possibilità di lavorare con delle finestre grafiche sulle quali si possono fare disegni bidimensionali o tridimensionali. Una finestra grafica viene aperta con il comando
Finestre grafiche MATLAB ha anche la possibilità di lavorare con delle finestre grafiche sulle quali si possono fare disegni bidimensionali o tridimensionali. Una finestra grafica viene aperta con il comando
Corso di Visione Artificiale. Matlab per Visione. Samuel Rota Bulò
 Corso di Visione Artificiale Matlab per Visione Samuel Rota Bulò Cos'è Matlab? MATLAB MATLAB - - MATrix MATrix LABoratory LABoratory Ambiente Ambiente di di sviluppo sviluppo ed ed esecuzione esecuzione
Corso di Visione Artificiale Matlab per Visione Samuel Rota Bulò Cos'è Matlab? MATLAB MATLAB - - MATrix MATrix LABoratory LABoratory Ambiente Ambiente di di sviluppo sviluppo ed ed esecuzione esecuzione
Controlli Automatici T. Trasformata di Laplace e Funzione di trasferimento. Parte 3 Aggiornamento: Settembre 2010. Prof. L.
 Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo
 SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html it/~lbiagiotti/sistemicontrollo html INTRODUZIONE A MATLAB Ing. e-mail: luigi.biagiotti@unimore.it
SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html it/~lbiagiotti/sistemicontrollo html INTRODUZIONE A MATLAB Ing. e-mail: luigi.biagiotti@unimore.it
Lab. 1 - Introduzione a Matlab
 Lab. 1 - Introduzione a Matlab Alcune informazioni su Matlab Matlab è uno strumento per il calcolo scientifico utilizzabile a più livelli, dalla calcolatrice tascabile, alla simulazione ed analisi di sistemi
Lab. 1 - Introduzione a Matlab Alcune informazioni su Matlab Matlab è uno strumento per il calcolo scientifico utilizzabile a più livelli, dalla calcolatrice tascabile, alla simulazione ed analisi di sistemi
Introduzione al Foglio Elettronico
 Microsoft Excel Introduzione al Foglio Elettronico Il Foglio Elettronico Si presenta come una grande tabella su un foglio di carta Le celle contengono differenti dati Numeri Testo Date Ecc I dati possono
Microsoft Excel Introduzione al Foglio Elettronico Il Foglio Elettronico Si presenta come una grande tabella su un foglio di carta Le celle contengono differenti dati Numeri Testo Date Ecc I dati possono
Dati importati/esportati
 Dati importati/esportati Dati importati Al workspace MATLAB script Dati esportati file 1 File di testo (.txt) Spreadsheet Database Altro Elaborazione dati Grafici File di testo Relazioni Codice Database
Dati importati/esportati Dati importati Al workspace MATLAB script Dati esportati file 1 File di testo (.txt) Spreadsheet Database Altro Elaborazione dati Grafici File di testo Relazioni Codice Database
if t>=0 x=1; else x=0; end fornisce, nella variabile x, il valore della funzione gradino a tempi continui, calcolata in t.
 Il programma MATLAB In queste pagine si introduce in maniera molto breve il programma di simulazione MAT- LAB (una abbreviazione di MATrix LABoratory). Introduzione MATLAB è un programma interattivo di
Il programma MATLAB In queste pagine si introduce in maniera molto breve il programma di simulazione MAT- LAB (una abbreviazione di MATrix LABoratory). Introduzione MATLAB è un programma interattivo di
INTRODUZIONE A MATLAB
 INTRODUZIONE A MATLAB INTRODUZIONE A MATLAB MATLAB (MATrix LABoratory) è un linguaggio di programmazione per applicazioni scientifiche (elaborazione numerica dei segnali, progetto di simulatori, sintesi
INTRODUZIONE A MATLAB INTRODUZIONE A MATLAB MATLAB (MATrix LABoratory) è un linguaggio di programmazione per applicazioni scientifiche (elaborazione numerica dei segnali, progetto di simulatori, sintesi
Laboratorio di Informatica
 Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
EXCEL PER WINDOWS95. sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area di lavoro, detta foglio di lavoro,
 EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Interpolazione ed approssimazione di funzioni
 Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
FORMULE: Operatori matematici
 Formule e funzioni FORMULE Le formule sono necessarie per eseguire calcoli utilizzando i valori presenti nelle celle di un foglio di lavoro. Una formula inizia col segno uguale (=). La formula deve essere
Formule e funzioni FORMULE Le formule sono necessarie per eseguire calcoli utilizzando i valori presenti nelle celle di un foglio di lavoro. Una formula inizia col segno uguale (=). La formula deve essere
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Grafici tridimensionali
 MatLab Lezione 3 Grafici tridimensionali Creazione di un Grafico 3D (1/4) Si supponga di voler tracciare il grafico della funzione nell intervallo x = [0,5]; y=[0,5] z = e -(x+y)/2 sin(3x) sin(3y) Si può
MatLab Lezione 3 Grafici tridimensionali Creazione di un Grafico 3D (1/4) Si supponga di voler tracciare il grafico della funzione nell intervallo x = [0,5]; y=[0,5] z = e -(x+y)/2 sin(3x) sin(3y) Si può
Laboratorio di Matematica Computazionale A.A. 2008-2009 Lab. 1 - Introduzione a Matlab
 Laboratorio di Matematica Computazionale A.A. 2008-2009 Lab. 1 - Introduzione a Matlab Alcune informazioni su Matlab Matlab è uno strumento per il calcolo scientifico utilizzabile a più livelli, dalla
Laboratorio di Matematica Computazionale A.A. 2008-2009 Lab. 1 - Introduzione a Matlab Alcune informazioni su Matlab Matlab è uno strumento per il calcolo scientifico utilizzabile a più livelli, dalla
Fondamenti di Automatica
 Fondamenti di Automatica Prof. Bruno Picasso Eserc. Ing. Stefano Bottelli Thanks to Prof. S. Strada Introduzione a Matlab, Vettori, Matrici, Polinomi, Sistemi dinamici nel tempo, Rappresentazione grafica
Fondamenti di Automatica Prof. Bruno Picasso Eserc. Ing. Stefano Bottelli Thanks to Prof. S. Strada Introduzione a Matlab, Vettori, Matrici, Polinomi, Sistemi dinamici nel tempo, Rappresentazione grafica
Documentazione esterna al software matematico sviluppato con MatLab
 Documentazione esterna al software matematico sviluppato con MatLab Algoritmi Metodo di Gauss-Seidel con sovrarilassamento Metodo delle Secanti Metodo di Newton Studente Amelio Francesco 556/00699 Anno
Documentazione esterna al software matematico sviluppato con MatLab Algoritmi Metodo di Gauss-Seidel con sovrarilassamento Metodo delle Secanti Metodo di Newton Studente Amelio Francesco 556/00699 Anno
Esame di Informatica CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO. Facoltà di Scienze Motorie
 Facoltà di Scienze Motorie CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche e funzioni statistiche. Esame di Informatica
Facoltà di Scienze Motorie CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche e funzioni statistiche. Esame di Informatica
Introduzione al Python
 Andrea Passerini passerini@disi.unitn.it Informatica Caratteristiche procedurale si specifica la procedura da eseguire sui dati strutturato concetto di visibililtà delle variabili orientato agli oggetti
Andrea Passerini passerini@disi.unitn.it Informatica Caratteristiche procedurale si specifica la procedura da eseguire sui dati strutturato concetto di visibililtà delle variabili orientato agli oggetti
Automatizzare i compiti ripetitivi. I file batch. File batch (1) File batch (2) Visualizzazione (2) Visualizzazione
 Automatizzare i compiti ripetitivi I file batch Anno accademico 2000-01 1 Spesso capita di dover eseguire ripetutatmente una data sequenza di comandi Introdurli uno a uno da tastiera è un processo lento
Automatizzare i compiti ripetitivi I file batch Anno accademico 2000-01 1 Spesso capita di dover eseguire ripetutatmente una data sequenza di comandi Introdurli uno a uno da tastiera è un processo lento
Fondamenti di Automatica
 Fondamenti di Automatica Cenni su Matlab (e toolbox Control Systems + Symbolic) Dott. Ingg. Marcello Bonfè e Silvio Simani Dipartimento di Ingegneria - Università di Ferrara Tel. +39 0532 974839 / 974844
Fondamenti di Automatica Cenni su Matlab (e toolbox Control Systems + Symbolic) Dott. Ingg. Marcello Bonfè e Silvio Simani Dipartimento di Ingegneria - Università di Ferrara Tel. +39 0532 974839 / 974844
Obiettivi d esame PHP Developer Fundamentals on MySQL Environment
 Obiettivi d esame PHP Developer Fundamentals on MySQL Environment 1.0 Ambiente di sviluppo 1.1 Web server e database MySQL Comprendere la definizione dei processi che si occupano di fornire i servizi web
Obiettivi d esame PHP Developer Fundamentals on MySQL Environment 1.0 Ambiente di sviluppo 1.1 Web server e database MySQL Comprendere la definizione dei processi che si occupano di fornire i servizi web
Laboratorio di Fondamenti di Automatica Ingegneria Elettrica Sessione 2/3. Danilo Caporale [caporale@elet.polimi.it]
![Laboratorio di Fondamenti di Automatica Ingegneria Elettrica Sessione 2/3. Danilo Caporale [caporale@elet.polimi.it] Laboratorio di Fondamenti di Automatica Ingegneria Elettrica Sessione 2/3. Danilo Caporale [caporale@elet.polimi.it]](/thumbs/24/2724545.jpg) Laboratorio di Fondamenti di Automatica Ingegneria Elettrica Sessione 2/3 Danilo Caporale [caporale@elet.polimi.it] Outline 2 Funzione di trasferimento e risposta in frequenza Diagrammi di Bode e teorema
Laboratorio di Fondamenti di Automatica Ingegneria Elettrica Sessione 2/3 Danilo Caporale [caporale@elet.polimi.it] Outline 2 Funzione di trasferimento e risposta in frequenza Diagrammi di Bode e teorema
Rapida Introduzione all uso del Matlab Ottobre 2002
 Rapida Introduzione all uso del Matlab Ottobre 2002 Tutti i tipi di dato utilizzati dal Matlab sono in forma di array. I vettori sono array monodimensionali, e così possono essere viste le serie temporali,
Rapida Introduzione all uso del Matlab Ottobre 2002 Tutti i tipi di dato utilizzati dal Matlab sono in forma di array. I vettori sono array monodimensionali, e così possono essere viste le serie temporali,
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
Esempi di uso e applicazioni di Matlab e simulink. 1) Uso delle funzioni ode23 e ode45 per l'integrazione di equazioni differenziali con Matlab
 Esempi di uso e applicazioni di Matlab e simulink ) Uso delle funzioni ode23 e ode45 per l'integrazione di equazioni differenziali con Matlab Sia dato da integrare una equazione differenziale scalare di
Esempi di uso e applicazioni di Matlab e simulink ) Uso delle funzioni ode23 e ode45 per l'integrazione di equazioni differenziali con Matlab Sia dato da integrare una equazione differenziale scalare di
Microsoft Excel. Sommario. Cosa è un foglio elettronico. L interfaccia Utente. La cartella di Lavoro. Corso di introduzione all informatica
 Corso di introduzione all informatica Microsoft Excel Gaetano D Aquila Sommario Cosa è un foglio elettronico Caratteristiche di Microsoft Excel Inserimento e manipolazione dei dati Il formato dei dati
Corso di introduzione all informatica Microsoft Excel Gaetano D Aquila Sommario Cosa è un foglio elettronico Caratteristiche di Microsoft Excel Inserimento e manipolazione dei dati Il formato dei dati
Introduzione a Matlab
 Introduzione a Matlab 1 Introduzione Matlab (MATrix LABoratory) è un software per il calcolo scientifico, particolarmente sviluppato per quanto riguarda la gestione ed elaborazione di vettori e matrici.
Introduzione a Matlab 1 Introduzione Matlab (MATrix LABoratory) è un software per il calcolo scientifico, particolarmente sviluppato per quanto riguarda la gestione ed elaborazione di vettori e matrici.
Test Excel conoscenze di Base
 Test Excel conoscenze di Base 1)Che tipo di barra ha un foglio di calcolo, che un elaboratore testi non ha? a. La barra dei menu b. La barra della formula c. La barra del titolo d. La barra della formattazione
Test Excel conoscenze di Base 1)Che tipo di barra ha un foglio di calcolo, che un elaboratore testi non ha? a. La barra dei menu b. La barra della formula c. La barra del titolo d. La barra della formattazione
FONDAMENTI DI AUTOMATICA
 FONDAMENTI DI AUTOMATICA A c osa serve quest a present azione Scopi di questo materiale: fornire le informazioni necessarie per l uso di Matlab e Simulink in relazione ai Laboratori di Fondamenti di Automatica;
FONDAMENTI DI AUTOMATICA A c osa serve quest a present azione Scopi di questo materiale: fornire le informazioni necessarie per l uso di Matlab e Simulink in relazione ai Laboratori di Fondamenti di Automatica;
LA FUNZIONE DI TRASFERIMENTO
 LA FUNZIONE DI TRASFERIMENTO Può essere espressa sia nel dominio della s che nel dominio della j Definizione nel dominio della s. è riferita ai soli sistemi con un ingresso ed un uscita 2. ha per oggetto
LA FUNZIONE DI TRASFERIMENTO Può essere espressa sia nel dominio della s che nel dominio della j Definizione nel dominio della s. è riferita ai soli sistemi con un ingresso ed un uscita 2. ha per oggetto
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
A.1 Definizione e rappresentazione di un numero complesso
 441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
Cosa è un foglio elettronico
 Cosa è un foglio elettronico Versione informatica del foglio contabile Strumento per l elaborazione di numeri (ma non solo...) I valori inseriti possono essere modificati, analizzati, elaborati, ripetuti
Cosa è un foglio elettronico Versione informatica del foglio contabile Strumento per l elaborazione di numeri (ma non solo...) I valori inseriti possono essere modificati, analizzati, elaborati, ripetuti
E possibile modificare la lingua dei testi dell interfaccia utente, se in inglese o in italiano, dal menu [Tools
 Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda
 Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
ESTRAZIONE DI RADICE
 ESTRAZIONE DI RADICE La radice è l operazione inversa dell elevamento a potenza. L esponente della potenza è l indice della radice che può essere: quadrata (); cubica (); quarta (4); ecc. La base della
ESTRAZIONE DI RADICE La radice è l operazione inversa dell elevamento a potenza. L esponente della potenza è l indice della radice che può essere: quadrata (); cubica (); quarta (4); ecc. La base della
Lezione 5. Fogli di calcolo
 Lezione 5 Fogli di calcolo Cos'e' un foglio di calcolo E' una tabella che permette di fare operazioni complesse sui dati Lo scopo e' la manipolazione dei dati Programmi EXCEL (commerciale) WORKS (commerciale)
Lezione 5 Fogli di calcolo Cos'e' un foglio di calcolo E' una tabella che permette di fare operazioni complesse sui dati Lo scopo e' la manipolazione dei dati Programmi EXCEL (commerciale) WORKS (commerciale)
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
La grafica. La built-in funzione grafica plot. x spezzata poligonale. discretizzato
 La grafica. Il Matlab possiede un ambiente grafico abbastanza potente paragonabile a software grafici operanti in altri contesti. In questo corso ci limiteremo ad illustrare solo una funzione grafica,
La grafica. Il Matlab possiede un ambiente grafico abbastanza potente paragonabile a software grafici operanti in altri contesti. In questo corso ci limiteremo ad illustrare solo una funzione grafica,
3 - Variabili. Programmazione e analisi di dati Modulo A: Programmazione in Java. Paolo Milazzo
 3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
3 - Variabili Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://www.di.unipi.it/ milazzo milazzo di.unipi.it Corso di
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
31/10/2012. Lo studio delle funzioni permette di interpretare la variazione di due grandezze, l una rispetto l altra, quando
 FUNZIONI MATEMATICHE Introduzione Lo studio delle funzioni permette di interpretare la variazione di due grandezze, l una rispetto l altra, quando tra le due esiste un legame di tipo matematico. La teoria
FUNZIONI MATEMATICHE Introduzione Lo studio delle funzioni permette di interpretare la variazione di due grandezze, l una rispetto l altra, quando tra le due esiste un legame di tipo matematico. La teoria
Parte IV. I fogli elettronici e Excel
 Parte IV I fogli elettronici e Excel Caratteristiche principali dei fogli elettronici Organizzazione dei dati in forma tabellare. Ogni cella può contenere: numeri, testi, formule il cui calcolo è aggiornato
Parte IV I fogli elettronici e Excel Caratteristiche principali dei fogli elettronici Organizzazione dei dati in forma tabellare. Ogni cella può contenere: numeri, testi, formule il cui calcolo è aggiornato
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Appunti di: MICROSOFT EXCEL
 Appunti di: MICROSOFT EXCEL INDICE PARTE I: IL FOGLIO ELETTRONICO E I SUOI DATI Paragrafo 1.1: Introduzione. 3 Paragrafo 1.2: Inserimento dei Dati....4 Paragrafo 1.3: Ordinamenti e Filtri... 6 PARTE II:
Appunti di: MICROSOFT EXCEL INDICE PARTE I: IL FOGLIO ELETTRONICO E I SUOI DATI Paragrafo 1.1: Introduzione. 3 Paragrafo 1.2: Inserimento dei Dati....4 Paragrafo 1.3: Ordinamenti e Filtri... 6 PARTE II:
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO
 SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
Potenzialità statistiche Excel
 Potenzialità statistiche Excel INTRODUZIONE A MS EXCEL Prof. Raffaella Folgieri Email folgieri@mtcube.com Fogli di calcolo MS Excel Prof. Folgieri 1 I Fogli Elettronici (Microsoft Excel) Sono strumenti
Potenzialità statistiche Excel INTRODUZIONE A MS EXCEL Prof. Raffaella Folgieri Email folgieri@mtcube.com Fogli di calcolo MS Excel Prof. Folgieri 1 I Fogli Elettronici (Microsoft Excel) Sono strumenti
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
Parte II Indice. Operazioni aritmetiche tra valori rappresentati in binario puro. Rappresentazione di numeri con segno
 Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Lezioni su MATLAB. Ingegneria Civile/Meccanica
 Lezioni su ali in Ingegneria Civile/Meccanica Corso di laboratorio di informatica 06/07 Sommario ali in 1 2 3 4 ali 5 6 in ali in : MATrix LABoratory È un ambiente per l analisi e la simulazione dei sistemi
Lezioni su ali in Ingegneria Civile/Meccanica Corso di laboratorio di informatica 06/07 Sommario ali in 1 2 3 4 ali 5 6 in ali in : MATrix LABoratory È un ambiente per l analisi e la simulazione dei sistemi
LEZIONE DI MATLAB 2.0. Ing.Irene Tagliente E-mail: irene.tagliente@opbg.net
 LEZIONE DI MATLAB 2.0 Ing.Irene Tagliente E-mail: irene.tagliente@opbg.net Cos è Matlab Il programma MATLAB si è imposto in ambiente ingegneristico come strumento per la simulazione e l'analisi dei sistemi
LEZIONE DI MATLAB 2.0 Ing.Irene Tagliente E-mail: irene.tagliente@opbg.net Cos è Matlab Il programma MATLAB si è imposto in ambiente ingegneristico come strumento per la simulazione e l'analisi dei sistemi
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Microsoft Excel. Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle. Numeri, date, formule, testo, funzioni
 Microsoft Excel Sommario Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle Numeri, date, formule, testo, funzioni Formattazione dei dati Creazione di serie di
Microsoft Excel Sommario Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle Numeri, date, formule, testo, funzioni Formattazione dei dati Creazione di serie di
Excel. Excel. Videata iniziale Fogli elettronici. Fogli elettronici. Come si inserisce un dato
 Excel Excel he cos è? È un programma che appartiene alla famiglia dei fogli elettronici. Dove si esegue? Excel gira in ambiente Windows. che cosa serve? Serve a realizzare tabelle numeriche. Videata iniziale
Excel Excel he cos è? È un programma che appartiene alla famiglia dei fogli elettronici. Dove si esegue? Excel gira in ambiente Windows. che cosa serve? Serve a realizzare tabelle numeriche. Videata iniziale
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Introduzione a MATLAB INTRODUZIONE A MATLAB
 INTRODUZIONE A MATLAB 1 Il programma MATLAB: indice Introduzione, help e files Punteggiatura e variabili Operatori Matrici Polinomi Istruzione IF-THEN-ELSE e Cicli Stringhe di testo, input ed output Grafici
INTRODUZIONE A MATLAB 1 Il programma MATLAB: indice Introduzione, help e files Punteggiatura e variabili Operatori Matrici Polinomi Istruzione IF-THEN-ELSE e Cicli Stringhe di testo, input ed output Grafici
Funzioni in C. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
PULSANTI E PAGINE Sommario PULSANTI E PAGINE...1
 Pagina 1 Sommario...1 Apertura...2 Visualizzazioni...2 Elenco...2 Testo sul pulsante e altre informazioni...3 Comandi...3 Informazioni...4 Flow chart...5 Comandi...6 Pulsanti Principali e Pulsanti Dipendenti...6
Pagina 1 Sommario...1 Apertura...2 Visualizzazioni...2 Elenco...2 Testo sul pulsante e altre informazioni...3 Comandi...3 Informazioni...4 Flow chart...5 Comandi...6 Pulsanti Principali e Pulsanti Dipendenti...6
la scienza della rappresentazione e della elaborazione dell informazione
 Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
L analisi dei dati. Capitolo 4. 4.1 Il foglio elettronico
 Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Introduzione a Matlab Parte 1
 Introduzione a Matlab Parte 1 Ing. Roberto Naldi DEIS-Università di Bologna Tel. 051 2093876 Email: roberto.naldi@unibo.it URL: www-lar.deis.unibo.it/~rnaldi 1 Cosa è Matlab? Matlab (= Matrix Laboratory)
Introduzione a Matlab Parte 1 Ing. Roberto Naldi DEIS-Università di Bologna Tel. 051 2093876 Email: roberto.naldi@unibo.it URL: www-lar.deis.unibo.it/~rnaldi 1 Cosa è Matlab? Matlab (= Matrix Laboratory)
Introduzione alla programmazione in C
 Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Programmazione dinamica
 Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
SPECIFICHE E LIMITI DI EXCEL
 SPECIFICHE E LIMITI DI EXCEL Un "FOGLIO DI CALCOLO" è un oggetto di un programma per computer costituito da un insieme di celle, organizzate in righe e colonne, atte a memorizzare dati ed effettuare operazioni
SPECIFICHE E LIMITI DI EXCEL Un "FOGLIO DI CALCOLO" è un oggetto di un programma per computer costituito da un insieme di celle, organizzate in righe e colonne, atte a memorizzare dati ed effettuare operazioni
Introduzione al MATLAB c Parte 1
 Introduzione al MATLAB c Parte 1 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ Lezione 1-2 maggio 2007 Outline 1 Cos è il MATLAB Componenti principali di MATLAB 2 Avvio Avviare
Introduzione al MATLAB c Parte 1 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ Lezione 1-2 maggio 2007 Outline 1 Cos è il MATLAB Componenti principali di MATLAB 2 Avvio Avviare
Introduzione allo Scilab Parte 3: funzioni; vettori.
 Introduzione allo Scilab Parte 3: funzioni; vettori. Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro felix@dm.uniba.it 13 Giugno 2007 Felice Iavernaro (Univ.
Introduzione allo Scilab Parte 3: funzioni; vettori. Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro felix@dm.uniba.it 13 Giugno 2007 Felice Iavernaro (Univ.
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo
 Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
LAB LEZ. 1 STATISTICA DESCRITTIVA CON R
 LAB LEZ. 1 STATISTICA DESCRITTIVA CON R 1 2 L AMBIENTE DI SVILUPPO DI RStudio 1 3 4 2 1 FINESTRA PER GLI SCRIPT E PER VISUALIZZARE I DATI 2 CONSOLE DEI COMANDI 3 VARIABILI PRESENTI NELLA MEMORIA DEL PROGRAMMA
LAB LEZ. 1 STATISTICA DESCRITTIVA CON R 1 2 L AMBIENTE DI SVILUPPO DI RStudio 1 3 4 2 1 FINESTRA PER GLI SCRIPT E PER VISUALIZZARE I DATI 2 CONSOLE DEI COMANDI 3 VARIABILI PRESENTI NELLA MEMORIA DEL PROGRAMMA
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL
 RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Sistemi di Numerazione
 Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Analisi Matematica di circuiti elettrici
 Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
Sistema di numerazione binario, operazioni relative e trasformazione da base due a base dieci e viceversa di Luciano Porta
 Sistema di numerazione binario, operazioni relative e trasformazione da base due a base dieci e viceversa di Luciano Porta Anche se spesso si afferma che il sistema binario, o in base 2, fu inventato in
Sistema di numerazione binario, operazioni relative e trasformazione da base due a base dieci e viceversa di Luciano Porta Anche se spesso si afferma che il sistema binario, o in base 2, fu inventato in
