Modelli probabilistici per la percezione
|
|
|
- Brigida Paoli
- 6 anni fa
- Visualizzazioni
Transcript
1 Modelli probabilistici per la percezione Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Problemi mal posti Un piccolo test: x + 3 = 8 quanto vale x?
2 Problemi mal posti Un piccolo test: 2x + 2 =10 quanto vale x? Problemi mal posti Un piccolo test: x + y = 9 quanto valgono x e y?
3 Problemi mal posti Un piccolo test: x + y = 9 quanto valgono x e y? Questo è un esempio di problema mal posto Problemi mal posti Un piccolo test: x + y = 9 quanto valgono x e y? Questo è un esempio di problema mal posto: - non ha soluzione unica
4 a riflettanza spettrale // inferenza: un problema mal posto E R E x R = N fotoni emessi % fotoni riflessi N fotoni riflessi Spettro di irradiamento x x Spettro di riflettanza = = Spettro di radianza a riflettanza spettrale // inferenza: un problema mal posto E R E x R = 100 x N fotoni emessi % fotoni riflessi N fotoni riflessi E=? R=? =
5 Problemi mal posti //soluzione probabilistica Posso provare a utilizzare osservazioni precedenti : x + y = 9 Problemi mal posti //soluzione probabilistica Posso provare a utilizzare osservazioni precedenti : x + y = 9 x = 2, y = 7
6 Problemi mal posti //soluzione probabilistica Posso provare a utilizzare osservazioni precedenti : x + y = 9 x = 2, y = 7 Quanto ci fidiamo del risultato ottenuto? Probabilità e scienze cognitive //tre problemi per i modelli cognitivi Percezione e azione hanno a che fare con eventi incerti: rumore, incertezza ignoranza sulle condizioni al contorno stesso oggetto immagini diverse
7 Probabilità e scienze cognitive //tre problemi per i modelli cognitivi Percezione e azione hanno a che fare con eventi incerti: rumore, incertezza ignoranza sulle condizioni al contorno oggetti diversi immagini identiche Probabilità e scienze cognitive //tre problemi per i modelli cognitivi Percezione e azione hanno a che fare con eventi incerti: rumore, incertezza ignoranza sulle condizioni al contorno incertezze conoscenza }? modularità Module design Module integration
8 a logica dell incerto Come già osservava ocke ( ), anche gli agenti più razionali prendono le loro decisioni non nella chiara luce della certezza nel crepuscolo delle probabilità. Merita forse anche il titolo di conoscenza l'opinione fondata sulla plausibilità; [ ] Per questo credo che la ricerca sui gradi di probabilità sia estremamente importante; [ ] Così, quando non si potesse decidere con assoluta certezza una questione, si potrebbe almeno determinare il grado di probabilità alla luce dell'evidenza. (G.W. eibniz, Nuovi Saggi sull Intelletto Umano). Probabilità e scienze cognitive //percezione come inferenza inconscia Come già osservava ocke ( ), anche gli agenti più razionali prendono le loro decisioni non nella chiara luce della certezza nel crepuscolo delle probabilità. incertezze T e o r i a d e l l a probabilità conoscenza modularità Module design }? Module integration
9 Quale probabilità //Tre concetti di probabilità: la definizione classica a probabilità di un evento è il rapporto tra il numero dei casi favorevoli e il numero dei casi possibili, purché questi ultimi siano ugualmente possibili. Quindi se i casi possibili sono n e i casi favorevoli sono na, per la teoria classica la probabilità che accada l'evento A sarà: Tre concetti di probabilità: la definizione frequentista a probabilità di un evento è il limite della frequenza (relativa) dei successi, cioè del verificarsi dell'evento, quando il numero delle prove tende all'infinito.
10 Tre concetti di probabilità: la definizione soggettivista a probabilità di un evento è il prezzo che un individuo razionale ritiene equo pagare per ricevere 1 se l'evento si verifica (e 0 altrimenti). Alessio è disposto a scommettere 1 contro 20 sul fatto che nel pomeriggio arrivi finalmente l'idraulico a riparare il rubinetto che perde da una settimana: attribuisce cioè a tale evento una probabilità 1/21 (meno del 5%). È come se ci trovassimo ad effettuare un sorteggio da un'urna con 1 pallina rossa (evento positivo = arrivo dell'idraulico) e 20 palline nere (eventi negativi = assenza dell'idraulico). Come si valuta la probabilità? Immaginiamo che ci sia una partita di calcio. o spazio degli eventi comprende (1) la vittoria della squadra di casa, (2) la vittoria della squadra ospite e (3) il pareggio. Secondo la teoria classica esiste 1 probabilità su 3 che abbia luogo il primo evento secondo la teoria frequentista ci si può dotare di un almanacco e controllare tutte le partite precedenti e calcolare la frequenza dell evento vittoria della squadra di casa. Secondo la teoria soggettivista, ci si può documentare sullo stato di forma dei calciatori, sul terreno di gioco e così via fino ad emettere una probabilità soggettiva.
11 Probabilità e scienze cognitive //percezione come inferenza inconscia Probabilità soggettiva: mette in relazione le asserzioni fatte sul mondo con lo stato di conoscenza dell agente incertezze T e o r i a d e l l a probabilità conoscenza modularità Module design }? Module integration Probabilità e scienze cognitive //percezione come inferenza inconscia...(helmholtz, 1925) I called the connections of ideas which take place in these processes unconscious inferences. These inferences are unconscious insofar as their major premise is not necessarily expressed in the form of a proposition; it is formed from a series of experiences whose individual members have entered consciousness only in the form of sense impressions which have long since disappeared from memory. Some fresh sense impression forms the minor premise, to which the rule impressed upon us by previous observations is applied
12 Probabilità e scienze cognitive //percezione come inferenza inconscia...(helmholtz, 1925) (T. Bayes, ) unconscious inferences fresh sense impression forms the minor premise rule impressed upon us by previous observations P( osservazioni P (observation knowledge)p conoscenza) x P( (knowledge) conoscenza) P (knowledge observation) = = P (observation) P( conoscenza osservazioni) P( osservazioni ) Probabilità e scienze cognitive //percezione come inferenza inconscia Probabilità soggettiva: mette in relazione le asserzioni fatte sul mondo con lo stato di conoscenza dell agente = grado di credenza incertezze conoscenza modularità Module design Teoria Bayesiana della probabilità Module integration
13 Problemi mal posti //soluzione probabilistica Supponiamo di voler ricostruire il mondo 3D a partire dall ombreggiatura Questo è il mondo che osserviamo, le ombre proiettate nella caverna di Platone... Problemi mal posti //soluzione probabilistica Supponiamo di voler ricostruire il mondo 3D a partire dall ombreggiatura Questa è l immagine di un oggetto concavo o convesso? Questo è il mondo che osserviamo, le ombre proiettate nella caverna di Platone...
14 Probabilità //sintassi Proposizioni elementari C = IN, la curvatura è di tipo IN Proposizioni complesse =sopra C = IN C I Curvatura C={IN, OUT} Posizione sorgente di luce ={sopra, sotto} Immagine I ={, } C,, I le possiamo considerare variabili aleatorie che assumono un valore (discreto/continuo) rispetto agli eventi che accadono nel mondo. Il risultato numerico di un esperimento Probabilità //assiomi P(A) 0 P (A A) = 0 P ( A) = 1 - P(A) P(A B) = P(A) + P(B) - P(A B)
15 Probabilità //modellare la percezione del mondo Probabilità //modellare la percezione del mondo C a scelta delle variabili aleatorie di interesse discrete continue C={IN, OUT} ={sopra, sotto} Immagine I ={, } I
16 Probabilità //la probabilità del tutto: congiunta P(I C )=P(I, C, ) P(I, C, ) I C C IN IN sopra sopra OUT sopra C={IN, OUT} ={sopra, sotto} Immagine I ={, } I OUT IN IN OUT OUT sopra sotto sotto sotto sotto Probabilità //la probabilità condizionata Probabilità condizionata di A dato B (posto che conosco il valore di B) P(A B) = P(A B) / P(B) = P(A, B) / P(B) Ci consente di strutturare la conoscenza sul mondo Regola del prodotto B A P(A, B) = P(A B) P(B) = P(B A) P(A) P(A, B, C) = P(A B, C) P(B C) P(C) poichè P(A B) = P(B A) (chain rule) semplifica una query difficile in query più semplici
17 Probabilità //la probabilità condizionata Da un punto di vista strettamente Bayesiano esistono solo probabilità condizionate P(A ) -> P(A H ) H è l insieme di ipotesi che ci consentono di esplicitare la conoscenza sul mondo Posizionamento luci possibile Alcune delle ipotesi in H Posizionamento luci inammissibile P( H) 0,9 sopra 0,1 sotto P( H) 0,9 sopra 0,1 sotto
18 P( H) 0,9 sopra 0,1 sotto Probabilità //la probabilità condizionata Da un punto di vista strettamente Bayesiano esistono solo probabilità condizionate P(A ) -> P(A H ) H è l insieme di ipotesi che ci consentono di esplicitare la conoscenza sul mondo C Oggetti che esistono nel mondo osservato Alcune delle ipotesi in H Oggetti che non esistono nel mondo osservato P(C H) C 0,5 IN 0,5 OUT
19
20
21 Probabilità //specificare un modello del mondo: struttura P(I C )=P(I, C, ) = P(I C, ) P(C ) P() C Indipendenza di C da P(C ) = P(C) P(I, C, ) = P(I C, ) P(C ) P() I questo è il mio modello del mondo C={IN, OUT} ={sopra, sotto} Immagine I ={, } Probabilità //specificare un modello del mondo Il modello del mondo mi semplifica la probabilità del tutto (2 3-1 stati) P(I, C, ) I C IN sopra IN sopra OUT sopra OUT sopra IN sotto IN sotto OUT sotto OUT sotto
22 Probabilità //specificare un modello del mondo P(I, C, ) = P(I C, ) P(C ) P() P(C ) C P( ) 0,5 IN 0,5 OUT C 0,9 sopra 0,1 sotto I P(I C, ) I C 0 IN sopra 1 IN sopra 1 OUT sopra 0 OUT sopra 1 IN sotto 0 IN sotto 0 OUT sotto 1 OUT sotto Probabilità //specificare un modello del mondo P(I, C, ) = P(I C, ) P(C ) P() P(C ) C P( ) 0,5 IN 0,5 OUT C 0,9 sopra 0,1 sotto I Probabilità a priori= la mia conoscenza del mondo
23 Probabilità //specificare un modello del mondo P(I, C, ) = P(I C, ) P(C ) P() C Verosimiglianza= la mia osservazione del mondo I P(I C, ) I C 0 IN sopra 1 IN sopra 1 OUT sopra 0 OUT sopra 1 IN sotto 0 IN sotto 0 OUT sotto 1 OUT sotto Probabilità //fare inferenze: la regola di Bayes Dalla Regola del prodotto: P(A, B) = P(A B) P(B) = P(B A) P(A) poichè P(A B) = P(B A) B B A A Probabilità inversa
24 Probabilità //fare inferenze: la regola di Bayes probabilità a posteriori verosimiglianza probabilità a priori { P( dati P (observation knowledge)p sensoriali cosa c è nel mondo) x P( cosa (knowledge) c è nel mondo) P (knowledge observation) = = P (observation) P( cosa c è nel mondo dati sensoriali) { P( dati sensoriali ) { Probabilità //Indipendenza (marginale) C Indipendenza di C da P(C ) = P(C) P(C, ) = P(C ) P() = P(C) P() C={IN, OUT} ={sopra, sotto} Immagine I ={, }
25 Probabilità //Indipendenza (marginale) Eventi mutualmente esclusivi P(A, B) =P(A B) =0 P (, ) = 0 Si semplifica la regola della somma: P(A B) = P(A) + P(B) - P(A B) = P(A) + P(B) P ( ) = P ( ) + P ( ) Generalizzata: P(A1 A2... AN ) = i=1;..;n P(Ai ) Probabilità //Marginalizzazione Dalla probabilità congiunta possiamo ottenere la probabilità (marginale) di una variabile sommando su tutti i possibili valori delle altre variabili P(X) = Y P(X, Y) P(X) = Y P(X, Y) = Y P(X Y) P(Y)
26 Probabilità //Marginalizzazione a marginalizzazione ci consente inferenze: Se osservo I=, qual è la probabilità di P( C = OUT I = ) P( C = OUT I = ) = P( I =, C = OUT ) P( I = ) C ={sopra, sotto} P( I =, C = OUT, ) = ={sopra, sotto} P( I = C = OUT, ) P(C ) P() 0,5{ 0,9{ = P(C = 0UT ) [ P( I = C = OUT, = sopra ) P( =sopra) + P( I = C = OUT, = sotto ) P( = sotto) ] { 0 Probabilità //Problema per l inferenza Bayesiana a marginalizzazione ci consente inferenze: Se osservo I=, qual è la probabilità di P( C = OUT I = ) P( I = ) P( I =, C = OUT ) P( C = OUT I = ) = P( I = ) = C={IN, OUT} ={sopra, sotto} P( I =, C, ) Hic sunt leones = [ P( I = C = OUT, = sopra ) P( =sopra) P( C = OUT) + P( I = C = OUT, = sotto ) P( = sotto) P( C = OUT) + P( I = C = IN, = sopra ) P( =sopra) P( C = IN) + P( I = C = IN, = sotto ) P( = sotto) P( C = IN)]
27 Modelli nelle scienze cognitive e nella percezione //da Marr a Bayes Qual è il goal della computazione? ivelli di spiegazione secondo Marr Quale rappresentazione e quale algoritmo? Come realizzarla fisicamente? Modelli nelle scienze cognitive e nella percezione //da Marr a Bayes Teoria Bayesiana ivelli di spiegazione (Kersten e Yuille) Vincoli e ipotesi Implementazione
28 Modelli nelle scienze cognitive e nella percezione //da Marr a Bayes Modelli teorici Bayesiani: Modello Grafico + PDF C I P(I, C, ) = P(I C, ) P(C ) P() ivelli di spiegazione (Boccignone e Cordeschi) Inferenza su MG SIMUAZIONE Modello implementativo
La PROBABILITA è un numero che si associa ad un evento E ed esprime il grado di aspettativa circa il suo verificarsi.
 La maggior parte dei fenomeni, ai quali assistiamo quotidianamente, può manifestarsi in vari modi, ma è quasi sempre impossibile stabilire a priori quale di essi si presenterà ogni volta. La PROBABILITA
La maggior parte dei fenomeni, ai quali assistiamo quotidianamente, può manifestarsi in vari modi, ma è quasi sempre impossibile stabilire a priori quale di essi si presenterà ogni volta. La PROBABILITA
Probabilità. Ing. Ivano Coccorullo
 Ing. Ivano Coccorullo PROBABILITA Teoria della Eventi certi, impossibili e casuali Nella scienza e nella tecnologia è fondamentale il principio secondo il quale ogni volta che si realizza un insieme di
Ing. Ivano Coccorullo PROBABILITA Teoria della Eventi certi, impossibili e casuali Nella scienza e nella tecnologia è fondamentale il principio secondo il quale ogni volta che si realizza un insieme di
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio. M. Besozzi - IRCCS Istituto Auxologico Italiano
 Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio. M. Besozzi - IRCCS Istituto Auxologico Italiano
 Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
ESPONENZIALI E LOGARITMI. chiameremo logaritmica (e si legge il logaritmo in base a di c è uguale a b ).
 ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere:
 PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
CORSO DI LAUREA IN MATEMATICA
 CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
Richiami di teoria della probabilitá e Modelli Grafici
 Modelli di computazione affettiva e comportamentale Data: 23 Aprile 2010 Richiami di teoria della probabilitá e Modelli Grafici Docente: Prof. Giuseppe Boccignone Scriba: Matteo Battistini 1 Richiami di
Modelli di computazione affettiva e comportamentale Data: 23 Aprile 2010 Richiami di teoria della probabilitá e Modelli Grafici Docente: Prof. Giuseppe Boccignone Scriba: Matteo Battistini 1 Richiami di
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti
 FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
8a. Teorema di Bayes, rapporto di verosimiglianza (likelihood ratio, LR) e odds
 8a. Teorema di Bayes, rapporto di verosimiglianza (likelihood ratio, LR) e odds Se partiamo dalla forma classica (5.13) del teorema di Bayes che possiamo anche riscrivere come e se consideriamo il rapporto
8a. Teorema di Bayes, rapporto di verosimiglianza (likelihood ratio, LR) e odds Se partiamo dalla forma classica (5.13) del teorema di Bayes che possiamo anche riscrivere come e se consideriamo il rapporto
Introduzione alla probabilità
 Introduzione alla probabilità Osservazione e studio dei fenomeni naturali: a. Caso deterministico: l osservazione fornisce sempre lo stesso risultato. b. Caso stocastico o aleatorio: l osservazione fornisce
Introduzione alla probabilità Osservazione e studio dei fenomeni naturali: a. Caso deterministico: l osservazione fornisce sempre lo stesso risultato. b. Caso stocastico o aleatorio: l osservazione fornisce
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE
 PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE
 ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
Anno 3. Funzioni esponenziali e logaritmi: le 4 operazioni
 Anno 3 Funzioni esponenziali e logaritmi: le 4 operazioni 1 Introduzione In questa lezione impareremo a conoscere le funzioni esponenziali e i logaritmi; ne descriveremo le principali caratteristiche e
Anno 3 Funzioni esponenziali e logaritmi: le 4 operazioni 1 Introduzione In questa lezione impareremo a conoscere le funzioni esponenziali e i logaritmi; ne descriveremo le principali caratteristiche e
Il sole e le ombre. Un percorso in costruzione, modifiche ed adeguamenti. Claudia Iacopini, Lorella Cesare. Scuola Primaria Vinci 2014
 Il sole e le ombre Un percorso in costruzione, modifiche ed adeguamenti Scuola Primaria Vinci 2014 Claudia Iacopini, Lorella Cesare Attività per la classe quarta Indagine individuale: Cos è per te l ombra?
Il sole e le ombre Un percorso in costruzione, modifiche ed adeguamenti Scuola Primaria Vinci 2014 Claudia Iacopini, Lorella Cesare Attività per la classe quarta Indagine individuale: Cos è per te l ombra?
1 Definizione di sistema lineare omogeneo.
 Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo. Calcolo Combinatorio
 Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Funzioni elementari: funzioni potenza
 Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
Capitolo 6. La distribuzione normale
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Capitolo 6 Economia dell informazione e scelta in condizioni di incertezza
 Capitolo 6 Economia dell informazione e scelta in condizioni di incertezza COSA ABBIAMO FATTO FINORA Concetti introduttivi della microeconomia Teoria della scelta razionale del consumatore in condizioni
Capitolo 6 Economia dell informazione e scelta in condizioni di incertezza COSA ABBIAMO FATTO FINORA Concetti introduttivi della microeconomia Teoria della scelta razionale del consumatore in condizioni
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
La probabilità matematica
 1 La probabilità matematica In generale parliamo di eventi probabili o improbabili quando non siamo sicuri se si verificheranno. DEFINIZIONE. Un evento (E) si dice casuale, o aleatorio, quando il suo verificarsi
1 La probabilità matematica In generale parliamo di eventi probabili o improbabili quando non siamo sicuri se si verificheranno. DEFINIZIONE. Un evento (E) si dice casuale, o aleatorio, quando il suo verificarsi
Potenze - Monomi - Polinomi - Operazioni tra Polinomi - Quadrato e Cubo del Binomio - Quadrato del Trinomio
 Potenze - Monomi - Polinomi - Operazioni tra Polinomi - Quadrato e Cubo del Binomio - Quadrato del Trinomio Francesco Zumbo www.francescozumbo.it http://it.geocities.com/zumbof/ Questi appunti vogliono
Potenze - Monomi - Polinomi - Operazioni tra Polinomi - Quadrato e Cubo del Binomio - Quadrato del Trinomio Francesco Zumbo www.francescozumbo.it http://it.geocities.com/zumbof/ Questi appunti vogliono
Lezione 4. Sommario. L artimetica binaria: I numeri relativi e frazionari. I numeri relativi I numeri frazionari
 Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE
 ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
TEOREMA DEL RESTO E REGOLA DI RUFFINI
 TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
EQUAZIONI E PROBLEMI: GUIDA D'USO
 P.1\5- EQUAZIONI E PROBLEMI: GUIDA D'USO - Prof. I.Savoia, Maggio 2011 EQUAZIONI E PROBLEMI: GUIDA D'USO EQUAZIONI LINEARI INTERE: PROCEDURA RISOLUTIVA Per risolvere le equazioni numeriche intere, si può
P.1\5- EQUAZIONI E PROBLEMI: GUIDA D'USO - Prof. I.Savoia, Maggio 2011 EQUAZIONI E PROBLEMI: GUIDA D'USO EQUAZIONI LINEARI INTERE: PROCEDURA RISOLUTIVA Per risolvere le equazioni numeriche intere, si può
= < < < < < Matematica 1
 NUMERI NATURALI N I numeri naturali sono: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,... L insieme dei numeri naturali è indicato con la lettera. Si ha cioè: N= 0,1,2,3,4,5,6,7,.... L insieme dei naturali privato
NUMERI NATURALI N I numeri naturali sono: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,... L insieme dei numeri naturali è indicato con la lettera. Si ha cioè: N= 0,1,2,3,4,5,6,7,.... L insieme dei naturali privato
Distribuzioni campionarie. Antonello Maruotti
 Distribuzioni campionarie Antonello Maruotti Outline 1 Introduzione 2 Concetti base Si riprendano le considerazioni fatte nella parte di statistica descrittiva. Si vuole studiare una popolazione con riferimento
Distribuzioni campionarie Antonello Maruotti Outline 1 Introduzione 2 Concetti base Si riprendano le considerazioni fatte nella parte di statistica descrittiva. Si vuole studiare una popolazione con riferimento
ARROTONDANDO FIGURE CON TRIANGOLI EQUILATERI
 ARROTONDANDO Cosa succede ad accostare figure identiche una all altra? Le figure ottenute che proprietà presentano? Posso trovare un qualche tipo di legge generale? Per rispondere a questa ed altre domande
ARROTONDANDO Cosa succede ad accostare figure identiche una all altra? Le figure ottenute che proprietà presentano? Posso trovare un qualche tipo di legge generale? Per rispondere a questa ed altre domande
Test di sopravvivenza
 Dipartimento di Fisica a.a. 24/25 Fisica Medica 2 Test di sopravvivenza 9/5/24 Analisi della sopravvivenza Esiste un punto di partenza ben identificabile ad esempio: inizio di un mal di schiena? primo
Dipartimento di Fisica a.a. 24/25 Fisica Medica 2 Test di sopravvivenza 9/5/24 Analisi della sopravvivenza Esiste un punto di partenza ben identificabile ad esempio: inizio di un mal di schiena? primo
Esercizio. Sia a R non nullo e siano m, n numeri interi non nulli con m n. Allora a m /a n è uguale a. [1] 1/a n m [2] 1/a m n [3] 1/a n m [4] a n m
![Esercizio. Sia a R non nullo e siano m, n numeri interi non nulli con m n. Allora a m /a n è uguale a. [1] 1/a n m [2] 1/a m n [3] 1/a n m [4] a n m Esercizio. Sia a R non nullo e siano m, n numeri interi non nulli con m n. Allora a m /a n è uguale a. [1] 1/a n m [2] 1/a m n [3] 1/a n m [4] a n m](/thumbs/49/24983931.jpg) Sia a R non nullo e siano m, n numeri interi non nulli con m n. Allora a m /a n è uguale a [1] 1/a n m [2] 1/a m n [3] 1/a n m [4] a n m Vale la [1] perché per le proprietà delle potenze risulta a m a
Sia a R non nullo e siano m, n numeri interi non nulli con m n. Allora a m /a n è uguale a [1] 1/a n m [2] 1/a m n [3] 1/a n m [4] a n m Vale la [1] perché per le proprietà delle potenze risulta a m a
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo. Calcolo Combinatorio
 Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 13/9/2012 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 13/9/2012 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
I RADICALI QUADRATICI
 I RADICALI QUADRATICI 1. Radici quadrate Definizione di radice quadrata: Si dice radice quadrata di un numero reale positivo o nullo a, e si indica con a, il numero reale positivo o nullo (se esiste) che,
I RADICALI QUADRATICI 1. Radici quadrate Definizione di radice quadrata: Si dice radice quadrata di un numero reale positivo o nullo a, e si indica con a, il numero reale positivo o nullo (se esiste) che,
04 - Numeri Complessi
 Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
ESERCIZI DI CALCOLO COMBINATORIO
 ESERCIZI DI CALCOLO COMBINATORIO (G.T.Bagni) Sintesi delle nozioni teoriche da utilizzare a) Dati n elementi e k n, si dicono disposizioni semplici di n elementi di classe k tutti i raggruppamenti ottenuti
ESERCIZI DI CALCOLO COMBINATORIO (G.T.Bagni) Sintesi delle nozioni teoriche da utilizzare a) Dati n elementi e k n, si dicono disposizioni semplici di n elementi di classe k tutti i raggruppamenti ottenuti
EQUAZIONI CON VALORE ASSOLUTO DISEQUAZIONI CON VALORE ASSOLUTO
 EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
1) D0MINIO. Determinare il dominio della funzione f (x) = ln ( x 3 4x 2 3x). Deve essere x 3 4x 2 3x > 0. Ovviamente x 0.
 D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
Giovanna Carnovale. October 18, Divisibilità e massimo comun divisore
 MCD in N e Polinomi Giovanna Carnovale October 18, 2011 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore
MCD in N e Polinomi Giovanna Carnovale October 18, 2011 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore
Economia, Corso di Laurea Magistrale in Ing. Elettrotecnica, A.A Prof. R. Sestini SCHEMA DELLE LEZIONI DELLA PRIMA SETTIMANA
 Economia, Corso di Laurea Magistrale in Ing. Elettrotecnica, A.A. 2013-2014. Prof. R. Sestini SCHEMA DELLE LEZIONI DELLA PRIMA SETTIMANA ALCUNE PREMESSE Cosa e la microeconomia? E la disciplina che studia
Economia, Corso di Laurea Magistrale in Ing. Elettrotecnica, A.A. 2013-2014. Prof. R. Sestini SCHEMA DELLE LEZIONI DELLA PRIMA SETTIMANA ALCUNE PREMESSE Cosa e la microeconomia? E la disciplina che studia
Istituzioni di Statistica 1 Esercizi su strumenti grafici e funzione di frequenza relativa cumulata
 Istituzioni di Statistica 1 Esercizi su strumenti grafici e funzione di frequenza relativa cumulata Esercizio 1 La seguente tabella riguarda il tempo per passare da 0 a 100 km/h di 17 automobili tedesche
Istituzioni di Statistica 1 Esercizi su strumenti grafici e funzione di frequenza relativa cumulata Esercizio 1 La seguente tabella riguarda il tempo per passare da 0 a 100 km/h di 17 automobili tedesche
Matematica e-learning - Corso Zero di Matematica. Gli Insiemi. Prof. Erasmo Modica A.A.
 Matematica e-learning - Gli Insiemi Prof. Erasmo Modica http://www.galois.it erasmo@galois.it A.A. 2009/2010 1 Simboli Matematici Poiché in queste pagine verranno utilizzati differenti simboli matematici,
Matematica e-learning - Gli Insiemi Prof. Erasmo Modica http://www.galois.it erasmo@galois.it A.A. 2009/2010 1 Simboli Matematici Poiché in queste pagine verranno utilizzati differenti simboli matematici,
1 1+e ξ, (1) P A (ξ) = P B (ξ) = 1 1+e ξ (3) In figura (1) riportiamo l andamento delle probabilità P A (ξ) e P B (ξ). P A,P B
 Algoritmo di Elo generalizzato AEg Marcello Colozzo Siano A e B due giocatori che eseguono un gioco a somma zero G. La probabilità di vittoria per A è: dove P A ξ = +e ξ ξ = βr A R B 2 In questa equazione
Algoritmo di Elo generalizzato AEg Marcello Colozzo Siano A e B due giocatori che eseguono un gioco a somma zero G. La probabilità di vittoria per A è: dove P A ξ = +e ξ ξ = βr A R B 2 In questa equazione
Distribuzioni di Probabilità
 Distribuzioni di Probabilità Distribuzioni discrete Distribuzione uniforme discreta Distribuzione di Poisson Distribuzioni continue Distribuzione Uniforme Distribuzione Gamma Distribuzione Esponenziale
Distribuzioni di Probabilità Distribuzioni discrete Distribuzione uniforme discreta Distribuzione di Poisson Distribuzioni continue Distribuzione Uniforme Distribuzione Gamma Distribuzione Esponenziale
Analisi. Calcolo Combinatorio. Ing. Ivano Coccorullo
 Analisi Ing. Ivano Coccorullo Prof. Ivano Coccorullo ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli possibili. Quando le situazioni diventano
Analisi Ing. Ivano Coccorullo Prof. Ivano Coccorullo ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli possibili. Quando le situazioni diventano
Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata
 Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata Stefano Patti 1 19 ottobre 2005 Definizione 1 Sia (Ω, F) uno spazio probabilizzabile.
Esercitazioni del Corso di Probabilitá e Statistica Lezione 2: Eventi disgiunti, eventi indipendenti e probabilitá condizionata Stefano Patti 1 19 ottobre 2005 Definizione 1 Sia (Ω, F) uno spazio probabilizzabile.
Disequazioni - ulteriori esercizi proposti 1
 Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA
 Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione = f(), l'insieme di tutti i valori reali che assegnati
Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione = f(), l'insieme di tutti i valori reali che assegnati
Fenomeni deterministici e aleatori
 Fenomeni deterministici e aleatori Problemi di predizione fenomeni deterministici: data la legge di evoluzione di un sistema, e note le condizioni iniziali, prevedo con buona precisione il comportamento
Fenomeni deterministici e aleatori Problemi di predizione fenomeni deterministici: data la legge di evoluzione di un sistema, e note le condizioni iniziali, prevedo con buona precisione il comportamento
Capitolo 11 Test chi-quadro
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Esame di Probabilità e Statistica del 30 marzo 2009 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esame di Probabilità e Statistica del 30 marzo 2009 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione:
Esame di Probabilità e Statistica del 30 marzo 2009 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione:
Correzione primo compitino, testo A
 Correzione primo compitino, testo A Parte Esercizio Facciamo riferimento alle pagine 22 e 2 del libro di testo Quando si ha a che fare con la moltiplicazione o la divisione di misure bisogna fare attenzione,
Correzione primo compitino, testo A Parte Esercizio Facciamo riferimento alle pagine 22 e 2 del libro di testo Quando si ha a che fare con la moltiplicazione o la divisione di misure bisogna fare attenzione,
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U 1. 2. 3. U 4. 5. 6
 EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
Modulo 2 Data Base - Modello Relazionale
 Modulo 2 Data Base - Modello Relazionale Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2004/2005 Modello Relazionale
Modulo 2 Data Base - Modello Relazionale Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2004/2005 Modello Relazionale
Esame di INFORMATICA (*) Operazioni Aritmetiche: Somma. Lezione 3. Operazioni Aritmetiche: Somma. Operazioni Aritmetiche: Somma
 Università degli Studi di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA A.A. 2008/09 Lezione 3 Operazioni Aritmetiche: Somma + 1 0 1 0 (*) 1 0 1 0 (*) con riporto di 1 2 Operazioni Aritmetiche:
Università degli Studi di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA A.A. 2008/09 Lezione 3 Operazioni Aritmetiche: Somma + 1 0 1 0 (*) 1 0 1 0 (*) con riporto di 1 2 Operazioni Aritmetiche:
IL CALCOLO DELLE PROBABILITA
 IL CLCOLO DLL ROILIT Il concetto di probabilità di un evento casuale si può definire come un opportuno numero indice, compreso fra zero e uno, che intende esprimere la possibilità che l evento medesimo
IL CLCOLO DLL ROILIT Il concetto di probabilità di un evento casuale si può definire come un opportuno numero indice, compreso fra zero e uno, che intende esprimere la possibilità che l evento medesimo
1 L estrazione di radice
 1 L estrazione di radice Consideriamo la potenza 3 2 = 9 di cui conosciamo: Esponente 3 2 = 9 Valore della potenza Base L operazione di radice quadrata consiste nel chiedersi qual è quel numero x che elevato
1 L estrazione di radice Consideriamo la potenza 3 2 = 9 di cui conosciamo: Esponente 3 2 = 9 Valore della potenza Base L operazione di radice quadrata consiste nel chiedersi qual è quel numero x che elevato
Variabili aleatorie Parte I
 Variabili aleatorie Parte I Variabili aleatorie Scalari - Definizione Funzioni di distribuzione di una VA Funzioni densità di probabilità di una VA Indici di posizione di una distribuzione Indici di dispersione
Variabili aleatorie Parte I Variabili aleatorie Scalari - Definizione Funzioni di distribuzione di una VA Funzioni densità di probabilità di una VA Indici di posizione di una distribuzione Indici di dispersione
ESAME DI STATO LICEO SCIENTIFICO MATEMATICA 2011
 ESAME DI STATO LICEO SCIENTIFICO MATEMATICA PROBLEMA La funzione f ( ) ( )( ) è una funzione dispari di terzo grado Intercetta l asse nei punti ;, ; e ; Risulta f per e per è invece f per e per f ' risulta
ESAME DI STATO LICEO SCIENTIFICO MATEMATICA PROBLEMA La funzione f ( ) ( )( ) è una funzione dispari di terzo grado Intercetta l asse nei punti ;, ; e ; Risulta f per e per è invece f per e per f ' risulta
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio. M. Besozzi - IRCCS Istituto Auxologico Italiano
 Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Somma di numeri floating point. Algoritmi di moltiplicazione e divisione per numeri interi
 Somma di numeri floating point Algoritmi di moltiplicazione e divisione per numeri interi Standard IEEE754 " Standard IEEE754: Singola precisione (32 bit) si riescono a rappresentare numeri 2.0 10 2-38
Somma di numeri floating point Algoritmi di moltiplicazione e divisione per numeri interi Standard IEEE754 " Standard IEEE754: Singola precisione (32 bit) si riescono a rappresentare numeri 2.0 10 2-38
Disequazioni in una incognita. La rappresentazione delle soluzioni
 Disequazioni in una incognita Una disequazione in una incognita è una disuguaglianza tra due espressioni contenenti una variabile (detta incognita) verificata solo per particolari valori attribuirti alla
Disequazioni in una incognita Una disequazione in una incognita è una disuguaglianza tra due espressioni contenenti una variabile (detta incognita) verificata solo per particolari valori attribuirti alla
La domanda di mercato: surplus del consumatore; Elasticità della domanda
 La domanda di mercato: surplus del consumatore; Elasticità della domanda ELASTICITA ε L elasticità diretta della domanda rispetto al prezzo è una misura della reattività della domanda di un bene a variazioni
La domanda di mercato: surplus del consumatore; Elasticità della domanda ELASTICITA ε L elasticità diretta della domanda rispetto al prezzo è una misura della reattività della domanda di un bene a variazioni
Progettazione di Algoritmi
 Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 1/01/016 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via avrai
Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 1/01/016 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via avrai
ANALISI CHIMICO FARMACEUTICA I
 Prof. Gianluca Sbardella : 089 969770 : gsbardella@unisa.it L INCERTEZZA E LE CIFRE SIGNIFICATIVE Tutte le misure sono affette da un certo grado di incertezza la cui entità può dipendere sia dall operatore
Prof. Gianluca Sbardella : 089 969770 : gsbardella@unisa.it L INCERTEZZA E LE CIFRE SIGNIFICATIVE Tutte le misure sono affette da un certo grado di incertezza la cui entità può dipendere sia dall operatore
Andamento e periodo delle funzioni goniometriche
 Andamento e periodo delle funzioni goniometriche In questa dispensa ricaviamo gli andamenti delle funzioni goniometriche seno, coseno, tangente e cotangente tra 0 e 360, detti, rispettivamente, sinusoide,
Andamento e periodo delle funzioni goniometriche In questa dispensa ricaviamo gli andamenti delle funzioni goniometriche seno, coseno, tangente e cotangente tra 0 e 360, detti, rispettivamente, sinusoide,
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
INSIEME N. L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi.
 INSIEME N L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi. N = {0;1;2;3... Su tale insieme sono definite le 4 operazioni di base: l'addizione (o somma), la sottrazione, la moltiplicazione
INSIEME N L'insieme dei numeri naturali (N) è l'insieme dei numeri interi e positivi. N = {0;1;2;3... Su tale insieme sono definite le 4 operazioni di base: l'addizione (o somma), la sottrazione, la moltiplicazione
Corso di Fondamenti di Informatica Classi di istruzioni 2
 Corso di Informatica Classi di istruzioni 2 Anno Accademico 2010/2011 Francesco Tortorella Strutture di controllo Caratteristica essenziale degli algoritmi è la possibilità di decidere le operazioni da
Corso di Informatica Classi di istruzioni 2 Anno Accademico 2010/2011 Francesco Tortorella Strutture di controllo Caratteristica essenziale degli algoritmi è la possibilità di decidere le operazioni da
Costruiamo la STRISCIA DELLE MISURE. decametro metro decimetro. Tm Gm Mm km hm dam m dm cm mm µm nm pm
 Terametro Gigametro Megametro chilometro ettometro decametro metro decimetro micrometro millimetro milcrometro nanometro picometro Costruiamo la STRISCIA DELLE MISURE. Tm Gm Mm km hm dam m dm cm mm µm
Terametro Gigametro Megametro chilometro ettometro decametro metro decimetro micrometro millimetro milcrometro nanometro picometro Costruiamo la STRISCIA DELLE MISURE. Tm Gm Mm km hm dam m dm cm mm µm
Esercitazioni di Metodologia
 Esercitazioni di Metodologia Dott.ssa Gabriella Agrusti Università degli Studi Roma Tre Riprendiamo il discorso Centili Rango centile Punti z.. Punti T Repetita iuvant Il centile è il valore al di sotto
Esercitazioni di Metodologia Dott.ssa Gabriella Agrusti Università degli Studi Roma Tre Riprendiamo il discorso Centili Rango centile Punti z.. Punti T Repetita iuvant Il centile è il valore al di sotto
TOLLERANZE DIMENSIONALI DESIGNAZIONE DI FORI E ALBERI
 TOLLERANZE DIMENSIONALI DESIGNAZIONE DI FORI E ALBERI Nel ciclo di lavorazione di un pezzo meccanico ci sono inevitabili errori che rendono impossibile il rispetto delle esatte misure riportate nel disegno.
TOLLERANZE DIMENSIONALI DESIGNAZIONE DI FORI E ALBERI Nel ciclo di lavorazione di un pezzo meccanico ci sono inevitabili errori che rendono impossibile il rispetto delle esatte misure riportate nel disegno.
Esercitazioni di Statistica
 Esercitazioni di Statistica Variabili casuali Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio Determinare se le funzioni seguenti: 0.0 se x < 0. se x = g(x) = 0.5 se x = 0.7 se x = 3 se x =
Esercitazioni di Statistica Variabili casuali Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio Determinare se le funzioni seguenti: 0.0 se x < 0. se x = g(x) = 0.5 se x = 0.7 se x = 3 se x =
Esame di Statistica (10 o 12 CFU) CLEF 11 febbraio 2016
 Esame di Statistica 0 o CFU) CLEF febbraio 06 Esercizio Si considerino i seguenti dati, relativi a 00 clienti di una banca a cui è stato concesso un prestito, classificati per età e per esito dell operazione
Esame di Statistica 0 o CFU) CLEF febbraio 06 Esercizio Si considerino i seguenti dati, relativi a 00 clienti di una banca a cui è stato concesso un prestito, classificati per età e per esito dell operazione
Dadi, carte, diagrammi e frazioni.
 Dadi, carte, diagrammi e frazioni..i primi passi nella probabilità Relatore: Prof.ssa Ana Millán Gasca Laura Sol Minicorso Insegnare la matematica ai bambini a partire dall esperienza Roma, Università
Dadi, carte, diagrammi e frazioni..i primi passi nella probabilità Relatore: Prof.ssa Ana Millán Gasca Laura Sol Minicorso Insegnare la matematica ai bambini a partire dall esperienza Roma, Università
Teoria della probabilità: eventi, proprietà additiva e moltiplicativa. L incertezza
 La probabilità Teoria della probabilità: eventi, proprietà additiva e moltiplicativa L incertezza Nella maggior parte delle situazioni la nostra condizione è caratterizzata dallincertezza Incertezza relativa
La probabilità Teoria della probabilità: eventi, proprietà additiva e moltiplicativa L incertezza Nella maggior parte delle situazioni la nostra condizione è caratterizzata dallincertezza Incertezza relativa
CURRICOLO DI MATEMATICA CLASSE PRIMA
 CURRICOLO DI MATEMATICA CLASSE PRIMA INDICATORI OBIETTIVI SPECIFICI CONTENUTI NUMERI Eseguire le quattro operazioni con i numeri interi. Elevare a potenza numeri naturali e interi. Comprendere il significato
CURRICOLO DI MATEMATICA CLASSE PRIMA INDICATORI OBIETTIVI SPECIFICI CONTENUTI NUMERI Eseguire le quattro operazioni con i numeri interi. Elevare a potenza numeri naturali e interi. Comprendere il significato
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di Mercoledì giugno 4 (tempo a disposizione: ore. Scrivere su ogni foglio NOME e COGNOME. Le
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di Mercoledì giugno 4 (tempo a disposizione: ore. Scrivere su ogni foglio NOME e COGNOME. Le
Grandezze fotometriche 1
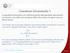 Grandezze fotometriche 1 Le grandezze fotometriche sono definite partendo dalle grandezze radiometriche ma tenendo conto della curva di risposta dell occhio umano, che agisce come un fattore di peso. In
Grandezze fotometriche 1 Le grandezze fotometriche sono definite partendo dalle grandezze radiometriche ma tenendo conto della curva di risposta dell occhio umano, che agisce come un fattore di peso. In
Richiami di aritmetica
 Richiami di aritmetica I numeri naturali L insieme dei numeri naturali, che si indica con N, comprende tutti i numeri interi maggiori di zero. Operazioni fondamentali OPERAZIONE SIMBOLO RISULTATO TERMINI
Richiami di aritmetica I numeri naturali L insieme dei numeri naturali, che si indica con N, comprende tutti i numeri interi maggiori di zero. Operazioni fondamentali OPERAZIONE SIMBOLO RISULTATO TERMINI
Rappresentazioni numeriche
 Rappresentazioni numeriche Un numero è dotato di un valore una rappresentazione La rappresentazione di un numero è il sistema che utilizziamo per indicarne il valore. Normalmente è una sequenza (stringa)
Rappresentazioni numeriche Un numero è dotato di un valore una rappresentazione La rappresentazione di un numero è il sistema che utilizziamo per indicarne il valore. Normalmente è una sequenza (stringa)
Lezione 4 a - Misure di dispersione o di variabilità
 Lezione 4 a - Misure di dispersione o di variabilità Abbiamo visto che la media è una misura della localizzazione centrale della distribuzione (il centro di gravità). Popolazioni con la stessa media possono
Lezione 4 a - Misure di dispersione o di variabilità Abbiamo visto che la media è una misura della localizzazione centrale della distribuzione (il centro di gravità). Popolazioni con la stessa media possono
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
Esercizi con catene di Markov Pietro Caputo 12 dicembre 2006
 Esercizi con catene di Markov Pietro Caputo dicembre 006 Esercizio. Si considerino i lanci di un dado (6 facce equiprobabili). Sia X n il minimo tra i risultati ottenuti nei lanci,,..., n. Si calcoli la
Esercizi con catene di Markov Pietro Caputo dicembre 006 Esercizio. Si considerino i lanci di un dado (6 facce equiprobabili). Sia X n il minimo tra i risultati ottenuti nei lanci,,..., n. Si calcoli la
Introduzione. Il Dirigente Scolastico
 Introduzione La L.107/2015, cosiddetta della Buona scuola, prevede che, ogni Istituzione scolastica, entro il 16 gennaio 2016, approvi il P.t.o.f. (Piano triennale dell offerta formativa), contenente le
Introduzione La L.107/2015, cosiddetta della Buona scuola, prevede che, ogni Istituzione scolastica, entro il 16 gennaio 2016, approvi il P.t.o.f. (Piano triennale dell offerta formativa), contenente le
SECONDA PROVA PARZIALE DI MACROECONOMIA Del 1 Giugno 2015 (VERSIONE C) CLEC COGNOME NOME
 SECONDA PROVA PARZIALE DI MACROECONOMIA Del 1 Giugno 2015 (VERSIONE C) CLEC COGNOME NOME MATRICOLA 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10)
SECONDA PROVA PARZIALE DI MACROECONOMIA Del 1 Giugno 2015 (VERSIONE C) CLEC COGNOME NOME MATRICOLA 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10)
I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito.
 TEST DI AUTOVALUTAZIONE - SETTIMANA I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
TEST DI AUTOVALUTAZIONE - SETTIMANA I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
La probabilità non esiste Riflessioni e percorsi sul tema Dati e previsioni
 La probabilità non esiste Riflessioni e percorsi sul tema Dati e previsioni Mathesis Milano, 21/1/2015 La mia tesi, paradossale e un po' provocatoria, ma genuina, è che semplicemente LA PROBABILITÀ NON
La probabilità non esiste Riflessioni e percorsi sul tema Dati e previsioni Mathesis Milano, 21/1/2015 La mia tesi, paradossale e un po' provocatoria, ma genuina, è che semplicemente LA PROBABILITÀ NON
L'ATMOSFERA un involucro eccezionale
 DIESSE FIRENZE Didattica e Innovazione Scolastica Centro per la formazione e l aggiornamento SCIENZAFIRENZE QUARTA EDIZIONE Docenti e studenti a confronto su: L'ATMOSFERA un involucro eccezionale Aula
DIESSE FIRENZE Didattica e Innovazione Scolastica Centro per la formazione e l aggiornamento SCIENZAFIRENZE QUARTA EDIZIONE Docenti e studenti a confronto su: L'ATMOSFERA un involucro eccezionale Aula
Modelli descrittivi, statistica e simulazione
 Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 18 febbraio 2016 (9.00/13.00)
Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 18 febbraio 2016 (9.00/13.00)
Ingegneria Meccatronica. M. Da Lio
 Ingegneria Meccatronica M. Da Lio Ingegneria Meccatronica Dall Idea al Prodotto finito (sito web) Innovazione ritmo di rinnovamento dei prodotti industriali sempre più rapido nel triennio 94-96 il 49.7%
Ingegneria Meccatronica M. Da Lio Ingegneria Meccatronica Dall Idea al Prodotto finito (sito web) Innovazione ritmo di rinnovamento dei prodotti industriali sempre più rapido nel triennio 94-96 il 49.7%
Circonferenze del piano
 Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Equazioni di II grado come strumento per risolvere problemi
 Equazioni di II grado come strumento per risolvere problemi Presentazione per il corso di perfezionamento 200/06 Anna Lisa Granata Obiettivi principali proporre le equazioni di secondo grado come traduzione
Equazioni di II grado come strumento per risolvere problemi Presentazione per il corso di perfezionamento 200/06 Anna Lisa Granata Obiettivi principali proporre le equazioni di secondo grado come traduzione
Distribuzioni di probabilità
 Distribuzioni di probabilità Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Distribuzioni di probabilità Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
m = a k n k + + a 1 n + a 0 Tale scrittura si chiama rappresentazione del numero m in base n e si indica
 G. Pareschi COMPLEMENTI ED ESEMPI SUI NUMERI INTERI. 1. Divisione con resto di numeri interi 1.1. Divisione con resto. Per evitare fraintendimenti nel caso in cui il numero a del Teorema 0.4 sia negativo,
G. Pareschi COMPLEMENTI ED ESEMPI SUI NUMERI INTERI. 1. Divisione con resto di numeri interi 1.1. Divisione con resto. Per evitare fraintendimenti nel caso in cui il numero a del Teorema 0.4 sia negativo,
Mini-Corso di Informatica
 Mini-Corso di Informatica CALCOLI DI PROCESSO DELL INGEGNERIA CHIMICA Ing. Sara Brambilla Tel. 3299 sara.brambilla@polimi.it Note sulle esercitazioni Durante le esercitazioni impareremo a implementare
Mini-Corso di Informatica CALCOLI DI PROCESSO DELL INGEGNERIA CHIMICA Ing. Sara Brambilla Tel. 3299 sara.brambilla@polimi.it Note sulle esercitazioni Durante le esercitazioni impareremo a implementare
2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi)
 2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi) La circonferenza è la curva di 2^ grado che viene individuata univocamente da tre punti non allineati e possiede la seguente proprietà:
2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi) La circonferenza è la curva di 2^ grado che viene individuata univocamente da tre punti non allineati e possiede la seguente proprietà:
