Imetodi usati per la produzione
|
|
|
- Giuliana Santi
- 8 anni fa
- Visualizzazioni
Transcript
1 Un software per ottimizzare la rigidezza d ingranamento In questo articolo si presenta il calcolo delle geometria dei denti usando utensili diversi; sulla base di questa geometria, si calcolano la rigidezza effettiva di ingranamento sotto carico e le sollecitazioni. g Ulrich Kissling, Marcus Raabe, Michael Fish Imetodi usati per la produzione delle ruote dentate sono in costante sviluppo. Negli ultimi anni è diventata una tendenza la rettifica di forma, un alternativa alla classica rettifica con generazione. Un altro esempio è un metodo usato per lo più nell industria automobilistica: per migliorare la vita operativa degli utensili e ottenere una forma dei denti con più alta resistenza al piede, le ruote dentate vengono prodotti con uno, due o tre processi di pre-fresatura diversi seguiti da honing o rettifica finali. Una delle più recenti tendenze nello sviluppo di ruote dentate ottimizzate è quella di applicare, nel processo di finitura, una modifica del profilo di forma ondulatoria in modo da ridurre l errore di trasmissione. Questi metodi di produzione richiedono lo sviluppo di metodi di calcolo appropriati. Durante il funzionamento, la variazione della rigidezza di ingranamento provoca una deviazione sull angolo di rotazione della ruota di uscita rispetto al rapporto di trasmissione nominale (errore di trasmissione), che causa vibrazioni e rumore. La variazione della rigidezza di ingranamento può essere ridotta ottimizzando la geometria della dentatura (rapporto di condotta trasversale εα e rapporto di ricoprimento εβ), ma per la rigidezza sotto carico è anche molto importante il tipo di modifica del profilo. Il metodo di calcolo corrente per la resistenza dei denti secondo AGMA 2001 [1] o ISO 6336 [2] si basa sull assunzione di una forma del dente prodotta da un solo utensile in un processo di generazione. Quando si usa un utensile con protuberanza, il metodo comprende anche un processo di pre-fresatura (con sovrametallo per la finitura) e un processo finale di rettifica oppure di honing. Ciò comporta che, nel caso delle ruote dentate prodotte con rettifica di forma o altri metodi non convenzionali, non si possano applicare le formule per il calcolo della resistenza previsto dai metodi AGMA o ISO. Il problema è che per il calcolo delle sollecitazioni al piede del 54 Organi di trasmissione - gennaio 2007
2 dente si devono conoscere alcuni valori, per esempio lo spessore del dente e il raccordo al piede. Il metodo di calcolo assume che la forma del dente sia conosciuta non esattamente e presenta pertanto formule che consentono il calcolo della forma del dente solo nella sezione considerata del dente. Queste formule presuppongono la fabbricazione con un processo di generazione. Ma in linea di principio, se si conosce la forma del dente, il dente può essere calcolato usando direttamente le formule proposte dalle norme. Pertanto, se il calcolo della forma del dente viene integrato nel software di calcolo della resistenza, le norme AGMA o ISO possono essere usate per qualsiasi metodo di produzione. Fig. 1 - Forma del dente generata con un ciclo di fabbricazione con tre utensili. 1: Pre-fresa m n = 1,0368, α n = 25 (verde) 2: Fresa con protuberanza m n = 1,0, α n = 20,0 (marrone) 3: Processo finale di rettifica (azzurro) Calcolo della forma del dente con diversi utensili Nella maggior parte dei programmi disponibili per il calcolo degli ingranaggi, è possibile calcolare la forma del dente quando si usa un utensile standard (creatore, fresa di generazione o pignone utensile). Normalmente è anche possibile introdurre un sovrametallo di rettifica e simulare così un processo di produzione a due stadi (taglio più rettifica). In risposta alle frequenti richieste degli utilizzatori del software di calcolo delle ruote dentate largamente apprezzato KISSsoft [3], si è deciso di implementare nel software un nuovo approccio per il calcolo della forma del dente. Si può definire, in qualsiasi sequenza desiderata, un numero illimitato di utensili, quali creatore, fresa, pignone utensile, disco di rettifica (rettifica con generazione o di forma) e utensile per honing. Dopo ogni fase, può essere visualizzata la forma del dente e diverse forme possono essere sovrapposte per illustrare l asportazione di materiale da una fase all altra. Viene anche visualizzato il processo di fabbricazione dall utensile all ingranaggio e, per ottimizzare la durata dell utensile, vengono visualizzati i vettori delle velocità di strisciamento e di rotolamento. In figura 1 sono indicati i diversi stadi per ottenere la forma definitiva del dente quando si usano due frese e un processo finale di rettifica. Per la ruota dentata con angolo di pressione án 20 si usa una pre-fresa con α n 25. Ciò determina un miglioramento della vita operativa dell utensile e crea un migliore raccordo al piede del dente. Dato che la forma del fianco deve essere identica al disegno finale, il diametro di base bd della ruota dentata deve rimanere identico. Pertanto il modulo della prefresa deve essere aumentato del rapporto cos20 /cos25. Alcune altre particolarità del calcolo della forma del dente sono: Vita operativa dell utensile: Per il miglioramento della vita operativa dell utensile (numero di ruote tagliate prima che l utensile debba essere riaffilato o sostituito) è molto importante la visualizzazione dello strisciamento sul fianco di taglio dell utensile (figura 2). Molti sono i fattori che influenzano la vita operativa dell utensile. Uno di essi è lo strisciamento specifico locale sull utensile. Uno strisciamento specifico negativo elevato sull utensile comporta che una piccola Fig. 2 - Disegno di un dente della fresa per il processo di pretaglio (angolo di pressione 25 ) e di taglio finale (angolo di pressione 20 ) con indicazione dello strisciamento specifico (tra fresa e ruota dentata) durante la fabbricazione. Uno strisciamento specifico positivo elevato (in questo caso sul dedendum) indica rischio di usura più alto. Lo strisciamento sulla fresa da 20 è il doppio di quello sulla pre-fresa da 25. sezione del tagliente dell utensile produca una grande sezione sulla ruota dentata. Ciò significa che questa parte dell utensile viene utilizzata fortemente e di conseguenza è soggetta a notevole usura. Come si vede in figura 2, la prefresa con un angolo di pressione più elevato (come indicato in figura 1), presenta uno strisciamento specifico sensibilmente ridotto. Intaglio di rettifica: per la massima resistenza è importante sapere se nel pro- gennaio Organi di trasmissione 55
3 cesso di rettifica si provoca il cosiddetto intaglio di rettifica (ISO , fattore Ysg). Pertanto, nel calcolo del processo di rettifica bisogna tenere conto dell intaglio. Questo intaglio può ridurre notevolmente il fattore di sicurezza per la sollecitazione a flessione. Nel programma KISSsoft i dati pertinenti vengono automaticamente trasferiti al calcolo della resistenza e il fattore intaglio viene incluso nei risultati. Fig. 3 - Rappresentazione della coppia di ruote dentate usate per il calcolo dell errore di trasmissione. Fig. 4 - Errore di trasmissione calcolato considerando la rigidezza sotto carichi di 0, 25, 50, 75 e 100% della potenza nominale. In alto: ingranaggio con profilo non modificato. Al centro: ingranaggio con modifica simmetrica piccola del profilo (13 µm). In basso: ingranaggio con modifica simmetrica normale del profilo (26 µm). Vibrazioni In molte applicazioni il livello di rumore è oggi molto critico e deve essere mantenuto quanto più basso possibile. Il rumore è generato dagli errori di trasmissione che producono una variazione incrementale della velocità del rotismo rispetto al valore nominale. Questo effetto provoca un istantanea accelerazione/decelerazione nella catena di trasmissione da cui si originano vibrazioni. L errore di trasmissione viene determinato dalla variazione della rigidezza durante un ciclo di ingranamento. È ben noto che anche gli errori di fabbricazione generano un certo errore di trasmissione. Migliorando la qualità degli ingranaggi si contribuisce al miglioramento della situazione, ma anche con un rotismo della massima qualità si hanno errori di trasmissione dovuti alla variazione della rigidezza. In questo contesto, il software calcola la rigidezza del singolo dente per ogni forma del dente e determina la linea di contatto reale sotto carico. Da queste informazioni si ricava l errore reale di trasmissione della coppia di ruote. È possibile studiare molto rapidamente l effetto della proposta di modifica del profilo sul comportamento di un ingranaggio sotto diversi carichi. Il calcolo della rigidezza della coppia di denti sotto carico permette di confrontare diverse geometrie di dentatura per trovare la soluzione migliore. In figura 4 è illustrato un tipico caso di un ingra- 56 Organi di trasmissione - gennaio 2007
4 Fig. 5 - Ingranaggio con modifica simmetrica piccola del profilo (13 µm) come in figura 4, ma con una modifica supplementare di forma sinusoidale nella regione di contatto singolo del fianco del dente. A sinistra: la forma modificata del dente (esagerata nel disegno) con spessore supplementare di 10 µm. A destra: il conseguente errore di trasmissione per diversi carichi. Fig. 6 - Calcolo dell errore di trasmissione di una coppia di ruote dentate sotto carico. naggio standard (forma dei denti di figura 3) con rapporto di condotta trasversale (εα) = 1,67 (z: 25/76; P: 4,2333; modulo: 6,0). L errore di trasmissione è piccolo (la rigidezza è elevata) durante il 67% del ciclo, quando due coppie di denti sono in presa, e per il resto è grande, quando una sola coppia di denti è in presa. (Osservazione: un valore teorico del rapporto di condotta trasversale di 1,67 significa che durante il 67% del tempo due coppie di denti sono in presa e durante il 33% del tempo solo una coppia). L ingranaggio senza modifica del profilo è soggetto a un salto da piccolo a elevato errore di trasmissione, come si vede in figura 4. Una modifica del profilo ben studiata ridurrebbe la pendenza di questo salto, producendo una variazione più dolce della rigidezza, ma non cambierebbe il livello delle fasi di bassa e alta rigidezza. Perciò la modifica del profilo è utile, ma non è la soluzione del problema. Il metodo migliore per ridurre la variazione della rigidezza è quello di usare un alto profilo del dente con, teoricamente, un rapporto di condotta trasversale di 2,0. In questo caso, dato che sono sempre in presa due coppie di denti, il salto viene eliminato. Risultati ottimi si ottengono quando il terzo dente che entra in presa è scarico. Questo è possibile se si applica una modifica del profilo appropriata. In questo gennaio Organi di trasmissione 57
5 caso, il rapporto di condotta trasversale teorico deve essere maggiore di 2,0, a seconda della lunghezza della correzione del profilo prevista. Fig. 7 - Determinazione della sollecitazione al piede del dente per qualsiasi punto del piede tra Y F (r) e Y S (r). Il calcolo dell errore di trasmissione La rigidezza del singolo dente è costituita dai seguenti quattro importanti effetti: Flessione del dente Deformazione di taglio del dente Pressione hertziana sul contatto Inclinazione del dente nel corpo dell ingranaggio Le equazioni per il calcolo di questi effetti sono state sviluppate da Peterson [4] per gli ingranaggi a evolvente. Il metodo può essere adattato anche a ingranaggi con modifica del profilo e a ingranaggi non a evolvente. La rigidezza di due denti in presa viene chiamata rigidezza del dente combinata di una coppia di denti (c ) e la rigidezza totale di tutti i denti in presa è la rigidezza di ingranamento (c y ). È importante il calcolo dell andamento della rigidezza di ingranamento durante un ciclo. Per gli ingranaggi a evolvente non caricati senza modifica del profilo, la linea di contatto è una retta, ma per gli ingranaggi reali sotto carico trovare la linea di contatto effettiva è complicato. A causa della flessione dei denti, il rapporto di condotta trasversale εα reale aumenta. Pertanto la linea di contatto deve essere calcolata tratto dopo tratto; e per ogni singolo tratto, deve essere determinato il numero effettivo di denti in presa. Dato che la rigidezza dei denti dipende dal carico e che il carico su un singolo dente (con coppia costante sul pignone) dipende dal numero di denti in presa, la soluzione deve essere trovata mediante iterazione (figura 6). Il calcolo è lungo perché la rigidezza stessa dipende dalla forza normale applicata (dovuta alla pressione hertziana); pertanto, ogni singolo tratto sulla linea di contatto deve essere trovato mediante doppia iterazione. Il risultato è interessante. In figura 4 è illustrato un tipico esempio di ingranaggio senza (in alto) e con diversi gradi di modifica del profilo (al centro e in basso). La tecnica di indicare l errore di trasmissione sotto carico variabile, per esempio 25, 50, 75 e 100% della coppia nominale di carico, e definita da Harris [5] già nel 1958, è una presentazione utilissima per valutare il comportamento di una modifica del profilo proposta. La maggior parte dei riduttori non funziona sempre con carico costante, per cui le prestazioni devono essere ottimali all interno di un certo intervallo di coppie. L errore di trasmissione non modificato di figura 4 fa anche vedere una particolarità spesso discussa: a causa della flessione dei denti, all aumentare della coppia il rapporto trasversale di contatto (εα) aumenta da 1,67 a circa 1,78 (per carico 58 Organi di trasmissione - gennaio 2007
6 50%) e a 1,81 (per carico 100%). Ogni piccola modifica del profilo del dente ha un influenza importante sulla curva, come si vede nel confronto di figura 4. Una nuova tendenza nello sviluppo di ingranaggi ottimizzati è quella di applicare una speciale modifica del profilo nel processo di finitura per ridurre l errore di trasmissione. Quando si aumenta lo spessore del dente tra i limiti dei singoli diametri di contatto (la parte del fianco del dente con una coppia di denti in presa), si può ridurre il valore dell errore di trasmissione in questa parte. Per dimostrare questo effetto, la figura 5 presenta l errore di trasmissione determinato da una modifica di tipo sinusoidale. È evidente che questo genere di modifica produce errori di trasmissione più elevati in condizioni di basso carico, ma nel campo della coppia nominale la variazione dell errore di trasmissione risulta notevolmente ridotta. Il comportamento dell errore di trasmissione può essere ulteriormente migliorato quando si applicano forme di modifica diverse. La sinusoide è stata scelta per dimostrare questo principio. È ben noto che gli errori di fabbricazione (per esempio, l errore di passo) hanno un influenza importante sull errore di trasmissione delle ruote dentate reali. Questi effetti possono essere studiati applicando un errore alla forma del dente. Per esempio, prima di calcolare l errore di trasmissione, si può aumentare la distanza tra due fianchi di un valore pari all errore di passo (fig. 6). Analisi delle sollecitazioni Per il calcolo della resistenza delle ruote dentate ottimizzate è stato sviluppato un algoritmo. Tutte le normali procedure di calcolo determinano la sollecitazione al piede del dente mediante un modello semplificato delle condizioni reali. Secondo ISO 6336, la sezione trasversale critica al piede del dente deve trovarsi sul punto di contatto della tangente a 30 al Fig. 8 - Sollecitazioni (e pressione di Hertz) al piede del dente, calcolate sulla base della forma effettiva del dente e delle condizioni di ingranamento. profilo del piede. Secondo AGMA 2001 (con AGMA 908-B89), alla forma del dente viene applicata la parabola di Lewis, in cui il punto di contatto della parabola con il raccordo al piede del dente definisce la sezione trasversale critica. A seconda della forma effettiva del raccordo al piede del dente si ha un errore più o meno grande. Nella pubblicazione di B. Obsieger [6] di alcuni anni or sono, è stato proposto un metodo di calcolo notevolmente migliorato. Sulla base della forma effettiva del dente, per ogni punto nella regione del piede del dente si calcolano il fattore di forma del dente (ISO: YF, AGMA: Y) e il fattore di correzione della sollecitazione (ISO: YS, AGMA: Kf) e si determina quindi la posizione del massimo del prodotto (ISO: YF* YS, AGMA: Y/Kf) (figura 7). Questa procedura di calcolo è integrata nel software KISSsoft. La sezione trasversale critica al piede del dente può essere determinata, secondo AG- MA, sulla base dell applicazione della forza sulla testa del dente o sul punto di contatto singolo più esterno. Con questo dato specifico, si effettua completamente il calcolo della resistenza secondo ISO o AGMA. L andamento delle sollecitazioni può essere presentato anche in forma grafica (figura 8). Questo metodo dà buoni risultati rispetto ai calcoli FEM. In questa procedura è anche incluso l effetto dell intaglio di rettifica. Per una verifica della resistenza secondo AGMA o ISO, si identifica il punto di massima sollecitazione e si esegue il calcolo su questo punto specifico. Dato che la norma ISO stabilisce esplicitamente un metodo A, per avere un algoritmo migliorato sulla base della stessa filosofia fondamentale, questo tipo di calcolo è conforme al 100%. Anche il valore della pressione di Hertz lungo il fianco del dente viene calcolato sulla base della forma effettiva del dente. Per ogni punto di azione si determinano i raggi di curvatura di entrambe le ruote dentate e la pressione viene calcolata gennaio Organi di trasmissione 59
7 partendo da questi valori. Con gli stessi dati è possibile calcolare la velocità di strisciamento e anche di simulare la temperatura locale di contatto, il rendimento e il fattore di sicurezza al grippaggio per qualsiasi coppia di ruote. Fig. 9 - A sinistra: forza normale; a destra: pressione di Hertz e sollecitazione al piede del dente durante un ciclo di ingranamento (stesse ruote dentate della figura 4 per carico 100%). Sollecitazioni lungo la linea di contatto La procedura per il calcolo dell errore di trasmissione (figura 6) fornisce anche la forza normale e il punto di contatto sul dente durante il ciclo di ingranamento, consentendo così un analisi ancora più precisa. In figura 8 sono riportate la pressione hertziana e la massima sollecitazione sul dente, calcolate con la forza normale effettiva. Dato che le norme (AGMA e ISO) si basano sul calcolo di una sola situazione, cioè l applicazione della forza normale sul punto del contatto singolo del dente, è di gran lunga più preciso il calcolo più realistico della forza normale e delle corrispondenti sollecitazioni in ogni posizione. Si noti, comunque, che il risultato può essere abbastanza differente da quello della procedura prevista dalle norme. Conclusione Con un software avanzato per la simulazione del processo di fabbricazione con uno o più diversi utensili e metodi di produzione, si calcola la forma effettiva del dente. Sulla base di questi dati si effettua il calcolo della resistenza al piede e dell errore di trasmissione. Viene proposta un estensione del calcolo della resistenza al piede, in modo che le norme AGMA o ISO possano essere applicate a qualsiasi forma del dente, per esempio anche a ruote dentate rettificate di forma. Per lo sviluppo di ingranaggi silenziosi, è molto importante il calcolo dell errore di trasmissione sotto diversi carichi. Il software permette di studiare gli effetti di diverse modifiche del profilo sotto carico e di trovare la soluzione migliore per il campo di coppie richiesto. Bibliografia [1] AGMA 2001-C95: Fattori fondamentali di funzionamento e metodi di calcolo per denti diritti a evolvente e denti elicoidali. Norma AGMA, [2] ISO 6336, Parte 1-3: Calcolo della capacità di carico di ingranaggi cilindrici a denti diritti ed elicoidali [3] Progettazione di ingranaggi e riduttori (con KISSsoft). Gear Technology, gennaio [4] Peterson, D.: Auswirkung der Lastverteilung auf die Zahnfusstragfähigkeit von Stirnradpaarungen. Tesi, Braunschweig, Germania, [5] Harris, S.L.: Dynamics Loads on the Teeth of Spur Gears. Atti Inst. Mech. Eng., vol. 172, 1958, pp [6] Obsieger, B.: Zahnformfactoren von Aussen-und Innenverzahnungen. Konstruction 32 (1980), pp Organi di trasmissione - gennaio 2007
KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici e conici, dimensionamento e ottimizzazione
 KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici e conici, dimensionamento e ottimizzazione Due giorni Il 18/03/13 dalle 09.30 alle 17.30 e il 19/03/13 dalle 09.00 alle 17.00. KISSsoft AG
KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici e conici, dimensionamento e ottimizzazione Due giorni Il 18/03/13 dalle 09.30 alle 17.30 e il 19/03/13 dalle 09.00 alle 17.00. KISSsoft AG
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
SIMULAZIONI LTCA MEDIANTE METODI F.E.M. PER L ANALISI DI INGRANAGGI CILINDRICI A DENTI DRITTI
 Autori: SIMULAZIONI LTCA MEDIANTE METODI F.E.M. PER L ANALISI DI INGRANAGGI CILINDRICI A DENTI DRITTI Marco Beghini Fabio Presicce Ciro Santus Marco Facchini Collaborazione fra DIMNP, Università di Pisa
Autori: SIMULAZIONI LTCA MEDIANTE METODI F.E.M. PER L ANALISI DI INGRANAGGI CILINDRICI A DENTI DRITTI Marco Beghini Fabio Presicce Ciro Santus Marco Facchini Collaborazione fra DIMNP, Università di Pisa
RUOTE DENTATE. Introduzione
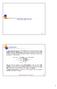 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
INGRANAGGI CILINDRICI E CREMAGLIERE
 INGRANAGGI CILINDRICI E CREMAGLIERE INGRANAGGI CILINDRICI CON MOZZO LATERALE pag. 4 INGRANAGGI CILINDRICI SENZA MOZZO pag. 7 CREMAGLIERE pag. 9 INGRANAGGI CILINDRICI E CREMAGLIERE INGRANAGGI CILINDRICI
INGRANAGGI CILINDRICI E CREMAGLIERE INGRANAGGI CILINDRICI CON MOZZO LATERALE pag. 4 INGRANAGGI CILINDRICI SENZA MOZZO pag. 7 CREMAGLIERE pag. 9 INGRANAGGI CILINDRICI E CREMAGLIERE INGRANAGGI CILINDRICI
Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon
 Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon I tre programmi sono utility generali preparate appositamente per gli studenti (ma che potrebbero essere utili anche per professionisti). MomCad
Istruzioni per l uso dei programmi MomCad, TraveCon, TraveFon I tre programmi sono utility generali preparate appositamente per gli studenti (ma che potrebbero essere utili anche per professionisti). MomCad
e-dva - eni-depth Velocity Analysis
 Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
RUOTE DENTATE CILINDRICHE A DENTI DIRITTI E CREMAGLIERE
 RUOTE DENTATE CILINDRICHE A DENTI DIRITTI E CREMAGLIERE Gli ingranaggi cilindrici e le cremagliere sono gli elementi classici per la trasmissione meccanica dei movimenti di rotazione e di traslazione tra
RUOTE DENTATE CILINDRICHE A DENTI DIRITTI E CREMAGLIERE Gli ingranaggi cilindrici e le cremagliere sono gli elementi classici per la trasmissione meccanica dei movimenti di rotazione e di traslazione tra
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Progetto e costruzione di macchine Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas Copyright 2005 The McGraw-Hill Companies srl
 Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
RESISTENZA DEI MATERIALI TEST
 RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
RUOTE DENTATE Perdite e rendimento
 Dipartimento di Ingegneria eccanica, Nucleare e della Produzione UOTE DENTATE Perdite e rendimento Prof. Ing. Enrico ANFEDI Integrazione degli argomenti trattati al Cap. 5 del testo di Juvinall e arshek:
Dipartimento di Ingegneria eccanica, Nucleare e della Produzione UOTE DENTATE Perdite e rendimento Prof. Ing. Enrico ANFEDI Integrazione degli argomenti trattati al Cap. 5 del testo di Juvinall e arshek:
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi.
 IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
Schede tecniche - Ingranaggi di precisione
 Schede tecniche Ingranaggi di precisione Ingranaggi a denti dritti ed elicoidali Formula Formula Descrizione Simbolo Unità Ingranaggi a denti diritti Ingranaggi elicoidali Modulo reale m n Modulo apparente
Schede tecniche Ingranaggi di precisione Ingranaggi a denti dritti ed elicoidali Formula Formula Descrizione Simbolo Unità Ingranaggi a denti diritti Ingranaggi elicoidali Modulo reale m n Modulo apparente
Sistemi di bloccaggio idraulici -- Mandrini idraulici
 Sistemi di bloccaggio idraulici -- Mandrini idraulici La tecnologia del serraggio idraulico ad espansione si è evoluto fino a raggiungere livelli di precisione e di affidabilità tali da poter soddisfare
Sistemi di bloccaggio idraulici -- Mandrini idraulici La tecnologia del serraggio idraulico ad espansione si è evoluto fino a raggiungere livelli di precisione e di affidabilità tali da poter soddisfare
ELEMENTI DI UNA RUOTA DENTATA A DENTI DIRITTI
 1 Ruote dentate Le ruote dentate servono per la trasmissione del moto rotatorio continuo fra due alberi a distanza ravvicinata, con assi paralleli, concorrenti o sghembi. I denti della ruota motrice spingono,
1 Ruote dentate Le ruote dentate servono per la trasmissione del moto rotatorio continuo fra due alberi a distanza ravvicinata, con assi paralleli, concorrenti o sghembi. I denti della ruota motrice spingono,
Piani di input e piani di calcolo reale in FaTA-e
 0 1 Piani di input e piani di calcolo reali in FaTA-e Dalla versione XX di FaTA-e è presente una nuova implementazione per il calcolo dei baricentri di massa e rigidezza. La nuova procedura consente di
0 1 Piani di input e piani di calcolo reali in FaTA-e Dalla versione XX di FaTA-e è presente una nuova implementazione per il calcolo dei baricentri di massa e rigidezza. La nuova procedura consente di
Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO TUBI VORTEX FRIGID-X TM VORTEX TUBE
 Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO DC COOLING TUBI VORTEX FRIGID-X TM VORTEX TUBE Documentazione non registrata, soggetta a modifiche
Sez. J.1 Sistemi e tecnologie ad aria compressa, di ausilio alla produzione SISTEMI DI RAFFREDDAMENTO DC COOLING TUBI VORTEX FRIGID-X TM VORTEX TUBE Documentazione non registrata, soggetta a modifiche
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE
 DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE
 30.11.2011 Gazzetta ufficiale dell Unione europea L 317/17 REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE del 29 novembre 2011 recante modifica del regolamento (CE) n. 1222/2009 del Parlamento europeo
30.11.2011 Gazzetta ufficiale dell Unione europea L 317/17 REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE del 29 novembre 2011 recante modifica del regolamento (CE) n. 1222/2009 del Parlamento europeo
La rumorosità degli ingranaggi (Parte 1^)
 La rumorosità degli ingranaggi (Parte 1^) Il problema del rumore generato dalle trasmissioni è diventato sempre più pressante negli ultimi anni, anche a causa della maggiore esigenza di combattere l inquinamento
La rumorosità degli ingranaggi (Parte 1^) Il problema del rumore generato dalle trasmissioni è diventato sempre più pressante negli ultimi anni, anche a causa della maggiore esigenza di combattere l inquinamento
Gradi imbattibili per produttività ultra
 Gradi imbattibili per produttività ultra Inserti tangenziali positivi per la fresatura di Acciai 3 1 4 08 13 16 2 Esclusivo inserto con 6 taglienti per Avanzamenti Super 2 3 5 6 1 4 Angoli di attacco positivi
Gradi imbattibili per produttività ultra Inserti tangenziali positivi per la fresatura di Acciai 3 1 4 08 13 16 2 Esclusivo inserto con 6 taglienti per Avanzamenti Super 2 3 5 6 1 4 Angoli di attacco positivi
TRASMISSIONE AD INGRANAGGI. Università degli Studi di Bergamo Corso di Laurea in Ingegneria Meccanica Prof. Sergio Baragetti
 TRASMISSIONE AD INGRANAGGI Corso di Laurea in Ingegneria Meccanica Prof. Sergio Baragetti GEOMETRIA DELLE RUOTE DENTATE La geometria delle ruote dentate si fonda sul modulo, m, dato da Dal modulo dipendono
TRASMISSIONE AD INGRANAGGI Corso di Laurea in Ingegneria Meccanica Prof. Sergio Baragetti GEOMETRIA DELLE RUOTE DENTATE La geometria delle ruote dentate si fonda sul modulo, m, dato da Dal modulo dipendono
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Il modello generale di commercio internazionale
 Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
PROGRAMMAZIONE ASSISTITA DAL COMPUTER (CAD/CAM)
 PROGRAMMAZIONE ASSISTITA DAL COMPUTER (CAD/CAM) Con la programmazione manuale, il programmatore descrive un ciclo di lavoro nella sequenza voluta ed in un linguaggio comprensibile all unità di governo.
PROGRAMMAZIONE ASSISTITA DAL COMPUTER (CAD/CAM) Con la programmazione manuale, il programmatore descrive un ciclo di lavoro nella sequenza voluta ed in un linguaggio comprensibile all unità di governo.
LEZIONI N 24 E 25 UNIONI SALDATE
 LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
LEZIONI N 24 E 25 UNIONI SALDATE Le saldature si realizzano prevalentemente con il metodo dell arco elettrico, utilizzando elettrodi rivestiti, che forniscono il materiale di apporto. Il collegamento è
METODO PER LA DESCRIZIONE DEL CAMPO MAGNETICO ROTANTE
 Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
COPPIE CONICHE PER TRASMISSIONI TRA ASSI ORTOGONALI
 DICHIARAZIONE DI INTENTI Il progetto modifica dell attuale assortimento di coppie coniche, sviluppato con l intento di unificare l esecuzione di questo prodotto e di ridurre il numero delle posizioni di
DICHIARAZIONE DI INTENTI Il progetto modifica dell attuale assortimento di coppie coniche, sviluppato con l intento di unificare l esecuzione di questo prodotto e di ridurre il numero delle posizioni di
ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato
 ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato Nella presente esercitazione si redige il programma CNC per la fresatura del pezzo illustrato nelle Figure 1 e 2. Figura
ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato Nella presente esercitazione si redige il programma CNC per la fresatura del pezzo illustrato nelle Figure 1 e 2. Figura
Il Campionameto dei segnali e la loro rappresentazione. 1 e prende il nome frequenza di
 Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici, conici e viti senza fine
 KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici, conici e viti senza fine Primi tre giorni 15/02/16 dalle 09.30 alle 17.30, 16/02/16 dalle 09.00 alle 17.30 ed 17/02/16 dalle 08.30 alle
KISSsoft- Seminario d approfondimento su: Ingranaggi cilindrici, conici e viti senza fine Primi tre giorni 15/02/16 dalle 09.30 alle 17.30, 16/02/16 dalle 09.00 alle 17.30 ed 17/02/16 dalle 08.30 alle
VALORE DELLE MERCI SEQUESTRATE
 La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
CHRYSO Flexò la tecnologia avanzata per pannelli a taglio termico
 la tecnologia avanzata per pannelli a taglio termico CHRYSO Flexò: la tecnologia avanzata per pannelli a taglio termico IL SISTEMA, COPERTO DA BREVETTO INTERNAZIONALE, PER OTTIMIZZARE LA PRESTAZIONE TERMICA
la tecnologia avanzata per pannelli a taglio termico CHRYSO Flexò: la tecnologia avanzata per pannelli a taglio termico IL SISTEMA, COPERTO DA BREVETTO INTERNAZIONALE, PER OTTIMIZZARE LA PRESTAZIONE TERMICA
L Unità didattica in breve
 L Unità didattica in breve Trasmissione del moto mediante ruote dentate Si definisce ingranaggio l accoppiamento di due ruote dentate ingrananti fra loro, montate su assi la cui posizione relativa resta
L Unità didattica in breve Trasmissione del moto mediante ruote dentate Si definisce ingranaggio l accoppiamento di due ruote dentate ingrananti fra loro, montate su assi la cui posizione relativa resta
FIRESHOP.NET. Gestione del taglia e colore. www.firesoft.it
 FIRESHOP.NET Gestione del taglia e colore www.firesoft.it Sommario SOMMARIO Introduzione... 3 Configurazione iniziale... 5 Gestione delle varianti... 6 Raggruppamento delle varianti... 8 Gestire le varianti
FIRESHOP.NET Gestione del taglia e colore www.firesoft.it Sommario SOMMARIO Introduzione... 3 Configurazione iniziale... 5 Gestione delle varianti... 6 Raggruppamento delle varianti... 8 Gestire le varianti
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
DETERMINAZIONE DI V S30 ReMi software
 DETERMINAZIONE DI V S30 ReMi software Il calcolo di questo parametro dinamico può essere effettuato attraverso le classiche prove sismiche in foro del tipo DOWN-HOLE oppure con metodi innovativi indiretti.
DETERMINAZIONE DI V S30 ReMi software Il calcolo di questo parametro dinamico può essere effettuato attraverso le classiche prove sismiche in foro del tipo DOWN-HOLE oppure con metodi innovativi indiretti.
Normative sulla Tenuta dei Serramenti ad Aria, Acqua e Vento
 UNI EN 12208 La tenuta all acqua di un serramento, descrive la sua capacità di essere impermeabile sotto l azione di pioggia battente e in presenza di una determinata velocità del vento. La norma, la UNI
UNI EN 12208 La tenuta all acqua di un serramento, descrive la sua capacità di essere impermeabile sotto l azione di pioggia battente e in presenza di una determinata velocità del vento. La norma, la UNI
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Scheduling della CPU. Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux
 Scheduling della CPU Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux Sistemi multiprocessori Fin qui si sono trattati i problemi di scheduling su singola
Scheduling della CPU Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux Sistemi multiprocessori Fin qui si sono trattati i problemi di scheduling su singola
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Sensori a effetto Hall bipolari con ritenuta stabilizzati e non stabilizzati con circuito chopper
 Sensori a effetto Hall bipolari con ritenuta stabilizzati e non stabilizzati con circuito chopper I risultati dei test mostrano che è possibile ottenere prestazioni significativamente maggiori impiegando
Sensori a effetto Hall bipolari con ritenuta stabilizzati e non stabilizzati con circuito chopper I risultati dei test mostrano che è possibile ottenere prestazioni significativamente maggiori impiegando
GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain.
 *+33(GLWRU GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain. Il programma si basa su un architettura di tasti funzionali presenti
*+33(GLWRU GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain. Il programma si basa su un architettura di tasti funzionali presenti
REATTANZE INDUTTIVE DI LINEA Filtri elettrici di potenza per l automazione industriale
 INDUCTIVE COMPONENTS Tensione di rete Corrente di linea Tensione di rete Corrente di linea REATTANZE INDUTTIVE DI LINEA Filtri elettrici di potenza per l automazione industriale Reattanze induttive per
INDUCTIVE COMPONENTS Tensione di rete Corrente di linea Tensione di rete Corrente di linea REATTANZE INDUTTIVE DI LINEA Filtri elettrici di potenza per l automazione industriale Reattanze induttive per
Ricerca di outlier. Ricerca di Anomalie/Outlier
 Ricerca di outlier Prof. Matteo Golfarelli Alma Mater Studiorum - Università di Bologna Ricerca di Anomalie/Outlier Cosa sono gli outlier? L insieme di dati che sono considerevolmente differenti dalla
Ricerca di outlier Prof. Matteo Golfarelli Alma Mater Studiorum - Università di Bologna Ricerca di Anomalie/Outlier Cosa sono gli outlier? L insieme di dati che sono considerevolmente differenti dalla
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Il controllo della visualizzazione
 Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda
 Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
GUIDA ALLA RILEVANZA
 GUIDA ALLA RILEVANZA Posizionamento per Rilevanza Suggerimenti per una migliore visibilità su ebay www.egolden.it Vers. 1.1 Questa guida puo essere ridistribuita con l obbligo di non modificarne contenuto
GUIDA ALLA RILEVANZA Posizionamento per Rilevanza Suggerimenti per una migliore visibilità su ebay www.egolden.it Vers. 1.1 Questa guida puo essere ridistribuita con l obbligo di non modificarne contenuto
Il modello generale di commercio internazionale
 Capitolo 6 Il modello generale di commercio internazionale adattamento italiano di Novella Bottini 1 Struttura della presentazione Domanda e offerta relative Benessere e ragioni di scambio Effetti della
Capitolo 6 Il modello generale di commercio internazionale adattamento italiano di Novella Bottini 1 Struttura della presentazione Domanda e offerta relative Benessere e ragioni di scambio Effetti della
GRANDEZZE SINUSOIDALI
 GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
Analisi del trivai point
 Analisi del trivai point Strategia di controllo: il valore trivai (punto di trivalenza) Questa strategia di controllo, basata sul valore trivai, è generalmente usata se è disponibile come generatore ausiliario
Analisi del trivai point Strategia di controllo: il valore trivai (punto di trivalenza) Questa strategia di controllo, basata sul valore trivai, è generalmente usata se è disponibile come generatore ausiliario
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
--- durezza --- trazione -- resilienza
 Proprietà meccaniche Necessità di conoscere il comportamento meccanico di un certo componente di una certa forma in una certa applicazione prove di laboratorio analisi del comportamento del componente
Proprietà meccaniche Necessità di conoscere il comportamento meccanico di un certo componente di una certa forma in una certa applicazione prove di laboratorio analisi del comportamento del componente
Librerie digitali. Video. Gestione di video. Caratteristiche dei video. Video. Metadati associati ai video. Metadati associati ai video
 Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
Sistema di diagnosi CAR TEST
 Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Progettazione di una base di dati Ufficio della Motorizzazione
 Corso di Gestione dell Informazione Studenti NON frequentanti A.A. 2008/2009 1 Scopo del progetto Progettazione di una base di dati Ufficio della Motorizzazione Si vuole realizzare un applicazione base
Corso di Gestione dell Informazione Studenti NON frequentanti A.A. 2008/2009 1 Scopo del progetto Progettazione di una base di dati Ufficio della Motorizzazione Si vuole realizzare un applicazione base
M296 ESAME DI STATO DI ISTITUTO TECNICO INDUSTRIALE CORSO DI ORDINAMENTO
 M29 ESME DI STTO DI ISTITUTO TECNICO INDUSTRILE CORSO DI ORDINMENTO Indirizzo: MECCNIC Tema di: DISEGNO, PROGETTZIONE ED ORGNIZZZIONE INDUSTRILE Nel disegno allegato è rappresentato un albero che trasmette
M29 ESME DI STTO DI ISTITUTO TECNICO INDUSTRILE CORSO DI ORDINMENTO Indirizzo: MECCNIC Tema di: DISEGNO, PROGETTZIONE ED ORGNIZZZIONE INDUSTRILE Nel disegno allegato è rappresentato un albero che trasmette
Dispositivo di conversione di energia elettrica per aerogeneratori composto da componenti commerciali.
 Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Soluzione di equazioni quadratiche
 Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Ruote dentate elicoidali e loro controllo con micrometro a piattelli
 Ruote dentate elicoidali e loro controllo con micrometro a piattelli Nella ruota dentata cilindrica a denti elicoidali le linee dei fianchi, essendo delle eliche, sono inclinate di un angolo β rispetto
Ruote dentate elicoidali e loro controllo con micrometro a piattelli Nella ruota dentata cilindrica a denti elicoidali le linee dei fianchi, essendo delle eliche, sono inclinate di un angolo β rispetto
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
APP_PIT_Comparazione Pile Dynamics Inc. Rev.01-012015
 Pile Integrity Tester PIT Caratteristiche Tecniche Serie PIT-X, PIT-X2, PIT-V e PIT-FV La strumentazione Pile Integrity Tester serie PIT è disponibile in 4 versioni, con 1 (PIT-X e PIT- V) o 2 (PIT-X2
Pile Integrity Tester PIT Caratteristiche Tecniche Serie PIT-X, PIT-X2, PIT-V e PIT-FV La strumentazione Pile Integrity Tester serie PIT è disponibile in 4 versioni, con 1 (PIT-X e PIT- V) o 2 (PIT-X2
Rendering air show e verifica della sincronizzazione
 Capitolo 5 Rendering air show e verifica della sincronizzazione 5.1 Introduzione Il Rendering 3D dell evoluzioni acrobatiche costituisce uno degli aspetti cruciali dell applicazione realizzata. L ambiente
Capitolo 5 Rendering air show e verifica della sincronizzazione 5.1 Introduzione Il Rendering 3D dell evoluzioni acrobatiche costituisce uno degli aspetti cruciali dell applicazione realizzata. L ambiente
FRESATRICI CLASSIFICAZIONE DELLE FRESATRICI
 FRESATRC CLASSFCAZONE DELLE FRESATRC Le fresatrici si distinguono principalmente per la disposizione dell albero portafresa e per le possibilità di movimento della tavola portapezzo. Si classificano in
FRESATRC CLASSFCAZONE DELLE FRESATRC Le fresatrici si distinguono principalmente per la disposizione dell albero portafresa e per le possibilità di movimento della tavola portapezzo. Si classificano in
Corso di Automazione industriale
 Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Funzioni in C. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Nuova funzione di ricerca del sito WIKA.
 Nuova funzione di ricerca del sito WIKA. Il sito WIKA dispone ora di una funzione di ricerca completamente riprogettata. Essa è uno strumento particolarmente importante in quanto deve fornire al navigatore
Nuova funzione di ricerca del sito WIKA. Il sito WIKA dispone ora di una funzione di ricerca completamente riprogettata. Essa è uno strumento particolarmente importante in quanto deve fornire al navigatore
VIRTUAL DYNO - presentazione. VIRTUAL DYNO - inserimento dati
 VIRTUAL DYNO - presentazione All'apertura il software VIRTUAL DYNO si presenta in questo modo. A seguire vi mostreremo come l'utilizzo sia estremamente semplice ed i risultati vi consentano di sfruttare
VIRTUAL DYNO - presentazione All'apertura il software VIRTUAL DYNO si presenta in questo modo. A seguire vi mostreremo come l'utilizzo sia estremamente semplice ed i risultati vi consentano di sfruttare
Informazioni tecniche. QWD Macchine per la fabbricazione e la manutenzione degli utensili in PCD con processo di elettroerosione a filo
 Informazioni tecniche QWD Macchine per la fabbricazione e la manutenzione degli utensili in PCD con processo di elettroerosione a filo QWD 750/760 Una concezione versatile di macchina per le più elevate
Informazioni tecniche QWD Macchine per la fabbricazione e la manutenzione degli utensili in PCD con processo di elettroerosione a filo QWD 750/760 Una concezione versatile di macchina per le più elevate
Application note. CalBatt NomoStor per i sistemi di accumulo di energia
 1. Panoramica Application note CalBatt NomoStor per i sistemi di accumulo di energia Gli Energy Management Systems () sono dispositivi atti al controllo dei flussi di energia dalle sorgenti di produzione
1. Panoramica Application note CalBatt NomoStor per i sistemi di accumulo di energia Gli Energy Management Systems () sono dispositivi atti al controllo dei flussi di energia dalle sorgenti di produzione
Teste regolabili per tornire
 DREX -TOOLS Teste regolabili per tornire ETA-MEC.SRL REPUBBLICA DI SAN MARINO www.eta-mec.sm - e-mail: info@eta-mec.sm Indice Pag. - Introduzione 1 - Teste GEN-DEX 2 - Teste GEN-DEX - dimensioni 3 - Teste
DREX -TOOLS Teste regolabili per tornire ETA-MEC.SRL REPUBBLICA DI SAN MARINO www.eta-mec.sm - e-mail: info@eta-mec.sm Indice Pag. - Introduzione 1 - Teste GEN-DEX 2 - Teste GEN-DEX - dimensioni 3 - Teste
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
20.18-ITA Assemblaggio valvole AGS a triplo servizio
 TM Le valvole a servizio triplo AGS Victaulic sono costituite da una valvola a farfalla Vic-300 AGS Serie W761 e da una valvola Vic-Check AGS serie W715 (componenti spediti singolarmente, non assiemati).
TM Le valvole a servizio triplo AGS Victaulic sono costituite da una valvola a farfalla Vic-300 AGS Serie W761 e da una valvola Vic-Check AGS serie W715 (componenti spediti singolarmente, non assiemati).
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti. Enrico Saltari Università di Roma La Sapienza
 MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Valutazione delle Prestazioni. Valutazione delle Prestazioni. Architetture dei Calcolatori (Lettere. Tempo di risposta e throughput
 Valutazione delle Prestazioni Architetture dei Calcolatori (Lettere A-I) Valutazione delle Prestazioni Prof. Francesco Lo Presti Misura/valutazione di un insieme di parametri quantitativi per caratterizzare
Valutazione delle Prestazioni Architetture dei Calcolatori (Lettere A-I) Valutazione delle Prestazioni Prof. Francesco Lo Presti Misura/valutazione di un insieme di parametri quantitativi per caratterizzare
COLLEGAMENTI ALBERO-MOZZO
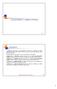 COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
Esercizio 1: trading on-line
 Esercizio 1: trading on-line Si realizzi un programma Java che gestisca le operazioni base della gestione di un fondo per gli investimenti on-line Creazione del fondo (con indicazione della somma in inizialmente
Esercizio 1: trading on-line Si realizzi un programma Java che gestisca le operazioni base della gestione di un fondo per gli investimenti on-line Creazione del fondo (con indicazione della somma in inizialmente
MService La soluzione per ottimizzare le prestazioni dell impianto
 MService La soluzione per ottimizzare le prestazioni dell impianto Il segreto del successo di un azienda sta nel tenere sotto controllo lo stato di salute delle apparecchiature degli impianti. Dati industriali
MService La soluzione per ottimizzare le prestazioni dell impianto Il segreto del successo di un azienda sta nel tenere sotto controllo lo stato di salute delle apparecchiature degli impianti. Dati industriali
Scheda. Descrizione della macchina
 Scheda 1 Lavorazione: Macchina: TORNITURA TORNIO PARALLELO Descrizione della macchina I torni sono macchine che eseguono l asportazione di truciolo: lo scopo è ottenere superfici esterne e interne variamente
Scheda 1 Lavorazione: Macchina: TORNITURA TORNIO PARALLELO Descrizione della macchina I torni sono macchine che eseguono l asportazione di truciolo: lo scopo è ottenere superfici esterne e interne variamente
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
IL DIMENSIONAMENTO DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione
 FOCUS TECNICO IL DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione CRITERI DI CALCOLO DELLA PORTATA DI PROGETTO Lo scopo principale del dimensionamento di una rete idrica è quello di assicurare
FOCUS TECNICO IL DEGLI IMPIANTI IDROSANITARI Miscelatori e riduttori di pressione CRITERI DI CALCOLO DELLA PORTATA DI PROGETTO Lo scopo principale del dimensionamento di una rete idrica è quello di assicurare
Aspettative, consumo e investimento
 Aspettative, consumo e investimento In questa lezione: Studiamo come le aspettative di reddito e ricchezza futuro determinano le decisioni di consumo e investimento degli individui. Studiamo cosa determina
Aspettative, consumo e investimento In questa lezione: Studiamo come le aspettative di reddito e ricchezza futuro determinano le decisioni di consumo e investimento degli individui. Studiamo cosa determina
