Esercizi di consolidamento
|
|
|
- Federico Federici
- 7 anni fa
- Visualizzazioni
Transcript
1 Esercizi di consolidamento Risolvi le seguenti disequazioni intere di secondo grado. esercizio guidato 0 þ 0 ffiffiffiffiffiffiffiffiffiffiffiffiffiffi 9 þ 0 Risolviamo l equazione associata ¼ ¼ 0 Disegniamo la arabola evidenziandone la osizione risetto all asse L intervallo delle soluzioni è quello che corrisonde ai valori di che rendono ositivo o nullo il trinomio, cioè _ 9 < 0 þ < 0 6 þ > 0 þ 0 6 þ þ 0 7 þ < 0 6 < 0 9 > þ 6 þ > 0 0 þ 9 9 < 0 < < þ 0 ¼ 6 7 > 0 < _ > 7 þ 9 þ < þ 6 þ < _ > 7 ½ Š < < < 0 ð Þþ ð9 Þ ½RŠ Caitolo - Le disequazioni di secondo grado
2 ð Þþ < ½Š þ þ ffiffiffi 6 ð Þ > 6 ð Þ þ 7 ffiffiffi ffiffiffi _ 9 þ 6 < ffiffiffi ffiffiffi 9 < < 7 ½ < < Š ffiffiffi ffiffiffi _ þ ð þ Þ þ ð þ Þ ð Þð Þ ffiffiffi < ffiffiffi ½0 < < Š 9 þ ffiffiffi ð Þ > ð Þ < _ > ffiffiffi Risolvi le seguenti disequazioni frazionarie. 0 esercizio guidato þ þ 0 Per il dominio della disequazione dobbiamo imorre che sia 6¼ Studiamo adesso il segno dei fattori al numeratore e al denominatore onendo quello al numeratore maggiore o uguale a zero, quello al denominatore solo maggiore di zero þ þ 0! _ > 0! > Per indicare nella tabella dei segni che il numero non aartiene al dominio abbiamo messo una doia linea verticale in corrisondenza di questo numero. L insieme delle soluzioni è quello che rende ositiva la frazione _ > ð Þ þ 0 ½0 Š > 0 0 < < _ > Caitolo - Le disequazioni di secondo grado
3 þ þ þ esercizio guidato > 0 ½ < _ > 0Š þ 6 < þ Trasortiamo darima tutti i fattori al rimo membro þ 6 < 0 Facciamo il denominatore comune e svolgiamo i calcoli þ 6 < 0! þ 6 Cambiamo i segni al numeratore in modo da avere il coefficiente di ositivo e cambiamo verso alla disequazione þ 6 > 0 Continua adesso come negli esercizi recedenti. ½ 6 < < 0 _ > Š < 0 7 þ _ 6 7 < þ > < ffiffiffi ffiffiffi _ > ½ < _ > Š þ 6 þ þ 9 þ < 0 ½Š ffiffiffiffiffi 0 < _ ffiffiffiffiffi 0 < 0 þ > þ ½ < _ < < _ > 0Š þ < 6 ð Þ þ ½ < < 0 _ < < Š ½ _ < < _ Š þ < ½0 < < Š þ þ þ 7 6 < þ ½ _ < 0 _ > Š < _ > 7 6 þ ½ < < Š Caitolo - Le disequazioni di secondo grado
4 Risolvi i seguenti sistemi di disequazioni. 7 esercizio guidato > ðaþ ðbþ Per risolvere un sistema di disequazioni si deve risolvere ciascuna disequazione e trovare oi l intersezione delle soluzioni disequazione A > 0! < 0 _ > disequazione B 9 0! Costruiamo la tabella delle soluzioni L insieme delle soluzioni è formato dagli intervalli in cui entrambe le disequazioni A e B sono verificate, cioè < 0 _ < < 0 < ð7 Þþ 6 6 < 0 þ þ < 0 0 > ð þ Þ þ þ ð þ Þ < > 0 þ þ < 6 ½ < Š < _ < ½ < < Š ½Š < _ < ½RŠ < _ < 9 < _ _ Caitolo - Le disequazioni di secondo grado
5 < þ > þ < þ 6 þ 0 > 7 ð Þð Þþ ð þ Þ 0 6 þ < 0 < 6 > 0 > > < þ ð Þ > 0 < 0 < þ ð Þ þ ð Þ > 0 < þ þ < ð Þ ð Þ þ 7 > 0 9 þ ð Þ þ > þ ð Þ þ ð Þ 0 9 ð Þ ð Þ < 0 ð þ Þ ð Þð þ Þ < 0 ð Þ 9 ½ _ > Š 6 ½ < < Š ½ < < Š ½Š < < ½ _ > Š ½ _ < Š < _ Caitolo - Le disequazioni di secondo grado
6 < < þ þ > < ð þ Þ < þ 6 < ð þ Þ < þ þ 0 ð þ Þþ < ð þ Þð Þ > ð Þ þ < þ > > ð þ Þ þ > 0 < þ þ 0 > þ þ < þ þ 0 < < _ > 7 < 6 _ < < 0 ½ > 6Š < ½ Š ½Š ½ < < Š ½Š ½ < < _ < < Š Caitolo - Le disequazioni di secondo grado
7 Stabilisci er quali valori del arametro k le seguenti equazioni ammettono radici reali e distinte. 7 k þ ðk Þ þ ¼ 0 k < ffiffiffi ffiffiffi _ k > þ 79 k þ ðk þ Þ ¼ 0 ½k RŠ 0 þ ðk Þ k ¼ 0 k 6¼ ½ Š ðk þ Þ ffiffiffiffiffi 6k þ k ¼ 0 < k < Determina i valori di k er i quali le seguenti equazioni soddisfano alla condizione indicata. ðk þ Þ k ¼ 0 ammette soluzioni reali k ffiffiffi ffiffiffi _ k þ k ðk þ Þ ¼ 0 non ammette soluzioni reali ffiffiffi ffiffiffi þ < k < ðk þ Þ þ k ¼ 0 ammette soluzioni reali distinte ½ < k < Š ð kþ þðk Þ þ ¼ 0 ammette soluzioni reali coincidenti oure non ammette soluzioni reali ½ k Š Caitolo - Le disequazioni di secondo grado
LA PARABOLA E LE DISEQUAZIONI
 LA PARABOLA E LE DISEQUAZIONI DI SECONDO GRADO 6 Per ricordare H Una funzione di secondo grado la cui equazione assume la forma y ˆ a b c si chiama arabola. Le sue caratteristiche sono le seguenti (osserva
LA PARABOLA E LE DISEQUAZIONI DI SECONDO GRADO 6 Per ricordare H Una funzione di secondo grado la cui equazione assume la forma y ˆ a b c si chiama arabola. Le sue caratteristiche sono le seguenti (osserva
Esercizi di consolidamento
 Esercizi di consolidamento Equazioni di grado sueriore al secondo Risolvi in R, mediante scomosizione, le seguenti equazioni di grado sueriore al secondo. esercizio guidato þ 9 ¼ 0 Scomoniamo il olinomio
Esercizi di consolidamento Equazioni di grado sueriore al secondo Risolvi in R, mediante scomosizione, le seguenti equazioni di grado sueriore al secondo. esercizio guidato þ 9 ¼ 0 Scomoniamo il olinomio
LE DISEQUAZIONI DI SECONDO GRADO. Prof. Stefano Spezia
 LE DISEQUAZIONI DI SECONDO GRADO 1. L EQUAZIONE ASSOCIATA 4x + 3x 2 + 6 > + 2x 3x 2 + 4x + 6 > + 2x 3x 2 + 4x 2x + 6 > 0 3x 2 + 2x + 6 > 0 Forma normale Ogni disequazione di secondo grado può essere ricondotta
LE DISEQUAZIONI DI SECONDO GRADO 1. L EQUAZIONE ASSOCIATA 4x + 3x 2 + 6 > + 2x 3x 2 + 4x + 6 > + 2x 3x 2 + 4x 2x + 6 > 0 3x 2 + 2x + 6 > 0 Forma normale Ogni disequazione di secondo grado può essere ricondotta
5. EQUAZIONI e DISEQUAZIONI
 5. EQUAZIONI e DISEQUAZIONI 1. Per ognuna delle affermazioni seguenti, indicare se e vera o falsa, motivando la risposta (a) L equazione di primo grado (1 2)x = 2 ha soluzione x = 2(1+ 2). V F (b) La disequazione
5. EQUAZIONI e DISEQUAZIONI 1. Per ognuna delle affermazioni seguenti, indicare se e vera o falsa, motivando la risposta (a) L equazione di primo grado (1 2)x = 2 ha soluzione x = 2(1+ 2). V F (b) La disequazione
Esercizi di consolidamento
 Esercizi di consolidamento Il sistema di riferimento cartesiano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð,
Esercizi di consolidamento Il sistema di riferimento cartesiano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð,
I fasci di circonferenze
 A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
Esercizi di consolidamento
 Esercizi di consolidamento Il sistema di riferimento nel iano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð, Þ
Esercizi di consolidamento Il sistema di riferimento nel iano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð, Þ
Disequazioni di II grado
 Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
A Ripasso. Nella seguente tabella sono riassunti gli schemi risolutivi per le equazioni di secondo grado incomplete.
 A Riasso Scheda Equazioni di secondo grado comlete e incomlete Un equazione di secondo grado, in forma normale, nell incognita è del tio: a þ b þ c ¼ 0, con a 6¼ 0 Nella seguente tabella sono riassunti
A Riasso Scheda Equazioni di secondo grado comlete e incomlete Un equazione di secondo grado, in forma normale, nell incognita è del tio: a þ b þ c ¼ 0, con a 6¼ 0 Nella seguente tabella sono riassunti
1 Funzioni algebriche fratte
 1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
Studio del segno di un prodotto
 Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
Nozioni fondamentali sulle disequazioni
 Capitolo 1 n n n n Nozioni fondamentali sulle disequazioni Disequazioni intere di primo e di secondo grado Sistemi. Regola dei segni Disequazioni binomie e trinomie n Nozioni fondamentali sulle disequazioni
Capitolo 1 n n n n Nozioni fondamentali sulle disequazioni Disequazioni intere di primo e di secondo grado Sistemi. Regola dei segni Disequazioni binomie e trinomie n Nozioni fondamentali sulle disequazioni
Disequazioni di secondo grado
 Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 4 Novembre Trinomi di secondo grado
 Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
1 Disquazioni di primo grado
 1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
Disequazioni di secondo grado
 Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica [email protected] EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica [email protected] EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
Disequazioni. 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese
 Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Identità ed equazioni
 Matematica e-learning - Identità ed equazioni Prof. [email protected] A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
Matematica e-learning - Identità ed equazioni Prof. [email protected] A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE. Le FUNZIONI RAZIONALI INTERE (i polinomi) hanno come insieme di definizione R.
 ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
Capitolo 2. Funzioni
 Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
3 Equazioni e disequazioni.
 3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
LE DISEQUAZIONI LINEARI
 LE DISEQUAZIONI LINEARI Per ricordare H Una disequazione si rappresenta come una disuguaglianza fra due espressioni algebriche A e B ; essa assume dunque la forma A Per risolvere una disequazione
LE DISEQUAZIONI LINEARI Per ricordare H Una disequazione si rappresenta come una disuguaglianza fra due espressioni algebriche A e B ; essa assume dunque la forma A Per risolvere una disequazione
Docente: Vincenzo Pappalardo Materia: Matematica. Algebra. Disequazioni valore assoluto
 Docente: Vincenzo Pappalardo Materia: Matematica Algebra Disequazioni valore assoluto DEFINIZIONI Il valore assoluto di un numero è uguale al numero stesso se il numero è positivo o nullo, è l opposto
Docente: Vincenzo Pappalardo Materia: Matematica Algebra Disequazioni valore assoluto DEFINIZIONI Il valore assoluto di un numero è uguale al numero stesso se il numero è positivo o nullo, è l opposto
1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari
 Secondo modulo: Algebra Obiettivi 1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari 2. risolvere equazioni intere e frazionarie di primo grado, secondo grado, grado superiore
Secondo modulo: Algebra Obiettivi 1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari 2. risolvere equazioni intere e frazionarie di primo grado, secondo grado, grado superiore
PALESTRA PER IL RECUPERO
 PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
PALESTRA PER IL RECUPERO
 PIAN CARTESIAN E RETTA PALESTRA PER IL RECUPER SVLTI Determinare l equazione della retta passante per ð 3; Þ e per il punto P d intersezione della retta r di equazione 0 e della retta s di equazione 0.
PIAN CARTESIAN E RETTA PALESTRA PER IL RECUPER SVLTI Determinare l equazione della retta passante per ð 3; Þ e per il punto P d intersezione della retta r di equazione 0 e della retta s di equazione 0.
DISEQUAZIONI DI SECONDO GRADO
 DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio Studio di Funzione
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercitazione 2 - Soluzioni
 Esercitazione - Soluzioni Francesco Davì ottobre 0 Esercizio (a) Si deve avere + x 0 x, che è verificato x R, in quanto il valore del modulo di un espressione non è mai negativo. L espressione al numeratore
Esercitazione - Soluzioni Francesco Davì ottobre 0 Esercizio (a) Si deve avere + x 0 x, che è verificato x R, in quanto il valore del modulo di un espressione non è mai negativo. L espressione al numeratore
Esercizi 2016/17 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi
 Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
Mutue posizioni della parabola con gli assi cartesiani
 Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
Esercizi sulle Disequazioni
 Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
ESERCIZI SULLO STUDIO DI FUNZIONI
 ESERCIZI SULLO STUDIO DI FUNZIONI 0 novembre 206 Esercizi Esercizio n. Si consideri la funzione f(x) = 7 x 2 + 3 Dominio: R Intersezioni con gli assi: Intersezioni con l asse x: { y = 0 y = 7 x 2 + 3.
ESERCIZI SULLO STUDIO DI FUNZIONI 0 novembre 206 Esercizi Esercizio n. Si consideri la funzione f(x) = 7 x 2 + 3 Dominio: R Intersezioni con gli assi: Intersezioni con l asse x: { y = 0 y = 7 x 2 + 3.
LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI
 Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
Disequazioni - ulteriori esercizi proposti 1
 Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
MODULI DI LINEAMENTI DI MATEMATICA
 N. DODERO - P. BARONCINI - R. MANREDI TRIENNIO licei scientifici MODULI DI LINEAMENTI DI MATEMATICA er il triennio della scuola secondaria di secondo grado A DISEQUAZIONI ALGEBRICHE UNZIONI SUCCESSIONI
N. DODERO - P. BARONCINI - R. MANREDI TRIENNIO licei scientifici MODULI DI LINEAMENTI DI MATEMATICA er il triennio della scuola secondaria di secondo grado A DISEQUAZIONI ALGEBRICHE UNZIONI SUCCESSIONI
DISEQUAZIONI. Una disuguaglianza può essere Vera o Falsa. Per esempio:
 DISEQUAZIONI Prima di vedere cosa sono le disequazioni è necessario dare uno sguardo alle disuguaglianze numeriche. Al contrario delle uguaglianze numeriche, dove tra i numeri è presente il segno di uguaglianza
DISEQUAZIONI Prima di vedere cosa sono le disequazioni è necessario dare uno sguardo alle disuguaglianze numeriche. Al contrario delle uguaglianze numeriche, dove tra i numeri è presente il segno di uguaglianza
Equazioni e disequazioni. M.Simonetta Bernabei, Horst Thaler
 Equazioni e disequazioni M.Simonetta Bernabei, Horst Thaler A(x)=0 x si chiama incognita dell equazione. Se oltre all incognita non compaiono altre lettere l equazione si dice numerica, altrimenti letterale.
Equazioni e disequazioni M.Simonetta Bernabei, Horst Thaler A(x)=0 x si chiama incognita dell equazione. Se oltre all incognita non compaiono altre lettere l equazione si dice numerica, altrimenti letterale.
Massimi e minimi di una funzione razionale fratta Francesco Daddi - 18 maggio 2010
 Francesco Daddi - 18 maggio 2010 Esempio 1. Studiare la funzione f x 4 x 8 x 2 3 x 3. R (si osservi che il denominatore non si annulla mai); la funzione ha uno zero in x 2. La funzione è positiva per x
Francesco Daddi - 18 maggio 2010 Esempio 1. Studiare la funzione f x 4 x 8 x 2 3 x 3. R (si osservi che il denominatore non si annulla mai); la funzione ha uno zero in x 2. La funzione è positiva per x
DISEQUAZIONI DI SECONDO GRADO. Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono ad essa):
 P. \ Disequazioni di secondo grado Maggio 0 Copyright-I.S. DISEQUAZIONI DI SECONDO GRADO DISEQUAZIONI INTERE DI SECONDO GRADO Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono
P. \ Disequazioni di secondo grado Maggio 0 Copyright-I.S. DISEQUAZIONI DI SECONDO GRADO DISEQUAZIONI INTERE DI SECONDO GRADO Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono
EQUAZIONI, DISEQUAZIONI E SISTEMI
 EQUAZIONI, DISEQUAZIONI E SISTEMI RICHIAMI DI TEORIA Definizione: sia f una funzione reale di variabile reale. Gli elementi del dominio di f su cui la funzione assume valore nullo costituiscono l' insieme
EQUAZIONI, DISEQUAZIONI E SISTEMI RICHIAMI DI TEORIA Definizione: sia f una funzione reale di variabile reale. Gli elementi del dominio di f su cui la funzione assume valore nullo costituiscono l' insieme
RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI. Angela Donatiello 1
 RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI Angela Donatiello 1 Una funzione del tipo f() = m + q, con m e q numeri reali, è una FUNZIONE LINEARE. Il numero q è detto INTERCETTA o ORDINATA ALL ORIGINE,
RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI Angela Donatiello 1 Una funzione del tipo f() = m + q, con m e q numeri reali, è una FUNZIONE LINEARE. Il numero q è detto INTERCETTA o ORDINATA ALL ORIGINE,
Disequazioni di 1 grado
 Matematica Disequazioni di 1 grado Autore: Prof. Pappalardo Vincenzo docente di Matematica e Fisica 1. DEFINIZIONI Si dice disequazione di 1 grado un espressione algebrica nella quale compare il segno
Matematica Disequazioni di 1 grado Autore: Prof. Pappalardo Vincenzo docente di Matematica e Fisica 1. DEFINIZIONI Si dice disequazione di 1 grado un espressione algebrica nella quale compare il segno
Le disequazioni frazionarie (o fratte)
 Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
Disequazioni fratte. Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria.
 1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
f(x) = 1 x 2 Per determinare il dominio di f(x) dobbiamo imporre che il determinante sia diverso da zero
 . Data la funzione approssimarne il grafico. f() = 2 Per determinare il dominio di f() dobbiamo imporre che il determinante sia diverso da zero 2 0 = 2 = ± perciò il dominio ` D = R \ {, } =], [ ], [ ],
. Data la funzione approssimarne il grafico. f() = 2 Per determinare il dominio di f() dobbiamo imporre che il determinante sia diverso da zero 2 0 = 2 = ± perciò il dominio ` D = R \ {, } =], [ ], [ ],
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
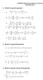 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
Dr. Erasmo Modica
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI PRIMO GRADO Dr. Erasmo Modica [email protected] IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI PRIMO GRADO Dr. Erasmo Modica [email protected] IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
lineamenti di matematica
 Nella Dodero Paolo Baroncini Roberto Manfredi lineamenti di matematica geometria analitica e comlementi di algebra er il triennio del liceo scientifico internet: www.ghisettiecorvi.it e-mail: [email protected]
Nella Dodero Paolo Baroncini Roberto Manfredi lineamenti di matematica geometria analitica e comlementi di algebra er il triennio del liceo scientifico internet: www.ghisettiecorvi.it e-mail: [email protected]
1 Fattorizzazione di polinomi
 1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
Matematica per le scienze sociali Equazioni e disequazioni. Francesco Lagona
 Matematica per le scienze sociali Equazioni e disequazioni Francesco Lagona University of Roma Tre F. Lagona ([email protected]) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Matematica per le scienze sociali Equazioni e disequazioni Francesco Lagona University of Roma Tre F. Lagona ([email protected]) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Esercizi SINTESI E RIEPILOGO. Parole chiave. Formule e proprietà importanti. Tema B. In più: esercizi interattivi
 Unità Esercizi In iù: esercizi interattivi Tema B SINTESI E RIEPILG Parole chiave Ascissa. 17 Asse delle ascisse. 17 Asse delle ordinate. 17 Asse. 17 Asse. 17 Coefficiente angolare. 10 Coordinata. 17 Distanza
Unità Esercizi In iù: esercizi interattivi Tema B SINTESI E RIEPILG Parole chiave Ascissa. 17 Asse delle ascisse. 17 Asse delle ordinate. 17 Asse. 17 Asse. 17 Coefficiente angolare. 10 Coordinata. 17 Distanza
Equazioni di secondo grado
 Equazioni di secondo grado www.competenzamatematica.it E. Modica A.S. 018/019 1 Equazioni di secondo grado Definizione 1. Dicesi equazione di secondo grado, un equazione del tipo: ax + bx + c = 0 con a,
Equazioni di secondo grado www.competenzamatematica.it E. Modica A.S. 018/019 1 Equazioni di secondo grado Definizione 1. Dicesi equazione di secondo grado, un equazione del tipo: ax + bx + c = 0 con a,
Esercizi di Matematica. Studio di Funzioni
 Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 2 I SISTEMI LINEARI
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
DISEQUAZIONI ALGEBRICHE
 DISEQUAZIONI ALGEBICHE Classe II a.s. 00/0 prof.ssa ita Schettino INTEVALLI DI Impariamo cosa sono gli intervalli di numeri reali Sono sottoinsiemi continui di numeri reali e possono essere limitati o
DISEQUAZIONI ALGEBICHE Classe II a.s. 00/0 prof.ssa ita Schettino INTEVALLI DI Impariamo cosa sono gli intervalli di numeri reali Sono sottoinsiemi continui di numeri reali e possono essere limitati o
Le disequazioni di primo grado. Prof. Walter Pugliese
 Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Calcolo letterale. 1. Quale delle seguenti affermazioni è vera?
 Calcolo letterale 1. Quale delle seguenti affermazioni è vera? (a) m.c.m.(49a b 3 c, 4a 3 bc ) = 98a 3 b 3 c (b) m.c.m.(49a b 3 c, 4a 3 bc ) = 98a 3 b 3 c (XX) (c) m.c.m.(49a b 3 c, 4a 3 bc ) = 49a bc
Calcolo letterale 1. Quale delle seguenti affermazioni è vera? (a) m.c.m.(49a b 3 c, 4a 3 bc ) = 98a 3 b 3 c (b) m.c.m.(49a b 3 c, 4a 3 bc ) = 98a 3 b 3 c (XX) (c) m.c.m.(49a b 3 c, 4a 3 bc ) = 49a bc
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO
 MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
Problemi geometrici che hanno come modello sistemi parametrici misti
 Problemi geometrici che hanno come modello sistemi arametrici misti Discussione di un roblema con arametro lcuni roblemi, er essere esressi nel modo iù generale ossibile, contengono un arametro. In questi
Problemi geometrici che hanno come modello sistemi arametrici misti Discussione di un roblema con arametro lcuni roblemi, er essere esressi nel modo iù generale ossibile, contengono un arametro. In questi
1 Identità ed equazioni
 1 Identità ed equazioni Consideriamo l uguaglianza espressa dalla seguente frase: Trova un numero tale che il suo doppio sommato con se stesso sia uguale al suo triplo. x > 2x + x = 3x La relazione: 2x
1 Identità ed equazioni Consideriamo l uguaglianza espressa dalla seguente frase: Trova un numero tale che il suo doppio sommato con se stesso sia uguale al suo triplo. x > 2x + x = 3x La relazione: 2x
