# $$ % % # & ' # $ $$ % ( # ( % % $
|
|
|
- Maria Teresa Sarti
- 4 anni fa
- Visualizzazioni
Transcript
1 !"
2 # $$% % # & ' # $$$% # % %$
3 !" # X F = f x ˆ ι F = f = f x x F x F x >, f x < <, f x > F = k xιˆ F = k r F = k r r # * +*,-+. /,
4 $! x k k x + x = pongo ω = > Equazione oraria x t = l cos ωt + φ +l -l F = k xιˆ a = xιˆ F = a k x = x x + kx = x + x x = ω x = l cos φ ω = k φ = v l = x + ω arctan v ωx T π = = ω π k
5 % x + ω x = x t = Acos ω t + ϕ Pulsazione, fase, fase iniziale. Moto periodico T = k con ω ; ; tan = A = + x ϕ = ω ωx ˆi ˆj kˆ f e = capo conservativo U x y z kx π ω p
6 B A B LAB = kx dx = k xa x A B U p U p U p x = kx + cost x t = Acos ωt + ϕ Acosϕ ϕ x t = ω Asinϕ Conservazione dell energia eccanica e trasforazioni K = x = A ω sin ϕ = k A sin ϕ U p = kx = k A cos ϕ EM = K + U p = k A sin ϕ cos ϕ k A ω A + = = cioè, proporzionale al quadrato dell apiezza e al quadrato della pulsazione
7 "
8 Circuito LC R trascurabile Le stesse relazioni si hanno in un circuito LC, con ω = LC All inizio condensatore carico con Q. Dopo, oscillazione elettroagnetica. Q t di VC = VL = L C dt Q d Q d Q L C dt dt LC = + Q = k Uguale a quella di una olla oscillante: + x x = L ; k C ω
9 Q = Q cos ω t + ϕ ; ove ω = Soluzione: carica LC La corrente nell induttanza: dq i = = ω Q sinϕ dt corrente 3
10 Riguardo all energia: Q Q U E = = cos C C ϕ U B = Li = Lω Q sin ϕ = Q = L Q = LC C sin ϕ sin Q = Q cosϕ i = Q ω sinϕ ω = ϕ LC e la soa è costante nel tepo: U E + U = B Q C
11 ! # 4 '%5 $ 6 $ &$%% $ f x F = f xˆ ι f x = Punti di equilibrio f x B > x B punto instabile A B x f x A < x A punto stabile f x f x + f x x x + O x x f x k x x A A A A x x A A Moto oscillatorio attorno al punto di equilibrio stabile x A
12 !!$! Notevole seplificazione dei calcoli: per esepio, le equazioni integro-differenziali con soluzione sinusoidale diventano algebriche lineare Rappresentazione geoetrica di una coppia ordinata di nueri reali Assi: reale e iaginario z x + iy rappresentazione algebrica z = r cosϕ + isinϕ rappresentazione trigonoetrica odulo e un argoento Soa di due coplessi equivale alla soa dei due vettori.
13 z x + iy = r cosϕ + isinϕ cosϕ + isinϕ = z r definizione forula di Eulero z x e = e cos y + isin y cioè, in terini di odulo e fase, a in fora esponenziale iϕ z* = r e = r cosϕ i sinϕ è il coplesso coniugato iϕ e = cosϕ + isinϕ ϕ + ϕ z = i z = zz = A A e iϕ z = A e z A i ϕ ϕ z e iϕ = = z = Ae z A n n inϕ n z = A e = A cos nϕ + isin nϕ re iϕ
14 Se il vettore ruota con velocità angolare costante ω = ω, la proiezione oscilla aronicaente. Il oto aronico è descritto dalla parte reale del nuero coplesso r A: z t = Ae iϕ = Ae i ω t+ ϕ x t = Acosϕ = Re z t = Re Ae = iϕ iϕ iωt iωt A Ac = Re e e = Re e con A = Ae iϕ apiezza coplessa c i ω t+ ϕ Ae d = = ω ; = = dt i ωt+ ϕ z i z zdt Ae dt z iω z x = Re z = Re iω z ; xdt = Re zdt = Re iω
15 i i z + z* = A e ϕ + e ϕ = = A cosϕ + isinϕ + cosϕ isinϕ = Acosϕ e + e e e cos ϕ = ; sinϕ = i iϕ iϕ e + e x t = A iϕ iϕ iϕ iϕ Il etodo sibolico funziona solo se le equazioni considerate sono lineari nella funzione aronica: in tale caso, le operazioni lineari coutano con l operazione prendere la parte reale. No energia, potenza, perché? In particolare, sono lineari le equazioni di Kirchhoff, di Maxwell, delle onde coe vedreo.
16 λt t x λ t = λe λx t x + ω x = ; x t = e λt x t = λ e λ x t λ iω x t = λ + ω = + ω ω soluzione generale: z t = c e + c e i t e ± ω, = ± coplesse coniugate e linearente indipendenti i t i t c e c possono essere coplesse Se vogliao soluzioni reali, annulliao la parte iaginaria: * ω * + * + i t iω t z z c c e c c e I z = = = c i i A i c = ϕ e A + i ω t+ ϕ A i ω t+ ϕ z t = e + e = cioè: c = A e iϕ = c * + iϕ iϕ e + e = A = Acos t + ω ϕ 6
17 Punto ateriale soggetto ad una forza elastica e ad una forza di attrito viscoso. F ˆ EL = k xι F ˆ a = xιˆ S = β xι kx β x = x β k x + x + x = F + F = a EL S Equazione differenziale alle derivate seconde lineare ed oogenea. x t x t x t = C x t + C x t C, C Lineare ed oogenea: se e sono soluzioni, allora lo è anche t Cerco una soluzione nella fora: x t = e λ λ t λ λt x t = λe = λx t x t = λx t = λ e = λ x t β k λ x + λx + x = λ x = β k + λ + = Soluzione ovvia dell oogenea Polinoio caratteristico "
18 $! ' λ β k + λ + = = β 4 k λ, β = ± $ 5 > β < λ <, λ < reali Due soluzioni diverse, reali e negative λ t λ t x t = C e + C e C, C % % x t t
19 7 5 = β λ = λ = = η $! ' Due soluzioni uguali, reali e negative t x t = e η d x d λ x t = C e + C te = C + C t e C, C η t = x t = te È una soluzione η t η t η t % % x t t $ '$$$ $589:- $$%7 ; trip = 3 5 %5% β 3
20 $! '. %5 < β β λ = + i λ = i x t ηt+ iωt ηt iωt Due soluzioni diverse, coplesse e coniugate λ = η + iω λ = η iω iωt x t = C e + C e e = cosωt + i sinωt ηt ω ω ω ω ηt cosω sinω cos ω φ x t = e C cos t + ic sin t + C cos t ic sin t = = + = + ηt e D t D t Ae t + Ae ηt % Ae ηt t Negli aortizzatori dei veicoli, k β k ω = / 4 = < β,4 β cr
21 t Posto: τ k β ω x t = A e cos ωt + ϕ = ; γ = ; ω = ω γ / 4 < ω ; τ = = γ β Se τ è abbastanza grande, cioè lo sorzaento abbastanza piccolo γ / ω in uno pseudoperiodo si può ω ω, assuere l apiezza circa costante; in pratica, si t τ trascura nello pseudoperiodo la variazione di e. In quello pseudoperiodo il oto è quasi periodico: EM ω A t
22 Nel periodo successivo, però, l apiezza edia diinuisce: ovviaente, l energia eccanica non si conserva! t τ t ω e A t = A e A t A t = A e τ per cui EM A decadiento esponenziale τ viene quindi detta tepo di decadiento dell oscillatore: τ è il tepo dopo il quale l energia decresce di un fattore /e τ γ deterina la rapidità con cui l energia si dissipa! t τ
23 Le stesse considerazioni si possono fare per il circuito LRC, per il quale: d Q R dq + + Q = dt L dt LC Q x ; L ; k ; R γ = C L τ t τ Q t = Q e cos ωt + ϕ γ R ω = ω ω 4 4τ LC 4L Qui piccolo sorzaento significa R < L C
24 In più: forza periodica dipendente dal tepo, di pulsazione Ω x + βx + kx = f t con f t = F cos Ωt ogni funzione periodica può essere espressa coe sovrapposizione di funzioni sinusoidali Soluzione generale: integrale dell oogenea sorzato + integrale particolare F cos t Re F e iωt Ω = β γ = ω = k
25 F e i Ω Possiao risolvere z + γ z + ω z = t e prendere la parte reale della soluzione: x t = Re z t A tepi lunghi prevarrà la forza aggiunta. Cerchiao soluzione particolare del tipo: zt=ae λt Sostituendo, si trova iediataente che deve essere λ = iω iωt iωt z = AiΩ e = iω z z t = Ae A può essere iωt z = A Ω e = Ω z coplesso iωt F iωt da cui Ω + iγ Ω + ω Ae = e F / F F A = χ, Z coplessi Ω + ω i Z + iγ Ω χ Ω γ Ω χ = ω Ω + iγ Ω ha fase δ = arctan ω Ω
26 ω γ Ω Z = γ + iω ha fase δ Z = arctan Ω ω Ω ipedenza eccanica Soluzione particolare cercata: z t F F Ωt δ = = = = χ e χ iωt iωt i Ae e e iδ F / e i Ω t δ = ω Ω + γ Ω che ha parte reale F / x t = z t = Ωt δ Re cos tanδ = γ Ω ω Ω ω Ω + γ Ω
27 Soluzione generale: soa con la soluzione della oogenea x t = x t + x t = oo part F / τ = A ωt + ϕ + Ωt δ t e cos cos γ ω = ω 4 ω 4τ ω Ω + γ Ω La pria, però, diventa trascurabile dopo qualche τ. ed è l unica che dipende dalle condizioni iniziali A e ϕ "
28 F / x t Ωt δ cos ω Ω + γ Ω γ Ω δ = arctan ω Ω Questa è detta soluzione stazionaria: ha la pulsazione uguale a quella della forza esterna l apiezza non dipende dalle condizioni iniziali 3 l apiezza dipende olto dalla differenza delle pulsazioni: risonanza 4 l oscillazione è sfasata rispetto alla forza esterna
29 F / x t Ωt B Ωt δ cos δ cos ω Ω + γ Ω apiezza δ B γ Ω δ = arctan ω Ω F/k Ω = ω γ ax Ω per β γ l apiezza ax tende a 9 Ω
30 F / x t cos Ωt δ γ Ω δ = arctan ω Ω + γ Ω ω Ω F F F A = x t cos Ωt doina k Ω ω ω k ; k δ in fase con forza esterna F x t cos Ωt F doina Ω A Ω ω Ω ; in opposizione di fase δ π con forza esterna F F A x t sin Ωt doina β Ω ω β Ω ; βω δ π/ in quadratura con forza esterna
31 L energia totale edia, il quadrato dell apiezza di oscillazione e altre grandezze ancora possono essere scritte in terini della funzione di risposta R dell oscillatore: x t F / Ω = cos F γ Ω ω Ω + γ Ω ω Ω + γ Ω t δ t δ t δ = cos Ω = F β Ω = Ω Ω R cos γ Ω R Ω = γ Ω ω Ω + γ Ω ω F E = ka = R Ω β Ω
32 R Ω = γ Ω ω Ω + γ Ω γ = β Ω ax = ω γ β = = γ
33 L analogo elettrico è un circuito RLC, con forza elettrootrice Vt R x Q β = γ L con e ω = L LC τ = R L di + Ri + Q = V t Q + R Q + Q = V t dt C L LC L si può variare la frequenza propria del circuito ω con un condensatore a capacità variabile
34 Se arriva un segnale esterno da una antenna di pulsazione Ω, esso provoca oscillazioni elettriche apie quando ω Ω. La larghezza della curva è γ = R / L, che deterina la selettività; per valori dei segnali con Ω lontano da ω più di R/L, le oscillazioni generate sono olto piccole e i segnali non vengono rilevati. γ = R L
Oscillazioni. Definizione Moto circolare uniforme Moto armonico
 Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Fisica 1, a.a : Oscillatore armonico
 Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
1 Oscillazioni libere (oscillatore armonico)
 C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
Strumenti matematici. La forza intermolecolare. Introduzione al problema fisico Base di uno spazio vettoriale Serie di Fourier
 Struenti ateatici Struenti ateatici Introduzione al problea fisico Base di uno spazio vettoriale Serie di Fourier Serie di Taylor Nueri coplessi Stru. at. Stru. at. Forza di attrazione Forza di repulsione
Struenti ateatici Struenti ateatici Introduzione al problea fisico Base di uno spazio vettoriale Serie di Fourier Serie di Taylor Nueri coplessi Stru. at. Stru. at. Forza di attrazione Forza di repulsione
Fisica 1, a.a : Oscillatore armonico
 Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
cos( ωt + ϕ)= Re v t = V o e jωt cos ωt + ϕ vt ()=V o e jϕ che è un numero complesso costante, di modulo V O ed e jωt = cos ωt + j sinωt
 . METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
. METODO SIMBOLIO, O METODO DEI FASORI..Introduzione Questo metodo applicato a reti lineari permanenti consente di determinare la soluzione in regime sinusoidale solamente per quanto attiene il regime
Oscillazioni e Onde Forza elastica
 Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
2. calcolare l energia cinetica del corpo e tracciare il suo andamento nel tempo;
 1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
Di seguito, per semplicità, mostreremo esempi in cui il termine di destra della (*) f è costante nel tempo. %%%%%%%
 Note su uso delle equazioni differenziali in eccanica Spesso la risoluzione delle equazioni del oto si ottiene attraverso la risoluzione di equazioni differenziali lineari a coefficienti costanti. L uso
Note su uso delle equazioni differenziali in eccanica Spesso la risoluzione delle equazioni del oto si ottiene attraverso la risoluzione di equazioni differenziali lineari a coefficienti costanti. L uso
Esperienza 12: oscillatore. forzato e risonanza. Laboratorio di Fisica 1 A. Baraldi, M. Riccò. Università di Parma. a.a. 2011/2012. Copyright M.
 Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Esperienza 1: oscillatore Università di Parma forzato e risonanza a.a. 11/1 Laboratorio di Fisica 1 A. Baraldi, M. Riccò Copyright M.Solzi Oscillazioni libere smorzate a.a. 11/1 1: Oscillatore forzato
Lez.21 Circuiti dinamici di ordine due. 1. Università di Napoli Federico II, CdL Ing. Meccanica, A.A , Elettrotecnica. Lezione 21 Pagina 1
 Lez.21 Circuiti dinamici di ordine due. 1 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 21 Pagina 1 Circuito RLC serie All istante t=0 inseriamo il generatore
Lez.21 Circuiti dinamici di ordine due. 1 Università di Napoli Federico II, CdL Ing. Meccanica, A.A. 2017-2018, Elettrotecnica. Lezione 21 Pagina 1 Circuito RLC serie All istante t=0 inseriamo il generatore
Oscillazioni. Definizioni Mo/ armonici Propagazione delle onde
 Oscillazioni Definizioni Mo/ aronici Propagazione delle onde Il oto aronico e il oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizioni Mo/ aronici Propagazione delle onde Il oto aronico e il oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Moti oscillatori. Parte I Oscillatore armonico
 1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
Esercizio (tratto dal Problema 2.6 del Mazzoldi)
 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
Esercizio (tratto dal Problema 2.6 del Mazzoldi)
 1 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
1 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
Esercizio (tratto dal Problema 4.7 del Mazzoldi 2)
 1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
si ottiene (come si può facilmente verificare sostituendo la soluzione proposta nell equazione): 1
 Prisa: legge di Cauchy Per deterinare la relazione tra l indice di rifrazione e la lunghezza d onda delle onde e- si utilizza un odello classico olto seplice, valido per atoi in un gas a che è counque
Prisa: legge di Cauchy Per deterinare la relazione tra l indice di rifrazione e la lunghezza d onda delle onde e- si utilizza un odello classico olto seplice, valido per atoi in un gas a che è counque
Lezione 15 - Onde. Fisica 1 - R. De Renzi - Onde 1
 Lezione 15 - Onde onde su una corda, sulla superficie dell acqua lunghezza d onda, periodo, vettor d onda, frequenza funzione d onda equazione delle onde e velocità dell onda esempio di equazione delle
Lezione 15 - Onde onde su una corda, sulla superficie dell acqua lunghezza d onda, periodo, vettor d onda, frequenza funzione d onda equazione delle onde e velocità dell onda esempio di equazione delle
Meccanica Dinamica del punto materiale
 Meccanica 17-18 8 Legge fondaentale della dinaica (II legge di Newton) Nota la forza possiao deterinare l equazione del oto d r F a dt al oviento (accelerazione) risaliao alla forza che lo produce Tipi
Meccanica 17-18 8 Legge fondaentale della dinaica (II legge di Newton) Nota la forza possiao deterinare l equazione del oto d r F a dt al oviento (accelerazione) risaliao alla forza che lo produce Tipi
Equazioni Differenziali
 Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Meccanica Dinamica del punto materiale
 Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
Meccanica 18-19 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente (statico,
m O Esercizio (tratto dal Problema 4.29 del Mazzoldi 2)
 Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Prova Scritta di Fondamenti di Automatica del 21 Giugno 2006 B
 Prova Scritta di Fondaenti di Autoatica del Giugno 6 Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt G () s I( (.s +.8s
Prova Scritta di Fondaenti di Autoatica del Giugno 6 Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt G () s I( (.s +.8s
Oscillatori armonici smorzati e forzati
 Oscillatori armonici smorzati e forzati Giuseppe Dalba Sommario In questi appunti prenderemo in esame l utilizzo delle funzioni complesse nella risoluzione delle equazioni lineari a coefficienti reali,
Oscillatori armonici smorzati e forzati Giuseppe Dalba Sommario In questi appunti prenderemo in esame l utilizzo delle funzioni complesse nella risoluzione delle equazioni lineari a coefficienti reali,
Misure con circuiti elettrici
 Misure con circuiti elettrici Samuele Straulino Laboratorio di Fisica II - S.S.I.S. 2008 2009 http://hep.fi.infn.it/ol/samuele/dida.php Descriverò in particolare questi aspetti: comportamento a regime
Misure con circuiti elettrici Samuele Straulino Laboratorio di Fisica II - S.S.I.S. 2008 2009 http://hep.fi.infn.it/ol/samuele/dida.php Descriverò in particolare questi aspetti: comportamento a regime
T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale. Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4).
 T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 1 Secondo Appello 25 Giugno 2018 Compito A Docente: # iscrizione: Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4). T.(a) Enunciare e
T.(a) T.(b) Es.1 Es.2 Es.3 Es.4 Totale Analisi e Geometria 1 Secondo Appello 25 Giugno 2018 Compito A Docente: # iscrizione: Cognome: Nome: Matricola: Prima parte: Teoria (punti 4+4). T.(a) Enunciare e
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA REGIMI DI FUNZIONAMENTO DEI CIRCUITI ELETTRICI: CORRENTE ALTERNATA SINUSOIDALE
 APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURA Per far produrre laoro elettrico ad un utilizzatore (anche detto bipolo), usando i generatori elettrici (per esepio gli alternatori) engono innanzitutto
APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURA Per far produrre laoro elettrico ad un utilizzatore (anche detto bipolo), usando i generatori elettrici (per esepio gli alternatori) engono innanzitutto
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Esercitazione 09: Forze d inerzia e oscillatore armonico
 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 09: Forze d inerzia e oscillatore aronico Indice 1 Moto relativo
Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 09: Forze d inerzia e oscillatore aronico Indice 1 Moto relativo
Fisica 2C. 3 Novembre Domande
 Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Fisica 2C 3 Novembre 2006 Domande ˆ i) Si consideri un oscillatore armonico smorzato e forzato da una sollecitazione sinusoidale esterna, la cui equazione é tipicamente s + 2γṡ + ω0s 2 = F cos ωt m 1)
Note sui circuiti a corrente alternata
 Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Note sui circuiti a corrente alternata Versione provvisoria. Novembre 018 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Indice 1 Corrente alternata 1.1 Circuito
Analisi e Geometria 1 Secondo Appello 25 Giugno 2018 SOLUZIONI
 Analisi e Geometria 1 Secondo Appello 25 Giugno 2018 SOLUZIONI Esercizi VERSIONE A Es. 1 Nello spazio euclideo R 3, si considerino i piani P e P, rispettivamente di equazioni cartesiane P : x y z 1 = 0,
Analisi e Geometria 1 Secondo Appello 25 Giugno 2018 SOLUZIONI Esercizi VERSIONE A Es. 1 Nello spazio euclideo R 3, si considerino i piani P e P, rispettivamente di equazioni cartesiane P : x y z 1 = 0,
Fondamenti di fisica
 Fondamenti di fisica Elettromagnetismo: 6-7 Circuiti in corrente alternata Tensioni e correnti alternate Vettori di fase, valori quadratici medi Potenza media Sicurezza nei circuiti domestici Circuiti
Fondamenti di fisica Elettromagnetismo: 6-7 Circuiti in corrente alternata Tensioni e correnti alternate Vettori di fase, valori quadratici medi Potenza media Sicurezza nei circuiti domestici Circuiti
Prova Scritta di di Meccanica Analitica. 3 luglio Un punto di massa unitaria si muove soggetto al potenziale. V (x) = k 2 x2 + l2 2x 2 x > 0
 Prova Scritta di di Meccanica Analitica 3 luglio 015 Problea 1 Un punto di assa unitaria si uove soggetto al potenziale V (x) = k x + l x x > 0 a) disegnare lo spazio delle fasi e calcolare la frequenza
Prova Scritta di di Meccanica Analitica 3 luglio 015 Problea 1 Un punto di assa unitaria si uove soggetto al potenziale V (x) = k x + l x x > 0 a) disegnare lo spazio delle fasi e calcolare la frequenza
UNIMOL Ingegneria edile Dinamica del punto materiale
 Le forze elastiche Molti oggetti solidi appaiono indeformabili (corpi rigidi) Nella realtà anche gli oggetti solidi subiscono delle deformazioni più o meno significative quando su di essi vengono esercitate
Le forze elastiche Molti oggetti solidi appaiono indeformabili (corpi rigidi) Nella realtà anche gli oggetti solidi subiscono delle deformazioni più o meno significative quando su di essi vengono esercitate
sono presenti ovunque onde marine onde sonore onde sismiche luce onde radio microonde onde umane?
 ONDE sono presenti ovunque onde marine onde sonore onde sismiche luce onde radio microonde onde umane? CARATTERISTICHE DELLE ONDE Oscillazioni in ogni punto dello spazio Una qualche grandezza fisica si
ONDE sono presenti ovunque onde marine onde sonore onde sismiche luce onde radio microonde onde umane? CARATTERISTICHE DELLE ONDE Oscillazioni in ogni punto dello spazio Una qualche grandezza fisica si
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici Sergio Benenti Prima versione settembre 2013 Revisione settembre 2017? ndice 21 Circuito elettrico elementare
Oscillatore semplice. ponendo. Vibrazioni armoniche libere o naturali
 Oscillatore seplice Vibrazioni aroniche libere o naturali k x Se il corpo di assa è spostato di x verso destra rispetto alla posizione di riposo, è soggetto alla forza elastica di richiao della olla kx
Oscillatore seplice Vibrazioni aroniche libere o naturali k x Se il corpo di assa è spostato di x verso destra rispetto alla posizione di riposo, è soggetto alla forza elastica di richiao della olla kx
Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com
![Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com Onde. Antonio Pierro. Per consigli, suggerimenti, eventuali errori o altro potete scrivere una a antonio.pierro[at]gmail.com](/thumbs/67/56787927.jpg) Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Onde Video Introduzione Onde trasversali e onde longitudinali. Lunghezza d'onda e frequenza. Interferenza fra onde. Battimenti. Moto armonico smorzato e forzato Antonio Pierro Per consigli, suggerimenti,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO
 Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Oscillazione Un oscillazione è la variazione,
Corso di Laurea in LOGOPEDIA FISICA ACUSTICA MOTO OSCILLATORIO Fabio Romanelli Department of Mathematics & Geosciences University of Trieste Email: romanel@units.it Oscillazione Un oscillazione è la variazione,
G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici)
 G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici). Oscillazioni smorzate Equazioni del moto di corpo soggetto a forza elastica e forza di viscosità β v (caso
G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici). Oscillazioni smorzate Equazioni del moto di corpo soggetto a forza elastica e forza di viscosità β v (caso
Induzione magne-ca. La legge di Faraday- Neumann- Lenz e l indu7anza
 Induzione magne-ca a legge di Faraday- Neumann- enz e l indu7anza Esperienza di Faraday Un filo percorso da corrente crea un campo magnetico. Con un magnete si può creare una corrente? a risposta è naturalmente
Induzione magne-ca a legge di Faraday- Neumann- enz e l indu7anza Esperienza di Faraday Un filo percorso da corrente crea un campo magnetico. Con un magnete si può creare una corrente? a risposta è naturalmente
Cap Moti oscillatori
 N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
N.Giglietto A.A. 005/06- Cap 16.1- Moti oscillatori - 1 Cap 16.1- Moti oscillatori Alcuni tipi di forze o alcune situazioni danno luogo a dei moti di tipo oscillante ovvero a dei moti che si ripetono regolarmente.
OSCILLAZIONI SMORZATE E FORZATE
 OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
OSCILLAZIONI SMORZATE E FORZATE Questo esperimento permette di studiare le oscillazioni armoniche di un pendolo e le oscillazioni smorzate e smorzate-forzate. Studiando il variare dell ampiezza dell oscillazione
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
III a Esperienza del Laboratorio di Fisica Generale II Oscillazioni libere e risonanza di un circuito LC-serie (Trattazione analitica del circuito LC-serie) Con questa breve nota si vuole fornire la trattazione
Meccanica Dinamica del punto materiale
 Meccanica 13-14 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente y m N mg mg
Meccanica 13-14 Dinamica del punto materiale 8 Dinamica del punto materiale Legge fondamentale della dinamica: d r ma m dt Tipi di forza: orza peso Reazione vincolare orza di attrito radente y m N mg mg
R = 2.2 kω / 100 kω Tensione di alimentazione picco-picco ε = 2 V (R int = 600 Ω)
 Strumentazione: oscilloscopio, generatore di forme d onda (utilizzato con onde sinusoidali), 2 sonde, basetta, componenti R,L,C Circuito da realizzare: L = 2 H (±10%) con resistenza in continua di R L
Strumentazione: oscilloscopio, generatore di forme d onda (utilizzato con onde sinusoidali), 2 sonde, basetta, componenti R,L,C Circuito da realizzare: L = 2 H (±10%) con resistenza in continua di R L
Equazioni differenziali lineari e oscillatori
 Equazioni differenziali lineari e oscillatori A.Gaudillière 1 Equazioni differenziali lineari 1.1 Equazione oogenea Un e.d.l. è un equazione d incognita x : I E = K n I intervallo di R, K = R o C della
Equazioni differenziali lineari e oscillatori A.Gaudillière 1 Equazioni differenziali lineari 1.1 Equazione oogenea Un e.d.l. è un equazione d incognita x : I E = K n I intervallo di R, K = R o C della
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Prova Scritta di Fondamenti di Automatica del 21 Giugno 2006 A
 Prova Scritta di Fondaenti di Autoatica del Giugno 6 A Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt F( G () s I(
Prova Scritta di Fondaenti di Autoatica del Giugno 6 A Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt F( G () s I(
Scopi del corso. lezione 1 2
 lezione 1 1 Scopi del corso Lo studente saprà analizzare circuiti elettrici dinamici per determinare il loro comportamento nel dominio del tempo e per ricavare le proprietà essenziali nel dominio della
lezione 1 1 Scopi del corso Lo studente saprà analizzare circuiti elettrici dinamici per determinare il loro comportamento nel dominio del tempo e per ricavare le proprietà essenziali nel dominio della
R = Esercizio n.6 di pagina 154. calcoliamo f: In quanto. quindi. Calcoliamo l accelerazione alle estremità; questa in generale è:
 Esercizio n.6 di pagina 154. V t = 3100 /s R = 4. 10 7 a =? v ax =? calcoliao f: In quanto velocità del satellite (tangenziale) raggio dell orbita del satellite frequenza del oto del punto accelerazione
Esercizio n.6 di pagina 154. V t = 3100 /s R = 4. 10 7 a =? v ax =? calcoliao f: In quanto velocità del satellite (tangenziale) raggio dell orbita del satellite frequenza del oto del punto accelerazione
che rappresenta l equazione differenziale del moto armonico. La soluzione dell equazione differenziale è espressa come
 Esperienza n. Forze elastiche Cenni teorici Si dicono elastici i corpi che quando vengono deforati con una copressione o dilatazione reagiscono con una forza di richiao proporzionale alla deforazione.
Esperienza n. Forze elastiche Cenni teorici Si dicono elastici i corpi che quando vengono deforati con una copressione o dilatazione reagiscono con una forza di richiao proporzionale alla deforazione.
Compito di febbraio 2004
 Copito di febbraio 004 Una laina oogenea di assa, avente la fora di un disco di raggio da cui è stato asportato il triangolo equilatero inscritto ABC, rotola senza strisciare lungo l asse delle ascisse
Copito di febbraio 004 Una laina oogenea di assa, avente la fora di un disco di raggio da cui è stato asportato il triangolo equilatero inscritto ABC, rotola senza strisciare lungo l asse delle ascisse
5.4 Larghezza naturale di una riga
 5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
Onde. Fisica Generale - L.Venturelli
 Onde Per descriere olti fenoeni fisici si ricorre a concetti (antitetici): particella onda Utili soprattutto per descriere i diersi odi in cui l energia iene trasferita: particella La ptc è pensata coe
Onde Per descriere olti fenoeni fisici si ricorre a concetti (antitetici): particella onda Utili soprattutto per descriere i diersi odi in cui l energia iene trasferita: particella La ptc è pensata coe
Calcolo del movimento di sistemi dinamici LTI
 Calcolo del movimento di sistemi dinamici LTI Analisi modale per sistemi dinamici LTI TC Modi naturali di un sistema dinamico Analisi modale Esercizio 1 Costante di tempo Esercizio 2 2 Analisi modale per
Calcolo del movimento di sistemi dinamici LTI Analisi modale per sistemi dinamici LTI TC Modi naturali di un sistema dinamico Analisi modale Esercizio 1 Costante di tempo Esercizio 2 2 Analisi modale per
LAVORO DI UNA FORZA (1)
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
Forza centrifuga. Funi e molle. Equazioni del moto
 La forza è un particolare tipo di forza apparente, presente quando il sistema non inerziale (SNI) è in moto rototraslatorio rispetto ad un sistema di riferimento inerziale (SI). Nel moto rototraslatorio
La forza è un particolare tipo di forza apparente, presente quando il sistema non inerziale (SNI) è in moto rototraslatorio rispetto ad un sistema di riferimento inerziale (SI). Nel moto rototraslatorio
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
meccanica delle vibrazioni laurea magistrale ingegneria meccanica parte 4 modelli matematici per sistemi MDOF
 E vietato ogni utilizzo diverso da quello inerente la preparazione dell esae del corso di @Units eccanica delle vibrazioni laurea agistrale ingegneria eccanica!! parte 4 odelli ateatici per sistei MDOF
E vietato ogni utilizzo diverso da quello inerente la preparazione dell esae del corso di @Units eccanica delle vibrazioni laurea agistrale ingegneria eccanica!! parte 4 odelli ateatici per sistei MDOF
G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici)
 G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici) 0.1 Oscillazioni smorzate Equazioni del moto di corpo soggetto a forza elastica e forza di viscosità β v
G. D Agostini Oscillatore smorzato e RCL impulsato (Appunti dal Corso di Fisica per Informatici) 0.1 Oscillazioni smorzate Equazioni del moto di corpo soggetto a forza elastica e forza di viscosità β v
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
α =ωt. =ωr in senso antiorario, dove ω indica la velocità angolare. Supponiamo che al tempo t 0
 Studio cinematico del moto armonico di un punto materiale per la determinazione di due relazioni utili all analisi di circuiti in corrente alternata. prof. Dario Benetti 1 Introduzione. In riferimento
Studio cinematico del moto armonico di un punto materiale per la determinazione di due relazioni utili all analisi di circuiti in corrente alternata. prof. Dario Benetti 1 Introduzione. In riferimento
CIRCUITI IN CORRENTE CONTINUA
 IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
FM210 - Fisica Matematica 1 Tutorato 11 ( )
 Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Sistemi continui oscillanti unidimensionali (corde vibranti)
 Edoardo Milotti 4/10/2005 Sistemi continui oscillanti unidimensionali (corde vibranti Consideriamo due oscillatori armonici accoppiati linearmente. Fisicamente ciò si può realizzare, ad esempio, con due
Edoardo Milotti 4/10/2005 Sistemi continui oscillanti unidimensionali (corde vibranti Consideriamo due oscillatori armonici accoppiati linearmente. Fisicamente ciò si può realizzare, ad esempio, con due
Dinamica del punto materiale
 Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Dinamica del punto materiale Formule fondamentali L. P. 5 Aprile 2010 N.B.: Le relazioni riportate sono valide in un sistema di riferimento inerziale. Princìpi della dinamica Secondo principio della dinamica
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Questa forza aumenta all aumentare della velocità del corpo ma la sua dipendenza dalla velocità è complessa ed è funzione di molti parametri
 Forze di attrito viscoso Durante le lezioni precedenti.. Per studiare i moti di caduta libera o qualsiasi moto possa avvenire nell esperienza quotidiana.. Tra le condizioni imposte c è stata sempre quella
Forze di attrito viscoso Durante le lezioni precedenti.. Per studiare i moti di caduta libera o qualsiasi moto possa avvenire nell esperienza quotidiana.. Tra le condizioni imposte c è stata sempre quella
Esperimenti computazionali con Mathematica: la trasformata di Fourier
 Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
CAMPO MAGNETICO ROTANTE
 CAPO AGNETICO ROTANTE Un solo avvolgimento percorso da corrente comunque variabile nel tempo sostiene una distribuzione di f.m.m. (e quindi di induzione) fissa nello spazio e con asse di simmetria diretto
CAPO AGNETICO ROTANTE Un solo avvolgimento percorso da corrente comunque variabile nel tempo sostiene una distribuzione di f.m.m. (e quindi di induzione) fissa nello spazio e con asse di simmetria diretto
Ricordiamo ora che a è legata ad x (derivata seconda) ed otteniamo
 Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
Moto armonico semplice Consideriamo il sistema presentato in figura in cui un corpo di massa m si muove lungo l asse delle x sotto l azione della molla ideale di costante elastica k ed in assenza di forze
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I
 ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
ELETTROTECNICA (10 CFU) CS INGEGNERIA MATEMATICA I prova in itinere 1 Novembre 008 SOLUZIONE - 1 - D1. (punti 8 ) Rispondere alle seguenti domande: punto per ogni risposta corretta, - 0.5 per ogni risposta
Prova Scritta di di Meccanica Analitica
 Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
Prova Scritta di di Meccanica Analitica 7 gennaio 015 Problema 1 Un punto di massa unitaria si muove sull asse x soggetto al potenziale V (x) = x e x a) Determinare le posizioni di equilibrio e la loro
Formulario Elettromagnetismo
 Formulario Elettromagnetismo. Elettrostatica Legge di Coulomb: F = q q 2 u 4 0 r 2 Forza elettrostatica tra due cariche puntiformi; ε 0 = costante dielettrica del vuoto; q = cariche (in C); r = distanza
Formulario Elettromagnetismo. Elettrostatica Legge di Coulomb: F = q q 2 u 4 0 r 2 Forza elettrostatica tra due cariche puntiformi; ε 0 = costante dielettrica del vuoto; q = cariche (in C); r = distanza
Tutorato 6 - FM210. avendo usato la condizione di puro rotolamento r φ = ẏ e. 2) I punti di equilibrio sono i punti critici del potenziale:
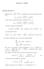 Tutorato 6 - FM10 Soluzione Esercizio 1 R l = l, applicando il teorema di Koenig abbi- 1 Abbiamo OC = amo T disco = 1 mẏ + 1 mr φ = 1 mẏ avendo usato la condizione di puro rotolamento r φ = ẏ e T asta
Tutorato 6 - FM10 Soluzione Esercizio 1 R l = l, applicando il teorema di Koenig abbi- 1 Abbiamo OC = amo T disco = 1 mẏ + 1 mr φ = 1 mẏ avendo usato la condizione di puro rotolamento r φ = ẏ e T asta
Soluzioni Prova Scritta di di Meccanica Analitica. 17 aprile Un punto di massa unitaria si muove lungo una retta soggetto al potenziale
 Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
Lezione XXVI Sistemi vibranti a 1 gdl 9,%5$=,21,75$16,725,(
 ezione XXVI 9,%5$=,,75$6,75,( Quando un sistema dinamico viene sollecitato da una eccitazione non periodica applicata improvvisamente, come nel caso di un impulso, le risposte a tali eccitazioni sono dette
ezione XXVI 9,%5$=,,75$6,75,( Quando un sistema dinamico viene sollecitato da una eccitazione non periodica applicata improvvisamente, come nel caso di un impulso, le risposte a tali eccitazioni sono dette
Prerequisiti e strumenti matematici e fisici per l elettronica delle telecomunicazioni I FASORI
 Ing. Nicola Cappuccio 214 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI 1 RIEPILOGO rappresentazione z = ρcos θ+ jρsin θ somma di due complessi con al regola del parallelogramma
Ing. Nicola Cappuccio 214 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI 1 RIEPILOGO rappresentazione z = ρcos θ+ jρsin θ somma di due complessi con al regola del parallelogramma
Oscillazioni LC Applicando la legge di Faraday: ma Φ B. in direzione I. ovvero. La soluzione di questa equazone e:
 Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
Oscillazioni Applicando la legge di Faraday: E d l d ma Φ B con d l in direzione d E dl ovvero ovvero d + q / n base alla nostra scelta di polarizzazione di pero', si ha' che: dq Segue che: A d d q Allora,
e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
Foglio di Esercizi 5 Meccanica Razionale a.a. 2017/18 Canale A-L (P. Buttà)
 Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
FM210 - Fisica Matematica 1. Esercizio 1. Si consideri il sistema di equazioni differenziali lineari
 TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
TUTORATO 1 (5-03-2019) FM210 - Fisica Matematica 1 sercizio 1. Si consideri il sistema di equazioni differenziali lineari ( ) ẋ = Ax, x R 2 3 2, A = 6 1 1. Si calcolino gli autovalori e gli autovettori.
Facoltà di Ingegneria Prova scritta di Fisica I
 Facoltà di Ingegneria Prova scritta di Fisica I 6..6 CMPIT C Esercizio n. Un blocco, assiilabile ad un punto ateriale di assa = kg, partendo da fero, scivola da un altezza h = 7 lungo una guida priva di.
Facoltà di Ingegneria Prova scritta di Fisica I 6..6 CMPIT C Esercizio n. Un blocco, assiilabile ad un punto ateriale di assa = kg, partendo da fero, scivola da un altezza h = 7 lungo una guida priva di.
Moto armonico. A.Solano - Fisica - CTF
 Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
Moto armonico Moti periodici Moto armonico semplice: descrizione cinematica e dinamica Energia nel moto armonico semplice Il pendolo Oscillazioni smorzate Oscillazioni forzate e risonanza Moto periodico
Induzione magne-ca. La legge di Faraday- Neumann- Lenz e l indu7anza
 Induzione magne-ca a legge di Faraday- Neumann- enz e l indu7anza egge di Faraday Un filo percorso da corrente crea un campo magnetico. Con un magnete si può creare una corrente? a risposta è naturalmente
Induzione magne-ca a legge di Faraday- Neumann- enz e l indu7anza egge di Faraday Un filo percorso da corrente crea un campo magnetico. Con un magnete si può creare una corrente? a risposta è naturalmente
DINAMICA DI SISTEMI AEROSPAZIALI
 DINAMICA DI SISTEMI AEROSPAZIALI Tema d esame 11-07 - 2014 g A l h M, J O d B M B, J B moto definita ai punti precedenti. C m Esercizio 1. Il sistema in figura, posto nel piano verticale, è costituito
DINAMICA DI SISTEMI AEROSPAZIALI Tema d esame 11-07 - 2014 g A l h M, J O d B M B, J B moto definita ai punti precedenti. C m Esercizio 1. Il sistema in figura, posto nel piano verticale, è costituito
La fisica di Feynmann Meccanica
 La fisica di Feynmann Meccanica 1.1 CINEMATICA Moto di un punto Posizione r = ( x, y, z ) = x i + y j + z k Velocità v = dr/dt v = vx 2 + vy 2 + vz 2 Accelerazione a = d 2 r/dt 2 Moto rettilineo Spazio
La fisica di Feynmann Meccanica 1.1 CINEMATICA Moto di un punto Posizione r = ( x, y, z ) = x i + y j + z k Velocità v = dr/dt v = vx 2 + vy 2 + vz 2 Accelerazione a = d 2 r/dt 2 Moto rettilineo Spazio
Università di Trieste Facoltà d Ingegneria. Esercizi sulle equazioni differenziali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria Esercizi sulle equazioni differenziali Dott Franco Obersnel Esercizio 1 Si classifichino le seguenti equazioni, come ordinarie o alle derivate parziali si dica
Università di Trieste Facoltà d Ingegneria Esercizi sulle equazioni differenziali Dott Franco Obersnel Esercizio 1 Si classifichino le seguenti equazioni, come ordinarie o alle derivate parziali si dica
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
Il modello di Lorentz e Drude
 Il odello di Lorentz e Drude Oscillatore di Lorentz Abbiao un elettrone di assa legato elasticaente al nucleo di assa M>>. L equazione del oto è 2 r t 2 Γ r t Ω 0 r e E loc (*) il terine viscoso ( r )
Il odello di Lorentz e Drude Oscillatore di Lorentz Abbiao un elettrone di assa legato elasticaente al nucleo di assa M>>. L equazione del oto è 2 r t 2 Γ r t Ω 0 r e E loc (*) il terine viscoso ( r )
Lezione 5: Sistemi ad un grado di libertà: l oscillatore elementare (5)
 Lezione 5: Sistei ad un grado di libertà: l oscillatore eleentare (5) Federico Cluni 7 arzo 25 Risposta sotto forzante qualsiasi - Integrale di Duhael. Sovrapposizione degli effetti L equazione del oto
Lezione 5: Sistei ad un grado di libertà: l oscillatore eleentare (5) Federico Cluni 7 arzo 25 Risposta sotto forzante qualsiasi - Integrale di Duhael. Sovrapposizione degli effetti L equazione del oto
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Appunti on-line del Corso di Onde e Oscillazioni
 Appunti on-line del Corso di Onde e Oscillazioni Docente Carlo Pagani http://wwwsrf.mi.infn.it/members/pagani/ Anno accademico 009-010 Redazione di Daniele Sertore degli appunti del docente per il corso
Appunti on-line del Corso di Onde e Oscillazioni Docente Carlo Pagani http://wwwsrf.mi.infn.it/members/pagani/ Anno accademico 009-010 Redazione di Daniele Sertore degli appunti del docente per il corso
