Pressione. F n. Pressione: è il rapporto P = F n
|
|
|
- Carlotta Ferretti
- 9 anni fa
- Visualizzazioni
Transcript
1 I FLUIDI
2 Pressione P = Pressione: è il rapporto P = F n /S tra la componente della forza ortogonale alla superficie e l area della superficie su cui la forza è applicata. È una grandezza scalare che ci dice quale può essere la forza esercitata dal fluido su una superficie (anche immaginaria in mezzo al fluido!) con cui si trova in contatto. Fn S S F F n Nel sistema SI si misura in pascal (Pa) 1 Pa = 1 N/m 2 Altre unità di misura sono: 1 bar = 10 5 Pa 1 atm = 1, Pa = 1,013 bar 1 atm = 760 mmhg 1 torr = 1 mmhg = 1/760 atm
3 Densità ρ = La densità dei solidi e dei liquidi dipende dalla temperatura ed è pressochè costante al variare della pressione. Normalmente ρ diminuisce al crescere della temperatura T perchè un aumento di T comporta un aumento di volume. m V Unità: kg/m 3 o g/cm 3 1 g/cm 3 = 1000 kg/m 3 ρ ρ 3 H = 1000 kg/m = 2 O Aria = kg/m 1g/cm 3 a T=4 0 C a T=0 0 C e p= 1 atm Peso specifico: mg [kg m -2 s -2 = N/m 3 ] σ = = ρg V
4 I FLUIDI: LIQUIDI E GAS Idrostatica: fluidi fermi Idrodinamica: fluidi in moto Definizione di fluido: mezzo continuo senza forma propria ma che si adatta a quella del recipiente che lo contiene. Può essere nella fase liquida (es. acqua) o gassosa (es. un gas). Anche se non possiede una forma propria, una massa M di fluido possiede un volume V. Differenze principali tra solidi, liquidi e gas: il libero cammino medio: le particelle che costituiscono i fluidi sono libere di muoversi, nei solidi sono legate tra loro a formare un reticolo cristallino la compressibilità: se esercito una forza su un corpo rigido non ottengo una variazione di volume V. Su un fluido sì. Per i liquidi V è piccolo, per i gas è grande.
5 Altra caratteristica del fluido è di esercitare la forza nella direzione perpendicolare ad una qualunque superficie toccata dallo stesso. F =0 altrimenti il liquido si muoverebbe a causa di F F =0 Esempi: l acqua contenuta in una bottiglia esercita una forza verso l esterno normale alla parete della stessa; l acqua del mare esercita sui pesci una forza diretta verso l interno del corpo; l'aria esercita su di noi una forza diretta verso l interno del nostro corpo.
6 I FLUIDI: LIQUIDI E GAS Descrizione macroscopica Poichè il fluido è un mezzo continuo senza forma propria, per descriverne il comportamento fisico dal punto di vista macroscopico è opportuno considerare volta per volta elementi di volume V a forma di parallelepipedo ed analizzare le forze che agiscono su di esso. P=forza peso F V =forze che agiscono su facce verticali F L =forze che agiscono su facce laterali P
7 In un qualsiasi elemento di liquido le condizioni di equilibrio comportano che le forze laterali F L = p S siano uguali, cioè: F =F p S =p S Se scelgo la forma di parallelepipedo allora sarà: S = S da cui p =p Idrostatica F y F y+dy F 1 P=mg F 2 Di conseguenza, la pressione in un fluido in equilibrio ha gli stessi valori nei punti alla stessa distanza dalla superficie libera
8 Le forze verticali sono in equilibrio se si ha F 1 + mg = F 2 quindi p 1 S+mg = p 2 S Legge di Stevino poichè m=ρv=ρs(y 2 -y 1 ) p 1 S+ ρs(y 2 -y 1 ) g = p 2 S p 2 -p 1 =ρg(y 2 -y 1 ) y 2 =y+dy F 1 P=mg y 1 =y Se y 1 = 0, y 2 =h p 1 p 0, p 2 p F 2 p=p 0 +ρgh o anche dp/dy = -ρg Di conseguenza, la pressione in un fluido in equilibrio non dipende dalla forma del contenitore ma solo dalla profondità p = p 0 + ρgh (pressione esterna e idrostatica). Due punti si trovano a diversa altezza nel fluido la pressione sarà maggiore nel punto di profondità maggiore, inoltre in due punti che si trovano alla stessa altezza nel fluido la pressione è la stessa.
9 La legge di Stevino spiega perché è consuetudine misurare le pressioni tramite altezze di fluidi: cmh 2 O, mmhg, p= ρ g h 1 cmh 2 O 10 3 kg/m 3 10 m/s m= 100 Pa 1 mmhg kg/m 3 10 m/s m=133 Pa La pressione IDROSTATICA gioca un ruolo non trascurabile anche nei sistemi biologici. Se assumiamo che la densità del sangue sia pari a quella dell acqua: 50 cm P CUORE = 100 mmhg 120 cm p capo = 100 mmhg /133 = 63 mmhg Legge di Stevino p piedi = 100 mmhg /133 = 190 mmhg
10 Problema Calcolare la pressione in una piscina piena d acqua (10 3 kg/m 3 ) alla profondità di 2 m. Soluzione: non appena conosciamo il valore della pressione in un punto della piscina, potremo applicare la legge di Stevino. Questo punto è la superficie dove l acqua è in contatto con l aria (altro fluido). Quindi sulla superficie la pressione è pari alla pressione atmosferica p o = 1, Pa. A due metri di profondità la pressione è di conseguenza: p = p o + ρgh = 1, Pa kg/m m/s 2 2 m = Pa Si noti che ogni 10 metri di profondità la pressione nell acqua aumenta di 1 atmosfera.
11 Misura della pressione Barometro a tubo aperto Barometro a mercurio
12 Principio di Pascal La legge di Pascal dice che una variazione di pressione p in un fluido incompressibile si trasmette inalterata a tutti i punti del fluido (e alle pareti del recipiente che lo contiene), qualunque sia la loro profondità: se p 0 = p 0 + p, si ha p = p 0 + p + ρgh. La pressa idraulica è un applicazione. p 1 F 2 p 2 F 1 S 1 S2 p 1 = p 2 quindi F S 1 1 F S 2 2 quindi Quindi se S 2»S 1 basta una piccola F 1 per ottenere F 2 molto grande = F 2 = F 1 S S 2 1
13 Principio di Archimede Galleggiamento dei corpi F S P F S P F S P Un elemento di fluido è in equilibrio perche` il suo peso è bilanciato da una forza di spinta uguale e contraria F S = P = mg = ρ f Vg. Un corpo immerso nel fluido è soggetto ad una spinta F s verso l alto pari al peso del volume di fluido spostato. Un corpo di galleggia se P + F s 0 e quindi se la sua densità ρ è minore di quella ρ f del fluido in cui è immerso (es. legno in acqua), altrimenti (se P + Fs 0 e quindi ρ ρ f ) affonda (es. pietra in acqua).
14 Galleggiamento dei corpi La parte emersa del galleggiante si ottiene eguagliando la spinta dovuta al liquido spostato dalla parte immersa F s = ρv*g al peso del corpo P= ρ'vg dove V* è il volume della parte immersa Problema Sapendo che un blocco di ghiaccio immerso in acqua galleggia e che la frazione del volume che rimane immersa è il 92%, calcolare la densità del ghiaccio ρ gh. Soluzione: posto V il volume del blocco di ghiaccio, l equilibrio delle forze a cui è soggetto si può scrivere come la somma vettoriale della forza peso e della spinta di Archimede generata dalla parte di ghiaccio immersa nell acqua P + F s = 0. V ρ V ρv im g ρ gh Vg = 0 ρ gh = im = 1 g/cm = 0.92 g/cm 3
15 Esercizio: quale volume di elio (ρ He =0.179 kg/m 3 ) è necessario per per un pallone che deve sollevare 100 kg in aria (ρ Aria =1.29 kg/m 3 )? La spinta verso l alto è data dal peso del fluido (aria) spostato: F A = m Aria g = ρ Aria V g La forza verso il basso è data dalla somma dei pesi del carico e dell elio F B = m He g + m carico g = ρ He V g + m carico g F A deve essere almeno pari a F B Per F A =F B, ρ Aria V g = ρ He V g + m carico g V = ρ m carico Aria ρ He
16 IDRODINAMICA Il flusso In generale la descrizione del movimento di un fluido è molto complicata: occorre definire un CAMPO VETTORIALE di VELOCITÁ che ad ogni punto (x,y,z) e ad ogni istante t associa un vettore v tangente alla direzione di movimento del fluido. Se il fluido attraversa A con velocità costante su tutta la superficie, e se v è perpendicolare ad A, Φ = va Noi considereremo per semplicità moti STAZIONARI, che cioè non variano nel tempo(v=cost in modulo, direzione, verso in ogni punto del condotto) e ASSIALI (in cui tutte le particelle si muovono nella medesima direzione lungo l asse del tubo).
17 IDRODINAMICA Linee di flusso Rappresentazione grafica del campo di velocità In ogni punto la velocità del flusso è tangente alla linea di flusso per quel punto. L intensità è proporzionale al numero di linee che attraversano una sezione trasversale Il concetto di flusso può essere esteso a qualunque campo vettoriale.
18 IDRODINAMICA Fluidi ideali Moto laminare v(t) = cost Il flusso non laminare è detto turbolento Fluido incomprimibile (ρ costante) Fluido non viscoso (non c è attrito) Un oggetto all interno del fluido non è soggetto a forze frenanti Flusso irrotazionale Se il flusso è irrotazionale, un oggetto posto in un punto non ruota attorno ad un asse passante per il suo centro di massa
19 IDRODINAMICA Portata Equazione di continuità: la massa m 1 che attraversa in un certo t una sezione S 1 del condotto è la stessa che attraversa nello stesso t qualunque altra sezione S 2. m = ρ V = ρ A 1 x 1 = ρ A 2 x 2 ρa 1 v 1 t = ρa 2 v 2 t da cui, dividendo per t, si ha A 1 v 1 = A 2 v 2. Legge della costanza della portata. Esprime il principio di conservazione della massa. La quantità di fluido che attraversa nell unità di tempo una qualunque sezione del condotto (portata), è costante (il fluido non si perde per strada!).
20 Portata volumica e massica Q = Sv = cost. (portata volumica) nel SI si misura in m 3 /s Q M = ρsv = cost. (portata massica) nel SI si misura in kg/s Nota bene Se S 1 = S 2 S 1 S 2 v 1 = v 2 Se S 2 < S 1 S 1 S 2 v 2 > v 1
21 Problema In un adulto normale a riposo, la velocità media del sangue attraverso l'aorta è v = 0.33 m/s. Calcolare la portata attraverso un'aorta di r = 9 mm. Soluzione: Q = Sv = πr 2 v = 3.14 ( ) 2 m m/s = m 3 /s Dall'aorta il sangue fluisce nelle arterie maggiori, poi in quelle più piccole e infine nei capillari. Ad ogni stadio successivo ciascuno di questi vasi si divide in molti vasi più piccoli e il flusso di sangue si ripartisce fra questi in modo che la portata totale sia costante. Se conosciamo la sezione complessiva di tutte le arterie S arterie e di tutti i capillari S capillari dovrà valere la relazione: Q = S arterie v arterie = S capillari v capillari Pertanto il sangue si muove più lentamente verso la periferia perché la sezione complessiva dei vasi sanguigni è maggiore.
22 Teorema di Bernoulli: conservazione dell energia nei fluidi ideali in moto stazionario in un condotto La forza F 1 =p 1 S 1 compie il lavoro L 1 = F 1 x 1 = p 1 S 1 x 1 = p 1 V sulla massa m (= ρv) nel volume V = S 1 x 1 La forza F 2 compie il lavoro L 2 = -F 2 x 2 = -p 2 S 2 x 2 = -p 2 V La forza di gravità compie L 3 = - U= -mg(h 2 -h 1 ) = -(ρv)g(h 2 -h 1 ) Il lavoro totale è L=L 1 +L 2 +L 3 L energia cinetica varia di E K = ½ m(v 22 -v 12 ) = ½ ρv(v 22 -v 12 ). F 2 v 1 S 2 h 2 x 1 h 1 F 1 m S 1 x2 v 2
23 Teorema di Bernoulli Applico il teorema dell energia cinetica L= K e, dividendo i termini per V, ottengo: p 1 + ρgh 1 + ½ ρv 1 2 = p 2 + ρgh 2 + ½ ρv 22, ossia p + ρgh + ½ρv 2 = costante ½ρv 2 = energia cinetica per unità di volume (pressione cinetica) ρgh =energia potenziale gravitazionale dell unità di volume (pressione di gravità) p = pressione dinamica In regime stazionario, la somma dei tre termini deve rimanere costante per ogni sezione. Nota: fissato h, a v alte corrispondono p basse e viceversa Se il fluido è statico, v 1 =v 2 =0 p + ρgh = p o + ρ gy o p p 0 = ρg(y o -y) Legge di Stevino
24 Problema Calcolare la velocità v con cui l acqua inizia ad uscire dal foro di scarico di una vasca da bagno dove il livello iniziale dell acqua è h = 30 cm. Soluzione: dobbiamo applicare l equazione di Bernoulli sul punto 1) dello scarico ed in un altro punto 2) della vasca dove conosciamo il valore per p, v e h. Il punto 2) in questione è il livello superiore dell acqua dove p 2 = p, h 2 = h e v 2 = 0 perché non appena l acqua inizia a defluire dal fondo, quella posta sulla superficie è ancora praticamente ferma. Al punto 1) vale invece h 1 = 0, v 2 = v e p 1 = p o perché la superficie del fronte d acqua che sta uscendo dallo scarico si trova in diretto contatto con l atmosfera. Quindi: 2 2 p 1 + ρgh 1 + ½ ρv 1 = p 2 + ρgh 2 + ½ ρv 2 p o + ½ ρv 2 = p o + ρgh v = 2 2 2gh = 2 9.8m/s m = m/s 2 1 h
25 Applicazioni dell equazione di Bernoulli: Condotto orizzontale - Stenosi y 1 = y 2 L equazione di Bernoulli si riduce a: p 1 + ½ ρv 1 2 = p 2 + ½ ρv 2 2 Se A 2 <A 1 (restringimento) A1 A1 dall equazione di continuità v 2 = v v 2 > v 1 >1 1 A2 dall equazione di Bernoulli: p 2 = p 1 - ½ ρ(v 22 -v 12 ) p 2 < p 1 Stenosi tendenza ad un ulteriore restringimento In presenza di un stenosi la sezione dell arteria S 2 è minore di quella naturale S 1 e quindi la pressione sanguigna p 2 all altezza della stenosi sarà minore di quella naturale p 1. Pertanto, nel punto dove c'è la stenosi, l'arteria può occludersi completamente. A 2
26 Applicazioni dell equazione di Bernoulli: Aneurisma Dilatazione congenita o patologica di un arteria p 1 v 1 A 1 p 2 v 2 A 2 Se A 2 > A 1 (dilatazione) 1 1 A2 dall equazione di continuità: v 2 = v 2 < v 1 <1 dall equazione di Bernoulli: p 2 = p 1 - ½ ρ(v 22 -v 12 ) p 2 > p 1 < 0 La pressione sanguigna p 2 all altezza dell aneurisma sarà maggiore di quella naturale p 1. Pertanto, nel punto dove c'è l'aneurisma, può rompersi la parete dell'arteria. v A A A 1 2
27 Problema Un arteria di raggio r = 2.5 mm è parzialmente ostruita da una placca, per modo che il suo raggio effettivo in quel punto vale 1.8 mm e la velocità del sangue è di 50 cm/s. Soluzione: La velocità media del sangue dove l arteria non è ostruita vale: v π r 2 = v π r 2 v = v ( r / r ) 2 = 50 cm/s ( 1.8 mm/ 2.5 mm) 2 = = circa 26 cm/ s (perché non è necessario passare nel S.I.? )
28 Altre applicazioni del teorema di Bernoulli Le ali dell aereo e la portanza La pressione dell aria è maggiore dove la velocità è più alta, ovvero dove le linee di campo si addensano. L angolo di attacco e la superficie arrotondata dell ala costringono le linee di flusso verso l alto ad addensarsi sopra l ala. Sezione dell ala La pressione nella parte inferiore dell ala è dunque più grande, per cui la forza risultante sarà diretta verso l alto Per un angolo di attacco superiore a 15 0, il regime diventa turbolento, aumenta l attrito e diminuisce la forza verso l alto. L aereo in queste condizioni va in stallo e precipita.
29 Altre applicazioni del teorema di Bernoulli (II) Il tiro ad effetto Mettiamoci nel S.R. della palla La palla, colpita ad un lato, ruota su se stessa, trascinando con sè uno strato d aria a causa dell attrito Nel punto B l aria trascinata dalla palla si muove come l aria che arriva, aumentandone la velocità. In A avviene il contrario Dunque la velocità in B sarà più grande che in A. Al contrario, la pressione sarà più grande in A, dunque la traiettoria della palla si incurverà verso B
30 Liquidi reali Attrito interno Flusso di un liquido ideale in un condotto La velocità è la stessa in tutti i punti di una sezione normale di un condotto Liquido reale in un tubo capillare L attrito sulle pareti fa sì che gli strati di liquido aderenti alle pareti abbiano velocità nulla. La velocità degli strati cresce andando verso l esterno. Moto laminare Regime di Poiseuille
31 Liquidi reali -Viscosità Viscosità: La definizione più intuitiva è quella data da Newton: una mancanza di scorrevolezza tra strati adiacenti di un fluido che si muovono con velocità diversa F A = dv η dy ΔS dv/dy: gradiente di velocità F A : forza d attrito agente sulla superficie di area S, appartenente ad uno degli strati in movimento η: coefficiente di viscosità In un fluido reale c e`perdita di carico dovuta alla dissipazione di energia. A causa della presenza dell attrito nel movimento sarà infattispeso del lavoro.
32 Liquidi reali -Viscosità η coefficiente di viscosità [η] = [ml -1 t -1 ] La viscosità viene misurata in Pa s nel SI oppure in poise (P) nel sistema CGS (1 P = 0.1 Pa s) Viscosità di alcune sostanze Acqua (e plasma): η 0.01 P a 20 0 C Olii: η 1P 10 P a 20 0 C Olii lubrificanti: η grande e poco sensibile alla temperatura Pece, vetro: η>10 8 P
33 Legge di Hagen-Poiseuille Per mantenere in movimento un volume di fluido reale V che fluisce in un tempo t, è necessario fare un lavoro, occorre cioè mantenere una differenza di pressione fra i punti d ingresso e d uscita. Nel caso di un condotto cilindrico di raggio costante R e lunghezza L la portata del condotto è legata alla differenza di pressione p agli estremi del condotto dall equazione: V = π 8 ΔpR ηl 4 t V/t=Q Q = π 8 ΔpR ηl 4 Valida in regime laminare gli strati di fluido scorrono gli uni sugli altri parallelamente senza mescolarsi. Approssimazione valida nei fluidi viscosi quando la velocità è molto bassa, all'aumentare della velocità gli strati di fluido si mescolano tra loro in moto vorticoso regime turbolento.
34 Numero di Reynolds Per stabilire se un fluido reale in movimento possa essere considerato in regime laminare occorre calcolare il numero di Reynolds: N R = 2ρ v R η _ dove Q v = è la velocità media del fluido di densità ρ e 2 πr viscosità η nel condotto cilindrico di raggio R, e verificare che sia 1000 < N R. Per valori maggiori a 3000 il moto è sicuramente turbolento mentre per valori intermedi il regime è instabile.
35 Problema Approssimando l'aorta di un adulto a riposo come un cilindro lungo L= 30 cm di raggio R= 9 mm, si calcoli la caduta di pressione nel sangue quando attraversa l'aorta. Si assuma la viscosità del sangue η= P e la portata del sangue nell aorta Q = 83 cm 3 /s. Soluzione: la caduta di pressione si ottiene applicando l equazione di Hagen-Poiseuille (passando al sistema SI): 3 8η LQ Pa s 0.3m Δp = = 3 4 πr π (9 10 m) 3 m /s 6 = Pa
36 Problema Calcolare il numero di Reynolds per il sangue che scorre con velocità media v=10 cm/s in un arteria di raggio R= 2 mm. Densità del sangue a 37 0 C ρ= 1.05 g/cm 3 e viscosità η = P. Soluzione: è sufficiente applicare la definizione di N R : _ 2ρ v R η g/cm 10cm/s P NR = = 2 Si tratta si un flusso laminare. 0.2cm 88
37 Problema Calcolare il numero di Reynolds nell ipotesi che nell arteria dell esercizio precedente sia presente una stenosi che riduca il raggio dell arteria a R = 2 mm. Soluzione: occorre anzitutto ricalcolare la velocità media del sangue nell ipotesi che la portata dell arteria sia costante: v π R 2 = v π R 2 v = v ( R / R ) 2 = 10 cm/s ( 2 mm / 0.2 mm) 2 = 10 3 cm/s e quindi applicare la definizione di N R _ ' R 2 NR = = 2 2ρ v η g/cm 10 cm/s P 0.02cm 884 con flusso prossimo ad essere turbolento.
38 Il moto dei corpi nei fluidi reali Oltre alle forze peso e di Archimede, c è una forza resistente al moto del corpo nel fluido, il cui modulo e : F R = bv che si oppone al moto del corpo. La costante b e proporzionale alla viscosita e alle dimensioni del corpo. Per corpi sferici di raggio R questa forza è data da: F = 6πηRv (Legge di Sokes) Sedimentazione Un corpo (di densità ρ) in un fluido viscoso di densità ρ è in equilibrio idrostatico se il suo peso e` bilanciato dalle forze di spinta e di resistenza viscosa P= F S + F R, ossia se ρvg = ρ Vg + bv, da cui si ricava la velocità di sedimentazione v sedim Spinta di Archimede: F s = ρ Vg = V(ρ ρ b * )g Forza di attrito: F R = bv Forza peso: P = mg = ρvg
39 Centrifugazione Immaginiamo dei corpuscoli di forma sferica in sospensione in un liquido posto in una provetta in rotazione intorno ad un asse verticale con velocità angolare ω. La legge di Stevino si modifica per tener conto del termine di rotazione: p = p 0 + ρgh + ρω 2 R 2 /2. Il corpuscolo in sospensione ad una distanza R dall asse di rotazione è soggetto ad una forza centripeta F C = mv 2 /R = mω 2 R = ρ Vω 2 R. Si puo dimostrare che: v S = V(ρ ρ b * )ω 2 R Velocità di separazione per centrifugazione
40 Centrifughe v v S = sedim 2 ω R g Centrifughe: ω 600 s -1, R 10 cm, 2 ω R g Ultracentrifughe: ω 10 5 minuti -1, a 10 6 g Usate per la separazione di corpuscoli con L < 1 µm(es. virus) e per lo studio del comportamento di sostanze macromolecolari.
41 Un esempio: la VES. La VELOCITA DI ERITROSEDIMENTAZIONE (VES) R = 3.5 µm d(glob)= g/cm 3 d(plasma)= g/cm 3 η= 0.01 cp v sedim = * V(ρ ρ )g 6π η R si trova una velocità di sedimentazione pari a v= 7 mm/h. La VES può aumentare di un ordine di grandezza in presenza di fatti patologici: ciò è legato all accresciuta concentrazione del fibrinogeno e delle globuline nel plasma che accrescono la tendenza degli eritrociti a formare rouleaux (sequenze di eritrociti che aderiscono l uno all altro) la cui velocità di sedimentazione è maggiore di quella delle singole particelle. Al contrario, l aumentata viscosità del plasma tenderebbe a ridurre la VES e non può quindi essere la causa dell osservato aumento della VES.
42 La misura della pressione arteriosa La misura non invasiva viene eseguita con lo sfigmomanometro di Riva-Rocci: intorno al braccio viene posto un manicotto gonfiabile, un manometro a mercurio permette di misurare la pressione di gonfiaggio. Il manicotto consente di esercitare una pressione tale da occludere l arteria brachiale. Quando la valvola viene rilasciata, la pressione decresce. Ponendo uno stetoscopio in prossimità del vaso è possibile percepire, per tutta la durata della compressione, dei rumori dovuti alle turbolenze del sangue (suoni di Korotkoff). La lettura del valore di pressione sul manometro quando tali suoni compaiono e scompaiono fornisce rispettivamente una misura della pressione sistolica e diastolica.
Meccanica dei Fluidi: statica e dinamica
 Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
Lezione 9. Statica dei fluidi
 Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Dinamica dei Fluidi. Moto stazionario
 FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
Densita. FLUIDI : liquidi o gas. macroscop.:
 6-SBAC Fisica 1/10 FLUIDI : liquidi o gas macroscop.: microscop.: sostanza che prende la forma del contenitore che la occupa insieme di molecole tenute insieme da deboli forze di coesione (primi vicini)
6-SBAC Fisica 1/10 FLUIDI : liquidi o gas macroscop.: microscop.: sostanza che prende la forma del contenitore che la occupa insieme di molecole tenute insieme da deboli forze di coesione (primi vicini)
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 15
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 15 Un fluido è un insieme di molecole tenute insieme da deboli forze di coesione e da forze esercitate dalla parete del contenitore (possono essere sia
Serway, Jewett Principi di Fisica IV Ed. Capitolo 15 Un fluido è un insieme di molecole tenute insieme da deboli forze di coesione e da forze esercitate dalla parete del contenitore (possono essere sia
IL MOTO DEI FLUIDI. con applicazione al sistema circolatorio
 IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
Meccanica dei Fluidi. stati di aggregazione della materia: solidi liquidi gas. fluidi assumono la forma del contenitore
 Meccanica dei luidi stati di aggregazione della materia: solidi liquidi gas fluidi assumono la forma del contenitore Caratteristiche di un fluido LUIDO sostanza senza forma propria (assume la forma del
Meccanica dei luidi stati di aggregazione della materia: solidi liquidi gas fluidi assumono la forma del contenitore Caratteristiche di un fluido LUIDO sostanza senza forma propria (assume la forma del
Esempi di esercizi per la preparazione al primo compito di esonero
 Esempi di esercizi per la preparazione al primo compito di esonero 1. Quanto sangue è approssimativamente presente in un essere umano? Esprimere il risultato in ml. 2. La densità dell etanolo e pare a
Esempi di esercizi per la preparazione al primo compito di esonero 1. Quanto sangue è approssimativamente presente in un essere umano? Esprimere il risultato in ml. 2. La densità dell etanolo e pare a
Fluidi (FMLP: Cap. 11 Meccanica dei fluidi)
 In un fluido Fluidi (FMLP: Cap. 11 Meccanica dei fluidi) le molecole non sono vincolate a posizioni fisse a differenza di quello che avviene nei solidi ed in particolare nei cristalli Il numero di molecole
In un fluido Fluidi (FMLP: Cap. 11 Meccanica dei fluidi) le molecole non sono vincolate a posizioni fisse a differenza di quello che avviene nei solidi ed in particolare nei cristalli Il numero di molecole
Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera
 PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 1 MISURA DELLA PRESSIONE ATMOSFERICA:
PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 1 MISURA DELLA PRESSIONE ATMOSFERICA:
Protezione Civile - Regione Friuli Venezia Giulia. Protezione Civile - Regione Friuli Venezia Giulia
 1 Principi di idraulica Definizioni MECCANICA DEI FLUIDI È il ramo della fisica che studia le proprietà dei fluidi, cioè liquidi, vapori e gas. Idrostatica Studia i fluidi in quiete Idrodinamica Studia
1 Principi di idraulica Definizioni MECCANICA DEI FLUIDI È il ramo della fisica che studia le proprietà dei fluidi, cioè liquidi, vapori e gas. Idrostatica Studia i fluidi in quiete Idrodinamica Studia
Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a Emanuele Biolcati
 Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
IL MOTO DEI FLUIDI. con applicazione al sistema circolatorio
 IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
Meccanica dei fluidi. ! definizioni; ! statica dei fluidi (principio di Archimede); ! dinamica dei fluidi (teorema di Bernoulli).
 Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Meccanica dei FLUIDI
 Meccanica dei FLUIDI Densità Portata Pressione Moto stazionario: equazione di continuità Legge di Stevino Pressione idrostatica Spinta di Archimede Teorema di Bernoulli Viscosità Moto laminare: equazione
Meccanica dei FLUIDI Densità Portata Pressione Moto stazionario: equazione di continuità Legge di Stevino Pressione idrostatica Spinta di Archimede Teorema di Bernoulli Viscosità Moto laminare: equazione
Dinamica dei fluidi. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Dinamica dei fluidi Universita' di Udine 1 Caratteristiche di un fluido In generale: FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene) liquido volume limitato dalla superficie
Dinamica dei fluidi Universita' di Udine 1 Caratteristiche di un fluido In generale: FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene) liquido volume limitato dalla superficie
è completamente immerso in acqua. La sua
 In un tubo scorre in regime stazionario un liquido ideale con densità 1.00 10 3 kg/m 3 ; in un punto A il tubo ha raggio R A = 2.00 cm, la velocità di scorrimento è v A = 5.00 m/se la pressione è P A =
In un tubo scorre in regime stazionario un liquido ideale con densità 1.00 10 3 kg/m 3 ; in un punto A il tubo ha raggio R A = 2.00 cm, la velocità di scorrimento è v A = 5.00 m/se la pressione è P A =
Dall idrostatica alla idrodinamica. Fisica con Elementi di Matematica 1
 Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
Legge di Stevino ( d.c.)
 Legge di Stevino (1548-1620 d.c.) PA =F A /A= (Ah)g/A= hg conosciuta come legge di Stevino che quindi afferma che la pressione esercitata dal liquido su una superficie interna e' proporzionale alla densita'
Legge di Stevino (1548-1620 d.c.) PA =F A /A= (Ah)g/A= hg conosciuta come legge di Stevino che quindi afferma che la pressione esercitata dal liquido su una superficie interna e' proporzionale alla densita'
Meccanica dei fluidi. Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso
 Meccanica dei fluidi Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso Densità m Unità di misura (S.I.): kg/m d = 3 V Funzione scalare di ogni punto del
Meccanica dei fluidi Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso Densità m Unità di misura (S.I.): kg/m d = 3 V Funzione scalare di ogni punto del
Cap Fluidi
 N.Giglietto A.A. 2005/06-15.4 - Legge di Stevino, fluidi a riposo - 1 Cap 15.1-15.2 - Fluidi Un fluido è una sostanza in grado di scorrere: i fluidi prendono la forma dei contenitori nei quali sono confinati.
N.Giglietto A.A. 2005/06-15.4 - Legge di Stevino, fluidi a riposo - 1 Cap 15.1-15.2 - Fluidi Un fluido è una sostanza in grado di scorrere: i fluidi prendono la forma dei contenitori nei quali sono confinati.
Stati di aggregazione della materia. Luca Stanco - Fisica 2015/16 Corso di Laurea in Igiene Dentale - Lezione 5
 Fluidi 1 Stati di aggregazione della materia 2 Densità (II) n La densità assoluta è definita dal rapporto tra la massa M di una sostanza omogenea ed il suo volume V: d = M / V n Nel sistema internazionale
Fluidi 1 Stati di aggregazione della materia 2 Densità (II) n La densità assoluta è definita dal rapporto tra la massa M di una sostanza omogenea ed il suo volume V: d = M / V n Nel sistema internazionale
CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI
 CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI Meccanica dei fluidi La meccanica dei fluidi si occupa sia della statica (idrostatica) sia del movimento (idrodinamica) dei fluidi. Per fluidi si intendono
CORSO DI FISICA dispensa n.2 MECCANICA DEI FLUIDI Meccanica dei fluidi La meccanica dei fluidi si occupa sia della statica (idrostatica) sia del movimento (idrodinamica) dei fluidi. Per fluidi si intendono
PRESSIONE ATMOSFERICA
 PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
1 bar = 10 Pa = 10 barie PRESSIONE PRESSIONE. N 10 dyn dyn. m 10 cm cm. Solido. Liquido. Gassoso. (pascal) m. kg 1000.
 STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 2013
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
Prova scritta di Fisica Generale I Corso di studio in Astronomia 16 luglio 013 Problema 1 Un cubo di legno di densità ρ = 800 kg/m 3 e lato a = 50 cm è inizialmente in quiete, appoggiato su un piano orizzontale.
Solidi, liquidi e gas. 0 In natura le sostanze possono trovarsi in tre stati di aggregazione:
 Solidi, liquidi e gas 0 In natura le sostanze possono trovarsi in tre stati di aggregazione: Caratteristiche di un fluido FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene)
Solidi, liquidi e gas 0 In natura le sostanze possono trovarsi in tre stati di aggregazione: Caratteristiche di un fluido FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene)
IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO
 A - IDRAULICA IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO' SUBIRE RILEVANTI VARIAZIONI
A - IDRAULICA IDRAULICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO' SUBIRE RILEVANTI VARIAZIONI
Facoltà di Farmacia - Anno Accademico A 18 febbraio 2010 primo esonero
 Facoltà di Farmacia - Anno Accademico 2009-2010 A 18 febbraio 2010 primo esonero Corso di Laurea: Laurea Specialistica in FARMACIA Nome: Cognome: Matricola Aula: Canale: Docente: Riportare sul presente
Facoltà di Farmacia - Anno Accademico 2009-2010 A 18 febbraio 2010 primo esonero Corso di Laurea: Laurea Specialistica in FARMACIA Nome: Cognome: Matricola Aula: Canale: Docente: Riportare sul presente
Meccanica dei Fluidi - Fluidostatica -
 Meccanica dei Fluidi - Fluidostatica - STATI DI AGGREGAZIONE DELLA MATERIA Stato Solido: La sostanza ha volume e forma ben definiti. Stato Liquido: La sostanza ha volume ben definito, ma assume la forma
Meccanica dei Fluidi - Fluidostatica - STATI DI AGGREGAZIONE DELLA MATERIA Stato Solido: La sostanza ha volume e forma ben definiti. Stato Liquido: La sostanza ha volume ben definito, ma assume la forma
Unità didattica 4. Quarta unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 4 Fisica dei fluidi Stati della materia 2 Condizione di riposo di un liquido 3 La pressione idrostatica. 4 Principio di Pascal. 5 Esercizio 7 Variazione di pressione con la profondità..
Unità didattica 4 Fisica dei fluidi Stati della materia 2 Condizione di riposo di un liquido 3 La pressione idrostatica. 4 Principio di Pascal. 5 Esercizio 7 Variazione di pressione con la profondità..
Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore
 Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore Legge di Stevino La pressione in un liquido a densità costante cresce linearmente con la profondità Il principio di
Statica dei fluidi & Termodinamica: I principio, gas perfetti e trasformazioni, calore Legge di Stevino La pressione in un liquido a densità costante cresce linearmente con la profondità Il principio di
Prima verifica A. v.limite o di sedimentazione : v sed = 2 9 gr2 d gl d pl
 Prima verifica F1) Un corpo di massa 200 g si muove lungo l asse x sotto l azione di una forza, parallela all asse x, la cui intensità in funzione di x è data nel grafico B Per quali valori di x l accelerazione
Prima verifica F1) Un corpo di massa 200 g si muove lungo l asse x sotto l azione di una forza, parallela all asse x, la cui intensità in funzione di x è data nel grafico B Per quali valori di x l accelerazione
I D R O S T A T I C A
 I D R O S T A T I C A Caratteristiche stato liquido (descr.) FLUIDI Massa volumica (def. + formula) Volume massico (def. + formula) Peso volumico (def. + formula) Legame massa volumica - peso volumico
I D R O S T A T I C A Caratteristiche stato liquido (descr.) FLUIDI Massa volumica (def. + formula) Volume massico (def. + formula) Peso volumico (def. + formula) Legame massa volumica - peso volumico
F > mg Il cubo galleggia
 LA LEGGE DI ARCHIMEDE Un corpo immerso in un liquido riceve una spinta dal basso verso l'alto pari al peso del liquido spostato Cubo di legno di pioppo V = 1 dm³ mg = 5N (forza peso) Legge di Archimede:
LA LEGGE DI ARCHIMEDE Un corpo immerso in un liquido riceve una spinta dal basso verso l'alto pari al peso del liquido spostato Cubo di legno di pioppo V = 1 dm³ mg = 5N (forza peso) Legge di Archimede:
Applicando al pistone una forza esterna, si esercita una pressione p ext sul fluido immediatamente sottostante al pistone.
 IL PRINCIPIO DI PASCAL Consideriamo un fluido incomprimibile come in figura contenuto in un cilindro chiuso superiormente da un pistone. Applicando al pistone una forza esterna, si esercita una pressione
IL PRINCIPIO DI PASCAL Consideriamo un fluido incomprimibile come in figura contenuto in un cilindro chiuso superiormente da un pistone. Applicando al pistone una forza esterna, si esercita una pressione
ATTRITO VISCOSO NEI FLUIDI
 ATTRITO VISCOSO NEI FLUIDI DOWNLOAD Il pdf di questa lezione (0319a.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/scamb/ 19/03/2012 VISCOSITÀ La viscosità è un fenomeno che si manifesta in
ATTRITO VISCOSO NEI FLUIDI DOWNLOAD Il pdf di questa lezione (0319a.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/scamb/ 19/03/2012 VISCOSITÀ La viscosità è un fenomeno che si manifesta in
Solido. Liquido. Gassoso STATI DI AGGREGAZIONE DELLA MATERIA. Il corpo ha volume e forma ben definiti
 FLUIDI Stati aggregazione materia Pressione Portata Moto stazionario Equazione di continuità Applicazione al sistema circolatorio Moto laminare e turbolento Legge Pascal Legge Stevino Legge Bernulli Legge
FLUIDI Stati aggregazione materia Pressione Portata Moto stazionario Equazione di continuità Applicazione al sistema circolatorio Moto laminare e turbolento Legge Pascal Legge Stevino Legge Bernulli Legge
Modulo B Unità 3 Equilibrio dei fluidi Pagina 1. Solidi, liquidi, aeriformi
 Modulo B Unità 3 Equilibrio dei fluidi Pagina Solidi, liquidi, aeriformi I solidi hanno forma e volume propri, i liquidi hanno volume proprio e forma del recipiente che li contiene, gli aeriformi hanno
Modulo B Unità 3 Equilibrio dei fluidi Pagina Solidi, liquidi, aeriformi I solidi hanno forma e volume propri, i liquidi hanno volume proprio e forma del recipiente che li contiene, gli aeriformi hanno
Lezione 11. Fluido dinamica
 Lezione 11 Fluido dinamica Equazione di Bernoulli per un fluido ideale L equazione di Bernoulli esprime la legge di conservazione dell energia totale di un fluido ideale che si muove in un condotto: Le
Lezione 11 Fluido dinamica Equazione di Bernoulli per un fluido ideale L equazione di Bernoulli esprime la legge di conservazione dell energia totale di un fluido ideale che si muove in un condotto: Le
I fluidi. Alberto Barbisan - Meccanica ITIS FERMI
 I fluidi Esercizio Una stanza ha dimensioni: 3.5 m (larghezza) e 4. m (lunghezza) ed una altezza di.4 m. (a) Quanto pesa l aria nella stanza se la pressione e.0 atm? SOLUZIONE: mg ( ρv)g (. kg / 48 N m
I fluidi Esercizio Una stanza ha dimensioni: 3.5 m (larghezza) e 4. m (lunghezza) ed una altezza di.4 m. (a) Quanto pesa l aria nella stanza se la pressione e.0 atm? SOLUZIONE: mg ( ρv)g (. kg / 48 N m
MODULO 3. La pressione
 MODULO 3 La pressione La pressione L obiettivo del modulo è comprendere gli effetti delle forze che dipendono dalla superficie su cui esse vengono applicate. Il grado di concentrazione di una forza sulla
MODULO 3 La pressione La pressione L obiettivo del modulo è comprendere gli effetti delle forze che dipendono dalla superficie su cui esse vengono applicate. Il grado di concentrazione di una forza sulla
EFFETTI FISIOLOGICI DELLA PRESSIONE IDROSTATICA
 LEZIONE n.5 ENERGIA NEI FLUIDI TEOREMA DI BERNOULLI E APPLICAZIONI PRESSIONE IDROSTATICA EFFETTI FISIOLOGICI DELLA PRESSIONE IDROSTATICA TEOREMA DI BERNOULLI IL TEOREMA DI BERNOULLI, ESPRIME LA LEGGE DI
LEZIONE n.5 ENERGIA NEI FLUIDI TEOREMA DI BERNOULLI E APPLICAZIONI PRESSIONE IDROSTATICA EFFETTI FISIOLOGICI DELLA PRESSIONE IDROSTATICA TEOREMA DI BERNOULLI IL TEOREMA DI BERNOULLI, ESPRIME LA LEGGE DI
Dall idrostatica alla idrodinamica. Fisica con Elementi di Matematica
 Dall idrostatica alla idrodinamica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo il valore della pressione atmosferica
Dall idrostatica alla idrodinamica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo il valore della pressione atmosferica
Densità e volume specifico
 Densità e volume specifico Si definisce densità di un corpo,, il rapporto tra la sua massa, m, e il suo volume, V; essa quantifica la massa dell unità di volume. m = = V [ kg] 3 [ m ] E utile considerare
Densità e volume specifico Si definisce densità di un corpo,, il rapporto tra la sua massa, m, e il suo volume, V; essa quantifica la massa dell unità di volume. m = = V [ kg] 3 [ m ] E utile considerare
PER ESERCITARSI Parte 2. Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica
 PER ESERCITARSI Parte 2 Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica ESERCIZIO n.1 Due forze uguali ed opposte sono applicate ad un oggetto lungo rette di azione tra loro
PER ESERCITARSI Parte 2 Esercizi su Corpo rigido, variabili angolari, momenti, fluidi, termodinamica ESERCIZIO n.1 Due forze uguali ed opposte sono applicate ad un oggetto lungo rette di azione tra loro
STATICA DEI FLUIDI G. ROBERTI
 STATICA DEI FLUIDI G. ROBERTI FLUIDI G. Roberti Definizione:sostanze che assumono la forma dei recipienti che le contengono oppure Definizione: sostanze che si deformano senza che si compia lavoro ΔV /
STATICA DEI FLUIDI G. ROBERTI FLUIDI G. Roberti Definizione:sostanze che assumono la forma dei recipienti che le contengono oppure Definizione: sostanze che si deformano senza che si compia lavoro ΔV /
Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI. Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013
 Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013 L'idraulica è la scienza che studia l'utilizzazione dei
Sussidi didattici per il corso di PROGETTAZIONE, COSTRUZIONI E IMPIANTI Prof. Ing. Francesco Zanghì ELEMENTI DI IDRAULICA AGGIORNAMENTO 26/11/2013 L'idraulica è la scienza che studia l'utilizzazione dei
CdL Professioni Sanitarie A.A. 2012/2013. Unità 4 (5 ore)
 L. Zampieri Fisica per CdL Professioni Sanitarie A.A. 12/13 CdL Professioni Sanitarie A.A. 2012/2013 Statica dei fluidi Fluidi e solidi Unità 4 (5 ore) Densità e pressione di un fluido Proprietà dei fluidi:
L. Zampieri Fisica per CdL Professioni Sanitarie A.A. 12/13 CdL Professioni Sanitarie A.A. 2012/2013 Statica dei fluidi Fluidi e solidi Unità 4 (5 ore) Densità e pressione di un fluido Proprietà dei fluidi:
Meccanica dei fluidi
 Meccanica dei fluidi Si definiscono fluidi I sistemi che si deformano continuamente sotto l'azione di una forza tangenziale, tendente a far scorrere uno strato del sistema sull'altro, indipendentemente
Meccanica dei fluidi Si definiscono fluidi I sistemi che si deformano continuamente sotto l'azione di una forza tangenziale, tendente a far scorrere uno strato del sistema sull'altro, indipendentemente
I Prova scritta di Fisica ( Scienze Biologiche ) Marzo 26, 2003
 I Prova scritta di Fisica ( Scienze Biologiche ) Marzo 26, 2003 Nome e Cognome: Gruppo: Problema 1 ( 1 Punto ) Un oggetto di massa m=10kg, partendo da fermo, si muove in linea retta sotto l azione di una
I Prova scritta di Fisica ( Scienze Biologiche ) Marzo 26, 2003 Nome e Cognome: Gruppo: Problema 1 ( 1 Punto ) Un oggetto di massa m=10kg, partendo da fermo, si muove in linea retta sotto l azione di una
PIANO DI STUDIO D ISTITUTO
 PIANO DI STUDIO D ISTITUTO Materia: FISICA Casse 2 1 Quadrimestre Modulo 1 - RIPASSO INIZIALE Rappresentare graficamente nel piano cartesiano i risultati di un esperimento. Distinguere fra massa e peso
PIANO DI STUDIO D ISTITUTO Materia: FISICA Casse 2 1 Quadrimestre Modulo 1 - RIPASSO INIZIALE Rappresentare graficamente nel piano cartesiano i risultati di un esperimento. Distinguere fra massa e peso
Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido.
 Fluidi Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido. In base a tale definizione, sia i gas che i liquidi
Fluidi Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido. In base a tale definizione, sia i gas che i liquidi
Applicazione delle leggi dell'idrodinamica alla circolazione del sangue. Idrodinamica a Emodinamica. complicazioni
 Lezione 1 IDROTATICA-UNITA' DI MIURA È grazie a sistemi fluidi che gli organismi riescono a trasportare, scambiare e assimilare ossigeno e sostanze nutritive. La conoscenza della meccanica dei fluidi è
Lezione 1 IDROTATICA-UNITA' DI MIURA È grazie a sistemi fluidi che gli organismi riescono a trasportare, scambiare e assimilare ossigeno e sostanze nutritive. La conoscenza della meccanica dei fluidi è
Problemi di Fisica per l ammissione alla Scuola Galileiana Problema 1
 Problemi di Fisica per l ammissione alla Scuola Galileiana 2015-2016 Problema 1 Un secchio cilindrico di raggio R contiene un fluido di densità uniforme ρ, entrambi ruotanti intorno al loro comune asse
Problemi di Fisica per l ammissione alla Scuola Galileiana 2015-2016 Problema 1 Un secchio cilindrico di raggio R contiene un fluido di densità uniforme ρ, entrambi ruotanti intorno al loro comune asse
elio giroletti effetti del sangue reale MECCANICA FLUIDI effetti del sangue reale MECCANICA FLUIDI
 UNIVERSITÀ DEGLI STUDI DI PAVIA dip. Fisica nucleare e teorica via bassi 6, 27100 pavia, italy - tel. 038298.7905 [email protected] - www.unipv.it/webgiro webgiro 1 elio giroletti effetti del sangue reale
UNIVERSITÀ DEGLI STUDI DI PAVIA dip. Fisica nucleare e teorica via bassi 6, 27100 pavia, italy - tel. 038298.7905 [email protected] - www.unipv.it/webgiro webgiro 1 elio giroletti effetti del sangue reale
a) Calcolare il modulo di F.
 1. (1-2-2011, 3-10-2011, 23-7-2013) Un getto d acqua che cade da un rubinetto si restringe verso il basso. Se l area di una sezione del flusso di acqua è A 1 =1.2 cm 2 e diventa A 2 = 0.35 cm 2 45 mm più
1. (1-2-2011, 3-10-2011, 23-7-2013) Un getto d acqua che cade da un rubinetto si restringe verso il basso. Se l area di una sezione del flusso di acqua è A 1 =1.2 cm 2 e diventa A 2 = 0.35 cm 2 45 mm più
( pi + σ ) nds = 0 (3)
 OLUZIONE IMULAZIONE EAME 0 DICEMBRE 05 I Parte Domanda (5 punti) Un fluido incomprimibile viene pompato in tubo orizzontale di lunghezza L e diametro D. La differenza di pressione agli estremi del tubo
OLUZIONE IMULAZIONE EAME 0 DICEMBRE 05 I Parte Domanda (5 punti) Un fluido incomprimibile viene pompato in tubo orizzontale di lunghezza L e diametro D. La differenza di pressione agli estremi del tubo
Esercizio 1 L/3. mg CM Mg. La sommatoria delle forze e dei momenti deve essere uguale a 0 M A. ω è il verso di rotazione con cui studio il sistema
 Esercizio 1 Una trave omogenea di lunghezza L e di massa M è appoggiata in posizione orizzontale su due fulcri lisci posti alle sue estremità. Una massa m è appoggiata sulla trave ad una distanza L/3 da
Esercizio 1 Una trave omogenea di lunghezza L e di massa M è appoggiata in posizione orizzontale su due fulcri lisci posti alle sue estremità. Una massa m è appoggiata sulla trave ad una distanza L/3 da
STATI DI AGGREGAZIONE DELLA MATERIA E PROPRIETÀ DEI FLUIDI
 STATI DI AGGREGAZIONE DELLA MATERIA E PROPRIETÀ DEI FLUIDI 14/01/2014 2 Una porzione di materia costituita da una sostanza la cui composizione chimica non varia da un punto all altro si dice costituita
STATI DI AGGREGAZIONE DELLA MATERIA E PROPRIETÀ DEI FLUIDI 14/01/2014 2 Una porzione di materia costituita da una sostanza la cui composizione chimica non varia da un punto all altro si dice costituita
Il Corso di Fisica per Scienze Biologiche
 Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 708 Ø E-mail: [email protected] Ø Web: http://www.fisica.unipg.it/~attilio.santocchia
Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 708 Ø E-mail: [email protected] Ø Web: http://www.fisica.unipg.it/~attilio.santocchia
IDRODINAMICA. Si chiama portata, il volume di fluido che defluisce attraverso una sezione nell unità di tempo; si indica con il simbolo Q [L 3 /T].
![IDRODINAMICA. Si chiama portata, il volume di fluido che defluisce attraverso una sezione nell unità di tempo; si indica con il simbolo Q [L 3 /T]. IDRODINAMICA. Si chiama portata, il volume di fluido che defluisce attraverso una sezione nell unità di tempo; si indica con il simbolo Q [L 3 /T].](/thumbs/55/36004854.jpg) IDRODINAMICA Portata e velocità media Si chiama portata, il volume di fluido che defluisce attraverso una sezione nell unità di tempo; si indica con il simbolo Q [L 3 /T]. In una corrente d acqua la velocità
IDRODINAMICA Portata e velocità media Si chiama portata, il volume di fluido che defluisce attraverso una sezione nell unità di tempo; si indica con il simbolo Q [L 3 /T]. In una corrente d acqua la velocità
INTRODUZIONE ALLA TERMODINAMICA. Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta
 INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
DINAMICA DEI FLUIDI G. ROBERTI
 DINAMICA DEI FLUIDI G. ROBERTI Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione)
DINAMICA DEI FLUIDI G. ROBERTI Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione)
1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5.
 Unità n 6 Le leggi dei gas 1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5. La legge di Gay-Lussac o legge
Unità n 6 Le leggi dei gas 1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5. La legge di Gay-Lussac o legge
Sesta esercitazione di Fisica I Fluidodinamica 1 PROBLEMI RISOLTI
 Sesta esercitazione di Fisica I Fluidodinamica 1 PROBLEMI RISOLTI 1. Un secchio colmo d'acqua pesa complessivamente 2 kg. Se è pesato mentre è sotto un rubinetto con una portata di 0.5 litri/s ed è raggiunto
Sesta esercitazione di Fisica I Fluidodinamica 1 PROBLEMI RISOLTI 1. Un secchio colmo d'acqua pesa complessivamente 2 kg. Se è pesato mentre è sotto un rubinetto con una portata di 0.5 litri/s ed è raggiunto
STATICA DEI FLUIDI (Giuseppe Frangiamore con la collaborazione di Michele Sorce)
 STATICA DEI FLUIDI (Giuseppe Frangiamore con la collaborazione di Michele Sorce) Definizione Di Pressione In questo capitolo si analizzeranno le caratteristiche meccaniche dei fluidi in condizioni di equilibrio
STATICA DEI FLUIDI (Giuseppe Frangiamore con la collaborazione di Michele Sorce) Definizione Di Pressione In questo capitolo si analizzeranno le caratteristiche meccaniche dei fluidi in condizioni di equilibrio
La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da:
 Statica Distribuzione delle pressioni La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da: z+p/γ= cost LEE DI STEVIN Il valore della costante è
Statica Distribuzione delle pressioni La distribuzione delle pressioni all interno di un fluido in quiete, pesante e incomprimibile, è governata da: z+p/γ= cost LEE DI STEVIN Il valore della costante è
3. Si dica per quali valori di p e q la seguente legge e` dimensionalmente corretta:
 Esercizi su analisi dimensionale: 1. La legge oraria del moto di una particella e` x(t)=a t 2 +b t 4, dove x e` la posizione della particella e t il tempo. Si determini le dimensioni delle costanti a e
Esercizi su analisi dimensionale: 1. La legge oraria del moto di una particella e` x(t)=a t 2 +b t 4, dove x e` la posizione della particella e t il tempo. Si determini le dimensioni delle costanti a e
Compito di Fisica Generale (Meccanica) 25/01/2011
 Compito di Fisica Generale (Meccanica) 25/01/2011 1) Un punto materiale di massa m è vincolato a muoversi su di una guida orizzontale. Il punto è attaccato ad una molla di costante elastica k. La guida
Compito di Fisica Generale (Meccanica) 25/01/2011 1) Un punto materiale di massa m è vincolato a muoversi su di una guida orizzontale. Il punto è attaccato ad una molla di costante elastica k. La guida
Fisica applicata Lezione 7
 Fisica applicata Lezione 7 Maurizio Tomasi [email protected] Dipartimento di Fisica Università degli studi di Milano 14 Novembre 2016 Parte I Fluidostatica (conclusione) Il tubo di Torricelli Un
Fisica applicata Lezione 7 Maurizio Tomasi [email protected] Dipartimento di Fisica Università degli studi di Milano 14 Novembre 2016 Parte I Fluidostatica (conclusione) Il tubo di Torricelli Un
Se la curvatura è minore, la tensione totale deve essere più grande per mantenere la stessa componente della tensione verso il basso
 Le Pressioni in emodinamica sono: Pressione di propulsione Pa Pv, responsabile del flusso Pressione transmurale (P tm ). Poiché i vasi sono distensibili la P tm può influenzare il raggio del vaso e per
Le Pressioni in emodinamica sono: Pressione di propulsione Pa Pv, responsabile del flusso Pressione transmurale (P tm ). Poiché i vasi sono distensibili la P tm può influenzare il raggio del vaso e per
Lavoro. Esempio. Definizione di lavoro. Lavoro motore e lavoro resistente. Lavoro compiuto da più forze ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE
 Lavoro ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE Cos è il lavoro? Il lavoro è la grandezza fisica che mette in relazione spostamento e forza. Il lavoro dipende sia dalla direzione della forza sia dalla
Lavoro ENERGIA, LAVORO E PRINCIPI DI CONSERVAZIONE Cos è il lavoro? Il lavoro è la grandezza fisica che mette in relazione spostamento e forza. Il lavoro dipende sia dalla direzione della forza sia dalla
Corso di Componenti e Impianti Termotecnici RETI DI DISTRIBUZIONE PERDITE DI CARICO CONTINUE
 RETI DI DISTRIBUZIONE PERDITE DI CARICO CONTINUE 1 PERDITE DI CARICO CONTINUE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
RETI DI DISTRIBUZIONE PERDITE DI CARICO CONTINUE 1 PERDITE DI CARICO CONTINUE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 2012
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Secondo Compitino di FISICA 15 giugno 01 1) FLUIDI: Un blocchetto di legno (densità 0,75 g/ cm 3 ) di dimensioni esterne (10x0x5)cm 3 è trattenuto mediante una fune
FISICA E LABORATORIO INDIRIZZO C.A.T. CLASSE PRIMA. OBIETTIVI U. D. n 1.2: La rappresentazione di dati e fenomeni
 FISICA E LABORATORIO INDIRIZZO C.A.T. CLASSE PRIMA Le competenze di base a conclusione dell obbligo di istruzione sono le seguenti: Osservare, descrivere ed analizzare fenomeni appartenenti alla realtà
FISICA E LABORATORIO INDIRIZZO C.A.T. CLASSE PRIMA Le competenze di base a conclusione dell obbligo di istruzione sono le seguenti: Osservare, descrivere ed analizzare fenomeni appartenenti alla realtà
Tratti (capillari) che consentono la fuoriuscita e l ingresso di liquido
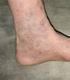 Le leggi dell idrostatica e dell idrodinamica spiegano i principi fisici che sono alla base del funzionamento del sistema cardio circolatorio, ma le caratteristiche particolari di questo sistema impediscono
Le leggi dell idrostatica e dell idrodinamica spiegano i principi fisici che sono alla base del funzionamento del sistema cardio circolatorio, ma le caratteristiche particolari di questo sistema impediscono
approfondimento Lavoro ed energia
 approfondimento Lavoro ed energia Lavoro compiuto da una forza costante W = F. d = F d cosθ dimensioni [W] = [ML T - ] Unità di misura del lavoro N m (Joule) in MKS dine cm (erg) in cgs N.B. Quando la
approfondimento Lavoro ed energia Lavoro compiuto da una forza costante W = F. d = F d cosθ dimensioni [W] = [ML T - ] Unità di misura del lavoro N m (Joule) in MKS dine cm (erg) in cgs N.B. Quando la
PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI)
 1 PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI) Qui di seguito viene riportata la risoluzione dei problemi presentati nel file Unità omonimo (enunciati). Si raccomanda di prestare molta attenzione ai ragionamenti
1 PROBLEMI E QUESITI DI TERMOLOGIA (SOLUZIONI) Qui di seguito viene riportata la risoluzione dei problemi presentati nel file Unità omonimo (enunciati). Si raccomanda di prestare molta attenzione ai ragionamenti
FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013
 FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013 1) Un corpo di massa m = 500 g scende lungo un piano scabro, inclinato di un angolo θ = 45. Prosegue poi lungo un tratto orizzontale
FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013 APPELLO 18 Luglio 2013 1) Un corpo di massa m = 500 g scende lungo un piano scabro, inclinato di un angolo θ = 45. Prosegue poi lungo un tratto orizzontale
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni (Parte I):
 Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
GALLERIA DEL VENTO SCOPI DELL ESPERIENZA
 GALLERIA DEL VENTO SCOPI DELL ESPERIENZA Con la galleria del vento ci si propone: la verifica delle leggi di continuità (o di Leonardo) e di Bernoulli la misura della resistenza aerodinamica di diversi
GALLERIA DEL VENTO SCOPI DELL ESPERIENZA Con la galleria del vento ci si propone: la verifica delle leggi di continuità (o di Leonardo) e di Bernoulli la misura della resistenza aerodinamica di diversi
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
GLI STATI DI AGGREGAZIONE DELLA MATERIA
 GLI STATI DI AGGREGAZIONE DELLA MATERIA AERIFORME (gas o vapore) Fluido: : non ha forma propria. Occupa tutto il volume del recipiente che lo contiene.. Le molecole sono legate da forze molto deboli FLUIDI
GLI STATI DI AGGREGAZIONE DELLA MATERIA AERIFORME (gas o vapore) Fluido: : non ha forma propria. Occupa tutto il volume del recipiente che lo contiene.. Le molecole sono legate da forze molto deboli FLUIDI
EQUILIBRIO DEI FLUIDI
 EQUILIBRIO DEI FLUIDI Pressione atmosferica, spinta di Archimede 1 Pressione atmosferica Bicchiere e cartoncino Cannuccia Uova Ventosa Emisferi di Magdeburgo 1 Emisferi di Magdeburgo 2 Unità D-Lez.2 Par
EQUILIBRIO DEI FLUIDI Pressione atmosferica, spinta di Archimede 1 Pressione atmosferica Bicchiere e cartoncino Cannuccia Uova Ventosa Emisferi di Magdeburgo 1 Emisferi di Magdeburgo 2 Unità D-Lez.2 Par
Problemi di Fisica per l ammissione alla Scuola Galileana Problema 1
 Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
Attrito statico e attrito dinamico
 Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
Forza di attrito La presenza delle forze di attrito fa parte dell esperienza quotidiana. Se si tenta di far scorrere un corpo su una superficie, si sviluppa una resistenza allo scorrimento detta forza
Proprieta meccaniche dei fluidi
 Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Corso di Fisica. Laurea in Scienze Infermieristiche Sede di Cassino
 Corso di Fisica Laurea in Scienze Infermieristiche Sede di Cassino Docente: Deborah Lacitignola Dipartimento di Scienze Motorie e della Salute Università di Cassino Email: [email protected] LEZIONE
Corso di Fisica Laurea in Scienze Infermieristiche Sede di Cassino Docente: Deborah Lacitignola Dipartimento di Scienze Motorie e della Salute Università di Cassino Email: [email protected] LEZIONE
ANNO SCOLASTICO CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA
 ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA LE FORZE: Ripasso degli argomenti della classe I: Grandezze scalari e vettoriali, concetto di forza, peso e
ANNO SCOLASTICO 2014-2015 CLASSE II E DISCIPLINA: FISICA DOCENTE: Romio Silvana A. PROGRAMMA LE FORZE: Ripasso degli argomenti della classe I: Grandezze scalari e vettoriali, concetto di forza, peso e
Test Esame di Fisica
 Test Esame di Fisica NOTA: per le domande a risposta multipla ogni risposta corretta viene valutata con un punto mentre una errata con -0.5 punti. 1) Una sola delle seguenti uguaglianze non e corretta?
Test Esame di Fisica NOTA: per le domande a risposta multipla ogni risposta corretta viene valutata con un punto mentre una errata con -0.5 punti. 1) Una sola delle seguenti uguaglianze non e corretta?
sfera omogenea di massa M e raggio R il momento d inerzia rispetto ad un asse passante per il suo centro di massa vale I = 2 5 MR2 ).
 ESERCIZI 1) Un razzo viene lanciato verticalmente dalla Terra e sale con accelerazione a = 20 m/s 2. Dopo 100 s il combustibile si esaurisce e il razzo continua a salire fino ad un altezza massima h. a)
ESERCIZI 1) Un razzo viene lanciato verticalmente dalla Terra e sale con accelerazione a = 20 m/s 2. Dopo 100 s il combustibile si esaurisce e il razzo continua a salire fino ad un altezza massima h. a)
FISICA-TECNICA Statica e dinamica dei fluidi
 FISICA-TECNICA Statica e dinamica dei fluidi Katia Gallucci I gas, insieme ai liquidi sono sostanze capaci di scorrere o di fluire e vengono compresi nella categoria detta dei FLUIDI. Per esempio, il gas
FISICA-TECNICA Statica e dinamica dei fluidi Katia Gallucci I gas, insieme ai liquidi sono sostanze capaci di scorrere o di fluire e vengono compresi nella categoria detta dei FLUIDI. Per esempio, il gas
Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido.
 Fluidi Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido. In base a tale definizione, sia i gas che i liquidi
Fluidi Una sostanza che non ha delle dimensioni definite, ma che prende la forma del contenitore entro la quale e confinata, prende il nome di fluido. In base a tale definizione, sia i gas che i liquidi
LEZIONE 17 ESERCIZI-FLUIDI
 LEZIONE 17 ESERCIZI-FLUIDI Qual è, in at, la pressione a 20 di profondità? (densità dell acqua = 1,0 gr/c ) P = 2 at. Sapendo che la densità del ghiaccio è 0,92 g/c e quella dell acqua di are 1,0 g/c,
LEZIONE 17 ESERCIZI-FLUIDI Qual è, in at, la pressione a 20 di profondità? (densità dell acqua = 1,0 gr/c ) P = 2 at. Sapendo che la densità del ghiaccio è 0,92 g/c e quella dell acqua di are 1,0 g/c,
