CLASSE 3 A APPUNTI DAL CORSO DI COSTRUZIONI LA DEFORMAZIONE DEI MATERIALI SOTTO CARICO
|
|
|
- Lazzaro Palma
- 6 anni fa
- Visualizzazioni
Transcript
1 the design of he Forth Bridge (Scotland) by Sir John Fowler and Sir Benjamin Baker Nessun effetto è in natura sanza ragione; intendi la ragione e non ti bisogna sperienzia. Leonardo da Vinci CLASSE 3 A APPUNTI DAL CORSO DI COSTRUZIONI LA DEFORMAZIONE DEI MATERIALI SOTTO CARICO L EQUILIBRIO TRA LE SOLLECITAZIONI ESTERNE E LE TENSIONI INTERNE DELLE SEZIONI RESISTENTI 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 1
2 Premessa Nel dimensionamento di un sistema strutturale resistente, la definizione della soluzione equilibrata del modello rigido (in pratica la soluzione delle reazioni vincolari) costituisce il primo passo della soluzione strutturale. I diagrammi delle sollecitazioni rappresentano la misura delle azioni che tendono a spostare la generica sezione dell elemento dalla configurazione iniziale (scarica) definita dagli assi locali. Lo spostamento può prevedere una traiettoria di traslazione lungo l asse locale x (sforzo normale assiale) oppure lungo l asse z (sforzo di taglio); una rotazione intorno all asse locale y o Z (momento flettente), una rotazione intorno all asse locale x (sforzo di torsione), oppure mista (sforzo di pressoflessione, flessione deviata, flessione associata al taglio). L esperienza mostra come la rottura interna sia causata dal superamento del limite di deformabilità del materiale impiegato nell elemento strutturale. Definite tutte le proprietà elastiche di un materiale, il contenimento delle deformazioni entro un limite definito si realizza attraverso la scelta della appropriata inerzia (in pratica la forma) della sezione resistente. Il modello elastico dei materiali I materiali impiegati nel campo delle costruzioni vengono studiati dal punto di vista del comportamento sotto carico attraverso delle prove di laboratorio (tipo UNI-EN) con provini e procedure standardizzate. La prova principale per valutare la deformabilità di un materiale sia sotto l aspetto qualitativo sia per quello quantitativo è la prova di trazione o compressione monoassiale. Per alcuni materiali (ad esempio il legno) la descrizione del comportamento elastico deve essere completata con prove di deformabilità a flessione. Il motivo di ciò risiede nel fatto che il legno presenta delle elasticità direzionali legate all andamento delle fibre rispetto alla direzione delle sollecitazioni. Prendiamo in esame un elemento rettilineo di un determinato materiale, lunghezza iniziale l 0, sezione A. Se applichiamo una forza crescente con incrementi lenti vediamo che per ogni misura di N (N 1, N 2, N 3, N 4,..) otteniamo un corrispondente valore dell allungamento L ( L1, L2, L3, L4, ). Se poniamo su di un sistema di assi cartesiani: 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 2
3 ε = L / l 0 in ascissa; σ = N / A in ordinata Otteniamo che il legame tra la forza e l allungamento viene descritto attraverso i termini σ (tensione normale) e ε ( deformazione unitaria) indipendenti dai valori di l 0 e A e per questo rappresentativi del comportamento del materiale e non dell elemento. La relazione tra σ e ε prende il nome di legame costitutivo. Possiamo ripetere la prova di carico invertendo la direzione della azione sottoponendo cosi l asta ad una sollecitazione di compressione. Se otteniamo un diagramma simmetrico questo vuol dire che il materiale si comporta indifferentemente a compressione o trazione. In questo caso si dice che il materiale ha un comportamento OMOGENEO. Se i grafici i sono diversi il comportamento del materiale può dirsi NON OMOGENEO. 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 3
4 Se consideriamo un diagramma N, L possiamo individuare in ogni prodotto Forza x Spostamento un area rettangolare rappresentativa di un lavoro meccanico compiuto dalla Forza applicata alla sezione. La superficie sottesa dal diagramma corrisponde al lavoro complessivo compiuto dalla forza variabile da zero a Nmax L TOT = i n N i x Li Per il principio di conservazione dell energia meccanica tale lavoro deve trovare compenso in una uguale energia immagazzinata dall asta. Alle stesse conclusioni si arriva utilizzando il diagramma tra σ, ε. Materiali dal comportamento perfettamente elastico Se carichiamo un asta con un azione variabile da zero ad N max otterremo in corrispondenza del valore massimo una deformazione massima L(MAX) Lo sforzo nel materiale (tensione normale) varierà anch essa da zero ad un valore σ MAX e cosi può dirsi della deformazione unitaria ε MAX. Se facciamo decrescere l azione N dal valore max a zero avremo un diagramma di ritorno in cui l energia precedentemente immagazzinata viene spesa dal sistema per riportare l asta nella configurazione iniziale indeformata. Se i diagrammi di carico e scarico risultano coincidenti allora si dice che il materiale ha un comportamento perfettamente elastico. In un materiale avente comportamento elastico lineare (cioè dove la curvatura del diagramma può approssimarsi ad una retta) le tensioni normali σ e le deformazioni unitarie ε sono direttamente proporzionali. Indicando con E la costante di proporzionalità si ottiene l equazione della retta rappresentata nel piano cartesiano (n.b. è uno spazio affine) : σ = ε x E (LEGGE DI HOOKE) 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 4
5 La costante E viene detta costante elastica di un dato materiale o più precisamente modulo elastico longitudinale e rappresenta un valore tipico per ogni tipo di materiale. Dato che la deformazione unitaria è un numero puro la unità di misura del modulo elastico è la stessa della tensione normale: N/mmq N.B. nei materiali perfettamente elastici è possibile applicare il principio di sovrapposizione degli effetti che consente di risolvere l equilibrio elastico della sezione nelle situazioni di sollecitazioni composte (come vedremo in seguito) Materiali dal comportamento perfettamente plastico Un materiale presenta un comportamento perfettamente plastico se la deformazione indotta dalla azione N permane totalmente al cessare di quest ultima. Materiali dal comportamento elasto-plastico I materiali dal comportamento elasto-plastico presentano un diagramma mistilineo in cui una prima parte di tipo elastico lineare è seguita da un tratto orizzontale raggiunto il quale la struttura al cessare delle azioni presenta una deformazione residua. L entità del tratto orizzontale del diagramma definisce una importante proprietà dei materiali da costruzione che prende il nome di DUTTILITA. La duttilità è preziosa perché costituisce una riserva di sicurezza nei riguardi dell evento della rottura dell elemento strutturale, che, in questo caso si verifica dopo evidenti segnali premonitori. 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 5
6 Nelle zone sismiche la duttilità delle sezioni resistenti costituisce una proprietà decisiva ai fini della resistenza strutturale poiché consente una maggiore capacità dissipativa dell energia meccanica prodotta dall evento sismico. STATI DI SOLLECITAZIONE NORMALE (perpendicolari alla sezione) Come descritto in precedenza ogni spostamento della sezione (ε) dovuto ad una traiettoria lineare o composta produce per effetto della legge di Hooke uno stato di sollecitazione σ che la sezione dovrà, con la propria inerzia, contenere, al fine di evitare il raggiungimento della deformazione limite di rottura. La rappresentazione di un moncone di trave realizzata con un materiale perfettamente elastico è la seguente: Gli assi locali x,y,z (assi principali) hanno origine nel baricentro della sezione della trave. per semplicità possiamo disporre l asse locale x in verticale (come se si trattasse di un pilastro). Aggiungiamo al sistema una risultante delle caratteristiche di sollecitazione N qualsiasi in modo da produrre una configurazione deformata. CASO GENERALE 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 6
7 Essendo il materiale di cui è composta la trave perfettamente elastico è possibile applicare il principio di sovrapposizione degli effetti (P.S.E.). Lo stato di sollecitazione indotto dalla azione N eccentrica è equivalente a quello prodotto da una forza N centrata a cui si sommano gli effetti prodotti da due momenti Mz e My prodotti rispettivamente dalle eccentricità y c e z c.. Per l equilibrio della sezione il sistema deve produrre una risposta per ognuna delle tre azioni elementari N produce una traslazione lungo l asse x-x My = N*Zc produce una rotazione intorno all asse y-y Mz = N*Yc produce una rotazione intorno all asse z-z La sezione per equilibrare le azioni N,Mz,My deve produrre delle forze e dei momenti uguali e contrari. Considerando un elementino i-esimo da di dimensione 1mm x 1mm, possiamo definire per questa areola un accorciamento (o allungamento unitario) ε i. Applicando la legge di Hooke, per ogni deformazione unitaria è associabile localmente una tensione normale: σ i = ε i x E Il prodotto tra σ i e una superficie da produce una forza i-esima del tipo,, per cui possiamo determinare la risposta della sezione, in termini di N, come la somma del contributo di tutte le areole di 1mm 2 La condizione di equilibrio alla traslazione verticale fornisce la seguente espressione:. Per quanto riguarda l equilibrio alle due rotazioni, ogni areola di 1mm 2 produce, rispetto all asse di riferimento un momento che è il risultato di prodotti del tipo: ; 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 7
8 La condizione di equilibrio rispetto alle due rotazioni è data dalle seguenti espressioni: Le incognite σ i del problema sono infinite dal momento che sono legate alle deformazioni unitarie ε sono diverse da una areola da ad un'altra. Se ipotizziamo la sezione infinitamente rigida nel proprio piano*. Potendo applicare il P.S.E. si può esprimere una generica deformazione unitaria dell elemento da i-esimo mediante la sommatoria di contributi elementari delle deformazioni prodotte da ogni azione singolarmente. Attraverso la legge di Hooke possiamo passare dalle deformazioni unitarie alle tensioni: 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 8
9 *N.B. ciò corrisponde nel ritenere valida l ipotesi di Bernoulli-Navier per cui le sezioni trasversali rette di una trave, piane prima della deformazione, rimangono tali anche all atto della deformazione, in questo modo le deformazioni in caso di traslazione rigida sono tutte uguali per gli elementini da. Nel caso di rotazione rigida la relazione che lega l entità delle deformazioni unitarie dalla distanza dell elementino da dall asse neutro è di tipo lineare Sostituendo ad ogni deformazione unitaria il proprio valore si ottiene: Possiamo sostituire il valore della σ i alle equazioni di equilibrio precedenti ottenendo: I termini tra parentesi hanno il seguente significato: Facendo le seguenti considerazioni le espressioni si semplificano: - Il momento statico di una sezione, calcolato rispetto ad un asse baricentrico risulta nullo - Il momento d inerzia misto (centrifugo) calcolato rispetto a due assi principali d inerzia (z,y) è nullo 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 9
10 Le equazioni di equilibrio diventano: : 0 0 : Quindi possiamo calcolare il valore della tensione normale in una generica areola da Sostituiamo: Che consente di calcolare la tensione normale in ogni punto della sezione. L espressione: prende il nome di formula trinomia di Navier. Il segno ± è legato alla posizione relativa delle coordinate y i e z i rispetto ad un asse detto asse neutro che rappresenta il luogo geometrico di tutti i punti della sezione con ε nulla e come tale rappresenta il riferimento rispetto al quale si misurano e si assegnano i segni alle coordinate y i e z i. Per determinare la posizione dell asse neutro basta porre la condizione: 0 Sostituendo le espressioni di, α, β e ponendo M y = N*z c e M z = N*y c Moltiplichiamo tutto x E Dividiamo tutto x N Le intersezioni della retta con gli assi di riferimento (principali) sono date da: sull asse z (y=0) mentre sull asse y (z=0) la retta che unisce i due punti è l asse neutro della sezione. L espressione che abbiamo visto rappresenta il caso generale, nei casi particolari l espressione si semplifica. 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 10
11 SFORZO NORMALE CENTRATO CASI PARTICOLARI In questa condizione la sezione è soggetta ad una sollecitazione semplice di carico normale centrato In questo caso l espressione generale che definisce il valore dello sforzo sull i-esimo clementino: Essendo: α = 0 ; β = 0 ; Diventa semplicemente: σ = E x ε = N/A essendo ε identiche in ogni areola da per l ipotesi di complanarità della sezione E possibile graficizzare l andamento delle deformazioni e la conseguente distribuzione dello stato tensionale delle areole da 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 11
12 FLESSIONE RETTA In questa condizione la sezione è soggetta ad una sollecitazione semplice di momento flettente retto In questo caso l espressione generale che definisce il valore dello sforzo sull i-esimo clementino: Essendo: α = 0 ; ; 0 Diventa semplicemente: σ = E x = M y z i / J y essendo variabile linearmente in ragione della distanza dell elementino da dal baricentro si ha un andamento delle deformazioni unitarie ed in conseguenza dello sforzo normale come in figura: L asse baricentrico Y-Y, nel caso di flessione retta agente su di un asse principale di una sezione omogenea, possiede la proprietà di contenere le fibre della sezione che pur deformandosi mantengono la loro lunghezza inalterata. N.B. con identica procedura si giunge ad analoghe conclusioni (basta scambiare le lettere) nel caso di flessione retta con momento agente intorno all asse Z 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 12
13 PRESSO (TENSO) FLESSIONE RETTA In questa condizione la sezione è soggetta ad una sollecitazione composta di sforzo assiale + momento flettente retto In questo caso l espressione generale che definisce il valore dello sforzo sull i-esimo clementino: Essendo: α = 0 ; ; σ = (E x ε) ± (E x ) = N/A ± M y z i / J y N.B. ovviamente per momenti flettenti agenti intorno all asse z l espressione diventa: σ = N/A ± M z y i / J z FLESSIONE DEVIATA In questa condizione la sezione è soggetta ad una sollecitazione composta di flessione deviata In questo caso l espressione generale che definisce il valore dello sforzo sull i-esimo clementino: Essendo: α = ; ; 0 σ = (E x ) ± (E x ) = M z y i / J z ± M y z i / J y STATI DI SOLLECITAZIONE TANGENZIALE (paralleli alla sezione) 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 13
14 Gli stati di sollecitazione tangenziale sono quelli prodotti dalle tensioni tangenziali (cioè ad andamento parallelo alla sezione ) nelle dimostrazioni sono indicate con la lettera greca τ seguita dalle lettere indicanti il piano che le contiene. Le tensioni tangenziali sono dovute a due tipi di risultanti: - TAGLIO - TORSIONE Nel caso del taglio le tensioni tangenziali sono prodotte dalla necessità di equilibrare l azione traslante indotta dalla sollecitazione sulla sezione stessa; Nel caso della torsione le tensioni tangenziali sono prodotte dalla necessità di equilibrare la rotazione intorno all asse locale X. Come evidenziato in figura, il meccanismo deformativo di una trave soggetta a flessione (e quindi anche taglio) vede la parte superiore della trave scivolare sulla parte sottostante. La forza risultante dall equilibrio delle due sezioni longitudinali prende il nome di forza di scorrimento, che, nella dimostrazione indicheremo con la lettera R. La forza di scorrimento risulterà dalla somma di tutti i contributi da*τ xy essendo le tensioni tangenziali di spigolo uguali (principio della reciprocità delle tensioni tangenziali). Negli spigoli vale la relazione τ zy = τ xy 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 14
15 Assumiamo una semplice trave inflessa soggetta da un carico uniformemente ripartito, rispetto alla quale abbiamo determinato i diagrammi di sollecitazione TAGLIO e MOM. FLETTENTE Se consideriamo il tronco di trave x possiamo analizzare la condizione di equilibrio di tutte le forze verticali: Z = 0 (equilibrio alla traslazione verticale) T (T+ T) = 0 ; in cui T = - q* x M = 0 (equilibrio alla rotazione) - M +(M+ M) = 0 ; in cui M = T* x La presenza del momento flettente produce delle tensioni normali sulla sezione: 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 15
16 Come visto nel caso delle sollecitazioni normali sommando tutti i prodotti da*σ i si ottiene una forza risultante N. Dove la tensione normale è il risultato della applicazione del momento flettente, sostituiamo alla σ i il valore calcolato con le formule viste in precedenza: La risultante N+ N vale: Se consideriamo la sola parte inferiore A 1 possiamo associare la N e la N+ N ad un volume come in figura: Poniamo l equazione di equilibrio rispetto alle traslazioni orizzontali con riferimento alla parte inferiore della trave X = 0 (equilibrio alla traslazione orizzontale) N + R - (N + N) = 0 ; in cui R = N La forza N vale per le considerazioni fatte in precedenza: 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 16
17 Essendo: R 0 ; R M = T* x ; = momento statico della sezione rispetto all asse y (S y ) Δ Δ x A questo punto abbiamo bisogno di una approssimazione circa l andamento delle tensioni tangenziali ripetto ad una corda di larghezza B. Si assume che le tensioni tangenziali distribuite lungo la corda siano costanti (approssimazione di Jourasky). Considerando la reciprocità delle tensioni tangenziali possiamo porre l uguaglianza tra le due espressioni della forza di scorrimento R : essendo: Δ Δ si può porre: Δ x applicando il principio di reciprocità si determina la relazione tra le tensioni tangenziali e le grandezze in gioco: Che rappresenta la formula generale di equilibrio per le sezioni soggette a taglio. 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 17
18 SEZIONE RETTANGOLARE SEZIONE A DOPPIO T CASI PARTICOLARI Nota: Seguono esercitazioni + aggiungere dimostrazione Torsione (analogia di Bredt) 93 Università degli Studi di Roma La Sapienza - appunti per una pubblicazione ad uso didattico S.CATASTA e P.ANTONINI 18
ELEMENTI MONODIMENSIONALI : TRAVE
 ELEMENTI MONODIMENSIONALI : TRAVE La trave è un elemento strutturale con una dimensione predominante sulle altre due. baricentro G sezione trasversale linea d asse rappresentazione schematica 1 ELEMENTI
ELEMENTI MONODIMENSIONALI : TRAVE La trave è un elemento strutturale con una dimensione predominante sulle altre due. baricentro G sezione trasversale linea d asse rappresentazione schematica 1 ELEMENTI
Geometria delle Aree. Finora ci si è occupati di determinare le sollecitazioni che agiscono su sezioni di elementi monodimensionali
 eometria delle ree Finora ci si è occupati di determinare le sollecitazioni che agiscono su sezioni di elementi monodimensionali In realtà lo studio della Meccanica delle Strutture non si accontenta di
eometria delle ree Finora ci si è occupati di determinare le sollecitazioni che agiscono su sezioni di elementi monodimensionali In realtà lo studio della Meccanica delle Strutture non si accontenta di
PRESSO-FLESSIONE RETTA
 PRESSO-FLESSIONE RETTA Consideriamo un elemento strutturale verticale (Pilastro) soggetto ad uno carico P eccentrico, cioè applicato nella sezione in un punto c (centro di pressione) che non corrisponde
PRESSO-FLESSIONE RETTA Consideriamo un elemento strutturale verticale (Pilastro) soggetto ad uno carico P eccentrico, cioè applicato nella sezione in un punto c (centro di pressione) che non corrisponde
4. Travi di fondazione
 4. Travi di fondazione Esempi Nelle applicazioni che seguono la fondazione è modellata come una trave continua appoggiata in corrispondenza dei pilastri e soggetta al carico lineare proveniente dal terreno
4. Travi di fondazione Esempi Nelle applicazioni che seguono la fondazione è modellata come una trave continua appoggiata in corrispondenza dei pilastri e soggetta al carico lineare proveniente dal terreno
ESERCIZIO SOLUZIONE. 13 Aprile 2011
 ESERCIZIO Un corpo di massa m è lasciato cadere da un altezza h sull estremo libero di una molla di costante elastica in modo da provocarne la compressione. Determinare: ) la velocità del corpo all impatto
ESERCIZIO Un corpo di massa m è lasciato cadere da un altezza h sull estremo libero di una molla di costante elastica in modo da provocarne la compressione. Determinare: ) la velocità del corpo all impatto
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
GEOMETRIA DELLE MASSE
 IL BARICENTRO GENERALITA' GEOMETRIA DELLE MASSE Un corpo può essere immaginato come se fosse costituito da tante piccole particelle dotate di massa (masse puntiformi); a causa della forza di gravità queste
IL BARICENTRO GENERALITA' GEOMETRIA DELLE MASSE Un corpo può essere immaginato come se fosse costituito da tante piccole particelle dotate di massa (masse puntiformi); a causa della forza di gravità queste
La composizione di isometrie
 La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM )
 Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM ) 1. Scrivere l'equazione della retta passante per i punti P1(-3,1), P2(2,-2). Dobbiamo applicare l'equazione di una retta passante per due
Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM ) 1. Scrivere l'equazione della retta passante per i punti P1(-3,1), P2(2,-2). Dobbiamo applicare l'equazione di una retta passante per due
COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI
 LEZIONI N 32 E 33 COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI Prima di addentrarci nei dettagli della teoria tecnica delle costruzioni di cemento armato, è utile richiamare
LEZIONI N 32 E 33 COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI Prima di addentrarci nei dettagli della teoria tecnica delle costruzioni di cemento armato, è utile richiamare
3 Geometria delle masse e momento di 2 ordine 3.3 Ellisse centrale d inerzia e nocciolo centrale d inerzia
 3 Geometria delle masse e momento di ordine ESERCIZI SVOLTI Considerata la sezione rappresentata in figura, calcolare i raggi d inerzia massimo e minimo, tracciare l ellisse d inerzia e il nocciolo centrale
3 Geometria delle masse e momento di ordine ESERCIZI SVOLTI Considerata la sezione rappresentata in figura, calcolare i raggi d inerzia massimo e minimo, tracciare l ellisse d inerzia e il nocciolo centrale
valore di a: verso l alto (ordinate crescenti) se a>0, verso il basso (ordinate decrescenti) se a<0;
 La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
La parabola è una particolare conica definita come è una curva aperta, nel senso che non può essere contenuta in alcuna superficie finita del piano; è simmetrica rispetto ad una retta, detta ASSE della
Esercitazione 3 - Calcolo delle azioni interne
 Università degli Studi di ergamo orso di Laurea in Ingegneria Tessile orso di Elementi di Meccanica Esercitazione - alcolo delle azioni interne Esercizio n. La struttura di figura.a è composta da due aste
Università degli Studi di ergamo orso di Laurea in Ingegneria Tessile orso di Elementi di Meccanica Esercitazione - alcolo delle azioni interne Esercizio n. La struttura di figura.a è composta da due aste
Circonferenze del piano
 Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Robotica industriale. Richiami di statica del corpo rigido. Prof. Paolo Rocco
 Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Disequazioni di secondo grado
 Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
ESPONENZIALI E LOGARITMI. chiameremo logaritmica (e si legge il logaritmo in base a di c è uguale a b ).
 ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
Questo paragrafo e quello successivo trattano gli stessi argomenti del capitolo B6 relativo alla soluzione grafica dei sistemi di primo grado.
 D1. Retta D1.1 Equazione implicita ed esplicita Ogni equazione di primo grado in due incognite rappresenta una retta sul piano cartesiano (e viceversa). Si può scrivere un equazione di primo grado in due
D1. Retta D1.1 Equazione implicita ed esplicita Ogni equazione di primo grado in due incognite rappresenta una retta sul piano cartesiano (e viceversa). Si può scrivere un equazione di primo grado in due
UNIVERSITA DEGLI STUDIO DI PADOVA Facoltà di Agraria Collegio dei Geometri CORSO DI AGGIORNAMENTO PROFESSIONALE DI PROGETTAZIONE COSTRUTTIVA
 UNIVERSITA DEGLI STUDIO DI PADOVA Facoltà di Agraria Collegio dei Geometri CORSO DI AGGIORNAMENTO PROFESSIONALE DI PROGETTAZIONE COSTRUTTIVA LEZIONE 4 STATI SEMPLICI DI TENSIONE E COMPORTAMENTO DEI MATERIALI:
UNIVERSITA DEGLI STUDIO DI PADOVA Facoltà di Agraria Collegio dei Geometri CORSO DI AGGIORNAMENTO PROFESSIONALE DI PROGETTAZIONE COSTRUTTIVA LEZIONE 4 STATI SEMPLICI DI TENSIONE E COMPORTAMENTO DEI MATERIALI:
Calcolo della deformazione a rottura di un tirante metallico
 MICHELE VINCI Calcolo della deformazione a rottura di un tirante metallico Collana Calcolo di edifici in muratura (www.edificiinmuratura.it) Articolo 1 Marzo 014 Bibliografia: Michele Vinci Metodi di calcolo
MICHELE VINCI Calcolo della deformazione a rottura di un tirante metallico Collana Calcolo di edifici in muratura (www.edificiinmuratura.it) Articolo 1 Marzo 014 Bibliografia: Michele Vinci Metodi di calcolo
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi)
 2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi) La circonferenza è la curva di 2^ grado che viene individuata univocamente da tre punti non allineati e possiede la seguente proprietà:
2. APPUNTI SUI FASCI DI CIRCONFERENZE (raccolti dal prof. G. Traversi) La circonferenza è la curva di 2^ grado che viene individuata univocamente da tre punti non allineati e possiede la seguente proprietà:
S 2 S 1 S 3 S 4 B S 5. Figura 1: Cammini diversi per collegare i due punti A e B
 1 ENERGI PTENZILE 1 Energia potenziale 1.1 orze conservative Se un punto materiale è sottoposto a una forza costante, cioè che non cambia qualunque sia la posizione che il punto materiale assume nello
1 ENERGI PTENZILE 1 Energia potenziale 1.1 orze conservative Se un punto materiale è sottoposto a una forza costante, cioè che non cambia qualunque sia la posizione che il punto materiale assume nello
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
determinare le coordinate di P ricordando la relazione che permette di calcolare le coordinate del punto medio di un segmento si
 PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
La corrente alternata
 La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
La corrente alternata Corrente continua e corrente alternata Le correnti continue sono dovute ad un generatore i cui poli hanno sempre lo stesso segno e pertanto esse percorrono un circuito sempre nello
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
Geometria analitica di base (seconda parte)
 SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE
 ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
LA RESISTENZA DEI MATERIALI
 Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì LA RESISTENZA DEI MATERIALI AGGIORNAMENTO DEL 30/09/2011 LEGAME COSTITUTIVO Il legame costitutivo rappresenta il collegamento
Sussidi didattici per il corso di COSTRUZIONI EDILI Prof. Ing. Francesco Zanghì LA RESISTENZA DEI MATERIALI AGGIORNAMENTO DEL 30/09/2011 LEGAME COSTITUTIVO Il legame costitutivo rappresenta il collegamento
SOLUZIONE DELLA TRACCIA N 2
 SOLUZIONE DELLA TRACCIA N La presente soluzione verrà redatta facendo riferimento al manuale: Caligaris, Fava, Tomasello Manuale di Meccanica Hoepli. - Studio delle sollecitazioni in gioco Si calcolano
SOLUZIONE DELLA TRACCIA N La presente soluzione verrà redatta facendo riferimento al manuale: Caligaris, Fava, Tomasello Manuale di Meccanica Hoepli. - Studio delle sollecitazioni in gioco Si calcolano
Proprietà meccaniche. Proprietà dei materiali
 Proprietà meccaniche Proprietà dei materiali Proprietà meccaniche Tutti i materiali sono soggetti a sollecitazioni (forze) di varia natura che ne determinano deformazioni macroscopiche. Spesso le proprietà
Proprietà meccaniche Proprietà dei materiali Proprietà meccaniche Tutti i materiali sono soggetti a sollecitazioni (forze) di varia natura che ne determinano deformazioni macroscopiche. Spesso le proprietà
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
APPUNTI DI MATEMATICA ALGEBRA \ CALCOLO LETTERALE \ MONOMI (1)
 LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
Le coniche: circonferenza, parabola, ellisse e iperbole.
 Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
ACCIAIO Calcolo Strutturale
 ISTITUTO TECNICO COSTRUZIONI AMBIENTE TERRITORIO Appunti per il corso di PROGETTAZIONE COSTRUZIONI IMPIANTI ACCIAIO Calcolo Strutturale Aggiornamento: Aprile 2016 Prof. Ing. Del Giudice Tony GENERALITA
ISTITUTO TECNICO COSTRUZIONI AMBIENTE TERRITORIO Appunti per il corso di PROGETTAZIONE COSTRUZIONI IMPIANTI ACCIAIO Calcolo Strutturale Aggiornamento: Aprile 2016 Prof. Ing. Del Giudice Tony GENERALITA
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti
 FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Il Principio dei lavori virtuali
 Il Principio dei lavori virtuali Il P..V. rientra nella classe di quei principi energetici che indicano che i sistemi evolvono nel senso di minimizzare l energia associata ad ogni stato di possibile configurazione.
Il Principio dei lavori virtuali Il P..V. rientra nella classe di quei principi energetici che indicano che i sistemi evolvono nel senso di minimizzare l energia associata ad ogni stato di possibile configurazione.
B6. Sistemi di primo grado
 B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
Il transistor come amplificatore
 Il transistor come amplificatore.doc rev. 1 del 24/06/2008 pagina 1 di 9 Il transistor come amplificatore Transistor BJT Continuiamo nel nostro studio dei transistor dando una dimostrazione grafica della
Il transistor come amplificatore.doc rev. 1 del 24/06/2008 pagina 1 di 9 Il transistor come amplificatore Transistor BJT Continuiamo nel nostro studio dei transistor dando una dimostrazione grafica della
x 2 + (x+4) 2 = 20 Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati per le EQUAZIONI di PRIMO GRADO.
 EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
Lezione PONTI E GRANDI STRUTTURE. Prof. Pier Paolo Rossi Università degli Studi di Catania
 Lezione PONTI E GRANDI TRUTTURE Prof. Pier Paolo Rossi Università degli tudi di Catania Linee di influenza Definizione Dicesi linea di influenza della grandezza G nella sezione, Il diagramma che indica
Lezione PONTI E GRANDI TRUTTURE Prof. Pier Paolo Rossi Università degli tudi di Catania Linee di influenza Definizione Dicesi linea di influenza della grandezza G nella sezione, Il diagramma che indica
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti sulla parabola
 Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 19 dicembre 011 Esercizi svolti sulla parabola Esercizio 1. Determinare l equazione della parabola avente fuoco in F(1, 1) e per direttrice
Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 19 dicembre 011 Esercizi svolti sulla parabola Esercizio 1. Determinare l equazione della parabola avente fuoco in F(1, 1) e per direttrice
Informatica Grafica. Un introduzione
 Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
TEOREMA DEL RESTO E REGOLA DI RUFFINI
 TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
Corso di meccanica, macchine e disegno VD 2013/2014 Modulo UD Lez. Esercizi svolti di statica pag. 1
 orso di meccanica, macchine e disegno VD 2013/2014 Modulo UD Lez. Esercizi svolti di statica pag. 1 1) Un triangolo rettangolo presenta l ipotenusa lunga 5m mentre l angolo formato con uno dei due cateti
orso di meccanica, macchine e disegno VD 2013/2014 Modulo UD Lez. Esercizi svolti di statica pag. 1 1) Un triangolo rettangolo presenta l ipotenusa lunga 5m mentre l angolo formato con uno dei due cateti
Francesco Zumbo
 La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
Unità Didattica realizzata dalla prof.ssa De Simone Marilena A.S. 2015/16
 Unità Didattica realizzata dalla prof.ssa De Simone Marilena A.S. 2015/16 La matematica finanziaria si occupa di tutti i problemi relativi al denaro e al suo impiego. Il denaro è lo strumento con cui possiamo
Unità Didattica realizzata dalla prof.ssa De Simone Marilena A.S. 2015/16 La matematica finanziaria si occupa di tutti i problemi relativi al denaro e al suo impiego. Il denaro è lo strumento con cui possiamo
Anno 2. Risoluzione di sistemi di primo grado in due incognite
 Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Unioni bullonate. 1 Tecnologia delle unioni bullonate. 1.1 Classificazione dei bulloni. Classificazione secondo D.M
 Unioni bullonate 1 Tecnologia delle unioni bullonate 1.1 Classificazione dei bulloni Classificazione secondo D.M. 9-1-96 Classificazione secondo CNR 10011 [#4.13] Stato limite ultimo Tensioni ammissibili
Unioni bullonate 1 Tecnologia delle unioni bullonate 1.1 Classificazione dei bulloni Classificazione secondo D.M. 9-1-96 Classificazione secondo CNR 10011 [#4.13] Stato limite ultimo Tensioni ammissibili
Svolgimento degli esercizi sulla circonferenza
 Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 1 ottobre 011 Svolgimento degli esercizi sulla circonferenza Esercizio 1. La circonferenza ha centro in C 4 ), 7, 7 ) e raggio + 7 57
Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 1 ottobre 011 Svolgimento degli esercizi sulla circonferenza Esercizio 1. La circonferenza ha centro in C 4 ), 7, 7 ) e raggio + 7 57
Problema 1: SOLUZIONE: 1) La velocità iniziale v 0 si ricava dal principio di conservazione dell energia meccanica; trascurando
 Problema : Un pallina di gomma, di massa m = 0g, è lanciata verticalmente con un cannoncino a molla, la cui costante elastica vale k = 4 N/cm, ed è compressa inizialmente di δ. Dopo il lancio, la pallina
Problema : Un pallina di gomma, di massa m = 0g, è lanciata verticalmente con un cannoncino a molla, la cui costante elastica vale k = 4 N/cm, ed è compressa inizialmente di δ. Dopo il lancio, la pallina
MURI DI SOSTEGNO. a cura del professore. Francesco Occhicone
 MURI DI SOSTEGNO a cura del professore Francesco Occhicone anno 2014 MURI DI SOSTEGNO Per muro di sostegno si intende un opera d arte con la funzione principale di sostenere o contenere fronti di terreno
MURI DI SOSTEGNO a cura del professore Francesco Occhicone anno 2014 MURI DI SOSTEGNO Per muro di sostegno si intende un opera d arte con la funzione principale di sostenere o contenere fronti di terreno
NUOVE NORME TECNICHE PER LE COSTRUZIONI
 NUOVE NORME TECNICHE PER LE COSTRUZIONI PILASTRI IN CEMENTO ARMATO (D.M. 14 Gennaio 2008) MATERIALI Conglomerato Non è ammesso l uso di conglomerati di classe inferiore a C20/25. Acciaio Si deve utilizzare
NUOVE NORME TECNICHE PER LE COSTRUZIONI PILASTRI IN CEMENTO ARMATO (D.M. 14 Gennaio 2008) MATERIALI Conglomerato Non è ammesso l uso di conglomerati di classe inferiore a C20/25. Acciaio Si deve utilizzare
2. Si Discretizzano i carichi in CARICHI CONCENTRATI in modo da riprodurre gli andamenti delle azioni interne. Si opera in pi passi: 2a.
 1 Prove Statiche Permettono la verifica del comportamento elastico struttura allo scopo di validare il modello numerico Le prove prevedono: 1. Struttura completa (full-scale) Sottostruttura (Es. solo centina,
1 Prove Statiche Permettono la verifica del comportamento elastico struttura allo scopo di validare il modello numerico Le prove prevedono: 1. Struttura completa (full-scale) Sottostruttura (Es. solo centina,
GEOMETRIA ANALITICA. Il Piano cartesiano
 GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
Funzioni di secondo grado
 Definizione della funzione di secondo grado 1 Funzioni di secondo grado 1 Definizione della funzione di secondo grado f: R R, = a +b +c dove a, b, c ǫ R e a definisce una funzione di secondo grado. A seconda
Definizione della funzione di secondo grado 1 Funzioni di secondo grado 1 Definizione della funzione di secondo grado f: R R, = a +b +c dove a, b, c ǫ R e a definisce una funzione di secondo grado. A seconda
VINCOLI CEDEVOLI ANELASTICAMENTE
 VINCOLI CEDEVOLI ANELASTICAMENTE IL cedimento anelastico detto anche cedimento impresso è indipendente dai carichi applicati ed è definito da un valore assegnato. Esso provoca sollecitazioni solo nelle
VINCOLI CEDEVOLI ANELASTICAMENTE IL cedimento anelastico detto anche cedimento impresso è indipendente dai carichi applicati ed è definito da un valore assegnato. Esso provoca sollecitazioni solo nelle
Graficazione qualitativa del luogo delle radici
 .. 5.3 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s + 1)(s + 8s + 5) y(t) Per una graficazione qualitativa
.. 5.3 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s + 1)(s + 8s + 5) y(t) Per una graficazione qualitativa
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
SOLUZIONE. Calcolo resistenze di progetto materiali: conglomerato: f ck = 200 dan / cm 2 (tab. 9.3_b); f ctk = 15daN / cm 2 f ctm = 22daN / cm 2
 (*)ESEMPIO 4. Sia data la trave di sezione rettangolare delle dimensioni di 20 cm x 40 cm, descritta all esempio 1 (vedere particolari in figura 16.22). Supponendo che la struttura sia stata confezionata
(*)ESEMPIO 4. Sia data la trave di sezione rettangolare delle dimensioni di 20 cm x 40 cm, descritta all esempio 1 (vedere particolari in figura 16.22). Supponendo che la struttura sia stata confezionata
Ellisse. DEF: "il luogo dei punti la cui somma delle distanze da due punti dati detti fuochi. è costante"; CONSIDERAZIONI:
 Ellisse DEF: "il luogo dei punti la cui somma delle distanze da due punti dati detti fuochi è costante"; CONSIDERAZIONI: Il punto P appartiene all'ellisse se, e solo se, la distanza del punto P dal fuoco
Ellisse DEF: "il luogo dei punti la cui somma delle distanze da due punti dati detti fuochi è costante"; CONSIDERAZIONI: Il punto P appartiene all'ellisse se, e solo se, la distanza del punto P dal fuoco
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Misure di spostamento e deformazione eseguite su pannelli sandwich durante prove di carico in flessione a quattro punti
 DISTART DIPARTIMENTO DI INGEGNERIA DELLE STRUTTURE, DEI TRASPORTI, DELLE ACQUE, DEL RILEVAMENTO, DEL TERRITORIO LABORATORIO PROVE STRUTTURE Bologna, 1//3 Pos. 73/3 Misure di spostamento e deformazione
DISTART DIPARTIMENTO DI INGEGNERIA DELLE STRUTTURE, DEI TRASPORTI, DELLE ACQUE, DEL RILEVAMENTO, DEL TERRITORIO LABORATORIO PROVE STRUTTURE Bologna, 1//3 Pos. 73/3 Misure di spostamento e deformazione
Funzioni goniometriche
 Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Utilizzare il ponte di Wheatstone per misurare la trazione di una barra Verificare l'insensibilità ad una sollecitazione in flessione
 Laboratorio di misure Applicazioni del ponte di Wheatstone Barra di trazione Scopo Compiti Prerequisiti Riferimenti Utilizzare il ponte di Wheatstone per misurare la trazione di una barra Verificare l'insensibilità
Laboratorio di misure Applicazioni del ponte di Wheatstone Barra di trazione Scopo Compiti Prerequisiti Riferimenti Utilizzare il ponte di Wheatstone per misurare la trazione di una barra Verificare l'insensibilità
1 La Geometria delle Masse
 1 La eometria delle Masse 1.1 Baricentri e Momenti Statici Due siste di forze vengono detti equivalenti quando generano la stessa risultante e lo stesso momento risultante rispetto ad un polo qualsiasi.
1 La eometria delle Masse 1.1 Baricentri e Momenti Statici Due siste di forze vengono detti equivalenti quando generano la stessa risultante e lo stesso momento risultante rispetto ad un polo qualsiasi.
Esercitazione per la prova di recupero del debito formativo
 LEZIONI ED ESERCITAZIONI DI MATEMATICA Prof. Francesco Marchi 1 Esercitazione per la prova di recupero del debito formativo 24 febbraio 2010 1 Per altri materiali didattici o per contattarmi: Blog personale:
LEZIONI ED ESERCITAZIONI DI MATEMATICA Prof. Francesco Marchi 1 Esercitazione per la prova di recupero del debito formativo 24 febbraio 2010 1 Per altri materiali didattici o per contattarmi: Blog personale:
Derivate delle funzioni di una variabile.
 Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
UNIVERSITÀ DEGLI STUDI DI TRIESTE
 UNIVERSITÀ DEGLI STUDI DI TRIESTE Laurea magistrale in ingegneria meccanica Corso di costruzione di macchine e affidabilità PRIMA ESERCITAZIONE Analisi FEM applicata alla ricerca della sezione maggiormente
UNIVERSITÀ DEGLI STUDI DI TRIESTE Laurea magistrale in ingegneria meccanica Corso di costruzione di macchine e affidabilità PRIMA ESERCITAZIONE Analisi FEM applicata alla ricerca della sezione maggiormente
IIS Moro Dipartimento di matematica e fisica
 IIS Moro Dipartimento di matematica e fisica Obiettivi minimi per le classi prime - Fisica Poiché la disciplina Fisica è parte dell Asse Scientifico Tecnologico, essa concorre, attraverso lo studio dei
IIS Moro Dipartimento di matematica e fisica Obiettivi minimi per le classi prime - Fisica Poiché la disciplina Fisica è parte dell Asse Scientifico Tecnologico, essa concorre, attraverso lo studio dei
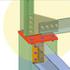
SOMMARIO. 1. VERIFICA DEL PARAPETTO (parodos occidentale) - DESCRIZIONE DELL OPERA - NORMATIVA DI RIFERIMENTO - MATERIALI ADOTTATI
 SOMMARIO 1. VERIFICA DEL PARAPETTO (parodos occidentale) - DESCRIZIONE DELL OPERA - NORMATIVA DI RIFERIMENTO - MATERIALI ADOTTATI 1.1 DIMENSIONAMENTO E VERIFICA DEGLI ELEMENTI STRUTTURALI - montante 1.1.1
SOMMARIO 1. VERIFICA DEL PARAPETTO (parodos occidentale) - DESCRIZIONE DELL OPERA - NORMATIVA DI RIFERIMENTO - MATERIALI ADOTTATI 1.1 DIMENSIONAMENTO E VERIFICA DEGLI ELEMENTI STRUTTURALI - montante 1.1.1
FISICA: Le Forze. Giancarlo Zancanella (2014)
 FISICA: Le Forze Giancarlo Zancanella (2014) 1 Cos è una forza 2 Il Principio D inerzia Un corpo mantiene inalterato il suo stato di quiete o di moto fino a quando non si gli applica una forza che ne cambia
FISICA: Le Forze Giancarlo Zancanella (2014) 1 Cos è una forza 2 Il Principio D inerzia Un corpo mantiene inalterato il suo stato di quiete o di moto fino a quando non si gli applica una forza che ne cambia
UNITA DIDATTICA. Conoscenze. Abilità
 Titolo: Problemi di geometria analitica : la parabola e l iperbole Codice: B1_S Ore previste:15 Equazione della parabola e coordinate del vertice Grafico di una parabola Equazione dell iperbole equilatera
Titolo: Problemi di geometria analitica : la parabola e l iperbole Codice: B1_S Ore previste:15 Equazione della parabola e coordinate del vertice Grafico di una parabola Equazione dell iperbole equilatera
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
Testi verifiche 3 C 3 I a. s. 2008/2009
 Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Risoluzione dei triangoli rettangoli
 Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Funzioni Pari e Dispari
 Una funzione f : R R si dice Funzioni Pari e Dispari PARI: se f( ) = f() R In questo caso il grafico della funzione è simmetrico rispetto all asse DISPARI: se f( ) = f() R In questo caso il grafico della
Una funzione f : R R si dice Funzioni Pari e Dispari PARI: se f( ) = f() R In questo caso il grafico della funzione è simmetrico rispetto all asse DISPARI: se f( ) = f() R In questo caso il grafico della
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
LA FORZA...SIA CON TE!
 LA FORZA...SIA CON TE! CHE COS'E' LA FORZA? E' UNA GRANDEZZA FISICA VETTORIALE. L'UNITA' DI MISURA NEL S.I. E' IL "NEWTON" ( N ), DAL CELEBRE SCIENZIATO INGLESE ISAAC NEWTON, CHE NE HA STUDIATO LE LEGGI,
LA FORZA...SIA CON TE! CHE COS'E' LA FORZA? E' UNA GRANDEZZA FISICA VETTORIALE. L'UNITA' DI MISURA NEL S.I. E' IL "NEWTON" ( N ), DAL CELEBRE SCIENZIATO INGLESE ISAAC NEWTON, CHE NE HA STUDIATO LE LEGGI,
MOLLE, MOLLE A SPIRALE E DI VARIA FOGGIA
 MOLLE, MOLLE A SPIRALE E DI VARIA FOGGIA Molla a spirale per compressione Molla a spirale per trazione (estensione) Molle con tante forme diverse! Leonardo da Vinci, Codice di Madrid, 1490-99 MOLLA A SPIRALE
MOLLE, MOLLE A SPIRALE E DI VARIA FOGGIA Molla a spirale per compressione Molla a spirale per trazione (estensione) Molle con tante forme diverse! Leonardo da Vinci, Codice di Madrid, 1490-99 MOLLA A SPIRALE
LA CIRCONFERENZA La circonferenza è il luogo geometrico dei punti equidistanti da un punto C, detto centro.
 Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
Geometria Analitica Le coniche Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di
Capitolo 2 Le misure delle grandezze fisiche
 Capitolo 2 Le misure delle grandezze fisiche Gli strumenti di misura Gli errori di misura Il risultato di una misura Errore relativo ed errore percentuale Propagazione degli errori Rappresentazione di
Capitolo 2 Le misure delle grandezze fisiche Gli strumenti di misura Gli errori di misura Il risultato di una misura Errore relativo ed errore percentuale Propagazione degli errori Rappresentazione di
L EQUILIBRIO DEL PUNTO MATERIALE
 1 L EQUILIBRIO DEL PUNTO MATERIALE La statica studia l equilibrio dei corpi. Un corpo è in equilibrio se è fermo e persevera nel suo stato di quiete al trascorrere del tempo. Un modello è la semplificazione
1 L EQUILIBRIO DEL PUNTO MATERIALE La statica studia l equilibrio dei corpi. Un corpo è in equilibrio se è fermo e persevera nel suo stato di quiete al trascorrere del tempo. Un modello è la semplificazione
Costi fissi, costi variabili, punto di pareggio e diagramma di redditività
 Cognome... Nome... Classe... Data... Costi fissi, costi variabili, punto di pareggio e diagramma di redditività Correlazione 1 Associa ciascun costo alla relativa tipologia. 1. Costo delle lavorazioni
Cognome... Nome... Classe... Data... Costi fissi, costi variabili, punto di pareggio e diagramma di redditività Correlazione 1 Associa ciascun costo alla relativa tipologia. 1. Costo delle lavorazioni
VERIFICA SECONDO UNI EN 13374
 Ferro-met SRL Via Medici 22/24/24a - 25080 Prevalle (BS) Tel. +39 030 6801973 Fax. +39 030 6801163 P.IVA - C.F. - C.C.I.A.A. BS: 01757240989 REA 349144 Cap. Soc. 300.000 Int. Vers. www.ferro-met.com info@ferro-met.com
Ferro-met SRL Via Medici 22/24/24a - 25080 Prevalle (BS) Tel. +39 030 6801973 Fax. +39 030 6801163 P.IVA - C.F. - C.C.I.A.A. BS: 01757240989 REA 349144 Cap. Soc. 300.000 Int. Vers. www.ferro-met.com info@ferro-met.com
Definizione: Dato un sottoinsieme non vuoti di. Si chiama funzione identica o identità di in sé la funzione tale che.
 Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Equazioni Polinomiali II Parabola
 Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
DIODO. La freccia del simbolo indica il verso della corrente.
 DIODO Si dice diodo un componente a due morsetti al cui interno vi è una giunzione P-N. Il terminale del diodo collegato alla zona P si dice anodo; il terminale collegato alla zona N si dice catodo. Il
DIODO Si dice diodo un componente a due morsetti al cui interno vi è una giunzione P-N. Il terminale del diodo collegato alla zona P si dice anodo; il terminale collegato alla zona N si dice catodo. Il
a b a : b Il concetto di rapporto
 1 Il concetto di rapporto DEFINIZIONE. Il rapporto fra due valori numerici a e b è costituito dal loro quoziente; a e b sono i termini del rapporto, il primo termine si chiama antecedente, il secondo si
1 Il concetto di rapporto DEFINIZIONE. Il rapporto fra due valori numerici a e b è costituito dal loro quoziente; a e b sono i termini del rapporto, il primo termine si chiama antecedente, il secondo si
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA. PROGRAMMA DI Matematica. Classe IIIB. Anno Scolastico
 LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IIIB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 DISEQUAZIONI Disequazioni razionali intere di secondo
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IIIB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 DISEQUAZIONI Disequazioni razionali intere di secondo
ECONOMIA APPLICATA ALL INGEGNERIA (Docente: Prof. Ing. Donato Morea) Microeconomia Esercitazione n. 1 - I FONDAMENTI DI DOMANDA E DI OFFERTA
 ESERCIZIO n. 1 - Equilibrio di mercato e spostamenti delle curve di domanda e di offerta La quantità domandata di un certo bene è descritta dalla seguente funzione: p (D) mentre la quantità offerta è descritta
ESERCIZIO n. 1 - Equilibrio di mercato e spostamenti delle curve di domanda e di offerta La quantità domandata di un certo bene è descritta dalla seguente funzione: p (D) mentre la quantità offerta è descritta
