CALCOLO DELLA STRUTTURA MOLECOLARE: 3. METODI DI CALCOLO PER LA SUPERFICIE DI ENERGIA POTENZIALE E(R)
|
|
|
- Geraldo Gallo
- 5 anni fa
- Visualizzazioni
Transcript
1 CALCOLO DELLA STRUTTURA MOLECOLARE: 3. METODI DI CALCOLO PER LA SUPERFICIE DI ENERGIA POTENZIALE E(R) 1
2 Lo studio teorico di un sistema molecolare in genere si sviluppa in tre fasi: 1. Selezione di un metodo di calcolo per descrivere le interazioni intraed inter-molecolari nel sistema. 2. Esecuzione del calcolo vero e proprio: individuazione della geometria più stabile (minimizzazione dell energia ed analisi conformazionale). 3. Analisi dei risultati del calcolo per determinare le proprietà chimiche ed elettroniche del sistema, da mettere in relazione con eventuali risultati sperimentali. 2
3 Scelta del metodo di calcolo: Metodi quantistici (metodi ab initio, DFT e semiempirici): permettono la determinazione delle caratteristiche geometriche, elettroniche ed energetiche dei sistemi molecolari. Sono estremamente costosi in termini di tempo di calcolo e carico computazionale, diventando in alcuni casi proibitivi per sistemi molto grandi. Metodi della meccanica molecolare (o dei campi di forza): si basano su modelli semplici in cui le molecole sono trattate come se fossero composte da masse e molle e le loro interazioni sono governate dalle leggi della meccanica classica (informazioni in tempi relativamente brevi anche per sistemi estesi). Forniscono informazioni di tipo strutturale (geometrico) o energetico e non di tipo elettronico (NO studio di reazioni). 3
4 Entrambi i metodi sono conseguenze diverse della separazione di Born- Oppenheimer del moto nucleare ed elettronico: Nei calcoli quantistici si parte ad una data geometria nucleare e si determina la migliore distribuzione degli elettroni nel potenziale generato dai nuclei. Con la meccanica molecolare, al contrario, si studia la posizione dei nuclei nel campo generato dagli elettroni. Gli elettroni non sono considerati esplicitamente e il loro campo non è effettivamente calcolato, ma piuttosto rappresentato da un potenziale efficace trattato secondo la meccanica classica. 4
5 MECCANICA MOLECOLARE: - le molecole sono trattate come se fossero composte da masse e molle; - le diverse interazioni nella molecola sono descritte con le leggi della meccanica classica secondo un modello che viene parametrizzato empiricamente. Un concetto chiave su cui si basano i campi di forze è quello della trasferibilità, che implica che parametri sviluppati e testati per un numero relativamente piccolo di casi modello possa essere usato per studiare molecole molto più grandi. 5
6 CAMPI DI FORZA (FORCE FIELDS): La costruzione di un campo di forza consiste di due parti: 1. La scelta della forma funzionale che descrive l energetica del sistema: l energia potenziale di una molecola = somma di termini associati ai vari tipi di deformazioni molecolari (variazioni di lunghezze di legami, angoli di valenza o di torsione) o interazioni atomo-atomo. L energia sterica calcolata dalla somma di questi termini rappresenta l energia addizionale associata alle deviazioni della struttura rispetto ad una situazione ideale dove tutti gli elementi geometrici sono in uno stato di riferimento. 2. La scelta dei parametri da inserire nella forma funzionale. Questa scelta è basata sull ipotesi che i parametri necessari per calcolare l energia molecolare possono essere derivati dalle informazioni ottenute da molecole piccole (lunghezze e angoli di legame) e che questi siano trasferibili a sistemi grandi. 6
7 CAMPI DI FORZA (FORCE FIELDS): La costruzione di un campo di forza consiste di due parti: 1. La scelta della forma funzionale che descrive l energetica del sistema: l energia potenziale di una molecola = somma di termini associati ai vari tipi di deformazioni molecolari (variazioni di lunghezze di legami, angoli di valenza o di torsione) o interazioni atomo-atomo. L energia sterica calcolata dalla somma di questi termini rappresenta l energia addizionale associata alle deviazioni della struttura rispetto ad una situazione ideale dove tutti gli elementi geometrici sono in uno stato di riferimento. 2. La scelta dei parametri da inserire nella forma funzionale. Questa scelta è basata sull ipotesi che i parametri necessari per calcolare l energia molecolare possono essere derivati dalle informazioni ottenute da molecole piccole (lunghezze e angoli di legame) e che questi siano trasferibili a sistemi grandi. 7
8 La maggior parte dei campi di forza usati attualmente per modellare molecole o insiemi di atomi e/o molecole può essere rappresentata come somma di quattro contributi, che descrivono le forze intra ed intermolecolari all interno del sistema: V tot ( r) = V + V + V + V stretching bending torsion non bonded Un campo di forza è generalmente disegnato per predire delle proprietà e deve essere parametrizzato di conseguenza. Va ricordato che i campi di forza sono empirici, non esiste dunque una forma esatta per un campo di forza. 8
9 1. Termine di stretching del legame ( V stretching ): descrive le interazioni tra le coppie di atomi legati ed è rappresentato da un potenziale che dà la variazione di energia a seconda della deviazione della lunghezza di legame dal suo valore di riferimento. L approccio più semplice per descrivere questo termine consiste nell usare la legge di Hooke in cui l energia varia con il quadrato della variazione dal valore di riferimento della lunghezza di legame r 0 : V stretch = k( r r ) 0 2 9
10 Approcci più raffinati: Morse V stretch = k [ ] α r r ) 1 e 2 ( 0 Cubica V stretch = k ( r r 0) + k3 ( r r 0) Morse quadratica -100 Quadratica Morse Cubica 10
11 2. Termine di bending ( V bending ) Si usano forme funzionali simili a quelle di stretching del legame, ma sono necessari tre atomi per definire l angolo. V angle = k ( θ θ 0 ) 2 E richiesta una minore energia per far deviare un angolo dal suo valore di equilibrio rispetto a quella richiesta per allungare o comprimere un legame: le costanti di forza sono proporzionalmente più piccole. 11
12 3. Termine torsionale ( V torsion ) descrive come varia l energia in seguito alla rotazione dei legami. I potenziali torsionali sono espressi come uno sviluppo in serie di coseni: V torsion = N n= 0 V 2 n [ 1+ cos( nω γ )] dove ω è l angolo di torsione; V n è l altezza della barriera; n è la periodicità della rotazione. 12
13 Esempio: Etano I tre minimi di energia delle conformazioni sfalsate e i tre massimi di energia delle strutture eclissate dell etano sono un classico esempio del modo in cui l energia cambia con la rotazione del legame. H1 H4 H C1 C2 1 H3 H6 0.5 H
14 Lo stretching e il bending dei legami sono gradi di libertà piuttosto rigidi: occorre una notevole quantità di energia per provocare deformazioni sostanziali dai valori di riferimento. La maggior parte delle variazioni nella struttura e nelle energie relative sono dovute al termine torsionale e ai termini di non legame. L esistenza di barriere di rotazione intorno ai legami chimici è fondamentale per capire le proprietà strutturali delle molecole e l analisi conformazionale. 14
15 4. Termini di non legame (V non-bonded ) Il termine non-bonded tiene conto delle interazioni tra coppie di atomi che si trovano in diverse molecole o che si trovano nella stessa molecola ma che sono separati da almeno tre legami. Nei campi di forza il termine non-bonded è di solito rappresentato usando: a) un potenziale di Coulomb per le interazioni elettrostatiche b) un potenziale Lennard-Jones per le interazioni di van der Waals. 15
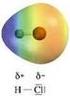
16 a) Interazioni elettrostatiche Gli elementi elettronegativi attraggono gli elettroni in misura maggiore degli elementi meno elettronegativi, dando luogo ad un ineguale distribuzione di carica nella molecola. Questa distribuzione di carica può essere rappresentata in vari modi; uno tra gli approcci più comuni consiste in un arrangiamento di cariche puntiformi frazionarie distribuite all interno della molecola. Queste cariche vengono introdotte in maniera da riprodurre le proprietà elettrostatiche della molecola. Se le cariche sono ristrette al centro del nucleo, sono spesso riportate come cariche atomiche parziali. 16
17 Le interazioni elettrostatiche tra due molecole (o tra differenti parti della stessa molecola) sono poi calcolate come una somma d interazioni tra coppie di cariche puntiformi usando la legge di Coulomb: V N N = A B q q i= 1 j= 1 0 i 4πε j r ij dove N A ed N B sono il numero di cariche puntiformi nelle due molecole. 17
18 b) Interazioni van der Waals Le interazioni elettrostatiche non tengono conto di tutte le interazioni che ci sono tra gli atomi non legati in un sistema (vedi atomi dei gas nobili: hanno momento dipolare uguale a zero, quindi non presentano interazioni dipolo-dipolo o interazioni dipolo-dipolo indotto). Funzione di Lennard-Jones 12-6: υ () r = 4ε σ r 12 σ r 6 σ = diametro di collisione (corrisponde ad una separazione tra gli atomi r tale che l energia di interazione sia nulla) ε = profondità della buca di potenziale. 18
19 4. Termini di non legame (V non-bonded ): legame idrogeno Alcuni campi di forza utilizzano una funzione simile a quella di Lennard- Jones 6-12 per riprodurre esplicitamente il legame idrogeno: potenziale di Lennard-Jones 10-12: υ A r C r () r = A e C sono parametri legati a σ e ε. 19
20 Esempio: energia di una conformazione del propano V(R) 10 termini di stretching 18 termini di bending 18 termini torsionali 27 termini non-bonded (21 H-H e 6 C-H) 20
21 CAMPI DI FORZA (FORCE FIELDS): La costruzione di un campo di forza consiste di due parti: 1. La scelta della forma funzionale che descrive l energetica del sistema: l energia potenziale di una molecola = somma di termini associati ai vari tipi di deformazioni molecolari (variazioni di lunghezze di legami, angoli di valenza o di torsione) o interazioni atomo-atomo. L energia sterica calcolata dalla somma di questi termini rappresenta l energia addizionale associata alle deviazioni della struttura rispetto ad una situazione ideale dove tutti gli elementi geometrici sono in uno stato di riferimento. 2. La scelta dei parametri da inserire nella forma funzionale. Questa scelta è basata sull ipotesi che i parametri necessari per calcolare l energia molecolare possono essere derivati dalle informazioni ottenute da molecole piccole (lunghezze e angoli di legame) e che questi siano trasferibili a sistemi grandi. 21
22 I parametri del campo di forza sono: atom type costanti di forza valori di equilibrio parametri di van der Waals cariche atomiche parziali 22
23 Atom Types Il concetto di atom types può essere considerato uno dei concetti fondamentali in meccanica molecolare e sta alla base di tutti gli aspetti dell approccio. I tipi di atomi, e non gli atomi stessi, sono fondamentali per calcolare le interazioni in meccanica molecolare. Definizione di Atom Type Gli atomi possono essere distinti a seconda di: Ibridizzazione sp 3 Carica formale sull atomo Atomi legati più vicini sp 2 sp 23
24 L ambiente chimico per un atomo all interno di una molecola è creato dal resto della molecola. I campi di forze usano concetti chimici per definire tipi di atomi generali. Per esempio, il campo di forze AMBER ( ) definisce 5 tipi di atomo per l ossigeno: O ossigeno carbonilico OH ossigeno idrossilico (alcol) O2 ossigeno di una acido carbossilico o ossigeno di un fosfato OS ossigeno di un etere o di un estere OW ossigeno dell acqua Le interazioni in meccanica molecolare sono quindi calcolate tra tipi di atomi e non tra elementi. Così si calcoleranno interazioni non-bonded diverse tra gli ossigeni di due molecole di acqua e l ossigeno dell acqua e quello di un estere. 24
25 Parametri di van der Waals La distanza di van der Waals σ AB e il parametro energetico ε AB dipendono da entrambi i tipi atomici. Questi parametri vengono in genere calcolati a partire da termini che dipendono dai singoli tipi atomici A e B. Esistono diversi modi per combinare i parametri atomici a dare i parametri diatomici, alcuni dei quali molto complicati. Un metodo comunemente impiegato consiste nel calcolare la minima distanza di van der Waals σ come somma dei due raggi di van der Waals e di calcolare il parametro energetico ε come media geometrica delle costanti atomiche. σ AB = ½(σ AA + σ BB ) ε AB = (ε AA ε BB ) ½ Per ciascun tipo atomico devono essere determinati due parametri: σ ed 25 ε.
26 Derivazione delle cariche parziali Un certo numero di schemi è stato sviluppato per assegnare le cariche atomiche in maniera sistematica. Tra gli schemi più diffusi abbiamo: 1: Trattare la carica come un qualunque parametro empirico. Questo approccio dà dei buoni risultati per il set di dati usato ma dà problemi per quanto riguarda la trasferibilità. 2: Usare considerazioni di elettronegatività. Anche questa tecnica è utile ma introduce una dipendenza dalla connettività e dalla topologia. 3: Usare cariche quantomeccaniche, dato che la densità di carica è una proprietà dello stato fondamentale della funzione d onda molecolare. 26
27 Parametrizzazione Un set di parametri iniziale è usato per calcolare un set di osservabili sperimentali: lunghezze o angoli di legame, ecc. I valori ottenuti sono quindi confrontati con quelli sperimentali e il set di parametri viene modificato per migliorare la correlazione tra il modello e l esperimento, si ripete il procedimento in maniera iterativa. Un altro schema consiste nell usare il metodo matematico dei minimi quadrati: i parametri vengono selezionati in maniera che la discrepanza tra i valori dei dati sperimentali e quelli ottenuti con i parametri sia minima: δ ( y ) 2 misurati y = w calc. La derivata di δ rispetto al set di parametri può essere calcolata in maniera da cambiare i parametri del force field in modo da minimizzare l errore. 27
28 Campi di forze più usati MM2/MM3 (Allinger, Universty of Georgia): molecole organiche non troppo grandi. Amber (Kollman, University of California, San Francisco): proteine e acidi nucleici. MMFF (Halgren, Merck): parametrizzato da calcoli quantomeccanici. UFF (Rappe, Casewit e Skiff): ha parametri per molti elementi della tavola periodica. 28
Rappresentazione grafica di sistemi atomici e molecolari: editor e visualizzatori ESERCITAZIONE 5
 Rappresentazione grafica di sistemi atomici e molecolari: editor e visualizzatori ESERCITAZIONE 5 Editor e visualizzatori Spesso è utile rappresentare graficamente la struttura atomica o molecolare del
Rappresentazione grafica di sistemi atomici e molecolari: editor e visualizzatori ESERCITAZIONE 5 Editor e visualizzatori Spesso è utile rappresentare graficamente la struttura atomica o molecolare del
Macromolecole Biologiche. Metodi di simulazione
 Metodi di simulazione Dinamica molecolare Tecnica di simulazione che permette lo studio del moto e delle proprietà di un sistema di particelle. Moti localizzati (da 0.01 a 5 Å, da 10-15 a 10-1 s) - fluttuazioni
Metodi di simulazione Dinamica molecolare Tecnica di simulazione che permette lo studio del moto e delle proprietà di un sistema di particelle. Moti localizzati (da 0.01 a 5 Å, da 10-15 a 10-1 s) - fluttuazioni
Perché H 2 e non H? He e non He 2? H 2 O e non H 3 O?
 IL LEGAME CHIMICO Perché H 2 e non H? He e non He 2? H 2 O e non H 3 O? Configurazione degli elettroni diversa ed energeticamente più favorevole di quella degli atomi isolati? Ionico (trasferimento di
IL LEGAME CHIMICO Perché H 2 e non H? He e non He 2? H 2 O e non H 3 O? Configurazione degli elettroni diversa ed energeticamente più favorevole di quella degli atomi isolati? Ionico (trasferimento di
Introduzione alla chimica organica. 1. Regola ottetto 2. Teoria del legame 3. Geometria delle molecole
 Introduzione alla chimica organica 1. Regola ottetto 2. Teoria del legame 3. Geometria delle molecole La chimica organica tratta di pochissimi atomi che si possono combinare in moltissimi modi Grande importanza
Introduzione alla chimica organica 1. Regola ottetto 2. Teoria del legame 3. Geometria delle molecole La chimica organica tratta di pochissimi atomi che si possono combinare in moltissimi modi Grande importanza
CORSO DI LAUREA IN INGEGNERIA GESTIONALE A.A Prova scritta del corso di Fondamenti di Chimica A-K Compito prova
 CORSO DI LAUREA IN INGEGNERIA GESTIONALE A.A. 2012-2013 Prova scritta del corso di Fondamenti di Chimica A-K Compito prova Cognome e nome.... n di matricola Nei quesiti a risposta multipla, verranno ANNULLATI
CORSO DI LAUREA IN INGEGNERIA GESTIONALE A.A. 2012-2013 Prova scritta del corso di Fondamenti di Chimica A-K Compito prova Cognome e nome.... n di matricola Nei quesiti a risposta multipla, verranno ANNULLATI
CALCOLO DELLA STRUTTURA MOLECOLARE: 1. LE SUPERFICI DI ENERGIA POTENZIALE E L APPROSSIMAZIONE DI BORN-OPPENHEIMER
 CALCOLO DELLA STRUTTURA MOLECOLARE: 1. LE SUPERFICI DI ENERGIA POTENZIALE E L APPROSSIMAZIONE DI BORN-OPPENHEIMER 1 COSA E UNA MOLECOLA Tutti gli atomi a piccola distanza si attraggono (forze di van der
CALCOLO DELLA STRUTTURA MOLECOLARE: 1. LE SUPERFICI DI ENERGIA POTENZIALE E L APPROSSIMAZIONE DI BORN-OPPENHEIMER 1 COSA E UNA MOLECOLA Tutti gli atomi a piccola distanza si attraggono (forze di van der
FORZE INTERMOLECOLARI
 FORZE INTERMOLECOLARI Oltre alle forze intramolecolari (legami) esistono nella materia forze intermolecolari (tra molecole diverse), anch esse dovute ad interazioni elettrostatiche. Le forze intermolecolari
FORZE INTERMOLECOLARI Oltre alle forze intramolecolari (legami) esistono nella materia forze intermolecolari (tra molecole diverse), anch esse dovute ad interazioni elettrostatiche. Le forze intermolecolari
I LEGAMI CHIMICI. Configurazione elettronica stabile: è quella in cui tutti i livelli energetici dell atomo sono pieni di elettroni
 I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
I LEGAMI CIMICI In natura sono pochi gli elementi che presentano atomi allo stato libero. Gli unici elementi che sono costituiti da atomi isolati si chiamano gas nobili o inerti, formano il gruppo VIII
Corso di Laurea in CHIMICA (L.T.) Esercitazione n. 1 - Struttura delle molecole e modo di scrivere le formule
 orso di Laurea in IMIA (L.T.) IMIA RGANIA I con Elementi di Laboratorio Esercitazione n. 1 - Struttura delle molecole e modo di scrivere le formule TERMINI ED ARGMENTI DA NSERE PER L SVLGIMENT DEGLI ESERIZI
orso di Laurea in IMIA (L.T.) IMIA RGANIA I con Elementi di Laboratorio Esercitazione n. 1 - Struttura delle molecole e modo di scrivere le formule TERMINI ED ARGMENTI DA NSERE PER L SVLGIMENT DEGLI ESERIZI
Geometria della distanza
 Geometria della distanza La geometria della distanza esplora lo spazio conformazionale generando casualmente molte matrici delle distanze, che sono poi convertite in conformazioni nello spazio cartesiano
Geometria della distanza La geometria della distanza esplora lo spazio conformazionale generando casualmente molte matrici delle distanze, che sono poi convertite in conformazioni nello spazio cartesiano
Diagramma di Ramachandran
 Chimica Biologica A.A. 2010-2011 Diagramma di Ramachandran Diagramma di Ramachandran Catena polipeptidica La formazione in successione di legami peptidici genera la cosiddetta catena principale o scheletro
Chimica Biologica A.A. 2010-2011 Diagramma di Ramachandran Diagramma di Ramachandran Catena polipeptidica La formazione in successione di legami peptidici genera la cosiddetta catena principale o scheletro
ORBITALE ATOMICO. Forma
 L ATOMO ORBITALE ATOMICO n (numero quantico principale) Energia e Dimensione l (numero quantico azimutale) Forma m l (numero quantico magnetico) Orientazione nello spazio l dipende da n assume n valori:
L ATOMO ORBITALE ATOMICO n (numero quantico principale) Energia e Dimensione l (numero quantico azimutale) Forma m l (numero quantico magnetico) Orientazione nello spazio l dipende da n assume n valori:
Metodi Pseudopotenziale
 Oltre HF Metodi Pseudopotenziale Il moto degli elettroni interni è poco influenzato dall'intorno molecolare Il calcolo può essere semplificato modificando lo hamiltonano: limitandosi a calcolare solo il
Oltre HF Metodi Pseudopotenziale Il moto degli elettroni interni è poco influenzato dall'intorno molecolare Il calcolo può essere semplificato modificando lo hamiltonano: limitandosi a calcolare solo il
FORMAZIONE DI LEGAMI. Il legame chimico si definisce quando fra due atomi esistono delle forze che danno luogo alla formazione di un aggregato.
 FORMAZIONE DI LEGAMI Il legame chimico si definisce quando fra due atomi esistono delle forze che danno luogo alla formazione di un aggregato. Presa r come distanza internucleare si osserva che l'energia
FORMAZIONE DI LEGAMI Il legame chimico si definisce quando fra due atomi esistono delle forze che danno luogo alla formazione di un aggregato. Presa r come distanza internucleare si osserva che l'energia
delle curve isoterme dell anidride carbonica
 COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
Un compostoè costituito da due o più elementi in proporzioni costanti, ottenibili dai composti per trasformazioni chimiche.
 Le Formule Chimiche Un compostoè costituito da due o più elementi in proporzioni costanti, ottenibili dai composti per trasformazioni chimiche. La formula minima(o empirica): indica gli elementi che formano
Le Formule Chimiche Un compostoè costituito da due o più elementi in proporzioni costanti, ottenibili dai composti per trasformazioni chimiche. La formula minima(o empirica): indica gli elementi che formano
1.La forma delle molecole 2.La teoria VSEPR 3.Molecole polari e apolari 4.Le forze intermolecolari 5.Legami a confronto
 1.La forma delle molecole 2.La teoria VSEPR 3.Molecole polari e apolari 4.Le forze intermolecolari 5.Legami a confronto 1 1. La forma delle molecole Molte proprietà delle sostanze dipendono dalla forma
1.La forma delle molecole 2.La teoria VSEPR 3.Molecole polari e apolari 4.Le forze intermolecolari 5.Legami a confronto 1 1. La forma delle molecole Molte proprietà delle sostanze dipendono dalla forma
CENNI SUL TIPO DI FORZE
 CENNI SUL TIPO DI FORZE Forze deboli che influenzano la struttura delle proteine: le interazioni di van der Waals repulsione attrazione Forze attrattive dovute a interazioni istantanee che si generano
CENNI SUL TIPO DI FORZE Forze deboli che influenzano la struttura delle proteine: le interazioni di van der Waals repulsione attrazione Forze attrattive dovute a interazioni istantanee che si generano
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici. Capitolo 10
 Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Chimica computazionale
 Chimica computazionale Loriano Storchi loriano@storchi.org http://www.storchi.org/ In questo caso le molecole vengono trattate come se costituite da atomi (considerati sfere) collegati da molle (i legami)
Chimica computazionale Loriano Storchi loriano@storchi.org http://www.storchi.org/ In questo caso le molecole vengono trattate come se costituite da atomi (considerati sfere) collegati da molle (i legami)
LCAO nella molecola d acqua. Teoria del funzionale di densità (DFT).
 Il programma cambia negli anni accademici. Questo file contiene i programmi dei vari A.A. Lo studente deve riferirsi al programma dell'anno in cui ha seguito il corso. Consultare Testi Consigliati per
Il programma cambia negli anni accademici. Questo file contiene i programmi dei vari A.A. Lo studente deve riferirsi al programma dell'anno in cui ha seguito il corso. Consultare Testi Consigliati per
Fondamenti di chimica organica Janice Gorzynski Smith Copyright 2009 The McGraw Hill Companies srl
 Soluzioni ai problemi proposti nel libro Capitolo 1 1.1 Il numero di massa è il numero dei protoni e dei neutroni. Il numero atomico è il numero dei protoni ed è identico per tutti gli isotopi. a. Numero
Soluzioni ai problemi proposti nel libro Capitolo 1 1.1 Il numero di massa è il numero dei protoni e dei neutroni. Il numero atomico è il numero dei protoni ed è identico per tutti gli isotopi. a. Numero
Legame chimico: covalente polare Legame covalente polare
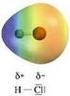
 Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame Covalente Polare e MOT. Polarità del legame aumenta con differenza di elettronegatività.
 Legame Covalente Polare e MOT Polarità del legame aumenta con differenza di elettronegatività. Legame Ionico Se differenza di elettronegatività è molto grande si ottiene un legame ionico. Legame Ionico
Legame Covalente Polare e MOT Polarità del legame aumenta con differenza di elettronegatività. Legame Ionico Se differenza di elettronegatività è molto grande si ottiene un legame ionico. Legame Ionico
Fluttuazioni. Descrizione molecolare e descrizione macroscopica Il concetto di insieme termodinamico Fluttuazioni in un insieme canonico
 Fluttuazioni Descrizione molecolare e descrizione macroscopica Il concetto di insieme termodinamico Fluttuazioni in un insieme canonico Cenni di meccanica statistica In questa lezione accenneremo ai principi
Fluttuazioni Descrizione molecolare e descrizione macroscopica Il concetto di insieme termodinamico Fluttuazioni in un insieme canonico Cenni di meccanica statistica In questa lezione accenneremo ai principi
Lezione n. 26. Principi generali della spettroscopia IR. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 26 Principi generali della spettroscopia IR 02/03/2008 Antonino Polimeno 1 Spettroscopia infrarossa (1) - La spettroscopia infrarossa studia
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 26 Principi generali della spettroscopia IR 02/03/2008 Antonino Polimeno 1 Spettroscopia infrarossa (1) - La spettroscopia infrarossa studia
2 HCl. H 2 + Cl 2 ATOMI E MOLECOLE. Ipotesi di Dalton
 Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Ipotesi di Dalton ATOMI E MOLECOLE 1.! Un elemento è formato da particelle indivisibili chiamate atomi. 2.! Gli atomi di uno specifico elemento hanno proprietà identiche. 3.! Gli atomi si combinano secondo
Prestazioni Errori medi
 Prestazioni Errori medi Per molecole nello stato fondamentale, closed-shell, formate da atomi da H a Ar Geometrie di equilibrio In vicinanza del minimo la superficie di potenziale a livello Hartee-Fock
Prestazioni Errori medi Per molecole nello stato fondamentale, closed-shell, formate da atomi da H a Ar Geometrie di equilibrio In vicinanza del minimo la superficie di potenziale a livello Hartee-Fock
Idrocarburi Saturi. Alcani
 Idrocarburi Saturi Alcani IDROCARBURI I principali componenti del petrolio e del gas naturale, risorse dalle quali proviene la maggior parte dei combustibili per la produzione di energia sono idrocarburi,
Idrocarburi Saturi Alcani IDROCARBURI I principali componenti del petrolio e del gas naturale, risorse dalle quali proviene la maggior parte dei combustibili per la produzione di energia sono idrocarburi,
FORZE INTERMOLECOLARI
 FORZE INTERMOLECOLARI Le forze intermolecolari sono forze di attrazione che si stabiliscono tra le molecole che costituiscono una sostanza Determinano la tendenza delle molecole ad avvicinarsi. Per ogni
FORZE INTERMOLECOLARI Le forze intermolecolari sono forze di attrazione che si stabiliscono tra le molecole che costituiscono una sostanza Determinano la tendenza delle molecole ad avvicinarsi. Per ogni
ORBITA ORBIT LI ALI MOLECOLARI
 ORBITALI MOLECOLARI Una molecola è dotata di una serie di orbitali detti orbitali molecolari Gli elettroni risiedono negli orbitali molecolari che, in molti casi, sono distribuiti (delocalizzati) su tutta
ORBITALI MOLECOLARI Una molecola è dotata di una serie di orbitali detti orbitali molecolari Gli elettroni risiedono negli orbitali molecolari che, in molti casi, sono distribuiti (delocalizzati) su tutta
Forze intermolecolari
 Forze intermolecolari Si vuole descrivere in modo semplice la forza che si esercita tra due molecole A e B, in particolare in base alle caratteristiche elettrostatiche delle molecole. Le forze elettriche
Forze intermolecolari Si vuole descrivere in modo semplice la forza che si esercita tra due molecole A e B, in particolare in base alle caratteristiche elettrostatiche delle molecole. Le forze elettriche
Legame covalente polare
 Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame covalente polare
 Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
= GEOMETRIA MOLECOLARE. (numero di legami) + (angolo di legame) = geometria. V.S.E.P.R.: Valence Shell Electron Pair Repulsion
 GEOMETRIA MOLECOLARE I legami covalenti sono direzionali I metodi sperimentali moderni permettono di conoscere sia la DISTANZA di legame (d) che l ANGOLO di legame (α), quindi una buona teoria del legame
GEOMETRIA MOLECOLARE I legami covalenti sono direzionali I metodi sperimentali moderni permettono di conoscere sia la DISTANZA di legame (d) che l ANGOLO di legame (α), quindi una buona teoria del legame
Ottimizzazione della geometria. Ottimizzazione della geometria A.A ! " B. Civalleri Chimica Computazionale a.a
 Ottimizzazione della geometria A.A. 2006-07 07! " B. Civalleri Chimica Computazionale a.a. 2006-07 1 Ottimizzazione della geometria Definizioni (I) Superficie di energia potenziale (PES) La PES descrive
Ottimizzazione della geometria A.A. 2006-07 07! " B. Civalleri Chimica Computazionale a.a. 2006-07 1 Ottimizzazione della geometria Definizioni (I) Superficie di energia potenziale (PES) La PES descrive
Lezione n. 22. Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
IL LEGAME CHIMICO. Per descrivere come gli elettroni si distribuiscono nell atomo attorno al nucleo si può far riferimento al MODELLO A GUSCI
 IL LEGAME CIMICO Come dagli atomi si costruiscono le molecole 02/19/08 0959 PM 1 Per descrivere come gli elettroni si distribuiscono nell atomo attorno al nucleo si può far riferimento al MODELLO A GUSCI
IL LEGAME CIMICO Come dagli atomi si costruiscono le molecole 02/19/08 0959 PM 1 Per descrivere come gli elettroni si distribuiscono nell atomo attorno al nucleo si può far riferimento al MODELLO A GUSCI
Legame chimico: covalente polare Legame covalente polare
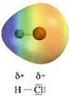 Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
Legame chimico: covalente polare Legame covalente polare Il passaggio dal legame covalente al legame ionico è il risultato di una distribuzione elettronica non simmetrica. Il simbolo δ (lettera greca delta
gruppo amminico Gli aminoacidi polimerizzano durante la sintesi delle proteine mediante la formazione di legami peptidici. gruppo carbossilico
 gruppo amminico Gli aminoacidi polimerizzano durante la sintesi delle proteine mediante la formazione di legami peptidici. gruppo carbossilico Il legame peptidico si ha quando il gruppo carbossilico (-
gruppo amminico Gli aminoacidi polimerizzano durante la sintesi delle proteine mediante la formazione di legami peptidici. gruppo carbossilico Il legame peptidico si ha quando il gruppo carbossilico (-
CAPITOLO 1 ELETTROSTATICA
 CAPITOLO 1 1.1 Introduzione Nell elettromagnetismo studieremo fenomeni elettrici e magnetici che rappresentano un altra interazione fondamentale della natura (dopo quella gravitazionale che abbiamo visto
CAPITOLO 1 1.1 Introduzione Nell elettromagnetismo studieremo fenomeni elettrici e magnetici che rappresentano un altra interazione fondamentale della natura (dopo quella gravitazionale che abbiamo visto
LEGAMI CHIMICI. Gli elettroni esterni sono implicati nella formazione dei legami chimici
 LEGAMI CHIMICI Gli elettroni esterni sono implicati nella formazione dei legami chimici La VALENZA di un elemento è data dal numero di elettroni che esso deve perdere, o acquistare, o mettere in comune
LEGAMI CHIMICI Gli elettroni esterni sono implicati nella formazione dei legami chimici La VALENZA di un elemento è data dal numero di elettroni che esso deve perdere, o acquistare, o mettere in comune
Legame nei cristalli. Cosa tiene insieme un cristallo?
 Legame nei cristalli Cosa tiene insieme un cristallo? L energia di coesione, dovuta all interazione elettrostatica attrattiva fra gli elettroni, carichi negativamente, e i nuclei, carichi positivamente
Legame nei cristalli Cosa tiene insieme un cristallo? L energia di coesione, dovuta all interazione elettrostatica attrattiva fra gli elettroni, carichi negativamente, e i nuclei, carichi positivamente
PROGRAMMAZIONE DIDATTICA ANNUALE DEL DIPARTIMENTO DATI GENERALI
 A.S.2016/17 Data: 27/0./2016 codice 21 0 edizione 1 del 5-05-2005 Pag. 1 di 10. REVISIONE 1 ORDINE SCOLASTICO DATI GENERALI MATERIA: CHIMICA CLASSI: SECONDE AFM TUR. DOCENTI DOCENTE RESPONSABILE : MARILINA
A.S.2016/17 Data: 27/0./2016 codice 21 0 edizione 1 del 5-05-2005 Pag. 1 di 10. REVISIONE 1 ORDINE SCOLASTICO DATI GENERALI MATERIA: CHIMICA CLASSI: SECONDE AFM TUR. DOCENTI DOCENTE RESPONSABILE : MARILINA
1. L energia di legame. 2. I gas nobili e a regola dell ottetto. 3. Il legame covalente. 4. Il legame covalente dativo. 5. Il legame covalente polare
 Capitolo 10 I legami chimici 1. L energia di legame 2. I gas nobili e a regola dell ottetto 3. Il legame covalente 4. Il legame covalente dativo 5. Il legame covalente polare 6. Il legame ionico 7. I composti
Capitolo 10 I legami chimici 1. L energia di legame 2. I gas nobili e a regola dell ottetto 3. Il legame covalente 4. Il legame covalente dativo 5. Il legame covalente polare 6. Il legame ionico 7. I composti
Dipartimento Scientifico-Tecnologico
 ISTITUTO TECNICO STATALE LUIGI STURZO Castellammare di Stabia - NA Anno scolastico 2012-13 Dipartimento Scientifico-Tecnologico CHIMICA, FISICA, SCIENZE E TECNOLOGIE APPLICATE Settore Economico Indirizzi:
ISTITUTO TECNICO STATALE LUIGI STURZO Castellammare di Stabia - NA Anno scolastico 2012-13 Dipartimento Scientifico-Tecnologico CHIMICA, FISICA, SCIENZE E TECNOLOGIE APPLICATE Settore Economico Indirizzi:
MOLECOLE. 2 - i legami chimici. Prof. Vittoria Patti
 MOLECOLE 2 - i legami chimici Prof. Vittoria Patti Gli stati di aggregazione della materia STATO SOLIDO molecole ravvicinate, struttura ordinata, volume proprio, forma propria STATO LIQUIDO molecole
MOLECOLE 2 - i legami chimici Prof. Vittoria Patti Gli stati di aggregazione della materia STATO SOLIDO molecole ravvicinate, struttura ordinata, volume proprio, forma propria STATO LIQUIDO molecole
Il Legame Chimico e la Struttura Molecolare
 A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
I Legami intermolecolari
 I Legami intermolecolari Legami tra gli atomi di una molecola riepilogando Ionico D >1,9 Legami forti Covalente D = differenza di elettronegatività tra gli atomi Metallico (dovuto alla dislocazione di
I Legami intermolecolari Legami tra gli atomi di una molecola riepilogando Ionico D >1,9 Legami forti Covalente D = differenza di elettronegatività tra gli atomi Metallico (dovuto alla dislocazione di
le SOSTANZE Sostanze elementari (ELEMENTI) COMPOSTI Costituiti da due o più atomi DIVERSI tra loro
 Il legame chimico In natura gli atomi sono solitamente legati ad altri in unità più complesse che, se aggregate fra loro costituiscono quello che macroscopicamente percepiamo come materia, le SOSTANZE
Il legame chimico In natura gli atomi sono solitamente legati ad altri in unità più complesse che, se aggregate fra loro costituiscono quello che macroscopicamente percepiamo come materia, le SOSTANZE
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2018-2019 2 Premessa TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2018-2019 2 Premessa TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CORSO DI LAUREA IN INGEGNERIA CIVILE A.A Prova scritta del corso di Chimica A-K Compito prova
 CORSO DI LAUREA IN INGEGNERIA CIVILE A.A. 2012-2013 Prova scritta del corso di Chimica A-K Compito prova Cognome e nome.... n di matricola Nei quesiti a risposta multipla, verranno ANNULLATI i quesiti
CORSO DI LAUREA IN INGEGNERIA CIVILE A.A. 2012-2013 Prova scritta del corso di Chimica A-K Compito prova Cognome e nome.... n di matricola Nei quesiti a risposta multipla, verranno ANNULLATI i quesiti
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN BIOTECNOLOGIE CORSO MONODISCIPLINARE: BIOCHIMICA (6CFU)
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN BIOTECNOLOGIE CORSO MONODISCIPLINARE: BIOCHIMICA (6CFU) Roberto Giacominelli Stuffler IL C.M. BIOCHIMICA È SUDDIVISO IN DUE UNITÀ DIDATTICHE: A) BIOCHIMICA
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN BIOTECNOLOGIE CORSO MONODISCIPLINARE: BIOCHIMICA (6CFU) Roberto Giacominelli Stuffler IL C.M. BIOCHIMICA È SUDDIVISO IN DUE UNITÀ DIDATTICHE: A) BIOCHIMICA
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L
 IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π
 IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
CAPITOLO 4 STRUTTURE MOLECOLARI
 APITL 4 STRUTTURE MLELARI 4.1 (a) Di seguito è mostrata la struttura di Lewis di P 3. Nella teoria VSEPR il numero di coppie di elettroni attorno all atomo centrale è fondamentale per determinare la struttura.
APITL 4 STRUTTURE MLELARI 4.1 (a) Di seguito è mostrata la struttura di Lewis di P 3. Nella teoria VSEPR il numero di coppie di elettroni attorno all atomo centrale è fondamentale per determinare la struttura.
L Atomo Nucleare. Rutherford protoni James Chadwick neutroni 1932
 Programma Misure ed Unità di misura. Incertezza della misura. Cifre significative. Notazione scientifica. Atomo e peso atomico. Composti, molecole e ioni. Formula molecolare e peso molecolare. Mole e massa
Programma Misure ed Unità di misura. Incertezza della misura. Cifre significative. Notazione scientifica. Atomo e peso atomico. Composti, molecole e ioni. Formula molecolare e peso molecolare. Mole e massa
Le idee della chimica
 G. Valitutti A.Tifi A.Gentile Seconda edizione Copyright 2009 Zanichelli editore Capitolo 10 I legami chimici 1. L energia di legame 2. I gas nobili e a regola dell ottetto 3. Il legame covalente 4. Il
G. Valitutti A.Tifi A.Gentile Seconda edizione Copyright 2009 Zanichelli editore Capitolo 10 I legami chimici 1. L energia di legame 2. I gas nobili e a regola dell ottetto 3. Il legame covalente 4. Il
I legami chimici. (parte seconda) Lezioni d'autore
 I legami chimici (parte seconda) Lezioni d'autore Introduzione (I) La teoria del legame di Lewis considera gli elettroni di valenza degli atomi che formano legami, ma prescinde totalmente dal fatto che
I legami chimici (parte seconda) Lezioni d'autore Introduzione (I) La teoria del legame di Lewis considera gli elettroni di valenza degli atomi che formano legami, ma prescinde totalmente dal fatto che
1.039 g g/mol g g/mol
 Un campione di un liquido di massa 0.5438 g, formato da C, H e O, viene bruciato in ossigeno puro. Si ottengono 1.039 g di CO 2 ed 0.6369 g di H 2 O. Determinare la formula chimica (molecolare) Se X(C,H,O)
Un campione di un liquido di massa 0.5438 g, formato da C, H e O, viene bruciato in ossigeno puro. Si ottengono 1.039 g di CO 2 ed 0.6369 g di H 2 O. Determinare la formula chimica (molecolare) Se X(C,H,O)
IBRIDAZIONE. MODELLO DELL ORBITALE di LEGAME
 IBRIDAZIONE MODELLO DELL ORBITALE di LEGAME Approccio più semplice per descrivere la struttura elettronica di una specie sfruttando il concetto di orbitale. METANO Gli atomi nel formare legami usano elettroni
IBRIDAZIONE MODELLO DELL ORBITALE di LEGAME Approccio più semplice per descrivere la struttura elettronica di una specie sfruttando il concetto di orbitale. METANO Gli atomi nel formare legami usano elettroni
Il Legame Chimico e la Struttura Molecolare
 A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
Valitutti, Falasca, Tifi, Gentile. Chimica. concetti e modelli.blu
 Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
IN UN ATOMO SI DISTINGUE UN NUCLEO CARICO POSITIVAMENTE ATTORNO AL QUALE RUOTANO PARTICELLE CARICHE NEGATIVAMENTE: GLI ELETTRONI (e - ) (-)
 LA VITA, LA CHIMICA E L ACQUA PER INIZIARE QUALCHE CENNO DI CHIMICA LA MATERIA E FATTA DI COMBINAZIONI DI ELEMENTI. GLI ELEMENTI SONO COMPOSTI DA SINGOLI ATOMI, LE PIU PICCOLE UNITA CHE MANTENGONO LE PROPRIETA
LA VITA, LA CHIMICA E L ACQUA PER INIZIARE QUALCHE CENNO DI CHIMICA LA MATERIA E FATTA DI COMBINAZIONI DI ELEMENTI. GLI ELEMENTI SONO COMPOSTI DA SINGOLI ATOMI, LE PIU PICCOLE UNITA CHE MANTENGONO LE PROPRIETA
Il legame ionico legame ionico
 Il legame ionico Il legame ionico è il legame che si realizza quando un atomo d un elemento fortemente elettropositivo (e quindi caratterizzato da bassa energia di ionizzazione) si combina con un atomo
Il legame ionico Il legame ionico è il legame che si realizza quando un atomo d un elemento fortemente elettropositivo (e quindi caratterizzato da bassa energia di ionizzazione) si combina con un atomo
ATOMI E MOLECOLE. Psicobiologia Lezione nr. 1. Prof. Lasaponara
 ATOMI E MOLECOLE Psicobiologia Lezione nr. 1 Prof. Lasaponara La struttura dell atomo I legami chimici e le molecole I componenti elementari della materia vivente 20 miliardi di anni fa Caratteristiche
ATOMI E MOLECOLE Psicobiologia Lezione nr. 1 Prof. Lasaponara La struttura dell atomo I legami chimici e le molecole I componenti elementari della materia vivente 20 miliardi di anni fa Caratteristiche
Unità didattica n 1 - Il primo principio della termodinamica
 PROGRAMMA PREVISTO Anno Scolastico 2006-2007 Testo di riferimento: Le Vie della Fisica voll. 2-3 (Battimelli G. Stilli R.) Unità didattica n 1 - Il primo principio della termodinamica Conoscenza dei concetti
PROGRAMMA PREVISTO Anno Scolastico 2006-2007 Testo di riferimento: Le Vie della Fisica voll. 2-3 (Battimelli G. Stilli R.) Unità didattica n 1 - Il primo principio della termodinamica Conoscenza dei concetti
Chimica Biologica A.A α-elica foglietto β reverse turn
 Chimica Biologica A.A. 2010-2011 α-elica foglietto β reverse turn Str. Secondaria sperimentalmente osservata: Si distinguono fondamentalmente tre tipi di strutture secondarie: α elica foglietto β reverse
Chimica Biologica A.A. 2010-2011 α-elica foglietto β reverse turn Str. Secondaria sperimentalmente osservata: Si distinguono fondamentalmente tre tipi di strutture secondarie: α elica foglietto β reverse
Riassunto modelli atomici.
 Lezione 6 1. La teoria atomica moderna 2. Il modello quantomeccanico dell atomo 3. Gli orbitali 4. Carica nucleare efficace 5. Principi di Pauli e Hund 6. Configurazioni elettroniche 7. AUFBAU Riassunto
Lezione 6 1. La teoria atomica moderna 2. Il modello quantomeccanico dell atomo 3. Gli orbitali 4. Carica nucleare efficace 5. Principi di Pauli e Hund 6. Configurazioni elettroniche 7. AUFBAU Riassunto
Coesione nei solidi, energia di coesione
 Coesione nei solidi, energia di coesione Cosa tiene insieme un cristallo? La coesione in un solido è un fenomeno complesso, dovuta al bilancio di forze repulsive fra cariche dello stesso segno (nuclei-nuclei,
Coesione nei solidi, energia di coesione Cosa tiene insieme un cristallo? La coesione in un solido è un fenomeno complesso, dovuta al bilancio di forze repulsive fra cariche dello stesso segno (nuclei-nuclei,
CAPITOLO 1 FORZA ELETTROSTATICA CAMPO ELETTROSTATICO
 CAPITOLO 1 FORZA ELETTROSTATICA CAMPO ELETTROSTATICO Elisabetta Bissaldi (Politecnico di Bari) A.A. 2018-2019 2 L elettromagnetismo INTERAZIONE ELETTROMAGNETICA = INTERAZIONE FONDAMENTALE Fenomeni elettrici
CAPITOLO 1 FORZA ELETTROSTATICA CAMPO ELETTROSTATICO Elisabetta Bissaldi (Politecnico di Bari) A.A. 2018-2019 2 L elettromagnetismo INTERAZIONE ELETTROMAGNETICA = INTERAZIONE FONDAMENTALE Fenomeni elettrici
Le proprietà delle sostanze dipendono dal tipo di legame che unisce gli atomi e dalla forma delle molecole.
 4.1 Angolo di legame e forma delle molecole Le proprietà delle sostanze dipendono dal tipo di legame che unisce gli atomi e dalla forma delle molecole. La forma e le dimensioni delle molecole, la disposizione
4.1 Angolo di legame e forma delle molecole Le proprietà delle sostanze dipendono dal tipo di legame che unisce gli atomi e dalla forma delle molecole. La forma e le dimensioni delle molecole, la disposizione
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
1. L energia di legame
 legami chimici 1. L energia di legame Nonostante l enorme numero di combinazioni possibili fra gli atomi, non tutte sono realizzabili: un composto si forma solo se la sua energia potenziale è minore dei
legami chimici 1. L energia di legame Nonostante l enorme numero di combinazioni possibili fra gli atomi, non tutte sono realizzabili: un composto si forma solo se la sua energia potenziale è minore dei
delle curve isoterme dell anidride carbonica
 COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
IL LEGAME A IDROGENO
 IL LEGAME A IDROGENO Il legame idrogeno è un particolare tipo di interazione fra molecole che si forma ogni volta che un atomo di idrogeno, legato ad un atomo fortemente elettronegativo (cioè capace di
IL LEGAME A IDROGENO Il legame idrogeno è un particolare tipo di interazione fra molecole che si forma ogni volta che un atomo di idrogeno, legato ad un atomo fortemente elettronegativo (cioè capace di
Aspetti generali della Chimica Organica 1 parte
 Aspetti generali della Chimica Organica 1 parte Struttura e Legame: Il Carbonio nella Tabella Periodica Il Modello di Lewis Calcolo delle cariche formali Teoria della Risonanza Dove troviamo il carbonio
Aspetti generali della Chimica Organica 1 parte Struttura e Legame: Il Carbonio nella Tabella Periodica Il Modello di Lewis Calcolo delle cariche formali Teoria della Risonanza Dove troviamo il carbonio
Il legame chimico. Energia di legame
 Il legame chimico Si definisce Legame chimico l effetto correlato alla forza che tiene uniti due atomi Elemento, o sostanza elementare, se vi è un legame tra atomi uguali Composto, o sostanza composta,
Il legame chimico Si definisce Legame chimico l effetto correlato alla forza che tiene uniti due atomi Elemento, o sostanza elementare, se vi è un legame tra atomi uguali Composto, o sostanza composta,
Comune ordine di riempimento degli orbitali di un atomo
 Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
strutture geometriche sperimentali
 Misure sperimentali strutture geometriche sperimentali principali metodi di misura fase gassosa Spettroscopia nelle microonde Diffrazione degli elettroni Spettroscopia infrarossa e Raman fase solida Diffrazione
Misure sperimentali strutture geometriche sperimentali principali metodi di misura fase gassosa Spettroscopia nelle microonde Diffrazione degli elettroni Spettroscopia infrarossa e Raman fase solida Diffrazione
IDROCARBURI: classificazione
 ALCANI 1 IDROCARBURI: classificazione 2 ALCANI Formula bruta: C n H 2n+2 1 C CH 4 2 C C 2 H 6 3 C C 3 H 8 4 C C 4 H 10 3 ALCANI: ibridazione Orbitali s, p e sp 3 z orbitale 2s y x z z z orbitali 2p y x
ALCANI 1 IDROCARBURI: classificazione 2 ALCANI Formula bruta: C n H 2n+2 1 C CH 4 2 C C 2 H 6 3 C C 3 H 8 4 C C 4 H 10 3 ALCANI: ibridazione Orbitali s, p e sp 3 z orbitale 2s y x z z z orbitali 2p y x
A.A Laboratorio 3 - Esercizio
 Laboratorio 3 Studio del dimero dell acqua A.A. 2007-08 08! " 1 Laboratorio 3 - Esercizio 1) Ottimizzazione della geometria e calcolo delle frequenze vibrazionali della molecola di acqua Confronto con
Laboratorio 3 Studio del dimero dell acqua A.A. 2007-08 08! " 1 Laboratorio 3 - Esercizio 1) Ottimizzazione della geometria e calcolo delle frequenze vibrazionali della molecola di acqua Confronto con
Formule e Strutture. Chimica Generale ed Inorganica. Chimica Inorganica 1. prof. Dario Duca
 Formule e Strutture Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca richiami su strutture molecolari, risonanza, cariche formali elettronegatività l elettronegatività origina da un
Formule e Strutture Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca richiami su strutture molecolari, risonanza, cariche formali elettronegatività l elettronegatività origina da un
Cos è un trasformazione chimica?
 Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
Chimica Lezione 1 Cos è un trasformazione chimica? Una reazione chimica è una trasformazione della materia che avviene senza variazioni misurabili di massa, in cui uno o più reagenti iniziali modificano
Stereochimica di alcani e cicloalcani
 di alcani e cicloalcani Conformazioni, conformeri Due conformazioni dell etano. Le conformazioni sono arrangiamenti diversi di atomi che interconvertono per rotazione attorno al legame C-C. Rappresentazione
di alcani e cicloalcani Conformazioni, conformeri Due conformazioni dell etano. Le conformazioni sono arrangiamenti diversi di atomi che interconvertono per rotazione attorno al legame C-C. Rappresentazione
Forze intermolecolari
 Forze intermolecolari Le forze intermolecolari sono forze attrattive tra molecole, tra ioni o tra ioni e molecole. In assenza di tali forze tutte le molecole sarebbero gas le molecole possono stabilire
Forze intermolecolari Le forze intermolecolari sono forze attrattive tra molecole, tra ioni o tra ioni e molecole. In assenza di tali forze tutte le molecole sarebbero gas le molecole possono stabilire
Teorie del legame chimico. Teorie del legame chimico
 Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Risultati della teoria di Hartree
 Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
3. Cicloalcani. Formula generale: C n H 2n in serie omologa C 9 C 10 C 11 C 12 >C 12. Es.: 1,1-dimetilciclopropano. Anelli. piccoli. Anelli.
 . Cicloalcani Formula generale: C n 2n in serie omologa ciclopropano ciclobutano ciclopentano Anelli piccoli C 9 C 10 C 11 C 12 cicloottano ciclononano ciclodecano cicloundecano ciclododecano Anelli medi
. Cicloalcani Formula generale: C n 2n in serie omologa ciclopropano ciclobutano ciclopentano Anelli piccoli C 9 C 10 C 11 C 12 cicloottano ciclononano ciclodecano cicloundecano ciclododecano Anelli medi
Le forze intermolecolari Manifestazione delle forze intermolecolari
 1 Le forze intermolecolari Manifestazione delle forze intermolecolari 2 I gas nobili (He, Ne, Ar...) che NON formano legami chimici dovrebbero restare gassosi a qualsiasi temperatura. Invece a T molto
1 Le forze intermolecolari Manifestazione delle forze intermolecolari 2 I gas nobili (He, Ne, Ar...) che NON formano legami chimici dovrebbero restare gassosi a qualsiasi temperatura. Invece a T molto
Olimpiadi di Chimica
 Olimpiadi di Chimica Acqua Oro Zucchero I Legami Chimici F N F F Il legame chimico il legame ionico Polare il legame covalente Dativo Gli elettroni di valenza sono gli elettroni del livello più esterno
Olimpiadi di Chimica Acqua Oro Zucchero I Legami Chimici F N F F Il legame chimico il legame ionico Polare il legame covalente Dativo Gli elettroni di valenza sono gli elettroni del livello più esterno
Il legame chimico. Energia di legame
 Il legame chimico Si definisce Legame chimico l effetto correlato alla forza che tiene uniti due atomi Elemento, o sostanza elementare, se vi è un legame tra atomi uguali Composto, o sostanza composta,
Il legame chimico Si definisce Legame chimico l effetto correlato alla forza che tiene uniti due atomi Elemento, o sostanza elementare, se vi è un legame tra atomi uguali Composto, o sostanza composta,
Esercizi sulle Geometrie Molecolari
 Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Esercizi sulle Geometrie Molecolari Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/education/general-chemistry-exercises/
Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Esercizi sulle Geometrie Molecolari Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/education/general-chemistry-exercises/
I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo
 La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
Gli Stati della Materia
 John C. Kotz Paul M. Treichel John Townsend http://academic.cengage.com/kotz Capitolo 1 Materia e Misure 1 Benvenuti nel Mondo della Chimica 2 Versione italiana a cura di Giaime Marongiu e Guido Ennas
John C. Kotz Paul M. Treichel John Townsend http://academic.cengage.com/kotz Capitolo 1 Materia e Misure 1 Benvenuti nel Mondo della Chimica 2 Versione italiana a cura di Giaime Marongiu e Guido Ennas
