18.3. Il nucleo del calore e altre applicazioni Il nucleo del calore.
|
|
|
- Giacinta Maggio
- 5 anni fa
- Visualizzazioni
Transcript
1 18.3. Il nucleo del calore e altre applicazioni Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita. Consideramo l equazione del calore 1 T t = D T x, Come abbiamo già sottolineato, questa equazione è ottenuta dall equazione di continuità T t = J x che esprime la conservazione locale della densità di energia T (x, t). Questo significa che vale la legge di conservazione T (x, t) dx = Θ Energia totale e quindi che l equazione del calore preserva la norma L 1 della temperatura. In altre parole, come abbiamo già messo in evidenza per la propagazione del calore in un filo finito, lo spazio funzionale adeguato per l equazione del calore è lo spazio di Banach L 1. Per un filo di lunghezza infinita, è lo spazio L 1 (R). Supponiamo di volere trovare una soluzione dell equazione del calore con i metodi dell analisi dimensionale: [D] = L T 1 è una costante del problema; Θ = Lθ (θ= temperatura), è proporzionale alla quantità iniziale di energia immessa nel sistema. Naturalmente, [x] = L e [t] = T. La quantità u = x/ Dt è adimensionale. La soluzione che cerchiamo è una temperatura: [T = θ. Cerchiamola come funzione di (t, D, Θ). Deve quindi valere [T ] = θ = [t] a [D b ][Θ c ] = T a L b T b θ c L c = L b+c T a b θ c da cui b + c = 0 a b = 0 c = 1 che ha soluzioni a = 1 b = 1 c = 1 Quindi l analisi dimensionale ci dice che la soluzione è della forma T (x, t) = Θ ( ) x Φ Dt Dt 1 Usiamo il simbolo T in vece di T perché tra poco faremo dell analisi dimensionale e T denoterà la dimensione del tempo. 1
2 dove Φ = Φ(u) è una funzione da terminare. Il punto importante è che Φ è una funzione di una variabile adimensionata, la combinazione u = x/ Dt, e non di x e t separatamente. Ora, f x = Θ 1 Dt Dt Φ (u) f t = 1 Θ [Φ(u) + Dt 3/ uφ (u)] Per l equazione del calore Θ 1 Dt Dt Φ (u) = D 1 Θ [Φ(u) + Dt 3/ uφ (u)] da cui Φ + u Φ + 1 Φ = 0 Con il vincolo (conservazione dell energia = norma L 1 ) Φ(u)du = 1 L equazione sembrerebbe difficile da risolvere, ma non lo è. Riconosciamo a primo membro un differenziale esatto: d [Φ + u ] du Φ = 0 Quindi Φ + u Φ = costante Tuttavia, ogni soluzione fisicamente ragionevole deve avere Φ 0 e Φ 0 quando u. Quindi la costante di integrazione deve essere zero. L equazione diventa Φ + u Φ = 0 Abbiamo già incontrato questa equazione nella lezione 10.1 quando abbiamo calcolato la trasformata di Fourier di una gaussiana con il metodo della derivazione sotto il segno di integrale. La soluzione è Ce u /4 Determiniamo C imponendo la normalizzazione C e u /4 du = C 4π = 1 Φ(u)du = 1, da cui E avevamo trovato + π e ax e ikx dx = a e k 4a
3 3 Dunque Φ(u) = 1 4π e u /4 Ritornando alle variabili originali, T (x, t) = Θ e x /4Dt soluzione generale È sorprendente che un po di analisi dimensionale ci abbia permesso di trovare una soluzione di f (1) t = D f x, E forse è ancora più sorprendente che la soluzione trovata, f(x, t) = T (x, t) = Θ e x /4Dt, per quanto non sia la soluzione generale, permetta agevolmente di generare tutte le soluzioni del problema al contorno, o di Cauchy, per la propagazione del calore in un filo illimitato, quando è specificato il valore della distribuzione di temperatura al tempo t = 0. Prima di mostrare questo, facciamoci un idea di che tipo di soluzione abbiamo. Posto n = 1/(4Dt), riconosciamo in () K(x, t) = 1 e x /4Dt un approssimante regolare della delta: per t 0 (n ), la funzione K diventa la delta di Dirac. Nel senso che lim K(x y, t)f(y)dy = f(y) t 0 per ogni funzione f buona, cioè in S (R). Quindi la soluzione T trovata con i metodi dell analisi dimensionale descrive la propagazione del tempo in cui tutto il calore Θ al tempo iniziale è concentrato in una sorgente puntiforme posta nell origine. La funzione K = K(x, t) definita dalla () è detta nucleo del calore ( heat kernel ) e interviene in una miriade di situazioni: dai processi stocastici (in particolare, il moto brwowniano), alla meccanica quantistica e alla teoria quantistica dei campi. Nel nostro caso, se consideriamo la convoluzione di K(x, t) con una funzione f 0 (x) e formiamo la funzione (3) 1 f(x, t) = K f 0 (x, t) = K(x y, t)f 0 (y)dy = e (x y) /4Dt f 0 (y)dy
4 raggiungiamo un triplice scopo: A. Otteniamo una classe più ampia di soluzioni di (1). B. Più precisamente, risolviamo completamente il problema di Cauchy di (1) per il dato iniziale f(x, 0) = f 0 (x), dove f 0 (x) è una funzione assegnata (possibilmente buona). Per queste soluzioni il calore totale Θ, anzichè essere concentrato in un punto è spalmato su tutto R, secondo la distribuzione iniziale di temperatura, e f(x, t) dx = f 0 (x) dx = Θ è preservato nel tempo. C. Come bonus, otteniamo la soluzione dell equazione di Schrödinger di una particella libera in una dimensione. Vediamo più in dettaglio questi punti. A. Se assumiamo che f 0 sia buona, possiamo scambiare senza problemi derivate e integrali. Poiché K(x, t) è soluzione dell equazione del calore anche K f 0 (x, t) = K(x y, t)f 0 (y)dy lo sarà (lo scambio vale anche per condizioni più deboli su f, ma adesso non vogliamo addentrarci in questo). B. Assumendo che la soluzione (1) sia unica (e lo è, ma non lo dimostriamo), f(x, t) è la soluzione di (1) che converge al dato iniziale f 0 (x) per t 0, in quanto, come abbiamo già mostrato, si ha lim K(x y, t)f 0 (y)dy = f 0 (y). t 0 C. Per rotazione t it nel piano complesso della variabile t, si ottiene 1 K(x, it) = e ix /4Dt def = G(x, t) 4πDit posto D = /m (come abbiamo già fatto per una particella in una scatola unidimensionale), si ottiene m / t (4) G(x, t) = π it eimx Si verifica facilmente per sostituzione che Ψ(x, t) = G(x, t) è soluzione dell equazione libera di Schrödinger i Ψ t = Ψ m x Tuttavia, prima di dire che le cose sono esattamente come per l equazione del calore, serve un po di cautela. Infatti, nella rotazione complessa si sono perse le proprietà di K come funzione buona: a differenza di K, la funzione G non è 4
5 buona e, al variare di t tendente a zero, non si ha più una successione regolare di approssimanti della delta. Si può tuttavia dimostrare che (ma per il momento non lo faremo) lim G(x y, t)ψ 0 (y)dy = Ψ 0 (x). t 0 Assodato questo, siamo nella stessa situazione di prima: Ψ(x, t) = G(x y, t)ψ 0 (y)dy è la soluzione dell equazione libera di Schrödinger per il dato iniziale Ψ(x, 0) = Ψ 0 (x). 5 Risolviamo il problema al contorno analisi di Fourier f t = D f x f(x, 0) = f 0 (x) con i metodi dell analisi di Fourier. Per comodità, lavoriamo con la convenzione 3 per la trasformata di Fourier: f(k) = 1 π f(x) = 1 π Allora la soluzione è data dallo schema: f(x)e ikx f(k)e ikx dx f(x, t) t = D f(x, t) x F soluzione f(x, t) = 1 π F 1 f 0 (k)e Dkt e ikx dx f(k, t) t = Dk f(k, t) soluzione f(k, t) = f0 (k)e Dk t
6 6 Possiamo adesso usare la trasformata inversa del dato iniziale e ottenere f(x, t) = 1 f 0 (k)e Dkt e ikx dx π = 1 [ 1 ] f 0 (y)e iky dy e Dkt e ikx dk π π = 1 π = 1 π = [ 1 e Dkt e ik(y x) dk [ π Dt e in accordo con quanto già trovato. ] (y x) 4Dt f 0 (y)dy e (x y) /4Dt f 0 (y)dy ] f 0 (y)dy Oscillazioni di temperatura nel suolo. È dato il problema al contornoper lo studio della propagazione del calore nel suolo (x = 0 è il livello del suolo, x > 0 misura la profondità): T t = D T per 0 < x < 3, t > 0 x T (0, t) = Ae iωt T (x, t) Si cerchi una soluzione del tipo allora che ha soluzione per Dunque (parte reale del secondo membro se T temperatura) funzione limitata in x e t T = u(x)e iωt Du (x) = iωu(x) u(x) = c 1 e i ω D x + c e i ω D x. i = e iπ/4 = cos π/4 + i sin(π/4) = 1 + i. ω u(x) = c 1 e D (1+i)x + c e ω D (1+i)x Le costanti c 1 e c si determinano imponendo le condizioni al contorno: u deve essere limitata per x e deve valere T (0, t) = Ae iωt, quindi deve essere u(0) = A. Si ha così c 1 = 0 e c = A e quindi T (x, t) = Ae ω D (1+i)x e iωt = Ae ω D x e iω t 1 x Dω
7 7 Passando alla parte reale (poiché T è una temperatura) u(x, t) = Ae ( ω D x cos t 1 ) x Dω Ne risulta che la temperatura T ad una qualsiasi profondità x è una funzione sinusoidale di t con ampiezza Ae ω D x minore dell ampiezza A in superficie, e la riduzione è tanto maggiore quanto maggiore è la profondità e quanto maggiore è la frequenza delle oscillazioni. La fase varia da punto a punto e, precisamente, le oscillazioni si risentono verso l interno con un ritardo x/( Dω) proporzionale alla distanza x dalla superficie, cosa che si può esprimere dicendo che le oscillazioni di temperatura si propagano nell interno con una velocità Dω (tanto maggiore quindi quanto maggiore è la frequenza ω). Ne deriva, in particolare che per x = π Dω le oscillazioni sono in opposizione di fase con quelle in superficie. Poiché il problema è lineare, se al suolo sono presenti due oscillazioni di frequenza ω 1 e ω, la temperatura sarà la sovrapposizione lineare delle temperatire per le due oscillazioni. Questo permette di confrontare le variazioni diurne e stagionali. Si trova così che l assorbimento e la velocità di propagazione delle oscillazioni diurne sono maggiori di quelle annue. Ad esempio, per un ordinario terreno umido (D = ) un escursione diurna di 0 0, si riduce a a soli 36 cm di profondità (dove le oscillazioni sono opposte a quelle superficiali) e a ad un metro. Un escursione annua di 0 0, invece, si ridurrebbe a a 30 cm, a ad un metro e a 0. 0 a 10 metri (a tale profondità si può dunque ritenere che la temperatura resti costante nel passaggio dall estate all inverno). È interessante osservare che la teoria (già sviluppata da Fourier) predice che ad una profondità di -3 metri circa le oscillazioni della temperatura sono in opposizione di fase di circa sei mesi (la temperatura nel terreno sarà più calda in inverno e più fredda in estate). Il che spiega perchè conviene avere la cantina di qualche metro sotto il livello del suolo Legge dei grandi numeri e limite centrale. Supponete di lanciare due dadi. La probabilità che la somma sia 7 è p(7) = p(1)p(7 1)+p()p(7 )+p(3)p(7 3)+p(4)p(7 4)+p(5)p(7 5)+p(6)p(7 6) Questa regola è del tutto generale: la probabilità della somma di due variabili casuali indipendenti, con distribuzioni di probabilità f(x) e g(y) rispettivamente, è il prodotto di convoluzione delle due distribuzioni di probabilità f g(x) = f(x)g(x y)dy
8 Se sommate N variabili casuali indipendenti, tutte con la stessa distribuzione di probabilità, la distribuzione della somma è p }.{{.. } p (x) = p N (x) N volte D ora in poi, per semplicità, assumeremo che p sia a media zero. Se moltiplicate per α una variabile casuale con distribuzione f(x), la sua distribuzione diventa (1/α)f(x/α). Quindi, se dividete per N la somma di N variabili casuali indipendenti, tutte con la stessa distribuzione p(x), questa variabile casuale, detta media empirica, ha distribuzione Np N (Nx) pe determinare che cosa diventa questa distribuzione per N grande, prendiamone la trasformata di Fourier N 1 N p(k/n)n = p(k/n) N Non è difficile vedere che questa funzione tende ad un valore costante e che quindi la p tende alla delta concentrata in zero (legge dei grandi numeri.../ SPIEGARE/) Limite centrale: dividiamo per N: Np N ( Nx) Passiamo alla trsformata di Fourier 8... /DA FINIRE/ p(k/ N) N
19.1. Il nucleo del calore e altre applicazioni Il nucleo del calore.
 19.1. Il nucleo del calore e altre applicazioni. 19.1.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
19.1. Il nucleo del calore e altre applicazioni. 19.1.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
Trasformata di Fourier e applicazioni
 Trasformata di Fourier e applicazioni Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio: Calcoliamo la trasformata di Fourier di f (x) = e x 2 x n f (x) L 1 (R) per ogni
Trasformata di Fourier e applicazioni Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio: Calcoliamo la trasformata di Fourier di f (x) = e x 2 x n f (x) L 1 (R) per ogni
LA TRASFORMATA DI FOURIER
 LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
Esame di Fisica Matematica 2, a.a (5/6/2012)
 Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
Esperimenti computazionali con Mathematica: la trasformata di Fourier
 Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
Matematica Open Source http://www.extrabyte.info Quaderni di Analisi Matematica 06 Esperimenti computazionali con Mathematica: la trasformata di Fourier Marcello Colozzo 3 0 5 5 0 Ω LA TRASFORMATA DI FOURIER
Dalla prova scritta del 18/01/2011
 Esercitazione 8 Lucia Pilleri /0/0 Dalla prova scritta del 8/0/0 Esercizio Determinare i valori di α e β che rendono ortogonali le matrici B ] α α C β ] β e, in corrispondenza di una coppia di tali valori,
Esercitazione 8 Lucia Pilleri /0/0 Dalla prova scritta del 8/0/0 Esercizio Determinare i valori di α e β che rendono ortogonali le matrici B ] α α C β ] β e, in corrispondenza di una coppia di tali valori,
2. Calcolare l area della regione Ω contenuta nel primo quadrante, delimitata dalle seguenti curve. : y = x 2 + x γ 2 : y = x 2 γ 3 : y = 1 x 2.
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Esercizi sul calcolo integrale. Calcolare l area della regione Ω contenuta nel primo quadrante, deitata dalle seguenti curve γ : y + γ :
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Esercizi sul calcolo integrale. Calcolare l area della regione Ω contenuta nel primo quadrante, deitata dalle seguenti curve γ : y + γ :
Il Principio di Indeterminazione di Heisenberg
 Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Fondamenti di Meccanica Quantistica (Prof. Tarantelli)
 Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ
 2/3 DISTRIBUZIONI SINGOLARI E "FUNZIONE" DELTA DI DIRAC 0/ DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ Consideriamo una distribuzione continua di una data quantità Q ad esempio la carica elettrica o la
2/3 DISTRIBUZIONI SINGOLARI E "FUNZIONE" DELTA DI DIRAC 0/ DISTRIBUZIONI SINGOLARI E FUNZIONE DENSITÀ Consideriamo una distribuzione continua di una data quantità Q ad esempio la carica elettrica o la
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. 2
 Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
f(x) = E chiaro che in questo caso, l integrale di f si puo fare ed e finito: f(x)dx = dx = b a
 1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
Appunti integrativi per il Corso di Metodi Matematici per l Ingegneria A.A. 2015/2016
 Appunti integrativi per il Corso di Metodi Matematici per l Ingegneria A.A. 5/6 Marco Bramanti Politecnico di Milano October 8, 5 Applicazioni della prima formula integrale di Cauchy al problema di Dirichlet
Appunti integrativi per il Corso di Metodi Matematici per l Ingegneria A.A. 5/6 Marco Bramanti Politecnico di Milano October 8, 5 Applicazioni della prima formula integrale di Cauchy al problema di Dirichlet
Analisi Vettoriale A.A Soluzioni del foglio 5. y = y 2, dy y 2 = x
 Analisi Vettoriale A.A. 2006-2007 - Soluzioni del foglio 5 5. Esercizio Assegnato il problema di Cauchy y = y 2, y(0) = k determinare per ogni k la soluzione y(x), determinare il suo insieme di esistenza,
Analisi Vettoriale A.A. 2006-2007 - Soluzioni del foglio 5 5. Esercizio Assegnato il problema di Cauchy y = y 2, y(0) = k determinare per ogni k la soluzione y(x), determinare il suo insieme di esistenza,
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
19 Problemi al contorno
 19 Problemi al contorno 19.1 Equazioni alle derivate parziali Una trattazione completa delle equazioni alle derivate parziali ( PDE, da adesso in poi 1 ) esula dagli scopi di questo corso. Qui ci limiteremo
19 Problemi al contorno 19.1 Equazioni alle derivate parziali Una trattazione completa delle equazioni alle derivate parziali ( PDE, da adesso in poi 1 ) esula dagli scopi di questo corso. Qui ci limiteremo
f(n)r n e inx lim Se f(x) C(T) allora f S (r) f(x) = lim e inx
 17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
La funzione di distribuzione Gaussiana normale
 La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
1. Scrivere l equazione di Schrödinger unidimensionale per una particella di massa m con energia potenziale V (x) = mω2
 1 Teoria Una particella di massa m = 1 g e carica elettrica q = 1 c viene accelerata per un tratto pari a l = m da una differenza di potenziale pari av = 0 volt Determinare la lunghezza d onda di De Broglie
1 Teoria Una particella di massa m = 1 g e carica elettrica q = 1 c viene accelerata per un tratto pari a l = m da una differenza di potenziale pari av = 0 volt Determinare la lunghezza d onda di De Broglie
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 10 2.11.2016 Equazione di Poisson Metodo delle cariche immagine Anno Accademico 2016/2017 Equazione di Poisson Tramite
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 10 2.11.2016 Equazione di Poisson Metodo delle cariche immagine Anno Accademico 2016/2017 Equazione di Poisson Tramite
FM210 / MA - Prima prova pre-esonero ( )
 FM10 / MA - Prima prova pre-esonero (4-4-018) 1. Una particella di massa m si muove in una dimensione sotto l effetto di una forza posizionale, come descritto dalla seguente equazione: mẍ = A x xx 0 3x
FM10 / MA - Prima prova pre-esonero (4-4-018) 1. Una particella di massa m si muove in una dimensione sotto l effetto di una forza posizionale, come descritto dalla seguente equazione: mẍ = A x xx 0 3x
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre nx 1 + n α x 2.
 Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre 7. Si consideri la successione di funzioni f n, dove f n : [, [ R è definita da e dove α >
Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre 7. Si consideri la successione di funzioni f n, dove f n : [, [ R è definita da e dove α >
1) D0MINIO FUNZIONE. Determinare il dominio della funzione f (x) = 4 x 2 4x + 3 x 2 6x + 8 Deve essere. x 2 6x + 5 (x 1) (x 5)
 ) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano:
 12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano: u = 0 in R u = g in R 12.3.1. Distribuzione di temperatura
12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano: u = 0 in R u = g in R 12.3.1. Distribuzione di temperatura
Funzioni Test, Distribuzioni e Applicazioni
 Capitolo 1 Funzioni Test, Distribuzioni e Applicazioni In questo capitolo discuteremo le distribuzioni, le funzioni test e loro applicazioni principali. Il motivo principale per introdurre le distribuzioni
Capitolo 1 Funzioni Test, Distribuzioni e Applicazioni In questo capitolo discuteremo le distribuzioni, le funzioni test e loro applicazioni principali. Il motivo principale per introdurre le distribuzioni
Analisi Reale e Complessa - a.a. 2008/2009
 Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
5π/2. 3π/2. y = f(x) π π. -5π/2-2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2 3π 7π. -π/2
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI /9/8) Docente: Claudia Anedda ) Data la funzione yx) x + π, x, π) prolungarla su tutto R in modo tale che sia una funzione π-periodica pari, disegnare
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI /9/8) Docente: Claudia Anedda ) Data la funzione yx) x + π, x, π) prolungarla su tutto R in modo tale che sia una funzione π-periodica pari, disegnare
Equazioni differenziali
 Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
Equazioni Differenziali
 Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
Equazioni Differenziali Carla A. Ferradini December 9, 217 1 Introduzione e notazioni Un equazione differenziale è un equazione che ha come incognita una funzione. In particolare un equazione differenziale
La Trasformata di Fourier
 La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
1 Introduzione all operatore di Laplace.
 CORSO DI ANALISI IN PIÙ VARIABILI II CORSO DI LAUREA IN MATEMATICA L OPERATORE DI LAPLACE 1 Introduzione all operatore di Laplace. Diamo un esempio di un problema di fisica matematica la cui equazione
CORSO DI ANALISI IN PIÙ VARIABILI II CORSO DI LAUREA IN MATEMATICA L OPERATORE DI LAPLACE 1 Introduzione all operatore di Laplace. Diamo un esempio di un problema di fisica matematica la cui equazione
Stati Coerenti. Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana. p = i d.
 1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
1 Stati Coerenti Definizione di stato coerente Consideriamo un oscillatore 1-dimensionale descritto dalla hamiltoniana H = 1 m p + 1 m ω x (1) Per semplicitá introduciamo gli operatori autoaggiunti adimensionali
(1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare)
 1 Spazi vettoriali (1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare) (a) R 5 (b) [0, ) (c) x R 2 : x 1 + 2x 2 = 0} (d) x R 2 : x 2 1 + 2x 2 = 0} (e) x R 2 : x 1 > x
1 Spazi vettoriali (1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare) (a) R 5 (b) [0, ) (c) x R 2 : x 1 + 2x 2 = 0} (d) x R 2 : x 2 1 + 2x 2 = 0} (e) x R 2 : x 1 > x
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
12 L equazione delle onde in una dimensione
 1 L equazione delle onde in una dimensione 1.1 L equazione omogenea delle onde L equazione delle onde è l equazione che descrive lo sviluppo di un onda che si propaga in un mezzo. Descrive, per esempio,
1 L equazione delle onde in una dimensione 1.1 L equazione omogenea delle onde L equazione delle onde è l equazione che descrive lo sviluppo di un onda che si propaga in un mezzo. Descrive, per esempio,
Metalli come gas di elettroni liberi
 Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Esercitazione del 6 Dicembre 2011
 Facoltà di Ingegneria dell Università degli Studi di Firenze CdS in Ingegneria per l Ambiente, le Risorse ed il Territorio Complementi di Analisi Matematica A.A. 11/1 Esercitazione del 6 Dicembre 11 Attenzione:
Facoltà di Ingegneria dell Università degli Studi di Firenze CdS in Ingegneria per l Ambiente, le Risorse ed il Territorio Complementi di Analisi Matematica A.A. 11/1 Esercitazione del 6 Dicembre 11 Attenzione:
La funzione di Green
 La funzione di Green Corso di Fisica Matematica 2, a.a. 203-204 Dipartimento di Matematica, Università di Milano 5/2/203 Vogliamo ora considerare l equazione del calore non omogenea, u t α 2 u xx = f(x,
La funzione di Green Corso di Fisica Matematica 2, a.a. 203-204 Dipartimento di Matematica, Università di Milano 5/2/203 Vogliamo ora considerare l equazione del calore non omogenea, u t α 2 u xx = f(x,
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
(ln 5)i 1 i. (c) (d) Scriviamo il numero complesso assegnato in forma algebrica:
 Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP
 Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP Docente:Alessandra Cutrì Equazione delle onde unidimensionale non omogenea u tt (x, t = a 2 u xx (x,
Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP Docente:Alessandra Cutrì Equazione delle onde unidimensionale non omogenea u tt (x, t = a 2 u xx (x,
1 Serie di Fourier uni-dimensionale
 Università di Roma La Sapienza Corso di Fisica Matematica Superiore Esercizi sulla serie di Fourier // Ottobre 2016 Gli Esercizi proposti sono risolubili utilizzando esclusivamente la teoria svolta durante
Università di Roma La Sapienza Corso di Fisica Matematica Superiore Esercizi sulla serie di Fourier // Ottobre 2016 Gli Esercizi proposti sono risolubili utilizzando esclusivamente la teoria svolta durante
Esame di Fisica Matematica III, a.a (27/9/2011)
 Esame di Fisica Matematica III, a.a. 010-011 (7/9/011) Tempo a disposizione: DUE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Si determini, attraverso
Esame di Fisica Matematica III, a.a. 010-011 (7/9/011) Tempo a disposizione: DUE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Si determini, attraverso
Trasformata di Fourier e proprietà-convoluzione ed equazione del calore-teorema di Shannon su Campionamento di segnali
 Trasformata di Fourier e proprietà-convoluzione ed equazione del calore-teorema di Shannon su Campionamento di segnali Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio:
Trasformata di Fourier e proprietà-convoluzione ed equazione del calore-teorema di Shannon su Campionamento di segnali Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio:
Teoria dei Segnali Trasmissione binaria casuale; somma di processi stocastici
 eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
Equazione di Laplace
 Equazione di Laplace. La funzione di Green Sia, indicati con x e y due punti di R 3 E(x, y) = x y Consideriamo la rappresentazione integrale di u(x) C 2 (), anche rinunciando all ipotesi che sia armonica
Equazione di Laplace. La funzione di Green Sia, indicati con x e y due punti di R 3 E(x, y) = x y Consideriamo la rappresentazione integrale di u(x) C 2 (), anche rinunciando all ipotesi che sia armonica
ANALISI C & Complementi di Analisi Matematica di Base. Prova scritta del 23 gennaio 2007
 Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
Forze Conservative. In generale il lavoro fatto da una forza (più precisamente, da un campo di forze):
 Forze Conservative In generale il lavoro fatto da una forza (più precisamente, da un campo di forze): L = f i F d r, può dipendere dal percorso seguito dalla particella. Se il lavoro fatto da una forza
Forze Conservative In generale il lavoro fatto da una forza (più precisamente, da un campo di forze): L = f i F d r, può dipendere dal percorso seguito dalla particella. Se il lavoro fatto da una forza
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Convergenza puntuale ed uniforme delle serie di Fourier
 Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2
![METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2 METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2](/thumbs/96/130608003.jpg) METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
Per determinare una soluzione particolare descriveremo un metodo che vale solo nel caso in cui la funzione f(x) abbia una forma particolare:
 42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
Soluzioni del Foglio 9
 ANALISI Soluzioni del Foglio 9 4 dicembre 9 9.. Esercizio. Si scriva il polinomio di Taylor T 5 (x, ), di punto iniziale x = e ordine n = 5 della funzione f(x) = ex e x La funzione f(x) assegnata é, generalmente,
ANALISI Soluzioni del Foglio 9 4 dicembre 9 9.. Esercizio. Si scriva il polinomio di Taylor T 5 (x, ), di punto iniziale x = e ordine n = 5 della funzione f(x) = ex e x La funzione f(x) assegnata é, generalmente,
Elementi di Probabilità e Statistica - 052AA - A.A
 Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
Equazioni differenziali
 Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
f(x)e 2πixy dx g(y)e 2πixy dy
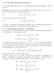 18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso
 Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano January 23, 2017 Parte 3. Teoria della misura e dell
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano January 23, 2017 Parte 3. Teoria della misura e dell
ANALISI MATEMATICA 1 ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 01/03/04
 ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
Le derivate parziali in termodinamica
 Capitolo 2 Le derivate parziali in termodinamica 2.1 La derivata di funzioni ad una variabile Sia f una funzione di una sola variabile La sua derivata è definita come f f(x (2.1 S(x = df dx = lim f(x +
Capitolo 2 Le derivate parziali in termodinamica 2.1 La derivata di funzioni ad una variabile Sia f una funzione di una sola variabile La sua derivata è definita come f f(x (2.1 S(x = df dx = lim f(x +
SOLUZIONE DELL EQUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME
 SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
SOLUZIONE DELL EUAZIONE DI FOURIER PER PER PIASTRA SOTTILE CON SORGENTE TERMICA IN MOTO UNIFORME Luca Ghezzi May 2 Abstract L equazione del calore di Fourier è risolta analiticamente nel caso di un mezzo
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Analisi II, a.a Soluzioni 4
 Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso
 Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy
 Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy 10 maggio 2010 Supponiamo che f(x, y) sia una funzione continua definita in un rettangolo del
Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy 10 maggio 2010 Supponiamo che f(x, y) sia una funzione continua definita in un rettangolo del
PNI 2002 QUESITO 1 QUESITO 2
 www.matefilia.it PNI 2002 QUESITO 1 Siano a>0 e b>0. Media aritmetica: Media geometrica: a b La media aritmetica di due numeri reali positivi è maggiore o uguale alla media geometrica dei due numeri (è
www.matefilia.it PNI 2002 QUESITO 1 Siano a>0 e b>0. Media aritmetica: Media geometrica: a b La media aritmetica di due numeri reali positivi è maggiore o uguale alla media geometrica dei due numeri (è
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA L-C, B-S
 ANALISI MAEMAICA L-C, B-S 25-6 SERIE DI FOURIER MASSIMO CICOGNANI Per la pubblicazione in rete di queste dispense si deve ringraziare Marco Frison che le ha trascritte interamente in Latex 1 Lo spazio
ANALISI MAEMAICA L-C, B-S 25-6 SERIE DI FOURIER MASSIMO CICOGNANI Per la pubblicazione in rete di queste dispense si deve ringraziare Marco Frison che le ha trascritte interamente in Latex 1 Lo spazio
L equazione di Schrödinger unidimensionale: soluzione analitica e numerica
 Chapter 3 L equazione di Schrödinger unidimensionale: soluzione analitica e numerica In questo capitolo verrà descritta una metodologia per risolvere sia analiticamente che numericamente l equazione di
Chapter 3 L equazione di Schrödinger unidimensionale: soluzione analitica e numerica In questo capitolo verrà descritta una metodologia per risolvere sia analiticamente che numericamente l equazione di
Introduzione euristica alla δ di Dirac e alle sue collegate.
 Introduzione euristica alla δ di Dirac e alle sue collegate. L antitrasformata di Fourier Se definiamo la trasformata di Fourier di una funzione assolutamente integrabile sulla retta reale con la formula:
Introduzione euristica alla δ di Dirac e alle sue collegate. L antitrasformata di Fourier Se definiamo la trasformata di Fourier di una funzione assolutamente integrabile sulla retta reale con la formula:
Limitiamoci dapprima a considerare una funzione f di periodo 2π. Cercheremo di approssimarla con polinomi trigonometrici di ordine n della forma
 Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Esercitazioni di Statistica Matematica A Lezione 7. Variabili aleatorie continue
 Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Secondo scritto. 8 luglio 2010
 Secondo scritto 8 luglio 010 1 Parte 1 Esercizio 1.1. Facciamo riferimento alle pagine e 3 del libro di testo. Quando si ha a che fare con la moltiplicazione o la divisione di misure bisogna fare attenzione,
Secondo scritto 8 luglio 010 1 Parte 1 Esercizio 1.1. Facciamo riferimento alle pagine e 3 del libro di testo. Quando si ha a che fare con la moltiplicazione o la divisione di misure bisogna fare attenzione,
2. la ricerca di funzioni che hanno una derivata assegnata.
 INTEGRALI PER FUNZIONI DI UNA VARIABILE Il calcolo integrale per funzioni reali di una variabile reale si occupa di risolvere due problemi:. il calcolo dell area di parti di piano qualsiasi, 2. la ricerca
INTEGRALI PER FUNZIONI DI UNA VARIABILE Il calcolo integrale per funzioni reali di una variabile reale si occupa di risolvere due problemi:. il calcolo dell area di parti di piano qualsiasi, 2. la ricerca
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
5.3 La δ di Dirac e cenni alle distribuzioni
 5.3 La δ di Dirac e cenni alle distribuzioni Le funzioni e iλx, con λ R, sono autofunzioni non quadrato sommabili dell operatore autoaggiunto id/ e costituiscono una base generalizzata in L 2 (R nel senso
5.3 La δ di Dirac e cenni alle distribuzioni Le funzioni e iλx, con λ R, sono autofunzioni non quadrato sommabili dell operatore autoaggiunto id/ e costituiscono una base generalizzata in L 2 (R nel senso
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO COGNOME: NOME: MATR.: 1) 7; C: x sin(x) dx è A: π ; B:2 ; C: 0 ; D: π/2; E: N.A.
 Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il
Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2011/12
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 0/ Esercizio Prova scritta del 7/06/0 Siano X e Y due v.a. indipendenti, con distribuzione continua Γ(, ). Si trovino la distribuzione di X Y e di (X Y ). Esercizio
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 0/ Esercizio Prova scritta del 7/06/0 Siano X e Y due v.a. indipendenti, con distribuzione continua Γ(, ). Si trovino la distribuzione di X Y e di (X Y ). Esercizio
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
