Formulazione matriciale dell ottica geometrica
|
|
|
- Donata Rizzo
- 8 anni fa
- Visualizzazioni
Transcript
1 Università di Pisa Corso di Laurea in Fisica Corso di Ottica Quantistica Riccardo GOTTARDI Formulazione matriciale dell ottica geometrica Docente del corso : Prof. D. Giulietti
2 Indice L approssimazione di Gauss 3. Alcune definizioni generali Il diottro sferico Il diottro sferico nell approssiamzione di Gauss Vergenza e matrice di rifrazione Un semplice esempio: il fuoco di un diottro Generalizzazione ai sistemi centrati 9 2. Matrice di traslazione Composizione di matrici e matrice di trasferimento Applicazione alle lenti 3 3. Lenti spesse Lenti sottili Il telescopio a rifrazione Applicazione agli specchi 7 4. Matrice di riflessione Il telescopio a riflessione Cavità risonanti Cavità sferica confocale Cavità sferica generica Onde sferiche e fasci gaussiani Onde sferiche Fasci gaussiani
3 Capitolo L approssimazione di Gauss L approssimazione di Gauss è l approssimazione lineare dell ottica geometrica. In queste condizioni è possibile sostituire le funzioni sinusoidali dell ottica geometrica con le loro approssimazioni lineari e, scelto un sistema di riferimento, trattare quindi un sistema ottico utilizzando il metodo delle matrici. Analizziamo un caso semplice dopo aver dato alcune definizioni generali.. Alcune definizioni generali Fascio omocentrico: un insieme di raggi con un punto comune d intersezione. Sistema ottico stigmatico: ad un fascio incidente omocentrico in A corrisponde un fascio emergente pure omocentrico in A 2. I sistemi ottici di uso corrente si possono considerare stigmatici. Punti coniugati: i punti A ed A 2 sono punti coniugati; A è l oggetto, A 2 è l immagine (Fig... A A2 Figura.: Sistema ottico stigmatico centrato. 3
4 Piani coniugati: il cammino ottico tra due punti su ciascun piano è lo stesso, indipendentemente dall inclinazione dei raggi uscenti dall uno ed entranti nell altro. Fuoco: il punto coniugato di un punto all infinito. Se il punto all infinito è l oggetto il suo coniugato si chiama secondo fuoco, se il punto all infinito è l immagine il suo coniugato si chiama primo fuoco. Sistema ottico centrato: un insieme di superfici rifrangenti o riflettenti, generalmente sferiche, che hanno simmetria cilindrica attorno ad un asse. Matrice ABCD: indicazione generica della matrice che rappresenta il passaggio attraverso un elemento ottico. Le lettere ABCD indicano le posizioni dei quattro elementi della matrice 2x2 come mostrato qui di seguito ( A B M ABCD = C D.2 Il diottro sferico La cosa più semplice che può succedere ad un raggio di luce è di trovarsi a passare da un mezzo con indice di rifrazione n ad un mezzo con un diverso indice di rifrazione n 2. Consideriamo quindi un raggio luminoso che incida su diottro sferico ad un certo angolo (Fig..2. Figura.2: Incidenza su un diottro sferico. Partendo dal raggio di incidenza, caratterizzato dal vettore u, si ricava il vettore del raggio diffratto, u 2, utilizzando le leggi di Descartes. Si calcola i (angolo d incidenza i = (N, u 4
5 se ne deduce i noti gli indici di rifrazione dei due mezzi, si valuta il coefficiente a i 2 = arcsin( n sin i n 2 e se ne deduce infine a = n 2 (N u 2 n (N u = n 2 cos i 2 n cos i u 2 = n 2 (n u an L intera procedura risulta piuttosto laboriosa e deve essere applicata a ciascun raggio luminoso. La determinazione dell immagine di un oggetto è quindi molto lunga, anche utilizzando un computer, in quanto risulta necessario ripetere lo stesso calcolo per molti raggi luminosi che partano da ciascun punto dell oggetto. Vediamo come le cose cambiano se utilizziamo l approssimazione di Gauss..3 Il diottro sferico nell approssiamzione di Gauss Consideriamo un sistema di assi Sxyz con Sz coincidente con l asse ottico ed il piano Sxy tangente al diottro in S (Fig..3. Figura.3: Incidenza su un diottro sferico considerato tridimensionalmente. Se i raggi luminosi sono poco inclinati sull asse ottico ed il punto di incidenza I non è molto distante da S possiamo approssimare linearmente la legge di Snell-Descartes n sin i = n 2 sin i 2 n i n 2 i 2 ed il coefficiente diventa a = n 2 n 5
6 per cui la relazione tra i vettori d incidenza e di rifrazione diventa IC n 2 u 2 n u = an = (n 2 n R ed in forma vettoriale, utilizzando le componenti del vettore u i = (α i, β i, γ i e le coordinate xyz del punto I n 2 α 2 β 2 n α β = (n 2 n x/r y/r γ 2 γ γ N Essendo i raggi poco discosti dall asse ottico si ha γ,γ 2 e γ N il che rende la terza riga una banale identità. Le altre due righe esprimono due equazioni lineari in cui, per la stessa approssimazione, α θ x e β θ y, dove θ x e θ y sono gli angoli che le proiezioni dei raggi luminosi sui piani Sxz e Syz rispettivamente formano con l asse ottico. Se definiamo con la notazione complessa ᾱ α + ıβ e x x + ıy possiamo condensare quanto succede durante la rifrazione nelle due seguenti equazioni x 2 = x (nᾱ 2 = (nᾱ n 2 n x R in quanto la coordinata x chiaramente non cambia nel corso della rifrazione.4 Vergenza e matrice di rifrazione Si definisce vergenza la quantità V n 2 n R in cui il segno di R è preso positivo nel senso della luce incidente. Quando R viene espresso in metri, l unità di misura conseguente della vergenza è la diottria (δ. La vergenza è una caratteristica intrinseca del diottro, indipendente dal senso di propagazione della luce, ed è positiva nei diottri converegenti e negativa per quelli divergenti. Se si definisce il vettore X che ha per elementi la posizione x del punto d intersezione del raggio luminoso con la superficie del diottro e l angolo ottico nᾱ, prodotto dell indice di rifrazione con l angolo definito precedentemente, si possono riscrivere le relazioni del paragrafo precedente come Dove ( x nᾱ 2 ( ( 0 x = V nᾱ R(S = è la matrice di rifrazione. ( 0 V (. (.2 6
7 .5 Un semplice esempio: il fuoco di un diottro Applichiamo il metodo delle matrici ad un caso semplice, ricerchiamo cioè il fuoco di un diottro prima col metodo tradizionale e poi utilizzando le matrici e confrontiamo i risultati. Sfruttando la condizione di parassialità dei raggi data dall approssimazione di Gauss, con alcune semplice relazioni di geometria elementare ed impiegando la legge di Snell approssimata, si ricava l equazione dei punti coniugati del diottro n p + n 2 q = n 2 n R (.3 dove p, q sono rispettivamente la distanza del punto oggetto e del punto immagine sull asse ottico dal vertice S, e R è il raggio di curvatura del diottro (Fig..4. x I R S C z p q Figura.4: Punti coniugati di un diottro sferico. Senza perdere di generalità abbiamo considerato qui un raggio sul piano Sxz. Dall equazione dei punti coniugati del diottro discende immediatamente la posizione dei fuochi del diottro. Per p si ha q = f 2 e la (.3 diventa n 2 = n 2 n f 2 R e quindi, come si vede in Fig. (.5 f 2 = n 2 R = n 2 n 2 n V (.4 7
8 Per q si ha p = f e la (.3 diventa e quindi n = n 2 n f R f = n R = n n 2 n V (.5 x 2 2 z f2 Figura.5: Secondo fuoco di un diottro sferico. Ripetiamo il procedimento ora utilizzando il metodo delle matrici. Riprendiamo l equazione (. limitandoci al piano Sxz ed inserendo i valori appropriati dell angolo α = 0 ed otteniamo. ( x 2 = x = n 2 α 2 = V x ( 0 V ( x n 0 (.6 Nell approssimazione di Gauss il punto di intersezione f 2 di questo raggio rifratto con l asse ottico è dato da x 2 f 2 α 2 ed essendo α 2 dalla (.6 esattamente si ha α 2 = V x n 2 f 2 = n 2 V (.7 Similmente si ottiene f f = n V Chiaramente i due procedimenti portano alle stesse conclusioni. (.8 8
9 Capitolo 2 Generalizzazione ai sistemi centrati 2. Matrice di traslazione La matrice di traslazione formalizza matematicamente la propagazione in un mezzo omogeneo del vettore X da un piano A xy ad un piano A 2 xy a lui parallelo (Fig. 2.. L introduzione di questa matrice si rende necessaria in quanto i sistemi ottici sono sistemi omogenei a tratti. Figura 2.: Propagazione in un mezzo omogeneo. Essendo i raggi luminosi delle rette poco inclinate rispetto all asse ottico, sfruttando l approssimazione lineare di Gauss, si vede come ad esempio la coordinata spaziale lungo l asse x diventi x 2 = x + α A A 2 mentre gli angoli ovviamente si conservano α 2 = α 9
10 Da cui, iterando i calcoli e raggruppandone i risultati, si ottiene la formulazione matriciale ( ( ( x A A = 2 /n x (2. nᾱ 0 nᾱ 2 e la matrice di traslazione è quindi ( A A τ(a A 2 = 2 /n ( Composizione di matrici e matrice di trasferimento Nel caso in cui si abbia un sistema ottico costituito da una successione di elementi semplici diversi (spazi omogenei, superfici diottriche, etc. le coordinate di un raggio subiranno i vari cambiamenti, ognuno governato da una matrice come quelle descritte sopra. Se iniziamo a scrivere i vari passaggi da un elemento all altro, indicati con delle matrici generiche M i si ha X(s = M X(s0 X(s 2 = M 2 X(s = M 2 M X(s0 e così di seguito. Si deduce immediatamente la regola di composizione delle matrici. La matrice globale di trasferimento del sistema ottico, indicata con T ( ES (Fig. 2.2 è data dal prodotto matriciale, ordinato in senso inverso rispetto a quello in cui il raggio incontra i vari elementi ottici, delle matrici di trasferimento dei singoli elementi ottici. no x E S z Figura 2.2: Sistema ottico generico. In formule, numerando le matrici da sinistra a destra, T(ES = M n M n... M 2 M (2.3 0
11 con M n = M(E e M = M(S. Utilizzando quanto sopra, esprimiamo la matrice di trasferimento tra due piani A xy e A 2 xy di indici rispettivamente n 0 ed n come in fig. ( 2.3. x no ni A z E S A2 z2 z Figura 2.3: Trasferimento tra due piani esterni ad un sistema ottico. Si ha T(A A 2 = τ(sa 2 T(ESτ(A E (2.4 che diventa in maniera esplicita T(A A 2 = ( ( ( z2 /n i T T 2 z /n 0 0 T 2 T 22 0 (2.5 Dei quattro elementi della matrice T(A A 2 solo l elemento C risulta indipendente da z e z 2, e quindi risulta indipendente dai piani scelti. Esso è esattamente l elemento T 2 della matrice T(ES ed è una caratteristica intrinseca del sistema. Per definizione si chiama vergenza, come per il diottro sferico, V T 2 Spingiamoci oltre supponendo che i due piani A xy e A 2 xy siano coniugati e prendiamo due punti, B 0 e B, su questi piani ed esplicitiamo la relazione matriciale X i = T(A A 2 X 0 x i = T x 0 + T 2 n 0 α 0 (2.6 n i α i = V x 0 + T 22 n 0 α 0 (2.7 Essendo la posizione x i dell immagine B i indipendente dall inclinazione α 0 si ha T 2 = 0 (2.8
12 e risulta che T è proprio il rapporto x i /x 0, cioè l ingrandimento trasversale G t. Se consideriamo poi il caso x 0 = 0 abbiamo T 22 = n iα i n 0 α 0 ] x0 =0 (2.9 Che in funzione dell ingrandimento angolare G a = α i α 0 ] x0 =0 diventa T 22 = n i n 0 G a (2.0 Concludendo la matrice di trasferimento tra due piani coniugati diventa ( Gt 0 T(A A 2 = (2. V n i /n o G a In maniera generale si definiscono anche le lunghezze focali immagine ed oggetto, che algebricamente risultano f i n i V (2.2 f 0 n 0 (2.3 V Una volta stabiliti i valori della matrice di trasferimento, è quindi possibile dedurre immediatamente alcune caratteristiche dell immagine senza in realtà dover fare il conto vero e proprio di trasferimento dei raggi vettore. 2
13 Capitolo 3 Applicazione alle lenti 3. Lenti spesse Ciò che viene naturale fare ora è di costruire la matrice di trasferimento di una lente in aria (il caso in cui la lente non sia in aria porta semplicemente all aggiunta dei relativi indici di rifrazione. Una lente è formata da due diottri sferici, di raggio R ed R 2, e da una certa quantità di materiale tra essi con indice di rifrazione n. Come da fig. ( 3. indichiamo con e la distanza tra i vertici dei due diottri ES ed inoltre con V e V 2 la vergenza di ciascun diottro. R R2 E S e z Figura 3.: Lente spessa. La matrice di trasferimento dal piano passante per E al piano passante per S sarà, usando le notazione dei paragrafi.4 e 2., e in forma esplicita T (ES = R(Sτ(ESR(E 3
14 T(ES = ( 0 V 2 dove la vergenza V è V = V + V 2 ev V 2 n ( e/n 0 ( ( 0 ev /n e/n = V V ev 2 /n (3. = (n ( R R 2 + n n e (3.2 R R 2 essendo la lente in aria dalle equazioni ( 2.2, ( 2.3 si ha semplicemente f f i = V ergo 3.2 Lenti sottili f = (n ( + n e (3.3 R R 2 n R R 2 E spesso possibile introdurre un ulteriore approssimazione, ossia considerare una lente sottile, in cui e sia trascurabile. La matrice di trasferimento, che indicheremo con R(L, diventa ( 0 R(L = (3.4 /f in quanto la vergenza nell equazione ( 3.2 diventa semplicemente la somma delle vergenze dei due diottri V = V + V 2 = (n ( R R 2 = f che è la stessa espressione per la lunghezza focale che si ricava utilizzando la geometria e la legge di Snell senza fare impiego della formulazione matriciale. Infatti l equazione che si ricava col metodo tradizionale per una lente sottile è la ben nota p + q = (n ( R R 2 = f (3.5 che, quando p (o equivalentemente per una lente in aria q, diventa esattamente f = (n ( R R 2 come già dedotto col metodo delle matrici. Delle lenti sottili è anche ben nota la formula dell ingrandimento trasversale di un oggetto (fig. 3.2 che è dato da G t = x i x 0 = q p 4
15 Bo L p f q Bi z Figura 3.2: Rifrazione attraverso una lente sottile. Guardando la matrice di trasferimento dal piano contenente B 0 al piano contenente B i si ottiene lo stesso risultato. Costruiamo la matrice di trasferimento come T (B 0 B i = τ(b i LR(Lτ(LB 0 che denotiamo con R e che esplicitamente diventa, essendo la lente in aria e quindi n =, ( ( ( ( q 0 p q/f p + q( p/f R(B 0 B i = = 0 /f 0 /f p/f (3.6 ed applicando l equazione ( 3.5 si ottiene ( (q/p 0 R(B 0 B i = (3.7 (/f (p/q Il termine A di questa matrice ABCD dà, come già visto, l ingrandimento trasversale, G t = (q/p. Il valore negativo dell ingrandimento sta ad indicare che l immagine viene capovolta. 3.3 Il telescopio a rifrazione Il telescopio rifrattore è in generale composto da due sistemi ottici: un obiettivo, ossia un sistema convergente di grande focale (f m che di un oggetto posto a grande distanza dà un immagine nel proprio piano focale, e un oculare che pure è un sistema convergente con lo stesso asse ottico, ma la cui lunghezza focale è molto più piccola (f 2 cm e la cui distanza dall obiettivo può essere regolata (fig L oculare viene sistemato in modo da portare il suo primo fuoco in prossimità dell immagine formata dall obiettivo che sarà circa sul secondo fuoco dell obiettivo stesso. Come si vede in figura, data la grande distanza dell oggetto, l angolo α sotto cui si vede ad occhio nudo l oggetto è praticamente coincidente con l angolo con cui lo stesso oggetto è 5
16 Obiettivo Oculare Bo E S z p f f2 grande distanza Figura 3.3: Principio del telescopio a rifrazione. Per chiarezza di rappresentazione le distanza non sono in scala. visto dal centro dell obiettivo. Tenendo presente quest approssimazione scriviamo la matrice di trasferimento del sistema T(ES = R(Sτ(ESR(E che in forma esplicita, essendo e la distanza tra le due lenti e trovandoci in aria (n =, è T(ES = ( 0 V 2 ( e 0 ( ( 0 = V ev e (V + V 2 ev V 2 ev 2 (3.8 Siccome poi V = /f e V 2 = /f 2 avremo che V = (V +V 2 ev V 2 = 0, inoltre e f + f 2 e quindi T(ES = ( f2 /f f + f 2 0 f /f 2 (3.9 L ingrandimento trasversale dell immagine, G t, è dato esattamente dal rapporto tra le focali G t = f 2 f (3.0 il segno meno indica semplicemente, di nuovo, che l immagine è invertita. L ingrandimento angolare (quello che interessa per vedere un oggetto distante come se fosse vicino è semplicemente G a = β/α = G t che con le lunghezze focali che abbiamo considerato diventa, a meno del segno, G a = f f 2 = m cm = 0 2 m = 00 (3. 6
17 Capitolo 4 Applicazione agli specchi 4. Matrice di riflessione Con un po di geometria elementare, applicando l approssimazione di Gauss ad uno specchio sferico, si ritrova senza difficoltà la nota equazione degli specchi sferici p q = 2 R (4. Da cui segue immediatamente la posizione dei due fuochi quando, a turno, p e q f = R 2 f 2 = R 2 Utilizzando lo stesso procedimento impiegato per il diottro (che qui non ripeteremo se si definisce come vergenza V = 2n 0 R si ricava semplicemente la matrice di riflessione per uno specchio sferico ( 0 R s (S = (4.2 V 4.2 Il telescopio a riflessione Il telescopio a riflessione è uno strumento analogo al telescopio a rifrazione, il cui obiettivo è però costituito da uno specchio M p, lo specchio primario, il cui fuoco è F p ed al quale è spesso associato un secondo specchio M s, lo specchio secondario. In fig. ( 4. si vede il montaggio alla Cassegrain, in cui il fascio passa attraverso un apertura in M p e converge al fuoco Cassegrain F C. I vantaggi dei telescopi a riflessione rispetto a quelli a rifrazione sono essenzialmente due: 7
18 . non vi è aberrazione cromatica in quanto i fasci non passano attraverso un mezzo rifrangente, 2. il diametro d apertura può essere molto più grande, in quanto è più facile costruire uno specchio di grandi dimensioni piuttosto che una lente. Mp Fp Ms Ss Sp Fc Figura 4.: Principio del telescopio a riflessione. La matrice di trasferimento dal vertice S p di M p prima della riflessione al vertice S s di M s dopo la riflessione è T(S p S s = R m (S s τ(s p S s R m (S p che esplicitamente diventa, considerando V p e V s la vergenza rispettiva di ciascun diottro, ( ( ( ( 0 e 0 e V T(S p S s = = p V s 0 V p V e e V s (4.3 dove V = V p + V s e V p V s. Se prendiamo R p = 20m, e = 8m e R s = 4, 5m, avremo T(S p S s = ( (4.4 da cui si deduce che la vergenza del sistema è V = 0.02δ, il fuoco immagine è f i = /V = 83.3m, il fuoco oggetto f 0 = /V = 83.3m. Con un osservazione oculare si costituisce un sistema afocale simile a quello del telescopio a rifrazione in cui il fuoco immagine dell obiettivo coincida con il fuoco oggetto dell oculare in modo che i raggi emergenti dall obiettivo ed incidenti sull occhio siano tra loro paralleli. Adottando come entrata E il punto principale oggetto dell obiettivo e come uscita S il punto principale immagine dell oculare ed e come distanza tra i due 8
19 si ritrova la stessa matrice di trasferimento del telescopio a rifrazione che è in realtà caratteristica di ogni costruzione afocale ( eve e T(ES = (4.5 V ev S con V = V E + V S ev E V S = 0 ed e = f + f 2, per cui ( f2 /f T(ES = f 2 + f 0 f /f 2 (4.6 Prendendo i valori del caso in esame, con un oculare di focale f 2 = 8cm si ha un ingrandimento angolare G a = f /f 2 = Cavità risonanti 4.3. Cavità sferica confocale Consideriamo come esempio una cavità confocale simmetrica (fig I due fuochi sono coincidenti a metà della distanza S 2 S, al centro C S2 F S C2 Figura 4.2: Cavità confocale simmetrica. della cavità, i centri di curvatura C e C 2 sono situati ai vertici S 2 ed S. Si vede semplicemente dalla figura che l immagine di un oggetto su uno specchio torna a coincidere con l immagine stessa dopo due round trip della luce in cavità. In queste condizioni siamo certi che il fascio non diverga lateralmente il che assicura una buona intensità del fascio uscente da una delle superfici semi-riflettenti. In altri tipi di cavità che danno delle performances migliori l ingrandimento risulta uguale all unità solo dopo un gran numero di round trip. Costruiamo la matrice di trasferimento tra due punti, A i e A 0, su un piano interno alla cavità ottica. T(A 0 A i = τ(s 2 A i R m (S 2 τ(s S 2 R m (S τ(a 0 S 9
20 Sfruttando il fatto che un segmento può essere visto come somma di due segmenti e la relativa matrice di traslazione come prodotto delle due matrici di traslazione, abbiamo che τ(s 2 A i = τ(s A i τ(s 2 S che inserito nella precedente dà dove T(A 0 A i = τ(s A i T rt τ(a 0 S T rt = τ(s 2 S R m (S 2 τ(s S 2 R m (S è la matrice di round trip. Chiamando V e V 2 le vergenze dei due specchi ed e la loro distanza caratteristica che tiene conto anche dell indice di rifrazione del mezzo abbiamo esplicitamente ( ( ( ( e 0 e 0 T rt = 0 V 2 0 V ( ev e(v T rt = + V 2 ev V 2 e + e( ev 2 (V + V 2 ev V 2 ev 2 Nel caso della cavità confocale simmetrica abbiamo R = R 2 = e, V = V 2 = 2/e, V = 0 per cui ( 0 T rt = = I (4.7 0 Dopo un numero pari di riflessioni si ritrova appunto la coincidenza dell oggetto con l immagine in quanto A 0 ed A i sono coniugati ( ( ( S A T(A 0 A = i Trt 0 2m S A 0 S A = i S A 0 = I 0 0 ( Cavità sferica generica Quando non ci si trova nel caso particolarmente stabile di una cavità sferica confocale c è la possibilità che il raggio luminoso di riflessione in riflessione inizi a divergere ed esca dai lati della cavità. Si rende quindi necessario trovare una relazione che assicuri la stabilità della cavità. Consideriamo un piano β in cavità ed un raggio che parta da un punto P 0 su di esso (fig Dopo riflessione il raggio intersecherà il piano nel punto P. Se indichiamo con X 0 ed X i raggi vettore nei due punti si avrà ( A B X = C D X 0 (4.9 dove la matrice ABCD è la matrice di trasferimento per un round trip in cavità. Dopo un altra riflessione il raggio intersecherà il piano in un punto P 2 e si avrà ( A B X 2 = C D ( 2 A B X = X0 (4.0 C D 20
21 dopo n round trip il punto P n sarà dato da ( n A B X n = X0 (4. C D Perché si abbia stabilità serve che la matrice ABCD non diverga all aumentare di n. Dalle proprietà del calcolo matriciale, dopo alcune elaborazioni, si trova che, affinché la matrice non diverga, deve essere < (A + D < (4.2 2 P0 R P R2 L Figura 4.3: Cavità sferica generica. Applichiamo quanto visto ora in generale alla cavità che stiamo considerando ponendo il piano β appena di fronte al primo specchio. La matrice di trasferimento sarà T(β = τ(lr m (2τ(LR m ( che esplicitamente diventa T(β = ( L 2/R (2L/R ( L 2/R 2 (2L/R 2 ed una volta svolta l ultima moltiplicazione si ha A + D 2 che diventa infine A + D L equazione ( 4.2 può essere riscritta come (4.3 = 2L R 2L R 2 + 2L2 R R 2 (4.4 = ( L R ( L R 2 = g g 2 (4.5 0 < A + D + 2 < (4.6 4 e quindi si ritrova la condizione di stabilità 0 < g g 2 < (4.7 2
22 Capitolo 5 Onde sferiche e fasci gaussiani 5. Onde sferiche La formulazione matriciale può essere utile non solo per studiare il comportamento di raggi luminosi, ma anche la propagazione di onde sferiche attraverso un sistema ottico. Consideriamo due raggi coniugati X ed X 2 in aria di due onde sferiche con centro in P e P 2 (fig. 5.. I P x x2 P2 z z2 Figura 5.: Propagazione di un onda sferica attraverso un sistema ottico. raggi di curvatura delle due onde saranno R = x α R 2 = x 2 α 2 ed utilizzando queste relazioni sul prodotto ( A B X 2 = C D X (5. 22
23 si ottiene, con alcuni passaggi ed utilizzando proprietà delle matrici, R 2 = AR + B CR + D (5.2 Quindi, data la matrice di trasferimento di un sistema ottico, si può ricavare il raggio di curvatura R 2 dell onda in uscita, noto R dell onda incidente. Consideriamo due esempi banali. Propagazione nello spazio Utilizziamo come matrice ABCD la matrice di traslazione tra due punti z e z 2. La ( 5.2 diventa la banale R 2 = R + (z 2 z (5.3 Propagazione attraverso una lente sottile Utilizziamo come matrice ABCD la matrice di rifrazione della lente sottile. La ( 5.2 diventa R R 2 = R f + = fr (5.4 R + f che con una minima elaborazione dà la familiare 5.2 Fasci gaussiani p + q = f (5.5 Introduciamo nella trattazione dei fasci gaussiani il parametro complesso q, chiamato raggio complesso del fascio gaussiano, dato da q = R ı λ πw 2 Utilizzando il parametro q per descrivere un fascio gaussiano si può trattare in modo semplice il passaggio attraverso un sistema ottico. Si trova infatti che se q è il raggio incidente e q 2 è il raggio emergente si ha un equazione simile a quella per i fasci sferici q 2 = Aq + B Cq + D (5.6 nota come relazione ABCD di propagazione per fasci gaussiani. Come semplice esempio consideriamo un fascio gaussiano con waist w su una lente sottile di lunghezza focale f. Cerchiamo la posizione e la taglia del waist w 2 dopo la lente. La matrice ABCD del sistema ottico è la composizione di una matrice di traslazione di una matrice di rifrazione della lente ed è ( z/f z M ABCD = (5.7 /f 23
24 Applichiamo ora la relazione ( 5.6 riscritta come segue = C + D(/q q 2 A + B(/q (5.8 dove (/q è dato da = ı q λ πw 2 = ı z R (5.9 dove z R è il range di Rayleigh corrispondente al waist w. Imponendo che (/q 2 sia immaginario puro si ottiene il valore z M z M = f + (f/z R 2 (5.0 Come noto si ottiene che la taglia più piccola del raggio occorre ad una distanza z M che è minore di f. In condizioni tipiche però z R f cosicché z M f e con questa approssimazione si ottiene w 2 λf πw (5. 24
I raggi luminosi. Per secoli si sono contrapposti due modelli della luce. il modello ondulatorio (Christiaan Huygens)
 I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
I raggi luminosi Per secoli si sono contrapposti due modelli della luce il modello corpuscolare (Newton) * la luce è un flusso di particelle microscopiche il modello ondulatorio (Christiaan Huygens) *
d >> λ rettilinea raggio luminoso riflessione rifrazione
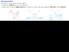 Ottica geometrica Proprietà più macroscopiche della luce d >> λ Propagazione rettilinea della luce (no diffrazione) Fondamentale concetto di raggio luminoso il cui percorso è determinato dalle leggi della
Ottica geometrica Proprietà più macroscopiche della luce d >> λ Propagazione rettilinea della luce (no diffrazione) Fondamentale concetto di raggio luminoso il cui percorso è determinato dalle leggi della
Esercizi di Fisica LB - Ottica
 Esercizi di Fisica LB - Ottica Esercitazioni di Fisica LB per ingegneri - A.A. 2003-2004 Esercizio Un sistema ottico centrato è costituito (da sinistra a destra) da una lente sottile biconcava (l indice
Esercizi di Fisica LB - Ottica Esercitazioni di Fisica LB per ingegneri - A.A. 2003-2004 Esercizio Un sistema ottico centrato è costituito (da sinistra a destra) da una lente sottile biconcava (l indice
GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI
 GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI Specchi sferici In approssimazione parassiale l equazione dei punti coniugati in uno specchio sferico è l: posizione oggetto (S nella figura) l
GLI SPECCHI SPECCHI SFERICI (CONCAVI E CONVESSI) E PIANI Specchi sferici In approssimazione parassiale l equazione dei punti coniugati in uno specchio sferico è l: posizione oggetto (S nella figura) l
ESERCIZI DI OTTICA GEOMETRICA
 ESERCIZI DI OTTICA GEOMETRICA Prima di ogni argomento sono raccolte alcune formule utili, e non banali, per lo svolgimento degli esercizi. Si presuppongono lo studio e la comprensione teorica delle stesse.
ESERCIZI DI OTTICA GEOMETRICA Prima di ogni argomento sono raccolte alcune formule utili, e non banali, per lo svolgimento degli esercizi. Si presuppongono lo studio e la comprensione teorica delle stesse.
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
LE LENTI GLI ELEMENTI CARATTERISTICI DI UNA LENTE
 LE LENTI Le lenti sono corpi omogenei trasparenti costituiti da due superfici curve oppure una curva e una piana; di solito si utilizzano sistemi di lenti con superfici sferiche, attraverso cui la luce
LE LENTI Le lenti sono corpi omogenei trasparenti costituiti da due superfici curve oppure una curva e una piana; di solito si utilizzano sistemi di lenti con superfici sferiche, attraverso cui la luce
5 Lenti e Specchi. Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali
 Laboratorio di didattica della Fisica (III modulo): Metodologie di insegnamento del Laboratorio di Ottica Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali 5
Laboratorio di didattica della Fisica (III modulo): Metodologie di insegnamento del Laboratorio di Ottica Formazione immagini Specchi Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali 5
Esercizi svolti sulla parabola
 Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 19 dicembre 011 Esercizi svolti sulla parabola Esercizio 1. Determinare l equazione della parabola avente fuoco in F(1, 1) e per direttrice
Liceo Classico Galilei Pisa - Classe a A - Prof. Francesco Daddi - 19 dicembre 011 Esercizi svolti sulla parabola Esercizio 1. Determinare l equazione della parabola avente fuoco in F(1, 1) e per direttrice
Corso di Laurea in Astronomia. Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA 2
 Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
Corso di Laurea in Astronomia Laurea Triennale DISPENSE DI ESPERIMENTAZIONI DI FISICA A.A. 01-013 Indice 1 Introduzione 5 1.1 Indice di rifrazione.............................. 5 1. Riflessione e rifrazione............................
5 Fondamenti di Ottica
 Laboratorio 2B A.A. 2012/2013 5 Fondamenti di Ottica Formazione immagini Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali Ottica geometrica In ottica geometrica si analizza la formazione
Laboratorio 2B A.A. 2012/2013 5 Fondamenti di Ottica Formazione immagini Superfici rifrangenti Lenti sottili Lenti spessi Punti cardinali Ottica geometrica In ottica geometrica si analizza la formazione
Ottica geometrica. Propagazione per raggi luminosi (pennello di luce molto sottile)
 Ottica geometrica Propagazione per raggi luminosi (pennello di luce molto sottile) All interno di un mezzo omogeneo la propagazione e rettilinea: i raggi luminosi sono pertanto rappresentati da tratti
Ottica geometrica Propagazione per raggi luminosi (pennello di luce molto sottile) All interno di un mezzo omogeneo la propagazione e rettilinea: i raggi luminosi sono pertanto rappresentati da tratti
Il diottro : c s o t s r t u r zi z on o e gra r f a i f ca c a dell immag a ine
 Il diottro : costruzione grafica dell immagine Il diottro: superficie sferica che separa due mezzi con diversi indici di rifrazione Deviazione della luce sulla superficie di separazione Legge di Snell
Il diottro : costruzione grafica dell immagine Il diottro: superficie sferica che separa due mezzi con diversi indici di rifrazione Deviazione della luce sulla superficie di separazione Legge di Snell
Note di ottica geometrica.
 Note di ottica geometrica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, novembre 2012. Indice 1 ttica geometrica 1 2 Riflessione. 2 2.1 La legge della riflessione..............................
Note di ottica geometrica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, novembre 2012. Indice 1 ttica geometrica 1 2 Riflessione. 2 2.1 La legge della riflessione..............................
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
OTTICA GEOMETRICA. Ovvero la retta perpendicolare alla superficie riflettente. Figura 1. Figura 2
 OTTICA GEOMETRICA L ottica geometrica si occupa di tutta quella branca della fisica che ha a che fare con lenti, specchi, vetri e cose simili. Viene chiamata geometrica in quanto non interessa la natura
OTTICA GEOMETRICA L ottica geometrica si occupa di tutta quella branca della fisica che ha a che fare con lenti, specchi, vetri e cose simili. Viene chiamata geometrica in quanto non interessa la natura
Lezione 7 Specchi Sferici Concavi, Convessi e Piani
 Lezione 7 Specchi Sferici Concavi, Convessi e Piani 1/13 Per determinare l immagine prodotta da uno specchio è necessario applicare la legge della riflessione di Snell Angolo di incidenza (misurato rispetto
Lezione 7 Specchi Sferici Concavi, Convessi e Piani 1/13 Per determinare l immagine prodotta da uno specchio è necessario applicare la legge della riflessione di Snell Angolo di incidenza (misurato rispetto
1 p. 1 q 1 R. altrimenti se il mezzo circostante ha un indice di rifrazione n 0. , al posto di n si deve usare
 2 Lenti Le lenti sono costituite da un mezzo rifrangente, di indice di rifrazione n, omogeneo, delimitato da superfici sferiche nel caso in cui il mezzo circostante é l aria: l equazione delle lenti é
2 Lenti Le lenti sono costituite da un mezzo rifrangente, di indice di rifrazione n, omogeneo, delimitato da superfici sferiche nel caso in cui il mezzo circostante é l aria: l equazione delle lenti é
Effetto convergente di uno specchio concavo: osservazione. Dimostrare la riflessione di raggi paralleli su uno specchio concavo
 ESPERIENZA 7 Effetto convergente di uno specchio concavo: osservazione 1. Argomenti Dimostrare la riflessione di raggi paralleli su uno specchio concavo 2. Montaggio Fig. 1 3. Note al montaggio 3.1 Fissare
ESPERIENZA 7 Effetto convergente di uno specchio concavo: osservazione 1. Argomenti Dimostrare la riflessione di raggi paralleli su uno specchio concavo 2. Montaggio Fig. 1 3. Note al montaggio 3.1 Fissare
LE LENTI E L OCCHIO UMANO Prof. Erasmo Modica erasmo@galois.it
 LE LENTI E L OCCHIO UMANO Prof. Erasmo Modica erasmo@galois.it LE LENTI E LE LORO PROPRIETÀ Una lente è uno strumento costituito da un mezzo trasparente delimitato da due superfici curve, oppure da una
LE LENTI E L OCCHIO UMANO Prof. Erasmo Modica erasmo@galois.it LE LENTI E LE LORO PROPRIETÀ Una lente è uno strumento costituito da un mezzo trasparente delimitato da due superfici curve, oppure da una
Definizioni riguardo alle lenti sferiche Una lente è un mezzo trasparente limitato da due superfici di cui almeno una curva.
 1 Le lenti Definizioni riguardo alle lenti sferiche Una lente è un mezzo trasparente limitato da due superfici di cui almeno una curva. Si chiama asse ottico della lente la retta che congiunge i centri
1 Le lenti Definizioni riguardo alle lenti sferiche Una lente è un mezzo trasparente limitato da due superfici di cui almeno una curva. Si chiama asse ottico della lente la retta che congiunge i centri
Problemi sulla circonferenza verso l esame di stato
 Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tr
 1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tra le due rifrazioni. In analogia al caso di lente sottile,
1 LENTE SPESSA Calcoliamo la matrice dei raggi di una lente spessa, ovvero di una lente in cui non sia possibile trascurare la propagazione interna tra le due rifrazioni. In analogia al caso di lente sottile,
Esercizi Ottica: la rifrazione
 Esercizi Ottica: la rifrazione " = = = "# "# 1) Scrivere la legge di snell tra due superfici di indice di rifrazione n1 (mezzo dove parte l onda) e n2 (mezzo dove l onda arriva). Se l indice di rifrazione
Esercizi Ottica: la rifrazione " = = = "# "# 1) Scrivere la legge di snell tra due superfici di indice di rifrazione n1 (mezzo dove parte l onda) e n2 (mezzo dove l onda arriva). Se l indice di rifrazione
MATEMATICA LA CIRCONFERENZA GSCATULLO
 MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW ,
 Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW 19.1-19.2, 19.5-19.7 1 1. Fronti d'onda e raggi Se lasciamo cadere un sasso in una pozza, dal punto di impatto partono onde circolari. Le circonferenze
Ottica (1/2) Ottica geometrica Lezione 17, 3/12/2018, JW 19.1-19.2, 19.5-19.7 1 1. Fronti d'onda e raggi Se lasciamo cadere un sasso in una pozza, dal punto di impatto partono onde circolari. Le circonferenze
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33
 ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
ONDE ELETTROMAGNETICE OTTICA LEZIONE 33 L'Ottica Geometrica è la più antica branca dell'ottica: essa studia i fenomeni ottici assumendo che la luce si propaghi mediante raggi rettilinei. Dal punto di vista
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Esperimento sull ottica
 Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
Matematica Lezione 6
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 6 Sonia Cannas 25/10/2018 Retta passante per un punto e direzione assegnata Data l equazione di una retta in forma esplicita y = mx
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 6 Sonia Cannas 25/10/2018 Retta passante per un punto e direzione assegnata Data l equazione di una retta in forma esplicita y = mx
Lezione 22 - Ottica geometrica
 Lezione 22 - Ottica geometrica E possibile, in certe condizioni particolari, prescindere dal carattere ondulatorio della radiazione luminosa e descrivere la propagazione della luce usando linee rette e
Lezione 22 - Ottica geometrica E possibile, in certe condizioni particolari, prescindere dal carattere ondulatorio della radiazione luminosa e descrivere la propagazione della luce usando linee rette e
Lenti. Capitolo Lenti sottili
 Capitolo 3 Lenti 3. Lenti sottili Indichiamo con il termine lente un sistema ottico costituito da materiale trasparente e omogeneo limitato da due superfici che possono essere entrambe sferiche oppure
Capitolo 3 Lenti 3. Lenti sottili Indichiamo con il termine lente un sistema ottico costituito da materiale trasparente e omogeneo limitato da due superfici che possono essere entrambe sferiche oppure
I Esonero di Elementi di Ottica del 13/06/2011
 I Esonero di Elementi di Ottica del 13/06/2011 1) L onda elettromagnetica piana sinusoidale di frequenza f= 100 khz emessa da un sottomarino in superficie, si propaga orizzontalmente sia nell aria che
I Esonero di Elementi di Ottica del 13/06/2011 1) L onda elettromagnetica piana sinusoidale di frequenza f= 100 khz emessa da un sottomarino in superficie, si propaga orizzontalmente sia nell aria che
Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) 21 giugno 2018
 Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) giugno 08 Problema Due lenti sottili, biconvesse e simmetriche, hanno raggio di curvatura R = 0.0 cm e indice di rifrazione n =.5. Queste
Corso di Laurea in Fisica Compito di Fisica 3 (Prof. E. Santovetti) giugno 08 Problema Due lenti sottili, biconvesse e simmetriche, hanno raggio di curvatura R = 0.0 cm e indice di rifrazione n =.5. Queste
Esercizi di Ottica. Università di Cagliari Laurea Triennale in Biologia Corso di Fisica
 Università di Cagliari Laurea Triennale in Biologia Corso di Fisica Esercizi di Ottica 1. Un fascio di luce di lunghezza λ passa attraverso una fenditura rettangolare di larghezza a. La sua immagine viene
Università di Cagliari Laurea Triennale in Biologia Corso di Fisica Esercizi di Ottica 1. Un fascio di luce di lunghezza λ passa attraverso una fenditura rettangolare di larghezza a. La sua immagine viene
OTTICA GEOMETRICA. L ottica geometrica è valida quando la luce interagisce solo con oggetti di dimensioni molto maggiori della sua lunghezza d onda.
 Un raggio di luce si propaga rettilineamente in un mezzo omogeneo ed isotropo con velocità: c v =, n > 1 n OTTICA GEOMETRICA L ottica geometrica è valida quando la luce interagisce solo con oggetti di
Un raggio di luce si propaga rettilineamente in un mezzo omogeneo ed isotropo con velocità: c v =, n > 1 n OTTICA GEOMETRICA L ottica geometrica è valida quando la luce interagisce solo con oggetti di
il discriminante uguale a zero; sviluppando i calcoli si ottiene che deve essere
 Macerata maggio 0 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI QUESITO Considera il fascio di curve di equazione: x y (.) = k + k 6 a) Trova per quali valori di k si hanno delle ellissi. Deve essere
Macerata maggio 0 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI QUESITO Considera il fascio di curve di equazione: x y (.) = k + k 6 a) Trova per quali valori di k si hanno delle ellissi. Deve essere
I esonero di Ottica Geometria a.a compito A
 I esonero di Ottica Geometria a.a. 2016-17 compito A Un onda elettromagnetica piana con frequenza 5x10 12 Hz entra con incidenza normale in un mezzo spesso 10 Km. Sapendo che la luce impiega un tempo t=50
I esonero di Ottica Geometria a.a. 2016-17 compito A Un onda elettromagnetica piana con frequenza 5x10 12 Hz entra con incidenza normale in un mezzo spesso 10 Km. Sapendo che la luce impiega un tempo t=50
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
1 Introduzione alla geometria analitica
 1.1 Il piano cartesiano 1 Introduzione alla geometria analitica Se R è l'insieme di tutti i numeri reali (rappresentabile su una retta), allora R R = R rappresenta il piano euclideo; infatti ciascun punto
1.1 Il piano cartesiano 1 Introduzione alla geometria analitica Se R è l'insieme di tutti i numeri reali (rappresentabile su una retta), allora R R = R rappresenta il piano euclideo; infatti ciascun punto
RIFLESSIONE. Riflessione - 1/17
 RIFLESSIONE Sommario Leggi della riflessione... 2 Specchi piani... 3 Specchi sferici... 6 Lunghezza focale di specchi sferici... 9 Immagine generata da specchi sferici... 11 Ingrandimento generato da specchi
RIFLESSIONE Sommario Leggi della riflessione... 2 Specchi piani... 3 Specchi sferici... 6 Lunghezza focale di specchi sferici... 9 Immagine generata da specchi sferici... 11 Ingrandimento generato da specchi
7 Cenni di ottica per la fotografia
 7 Cenni di ottica per la fotografia 7.1 Schematizzazione di un obiettivo fotografico Gli obiettivi fotografici sono generalmente composti da un numero elevato di lenti. Tuttavia per semplicità possiamo
7 Cenni di ottica per la fotografia 7.1 Schematizzazione di un obiettivo fotografico Gli obiettivi fotografici sono generalmente composti da un numero elevato di lenti. Tuttavia per semplicità possiamo
LEZIONE 9. k, tenendo conto delle formule che permettono di calcolare il prodotto scalare ed il prodotto vettoriale, otteniamo
 LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
Trigonometria angoli e misure
 Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Piano cartesiano e Retta
 Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
CORSI I.D.E.I. - LA PARABOLA CLASSI QUARTE Prof. E. Modica
 ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEDE DI VIA FATTORI CORSI I.D.E.I. - LA PARABOLA CLASSI QUARTE Prof. E. Modica erasmo@galois.it DEFINIZIONI Definizione. Dicesi parabola il luogo
ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEDE DI VIA FATTORI CORSI I.D.E.I. - LA PARABOLA CLASSI QUARTE Prof. E. Modica erasmo@galois.it DEFINIZIONI Definizione. Dicesi parabola il luogo
Geometria BAER Canale I Esercizi 12
 Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
Lezione 13: I sistemi di riferimento
 Lezione 13: I sistemi di riferimento Cambiamenti di coordinate In questa lezione proveremo a vedere le trasformazioni lineari sotto un altra luce Quando abbiamo visto l esempio di un oggetto che, soggetto
Lezione 13: I sistemi di riferimento Cambiamenti di coordinate In questa lezione proveremo a vedere le trasformazioni lineari sotto un altra luce Quando abbiamo visto l esempio di un oggetto che, soggetto
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
ALGEBRA VETTORIALE Corso di Fisica per la Facoltà di Farmacia, Università Gabriele D Annunzio, Chieti-Pescara, Cosimo Del Gratta 2008
 LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno 11 febbraio 2013.
 Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Marco Martini. 18 March Definiamo l ellisse come il luogo geometrico dei punti del piano per i quali è costante
 Marco Martini L'ELLISSE 18 March 2006 Articolo n 4 su 6 del corso "Le coniche". Vai all'indice del corso. Paragrafi dell'articolo: 1. L'ellisse come luogo geometrico 2. Costruzione secondo il metodo del
Marco Martini L'ELLISSE 18 March 2006 Articolo n 4 su 6 del corso "Le coniche". Vai all'indice del corso. Paragrafi dell'articolo: 1. L'ellisse come luogo geometrico 2. Costruzione secondo il metodo del
a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006
 a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006 Leggi dell ottica 1. Il raggio incidente, il raggio riflesso e il raggio rifratto giacciono sullo stesso piano 2.
a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Ottica 28/2/2006 Leggi dell ottica 1. Il raggio incidente, il raggio riflesso e il raggio rifratto giacciono sullo stesso piano 2.
Lezione 04. Costruzione grafica dei cammini ottici
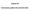 Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
Lezione 04 Costruzione grafica dei cammini ottici Riflessione e rifrazione della luce su una superficie di separazione tra due mezzi La luce si propaga in linea retta, Il raggio luminoso è la direzione
Circonferenze del piano
 Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
La parabola terza parte Sintesi
 La parabola terza parte Sintesi [ ] Qual è l equazione generale della parabola con l asse di simmetria orizzontale ( cioè parallelo all asse x )? Con quale trasformazione si ricava questa equazione da
La parabola terza parte Sintesi [ ] Qual è l equazione generale della parabola con l asse di simmetria orizzontale ( cioè parallelo all asse x )? Con quale trasformazione si ricava questa equazione da
Ottica fisiologica, ovvero perché funzionano i Google Glass (parte 2)
 Ottica fisiologica, ovvero perché funzionano i Google Glass (parte 2) Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Ottica fisiologica, ovvero perché funzionano i Google Glass (parte 2) Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
La luce Pagina 1 di 12. I raggi di luce
 La luce Pagina di I raggi di luce L ottica è quella parte della fisica che studia la propagazione della luce e la sua interazione con i corpi materiali. L esperienza comune ci consente di affermare che
La luce Pagina di I raggi di luce L ottica è quella parte della fisica che studia la propagazione della luce e la sua interazione con i corpi materiali. L esperienza comune ci consente di affermare che
ONDE ELETTROMAGNETICHE
 Fisica generale II, a.a. 01/014 OND LTTROMAGNTICH 10.1. Si consideri un onda elettromagnetica piana sinusoidale che si propaga nel vuoto nella direzione positiva dell asse x. La lunghezza d onda è = 50.0
Fisica generale II, a.a. 01/014 OND LTTROMAGNTICH 10.1. Si consideri un onda elettromagnetica piana sinusoidale che si propaga nel vuoto nella direzione positiva dell asse x. La lunghezza d onda è = 50.0
Schede di. dal LABORATORIO DI FISICA Docente Claudio Oleari AA 1999-2000
 Schede di 77,&$*(0(75,&$ dal LABORATORO D FSCA Docente Claudio Oleari AA 999-000 n costruzione - Aggiornamento a marzo 006 Si prega di comunicare errori, inesattezze, oscurità, suggerimenti oleari@fis.unipr.it
Schede di 77,&$*(0(75,&$ dal LABORATORO D FSCA Docente Claudio Oleari AA 999-000 n costruzione - Aggiornamento a marzo 006 Si prega di comunicare errori, inesattezze, oscurità, suggerimenti oleari@fis.unipr.it
GEOMETRIA ANALITICA
 GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
LA CIRCONFERENZA E LA SUA EQUAZIONE
 LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
(i) Determinare l equazione cartesiana dell unica circonferenza C passante per i tre punti dati.
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Informatica Grafica. Un introduzione
 Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
METODO DI CAVALIERI-SIMPSON (o delle parabole) (per il calcolo approssimato 1 di integrali definiti)
 METODO DI CVLIERI-SIMPSON (o delle parabole) (per il calcolo approssimato di integrali definiti) ssieme ai metodi dei Rettangoli e dei Trapezi costituisce l insieme dei metodi di Integrazione Numerica
METODO DI CVLIERI-SIMPSON (o delle parabole) (per il calcolo approssimato di integrali definiti) ssieme ai metodi dei Rettangoli e dei Trapezi costituisce l insieme dei metodi di Integrazione Numerica
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4.1 CAPITOLO 4 APPROSSIMAZIONE PARASSIALE
 4.1 CAPITOLO 4 APPROSSIMAZIONE PARASSIALE Quando i raggi, intercettati da un sistema ottico centrato, si propagono dal piano oggetto al piano immagine rimanendo confinati in una regione molto prossima
4.1 CAPITOLO 4 APPROSSIMAZIONE PARASSIALE Quando i raggi, intercettati da un sistema ottico centrato, si propagono dal piano oggetto al piano immagine rimanendo confinati in una regione molto prossima
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
Esercizi di Geometria Affine
 Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
LENTI SOTTILI. Le lenti sottili sono gli strumenti ottici più importanti tra quelli più semplici.
 LENTI SOTTILI Chiamiamo lente un qualsiasi corpo trasparente limitato da due superfici curve o da una superficie piana ed una curva, in grado di trasmettere un fascio di luce focalizzandolo in modo da
LENTI SOTTILI Chiamiamo lente un qualsiasi corpo trasparente limitato da due superfici curve o da una superficie piana ed una curva, in grado di trasmettere un fascio di luce focalizzandolo in modo da
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Capitolo 4. Sistemi ottici
 Capitolo 4 Sistemi ottici Si chiama sistema ottico un sistema di lenti e specchi, cioé dispositivi riflettenti e rifrangenti, quindi una successione di superfici riflettenti e rifrangenti che delimitano
Capitolo 4 Sistemi ottici Si chiama sistema ottico un sistema di lenti e specchi, cioé dispositivi riflettenti e rifrangenti, quindi una successione di superfici riflettenti e rifrangenti che delimitano
CONICHE. Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oxy sia data la conica C di equazione
 CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Fisica Generale B. 3. Esercizi di Ottica. Esercizio 1. Esercizio 1 (III) Esercizio 1 (II) ! 1. = v = c 2.
 Fisica Generale B 3. Esercizi di Ottica http://campus.cib.unibo.it/490/ May 7, 0 Esercizio La fiamma di un fornello, continuamente e regolarmente rifornita di sale da cucina, costituisce una sorgente estesa
Fisica Generale B 3. Esercizi di Ottica http://campus.cib.unibo.it/490/ May 7, 0 Esercizio La fiamma di un fornello, continuamente e regolarmente rifornita di sale da cucina, costituisce una sorgente estesa
24 giugno Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
Geometria BAER Canale A-K Esercizi 9
 Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Geometria BAER Canale I Esercizi 10
 Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
LEZIONE 10. S(C,ρ) Figura 10.1
 LEZIONE 10 10.1. Sfere nello spazio. In questa lezione studieremo alcuni oggetti geometrici non lineari, circonferenze e sfere nello spazio A 3. Poiché le proprietà delle circonferenze nel piano sono del
LEZIONE 10 10.1. Sfere nello spazio. In questa lezione studieremo alcuni oggetti geometrici non lineari, circonferenze e sfere nello spazio A 3. Poiché le proprietà delle circonferenze nel piano sono del
