SPUNTI SULL'INFINITO nei linguaggi di matematica e fisica
|
|
|
- Erico Messina
- 8 anni fa
- Visualizzazioni
Transcript
1 SPUNTI SULL'INFINITO nei linguaggi di matematica e fisica Un monaco medievale racconta di aver trovato il punto in cui cielo e terra si toccano (C. Flammarion)
2 UNA QUESTIONE LINGUISITICA Il linguaggio scientifico può dar luogo ad equivoci, se non correttamente interpretato. Motivo: i termini utilizzati in ambito scientifico non significano quello che comunemente si intende. Anzi, proprio averli svincolati dal loro senso comune li rende utili in ambito scientifico, dove servono a richiamare in forma concisa concetti spesso espressi da lunghe e laboriose definizioni.
3 Linguaggio naturale: infinito è qualcosa 1. che non ha principio né fine; che si protrae senza limiti; 2. innumerevole, immenso, grandissimo; come l'immensa grandezza del cosmo. 3. che non comporta limiti di spazio o di tempo. L'universo, la maggiore entità che si offre alla nostra osservazione, è spesso associato all'idea di infinito; ecco, forse, perché la scienza è sovente sollecitata a darne una sua interpretazione. Ma l'infinito scientifico rischia di deludere da al tre prospettive, ad esempio, quella letteraria.
4 Iniziamo con un gioco: Vero o Falso? Questa pagina è gialla. V o F? Domani pioverà. V o F? In un caso, si può rispondere subito; nell'altro si deve attendere il tempo necessario. A volte non si può proprio rispondere, perché servirebbe una quantità infinita di informazione, ovvero un processo senza limite per acquisirla.
5 Sopra o sotto?
6 Fiocco di neve di von Koch. Sono note molte figure costruite iterativamente, senza limite al numero di iterazioni. Per es. Tappeto di Sierpinski....
7 Ma esiste questa figura? C'è un senso in cui si può dire che: una successione di oggetti (astratti) converge a, magari senza mai raggiungere, un oggetto limite. Può dunque esistere, astrattamente, senza dover essere costruita. Se il nostro punto finsce sotto la linea frastagliata dopo n iterazioni, si ha la risposta, ma questo n potrebbe non arrivare mai!
8 Matematicamente, sono figure note come FRATTALI Si rappresentano graficamente e con formule, quasi come le figure elementari: retta, parabola, circonferenza... ma hanno propriètà molto peculiari, perché non si finisce mai di costruirle. Il nome indica che hanno dimensione intermedia fra quelle solite: La curva di von Koch è una linea, infinitamente lunga eppure contenuta entro un'area finita. Il tappeto è un'area, ma uguale a zero. (ACCARTOCCIARE)
9 Insieme di Mandelbrot
10 Numeri complessi (x,y) 1. (a,b)=(c,d) significa a=c e b=d 2. (a,b)+(c,d)=(a+c,b+d) 3. (a,b) (c,d)=(ac-bd,ad+bc) Allora posso indicare i numeri reali con (x,0) E cosa sarà il prodotto (0,1) (0,1)? (0,1) (0,1)=( , )=(-1,0) È il numero reale -1. Chiamo i=(0,1) unità immaginaria Il suo quadrato vale -1
11 Se Z=x+iy resta vicino all'origine, C=a+ib appartien all'insieme. Se Z scappa verso l'infinito, no. Basta poi dare colori diversi ai punti che scappano con velocità diverse e colorare di nero quelli che restano.
12 Cambio Z iniziale
13 Cambio C Sfuggirà o resterà?
14 Ingrandisco un dettaglio
15 E ancora...
16 E ancora...
17 e ancora...
18 e ancora...
19 Nella filosofia Paradosso di Zenone; primo argomento contro il movimento: non si può giungere all'estremità di uno stadio senza prima averne raggiunto la metà, ma prima si dovrebbe raggiungere la metà della metà ecc. Ci vorrebbero infiniti passi: mai si raggiungerà l'estremità dello stadio.
20 Soluzione matematica moderna: si introduca la velocità, V=distanza/tempo, se V è costante, metà distanza richiede metà tempo. Le distanze e i tempi seguiranno A farla in pratica, la somma resterebbe sempre minore di 1, solo avvicinandocisi via via di più. Il tempo, invece, scorre inesorabilmente, raggiunge 1, e allora anche la distanza percorsa si completa: Infiniti passi fatti in una unità di tempo: che senso ha? Teoria delle serie infinite: Il paradosso rimane, ma si ha un modo di sommare infiniti addendi, senza doverlo veramente fare. Ipotesi del continuo. Idea già presente nel calcolo di di Archimede.
21 Metafisica di Aristotele: Ed è evidente altresì l'impossibilità dell'esistenza attuale dell'infinito. Altrimenti una qualunque sua parte, presa separatamente, sarebbe infinita. Per Boezio l'infinito sarebbe addirittura una mostruosità. Per esempio, nei processi numerativi, ammettiamo l'infinito in potenza: 1, 2, 3, 4, 5,... ma non ammettiamo un infinito in atto (non sconfessato dalla teoria delle serie). L'infinito in potenza non può essere generato da un finito in atto perché: la causa non può essere meno perfetta dell'effetto.
22 Occam, però, si accorse del fatto che il principio per cui la parte è minore del tutto non è universale e, perciò, non esprime una verità metafisica. Non si può dimostrare (razionalmente) l'impossibilità di andare all'infinito, come per es. da un uomo generato a uno che lo genera. Ciò non comporta che esistano in atto infiniti esseri, perchè una causa efficiente può anche corrompersi e scomparire dopo aver prodotto il suo effetto.
23 Galileo osservò, ma non comprese, la corrispondenza 1:1 fra numeri naturali e loro quadrati: Ma sono di più gli interi o i quadrati? Per Cantor la corrispondenza significa che la loro quantità (potenza) è la stessa. Com'è possibile? 2,3,5... stanno sotto ma non sopra. Eppure ogni numero sotto ha un corrispondente sopra. Una parte propria tanto potente quanto il tutto?
24 Forse è per via dello spazio vuoto fra interi? No! I razionali m/n sono densi nei reali: dati due numeri reali qualunque, fra loro c'è sempre un razionale. Non lasciano vuoti! Ma si numerano Cantor: Lo vedo e non lo credo
25 Se la parte propria di un insieme di oggetti è equipotente al tutto diciamo che l'insieme è INFINITO Cantor poi farà vedere che non tutti gli infiniti sono uguali (idea già presente nella matematica jaina all'inizio dell'era cristiana)
26 Ci sono tanti numeri reali in un intervallo (segmento di retta), quanti tutti i numeri reali (l'intera retta). È un infinito diverso dagli interi. Quanti reali in [0,1]? Asumiamoli numerabili ordiniamoli (anche se senza limite): 0.a1a2a3a b1b2b3b c1c2c3c4... e prendiamo il numero 0.d1d2d3d4... con d1=/=a1; d2=/=b2; d3=/=c3;... Non c'è nella lista!! NON-NUMERABILI!
27 Si tratta di insiemi di oggetti, precisamente numeri. Cantor si era trovato alle soglie di un paradosso, nel definire l'insieme più grade possibile: L'insieme di tutti gli insiemi. Bertrand Russell introdusse l'insieme S, per es. di tutti gli oggetti descrivibili in esattamente otto parole il quale contiene se stesso e quello R di tutti gli insiemi che non appartengono a se stessi (barbiere rade tutti quelli che non radono se stessi). Rade se stesso? Se si, contraddice la definizione, se no, si deve radere... Problema di carattere linguistico evidente nel comprendere un tutto o l'infinito.
28 Nel definire un insieme, allora, non si può usare l'insieme stesso: qualunque cosa contenga tutto di una collezione di oggetti, non deve appartenere alla collezione. Ma non basta a evitare paradossi. Zermelo e Fränkel tentarono un'assiomatizzazione degli insiemi, simile in scopo a quella di Euclide per la geometria. Dei loro 9 assiomi, quello detto di scelta ha generato forti controversie: Se S è un insieme (finito o no) di insiemi non vuoti e senza elementi in comune, allora si può creare l'insieme di scelta prendendo da ogni insieme di S precisamente un solo elemento. Ma come si può fare questa scelta, se gli insiemi di S sono infiniti?
29 Gödel: il nono assioma non contraddice gli altri, Cohen: non può essere dimostrato a partire da essi: è indipendente dagli altri, come il Postulato di Euclide delle parallele (infinitamente lunghe). Ancora una volta, il concetto di infinito impone un mutamento al corso dello sviluppo della matematica. Come non c'è una unica geometria logicamente coerente, così non c'è un'unica teoria logicamente coerente degli insiemi. L'infinito ci forzerà, tramite il lavoro di Gödel, ad ammettere che certe proposizioni, anche se vere, non possono essere dimostrate. Conseguenze di ciò, fra cui il fatto che l'ipotesi del continuo è indecidibile, restano ancora da capire.
30 IL CAOS Fare previsioni sulla base di leggi note, richiede prima delle misure, per conoscere la situazione di partenza, ovvero la condizione iniziale. Fare previsioni ed effettuare le necessarie misure, sono attività umane e, dato che ogni misura che si può fare va soggetta a incertezze, accuratezza finita, le previsioni sono sempre affette da un margine d'errore, che ci ricordala nostra finitezza e i nostri limiti. L'incertezza appare anche nei fenomeni più semplici. Se questi hanno particolari caratteristiche, che ne impediscono la prevedibilità anche in linea di principio, si parla di: Caos Deterministico.
31 Anche i moti più semplici diventano imprevedibili. Crescita lineare delle incertezze iniziali: distanza doppia implica incertezza doppia; dimezzare l'incertezza iniziale la dimezza a tutte le distanze A sufficiente distanza un punto nel bersaglio o un altro, è indifferente. Ma questo non è chiamato caos, oggi.
32 Caos: dipendenza esponenziale dalle condizioni iniziali Esponenziale: distanza unitaria, incertezza 3; doppia, incertezza 9 tripla, 27. Migliorare la previsione richiederebbe uno sforzo sovrumano! Notare la taglia finita del bersaglio.
33 Una evoluzione continua nel tempo, può essere espressa in termini di una successione di simboli, che codificano le regioni visitate nella evoluzione temporale. N R V a g f e Y T...
34 Se la dinamica è caotica, traiettorie vicine si separano rapidamente, hanno sequenze simboliche diverse e ad ogni sequenza si associa una data traiettoria. L'informazione di una sequenza intera equivale alla conoscenza della condizione iniziale. Più lunga è la sequenza, più precisa è tale conoscenza. Traiettorie tipiche danno sequenze che non si ripetono nel tempo.
35 Questo perché i punti dello spazio, ovvero gli stati del sistema di interesse, sono infiniti. Fossero finiti, dopo un certo tempo, qualunque traiettoria tornerebbe sui suoi passi e proseguirebbe per un cammino già percorso in passato. Questo avviene con gli automi cellulari: Tutte le loro evoluzioni sono periodiche, tranne che nel limite in cui lo spazio dei loro stati diventi infinito.
36 Quando le dinamiche sono caotiche, producono sequenze di simboli apparentemente casuali. Dato un pezzo finito di sequenza simbolica, come si può evidenziare se è casuale (prodotta per es. nel gioco del testa o croce) o se segue una regola? Non si può: solo l'analisi dell'intera sequenza infinita potrebbe rispondere alla nostra domanda, perché: a. una sequenza casuale infinita contiene al suo interno ogni sotto-sequenza anche ordinata (anche la Divina Commedia) b. per qualunque sequenza finita si può trovare una regola.
37 Date due foto di un certo numero di bocce? È come nel moto delle molecole di un gas, di cui la Fisica dice: l'entropia (disordine) cresce: irreversibilità: freccia del tempo. Evoluzione verso distribuzione disordinata, cioè uniforme, cioè casuale delle molecole nel loro spazio.
38 Se ci sono pochi oggetti, non si parla neanche di ordine o disordine: non fa differenza. Se sono tanti e interagiscono (condividono la propria energia) evolvono. Come si equilibra le densità, così si trasporta calore, per equilibrare la temperatura, ecc. e si genera la freccia del tempo: tendenza verso un crescente disordine, grazie alla infinità dei possibili stati.
39 A cosa si deve che tutto nell'universo evolva in modo da non tornare indietro? Perchè il calore flusice dai corpi caldi a quelli freddi e non torna mai indietro? Perchè se metto del latte nel caffè, non li separo più? Innanzitutto, meno male che è così!
40 Meno male che è così! Ma perché? Per lo stesso motivo per il quale è facile mettere una camera in disordine e richiede lavoro (energia) rimetterla in ordine. Le combinazioni disordinate (uniformi) sono tante di più di quelle ordinate! Soprattutto quando gli oggetti sono tanti.
41 I moti caotici sono come casuali e il casuale preferisce l'uniformità. Praticamente tutta la materia è soggetta a moti caotici, quindi tende verso l'uniformità, se lasciata a se stessa (isolata). Ci vuole lavoro, energia, per vincere questa tendenza. Sulla Terra l'energia è fornita dal Sole. Una grande parte viene dissipata (restituita all'universo). Questo consente il miracolo di ordine ed armonia che è la vita. Lo stesso accade nel resto dell'universo.
42 Cat's Eye Nebula: stella morente; il Sole fra 5 miliardi anni.
43 Nebulosa del Granchio: resti di supernova
44 Nebulosa Rosetta: giovani stelle a 5000 anni luce
45 Nebulosa Testa di Cavallo: una nube di polveri a 1500 anni luce.
46 NGC2440: più caotica di NGC2346; la vogliamo chiamare dis-ordinata?
47 Era questo che intendevamo per INFINITO? Forse dobbiamo ammettere che c'è una questione di carattere linguistico: la scienza parla di altro
48 Noi scopriremo il semplice sotto il complesso, poi il complesso sotto il semplice, poi di nuovo il semplice sotto il complesso, e così via, senza poter prevedere quale sarà l'ultimo termine. Ma dovremo pure fermarci da qualche parte e, perchè la scienza sia possibile, occorre farlo quando si incontra la semplicità... Ma se la semplicità è solo apparente, questo terreno sarà abbastanza solido? È quanto conviene investigare. (H. Poincarè)
49 Riferimenti bibliografici D.R. Hofstadter, Gödel, Escher, Bach, Adelphi, Milano (1984) R. Penrose, The emperor's new mind, Vintage Books, London (1990) J.P. Luminet, M. Lachièze-Rey, Finito o infinito?, Mondadori, Milano (2005) E. Maor, To infinity and beyond, Birkhäuser, Stuttgart (1986) L. Rondoni, Caos, informazione e calore, Bollettino della Unione Matematica Italiana Vol. 8 Sez. A, (2005) L. Rondoni, Complessità, caos e la presunta supremazia dell'informazione sulla materia (Serie SEFIR, in stampa) L. Rondoni, Sistemi complessi nella fisica odierna e cenni alla complessità nelle scienze contemporanee (Serie SEFIR, in stampa)
50
51
52
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
Energia potenziale elettrica e potenziale. In queste pagine R indicherà una regione in cui è presente un campo elettrostatico.
 Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Dall italiano al linguaggio della logica proposizionale
 Dall italiano al linguaggio della logica proposizionale Dall italiano al linguaggio della logica proposizionale Enunciati atomici e congiunzione In questa lezione e nelle successive, vedremo come fare
Dall italiano al linguaggio della logica proposizionale Dall italiano al linguaggio della logica proposizionale Enunciati atomici e congiunzione In questa lezione e nelle successive, vedremo come fare
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Moto circolare uniforme
 Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali 01 - Grandezze scalari e grandezze vettoriali. Le grandezze fisiche, gli oggetti di cui si occupa la fisica, sono grandezze misurabili. Altri enti che non sono misurabili
Grandezze scalari e vettoriali 01 - Grandezze scalari e grandezze vettoriali. Le grandezze fisiche, gli oggetti di cui si occupa la fisica, sono grandezze misurabili. Altri enti che non sono misurabili
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
ci sono più problemi che programmi esiste un problema che non si può risolvere con un programma
 Calcolabilità problemi facili trovare la media di due numeri stampare le linee di un file che contengono una parola problemi difficili trovare il circuito minimo data una tabella determinare la migliore
Calcolabilità problemi facili trovare la media di due numeri stampare le linee di un file che contengono una parola problemi difficili trovare il circuito minimo data una tabella determinare la migliore
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
A intervalli regolari ogni router manda la sua tabella a tutti i vicini, e riceve quelle dei vicini.
 Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
4. Conoscere il proprio corpo
 4. Conoscere il proprio corpo Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
4. Conoscere il proprio corpo Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE
 I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
OSCURI PREDATORI DI LUCE
 OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
PROCESSO DI INDICIZZAZIONE SEMANTICA
 PROCESSO DI INDICIZZAZIONE SEMANTICA INDIVIDUAZIONE DEI TEMI/CONCETTI SELEZIONE DEI TEMI/CONCETTI ESPRESSIONE DEI CONCETTI NEL LINGUAGGIO DI INDICIZZAZIONE TIPI DI INDICIZZAZIONE SOMMARIZZAZIONE INDICIZZAZIONE
PROCESSO DI INDICIZZAZIONE SEMANTICA INDIVIDUAZIONE DEI TEMI/CONCETTI SELEZIONE DEI TEMI/CONCETTI ESPRESSIONE DEI CONCETTI NEL LINGUAGGIO DI INDICIZZAZIONE TIPI DI INDICIZZAZIONE SOMMARIZZAZIONE INDICIZZAZIONE
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
2 Rappresentazioni grafiche
 asi di matematica per la MPT 2 Rappresentazioni grafiche I numeri possono essere rappresentati utilizzando i seguenti metodi: la retta dei numeri; gli insiemi. 2.1 La retta numerica Domanda introduttiva
asi di matematica per la MPT 2 Rappresentazioni grafiche I numeri possono essere rappresentati utilizzando i seguenti metodi: la retta dei numeri; gli insiemi. 2.1 La retta numerica Domanda introduttiva
Bartoccini Marco 3 A
 Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
L infinito nell aritmetica. Edward Nelson Dipartimento di matematica Università di Princeton
 L infinito nell aritmetica Edward Nelson Dipartimento di matematica Università di Princeton Poi lo condusse fuori e gli disse: . E soggiunse:
L infinito nell aritmetica Edward Nelson Dipartimento di matematica Università di Princeton Poi lo condusse fuori e gli disse: . E soggiunse:
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi.
 E. Calabrese: Fondamenti di Informatica Problemi-1 Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi. L'informatica
E. Calabrese: Fondamenti di Informatica Problemi-1 Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi. L'informatica
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Scuola tedesca (1912) Si contrappone all elementismo di Wundt. Analisi vs sintesi
 Psicologia della forma (Gestalt) Scuola tedesca (1912) Si contrappone all elementismo di Wundt Esperienza Analisi vs sintesi Gestaltisti: quando una persona guarda fuori della finestra, essa vede immediatamente
Psicologia della forma (Gestalt) Scuola tedesca (1912) Si contrappone all elementismo di Wundt Esperienza Analisi vs sintesi Gestaltisti: quando una persona guarda fuori della finestra, essa vede immediatamente
CONOSCERE IL PROPRIO CORPO
 CONOSCERE IL PROPRIO CORPO Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
CONOSCERE IL PROPRIO CORPO Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
Processo di risoluzione di un problema ingegneristico. Processo di risoluzione di un problema ingegneristico
 Processo di risoluzione di un problema ingegneristico 1. Capire l essenza del problema. 2. Raccogliere le informazioni disponibili. Alcune potrebbero essere disponibili in un secondo momento. 3. Determinare
Processo di risoluzione di un problema ingegneristico 1. Capire l essenza del problema. 2. Raccogliere le informazioni disponibili. Alcune potrebbero essere disponibili in un secondo momento. 3. Determinare
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Lezione 14: L energia
 Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Psicometria (8 CFU) Corso di Laurea triennale STANDARDIZZAZIONE
 Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
LA CORRENTE ELETTRICA
 L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
La prof.ssa SANDRA VANNINI svolge da diversi anni. questo percorso didattico sulle ARITMETICHE FINITE.
 La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Mentore. Rende ordinario quello che per gli altri è straordinario
 Mentore Rende ordinario quello che per gli altri è straordinario Vision Creare un futuro migliore per le Nuove Generazioni Come? Mission Rendere quante più persone possibili Libere Finanziariamente Con
Mentore Rende ordinario quello che per gli altri è straordinario Vision Creare un futuro migliore per le Nuove Generazioni Come? Mission Rendere quante più persone possibili Libere Finanziariamente Con
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Algoritmo. I dati su cui opera un'istruzione sono forniti all'algoritmo dall'esterno oppure sono il risultato di istruzioni eseguite precedentemente.
 Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Studio di una funzione ad una variabile
 Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Un po di statistica. Christian Ferrari. Laboratorio di Matematica
 Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
Capitolo II. La forma del valore. 7. La duplice forma in cui si presenta la merce: naturale e di valore.
 Capitolo II La forma del valore 7. La duplice forma in cui si presenta la merce: naturale e di valore. I beni nascono come valori d uso: nel loro divenire merci acquisiscono anche un valore (di scambio).
Capitolo II La forma del valore 7. La duplice forma in cui si presenta la merce: naturale e di valore. I beni nascono come valori d uso: nel loro divenire merci acquisiscono anche un valore (di scambio).
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
I NUMERI DECIMALI. che cosa sono, come si rappresentano
 I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
La f(x) dovrà rimanere all interno di questo intorno quando la x è all interno di un intorno di x 0, cioè I(x 0 ), cioè:
 1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
Nascita e morte delle stelle
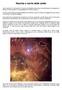 Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
IL TEMPO METEOROLOGICO
 VOLUME 1 CAPITOLO 4 MODULO D LE VENTI REGIONI ITALIANE IL TEMPO METEOROLOGICO 1. Parole per capire A. Conosci già queste parole? Scrivi il loro significato o fai un disegno: tempo... Sole... luce... caldo...
VOLUME 1 CAPITOLO 4 MODULO D LE VENTI REGIONI ITALIANE IL TEMPO METEOROLOGICO 1. Parole per capire A. Conosci già queste parole? Scrivi il loro significato o fai un disegno: tempo... Sole... luce... caldo...
Dispense di Informatica per l ITG Valadier
 La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
COMUNIC@CTION INVIO SMS
 S I G e s t S.r.l S e d e l e g a l e : V i a d e l F o r n o 3 19125 L a S p e z i a T e l e f o n o 0187/284510/15 - F a x 0187/525519 P a r t i t a I V A 01223450113 COMUNIC@CTION INVIO SMS GUIDA ALL
S I G e s t S.r.l S e d e l e g a l e : V i a d e l F o r n o 3 19125 L a S p e z i a T e l e f o n o 0187/284510/15 - F a x 0187/525519 P a r t i t a I V A 01223450113 COMUNIC@CTION INVIO SMS GUIDA ALL
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
NOME:... MATRICOLA:... Scienza dei Media e della Comunicazione, A.A. 2007/2008 Analisi Matematica 1, Esame scritto del 08.02.2008. x 1.
 NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
CALORE. Compie lavoro. Il calore è energia. Temperatura e calore. L energia è la capacità di un corpo di compiere un lavoro
 Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Come fare una scelta?
 Come fare una scelta? Don Alberto Abreu www.pietrscartata.com COME FARE UNA SCELTA? Osare scegliere Dio ha creato l uomo libero capace di decidere. In molti occasioni, senza renderci conto, effettuiamo
Come fare una scelta? Don Alberto Abreu www.pietrscartata.com COME FARE UNA SCELTA? Osare scegliere Dio ha creato l uomo libero capace di decidere. In molti occasioni, senza renderci conto, effettuiamo
Il modello generale di commercio internazionale
 Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
INTRODUZIONE AI CICLI
 www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
Teorie Etiche - Kant
 Teorie Etiche - Kant Gianluigi Bellin January 27, 2014 Tratto dalla Stanford Encyclopedia of Philosophy online alle voce Kant s Moral Philosophy. La filosofia morale di Immanuel Kant Immanuel Kant, visse
Teorie Etiche - Kant Gianluigi Bellin January 27, 2014 Tratto dalla Stanford Encyclopedia of Philosophy online alle voce Kant s Moral Philosophy. La filosofia morale di Immanuel Kant Immanuel Kant, visse
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
Uso dei modelli/template
 Uso dei modelli/template Il modello (o template, in inglese) non è altro che un normale file di disegno, generalmente vuoto, cioè senza alcuna geometria disegnata al suo interno, salvato con l estensione.dwt.
Uso dei modelli/template Il modello (o template, in inglese) non è altro che un normale file di disegno, generalmente vuoto, cioè senza alcuna geometria disegnata al suo interno, salvato con l estensione.dwt.
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 9 marzo 2010 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2010.html TEOREMI DI ESISTENZA TEOREMI DI ESISTENZA Teorema
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 9 marzo 2010 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2010.html TEOREMI DI ESISTENZA TEOREMI DI ESISTENZA Teorema
