A i è un aperto in E. i=1
|
|
|
- Letizia Carbone
- 9 anni fa
- Visualizzazioni
Transcript
1 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque se un punto è di accumulazione per A c deve per forza appartenere ad A c, ovvero (A c ) A c. = : se x o A allora x o A c e quindi, se per ipotesi A c è chiuso, x o non può essere di accumulazione per A c ; negando la condizione x o (A c ) si ottiene che esiste allora r > 0 tale che B(x o, r) A c =Ø, ovvero B(x o, r) A e quindi x o è interno ad A, il che prova che A è aperto. Proposizione A è aperto se e solo se A A =Ø. 2. C è chiuso se e solo se C C. Dimostrazione. Proviamo la condizione necessaria della 1. Se A è aperto, ogni x o A è interno, e quindi ceramente non appartiene alla frontiera. Viceversa, se A A =Ø, ogni elemento di A non appartiene a A e quindi è necessariamente interno. Proviamo la 2. Se C è chiuso per la Porposizione 1 A = C c è aperto; quindi per la 1, C c C c =Ø; Ma C c = C e quindi C c C =Ø, il che significa che C C. Viceversa, se C C, e A = C c allora A C = A c e quindi A A =Ø; di nuovo per la 1. allora A è aperto e per la Proposizione 1 C = A c è chiuso. Proposizione. C è chiuso se e solo se C = C. Dimostrazione. = : Dalla Proposizione 2 C C e poichè C = C C si ha C C C ovvero C = C. = Se C = C in particolare C C, cioè C C C e quindi C C; dalla Proposizione 2, allora, C è chiuso. Proposizione 4. Gli aperti di uno spazio normato (E, ) godono delle proprietà 1 Ø e E sono aperti; 2 Se {A α, α I} è una famiglia di sottoinsiemi aperti di E, allora α I A α è un aperto; Se A 1,, A n sono aperti in E anche n A i è un aperto in E. i=1 Dimostrazione Che tutto lo spazio E sia aperto è un immediata conseguenza della definizione, in quanto ogni x E è interno allo spazio; per questo motivo E =Ø, e quindi E E; dunque dalla Proposizione 2, E è anche chiuso, e quindi il suo complementare, cioè Ø, è aperto. 1
2 Per provare la 2, osserviamo che comunque scelto x α I A α deve esistere almeno un α I tale che x A α che è aperto; pertanto esiste anche r > 0 tale che B(x, r) A α α I A α e quindi x è interno all unione. Per provare la infine, osserviamo che se x n A i =Ø non si deve provare nulla; se invece i=1 n A i cioè x A i, i = 1,, n,allora esistono n raggi, r i tali che B(x, r i ) A i. i=1 Preso r = min{r 1,, r n } > 0 risulta chiaramente B(x, r) B(x, r i ) A i ovvero B(x, r) n A i, ovvero x è interno all intersezione.. Utilizzando la Proposizione 1 e le Leggi di De Morgan, si ottiene immediatamente il seguente Corollario. I chiusi di uno spazio normato (E, ) godono delle proprietà 1 Ø e E sono chiusi; 2 Se {C α, α I} è una famiglia di sottoinsiemi chiusi di E, allora α I C α è un chiuso; i=1 Se A 1,, A n sono chiusi in E anche n C i è un chiuso in E. Infine, come ultima caratterizzazione dei chiusi proviamo il seguente risultato. Proposizione 5. In uno spazio normato (E, ) sono equivalenti 1 C è chiuso in E; 2 per ogni successione (x n ) n C convergente a x o E risulta x o C. i=1 Dimostrazione. Proviamo innanzitutto che 1= 2. Supponiamo per assurdo che esista invece (x n ) C convergente a x o, ma che x o C; allora x o C c che per l ipotesi 1 è aperto; dunque esiste un raggio r tale che B(x o, r) C c ovvero B(x o, r) C =Ø, mentre per la convergenza dovrebbe contenere una coda della successione, e quindi dovrebbe contenere elementi di C. Passiamo all implicazione inversa; per provare che 2 = 1, proviamo che C C. Sia allora x o C fissato; consideriamo r 1 = 1 e applichiamo la definizione di punto di accumulazione; dunque B(x o, 1) C \ {x o } Ø, ovvero esiste x 1 C B(x o, 1) e x 1 x o ; allora ρ 1 = x o x 1 > 0 e scegliendo r 2 = ρ e iterando il procedimento si trova x 2 C B(x o, r 2 )\{x o } che di nuovo implica 0 < ρ 2 = x 2 x o < 1 ; proseguendo in questo modo si costruisce una 2 2
3 successione di punti x n C tali che x n x o 1 2 n e quindi tale che x n x o. Dall ipotesi 2, quindi x o C che è esattamente quello che ci proponevamo di provare.
4 Teorema 1. (Caratterizzazione dei connessi di R) Un sottoinsieme I di R è connesso se e solo se è un intervallo, o una semiretta o tutto R. Dimostrazione. Proviamo prima che se I è del tipo detto, allora I è connesso. A tale scopo, supponiamo per fissare le idee, che I sia limitato superiormente, e supponiamo per assurdo che I ammetta una sconnessione (A 1, A 2 ). Allora I A i Ø; di conseguenza, anche A i I o Ø, e quindi possiamo scegliere x A 1 I o e x A 2 I o ; poichè A 1 A 2 =Ø, necessariamente x x. Supponiamo per esempio che x < x, e poniamo H = {x I : x x e [x, x] A 1 }, x o = sup H. Poichè tra i punti di H vi è in particolare x, risulta certamente x x o. Proviamo ora che x > x o. Se infatti supponiamo per assurdo che x < x o esisterebbe necessariamente un elemento ξ H tale che ξ > x ; ciò significa che ξ I e che [x, ξ] A 1. Ma allora anche [x, x ] A 1 e quindi x A 1 il che è assurdo perchè A 1 e A 2 sono disgiunti. Se supponiamo d altra parte che x o = x, esiste una successione x n H tale che x n x, e quindi [x, x n ] A 1. D altra parte x A 2 che è aperto; dunque esiste un raggio r tale che B(x, r) A 2, e per la convergenza in questa boccia cade tutta una coda della successione (x n ) n ; poichè ciascun x n A 1 di nuovo perveniamo alla contraddizione A 1 A 2 Ø. Pertanto x x o < x. Ora, poichè x, x I o, x o [x, x [, necessariamente anche x o I o. Proviamo che [x, x o [ A 1 ; se x = x o l intervallo è vuoto e l inclusione è immediata; se invece x < x o, possiamo determinare una successione (ξ n ) n H convergente dal basso a x o (perchè I non è degenere e tutti i suoi punti interni sono di accumulazione sia da destra che da sinistra). Quindi tutti gli intervalli [x, ξ n [ sono contenuti in A 1 ; allora [x, x o [= n [x, ξ n [ A 1. (1) Se supponiamo che x o A 1, x o A 1 I o che è aperto, e quindi esiste certamente x 1 > x o tale che [x o, x 1 ] A 1 I o A 1 I (perchè contiene un intorno centrato in x o e dunque, a maggior ragione, contiene un intorno destro di x o ). Dalla (1), [x, x o [ [x o, x 1 ] = [x, x 1 ] A 1 ; ma allora x 1 H e questo contraddice il fatto che x o è un maggiorante di H. D altra parte se supponiamo che x o A 2, esiste certamente x 2 < x o tale che [x 2, x o ] A 2 (di nuovo perchè A 2 è aperto quindi contiene un intorno centrato in x o e dunque, a maggior ragione, contiene un intorno sinistro di x o ); senza restrizione di generalità si può supporre che x 2 x. Quindi [x 2, x o ] A 1 =Ø. Ma allora nessun elemento ξ x 2 può appartenere ad H, perchè in caso contrario [x 2, ξ] [x, ξ] A 1 e quindi x 2 A 1 ; cioè x 2 è un maggiorante di H. Allora sup H x 2 < x o che è di nuovo una contraddizione. In conclusione il punto x o I ma x o A 1 A 2 e questo contraddice l assunzione che (A 1, A 2 ) è una sconnessione per I. Viceversa, proviamo che se I è un connesso, allora è un insieme del tipo elencato. Per brevità trattiamo solo il caso di I connesso limitato, lasciando al lettore la trattazione dei rimanenti casi. 4
5 Poniamo allora a = inf I, b = sup I; negare che I sia uno qualsiasi degli intervalli determinati da a e da b, equivale a supporre che ci sia un punto x o ]a, b[\i; infatti, se al contrario fosse ]a, b[ I, I coinciderebbe con uno dei quattro intervalli [a, b], ]a, b[, [a, b[, ]a, b]. Prendiamo A 1 = (, x o [, A 2 =]x o, + ) e osserviamo che sono entrambe aperti, che sono disgiunti e la loro unione copre I; in altre parole abbiamo generato una sconnessione di I, il che nega l ipotesi che I sia connesso. 5
6 Teorema 2. Ogni insieme E stellato è connesso. Dimostrazione. Sia E stellato rispetto a x o e supponiamo per assurdo che E ammetta una sconnessione (A 1, A 2 ); allora x o appartiene ad uno solo dei due aperti, sia per esempio x o A 1. Poichè E A 2 Ø, possiamo scegliere x 1 E A 2 ; consideriamo I 1 = {t ]0, 1[: tx o + (1 t)x 1 A 1 }, I 2 = {t ]0, 1[: tx o + (1 t)x 1 A 2 }. Allora I 1 I 2 =]0, 1[ e I 1 I 2 =Ø; se proviamo che sono aperti e non vuoti abbiamo determinato una sconnessione di ]0, 1[ e quindi perveniamo ad un assurdo. Proviamo ora che sono entrambe non vuoti; basta provarlo per I 1 perchè la dimostrazione che I 2 Ø è analoga. Consideriamo la successione in ]0, 1[ definita da t n = n 1 n, e consideriamo corrispondentemente x n = t n x o + (1 t n )x 1 ; è facile verificare che x n x o. D altra parte, essendo A 1 aperto, e x o A 1 esiste certamente r > 0 tale che B(x o, r) A 1, mentre dalla convergenza, risulta x n B(x o, r) per n sufficientemente grande; dunque x n A 1 definitivamente, e di conseguenza t n I 1 definitivamente; ciò ci assicura che I 1 Ø. Proviamo per esempio che I 1 è aperto, cioè che se t o I 1 allora tutto un intorno di t o cade in I 1. Poniamo x = t o x o + (1 t o )x 1. Per definizione di I 1 si ha x A 1, ed essendo quest ultimo aperto, esiste r > 0 tale che B(x, r) A 1. Poichè x o x 1 (perchè appartengono a due insiemi disgiunti), risulta x o x 1 > 0. ] [ ] [ r Proviamo che t o x o x 1, t r r o + I 1 ; infatti se τ t o x o x 1 x o x 1, t r o + x o x 1 si ha τx o +(1 τ)x 1 x = (τ t o )x o +[(1 τ) (1 t o )]x 1 = (τ t o )x o (τ t o )x 1 = τ t o x o x 1 < r. Quindi τx o + (1 τ)x 1 B(x, r) A 1 che per definizione implica τ I 1. 6
7 Teorema. Se E è aperto e connesso, allora è connesso per poligonali. Dimostrazione. Consideriamo in E la relazione binaria x... y se e solo se esiste una poligonale S(x, y) tutta contenuta in E. E facile convincersi che si tratta di una relazione di equivalenza. Denotiamo con E[x] la classe di equivalenza del generico elemento x E ovvero E[x] = {y E : x... y}. Proviamo che E[x] è aperto per ogni x E. Infatti se y E[x], y E che è aperto, e quindi esiste r > 0 tale che B(y, r) E; ora B(y, r) è stellato rispetto a y quindi ogni suo punto z... y e poichè y... x per transitività z... x; così B(y, r) E[x] e quindi ogni punto di E[x] è interno. Ovviamente se x... y si ha E[x] E[y] =Ø; ma allora E[x] e E[y] sono due aperti y...x disgiunti la cui unione copre E, in altre parole costituiscono una sconnessione di E, il che contraddice l assunzione che E è connesso. Dunque non possono esistere due punti di E tali che x... y, ovvero x... y per ogni coppia di punti di E, il che assicura che E è connesso per poligonali. 7
8 Primo teorema di continuità globale. Siano V e W due spazi normati, D un sottoinsieme aperto di V e f : D W. Allora f è continua se e solo se per ogni aperto B W risulta f 1 (B) aperto in V. Dimostrazione. Proviamo prima la parte necessaria, cioè supponiamo f continua, e fissiamo un aperto B W. Se f 1 (B) è vuoto non vi è nulla da provare. Se f 1 (B) non è vuoto, vogliamo provare che ogni suo punto è interno. Sia allora x o f 1 (B); allora f(x o ) B e dunque esiste certamente r > 0 tale che B[f(x o ), r] B. Per l assunzione di continuità esiste in corrispondenza δ(r) > 0 tale che per ogni x D con x x o V < δ risulta f(x) f(x o ) W < r. D altra parte anche D è aperto; quindi esiste ρ > 0 tale che B(x o, ρ) D. Allora se scegliamo δ (r) = min{δ(r), ρ} risulta certamente B(x o, δ ) D ma anche f(x) B[f(x o ), r] per ogni x B(x o, δ ), e dunque B(x o, δ ) f 1 (B). Viceversa, proviamo la condizione sufficiente: fissato arbitrariamente x o D, per provare la continuità di f in x o, fissiamo ε > 0 e consideriamo l aperto in B = B[f(x o ), ε] W. Per l ipotesi risulta f 1 (B) aperto in V, e poichè ovviamente x o f 1 (B), deve esistere δ > 0 tale che B(x o, δ) f 1 (B). Ciò significa che per ogni x D con x x o V < δ risulta f(x) B = B[f(x o ), ε] cioè f(x) f(x o ) W < ε che è esattamente la definizione di continuità nel punto x o Secondo teorema di continuità globale. Siano V e W due spazi normati, D un sottoinsieme chiuso di V e f : D W una funzione continua. Allora per ogni chiuso C W risulta f 1 (C) chiuso in V. Dimostrazione. Fissato il chiuso C, sia x o [f 1 (C)], e sia (x n ) n una successione in f 1 (C) convergente a x o. Vogliamo provare che x o f 1 (C) ovvero che f 1 (C) contiene ogni suo punto di accumulazione. Sappiamo che x o D, in quanto D è chiuso, che f(x n ) C, e per la continuità, che f(x n ) f(x o ); dunque x o f 1 (C). 8
9 Teorema di conservazione della connessione. Siano V e W due spazi normati, C un sottoinsieme connesso di V e f : C W una funzione continua. Allora f(c) è connesso. Dimostrazione. Supponiamo per assurdo che esista una sconnessione (B 1, B 2 ) di f(c), e consideriamo C i = f 1 (B i ). Immediatamente si prova che C 1 e C 2 sono disgiunti, e che la loro unione ricopre C. Tuttavia non è detto che essi siano aperti, perchè per poter applicare il Primo teorema di continuità globale avremmo bisogno di sapere che anche C è aperto. Per questo motivo occorre costruire diversamente una sconnessione di C (in modo da pervenire ad una contraddizione). Per ogni x C consideriamo r(x) = { d(x, C2 ) se x C 1 d(x, C 1 ) se x C 2. Vogliamo provare innanzitutto che r(x) > 0 per ogni x C. Anche per questo passo procediamo per assurdo, e supponiamo per esempio, che esista x o C 1 tale che r(x o ) = 0; dunque deve esistere una successione (x n ) n C 2 tale che x o x n V 0; quindi si ha anche x n x o e per la continuità f(x n ) f(x o ). Poichè x o C 1 la sua immagine f(x o ) B 1 che è aperto; pertanto f(x n ) B 1 definitivamente; allora anche x n C 1 definitivamente, il che è assurdo perchè si era scelta x n C 2 e C 1 C 2 =Ø. Consideriamo ora gli insiemi A 1 = x C 1 B ( x, r(x) ), A 2 = ( B x, r(x) ). x C 2 Vogliamo provare che costituiscono una sconnessione di C. Intanto sono entrambe aperti, perchè sono unione di aperti; inoltre è evidente che C i A i per i = 1, 2 e quindi che C = C 1 C 2 A 1 A 2. Resta allora da provare che sono disgiunti. Supponiamo ancora per assurdo che ( A 1 A 2 contenga un punto x o ; allora debbono esistere x 1 C 1 e x 2 C 2 tali che x o B x 1, r(x ) ( 1) B x 2, r(x ) 2). Supponiamo per esempio r(x 1 ) r(x 2 ); allora x 1 x 2 V x 1 x o V + x o x 2 V < r(x 1) + r(x 2) < r(x 2 ). Ma x 1 C 1 e quindi r(x 2 ) = d(x 2, C 1 ) x 2 x 1 V < r(x 2 ) che è assurdo. 9
10 Teorema di Heine. Sia K un sottoinsieme sequenzialmente compatto di uno spazio normato (V, V ), e sia f : K (W, W ) una funzione continua. Allora f è uniformemente continua. Dim. Ciò che si vuole provare è che per ogni ε > 0 eiste δ(ε) > 0 tale che per ogni coppia di punti x, x K con x x V < δ risulta f(x ) f(x ) W < ε. Procediamo per assurdo, ovvero supponiamo che esista ε > 0 tale che per ogni δ > 0 esistono x δ, x δ D con x δ x δ V < δ ma f(x δ ) f(x δ ) W > ε. Applicando questa ipotesi assurda con δ = 1 n, n N+ si costruiscono quindi due successioni (x n) n, (x n) n D tali che x n x n V < 1 n e f(x n) f(x n) W > ε. Dalla compattezza sequenziale di K esiste una sottosuccessione (x n p ) p convergente a un elemento x o K; d altra parte se si considera la sottosuccessione (x n p ) p risulta x n p x o V x n p x n p V + x n p x o V < 1 n p + x n p x o V, e quindi immediatamente si ottine che anche converge a x o. Per la continuità di f (che come si è provato precedentemente comporta la continuità sequenziale), risulta allora che lim p + f(x n p ) = f(x o ), lim p + f(x n p ) = f(x o ). Dunque, in corrspondenza di ε esiste p tale che per ogni p > p risulta f(x n p ) f(x o ) W < ε, f(x n p ) f(x o ) W < ε e quindi, sempre per la disuguaglianza triangolare, f(x n p ) f(x n p ) W f(x n p ) f(x o ) W + f(x n p ) f(x o ) W < ε + ε < ε che contraddice l ipotesi inziale, cioè che f(x n) f(x n) W > ε per ogni n N. 10
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
Prodotto libero di gruppi
 Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
LEZIONE 14. a 1,1 v 1 + a 1,2 v 2 + a 1,3 v 3 + + a 1,n 1 v n 1 + a 1,n v n = w 1
 LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
Ancora sugli insiemi. Simbologia
 ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Introduzione Ordini parziali e Reticoli Punti fissi
 Introduzione Ordini parziali e Reticoli Punti fissi By Giulia Costantini (819048) & Giuseppe Maggiore (819050) Table of Contents ORDINE PARZIALE... 3 Insieme parzialmente ordinato... 3 Diagramma di Hasse...
Introduzione Ordini parziali e Reticoli Punti fissi By Giulia Costantini (819048) & Giuseppe Maggiore (819050) Table of Contents ORDINE PARZIALE... 3 Insieme parzialmente ordinato... 3 Diagramma di Hasse...
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
1. Intorni di un punto. Punti di accumulazione.
 1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
La f(x) dovrà rimanere all interno di questo intorno quando la x è all interno di un intorno di x 0, cioè I(x 0 ), cioè:
 1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
1 Insiemi e terminologia
 1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
x u v(p(x, fx) q(u, v)), e poi
 0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 26 marzo 2015 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2015.html COOPERAZIONE Esempio: strategie correlate e problema
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 26 marzo 2015 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2015.html COOPERAZIONE Esempio: strategie correlate e problema
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Finanza matematica - Lezione 01
 Finanza matematica - Lezione 01 Contratto d opzione Un opzione è un contratto finanziario stipulato al tempo, che permette di eseguire una certa transazione, d acquisto call o di vendita put, ad un tempo
Finanza matematica - Lezione 01 Contratto d opzione Un opzione è un contratto finanziario stipulato al tempo, che permette di eseguire una certa transazione, d acquisto call o di vendita put, ad un tempo
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
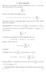 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Teoria degli insiemi
 Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
1 Definizione: lunghezza di una curva.
 Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
Appunti di LOGICA MATEMATICA (a.a.2009-2010; A.Ursini) Algebre di Boole. 1. Definizione e proprietá
 Appunti di LOGICA MATEMATICA (a.a.2009-2010; A.Ursini) [# Aii [10 pagine]] Algebre di Boole Un algebra di Boole è una struttura 1. Definizione e proprietá B =< B,,, ν, 0, 1 > in cui B è un insieme non
Appunti di LOGICA MATEMATICA (a.a.2009-2010; A.Ursini) [# Aii [10 pagine]] Algebre di Boole Un algebra di Boole è una struttura 1. Definizione e proprietá B =< B,,, ν, 0, 1 > in cui B è un insieme non
Algoritmi e strutture dati. Codici di Huffman
 Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
L anello dei polinomi
 L anello dei polinomi Sia R un anello commutativo con identità. È possibile costruire un anello commutativo unitario, che si denota con R[x], che contiene R (come sottoanello) e un elemento x non appartenente
L anello dei polinomi Sia R un anello commutativo con identità. È possibile costruire un anello commutativo unitario, che si denota con R[x], che contiene R (come sottoanello) e un elemento x non appartenente
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Soluzioni del giornalino n. 16
 Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
 Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
