CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
|
|
|
- Gianfranco Simone
- 8 anni fa
- Visualizzazioni
Transcript
1 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni e la indichiamo con il simbolo {f n (x)} n, una legge che ad ogni numero naturale n associa una funzione, che viene indicata con f n (x). dove f n : A R, n. Osserviamo che l insieme di definizione é lo stesso per ogni funzione dunque non dipende da n. Diremo che la successione {f n (x)} n converge puntualmente in A se x A lim n f n (x) = f(x), cioé se x A si ha che ε > 0 n = n (ε, x) : f n (x) f(x) < ε, n > n (quindi vale la relazione di limite a partire da un indice che puó variare al variare del punto x che si considera nell insieme A). Diremo poi che la successione {f n (x)} n converge uniformemente alla funzione f(x) in A se ε > 0 n = n(ε) : f n (x) f(x) < ε, n > n, x A. (in altre parole esiste un indice che va bene per tutti i punti dell insieme A a partire dal quale vale la relazione di limite) Esempi : 1) f n : (0, ) R cosí definita f n (x) = a se 0 < x < 1 n, f n(x) = b, se 1 n x <, essendo a, b due numeri reali distinti. Si ha lim n f n (x) = b, x (0, ) con convergenza non uniforme. ) f n : [0, 1] R cosí definita f n (x) = x n. Si ha lim n f n (1) = 1, lim n f n (x) = 0, x [0, 1) con convergenza non uniforme. 3) f n : R R cosí definite f n (x) = x n+x. Si ha lim n f n (x) = 0, x R con convergenza non uniforme. TEOREMA 74 : Data la successione di funzioni {f n (x)} n con f n : [a, b] R continua in [a, b], n, se c é convergenza uniforme alla funzione f(x) in [a, b], allora si ha che la funzione f(x) é continua in [a, b]. In altre parole la convergenza uniforme di funzioni continue mantiene la continuitá anche alla funzione limite. 1
2 Il Teorema é falso se la convergenza é solo puntuale come mostra l esempio ) oppure il seguente Esempio: 4) f n : R R cosí definita f n (x) = arctg (n x). Si ha lim n f n (0) = 0, lim n f n (x) = π, x > 0, lim n f n (x) = π, x < 0. Ovviamente non c é convergenza uniforme. Osserviamo che. in caso di una successione di funzioni continue considerate in un intervallo [a, b] vale la seguente Proprietá ; La successione di funzioni {f n (x)} n converge uniformemente a f(x) in [a, b] se e solo se lim n max x [a,b] f n (x) f(x) = 0. Data una successione di funzioni continue {f n (x)} n con f n : [a, b] R che converge puntualmente ad una funzione f(x) in [a, b], sappiamo che b a f n(x)dx, n ma i) b a f(x)dx? b ii) lim n a f n(x)dx? iii) in caso di risposta affermativa alle due precedenti domande, che relazioni b ci sono tra lim n a f n(x)dx e b a f(x)dx? In caso di uguaglianza tra queste due ultime quantitá si parla di passaggio al limite sotto il segno di integrale. TEOREMA 75 : Data la successione di funzioni {f n (x)} n con f n : [a, b] R continua in [a, b], n, se c é convergenza uniforme alla b funzione f(x) in [a, b], allora si ha che lim n a f n(x)dx = b a f(x)dx. Dimostrazione Valgono le seguenti disuguaglianze b b b 0 f n (x)dx f(x)dx f n (x) f(x) dx b a a a max x [a,b] f n (x) f(x) dx (b a)max x [a,b] f n (x) f(x) e quest ultima quantitá tende a zero al divergere di n per la convergenza uniforme. Esempi : 5) f n : [0, ] R cosí definita f n (0) = 0, f n (x) = n se 0 < x < 1 n, a
3 f n (x) = 0, se 1 n x. Si ha lim n f n (x) = f(x) = 0, x [0, ] e non vale il passaggio al limite sotto il segno di integrale. 6) f n : [0, + [ R cosí definita f n (x) = nxe nx. Si ha lim n f n (x) = f(x) = 0, x [0, ] e non vale il passaggio al limite sotto il segno di integrale. Il problema che abbiamo appena affrontato in relazione all operazione di integrazione, puó analogamente essere posto per l operazione di derivazione ed, in questo caso, una risposta é data dal seguente TEOREMA 76 : Data la successione di funzioni {f n (x)} n con f n : [a, b] R derivabili e con derivata continua in [a, b], n, se x 0 [a, b] : lim n f n (x 0 ) = l R, inoltre la successione {f n(x)} n converge uniformemente ad una funzione g(x) in [a, b], allora si ha che la successione {f n (x)} n converge uniformemente in [a, b] ad una funzione f(x) derivabile e si ha lim n f n(x) = f (x) = g(x). Anche in relazione a questo Teorema vediamo alcuni Esempi : 7) f n : R R cosí definita f n (x) = esiste f (0). x + 1 n. Si ha lim n f n (x) = x, e non 8) f n : [, +π] R cosí definita f n (x) = 1 n sin nx. Si ha lim n f n (x) = f(x) = 0, x [, +π] inoltre f n(x) = cos nx, pertanto f n(0) = 1 mentre f (0) = 0. SERIE DI FUNZIONI Dato un insieme A R ed una successione di funzioni {f n (x)} n definite su A, costruiamo la successione delle somme parziali {s n (x)} n cosí definita s 1 (x) = f 1 (x), s n (x) = s n 1 (x) + f n (x), x A. Osserviamo che, se il primo indice é zero oppure un altro numero naturale, il procedimento é identico (con le dovute modifiche). Abbiamo cosí costruito la serie di funzioni n f n(x)(ossia il procedimento usato per le serie numeriche va effettuato in ogni punto x A ). Studiare serie di funzioni n f n(x) equivale a studiare la successione di funzioni {s n (x)} n quindi possiamo trasportare alle serie di funzioni le definizioni ed i Teoremi enunciati per le successioni di funzioni. Parleremo quindi di convergenza puntuale della serie n f n(x) in un insieme A R se 3
4 x A lim n s n (x) = S(x). (limite puntuale) convergenza uniforme della serie n f n(x) in un insieme A R se lim n s n (x) = S(x) uniformemente in A. Vale poi il seguente TEOREMA 77 : Data la serie di funzioni n f n(x) con f n : [a, b] R continua in [a, b], n, se la serie converge uniformemente alla funzione S(x) in [a, b], allora si ha che la funzione S(x) é continua in [a, b]. Per le serie di funzioni si pone anche la seguente Definizione : la serie n f n(x) é detta totalmente convergente in A se esiste una successione numerica {b n } n tale che f n (x) b n, x A e n b n é convergente. Vale il Teorema 78 : La convergenza totale implica la convergenza uniforme. Osserviamo che la proprietá di convergenza totale é detta anche test di Weierstrass per la convergenza uniforme (é Condizione Sifficiente per la convergenza uniforme). Esempi : x 1) Sia f n (x) : R R cosí definita f n (x) = x 4 +3n. La serie 4 n f n(x) é totalmente convergente poiché si ha f n (x) 1 4n in quanto la funzione f 3 n (x) ha massimo per x = n. ) Sia f n (x) : [a, b] R cosí definita f n (x) = ( 1) n 1 n. La serie n f n(x) é convergente uniformemente ma non totalmente in quanto si ha f n (x) = 1 n, e é la serie armonica che diverge. n 1 n Teorema 79 : Se n f n(x) é una serie di funzioni continue che converge uniformemente in [a, b], allora la funzione somma é continua in [a, b] e vale la seguente uguaglianza b a n f n(x)dx = b n a f n(x)dx. ( serie integrata termine a termine). Teorema 80 : Se n f n(x) é una serie di funzioni derivabili con derivata continua in [a, b] inoltre x 0 [a, b] : n f n(x 0 ) converge e la serie n f n(x) converge uniformemente ad una funzione g(x) in [a, b], allora la serie n f n(x) converge uniformemente ad una funzione f(x) derivabile in [a, b] e vale la seguente uguaglianza n f n(x)dx = f (x) = g(x), x [a, b]. ( serie derivata termine a termine). 4
5 SERIE DI POTENZE Data una successione numerica {a n } n considerato un punto x 0 R, chiamiamo serie di potenze di centro x 0 la serie + a n(x x 0 ) n = a 0 + a 1 (x x 0 ) + a (x x 0 ) Si tratta dunque di una serie di funzioni nella quale si ha f n (x) = a n (x x 0 ) n. Per comoditá, considereremo x 0 = 0 ( ma tutto cio che diremo vale anche, con le dovute modifiche, se x 0 é un generico punto in R) cosí la serie diventa la seguente + a nx n che sicuramente converge ad a 0 per x = 0. Esempi : 1) le serie + n!xn e + nn x n convergono solo per x = 0 )la serie + xn n! converge assolutamente x R (vedi criterio del rapporto) 3)la serie + xn n+1 converge asolutamente per x < 1, non converge per x > 1 oppure per x < 1, diverge per x = 1 e converge per x = 1. Dagli esempi emerge quella che é la proprietá caratteristica delle serie di potenze ossia Teorema 81 : Data la serie di potenze + a nx n si possono presentare i seguenti casi : i) essa converge solo per x = 0 ii) essa converge x R iii) r > 0 : la serie converge per x < r, non converge per x > r e c é convergenza totale e quindi uniforme in ogni intervallo chiuso contenuto in ( r, r). Il numero r é detto raggio di convergenza della serie. Osserviamo che, in generale, non si puó dire cosa succede per x = r. Vediamo che, nell esempio 3), la serie converge per x = 1 mentre non converge per x = 1. Ci chiediamo, ora, come sia possibile trovare il raggio di convergenza di una serie di potenze. Forniamo due metodi : uno che vale quando si ha a n 0, n, l altro che vale sempre. Teorema 8 - (di D Alembert) : Data la serie di potenze + a nx n con a n 0, n, se lim n a n+1 a n = L, allora si ha che r = + se L = 0, r = 0 se L = +, r = 1 L se L R+. Teorema 83 - (di Cauchy - Hadamard) : Data la serie di potenze 5
6 + a nx n se lim n n a n = L, allora si ha che r = + se L = 0, r = 0 se L = +, r = 1 L se L R+. Data la serie di potenze + a nx n, si dice serie derivata la nuova serie di potenze + n=1 na nx n 1. Se una serie di potenze ha raggio di convergenza r 0, poiché essa converge uniformemente in ogni intervallo chiuso [a, b] contenuto in ( r, r), in tale intervallo [a, b] essa é pure derivabile termine a termine inoltre vale il seguente Teorema 84 : Ogni serie di potenze e la relativa serie derivata hanno stesso raggio di convergenza Vediamo una applicazione del precedente Teorema : sia + a nx n, una serie di potenze con raggio di convergenza r 0 e sia f(x) la sua somma, dunque si ha + a nx n = f(x), x : x < r. Allora per precedenti proprietá enunciate, si ha che la funzione f(x) é derivabile e f (x) = + n=1 n a nx n 1, x : x < r ; inoltre si ha anche x 0 f(t)dt = + a n n+1 xn+1. SERIE DI TAYLOR Data una funzione f : [a, b] R, preso un punto x 0 (a, b), ci chiediamo se esiste una serie di potenze di centro x 0 che converge a f(x) almeno in un intorno di x 0. In caso affermativo, diremo che f é sviluppabile in serie di potenze di centro x 0. Per i Teoremi visti in precedenza, vale il seguente: Teorema 85 : Se la serie di potenze + a n(x x 0 ) n ha raggio di convergenza r > 0 (cioé converge nell insiema A = {x R : x x 0 < r} con convergenza uniforme in ogni intervallo chiuso contenuto in A), allora la sua funzione somma f(x) ha derivata di ogni ordine data dalla seguente serie f (i) (x) = + n=i n(n 1)...(n i + 1)a n(x x 0 ) n i, x : x < r e si ha a n = f (n) (x 0) n!, pertanto infine si ottiene che f(x) = f (n) (x 0 ) (x x 0 ) n ( ) n! In conclusione, se la funzione f é sviluppabile in serie di potenze, essa ha derivata di ogni ordine e la serie di potenze di cui essa é somma e del tipo (*). Tale serie é detta serie di Taylor di centro x 0. Osservazione : avere derivata di ogni ordine (anche in ogni punto del dominio), non basta perché una funzione sia sviluppabile in serie di Taylor come mostra il seguente 6
7 Esempio : Sia f : R R cosí definita f(x) = e 1 x se x 0, f(0) = 0. Per questa funzione si ha che f (n) (x), n e x, inoltre si ha f (n) (0) = 0. Pertanto non puó valere la relazione ( ) con x 0 = 0 in quanto il secondo membro é identicamente nullo. Vediamo ora una Condizione Sufficiente per la sviluppabilitá in serie di Taylor. Teorema 86 : Sia f : [a, b] R tale che f (n) (x), n, x (a, b) inoltre supponiamo che M, L > 0 : f (n) (x) M L n, n, x (a, b), ( ) allora la funzione f é sviluppabile in serie di Taylor di centro un qualunque punto x 0 (a, b). Osserviamo che, in particolare, la proprietá ( ) é verificata se le derivate della funzione f sono equilimitate in (a, b) ossia se K > 0 : f (n) (x) K, n, x (a, b). Osserviamo, inoltre, che, nelle ipotesi del Teorema 86, vale la formula di Taylor arrestata a qualunque n N con il resto R n scritto, ad esempio, nella forma di Lagrange. La sviluppabilitá in serie della funzione f equivale, allora, a provare che lim n R n = 0. Nel caso particolare di x 0 = 0 si parla di serie di Mac-Laurin e la formula diventa f (n) (0) f(x) = x n. n! Vediamo ora alcuni casi particolari notevoli 1) f(x) = e x. La funzione é sviluppabile in serie di Mac-Laurin e si ha e x = x n n! = 1 + x + x! + x3 +..., x R 3! poiché f (n) (x) = e x, n, x da cui f (n) (0) = 1, n. ) f(x) = sin x. La funzione é sviluppabile in serie di Mac-Laurin poiché le sue derivate sono equilimitate. Si ha sin x = xn+1 ( 1) n (n + 1)! = x x3 3! + x5..., x R 5! poiché f (r) (0) = 0 se r é pari, mentre f (r) (0) = ( 1) n se r = n
8 3) f(x) = cos x. La funzione é sviluppabile in serie di Mac-Laurin poiché le sue derivate sono equilimitate. Si ha cos x = ( 1) n xn (n)! = 1 x! + x4..., x R 4! poiché f (r) (0) = 0 se r é dispari, mentre f (r) (0) = ( 1) n se r = n. 4) f(x) = ln(1 + x), x > 1. Si ha la seguente uguaglianza ln(1 + x) = n=1 ( 1) n+1 xn n = x x + x3..., x ( 1, 1]. 3 Dalla precedente uguaglianza per x = 1 si ottiene ln = + n=1 ( 1)n+1 1 n, in altre parole la somma della serie armonica a segni alterni é ln. 5) f(x) = (1 + x) α, x > 1 essendo α un generico numero reale. Posto ( α 0 ) = 1, ( α n) = α(α 1)...(α n+1 n! n 1, si ha la seguente uguaglianza (1 + x) α = ( α n) x n, x ( 1, 1). Questo quinto caso ha sottocasi particolari importanti ) α = 1. 1+x = + ( x)n, x ( 1, 1). (somma della serie geometrica di ragione x.) 5.) α = x = 1 + x + + n= (n 3)!! (n)!! x n, x ( 1, 1), dove si é usato il simbolo di semifattoriale che é cosí definito (n)!! = (n), (prodotto di tutti i numeri pari da fino a n ), (n + 1)!! = (n + 1), (prodotto di tutti i numeri dispari da 3 fino a n + 1). 5.3) α = x = (n 1)!! n=1 (n)!! x n, x ( 1, 1). Possiamo ottenere altri importanti sviluppi in serie di funzioni particolari utilizzando il Teorema di integrazione per serie. Ad esempio, dalla uguaglianze 1 1+x = + ( x ) n, ( che si ottiene come somma della serie geometrica di ragione x ), si ha arctg x = x x3 3 + x = + n=1 n 1 xn 1 ( 1), x ( 1, 1]. n 1 8
9 Per x = 1 si ha π 4 = + n=1 ( 1)n 1 1 n 1. 1 Dalla uguaglianze = x arcsin x = x + n=1 n=1 ( 1)n (n 1)!! (n)!! (n 1)!! (n)!! x n+1 ( x ) n, si ha, x ( 1, 1). n + 1 SERIE DI FOURIER Ricordiamo che una funzione f : R R si dice periodica di periodo T se si ha f(x + T ) = f(x), x R. Ovviamente una funzione periodica di periodo T é anche periodica di periodo kt, k N. Le funzioni trigonometriche sin x e cos x sono funzioni periodiche di periodo π inoltre, dati due numeri reali a, b ed un numero naturale k, la funzione a cos k x + b sin k x é periodica di periodo π k. In molte applicazioni vengono utilizzate combinazioni lineari di funzioni trigonometriche ossia funzioni del tipo a0 + n k=1 (a k cos k x + sin k x) dove a 0, a 1,..., a n, b 1,..., b n sono numeri reali assegnati. Tali funzioni sono dette polinomi trigonometrici e sono funzioni periodiche di periodo π, n N. Date due successioni numeriche {a n } +, {b n} + n=10, chiamiamo serie trigonometrica la seguente serie a (a k cos k x + b k sin k x) ( ) k=1 Se la serie trigonometrica ( ) é convergente ad una dunzione f(x), x R, allora, per la periodicitá dei polinomi trigonometrici, la funzione somma f(x) é sicuramente una funzione periodica di periodo π. Vale il seguente Teorema 87 : Se valgono le proprietá + a n < +, + n=1 b n < +, allora la serie trigonometrica ( ) converge totalmente e quindi uniformemente e la sua funzione somma é una funzione continua. Supponendo che una serie trigonometrica converga uniformemente ad una funzione f(x), ci chiediamo se ci siano legami tra la funzione somma ed i coefficienti della serie stessa. Tenuto conto della periodicitá delle funzioni coinvolte, possiamo restringere le nostre considerazioni ad un intervallo di ampiezza π ; abitualmente si considera l intervallo [, π]. Partiamo dall uguaglianza f(x) = a0 + + k=1 (a k cos k x + sin k x), che é vera uniformemente nell intervallo [, π], la moltiplichiamo per cos mx, con 9
10 m numero naturale o nullo fissato, poi integriamo nell intervallo indicato ed otteniamo π a0 π f(x) cos mx dx = cos mx dx + + k=1 (a π k cos k x cos mx dx + π b k sin k x cos mx dx), ricordando che, per la convergenza uniforma, la serie puó essere integrata termine a termine. Utilizzando i seguenti risultati π cos kx cos mx dx = 0 se m k, π m = k 0, π sin kx cos mx dx = 0, m, k, si ottiene cos kx cos mx dx = π, se a 0 = 1 π π f(x) dx, a n = 1 π π f(x) cos nx dx. (1) Con procedimento analogo, moltiplicando per sin mx e ricordando che π sin kx sin mx dx = 0 se m k, π sin kx sin mx dx = π, se m = k 0, si ottiene b n = 1 π π f(x) sin nx dx. () Le quantitá definite dalle uguaglianze (1) e () sono chiamate coefficienti di Eulero-Fourier della funzione f. A questo punto possiamo pensare di invertire il procedimento ossia : presa una funzione f(x) integrabile nell intervallo [, π], costruiti i suoi coefficienti di Eulero-Fourier utilizzando le uguaglianze (1) e (), possiamo considerare la serie trigonometrica generata da tali coefficienti. Ovviamente la domanda é : la serie cosí costruita converge? e converge alla funzione f(x)? In caso di risposta affermativa a queste domande diremo che la funzione é sviluppabile in serie di Fourier. Ci proponiamo, ora, di fornire Condizioni Sufficienti affinché una funzione sia sviluppabile in serie di Fourier ed, a questo scopo, premettiamo la seguente : Definizione : Una funzione f : [a, b] R si dice regolare a tratti in [a, b] se esiste una suddivisione D = {x 0, x 1,..., x n } dell intervallo [a, b] tale che la funzione f é continua e monotona in (x r, x r+1 ), r = 0, 1,..., n 1 inoltre lim x x + r f(x), lim x x r f(x), e sono finiti. Una funzione f : R R si dice regolare a tratti su R se lo é in ogni intervallo chiuso e limitato [a, b] R. Se f é una funzione definita in un intorno di un punto x 0, poniamo f(x + 0 ) = lim x x + f(x), f(x 0 ) = lim 0 x x f(x), qualora tali limiti esistano. 0 Vale il seguente Teorema 88 : Se f : R R é una funzione periodica di periodo π regolare a tratti, allora la serie di Fourier ad essa associata converge a 10
11 1 [f(x+ ) + f(x )] (media aritmetica tra limite destro e limite sinistro) in ogni punto x R. In particolare la serie converge a f(x) in ogni punto x di continuitá della funzione. Osserviamo che se f é una funzione pari allora si ha b n = 0, n ; mentre se f é una funzione dispari allora si ha a n = 0, n. Vediamo ora alcuni Esempi : 1) sia f la funzione periodica di periodo π ottenuta prolungando su R la funzione tale che f(x) = 0, se < x 0, f(x) = 1, se 0 < x π. I cofficienti di Eulero-Fourier di questa funzione sono i seguenti a 0 = 1, a n = 0, b n = 1 ( 1)n nπ, n N pertanto la serie di Fourier associata a questa + sin(k+1)x k=0 k+1 che, per il Teorema 88 converge a funzione é la seguente 1 + π f(x) in tutti i punti x mπ, m Z. Osserviamo che nel punto x 0 = 0 la serie precedente converge a 1 esattamente come afferma il Teorema. Per x = π, per la convergenza della serie alla funzione assegnata, sempre in base al Teorema enunciato, si ottiene la seguente uguaglianza π = 4 + che fornisce una formula di approssimazione del numero π. k=0 ( 1) k k+1, ) sia f la funzione periodica di periodo π ottenuta prolungando su R la funzione tale che f(x) = 1, se < x 0, f(x) = 1, se 0 < x π. I cofficienti di Eulero-Fourier di questa funzione sono i seguenti a 0 = 0, a n = 0, b n = (1 ( 1)n ) nπ funzione é la seguente 4 π, n N pertanto la serie di Fourier associata a questa + sin(k+1)x k=0 k+1 che, per il Teorema 88 converge a f(x) in tutti i punti x mπ, m Z. Osserviamo che nel punto x 0 = 0 la serie precedente converge a 0 esattamente come afferma il Teorema. 3) sia f la funzione periodica di periodo π ottenuta prolungando su R la funzione f(x) = x, se < x π. I cofficienti di Eulero-Fourier di questa funzione sono i seguenti a 0 = 0, a n = 0, b n = n ( 1)n+1, n N pertanto la serie di Fourier associata a questa funzione é la seguente + n=1 sin n x n che, per il Teorema 88 converge a f(x) in tutti i punti x mπ, m Z {0}. Osserviamo che per x = ± π la serie precedente converge a 0. 4) sia f la funzione periodica di periodo π ottenuta prolungando su R la funzione f(x) = x, se < x π. I cofficienti di Eulero-Fourier di questa funzione sono i seguenti a 0 = π, a n = 0, se n é pari, a n = 4 π n, se n é dispari e b n = 0 n N, pertanto la serie di Fourier associata a questa funzione é la seguente π 4 + cos(k+1)x π k=0 (k+1). che, per il Teorema 88 converge a f(x) in tutti i punti x R. 11
12 Per x = π, si ha π = π uguaglianza π 8 = + k=0 1 (k+1). + 4 π + k=0 1 (k+1), da cui si ha la seguente Forniamo, ora, una Condizione sufficiente per la convergenza uniforme della seria di Fourier. Teorema 89 : Se f : R R é una funzione periodica di periodo π, derivabile (escluso al piú un numero finito di punti in ogni intervallo chiuso contenuto in R) con derivata regolare a tratti, allora la serie di Fourier associata alla funzione f converge totalmente e quindi uniformemente in ogni intervallo chiuso contenuto in R. Vogliamo ora scrivere la serie di Fourier in forma esponenziale. A questo scopo ricordiamo le formule di Eulero ( cos nx = einx +e inx, sin nx = einx e inx i ), per cui si ha a n=1 (a n cos n x+b n sin n x) = a0 + + n=1 (a n einx +e inx e +b inx e inx n i ) = = a0 + + n=1 [( an + bn i )einx + ( an bn i )e inx ] = + n= c ne inx, dove si é posto c 0 = a0, c n = an ibn, se n = 1,, 3..., c n = an+ibn, se n = 1,, 3,.... Tramite le precedenti uguaglianze si ha infine c n = 1 π π f(x)e inx dx. 1
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
SVILUPPO IN SERIE DI FOURIER. Prof. Attampato Daniele
 SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
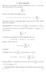 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Anno 5 4. Funzioni reali: il dominio
 Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
ESERCITAZIONI DI ANALISI 1 FOGLIO 1 FOGLIO 2 FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI. Marco Pezzulla
 ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
ESERCITAZIONI DI ANALISI FOGLIO FOGLIO FOGLIO 3 FOGLIO 4 FOGLIO 5 FOGLIO 6 FOGLIO 7 SVOLTI Marco Pezzulla gennaio 05 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) arccos x x + π/3.
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Diario del corso di Analisi Matematica 1 (a.a. 2015/16)
 Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
EQUAZIONI non LINEARI
 EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
24 : 3 = 8 con resto 0 26 : 4 = 6 con resto 2
 Dati due numeri naturali a e b, diremo che a è divisibile per b se la divisione a : b è esatta, cioè con resto 0. In questo caso diremo anche che b è un divisore di a. 24 : 3 = 8 con resto 0 26 : 4 = 6
Dati due numeri naturali a e b, diremo che a è divisibile per b se la divisione a : b è esatta, cioè con resto 0. In questo caso diremo anche che b è un divisore di a. 24 : 3 = 8 con resto 0 26 : 4 = 6
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Alcune note sulle serie di potenze 1
 Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
