, eccettuato al più il punto stesso, e sia L un numero reale. Si dice che f ha limite L per x che tende a x 0. L = lim f (x),
|
|
|
- Placido Fabbri
- 5 anni fa
- Visualizzazioni
Transcript
1 CAPITOLO FUNZIONI CONTINUE Ricordiamo la definizione di ite finito per x che tende a valore finito: Definizione Sia f una funzione definita in un intorno del punto x 0, eccettuato al più il punto stesso, e sia L un numero reale Si dice che f ha ite L per x che tende a x 0, e si scrive L = f x), x x 0 se per ogni ε > 0, δ > 0 0 < x x 0 < δ f x) L < ε Notiamo subito che la funzione può non essere definita in x 0, come per esempio nel caso della funzione f x) = x 6 x 4 x 6 x 4 x 4 = 8 nel punto x = 4, pur essendo 0 Una funzione si dice continua nel punto x 0, se questo è un punto interno all insieme di definizione della funzione e risulta: x x 0 f x) = f x 0 ) La definizione di ite viene modificata prevedendo la possibilità che x possa coincidere con x 0 : ε > 0, δ > 0 x x 0 < δ f x) L < ε Una definizione alternativa di funzione continua in un punto è la seguente: h 0 f x 0 + h) = f x 0 ) Di fondamentale importanza, come vedremo in seguito, è il concetto di funzione infinitesima Una funzione si dice infinitesima in x 0 se vale x x 0 funzione non è definita in x 0 f x) = 0, anche se la Questa ipotesi è essenziale per poter parlare in termini di ite, contrariamente al caso in cui x 0 è un punto isolato, dove convenzionalmente la funzione è ritenuta continua nel senso della definizione seguente: f è continua in x 0 se, ε > 0 esiste un intorno Ix 0 ) tale che f x per ogni x Ix 0 ) E evidente che tutto fila liscio se Ix 0 ) = { x 0 } ) f x 0 ) < ε,
2 Insieme di definizione e continuità In generale, una funzione è continua in un insieme se lo è in ognuno dei suoi punti, nel senso della definizione data Parrebbe quindi, che l insieme di definizione possa essere considerato, equivalentemente, come il più grande insieme in cui la funzione è continua nel senso della definizione con il concetto di ite Le cose, tuttavia, non stanno così Infatti, la continuità richiede primariamente la condizione che il punto x 0 sia un punto di accumulazione per l insieme di definizione della funzione, mentre esistono funzioni, come ad esempio f x) = cos x o g x) = x + x, che sono definite su insiemi di punti isolati e quindi continue!) In particolare, f x) = cos x è definita in D { x R, x = kπ k Z }, e g x) = x + x in D { x =} Esercizi Dire se le seguenti sono funzioni continue in 0 calcolare i iti destro e sinistro per x che tende a zero ): f x) = x + sin x si # f x) = & " 3 f x) = # # 4 f x) = & " 5 f x) = # " 6 f x) = # x, x 0 x x < 0 sin x x, x 0 x = 0 cos x, x > 0 x x 0 x x, x 0 0 x = 0 x x, x 0 0 x = 0 " no f x) = # si f x) = " # x + x x x 0 0 x = 0 arctan x x 0 π " sin x 0 si f x) = # x 0 x = 0 # x + si f x) = x x 0 & 0 x < 0 " no f x) = # log + x) x 0 x < 0 x = 0 no no no no si Un punto x 0 è di accumulazione per un sottoinsieme della retta reale, se ogni suo intorno completo contiene infiniti punti del sottoinsieme stesso
3 3 Punti di discontinuità I punti in cui una funzione non è continua si dicono punti di discontinuità Ci sono quattro tipi di punti di discontinuità Vediamoli nel dettaglio Punti di discontinuità einabile: sono punti in cui il ite di f x) per x x 0 esiste finito ma è diverso da f x 0 ), oppure la funzione non è definita in x 0 Esempi f x) = x x +, sin x f x) = x Punti di discontinuità di prima specie: sono punti in cui ite destro e ite sinistro esistono finiti e sono diversi tra loro In questo caso si dice che la funzione ha un salto nel punto di discontinuità dato da sx 0 ) = x x 0 + f x) x x 0 # Esempio f x) = & f x) lnx ) x 3 0 x < 3 Punti di discontinuità di seconda specie: sono punti in cui esistono ite destro e sinistro, ma almeno uno dei due è infinito Esempio f x) = e x Punti di discontinuità di terza specie: sono punti in cui uno o ambedue i iti, destro e sinistro, non esistono
4 4 Esempio f x) = sin x Esercizi Classificare le discontinuità delle seguenti funzioni nei punti indicati: f x) = x x x = ; f x) = 3 kx + 3; x 3 f x) = & x ; x < continua 4 f x) = x x 5 f x) = e Discontinuità di I specie x x = ; Discontinuità di II specie x+ 6 f x) = xn x x = ; ; Discontinuità di I specie se k altrimenti Discontinuità einabile x 3 x = 3 ; Discontinuità di II specie x = ; Discontinuità einabile
5 5 7 f x) = cos x cos x cosx x = 0 ; Discontinuità einabile 3 Un applicazione alla fisica: il campo elettrico dovuto a particolari distribuzioni di carica Esempio Indichiamo con σ la densità di carica distribuita uniformemente sulla superficie laterale di un cilindro di raggio r e altezza l Si determini l espressione del campo elettrico prodotto da tale distribuzione di carica, lontano dal bordo Applichiamo il teorema di Gauss: & Φ E = E πxl E = σ πrl x>r ε 0 πxl = σ r ε 0 x & ' E 0<x<r = 0 Esempio Due lastre rettangolari parallele molto estese hanno una densità di carica superficiale identica σ, e sono separate da una distanza a Si determini il campo elettrico in un punto a distanza x dal piano di simmetria delle due lastre 3 cos x cosx = cos x cos x + cos x = cos x cos x)+ + cos x) cos x) = cos x)cos x + cos x)
6 6 Esempio 3 Una quantità di carica positiva Q è distribuita uniformemente all interno di una corona sferica deitata da due superfici sferiche di raggi r < R Q Indicata con ρ = la densità di carica, si calcoli il valore del 4π 3 R3 r 3 ) campo elettrico in un punto a distanza x dal centro della corona sferica Si suddivida lo svolgimento in tre parti: 0 < x r, r < x R, x > R ) Analizziamo i singoli casi
7 7 r < x R 4πx E r<x R = x > R 4πx E x>r = Q ε 0 E x>r = ρ 4π x3 r 3 ) 3 ε 0 Q 4πε 0 x 0 < x r 4πx E 0<x r = 0 ε 0 E 0<x r = 0 E r<x R = ρ x 3 r 3 ) 3ε 0 x Teoremi sulle funzioni continue Diciamo che una funzione f è continua sull intervallo chiuso [ a,b] se è continua in a, in b ed in ogni punto a < x < b I teoremi che esamineremo quello di Weierstrass, quello degli zeri, e quello dei valori intermedi) riguarderanno proprio le funzioni continue definite su un intervallo chiuso e itato La continuità della somma e del prodotto di funzioni continue si dimostra senza troppe difficoltà, così come il quoziente nei punti in cui la funzione al denominatore è diversa da zero Occupiamoci adesso della continuità della funzione composta Teorema continuità della funzione composta) Siano f una funzione definita in un intorno aperto di x 0, e continua in x 0, e g una funzione definita in un intorno aperto di y 0 = f x 0 ) e continua in y 0 Se y 0 è un punto di accumulazione per l immagine della funzione f, allora, la funzione composta g f x)) è continua in x 0 A x 0 f!! B y 0 = f x 0 ) g!! C z 0 =g y 0 ) Dimostrazione Per ogni ε > 0 esiste un intorno di y 0 = f x 0 ), y 0 δ ;y 0 + δ ) tale che gy) gy 0 ) < ε, per ogni y y 0 δ ;y 0 + δ ) In corrispondenza di δ esiste, per la continuità dalla funzione f, un δ tale che f x) f x 0 ) < δ per ogni x x 0 δ ;x 0 + δ ) In definitiva, per ogni ε > 0 esiste un δ > 0 tale che g f x)) g f x 0 )) < ε per ogni x x 0 δ ;x 0 + δ ), di conseguenza g f x)) = g f x)) = g f x 0 )) = gy 0 x x 0 x x0 ) Esercizio Si studi la continuità della funzione x + log x) x +x x > 0 Il seguente risultato svela la relazione tra funzioni continue su intervalli chiusi e l esistenza di massimi e minimi:
8 8 Teorema di Weierstrass Ogni funzione continua su un intervallo chiuso a,b [ ] è ivi itata e assume massimo e minimo Per convincersi dell essenzialità dell ipotesi d intervallo chiuso, consideriamo il comportamento della funzione f x) = x, x 0,]: la funzione non ammette massimo, poiché + x = + Analogamente, se provassimo ad indebolire l ipotesi togliendo la continuità della funzione, la tesi del teorema salterebbe con il controesempio dato da f x) = x, x #, & Sempre con il metodo di bisezione degli intervalli e sempre grazie all assioma di continuità) è possibile dimostrare il seguente: Teorema degli zeri di funzioni continue Sia f una funzione continua su un intervallo chiuso [ a,b] e tale che f a) > 0, f b) < 0; allora esiste almeno un punto x 0 in a,b) tale che f x 0 ) = 0
9 9 Problema Si determini il numero di soluzioni dell equazione e x + x = 0, e s indichino con due cifre decimali esatte Dal confronto grafico di cui sopra, suggerito dall equazione e x = x, si vede che l equazione ammette una sola soluzione 0,6 < x < 0,5 Applichiamo il metodo di bisezione per determinare la soluzione con due cifre decimali esatte: a n f a n ) b n f b n ) m f m) -0,6-0,0588-0,5 0,0653-0,55 0, ,6-0,0588-0,55 0, ,575-0,095-0,575-0,095-0,55 0, ,565 0,0078-0,575-0,095-0,565 0,0078-0, ,0057 La soluzione con la precisione richiesta è x = 0,56 Un altro importante risultato che caratterizza le funzioni continue è il seguente Teorema dei valori intermedi Sia f una funzione continua su un intervallo chiuso! " a,b# Allora la funzione assume tutti i valori compresi tra il minimo m e il massimo M L immagine di! " a,b# è quindi l intervallo chiuso! " m, M#
10 0 Dimostrazione Siano c e d i punti rispettivamente di minimo e di massimo che esistono per il teorema di Weierstrass) Supponiamo che c<d Sia α un numero compreso tra m e M Proviamo che esiste x 0 in! " a,b# tale che f x 0 ) = α Per questo sarà sufficiente applicare il teorema degli zeri alla funzione gx) = f x) α, continua su! " c,d#, e tale che gc) = f c) α = m α < 0, gd ) = f d ) α > 0 Approfondimento: la continuità della funzione inversa Abbiamo già avuto modo di osservare che funzioni strettamente monotone sono invertibili, mentre non è necessariamente vero il viceversa: esistono, infatti, funzioni invertibili che non sono monotone Vediamo sotto quali ipotesi una funzione invertibile e continua, ammette inversa continua Cominciamo dicendo che la definizione su un intervallo è essenziale Infatti, esistono funzioni continue non definite su un intervallo, # con inversa non continua, come ad esempio f x) = & # chiaramente invertibile con inversa f x) = & sull intervallo! " 0,#, evidentemente discontinua in x = x 0 x < x + x x 0 x < x x 3 definita,
11 In generale, una funzione continua ed invertibile, definita su un intervallo che può essere itato, una semiretta, oppure tutto l insieme dei numeri reali), possiede inversa continua Esercizio E data la funzione f x) = ln x + e) a) Si determini il dominio della funzione e le intersezioni con gli assi; # ln x + e) # x + e e x + e > 0 & x R & D ;0) 0;+ ) La funzione è pari b) Si descriva il comportamento della funzione agli estremi del dominio; x ln x + e ) ln x + e) d) Si restringa il dominio della funzione al semiasse positivo delle ascisse e si determini l espressione analitica della funzione inversa y = ln x + e) ln x + e) = y ln x + e) = y y x = & e & e) Si tracci il grafico della funzione e della sua inversa y y ' e) )
12 Esercizio E data la funzione f x) = ln x a) Si tracci un grafico approssimativo; b) Si determini la funzione inversa e se ne tracci un grafico approssimativo; c) Si determini il punto di incontro delle curve grafico della funzione e della sua inversa Alcuni risultati generali Corollario La somma e la differenza di funzioni continue è una funzione continua Corollario 3 Il prodotto di funzioni continue è una funzione continua Corollario 3 Se f e g sono funzioni continue, allora la funzione f g è una funzione continua nei punti in cui f è positiva e g è definita Dimostrazione Si scrive la funzione nella forma! " f x)# = e g x )ln f x )), si applica il teorema della continuità della funzione composta, e si sfrutta la continuità del prodotto di funzioni continue Osservazione Un esempio in cui il teorema 3 non si può invertire è dato da f x) = x; gx) = x Corollario 4 Le funzioni polinomiali sono funzioni continue Corollario 4 Le funzioni seno e coseno sono funzioni continue si applichi la definizione f x h h) = f x 0 ) e le formule di addizione) ESERCITAZIONE FINALE PROBLEMA E data la circonferenza con centro nell origine degli assi cartesiani e raggio unitario Indichiamo i punti A ;0)e Q 0; ), e P sulla circonferenza, tale che PÔA := x La retta t, tangente alla circonferenza in P, e il segmento PQ incontrano l asse delle ascisse rispettivamente nei punti L e R Indicata con H la proiezione di P sull asse delle ascisse, si calcoli il Area QAH ) Area RPL ) g x )
13 3 ESERCIZI Si dimostri che l equazione xe x = 0 ammette una sola soluzione compresa tra zero e uno Si determini la soluzione in questione con un approssimazione alla prima cifra decimale, mostrando chiaramente il procedimento seguito Si calcoli il QUESITI cosx cosx cosx e Si dimostri il ite notevole x = x Si dica per quali valori del parametro a la funzione # x f x) ax; x = è continua su tutto il suo insieme di & ln x; x > definizione ln + x) 3 Si calcoli, al variare del parametro α R, il ite + x α CORREZIONE PROBLEMA E data la circonferenza con centro nell origine degli assi cartesiani e raggio unitario Indichiamo i punti A ;0 )e Q 0; ), e P sulla circonferenza, tale che PÔA := x La retta t, tangente alla circonferenza in P, e il segmento PQ incontrano l asse delle ascisse rispettivamente nei punti L e R Indicata Area QAH ) con H la proiezione di P sull asse delle ascisse, si calcoli il Area RPL )
14 4 Si determina OR applicando il teorema dei seni al triangolo OPR, essendo O ˆPR = π 4 x il triangolo OQP è isoscele): # sin π OR sin O ˆPR ) = OP sin O ˆRP ) OR = 4 x & cos x ' # sin 3π 4 x = sin x & cos x ' + sin x Area QAH ) Area RPL) = AH OQ ) OL OR) PH& ' = cosx & ) ' x cos cosx sin x + & - / cos x + sin x - sin x/ / - ), '/ ) cos x sin x cosx cos x sin x + - cos x + sin x - sin x -, = cosx tan x sin x = ESERCIZI Si dimostri che l equazione xe x = 0 ammette una sola soluzione compresa tra zero e uno Si determini la soluzione in questione con un approssimazione alla prima cifra decimale, mostrando chiaramente il procedimento seguito Si tracciano i grafici delle funzioni y = x e y = ex, e si osserva che si incontrano in un solo punto Di conseguenza l equazione xe x = 0 ammette una sola soluzione compresa tra zero e uno, che =
15 5 può essere determinata con la precisione richiesta applicando il teorema degli zeri per funzioni continue alla funzione y = xe x a n f a n 0 -, ,5-0, ,5 0,5-0, , ,75 0, ,75 0,5-0, ,75 0, ,65 0, ,6 0,5-0, ,65 0, ,565-0, ,56 0,565-0, ,65 0, , , ,59-3 ) b n f b n ) m f m) ZERO Si calcoli il cosx cosx cosx cosx cosx cosx = cosx cosx cos x + sin x = cosx) cosx cosx +cosx = 3 = QUESITI ) = ) + cos x e Si dimostri il ite notevole x = x Con la sostituzione e x = t x = lnt +) il ite è t 0 t ln+ t) = t 0 ln+ t) t = =
16 6 Si dica per quali valori del parametro a la funzione # x f x) ax; x = è continua su tutto il suo insieme di & ln x; x > definizione E sufficiente imporre la continuità in x =: f ) = a = +ln x = 0 a = x ) ln + x 3 Si calcoli, al variare del parametro α R, il ite + x α ) ln + x + x α ) ln + x = + x x α ) ln + x = + x x α = 0 + α < α = α > ESERCITAZIONE FINALE 3 Si determini, per via grafica al variare del parametro k R, il numero di soluzioni dell equazione x 3 + x k = 0 Si dimostri che un equazione polinomiale di grado dispari ammette sempre almeno una soluzione, indicando chiaramente i riferimenti teorici utilizzati 3 Si calcoli il valore approssimato di tan assumendo che π = 3,46 4 Si determini l insieme di definizione della funzione ) = ln cos x f x )), e se ne discuta la continuità 5 Calcolare e verificare con la definizione il ln x ) 6 Calcolare i seguenti iti di funzioni: + ) # cos arctan & x ' π, + - x sin x sinx x tan 3x
17 7 7 Si discuta, al variare del parametro α R, la continuità della # funzione f x) = x x > 0, classificandone gli eventuali punti di & e x α x 0 discontinuità 8 Calcolare, al variare del parametro α R il + x α sin x CORREZIONE Si determini, per via grafica al variare del parametro k R, il numero di soluzioni dell equazione x 3 + x k = 0 x 3 + x k = 0 x 0) x += k x Si dimostri che un equazione polinomiale di grado dispari ammette sempre almeno una soluzione, indicando chiaramente i riferimenti teorici utilizzati Sia P n x) = a n x n + a n x n + + a x + a 0 l espressione di una generica funzione polinomiale di grado n Se a n > 0, allora x x ± P n ) = ± ) = ) In ogni caso quindi, è possibile trovare un altrimenti P n x x ± intervallo di estremi a e b tali che P n a) P n b polinomiale è, ovviamente, continua Per il teorema degli zeri esiste almeno un x 0 a, b [ ] P n x 0 ) = 0 ) < 0, su cui la funzione
18 8 3 Si calcoli il valore approssimato di tan assumendo che π = 3,46 tan x Dal ite notevole = tan x x in un intorno di zero x Poiché = π 90 3,46 = 0, tan = 0, Si determini l insieme di definizione della funzione ) = ln cos x f x f x " # )) ) ) = ln cos x, e se ne discuta la continuità x = kπ D { x R x = ± kπ } ) 5 Calcolare e verificare con la definizione il ln x ln x ) = 0 ln x x < e ε ) 0 < ε x < e ε & '& x > e ε + & '& x R x < e ε ) # cos arctan & x ' π, Calcolare i seguenti iti di funzioni: sinx sin x x tan 3x t = arctan x π x = tan # t + π & = cost Di conseguenza, ' sint ) # & cos arctan π, + x ' - cost = cost # & t = + x t 0 t sint ' sin x sinx sin x cos x 3x) = = x tan 3x 9x 9 = 8 ) x tan3x) 7 Si discuta, al variare del parametro α R, la continuità della # funzione f x) = x x > 0, classificandone gli eventuali punti di & e x α x 0 discontinuità x
19 9 f 0) = e α = x α = 0 Se α 0 la funzione presenta + nell origine una discontinuità di salto 8 Calcolare, al variare del parametro α R il x α sin + x x α x α sin x xα x α sin + x = & ' 0 α > 0 / α 0 COMPITO DI MATEMATICA Classe V sezione B 04//04 Si discuta la continuità della funzione f x) = variare del parametro α R ) +! π tan# & x 0 " x + 4 ) x ln + x α x > 0, al Si enunci e si dimostri il teorema dei valori intermedi 3 Determinare il numero di zeri della funzione f x) = x x + Se ne determini il valore approssimato alla prima cifra decimale di uno a scelta 4 Calcolare il valore dei seguenti iti di funzioni: # & 3 x cosx + x ' a) x x ln sin x) b) tan 3 x
20 0 CORREZIONE Si discuta la continuità della funzione f x) = variare del parametro α R ) +! π tan# & x 0 " x + 4 ) x ln + x α x > 0, al f 0) = tan π 4 = α ) ln + x + x # = ln + x α + ) x = + α < IIspecie α = continua 0 α > Ispecie & ' Si enunci e si dimostri il teorema dei valori intermedi Sia f una funzione continua su un intervallo chiuso! " a,b# Allora la funzione assume tutti i valori compresi tra il minimo m e il massimo M L immagine di! " a,b# è quindi l intervallo chiuso! " m, M# Dimostrazione Siano c e d i punti rispettivamente di minimo e di massimo che esistono per il teorema di Weierstrass) Supponiamo che c<d Sia α un numero compreso tra m e M Proviamo che esiste x 0 in! " a,b# tale che f x ) = α Per questo sarà sufficiente applicare il 0 teorema degli zeri alla funzione gx) = f x) α, continua su! " c,d#, e tale che gc) = f c) α = m α < 0, gd ) = f d ) α > 0 3 Determinare il numero di zeri della funzione f x ) = x x + Se ne determini il valore approssimato alla prima cifra decimale di uno a scelta
21 Si applica il teorema degli zeri a f x ) = x x + in # 3 ; an fan) bn fbn) m fm) ZERO,50 0, ,75 0, ,75 -,5 0,45707,75 0, ,65 0, ,65,65 0, ,75 0, ,6875 0, ,6875! " &: 4 Calcolare il valore dei seguenti iti di funzioni: # & 3 x cosx + x ' 3 x ) + cosx a) = x x x ln sin x # ) x ln sin x & b) = ) cosx tan 3 x tan x sin x ' ) x = ln3 = ) =
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Infiniti e Infinitesimi
 Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Algebra dei limiti. quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha. lim. f (x)
 Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Funzioni Continue. se (e solo se) 0
 f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
y = x 3 infinitesimo per x 3 lim = l 0 allora f(x) è dello stesso ordine di g(x), ossia tendono a DEF. Una funzione y = f(x) si dice infinitesimo per
 INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
ESAME DI MATEMATICA PER LE APPLICAZIONI ECONOMICHE 14 GIUGNO 2016 FILA A
 ESAME DI MATEMATICA PER LE APPLICAZIONI ECONOMICHE 4 GIUGNO 206 FILA A Durata della prova: 2 ore e mezza. NOTA: Spiegare con molta cura le risposte. NOTAZIONE: log = ln = log e. Esercizio 5 punti) Sia
ESAME DI MATEMATICA PER LE APPLICAZIONI ECONOMICHE 4 GIUGNO 206 FILA A Durata della prova: 2 ore e mezza. NOTA: Spiegare con molta cura le risposte. NOTAZIONE: log = ln = log e. Esercizio 5 punti) Sia
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
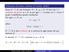 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Limiti di funzioni. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
2. Determina i valori delle funzioni trigonometriche seno e coseno di un angolo ottuso α sapendo che tan α = 15.
 Esercizi proposti di goniometria 1. Un settore circolare, in un cerchio di raggio 14 cm, ha area uguale a 42π cm 2. Determina la misura in gradi, primi e secondi dell angolo al centro corrispondente. 2.
Esercizi proposti di goniometria 1. Un settore circolare, in un cerchio di raggio 14 cm, ha area uguale a 42π cm 2. Determina la misura in gradi, primi e secondi dell angolo al centro corrispondente. 2.
1 Limiti e continuità per funzioni di una variabile
 1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
Esercizi sulle Funzioni
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Funzioni Esercizio svolto. Trovare i domini di definizione delle seguenti funzioni: a) f) sin + cos ; b) g) log ) ; c) h) sin + e sin. Soluzione. a) La
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Funzioni Esercizio svolto. Trovare i domini di definizione delle seguenti funzioni: a) f) sin + cos ; b) g) log ) ; c) h) sin + e sin. Soluzione. a) La
Teorema degli zeri. Essendo f continua in a e in b, per il teorema della
 Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Esercizi svolti. g(x) = sono una l inversa dell altra. Utilizzare la rappresentazione grafica di f e f 1 per risolvere l equazione f(x) = g(x).
 Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 008/09 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 4 ottobre 008 Dimostrare
Università degli Studi di Udine Anno Accademico 008/09 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 4 ottobre 008 Dimostrare
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Vogliamo analizzare diversi casi allo scopo di coinvolgere tutte le funzioni classiche che abbiamo incontrato finora..
 CAPITOLO 4 GRAFICI DI FUNZIONI Per tracciare il grafico di una funzione reale di variabile reale seguiremo il seguente schema generale: a. Dominio in realtà insieme di definizione ; b. Simmetrie e periodicità;
CAPITOLO 4 GRAFICI DI FUNZIONI Per tracciare il grafico di una funzione reale di variabile reale seguiremo il seguente schema generale: a. Dominio in realtà insieme di definizione ; b. Simmetrie e periodicità;
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica) Simulazione compito d esame
 COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio. A. Figà Talamanca
 ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Analisi Matematica 1
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 0/3 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi del 0 ottobre 0 La sottrazione
Università degli Studi di Udine Anno Accademico 0/3 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi del 0 ottobre 0 La sottrazione
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Proprietà globali delle funzioni continue
 Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
6. Asintoti e continuità
 6. Asintoti e continuità Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Asintoti Continuità Asintoto orizzontale: la retta y = l è l asintoto orizzontale a + (o destro) di
6. Asintoti e continuità Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Asintoti Continuità Asintoto orizzontale: la retta y = l è l asintoto orizzontale a + (o destro) di
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo.
![Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo. Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo.](/thumbs/100/143663280.jpg) FUNZIONI CONTINUE. PUNTI DI DISCONTINUITA. OPERAZIONI SUI LIMITI. CALCOLO DI LIMITI CHE SI PRESENTANO IN FORMA INDETERMINATA LIMITI NOTEVOLI E APPLICAZIONI Angela Donatiello DEF. di Funzione Continua in
FUNZIONI CONTINUE. PUNTI DI DISCONTINUITA. OPERAZIONI SUI LIMITI. CALCOLO DI LIMITI CHE SI PRESENTANO IN FORMA INDETERMINATA LIMITI NOTEVOLI E APPLICAZIONI Angela Donatiello DEF. di Funzione Continua in
PNI SESSIONE SUPPLETIVA QUESITO 1
 www.matefilia.it PNI - SESSIONE SUPPLETIVA QUESITO Si sa che certi uccelli, durante la migrazione, volano ad un altezza media di 6 metri. Un ornitologa osserva uno stormo di questi volatili, mentre si
www.matefilia.it PNI - SESSIONE SUPPLETIVA QUESITO Si sa che certi uccelli, durante la migrazione, volano ad un altezza media di 6 metri. Un ornitologa osserva uno stormo di questi volatili, mentre si
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Analisi Matematica 1 (Modulo) Prove Parziali A.A. 1999/2008
 Analisi 1 Polo di Savona Analisi Matematica 1 (Modulo) Prove Parziali A.A. 1999/2008 1- PrA1.TEX [] Analisi 1 Polo di Savona Prima prova Parziale 21/10/1998 Prima prova Parziale 21/10/1998 Si consideri
Analisi 1 Polo di Savona Analisi Matematica 1 (Modulo) Prove Parziali A.A. 1999/2008 1- PrA1.TEX [] Analisi 1 Polo di Savona Prima prova Parziale 21/10/1998 Prima prova Parziale 21/10/1998 Si consideri
Capitolo 3. Le funzioni elementari
 Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A Diario delle lezioni. Mercoledì 2 ottobre 2013 (2 ore)
 c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
Esercizio 1. Per quali valori di h e k le seguenti funzione sono derivabili? x 3 sin 1 x 0. 0 x = 0. x cos 1 x > 0
 Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
23 INVERTIBILITÀ E CONTINUITÀ
 23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R una funzione derivabile in 0 tale che f(0) = f (0) = 0. Si consideri la funzione g(x) = f(x). Allora, necessariamente sin x (a) lim g(x) = 0 (b) lim g(x) = 1 (c)
Test di autovalutazione 1. Sia f : R R una funzione derivabile in 0 tale che f(0) = f (0) = 0. Si consideri la funzione g(x) = f(x). Allora, necessariamente sin x (a) lim g(x) = 0 (b) lim g(x) = 1 (c)
Verso il calcolo dei limiti: alcuni risultati generali
 Verso il calcolo dei iti: alcuni risultati generali Ci proponiamo adesso di enunciare e dimostrare alcuni fatti di per sé piuttosto intuitivi, che trovano una giustificazione grazie al concetto di ite.
Verso il calcolo dei iti: alcuni risultati generali Ci proponiamo adesso di enunciare e dimostrare alcuni fatti di per sé piuttosto intuitivi, che trovano una giustificazione grazie al concetto di ite.
; c) log 3 5 (x 2 1) log 5 (x + 1). 1 log(x + 4) ; c) f(x) =
 Corso di Analisi Matematica I per Ingegneria Gestionale, a.a. 25-6 Esercizi per il ricevimento del 3 ottobre 25. Semplificare il più possibile le seguenti espressioni: a) 32x+4 9 ; b) x3 x 2 x+ ( x) 4
Corso di Analisi Matematica I per Ingegneria Gestionale, a.a. 25-6 Esercizi per il ricevimento del 3 ottobre 25. Semplificare il più possibile le seguenti espressioni: a) 32x+4 9 ; b) x3 x 2 x+ ( x) 4
Limiti di funzioni di due variabili
 Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
LIMITI E CONTINUITÀ 1 / ESERCIZI PROPOSTI
 ANALISI MATEMATICA I - A.A. 03/04 LIMITI E CONTINUITÀ / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili. Definizioni di ite e di continuità. Sia k>0un parametro reale fissato. Verificare
ANALISI MATEMATICA I - A.A. 03/04 LIMITI E CONTINUITÀ / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili. Definizioni di ite e di continuità. Sia k>0un parametro reale fissato. Verificare
06 - Continuitá e discontinuitá
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 06 - Continuitá e discontinuitá Anno Accademico 2013/2014 D. Provenzano
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 06 - Continuitá e discontinuitá Anno Accademico 2013/2014 D. Provenzano
Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/1/018 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 5 p.ti. 1. Determina
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/1/018 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 5 p.ti. 1. Determina
Università degli Studi di Verona
 Tipologia A 1.1 Si enunci il teorema di derivazione della funzione inversa e lo si applichi al calcolo della derivata della funzione log x. 1.2 Il ite vale 0; x + sin x 1 + xe x non esiste; vale + ; vale
Tipologia A 1.1 Si enunci il teorema di derivazione della funzione inversa e lo si applichi al calcolo della derivata della funzione log x. 1.2 Il ite vale 0; x + sin x 1 + xe x non esiste; vale + ; vale
Dispense di Matematica Analisi Matematica. Riccarda Rossi
 Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Topologia della retta reale. Concetto intuitivo di limite. Definizioni di limite. Teoremi sui limiti. Applicazioni. Angela Donatiello 1
 Topologia della retta reale. Concetto intuitivo di ite. Definizioni di ite. Teoremi sui iti. Applicazioni. Angela Donatiello TOPOLOGIA DELLA RETTA REALE Esiste una corrispondenza biunivoca tra l insieme
Topologia della retta reale. Concetto intuitivo di ite. Definizioni di ite. Teoremi sui iti. Applicazioni. Angela Donatiello TOPOLOGIA DELLA RETTA REALE Esiste una corrispondenza biunivoca tra l insieme
ORDINAMENTO SESSIONE SUPPLETIVA QUESITO 1
 www.matefilia.it ORDINAMENTO 0 - SESSIONE SUPPLETIVA QUESITO Si sa che certi uccelli, durante la migrazione, volano ad un altezza media di 60 metri. Un ornitologa osserva uno stormo di questi volatili,
www.matefilia.it ORDINAMENTO 0 - SESSIONE SUPPLETIVA QUESITO Si sa che certi uccelli, durante la migrazione, volano ad un altezza media di 60 metri. Un ornitologa osserva uno stormo di questi volatili,
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Corso di Analisi Matematica. Comportamenti asintotici
 a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 17/10/2013
 Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Università degli Studi di Verona
 Università degli Studi di Verona Dipartimento di Informatica Ca' Vignal 2 Strada le Grazie 15 37134 Verona - Italia Tel. +39 045 802 7069 Fax +39 045 802 7068 Corso di Laurea in Matematica Applicata PROVA
Università degli Studi di Verona Dipartimento di Informatica Ca' Vignal 2 Strada le Grazie 15 37134 Verona - Italia Tel. +39 045 802 7069 Fax +39 045 802 7068 Corso di Laurea in Matematica Applicata PROVA
DERIVATE. Rispondere ai seguenti quesiti. Una sola risposta è corretta. 1. Data la funzione f(x) =2+ x 7, quale delle seguente affermazioni èvera?
 DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 005/06 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 9 settembre 005 Dimostrare
Università degli Studi di Udine Anno Accademico 005/06 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 9 settembre 005 Dimostrare
Esercizi di Matematica per le Scienze Studio di funzione
 Esercizi di Matematica per le Scienze Studio di funzione A.M. Bigatti e G. Tamone Esercizi Studio di funzione Esercizio 1. Disegnare il grafico di una funzione continua f che soddisfi tutte le seguenti
Esercizi di Matematica per le Scienze Studio di funzione A.M. Bigatti e G. Tamone Esercizi Studio di funzione Esercizio 1. Disegnare il grafico di una funzione continua f che soddisfi tutte le seguenti
Corso di Laurea in Matematica Applicata PROVA DI ANALISI MATEMATICA 1 Mod. 1-1/12/2014 Tipologia A
 Tipologia A 1.1 Si enunci il teorema di Bolzano Weierstrass e si dia un esempio di successione itata che non ammette ite. 1.2 Il ite x 0 + x3 e 1/x non esiste; vale 0; vale 1; vale + ; 1.3 Sia f : R R
Tipologia A 1.1 Si enunci il teorema di Bolzano Weierstrass e si dia un esempio di successione itata che non ammette ite. 1.2 Il ite x 0 + x3 e 1/x non esiste; vale 0; vale 1; vale + ; 1.3 Sia f : R R
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 006/07 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 3 ottobre 006 Dimostrare
Università degli Studi di Udine Anno Accademico 006/07 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 3 ottobre 006 Dimostrare
Coordinate cartesiane nel piano
 Coordinate cartesiane nel piano O = (0, 0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate cartesiane nel piano O = (0, 0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I (corso tenuto dal Prof Alessandro Fonda) Università di Trieste, CdL Fisica e Matematica, aa 2012/2013 1 Principio di induzione 1 Dimostrare che per ogni numero naturale
Esercizi di Analisi Matematica I (corso tenuto dal Prof Alessandro Fonda) Università di Trieste, CdL Fisica e Matematica, aa 2012/2013 1 Principio di induzione 1 Dimostrare che per ogni numero naturale
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Lezioni del 29 settembre e 1 ottobre.
 Lezioni del 29 settembre e 1 ottobre. 1. Ricordiamo informalmente e brevemente la nozione di angolo e di misura di un angolo in radianti nel senso della geometria elementare. Per angolo intendiamo una
Lezioni del 29 settembre e 1 ottobre. 1. Ricordiamo informalmente e brevemente la nozione di angolo e di misura di un angolo in radianti nel senso della geometria elementare. Per angolo intendiamo una
Lezione 3 (2/10/2014)
 Lezione 3 (2/10/2014) Esercizi svolti a lezione Esercizio 1. Tracciando un grafico approssimativo, discutere qualitativamente l esistenza di radici reali dei seguenti polinomi, al variare del parametro
Lezione 3 (2/10/2014) Esercizi svolti a lezione Esercizio 1. Tracciando un grafico approssimativo, discutere qualitativamente l esistenza di radici reali dei seguenti polinomi, al variare del parametro
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
Analisi Matematica. Limiti di successioni numeriche e di funzioni
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Limiti di successioni numeriche e di funzioni Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Limiti di successioni numeriche e di funzioni Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Corso di Laurea in Ingegneria Civile Analisi Matematica I
 Corso di Laurea in Ingegneria Civile Analisi Matematica I Lezioni A.A. 2006/2007, prof. G. Stefani Primo periodo 18/09/06-15/12/06 Testi consigliati: M.Bertsch, R.Dal Passo - Elementi di Analisi Matematica
Corso di Laurea in Ingegneria Civile Analisi Matematica I Lezioni A.A. 2006/2007, prof. G. Stefani Primo periodo 18/09/06-15/12/06 Testi consigliati: M.Bertsch, R.Dal Passo - Elementi di Analisi Matematica
Analisi Matematica. Alcune funzioni elementari
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Alcune funzioni elementari Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
7. Studio elementare di funzioni
 7. Studio elementare di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria e la
7. Studio elementare di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria e la
13 LIMITI DI FUNZIONI
 3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
Limiti di funzioni. Parte 2 calcolo. prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, 10/2016
 Limiti di funzioni Parte calcolo prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, /6 L insieme R Il calcolo dei iti delle funzioni reali di variabile reale avviene nell insieme esteso dei numeri
Limiti di funzioni Parte calcolo prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, /6 L insieme R Il calcolo dei iti delle funzioni reali di variabile reale avviene nell insieme esteso dei numeri
