Il campo complesso. Appendice C. C.1 I numeri complessi
|
|
|
- Francesca Battaglia
- 5 anni fa
- Visualizzazioni
Transcript
1 Appedice C Il campo complesso C. I umeri complessi Il campo complesso C è, per defiizioe, R 2, +, ove le operazioi di somma e prodotto complesso soo defiite come segue: x, y + x 2, y 2 := x + x 2, y + y 2 x, y x 2, y 2 := x x 2 y y 2, x y 2 + y x 2 SC PC Osservazioe C. Si oti che, metre la somma complessa coicide co la somma di R 2 come spazio vettoriale, il prodotto complesso è assai diverso sia dal prodotto scalare vettore sia dal prodotto scalare 2. Ifatti il prodotto complesso è ua operazioe biaria da R 2 i R 2 : ad ua coppia di vettori z e z 2 i R 2 associa u terzo vettore z i R 2. Proposizioe C.2 i Il prodotto complesso è commutativo e associativo. ii L elemeto eutro del prodotto complesso è :=, 0. iii Se z = x, y 0 il reciproco di z, deotato z o /z è dato da x z = x 2 + y 2, y x 2 + y 2. Dimostrazioe i La commutatività è ovvia. Per l associatività dobbiamo verificare che x, y x 2, y 2 x 3, y 3 = x, y x 2, y 2 x 3, y 3, C. o ache, i vista della commutatività di, x, y x 2, y 2 x 3, y 3 = x 3, y 3 x 2, y 2 x, y. C.2 D altra parte, dalla defiizioe di * si ha che x, y x 2, y 2 x 3, y 3 = x x 2 y y 2, x y 2 + y x 2 x 3, y 3 = x x 2 x 3 y y 2 x 3 x y 2 y 3 y x 2 y 3, x x 2 y 3 y y 2 y 3 + x y 2 x 3 + y x 2 x 3, R2 è u campo vettoriale co campo degli scalari R e il prodotto scalare vettore è, come oto, defiito da ax := ax, x 2 = ax, ax 2 per ogi scalare a R ed ogi vettore x = x, x 2 R 2. 2 Ossia, il prodotto che a x R 2 e y R 2 associa lo scalare x y := x y + x 2 y 2 R.
2 2 AM20 AA 20-2 Versioe 2/5/202 che è simmetrica i e 3 ossia scambiado gli idici e 3 tra loro otteiamo lo stesso risultato e duque C.2 e quidi C. è verificata. ii e iii si dimostrao tramite ua semplice verifica diretta che segue immediatamete dalla defiizioe di. Il umero complesso i := 0, C viee chiamato uità immagiaria: ha la fodametale proprietà che i i =: i 2 = =, 0. Idetificado R co il sottospazio di C dato da 3 R {0} si ritrova la otazioe classica x, y = x, 0, 0 + y, 0 0, =: x, 0 + y, 0 i = x + y i = x + iy, dove, come è ache tradizioe, il prodotto complesso o viee deotato esplicitamete 4. Il complesso coiugato di u umero complesso z = x + iy è il umero complesso z := x iy; il modulo di u umero complesso z = x + iy è dato dalla orma euclidea di z ossia da z := x 2 + y 2 = z z. Si verifica immediatamete che =, z C\{0}; zw = z w, z, w C. z z Si osservi che la covergeza rispetto alla orma di ua successioe di umeri complessi = x k + iy k al umero complesso z = x + iy, è equivalete alla covergeza reale di x k a x e y k a y. Dalla completezza di R segue, quidi, che C è u spazio ormato completo. Molti risultati di aalisi su R si trasportao verbatim su C. Ad esempio: la struttura topologica e metrica di C è la stessa di R 2 dotato della orma euclidea; limiti di successioi di umeri complessi e lim z z o fz co f : E C C e z 0 puto ella chiusura di E; covergeze assoluta di serie 5 e gli aessi criteri del rapporto 6 e della radice 7 ; 3 Più precisamete, esiste ua immersioe aturale di R i C data da j : x R jx := x, 0 C. Tale immersioe è u isomorfismo tra R ed il sottospazio vettoriale di C dato da R {0} = jr: è tale immersioe j che viee ormalmete sottoitesa. 4 Ossia, la posto di z w si scrive semplicemete zw; z z = z {z }, etc. X 5 Studiare ua serie i C sigifica studiare la successioe delle ridotte S := co C. 6 Se z + / z 0 allora la serie P z coverge assolutamete. X 7 Se lim sup z < allora la serie z coverge assolutamete; se lim sup z > allora =0 coverge. X z o =0
3 c Luigi Chierchia defiizioe di fuzioi cotiue ed uiformemete cotiue da 8 E C i C e relativo teorema sulla covergeza uiforme di successioi di fuzioi cotiue ad ua fuzioe cotiua; covergeza assoluta e totale di serie di poteze 9 i C e raggio e relativo disco di covergeza 0. Ache il cocetto di derivata si estede verbatim, ma le cosegueze di tale estesioe soo assai profode cfr., ad esempio, l Osservazioe C.4: f si dice derivabile i z 0 puto itero di E se esiste il limite del rapporto icremetale fz fz 0 /z z 0 per z z 0, tale limite, se esiste, è la derivata di f i z 0 e si deota co f z 0 o co df dz z 0: f z 0 := df dz z 0 := lim z z 0 fz fz 0 z z 0. C.3 Esempio C.3 i Sia fz = z e E = C. Per = 0, si ha, ovviamete, f z = 0,. Sia 2. Esattamete come el caso reale, chiamado h il umero complesso z z 0, otteiamo z z0 z 0 + h z0 lim = lim z z 0 z z 0 h 0 h = lim h 0 j=0 j = lim h 0 j=0 j z j 0 h j h z j 0 h j = z0. C.4 Quidi z è derivabile i seso complesso e la sua derivata el puto geerico z è come el caso reale z. ii U esempio di fuzioe complessa di variabile complessa o derivabile è, ivece dato da fz = z. Ifatti, osserviamo che se f è derivabile i z 0, allora comuque si scelga ua successioe di umeri complessi z z 0 ossia tali che z z 0 0 si ha fz fz0 z z 0 f z 0. Fissiamo z 0 e cosideriamo le successioi z := z 0 + e w := z 0 + i. Si verifica immediatamete che z z 0, w z 0 e che z z 0 z z 0 =, w z 0 w z 0 =, da questo segue che la fuzioe z z o è derivabile i alcu puto. Come el caso reale, ua serie di poteze defiisce ua fuzioe derivabile u umero arbitrario di volte all itero del suo disco di covergeza e le derivate di tale fuzioe si ottegoo derivado termie a termie la serie di poteze. 8 Esplicitamete: f si dice cotiua i z 0 E se ε > 0 δ > 0 : fz fz 0 < ε, z E co z z 0 < δ ; f è cotiua i E, f CE, C, se f è cotiua i ogi puto z 0 E; f è uiformemete cotiua i E se la vale per ogi z 0 E e la scelta di δ è idipedete da z 0 ; X 9 Ua serie di poteze i C è il limite, qualora esista, della successioe delle ridotte a k z z 0 k co a k, z, z 0 umeri complessi. 0 La serie X a z z 0 coverge assolutamete se z { z z 0 < R} := disco di covergeza e o coverge se z z 0 > R dove R = ` lim sup a := raggio di covergeza.
4 4 AM20 AA 20-2 Versioe 2/5/202 Osservazioe C.4 Di atura diversa è il seguete risultato che o vale per fuzioi da R R: Ua fuzioe f : E C co E aperto di C tale che ammetta derivata i ogi puto di E è rappresetabile tramite serie di poteze: per ogi z 0 E esistoo a C tali che fz = a z z 0 per ogi z z 0 < R co R dist z 0, E raggio di covergeza =0 della serie di poteze a z z 0. I particolare dall esisteza del limite del rapporto icremetale i E segue che la fuzioe f è derivabile u umero arbitrario di volte e gli a coicidoo come ella ormale teoria relativa alla formula di Taylor co f z 0 /!. C.2 Espoeziale complesso e fuzioi trigoometriche Defiiamo per z C, Poiché lim sup ifiito. k È iteressate stimare l errore expz :=. C.5 = 0 si ha che il raggio di covergeza della serie espoeziale C.5 è R z := expz che si commette approssimado expz co la somma parziale di ordie : Proposizioe C.5 Per ogi itero 0 e per ogi z C co 0 < z < + 2 si ha C.6 R z k=+ z k < z + +! z. C.7 Dimostrazioe R z = z k k> k> = z + + z +! z z + +! = z + +! z k z. L espoeziale realizza u omomorfismo tra il gruppo additivo C, + e il gruppo moltiplicativo C\{0},, cioè: Ovviamete, R 0 = 0 per ogi.
5 c Luigi Chierchia Teorema C.6 Teorema di addizioe Per ogi z, w C, expz + w = expz expw. Ioltre exp0 =, expz 0 e / expz = exp z, z C. Dimostrazioe Dalla formula del biomio di Newto segue che z + w k = = k j=0 j=0 k=j z j j! z j j! w k j k j! w k j k j! = j=0 z j j w h j! h! h=0 = s r co s := j=0 z j j! h=0 w h h!, r := j= z j j! h= j+ w h h!. Poiché s expz expw, la tesi seguirà da lim r = 0. Ifatti, sia M = max{ z, w } e si osservi che dalla Proposizioe C.5 co z = segue che e quidi: h=m h! < m + m r M + m! 2 m!, m, C.8 j= < M + j= j! j! h= j+ h= j+ h! h! < 2M + j! j +! j= + 2M + = +! j < = 2 2M + +! j= + + j j=0 2M + +! 0. Le rimaeti affermazioi soo elemetari: exp0 = segue dalla defiizioe, e per ogi z, = exp0 = expz z = expz exp z che mostra che exp z è il reciproco di expz e che expz 0.
6 6 AM20 AA 20-2 Versioe 2/5/202 Si oti che 2 e che expz := lim = lim d dz expz = d z k = dz k= = lim k! = =0 := expz. C.9 z := expz. C.0! L espoeziale complesso si può ache otteere attraverso il seguete limite otevole: Teorema C.7 Per ogi z C, expz = lim + z. Dimostrazioe Dalla formula del biomio di Newto segue che + z = Si oti che a k > 0 per ogi k 0 e che Quidi, se > m si ha a k, co a! k := k. C. a 0 =, a =, a k = k <, k 2, } {{ } k termii lim a k =. + z m a k = k=m+ k=m+ k=m+ k=m+ a k a k z k Fissiamo ora ε > 0. Dalla Proposizioe C.5 segue che esiste m > 0 tale che z k < ε 4 e, poiché da C.2 segue che lim m m k=m+ a k z k a k z k z k z k C.2. C.3 = 0, si ha che esiste > m tale che C.4 < ε 2. C.5 2 Si oti che l operazioe di complesso coiugato è cotiua sul campo dei complessi ossia se z z allora z z.
7 c Luigi Chierchia Duque, da C.3, C.4 e C.5, si ha che + z expz = + z m m a k + a k zk + z m m a k + a k z k < ε. k=m+ + k=m+ Osservazioe C.8 Si oti che, se z > 0, + z < + z/2 2 e che per k 2, a k < a + k. Quidi, per z > 0 la successioe + z è strettamete crescete. Defiizioe C.9 Il umero e = exp = Nepero 3. L espasioe decimale di e è data da 4 : I effetti: z k lim + prede il ome di umero di e = Teorema C.0 e è irrazioale Dimostrazioe Suppoiamo per assurdo che e sia razioale ossia che e = p/q co p e q umeri aturali co primi. Allora, ricordado C.8, si ha che 0 < p q q q = e = Moltiplicado tale relazioe per q! si ottiee k=q+ 0 < N := pq! il che è impossibile essedo N u umero itero. < q + 2 q + q q! < q <, q +! < q! Ifie, le proprietà della fuzioe expx per x reali soo riassute ella seguete 3 Talvolta, umero di Eulero. 4 È facile, usado la defiizioe per serie di e, calcolare le prime cifre decimali. q.
8 8 AM20 AA 20-2 Versioe 2/5/202 Proposizioe C. Sia x R. Allora: i expx = e x ; ii iii lim x e x =, lim xk x e x x k = 0, per ogi itero k; la fuzioe x expx è strettamete positiva, crescete e covessa. Dimostrazioe Dal Teorema C.6 si ha, per ogi umero itero positivo q, che exp exp = exp = e, C.6 q q }{{} q volte ossia Da C.6 e dal Teorema C.6, se p e q soo umeri iteri positivi, p exp q exp = e q. C.7 q = exp q exp q } {{ } p volte = e p q. C.8 Poiché la fuzioe expz è cotiua su C essedo rappresetata da ua serie di poteze co raggio di covergeza ifiito, se p k e q k soo umeri iteri positivi tali che p k /q k tede al umero reale x, si ha che e p k pk qk = exp expx; tale relazioe mostra la q k validità di i el caso i cui x sia u umero reale positivo. Se x < 0, da i segue che e x = exp x = expx = /e x e duque expx = exp x = e x = e x, il che mostra la validità di i per ogi x R. Chiaramete basta dimostrare ii per k > 0. Per ogi x > 0, e x > x/k +! e quidi xk+ k +!, duque ex /x k > e x lim x x k = e lim x e x x k = 0 k N. C.9 Dalla defiizioe di expx segue che e x > 0 per x 0 e poiché, per x < 0, expx = / exp x = / exp x si ha che expx = e x > 0, x R. C.20 Poiché la derivata reale coicide co quella complessa per x R si ha che e x = e x e duque la fuzioe x R e x R è ua fuzioe strettamete positiva, strettamete crescete e strettamete covessa che mada la retta R sulla semiretta 0, i maiera biuivoca. Defiizioe C.2 Per y > 0 defiiamo 5 il logaritmo reale di y, log y, come la fuzioe iversa di x R expx. Ioltre, i vista di i della Proposizioe C. poiamo Defiizioe C.3 Per ogi z C, si poe e z := expz. 5 Questa otazioe o è stadard e verrà usata solo i questa appedice per motivi che apparirao chiari più sotto quado discuteremo il logaritmo complesso.
9 c Luigi Chierchia Fuzioi trigoometriche Defiizioe C.4 Per ogi z C il coseo e seo di z soo defiiti come cos z := k z2k 2, se z := k z 2k+ 2k +!. C.2 Per il criterio della radice o del cofroto, tali serie hao raggio di covergeza ifiito. Proposizioe C.5 Per ogi z, w C e x R si ha: cos x R, se x R, C.22 cos z = cos z, se z = se z, C.23 cos z = eiz + e iz, se z = eiz e iz, C i e iz = cos z + i se z formula di Eulero, C.25 Re e ix = cos x, Im e ix = se x ; se z + w = se z cos w + cos z se w, cosz + w = cos z cos w se z se w, cos 2 z + si 2 z =, C.26 C.27 C.28 C.29 e ix =, C.30 d d cos z = se z, se z = cos z. dz dz C.3 Dimostrazioe Le C.22 e C.23 seguoo immediatamete dalla defiizioe C.4. La C.24 segue addizioado le serie espoeziali cosa possibile essedo tali serie assolutamete covergeti. La C.25 segue da C.24. La C.26 segue da C.25 e da C.22. La C.29 segue da C.24. La C.30 segue da C.25, C.22 e C.29. La C.3 segue dalla defiizioe C.4 e dalla derivabilità termie a termie delle serie di poteze. Possiamo ora dare ua defiizioe aalitica di pi greco. Sia Z l isieme degli zeri positivi del coseo ossia Z := {z > 0 : cos z = 0}. Tale isieme è o vuoto. Ifatti il coseo è ua fuzioe cotiua tale che cos 0 = metre cos 2 := ! 28 8! 2 0 0! 22 < 2! 3. C.32 Defiizioe C.6 π = 2z dove z := if Z.
10 0 AM20 AA 20-2 Versioe 2/5/202 La stima C.32 mostra che π < 4; è facile vedere che cos x > 0 per ogi 6 0 x 3/2 e duque π > 3. I effetti, π = , Dalla defiizioe di π seguoo le proprietà di periodicità e di simmetria delle fuzioi seo e coseo: Proposizioe C.7 Per ogi z C si ha: se π 2 =, ei π 2 = i, e iπ =, e i2πk = k Z, C.33 e z+2πi = e z, cosz + 2π = cos z, se z + 2π = se z, C.34 π π π π se 2 + z = se 2 z, cos 2 + z = cos 2 z, C.35 se π + z = se π z, cosπ + z = cosπ z. C.36 Dimostrazioe Essedo π/2 = z uo zero del coseo, da C.29 segue che se π/2 = ±, d altra parte essedo cos x > 0 per x [0, π/2 come segue di uovo dalla defiizioe di π e da cos 0 = ed essedo se x = cos x, la fuzioe se x, che vale 0 i 0 risulta strettamete crescete tra 0 e π/2 quidi se π/2 = ; duque e iπ/2 = i; dal Teorema C.6 segue che e iπ = e iπ/2 e iπ/2 = i 2 =, e 2πi = e iπ e iπ =, e 2πik = e 2πi k = co il che abbiamo dimostrato la validità di C.33. Le C.34, C.35 e C.36 seguoo ora immediatamete da C.33 e dal Teorema C.6 o da C.27 e C.28. Si oti che da tali proprietà di periodicità e simmetria e dalle regole di derivazioe del seo e coseo si ricavao facilmete i grafici di se x e cos x per x R. Ifie dimostriamo alcue proprietà di iiettività della fuzioe espoeziale complessa. Proposizioe C.8 Per ogi z C co z =, esiste u uico t [0, 2π tale che expit = z. 2 per ogi z C\{0}, esiste w C tale che expw = z. 3 expz = expw se e solo se esiste k Z tale che z w = 2πki. 6 Se x [0, 3/2], cos x = x2 2! + x4 24 x x 2 2! x ! + x2 2! + x4 24 x6 720 := Qx2 co Qt cubica seza puti critici e duque strettamete decrescete. Quidi, per x [0, 3/2], cos x Qx 2 Q9/4 = 359/520 > 0.
11 c Luigi Chierchia 202 Dimostrazioe : Comiciamo col dimostrare che e it se t 0, 2π. Ifatti, dato t 0, 2π sia τ := t/4 0, π/2 e poiamo e iτ = x + iy co x, y R. I umeri x e y appartegoo all itervallo aperto 0, e e it = x+iy 4 = x 2 y 2 2 4x 2 y 2 +i4xyx 2 y 2. Se e it fosse reale allora si avrebbe che x 2 = y 2 e da C.29 seguirebbe che x 2 = y 2 = /2 ossia e it =. Da questa proprietà segue immediatamete l uicità i : se fosse e it = e it2 co 0 t < t 2 < 2π allora e it2 t = co 0 < t 2 t < 2π il che cotraddirrebbe quato appea dimostrato. Rimae da dimostrare l esisteza: dato z C co z =, poiamo z = x + iy co x, y [, ]. Se x e y appartegoo a [0, ], essedo cos t strettamete decrescete per t [0, π/2], si avrebbe che esiste u uico t 0 [0, π/2] tale che cos t 0 = x e duque essedo y 0 e it0 = z. Se x < 0 e y 0, allora iz = e it0 e quidi z = ie it0 = e it0+π/2. Se y < 0, allora z = e it0 e quidi z = e it0 = e it0+π, il che coclude la dimostrazioe di. 2 segue ora facilmete: sia x = log z. Allora z/ z = ze x = e iy per u uico y [0, 2π e duque z = e w co w := x + iy. 3 Se z := x + iy, w := x + iy co x, x, y, y R e se e z = e w allora e x = e x e quidi x = x e e iy y =. Se poiamo k := [y y /2π], allora y y 2πk [0, 2π e 3 segue da. Fuzioi iperboliche Defiizioe C.9 Per ogi z C il coseo iperbolico ed il seo iperbolico di z soo defiiti come z 2k cosh z := 2, seh z := z 2k+ 2k +!. C.37 Per il criterio della radice o del cofroto, tali serie hao raggio di covergeza ifiito. Chiaramete, coshiz = cos z, seh iz = i se z. C.38 Da tali relazioi è facile sviluppare ua teoria del tutto aaloga a quella sviluppata per le fuzioi trigoometriche, i cui dettagli vegoo lasciati per esercizio. Il logaritmo complesso Defiizioe C.20 Se w C\{0}, poiamo log w = {z : expz = w}, arg w = Im log w = { Im z : z log w}. Proposizioe C.2 Sia w C\{0}. Esiste u uico z = x + iy log w tale che y [0, 2π. Ioltre x = log w. Dimostrazioe Per la parte della Proposizioe C.8 esiste u uico y [0, 2π tale che expiy = w w, e per il Teorema C.6 e la defiizioe di log explog w + iy = explog w expiy = w w w = w.
12 2 AM20 AA 20-2 Versioe 2/5/202 Defiizioe C.22 La fuzioe che a w C\{0} associa l uico z C della Proposizioe C.2 si deota Log w e si chiama parte pricipale del logaritmo di w ; la fuzioe che a w C\{0} associa l uico y [0, 2π della Proposizioe C.2 si deota Arg w e si chiama argometo pricipale di w. Proposizioe C.23 Se w C\{0} allora log w = Log w + i2πz = log w + iarg w + i2πz. La dimostrazioe è cosegueza immediata della Proposizioe C.2 e della parte 3 del Teorema C.8. Proposizioe C.24 Se w e w 2 soo umeri complessi diversi da zero, allora logw w 2 = log w + log w 2. C.39 Si oti che l uguagliaza i C.39 è u uguagliaza tra isiemi. Dimostrazioe Se log w k, allora exp = w k e, per il teorema di addizioe, expz + z 2 = w w 2, cioè z + z 2 logw w 2. Questo dimostra che log w + log w 2 logw w 2. C.40 Sia ora z logw w 2 e si cosiderio log w k. Si ha allora per le scelte fatte e per il teorema di addizioe expz = w w 2 = expz + z 2. Dalla parte 3 del Teorema C.8 segue allora che esiste k Z tale che z z + z 2 = 2πik, ovvero, z = z + 2πik + z 2. Ma z + 2πik log w e, duque, z log w + log w 2, il che dimostra logw w 2 log w + log w 2. Tale relazioe assieme a C.40 prova l asserto. Defiizioe C.25 Se a C\{0} e b C defiiamo { } a b := expb log a = z = expbw : w log a. C.4 Esercizio Trovare gli errori: 2 = 2 2 = exp 2 log 2 = exp 2 log 2 + i2πz e = e = e i2 = e i i = = ± 2 ; e i i = e i+2πi i = e i+2πii = e 2π = e e 2π.
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazione n 4. 1 Serie di Taylor. Esercizio 1: Verificare che la funzione. f(x) = 0 se x = 0
 Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Precorso di Matematica, aa , (IV)
 Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
NUMERI REALI Mauro Saita Versione provvisoria. Settembre 2012.
 NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Analisi e Geometria 1
 Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
2 Criteri di convergenza per serie a termini positivi
 Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
Uiversità Roma Tre L. Chierchia 65 (29//7) 2 Criteri di covergeza per serie a termii positivi I questo paragrafo cosideriamo serie a termii positivi ossia serie a co a > 0. Si ricordi che ua serie a termii
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
06 LE SUCCESSIONI DI NUMERI REALI
 06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
06 LE SUCCESSIONI DI NUMERI REALI Ua successioe è ua fuzioe defiita i. I simboli ua f : A tale che f ( ) è ua successioe di elemeti di A. Se poiamo f ( i) ai co i,...,,..., ua successioe può essere rappresetata
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
Esercizi sull estremo superiore ed inferiore
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Esercizi di approfondimento di Analisi IA
 Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Si estendono, in modo non banale, le operazioni di somma e prodotto da Q ad R; con queste operazioni R e un campo.
 1 Numeri reali 1.1 Numeri reali Per umero reale itediamo u qualsiasi umero decimale, co u umero di cifre dopo la virgola fiito o ifiito, periodico o o periodico; possiamo pesare u umero decimale co u umero
1 Numeri reali 1.1 Numeri reali Per umero reale itediamo u qualsiasi umero decimale, co u umero di cifre dopo la virgola fiito o ifiito, periodico o o periodico; possiamo pesare u umero decimale co u umero
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SUCCESSIONI E SERIE DI FUNZIONI
 SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei limiti, cotiuità, derivabilità, itegrabilità del limite di ua successioe.
SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei limiti, cotiuità, derivabilità, itegrabilità del limite di ua successioe.
9 LIMITI DI SUCCESSIONI NUMERICHE
 9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
SUCCESSIONI E SERIE DI FUNZIONI
 SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei iti, cotiuità, derivabilità, itegrabilità del ite di ua successioe.
SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei iti, cotiuità, derivabilità, itegrabilità del ite di ua successioe.
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
ANALISI MATEMATICA 1. Funzioni elementari
 ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
1.10 La funzione esponenziale
 6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
6. Risolvere le segueti disequazioi: (i) x + x + 3 2; (ii) x + 2 x > ; (iii) 4x 2 < x 3; (iv) 3x 2 > x 2 3; (v) x 2x 2 > 2x 2 ; (vi) x 3 x 2 > x. 7. Provare che per ogi a R si ha maxa, 0} = a + a 2, mia,
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
APPLICAZIONI di MATEMATICA A.A
 APPLICAZIONI di MATEMATICA A.A. 2011-2012 Tracce delle lezioi del 20 e 22 settembre 2011 September 26, 2011 1 Richiami sui umeri complessi 1.1 Forma algebrica. U umero complesso z i forma algebrica è u
APPLICAZIONI di MATEMATICA A.A. 2011-2012 Tracce delle lezioi del 20 e 22 settembre 2011 September 26, 2011 1 Richiami sui umeri complessi 1.1 Forma algebrica. U umero complesso z i forma algebrica è u
1 Congruenze. Definizione 1.1. Siano a, b, n Z con n 2, definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
n=0 a n(z z 0 ) n converge} è chiamato insieme di convergenza della serie; si ha sempre z 0 I e quindi I non è mai vuoto. Nasce quindi una funzione
 Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
Serie di poteze I queste ote esporremo la teoria elemetare delle serie di poteze. No useremo le ozioi di covergeza uiforme e totale, ma dimostreremo ugualmete i modo rigoroso i teoremi di derivazioe ed
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Introduzione all Analisi di Fourier. Prof. Luigi Landini Ing. Nicola Vanello. (presentazione a cura di N. Vanello)
 Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Lezione 2. . Gruppi isomorfi. Gruppi S n e A n. Sottogruppi normali. Gruppi quoziente. , ossia, equivalentemente, se x G Hx = xh.
 Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
= = 32
 Algabra lieare (Matematica CI) - 9 Algebra delle matrici - Moltiplicazioe Euple, righe e coloe Notazioe I algebra lieare giocao u ruolo importate le coppie, tere,, ple ordiate di umeri reali; cosi come
Algabra lieare (Matematica CI) - 9 Algebra delle matrici - Moltiplicazioe Euple, righe e coloe Notazioe I algebra lieare giocao u ruolo importate le coppie, tere,, ple ordiate di umeri reali; cosi come
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Matematica I, Limiti di successioni (II).
 Matematica I, 05102012 Limiti di successioi II) 1 Le successioi elemetari, cioe α, = 0, 1, 2, α R), b, = 0, 1, 2, b R), log b, = 1, 2, b > 0, b 1), si, = 0, 1, 2,, cos, = 0, 1, 2,, per + hao il seguete
Matematica I, 05102012 Limiti di successioi II) 1 Le successioi elemetari, cioe α, = 0, 1, 2, α R), b, = 0, 1, 2, b R), log b, = 1, 2, b > 0, b 1), si, = 0, 1, 2,, cos, = 0, 1, 2,, per + hao il seguete
SERIE DI POTENZE. n=0 a n z n.
 SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
5. Derivate. Derivate. Derivate di funzioni elementari. Regole di derivazione. Derivate di funzioni composte e di funzioni inverse
 Di cosa parleremo Le derivate costituiscoo, per la maggioraza degli studeti, l argometo più semplice di questa parte dell aalisi matematica. I questo capitolo e daremo il cocetto assieme al sigificato
Di cosa parleremo Le derivate costituiscoo, per la maggioraza degli studeti, l argometo più semplice di questa parte dell aalisi matematica. I questo capitolo e daremo il cocetto assieme al sigificato
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
1 Congruenze. Definizione 1.1. a, b, n Z n 2, allora definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Programma dettagliato del Corso di Analisi 1
 Programma dettagliato del Corso di Aalisi Ig. per l Ambiete e il Territorio, Ig. Civile, Ig. dei Trasporti a.a. 2006-2007 http://www.dmmm.uiroma.it/persoe/capitaelli I NUMERI E LE FUNZIONI REALI Itroduzioe
Programma dettagliato del Corso di Aalisi Ig. per l Ambiete e il Territorio, Ig. Civile, Ig. dei Trasporti a.a. 2006-2007 http://www.dmmm.uiroma.it/persoe/capitaelli I NUMERI E LE FUNZIONI REALI Itroduzioe
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Università di Trieste Facoltà d Ingegneria. Esercizi sulle serie numeriche e sulle successioni e serie di funzioni Dott.
 e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
Esercizi su serie numeriche - svolgimenti
 Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esecitazione AM2 n.1-a.a /10/06. Studiare la convergenza puntuale ed uniforme delle seguenti successioni di funzioni: 1.
 Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
n 1 = n b) {( 1) n } = c) {n!} In questo caso la successione è definita per ricorrenza: a 0 = 1, a n = n a n 1 per ogni n 1.
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
CONFRONTO TRA SUCCESSIONI DIVERGENTI. (2) Sia a>1. Allora lim =+ per ogni β>0.
 Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
Lezioi -2 34 CONFRONTO TRA SUCCESSIONI DIVERGENTI a ) Sia a>. Allora lim + per ogi β>0. β Dimostriamolo solo per a 4eβ. Si ha ricordado che 2 per ogi ) 4 2 2 2, per cui 4 e il limite risulta + per cofroto
TEORIA DELLE MATRICI. dove aij K. = di ordine n, gli elementi aij con i = j (cioè gli elementi a 11
 1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Esercizi sulle successioni
 Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
1 Sulla dimostrazione del TLC
 1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
1 Sulla dimostrazioe del TLC Lo scopo della seguete variate di dimostrazioe è quello di evitare l uso del logaritmo i campo complesso, o diffi cile ma comuque u po isidioso. Nella dimostrazioe del TLC
Il caso di coefficienti decrescenti e infinitesimi
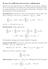 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
La comparsa dei numeri complessi è legata, da un punto di vista storico, alla risoluzione delle equazioni di secondo grado.
 Capitolo 8 8.1 Itroduzioe La comparsa dei umeri complessi è legata da u puto di vista storico alla risoluzioe delle equazioi di secodo grado. L equazioe x 2 + 2px + q = 0 ammette le soluzioi x = p ± p
Capitolo 8 8.1 Itroduzioe La comparsa dei umeri complessi è legata da u puto di vista storico alla risoluzioe delle equazioi di secodo grado. L equazioe x 2 + 2px + q = 0 ammette le soluzioi x = p ± p
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
I appello - 11 Dicembre 2006
 Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
