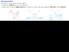
(x,y) Fig. 2.1 Un possibile cammino ottico tra due mezzi di indice di rifrazione diversi separati dalla superficie.

Transcript

1 CAPITOLO II.1 Il principio di Fermat Si tratta di un metodo molto potente per trattare i problemi di ottica geometrica. Si supponga di avere una superficie che trasmette e/o riflette i raggi luminosi. Il principio di Fermat afferma che la traiettoria seguita dal raggio luminoso sarà quella per cui il tempo necessario, per andare ad esempio dalla sorgente al piano focale, è minimo. Il principio di Fermat può essere esteso ad un sistema ottico più generale, e nella sua forma moderna asserisce che: La traiettoria vera seguita da un raggio luminoso è quella per cui il tempo, necessario per andare da un punto fisso A ad un altro punto fisso B, è stazionario rispetto a piccole variazioni dal percorso vero. In altre parole il tempo necessario per andare da un punto A ad un altro B non differisce più di un infinitesimo del secondo ordine dal tempo necessario per andare da A a B lungo un altro percorso molto prossimo al percorso vero. Quindi in prima approssimazione il tempo per il percorso vero è uguale a quello per un raggio adiacente al percorso vero. Il caso più semplice per illustrare il principio di Fermat è mostrato in Fig..1. Una superficie separa due punti P e P 1. n n (x,y) P 1 P Fig..1 Un possibile cammino ottico tra due mezzi di indice di rifrazione diversi separati dalla superficie. Le linee piene rappresentano la traiettoria vera, quelle tratteggiate una ad essa adiacente.il tempo per andare da P a P 1 sia. Affinchè sia verificata la condizione di stazionarietà per il percorso vero, deve essere: / x = / y = (.1) dove x,y sono le coordinate generiche dove il raggio incontra la superficie. In modo equivalente si può rimpiazzare la frase tempo di viaggio della luce con cammino ottico della luce. Se dt è un tempo infinitesimo allora cdt è il corrispondente cammino ottico. Il cammino ottico (OPL=Optical Path Length) è definito perciò dalla relazione: d(opl)=cdt=(c/v)vdt=nds (.) OPL= c dt = nds dove v è la velocità della luce nel mezzo di indice di rifrazione n. Il modo generico di enunciare il principio di Fermat è perciò = o (OPL)=, dove n può essere una funzione di tutte le coordinate che specificano la posizione.

2 Consideriamo ora il caso bidimensionale (D) dove n=n(y,z) e ds= y =dy/dz il principio di Fermat si scrive: dy + dz. Posto P1 n ( y, z ) (1 y ' ) dz (.3) P + = dove ds è stato rimpiazzato da dz (1 + y ' ). Assumendo F(y, y,z) sia l integrando della (.3) si ha: P1 P1 F( y, y ', z) dz = F( y, y ', z) dz = (.4) P P dove F F F F d F = y + y ' = y + y y y ' y y ' dz ( ) essendo z= agli estremi. Sostituendo F nella (.4) e integrando per parti si ottiene: F F d F ydz + y ydz = y y ' dz y ' P1 P P 1 1 P P P (.5) Il secondo termine nella (.5) è zero poiché y è nullo agli estremi. Possiamo perciò riscrivere: P1 F d F ydz P = y dz y ' (.6) Poiché quest espressione è nulla per ogni y deve essere: F d F = y dz y ' (.7) che è l equazione richiesta per soddisfare il principio di Fermat. Ora prendendo l eq. (.7) rimpiazzando la F ed eseguendo i differenziali si ottiene: n d ny ' n d y ' y ' dn + y = + y n = y dz (1 + y ' ) y dz (1 + y ' ) (1 + y ' ) dz (1 ' ) (1 ' ) (.8) Usando alcune sostituzioni trigonometriche la (.8) si semplifica notevolmente, infatti è: dy dy y ' tan = = y ' sin = = dz ds + y (1 ' ) dz 1 d d cos = = sin = cos ds (1 + y ' ) dz dz (.9) Per cui possiamo riscrivere la (1.8) come:

3 n n d sin ncos = cos y z dz (.1) Notiamo infine che la curvatura di un dato cammino ottico nello spazio è definita dall equazione: per cui la (.1) si può riscrivere: d d dz d = = = cos ds dz ds dz 1 cos d n n = n = sin n dz cos y z (.11) Quest equazione ci dice come varia la curvatura di un raggio luminoso in un mezzo il cui indice di rifrazione è una funzione uniformemente variabile con la posizione. Si noti che per n=cost la curvatura è zero ed il raggio viaggia in linea retta.. Applicazioni del principio di Fermat Vediamo ora alcune utili applicazioni del principio di Fermat...1 Legge della riflessione e della rifrazione Il principio di Fermat può essere usato per derivare la legge di Snell della riflessione e rifrazione di un raggio luminoso che attraversa una superficie piana di separazione tra due mezzi di indice di rifrazione n ed n. Esaminando la Fig.. si vede che il cammino ottico è stazionario se vale la relazione: y P (z z,y ) P (,y ) P 1 (z 1,) z Fig.. Un raggio attraversa una superficie piana che divide due mezzi di diverso indice di rifrazione. P P n ds + n ' ds = P 1 P

4 che diviene dopo il calcolo degli integrali: { n z1 y n z ( y y ) } + + ' + = (.1) Differenziando, essendo y la variabile indipendente si ottiene: d d ( ) ( ) n z1 + y + n' z + y y y = dy dy! poiché l espressione in parentesi è indipendente da y dovrà essere allora, eseguendo le derivate: n y ' y n y = ( z + y ) z + ( y y ) 1 (.13) da cui si vede che i due termini che moltiplicano n ed n sono rispettivamente sin(i) e sin(i ) e quindi la (.13) è proprio la legge di Snell della rifrazione n sin(i)=n sin(i ). Per ottenere la legge della riflessione basta allora porre n ' = n e si ottiene i ' = i. Si lascia allo studente provare che la (.13) è effettivamente una condizione di minimo... Il diottro sferico La superficie sferica di Fig..3 separa due mezzi omogenei di indice di rifrazione n ed n. B e B sono due punti coniugati, C è il centro di curvatura della superficie sferica. R B C B s Z s Fig..3 La rifrazione su una superficie sferica. Nel disegno si suppone di usare solo i raggi parassiali in modo da poter confondere la linea retta con la linea curva che rappresenta la superficie sferica. Rispettando la convenzione sui segni (vedi appendice) data dalle frecce il cammino ottico è L = nl+ n' l '. Usando la legge del coseno possiamo scrivere: ( ) ( ) l = R + R s R R s cos" ( ) ( ) l = R + s R + R s R ' ' ' cos "

5 Sostituendo ed in L si ha una espressione in cui è la variabile, per cui applicando il principio di Fermat si ottiene: dl nr( R s)sin " n' R( s ' R)sin" = = d" l l' (.14) che nel limite parassiale in cui sferico: l = s ed l = s ' dà immediatamente la nota relazione del diottro n' n n ' n =. 1 s ' s R..3 La lente sottile Come altro esempio dell uso del principio di Fermat vogliamo ora trovare la lunghezza focale di una lente sottile di indice di rifrazione n, con raggi di curvatura R 1 ed R. Ogni raggio che connette due punti coniugati deve soddisfare al principio di Fermat, in altre parole il cammino ottico OPL, dovendo essere lo stesso per tutti i raggi che connettono due punti coniugati, non è né un minimo né un massimo. Osservando la Fig..4 scriviamo l espressione del cammino ottico per il tragitto del raggio lungo l asse ottico e lungo un raggio parassiale a distanza y dall asse ottico: L = [BO 1] + n[o1o ] + f ' L = [BO ] + z + n[p P ] z + l p P 1 P O 1 O f Z Fig..4 Una lente sottile di spessore d è attraversata da due raggi, lungo l asse ottico, e a distanza y da questo, provenienti da un punto B a distanza infinita. z 1 (e z ) è la distanze tra il punto P 1 (P ) e la retta passante per O 1 perpendicolare all asse ottico. dove z < e z 1 > (per la convenzione sui segni) danno le distanze tra l asse y 1 e y e la superficie reale della lente. Posto L =L p si ha: nd + f ' = z + n( d z + z ) z + l (.15) Si noti la differenza con l eq. 1. del Capitolo I dovuta alla convenzione adotta sui segni.

6 - - in cui abbiamo sostituito d = [O1O ] e d z1 + z = [P1 P ]. Da questa svolgendo le operazioni si ottiene: l f ' = ( n 1)( z z ) (.16) 1 Essendo quindi i raggi di curvatura dati dalle relazioni: R = y + ( R z ) = R + y R z R = y + ( R + z ) = R + y R z dove y 1 =y =y per una lente sottile nell approssimazione parassiale. In questa approssimazione si ha pure che z 1 =y /R 1 e z = y /R. Dalla Fig..4 si vede inoltre che l = y + f ' = f ' (1 + y / f ' ), facendone la radice e l espansione binomiale si ha l f ' = y / f '. Sostituendo nella (1.16) le espressioni per z 1, z ed l f ' si ottiene infine: = ( n 1) f ' R1 R (.17) che è la ben nota relazione dei fabbricatori di lenti. In modo simile si può ricavare s ed s in funzione di f, esercizio che lasciamo allo studente..3 Il principio di Fermat e le superfici riflettenti Le applicazioni del principio di Fermat viste fino ad ora si applicano al dominio dei raggi parassiali ed hanno a che fare solo con superfici sferiche. Vediamo ora invece delle applicazioni che usano superfici riflettenti di forma differente e non hanno la limitazione imposta prima sull apertura del fascio luminoso..3.1 Specchio concavo (un punto coniugato all infinito) Consideriamo lo specchio concavo di Fig..5. I raggi paralleli provenienti da sinistra da distanza infinita sono fatti convergere dallo specchio ad una distanza f dal vertice dello specchio. Per convenienza assumiamo f,, e # positivi. Applicando il principio di Fermat ad i raggi lungo l asse ottico e a quelli distanti y da questo, vediamo che OPL uguali implicano che f = l + ( f # ), o l = f +#. Dalla geometria della figura si vede che: l = y + ( f # ). Eliminando si ottiene y = 4 f # che in termini di z diviene: = (.18) y 4 f z che è l equazione di un parabola con vertice in (,). Il paraboloide si ottiene facendo ruotare la parabola attorno all asse z.

7 - 1 - # y f Fig..5 Raggi riflessi da un riflettore concavo. Sostituendo R ad f usando l approssimazione parassiale f = -R/ si ha: y = R z dove R è il raggio di curvatura della superficie nel suo vertice e sia R che z hanno segno negativo in figura..3. Specchio concavo con due punti coniugati Se in Fig..5 si pensa all oggetto in un punto B distante s dal vertice, la sua immagine cade in un punto B distante s dal vertice. Allora dette ed le distanze percorse lungo il raggio che incide a distanza y dall asse ottico, si ha applicando il principio di Fermat: Essendo quindi: l+ l ' = ( s + s ') eliminando ed e posto l = y + ( s # ) l ' = y + ( s ' # ) # = z si ottiene: ss ' ss ' y 4z + 4z = s + s ' ( s + s ') (.19) che è l equazione di un ellisse con centro (,a) ed a,b semiassi maggiore e minore rispettivamente. Posto infatti a = s + s e b = ss la (.19) prende la forma canonica: ( z a) y + = 1 a b Il teorema di Fermat porta quindi a concludere che è l ellissoide la curva più appropriata per i punti coniugati. Si noti che la sfera ne rappresenta il caso particolare in cui s = s e a = b. Si noti inoltre che la parabola è pure un caso speciale della (.19) per s = e s = f.

8 Specchio convesso con due punti coniugati Nella Fig..6 è mostrato uno specchio convesso con un oggetto virtuale in B e la sua immagine in B sull asse ottico z. Assumendo la convenzione sui segni appropriata (lo studente verifichi quale deve essere) si ha applicando il principio di Fermat che: mentre la geometria della figura dà: l+ l ' = s ' d = y + ( s + #) l+ d = s ' s l ' = y + ( s ' +# ) P 1 B B S S Fig..6 Lo specchio convesso con due punti coniugati a distanza finita. Eliminando, e d da queste relazioni e ponendo # = z si ottiene: ss ' ss ' y 4z + 4z = s + s ' ( s + s ') (.) che è identica alla(.19), con una importante differenza sul segno di s ed s (lo studente dica quale). E facile vedere che questa è l equazione di un iperbole dove b = ss ' e a = s + s '..4 Le Sezioni coniche Ognuna delle curve studiate prima è una sezione conica. E quindi possibile ricavare una singola equazione da cui derivare tutti i casi particolari studiati. Partiamo dall equazione (1.3) dei punti coniugati che può anche scriversi: ss ' R s + s ' = (in approssimazione parassiale). Ricordando l equazione dell ellisse e le definizioni di a e b in termini di s ed s, e riprendendo la definizione di eccentricità e = c/a dell ellisse (dove c = a b ), si ha che:

9 - 3-4 ' ( ') 1 ss s e = = s ( s + s ') ( s + s ') e che insieme alla precedente danno: y Rz + (1 e ) z = (.1) che descrive tutta la famiglia delle coniche precedenti se si sceglie e opportunamente. Posto K = e le varie sezioni coniche si definiscono ponendo: Ellissoide oblato e < K > Sfera e= K = Ellissoide prolato < e<1 1< K < Paraboloide e=1 K = 1 Iperboloide e>1 K < 1 Nella discussione sulle aberrazioni che segue useremo K per descrivere tutte le sezioni coniche. Ricordando la definizione di ingrandimento m = s '/ s e sostituendo nelle precedenti si ha: ( m + 1) K = ( m 1) La superficie di rivoluzione generica sarà quindi descritta da un equazione del tipo: r Rz + (1 + K) z = (.) dove r = x + y. A questo punto è utile calcolare il raggio locale di curvatura R lc in un punto (r,z) della superficie dello specchio. La relazione per il raggio di curvatura è: R = + z z lc 3/ (1 ' ) / " dove z ' = dz / dr e z" = d z / dr. Risolvendo la (.) per z e svolgendo i calcoli si ha: 3/ 3/ Rlc = R 1 K( r / R ) = R 1 K( % /16 F ) (.3) dove F = f / D e r = % D / con <<1. Per K= si ha R lc =R. Esplorando la famiglia delle coniche si vede che andando dalla sfera all ellissoide, al paraboloide e all iperboloide si ha che R lc diviene progressivamente più grande per un dato r ed R. Alternativamente la curvatura locale 1/R lc decresce. Nel vertice si ha quindi che r & e Rlc & R. Vicino al vertice tutte le superfici considerate hanno la stessa forma e quindi in approssimazione parassiale sono identiche.

10 - 4 - In conclusione abbiamo visto che le superfici coniche riflettenti danno immagini perfette per una singola coppia di punti coniugati. Un dato specchio conico in generale non soddisferà al principio di Fermat per altre coppie di punti coniugati; questo implica la presenza di aberrazioni che esamineremo nei prossimi capitoli.