CALCOLO INTEGRALE IN PIÙ VARIABILI REALI
|
|
|
- Fabrizio Mariani
- 4 anni fa
- Visualizzazioni
Transcript
1 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI NTONIO INNIZZOTTO Sommario. Misura secondo Peano-Jordan in R n. Integrali doppi e tripli: funzioni integrabili secondo Riemann, formule di riduzione, domini normali, domini regolari, cambiamento di variabili. Calcolo di aree e volumi: solidi di rotazione. Integrali generalizzati. Queste note sono un mero supporto didattico, senza alcuna pretesa di completezza, originalità o precisione. Indice 1. Misura in R n 1. Integrali doppi 4 3. Integrali tripli 4. Integrali generalizzati 3 Riferimenti bibliografici 33 Versione del 18 maggio Misura in R n La scultura si prefigge la ricostruzione astratta dei piani e dei volumi che determinano le forme, non il loro valore figurativo. U. Boccioni La teoria dell integrazione secondo Riemann (non è l unica serve innanzitutto a determinare l estensione di un oggetto in uno spazio euclideo. Tale estensione corrisponde nello spazio di dimensione alla nozione geometrica di area, e nello spazio di dimensione 3 a quella di volume. Più in generale, mediante un integrale si calcola la quantità totale di una grandezza diffusa in una regione spaziale con densità variabile da punto a punto. Per i dettagli e alcune dimostrazioni, rimandiamo a [1]. Per definire rigorosamente il concetto di estensione, stabiliamo una teoria della misura (secondo Peano-Jordan in R n, che generalizza quella per R introdotta in [3]. In analogia col caso bidimensionale, chiameremo rettangoli gli insiemi del tipo R n [a i, b i ], dove a 1,... a n, b 1,... b n R e a i b i per ogni i {1,... n}. La misura di R è definita da R i1 n (b i a i. i1 1
2 . INNIZZOTTO Figura 1. Un pluri-rettangolo è un insieme P R n che si può esprimere nella forma k P R j, j1 dove R 1,... R k R n sono rettangoli t.c. R j R h per ogni j, h {1,... k}, j h. Denotiamo P la famiglia dei pluri-rettangoli di R n. La misura di P è definita da k P R j j1 (per ragioni formali, assumiamo anche P con. Sia ora R n un insieme limitato. Definiamo due famiglie di pluri-rettangoli: σ {P P : P }, Σ {Q P : Q} (ved. figura 1. Chiaramente si ha sup P inf Q. P σ Q Σ Diremo che è misurabile se sup P inf Q m, P σ Q Σ e in tal caso la sua misura è definita da m. Infine, se R è illimitato, diremo che è misurabile se [ k, k] n è misurabile per ogni k N, e porremo sup [ k, k] n k N (può essere +. La famiglia degli insiemi misurabili in R n si denota M(R n. Nel caso n la misura di un insieme è anche detta area, nel caso n 3 volume. La misura gode di alcune proprietà formali, analoghe a quelle viste in [3]: Lemma 1.1. Siano, B M(R n. llora B, B, \ B M(R n. Inoltre:
3 (i ; (ii B + B ; (iii B + B B ; (iv se B, B + B ; (v se B, B ; (vi se B, B \ B. CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 3 Osserviamo che non tutti i sottoinsiemi di R n sono misurabili. Esempio 1.. (Insieme di Dirichlet Sia {(x, y R : x, y Q}. Si vede facilmente che non contiene alcun pluri-rettangolo di misura positiva, mentre ogni pluri-rettangolo Q contenente contiene anche l insieme cl( [, 1], così che Q 1. Dunque si ha in questo caso sup σ, inf Σ 1 e non è misurabile. Inoltre, esistono insiemi compatti non misurabili (insieme di Smith-Volterra-Cantor, dalla complessa costruzione. Insomma, la teoria della misura qui introdotta non è del tutto soddisfacente sul piano astratto, tuttavia essa è sufficiente per gli scopi della presente trattazione. Una famiglia importante di insiemi misurabili: Lemma 1.3. Siano R n compatto, misurabile, f : R continua. llora gr(f è misurabile e gr(f. Dimostrazione. Per semplicità supponiamo f(x per ogni x. Per ogni ε > esiste un pluri-rettangolo Q R n, rappresentato come k Q R i, i1 dove R 1,... R k sono rettangoli t.c. R i R j per ogni i j, verificante le seguenti condizioni: Q Q \ < ε; posto per ogni i {1,... n}, Poniamo m i min R i f, M i max R i f, si ha M i m i < ε (quest ultima proprietà segue dal fatto che f è uniformemente continua, per il Teorema di Cantor-Heine, ved. [5]. Q k (R i [m i, M i ]. Dunque Q è un pluri-rettangolo in R n+1 t.c. gr(f Q e i1 Q < ε Q. Poiché ε è arbitrario, deduciamo che gr(f è misurabile e gr(f.
4 4. INNIZZOTTO Osservazione 1.4. Come visto nel Lemma 1.3, il grafico di una funzione di n variabili abbastanza regolare è un sottoinsieme di R n+1 di misura nulla. Similmente vedremo che una curva in R e una superficie in R 3 hanno, rispettivamente, area e volume nulli. Infatti la misura funziona come un indicatore di dimensione: un oggetto geometrico di dimensione intrinseca n si può pensare come sottoinsieme di R m per qualsiasi intero m n, ma può avere misura diversa da solo in R n. Il calcolo della lunghezza di una curva o dell area di una superficie non rientrano nella teoria della misura, ma vengono realizzati con tecniche diverse che tengono conto della curvatura (ved. [7]. Esercizio 1.5. Dimostrare il Lemma 1.1. Esercizio 1.6. (Difficile Sia R un insieme compatto e misurabile. Dimostrare che è misurabile con.. Integrali doppi Introduciamo ora l integrale di Riemann in R. Consideriamo inizialmente un rettangolo R [a, b] [c, d] (a, b, c, d R, a b, c d e una funzione limitata f : R R. Per ogni n N decomponiamo R in n rettangoli ponendo per ogni i, j {1,... n} x i a + b a n i, y j c + d c n j, R i,j [x i 1, x i ] [y j 1, y j ], così che R i,j è un rettangolo di misura Poiché f è limitata, esistono finiti R i,j (b a(d c n. m i,j inf R i,j f, M i,j sup R i,j f. Dunque definiamo le somme integrali (inferiore e superiore ponendo n n s n m i,j R i,j, S n M i,j R i,j. i,j1 Le successioni (s n, (S n sono limitate, e ovviamente si ha s n S n per ogni n N. In più si dimostra che gli insiemi delle somme inferiori e superiori sono separati (ved. []. i,j1 Definizione.1. La funzione f : R R è detta integrabile se e in tal caso il suo integrale è sup s n inf S n l, n N n N R f(x, y dx dy l. Una condizione necessaria e sufficiente per l integrabilità di una funzione: Teorema.. (Criterio di Riemann Siano R R un rettangolo, f : R R limitata. llora le seguenti condizioni sono equivalenti: (i f è integrabile; (ii per ogni ε > esiste n N t.c. S n s n < ε.
5 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 5 Figura. Dimostrazione. Dimostriamo che (i implica (ii. Fissato ε >, l integrabilità di f implica che esistono n, m N t.c. S n s m < ε. Sia dunque l mn. Si vede facilmente che ogni rettangolo della decomposizione indotta dal numero n è unione di m rettangoli della decomposizione indotta da l, e similmente ogni rettangolo della decomposizione indotta da m è unione di n rettangoli della decomposizione indotta da l. Pertanto si ha s m s l S l S n, da cui S l s l < ε. Dimostriamo che (ii implica (i. Poiché ε è arbitrario in (ii, si ha cioè f è integrabile. sup n N s n inf n N S n, L integrale della Definizione.1 è detto integrale doppio. Il suo significato geometrico è espresso dal seguente risultato (e dalla figura : Teorema.3. Sia f : R R integrabile t.c. f(x, y per ogni (x, y R. llora l insieme è misurabile e Dimostrazione. Poniamo T f {(x, y, z R 3 : (x, y R, z f(x, y} T f R R f(x, y dx dy. f(x, y dx dy l. Fissato ε >, per il Teorema. esiste n N t.c. l ε < s n S n < l + ε. È facile vedere che esistono due pluri-rettangoli P n, Q n in R 3 t.c. P n T f Q n, P n s n e Q n S n. Poiché ε > è arbitrario ne segue che T f è misurabile e T f l. In alcuni casi un integrale doppio si può calcolare direttamente:
6 6. INNIZZOTTO Esempio.4. Siano R R un rettangolo, c R, e f(x, y c una funzione costante. llora si ha per ogni n N, i, j {1,... m} che m i,j M i,j c, da cui s n S n c R. Pertanto f è integrabile e f(x, y dx dy c R. Esempio.5. Siano R [, 1] e f : R R definita da { 1 se y x f(x, y se y < x. R Fissato n N, il quadrato R è decomposto in n quadrati di area 1 n, così ripartiti: in n n quadrati si ha m i,j M i,j 1 in n n quadrati si ha m i,j M i,j nei restanti n quadrati si ha m i,j e M i,j 1. Pertanto s n n n n, S n n + n n. Per n entrambe le somme integrali tendono a 1, dunque f è integrabile e f(x, y dx dy 1. Esempio.6. (Funzione di Dirichlet Siano R [, 1] e f : R R definita da { 1 se x, y Q f(x, y se x / Q o y / Q. Fissato n N, per ogni i, j {1,... n} si ha m i,j e M i,j 1, da cui Pertanto f non è integrabile. Una condizione sufficiente per l integrabilità: R s n, S n 1. Lemma.7. Siano R R un rettangolo, f : R R continua. llora f è integrabile. Dimostrazione. Osserviamo che R è compatto. Per il Teorema di Weierstaß f è limitata, inoltre per il Teorema di Cantor-Heine essa è uniformemente continua (ved. [5]: fissato ε >, esiste δ > t.c. per ogni (x 1, y 1, (x, y R con d((x 1, y 1, (x, y < δ si ha f(x 1, y 1 f(x, y < Fissato n N abbastanza grande e decomposto come sopra R nei rettangoli R 1,1,... R n,n, si ha diam(r i,j < δ per ogni i, j {1,... n}, da cui M i,j m i,j < ε R. ε R. Questo implica S n s n < ε, così che f risulta integrabile per il Teorema..
7 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 7 L Esempio.5 prova che la condizione del Lemma.7 non è necessaria: osserviamo che in tale esempio l insieme dei punti di discontinuità della funzione integranda (ovvero la diagonale di R ha misura nulla. Invece, nell Esempio.6 l insieme dei punti di discontinuità è l intero quadrato R. In generale, infatti, vale il seguente risultato che estende il Lemma.7 (per la dimostrazione ved. [1]: Teorema.8. Siano R R un rettangolo, f : R R limitata t.c. l insieme D R dei punti di discontinuità di f sia misurabile con D. llora f è integrabile. Un modo efficace di calcolare un integrale doppio è quello di scomporlo in due integrali semplici, mediante le seguenti formule di riduzione: Lemma.9. Siano R [a, b] [c, d] un rettangolo, f : R R continua: (i posto per ogni x [a, b] si ha (ii posto per ogni y [c, d] si ha R R ϕ(x d c f(x, y dx dy ψ(y b a f(x, y dx dy f(x, y dy, b a f(x, y dx, d c ϕ(x dx; ψ(y dy. Dimostrazione. Proviamo (i (la dimostrazione di (ii è analoga. Per ogni x [a, b] la funzione f(x, è continua e quindi integrabile in [c, d], dunque ϕ è ben definita e a sua volta continua. Fissato n N e definiti x <... < x n, y <... < y n come sopra, per ogni i {1,... n} esiste ξ i [x i 1, x i ] t.c. xi ϕ(x dx ϕ(ξ i (x i x i 1 x i 1 n yj f(ξ i, y dy (x i x i 1 y j 1 Dunque si ha e similmente Pertanto si ha e si conclude. b a ϕ(x dx R i,j1 j1 n inf f (x i x i 1 (y j y j 1. R i,j j1 n inf f (x i x i 1 (y j y j 1 s n, R i,j b a ϕ(x dx S n. f(x, y dx dy b a ϕ(x dx,
8 8. INNIZZOTTO Esempio.1. Calcoliamo [,] [,1] (x y xy dx dy. Integriamo prima in y, ottenendo per ogni x [, ] [ x ϕ(x (x y xy y dy quindi applichiamo il Lemma.9: (x y xy dx dy [,] [,1] ( x x 3 xy3 ] 1 3 x x 3, dx [ x 3 x 6 ] 3. In particolare, se esistono g : [a, b] R, h : [c, d] R t.c. f(x, y g(xh(y per ogni (x, y R, le formule del Lemma.9 diventano b d (.1 f(x, y dx dy g(x dx h(y dy. Esempio.11. Calcoliamo R [,1] [1,] a e x y dx dy. Possiamo decomporre e x y e x e y e quindi applicare (.1: ( e 1. e x y dx dy [e x ] 1 [ e y ] 1 e [,1] [1,] Consideriamo ora domini di integrazione più generali: siano R compatto, f : R limitata. llora esiste un rettangolo R R t.c. R. Sia dunque f : R R definita per ogni (x, y R da { f(x, y se (x, y (. f(x, y se (x, y /. Definizione.1. La funzione f : R è detta integrabile se f : R R è integrabile, e in tal caso si pone f(x, y dx dy f(x, y dx dy. Osserviamo che l integrale definito sopra è indipendente dalla scelta di R. I Teoremi.,.3,.8 e il Lemma.7 si estendono facilmente al caso di un arbitrario dominio compatto. Inoltre valgono le seguenti proprietà, analoghe a quelle viste in [3]: Lemma.13. Siano R compatto, f, g : R integrabili: (i per ogni α, β R si ha ( αf(x, y + βg(x, y dx dy α (ii se f(x, y g(x, y per ogni (x, y, f(x, y dx dy R c f(x, y dx dy + β g(x, y dx dy; g(x, y dx dy;
9 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 9 (iii se B C, B, C R compatti misurabili t.c. B C, f(x, y dx dy f(x, y dx dy + f(x, y dx dy; (iv se, B f(x, y dx dy. In particolare, quindi, se f(x, y per ogni (x, y si ha f(x, y dx dy, e se f è positiva in un sottoinsieme di di misura non nulla la precedente diseguaglianza diventa stretta. Inoltre, se f è integrabile si ha f(x, y dx dy f(x, y dx dy. Esempio.14. L integrabilità di f non assicura quella di f. Per esempio, sia f : [, 1] R definita da { 1 se x, y Q f(x, y 1 se x / Q o y / Q. La funzione f non è integrabile, mentre f(x, y 1 ovviamente sì. Teorema.15. (Media integrale Siano R compatto e misurabile, f : R integrabile. llora si ha inf f f(x, y dx dy sup f. Dimostrazione. Dal Lemma.13 (ii, applicato alla funzione f e alle costanti inf f, sup f. Corollario.16. Siano R compatto, connesso e misurabile, f : R continua. llora esiste (x, y t.c. f(x, y dx dy f(x, y. Dimostrazione. Segue dal Teorema.15 e dal Teorema dei valori intermedi (ved. [5]. Mediante gli integrali forniamo una caratterizzazione della misurabilità in R : Lemma.17. Sia R compatto. llora le seguenti condizioni sono equivalenti: (i è misurabile; (ii la costante 1 è integrabile in. In tal caso si ha 1 dx dy. Dimostrazione. Proviamo che (i implica (ii. La costante 1 è continua, quindi per il Teorema.15 essa è integrabile in e vale l eguaglianza della tesi. Proviamo che (ii implica (i. Poniamo 1 dx dy m. C
10 1. INNIZZOTTO Figura 3. Sia R R un rettangolo t.c. R. Fissato ε >, per ogni n N introduciamo la decomposizione di R mediante i rettangoli R i,j (i, j {1,... n}. Per n abbastanza grande, si ha m ε < s n S n < m + ε. Denotiamo P l unione dei rettangoli R i,j contenuti in, e Q l unione di quelli che hanno con intersezione non vuota, così che P, Q sono plurirettangoli, P Q e m ε < P Q < m + ε. Poiché ε > è arbitrario, questo implica che è misurabile e m. Ovviamente il Lemma.9 non si applica direttamente a un dominio di forma arbitraria. Occorre definire alcune classi speciali di domini: Definizione.18. Sia R compatto. L insieme è detto (i dominio normale rispetto a x se esistono a, b R, a < b, e due funzioni continue g 1, g : [a, b] R t.c. g 1 (x g (x per ogni x [a, b] e {(x, y R : x [a, b], g 1 (x y g (x}; (ii dominio normale rispetto a y se esistono c, d R, c < d, e due funzioni continue h 1, h : [c, d] R t.c. h 1 (y h (y per ogni y [c, d] e {(x, y R : y [c, d], h 1 (y x h (y}; (iii dominio regolare se esistono k N, 1,... k R domini normali t.c. k i, i j per ogni i j. i1 Esempio.19. L insieme {(x, y R : x [, ], x y ex} è un dominio normale rispetto a x (ved. figura 3. Esempio.. L anello {(x, y R : 1 x + y 4} non è normale rispetto a x né rispetto a y. Tuttavia, possiamo decomporlo i 4 sottoinsiemi: 1 {(x, y : x 1}, {(x, y : 1 x 1, y },
11 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 11 Figura 4. 3 {(x, y : x }, 4 {(x, y : 1 x 1, y }, che sono tutti domini normali ( 1 e 3 rispetto a y, e 4 rispetto a x e tali che i j per ogni i j (ved. figura 4. Lemma.1. Siano R un dominio regolare, f : R continua. llora f è integrabile. Dimostrazione. Per semplicità supponiamo che sia un dominio normale del tipo (i. Poniamo c min [a,b] g 1, d max [a,b] g, così che è contenuto nel rettangolo R [a, b] [c, d]. Sia f : R R definita come in (., allora l insieme dei punti di discontinuità di f è gr(g 1 gr(g, misurabile con misura nulla per il Lemma 1.3. Dal Teorema.8 segue che f è integrabile, cioè f è integrabile (Definizione.1. In particolare, dunque, ogni dominio regolare è misurabile (Lemma.17. Inoltre, se è un dominio normale, vale la seguente estensione del Lemma.9: Lemma.. Siano R un dominio normale, f : R continua. llora: (i se (ii se si ha {(x, y R : x [a, b], g 1 (x y g (x}, ϕ(x f(x, y dx dy b a ϕ(x dx; {(x, y R : y [c, d], h 1 (y x h (y}, ψ(y g (x g 1 (x h (y h 1 (y f(x, y dy, f(x, y dx,
12 1. INNIZZOTTO si ha f(x, y dx dy d c ψ(y dy. Dimostrazione. Dimostriamo (i (la dimostrazione di (ii è analoga. Definiamo R e f come nella dimostrazione del Lemma.1. Sappiamo che f e f sono integrabili nei rispettivi insiemi di definizione. Per la Definizione.1 e il Lemma.9 si ha f(x, y dx dy f(x, y dx dy il che conclude la dimostrazione. Esempio.3. Siano R b a b a b a ( d c ( g (x g 1 (x ϕ(x dx, f(x, y dy dx f(x, y dy dx {(x, y R : x [, 1], x y x}, (ved. figura 5 e f : R definita da f(x, y 1 + xy. llora si ha, applicando la formula di riduzione (i, 1 ( x f(x, y dx dy (1 + xy dy dx x 1 ( x x + x3 x5 dx Esempio.4. Siano [ x 5 4. x3 3 + x4 8 x6 1 {(x, y R : x [, π], y sin(x}, (ved. figura 6 e f : R definita da f(x, y x y. llora si ha, applicando più volte la formula di integrazione per parti, π ( sin(x f(x, y dx dy x y dy dx π x sin(x dx [ x 3 1 x sin(x cos(x 4 π3 1 π 8. + x sin(x 4 ] 1 x 8 sin(x cos(x ] π + 8
13 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 13 Figura 5. Figura 6. Esempio.5. Siano R il parallelogramma di vertici (,, (1,, (1, 1, (, 1 e sia f : R definita da f(x, y cos(x + y. Il dominio è regolare in quanto possiamo decomporlo come 1, dove 1 {(x, y R : x 1, y x}, {(x, y R : 1 x, x 1 y 1} sono domini normali rispetto a x. Dunque si ha f(x, y dx dy f(x, y dx dy + f(x, y dx dy 1 1 ( x ( 1 (cos(x + y dy dx + 1 (x cos(x + x [x sin(x + cos(x + x3 6 cos(1 cos( 1. dx + La scelta fra le formule di riduzione (i e (ii non è indifferente: Esempio.6. Siano ] x 1 (cos(x + y dy dx (( x cos(x x + x dx [ + ( x sin(x cos(x x3 6 + x {(x, y R : x 1, x y 1}, e f : R definita da f(x, y sin(y 3. Il dominio è normale sia rispetto a x che rispetto a y (ved. figura 7. Tuttavia, la formula di riduzione (i produce un integrale alquanto complicato: f(x, y dx dy 1 ( x pplichiamo invece (ii, rappresentando il dominio come sin(y 3 dy dx... {(x, y R : y 1, x y } ] 1
14 14. INNIZZOTTO Figura 7. e ottenendo f(x, y dx dy [ 1 1 ( y sin(y 3 y dy cos(y3 3 1 cos(1. 3 sin(y 3 dx dy ] 1 Esempio.7. Calcoliamo l area dell insieme R delimitato dalle rette y, x 3, x e dalla curva y x ln(x 1 (ved. figura 8. Conviene decomporre in due domini normali: 1 {(x, y R : } 3 x 1, x ln(x 1 y, {(x, y R : 1 x, y x ln(x 1 y }, quindi calcolare le due aree separatamente. Si ha 1 ( 1 x ln(x [( 4x dy dx x ln(x 1 dx ln(3. ln(x 1 x + x 4 ] 3 1
15 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 15 Figura 8. Similmente si ricava da cui 15 8 ln(3 1, ln( Quando il dominio o la funzione integranda non permettono una facile rappresentazione, il metodo di integrazione per riduzione non è molto efficace. In questo caso si ricorre a un cambiamento di variabili, regolato dal seguente risultato: Teorema.8. Siano, B R domini regolari, f : R continua e integrabile, g : B un diffeomorfismo. llora la funzione (u, v (f g(u, v detj g (u, v è integrabile in B e f(x, y dx dy (f g(u, v detj g (u, v du dv. B Dimostrazione. Ci limitiamo a un caso speciale. Siano B [a, b] [c, d] un rettangolo (a < b, c < d e g : B R una trasformazione lineare definita da una matrice invertibile M R, cioè sia per ogni (u, v B [ ] u g(u, v M. v Sappiamo da [4] e [6] che g C 1 (B, R con matrice jacobiana J g (u, v M per ogni (u, v B, quindi per il Teorema di inversione locale g è un diffeomorfismo. L insieme g(b è un parallelogramma in R. Fissiamo una decomposzione di B mediante i punti a u <... < u n b, c v <... < v n d, ponendo R i,j [u i 1, u i ] [v j 1, v j ] (i, j 1,... n. Questa induce una decomposizione di in parallelogrammi P i,j g(r i,j, t.c. P i,j det M R i,j per ogni i, j {1,... n}. Sia ora f : R continua. Per il Corollario.16, per ogni i, j {1,... n} esiste ( x i,j, ȳ i,j P i,j t.c. P i,j f(x, y dx dy f( x i,j, ȳ i,j P i,j.
16 16. INNIZZOTTO Poiché g è suriettiva, esiste (ū i,j, v i,j R i,j t.c. ( x i,j, ȳ i,j g(ū i,j, v i,j, da cui P i,j f(x, y dx dy (f g(ū i,j, v i,j det M R i,j. ncora per il Corollario.16, per ogni i, j {1,... n} esiste (ũ i,j, ṽ i,j R i,j t.c. R i,j (f g(u, v det M du dv (f g(ũ i,j, ṽ i,j det M R i,j. Sia ora ε >. Poiché la funzione (f g det M è uniformemente continua in B (Teorema di Cantor-Heine, ved. [5], esiste δ > t.c. (f g(u, v det M (f g(u, v det M < ε per ogni (u, v, (u, v B con d((u, v, (u, v < δ. Scelto n N abbastanza grande nella decomposizione di, si ha diam(r i,j < δ per ogni i, j {1,... n}. Dunque, dalle relazioni precedenti abbiamo f(x, y dx dy (f g(u, v det M du dv n i,j1 B (f g(ūi,j, v i,j (f g(ũ i,j, ṽ i,j det M Ri,j ε det M B. L arbitrarietà di ε permette a questo punto di dedurre f(x, y dx dy (f g(u, v det M du dv, B concludendo. Nel caso di un dominio generico R e di una trasformazione non lineare g : B, il procedimento descritto sopra viene così adattato: (1 approssimiamo B con una famiglia (R h m h1 di rettangoli, in modo che l insieme B \ m h1 R h abbia misura piccola; ( per ogni h {1,... m} denotiamo (u h, v h il centro di R h, (x h, y h g(u h, v h e P h g(r h, quindi applichiamo a g la formula di Taylor centrata in (u h, v h e arrestata al primo ordine, approssimando g con la funzione lineare [ ] u uh g(u, v g(u h, v h + J g (u h, v h ; v v h (3 per ogni h {1,... m} applichiamo il metodo esposto sopra e otteniamo f(x, y dx dy (f g h (u, v det J g (u h, v h du dv; P h R h
17 (4 sommiamo tutti gli integrali ottenendo CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 17 m f(x, y dx dy f(x, y dx dy h1 P h m (f g h (u, v det J g (u h, v h du dv h1 R h m (f g(u, v det J g (u, v du dv h1 R h (f g(u, v det J g (u, v du dv. B La scelta della trasformazione g deve essere ponderata caso per caso, in modo da semplificare la forma del dominio. Di solito, scriveremo la trasformazione nella forma { x g 1 (u, v, (u, v B. y g (u, v Esempio.9. Siano il quadrato in R di vertici (1,, (, 1, ( 1,, (, 1 e f : R definita da f(x, y x. Poniamo B [ 1, 1] [ 1, 1] e x u + v y u v, (u, v B. Si vede facilmente che g : B è un diffeomorfismo con determinante jacobiano det J g (u, v 1/ 1/ 1/ 1/ 1. Per il Teorema.8 abbiamo f(x, y dx dy Esempio.3. Siano B 1 ( u + v 1 du dv ( u + du 3 1 {(x, y R : 1 x + y 4, y } (ved. figura 9 e f : R definita da f(x, y x + y. Poniamo B [1, ] [, π] e { x ρ cos(θ, (ρ, θ B y ρ sin(θ (si tratta della trasformazione da coordinate polari a coordinate cartesiane, già vista in [4] e in [6]. Si vede facilmente che g : B è un diffeomorfismo con determinante jacobiano det J g (ρ, θ ρ.
18 18. INNIZZOTTO Figura 9. Per il Teorema.8 f(x, y dx dy B π (ρ cos(θ + ρ sin(θρ dρ dθ ( 15 4 cos(θ sin(θ dθ [ 15 8 (θ + sin(θ cos(θ 7 ] π 3 cos(θ 15 8 π Esempio.31. Siano {(x, y R : x + y x, x 1} e f : R definita da f(x, y y x. Poniamo B [, 1] [ π, 3 π] e { x 1 + ρ cos(θ, (ρ, θ B. y ρ sin(θ Come sopra si ricava (y x dx dy B 3π π [ 3 π. (ρ sin(θ ρ cos(θ 1ρ dρ dθ ( sin(θ cos(θ 1 3 cos(θ + sin(θ 3 θ ] 3π π dθ
19 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 19 Esempio.3. Calcoliamo l area del dominio R delimitato dall ellisse Per il Lemma.17 si ha x 4 + y 1. 1 dx dy. Per calcolare l integrale poniamo B [, 1] [, π[ e { x ρ cos(θ, (ρ, θ B. y ρ sin(θ Si vede facilmente che g : B è un diffeomorfismo e det J g (ρ, θ ρ. Dunque 1 dx dy ρ dρ dθ π (in generale, la regione delimitata da un ellisse di semiassi a, b > ha area πab. Osserviamo che in questo caso B non è compatto, quindi non stiamo applicando il Teorema.8 alla lettera, ma una sua estensione (ved. [1]. Esercizio.33. Ricalcolare l integrale dell Esempio.5 usando la seguente rappresentazione di : {(x, y R : y [, 1], y x y + 1}. Esercizio.34. Calcolare l integrale cos(x + y dx dy, {(x, y R : x, y x, x + y }. Esercizio.35. Calcolare l integrale xy x + y dx dy, {(x, y R : x + y 1, y x}. Esercizio.36. Calcolare l integrale x + y 1 + x + y dx dy, {(x, y R : x + y 1, y x}. Esercizio.37. (Difficile Calcolare l integrale y dx dy, {(x, y R : y x, x + y x }. Esercizio.38. Calcolare l integrale xy dx dy, {(x, y R : x + 4y 1, y x }. Esercizio.39. Calcolare l area dell insieme R delimitato dalle rette x, x 1 e dalle curve y 1 x 1, y x +. B
20 . INNIZZOTTO Figura Integrali tripli In questa sezione trattiamo gli integrali del tipo f(x, y, z dx dy dz, dove R 3 è un insieme compatto e f : R è una funzione. La teoria è simile a quella svolta per il caso n, quindi non la ripetiamo: basti sapere che se f è continua e è di forma abbastanza regolare, allora f è integrabile. Ci concentriamo invece sull interpretazione geometrica e sulle tecniche di calcolo. Supponiamo f(x, y, z per ogni (x, y, z. Piuttosto che come misura in R 4 dell insieme T f {(x, y, z, w R 4 : (x, y, z, w f(x, y, z} come nel Teorema.3, conviene interpretare l integrale di f in come la massa di un corpo occupante la regione dello spazio R 3, e avente densità variabile espressa da f(x, y, z per ogni punto (x, y, z. Esempio 3.1. Sia {(x, y, z R 3 : x + y 1, z 1 x y } e f : R definita da f(x, y, z z. llora l integrale 1 dx dy dz rappresenta il volume di, mentre z dx dy dz rappresenta la massa totale del corpo con una densità crescente verso l alto (ved. figura 1.
21 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 1 In particolare, se f(x, y, z 1 per ogni (x, y, z, tale massa equivale al volume di : f(x, y, z dx dy dz. Le formule di riduzione per gli integrali tripli sono di due tipi: nella formula di riduzione per segmenti si considerano domini di integrazione normali rispetto al piano x y. Lemma 3.. Siano R un dominio regolare, g 1, g : R continue t.c. g 1 (x, y g (x, y per ogni (x, y, e f : R continua. llora: (i f è integrabile; (ii posto per ogni (x, y {(x, y, z R 3 : (x, y, g 1 (x, y z g (x, y} ϕ(x, y g (x,y g 1 (x,y f(x, y, z dz, la funzione ϕ : R è integrabile e f(x, y, z dx dy dz ϕ(x, y dx dy. Dimostrazione. naloga a quella del Lemma. (i. Esempio 3.3. Siano {(x, y, z R 3 : x + y + z 1, z }, e f : R definita da f(x, y, z xy z. Innanzitutto rappresentiamo in forma normale rispetto al piano x y, ponendo {(x, y R : x + y 1}, e per ogni (x, y g 1 (x, y, g (x, y 1 x y. Per il Lemma 3. abbiamo f(x, y, z dx dy dz ( 1 x y (xy z dz dx dy ( xy 1 x y + x + y 1 dx dy π 1 (ρ cos(θ sin(θ ρ ρ ρ dρ dθ ( π ( 1 cos(θ sin(θ dθ ρ ρ dρ + π (ρ 3 ρ dρ π 4, dove abbiamo usato il Teorema.8 e la formula (.1. Nella formula di riduzione per strati si considerano invece domini di integrazione normali rispetto all asse z:
22 . INNIZZOTTO Figura 11. Lemma 3.4. Siano c, d R, c < d, z R un dominio regolare per ogni z [c, d], e f : R continua. llora: {(x, y, z R 3 : z [c, d], (x, y z }, (i f è integrabile; (ii posto per ogni z [c, d] ψ(z f(x, y dx dy, z la funzione ψ : [c, d] R è integrabile e d f(x, y, z dx dy dz ψ(z dz. Dimostrazione. naloga a quella del Lemma. (ii. Esempio 3.5. Siano {(x, y, z R 3 : z [, 1], x + (y z 1} (ved. figura 11 e f : R definita da f(x, y, z 1 z. Posto per ogni z [, 1] per il Lemma 3.4 si ha f(x, y, z dx dy dz z {(x, y R : x + (y z 1}, 1 ( (1 z dx dy dz π z c 1 (1 z dz π. Ovviamente esistono versioni dei Lemmi 3., 3.4 per domini normali rispetto agli altri piani e assi coordinati. nche il metodo di integrazione per cambiamento di variabili si estende al caso n 3:
23 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 3 Teorema 3.6. Siano, B R 3 domini regolari, f : R continua e integrabile, g : B un diffeomorfismo. llora la funzione (u, v, w (f g(u, v, w det J g (u, v, w è integrabile in B e f(x, y, z dx dy dz B (f g(u, v, w det J g (u, v, w du dv dw. Quando il dominio di integrazione e la funzione integranda presentano una simmetria radiale, si può ricorrere alle coordinate polari sferiche (ved. [4]: x ρ sin(ϕ cos(θ y ρ sin(ϕ sin(θ z ρ cos(ϕ che definiscono una trasformazione g : (], + [ [, π] [, π[ (R 3 \ {} con determinante jacobiano sin(ϕ cos(θ ρ cos(ϕ cos(θ ρ sin(ϕ sin(θ det J g (ρ, ϕ, θ sin(ϕ sin(θ ρ cos(ϕ sin(θ ρ sin(ϕ cos(θ cos(ϕ ρ sin(ϕ ρ sin(ϕ. Esempio 3.7. Calcoliamo il volume della palla di raggio R > : {(x, y, z R 3 : x + y + z R }. Passando alle coordinate sferiche abbiamo 1 dx dy dz π ( π ( R π [ cos(ϕ ] [ π ρ πr3. ρ sin(ϕ dρ dϕ dθ Invece, se si ravvisa una simmetria assiale, si può ricorrere alle coordinate cilindriche: ] R x ρ cos(θ y ρ sin(θ z ζ che definiscono una trasformazione g : (], + [ [, π[ R (R 3 \ z con determinante jacobiano cos(θ sin(θ det J g (ρ, θ, ζ ρ sin(θ ρ cos(θ 1 ρ.,,
24 4. INNIZZOTTO Figura 1. Figura 13. Esempio 3.8. Calcoliamo l integrale dell Esempio 3.1: z dx dy dz π π π π ( 1 ( 1 ρ [ ζ ρ ] 1 ρ dρ (ρ ρ 3 + ρ 5 dρ ρζ dζ dρ dθ In generale, la trasformazione va scelta in base alla forma del dominio: Esempio 3.9. Calcoliamo il volume dell insieme R 3 delimitato dall ellissoide x + y 4 + z 9 1 (ved. figura 1. I semiassi dell ellissoide sono 1,, 3, dunque usiamo la trasformazione x ρ sin(ϕ cos(θ y ρ sin(ϕ sin(θ z ρ cos(ϕ,
25 con determinante jacobiano 6ρ sin(ϕ: 1 dx dy dz CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 5 π ( π ( 1 1π [ cos(ϕ ] [ π ρ 3 3 8π 6ρ sin(ϕ dρ dϕ dθ (in generale, se i semiassi sono a, b, c >, il volume è 4 3 πabc. Esempio 3.1. Calcoliamo il volume dell insieme delimitato dal piano x + z e dal paraboloide z 1 x y (ved. figura 13. In primo luogo troviamo una descrizione analitica di. L intersezione del piano e del paraboloide è un ellisse giacente sul piano, di equazione { x + y x 1 x + z, la cui proiezione sul piano x y è la circonferenza di equazione di centro ( 1, e raggio 5. Dunque poniamo e abbiamo la rappresentazione ] 1 x + y x 1, {(x, y R : x + y x 1 } {(x, y, z R 3 : (x, y, x z 1 x y }. Ora possiamo calcolare il volume usando le formule di riduzione e le coordinate polari (con centro opportuno: 1 dx dy dz Esempio Calcoliamo dove ( 1 x y 1 dz dx dy x (1 x x y dx dy π [ 5ρ π 5 3 π. ( 5 8 ρ4 4 ( 5 4 ρ + ρ3 dρ dθ ] 5 x dx dy dz, {(x, y, z R 3 : y 1 x, z y}.
26 6. INNIZZOTTO Poniamo {(x, y R : 1 x 1, y 1 x }. Bisogna applicare due volte le formule di riduzione: ( x y dx dy dz x dz dx dy x y dx dy x ( 1 x y dy dx 1 (x x 4 + x 6 dx 1 1 [ x 3 3 x5 5 + x7 ] Se un insieme R 3 rappresenta un corpo di densità f : R, il suo baricentro è il punto P di coordinate xf(x, y, z yf(x, y, z zf(x, y, z x dx, dy dz, y dx, dy dz, z dx, dy dz. Esempio 3.1. Consideriamo il cono {(x, y, z R 3 : x + y 1, z 1 x + y }, con densità f(x, y, z 1 z. Il volume di è 1 dx dy dz π 3. Calcoliamo inoltre Dove abbiamo posto x(1 z dx dy dz x(1 x + y dx dy π 1, {(x, y R : x + y 1}. ρ (1 ρ cos(θ dρ dθ Similmente y(1 z dx dy dz.
27 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 7 Infine z(1 z dx dy dz π 3 π 1 π. 1 ( (1 x + y (1 x + y 3 3 ( (1 ρ (1 ρ3 ρ dρ dθ 3 (ρ 3ρ 3 + ρ 4 dρ dx dy Dunque il baricentro è (,, 3. Consideriamo ora il caso particolare dei solidi di rotazione. Con questa espressione si indica l insieme delimitato (dalla superficie descritta dalla rotazione di una curva γ (ved. [7] intorno a una retta: per semplicità supponiamo che γ abbia parametrizzazione x f(t (3.1 y, t [a, b], z t dove a < b e f : [a, b] [, + [ è continua, e che la rotazione avvenga intorno all asse z. Vale in merito il seguente risultato: Teorema (Guldino Siano γ la curva di parametrizzazione (3.1 e llora {(x, y, z R 3 : z [a, b], x + y f(z}. π b Dimostrazione. Passiamo alle coordinate cilindriche: 1 dx dy dz da cui la conclusione. π π b a a f(t dt. ( b ( f(ζ a f(ζ dζ, ρ dρ dζ dθ Esempio Calcoliamo il volume dell insieme R 3 delimitato dalla rotazione intorno all asse z della curva di parametrizzazione x e t y, t [, ln(] z t (ved. figura 14. Si ha per il Teorema 3.13 π ln( e t dt 3 π.
28 8. INNIZZOTTO Figura 14. Figura 15. Il metodo descritto dal Teorema 3.13 si adatta in modo elementare ad altre rotazioni: Esempio Calcoliamo il volume dell insieme R 3 l insieme delimitato dalla rotazione intorno all asse x della curva di parametrizzazione x t y cosh(t, t [ 1, 1] z (ved. figura 15. Ragionando come nel Teorema 3.13, si ha: π 1 1 cosh(t dt [ t + cosh(t sinh(t π π (e 1 4 e + π. Quando è possibile utilizzare più metodi, l attenta osservazione dei dati consente in genere di scegliere il più adatto (ved. [8]. Esempio Calcoliamo il volume dell insieme {(x, y, z R 3 : x + y z x y }. Non conviene rappresentare come un solido di rotazione, in quanto la parametrizzazione della curva sarebbe assai complicata. È meglio porre ] 1 1 {(x, y R : x + y 1}
29 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 9 e poi calcolare il volume mediante le formule di riduzione e le coordinate polari: 1 dx dy dz ( x y x + y dx dy π ( 1 (ρ ρ 3 ρ dρ dθ π [ρ ρ4 4 ρ π. Esercizio Calcolare il volume dell insieme delimitato dal piano x + y z e dal paraboloide x + y + z 3/4. Esercizio Calcolare il volume dei seguenti insiemi: {(x, y, z R 3 : x + 4y 4, z y }, {(x, y, z R 3 : y 1 x, z x }, {(x, y, z R 3 : x 1, y 1, z ln(1 + x + y}, {(x, y, z R 3 : x + y 1, z xy}. Esercizio Calcolare il volume dell insieme delimitato dal piano z e dal paraboloide z x + y, che si proietta sull anello circolare Esercizio 3.. Calcolare ] 1 {(x, y R : 1 x + y 4}. z dx dy dz, dove R 3 è l insieme delimitato dai piani z, z y + 1 e dal cilindro x + y 1. Esercizio 3.1. Sia R 3 la sfera di centro (,, e raggio 1, con densità e (x +y +z 3. Calcolarne la massa. Esercizio 3.. Sia R 3 la sfera di centro (,, e raggio 1, con densità z 1. Calcolarne la massa e il baricentro. Esercizio 3.3. (Difficile Calcolare il volume dell insieme {(x, y, z R 3 : z [, π], x + (y sin(z π z}. Esercizio 3.4. (Difficile Calcolare il volume dell insieme delimitato dalla rotazione della curva dell Esempio 3.15 intorno all asse x.
30 3. INNIZZOTTO 4. Integrali generalizzati In questa sezione forniamo alcuni cenni sugli integrali di funzioni illimitate, o estesi a domini illimitati, in R n. Per semplicità, ci limitiamo al caso n (ved. [1] per un esposizione completa. Faremo uso della nozione di successione di insiemi, definita come una famiglia ( k t.c. per ogni k N k R. Definizione 4.1. (Integrale generalizzato del primo tipo Siano R illimitato, f : [, + [, ( k una successione di insiemi t.c. (i k1 k ; (ii k è un dominio regolare per ogni k N ; (iii f è integrabile in k per ogni k N ; (iv lim k k f(x, y dx dy l (l R {+, }. llora f è detta integrabile e si pone f(x, y dx dy l. Se l R diremo che l integrale converge. La Definizione 4.1 si estende come segue al caso di funzioni di segno variabile: se f : R, poniamo per ogni (x, y f + (x, y max{f(x, y, }, f (x, y max{ f(x, y, }, così che f ± : R sono funzioni non-negative. Diremo che f è integrabile se lo sono f ± e in tal caso porremo f(x, y dx dy f + (x, y dx dy f (x, y dx dy. Esempio 4.. (Funzione di Gauß in R Sia f : R R definita da f(x, y e x y. Poniamo k B k (, per ogni k N, quindi calcoliamo π ( k dx dy e ρ ρ dρ dθ Per k otteniamo x y e k x y e R [ π e ρ π(1 e k. ] k dx dy π. Questo notevole risultato permette di calcolare l integrale della funzione di Gauß anche in dimensione 1 (che non si può determinare con strumenti elementari, ved. [3]. Infatti si ha + ( + 1 ( + 1 e x dx e x dx e y dy ( π x y e R dx dy 1 (per svolgere questi calcoli, occorre però sapere che l integrale in questione è finito.
31 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 31 Definizione 4.3. (Integrale generalizzato del secondo tipo Siano R, f : [, + [ illimitata, ( k una successione di insiemi verificanti le condizioni (i - (iv della Definizione 4.1. llora f è detta integrabile e si pone f(x, y dx dy l. La Definizione 4.3 si estende alle funzioni di segno variabile come la 4.1. Esempio 4.4. Siano {(x, y R : < x + y 1} e f : R definita da f(x, y ln(x + y. Per ogni k N poniamo { k (x, y R 1 } : k < x + y 1, quindi calcoliamo π ( 1 f(x, y dx dy ln(ρ ρ dρ dθ 1 k k [ ρ ] 1 π (ln(ρ 1 1 k ( π 1 ln(k + 1 k. Per k otteniamo f(x, y dx dy π. Per sapere se l integrale converge, senza calcolarlo, si usano delle funzioni campione: Esempio 4.5. Siano e f : R n R definita da Per ogni intero k poniamo quindi consideriamo tre casi: se α > si ha da cui per k {(x, y R : x + y 1}, 1 f(x, y (x + y α (α >. k {(x, y R : 1 x + y k }, k f(x, y dx dy π ( k 1 ] k [ ρ α π α 1 π k α 1 α, f(x, y dx dy ρ 1 α dρ dθ π α ;
32 3. INNIZZOTTO se α < si ha come sopra da cui per k se α si ha da cui per k Esempio 4.6. Siano k f(x, y dx dy π k α 1 α, k f(x, y dx dy f(x, y dx dy + ; π ( k 1 π [ ln(ρ ] k 1 π ln(k, f(x, y dx dy +. 1 ρ dρ dθ {(x, y R : < x + y 1}, e f : R n R definita come nell Esempio 4.5. Come si vede facilmente, la situazione si capovolge: π se α ], [ f(x, y dx dy α + se α. La convergenza di un integrale generalizzato può talvolta essere stabilita mediante confronto con le funzioni degli Esempi 4.5, 4.6. Esempio 4.7. Sia f : R R definita da f(x, y x + y x 4 + y La funzione f è continua, quindi integrabile in B 1 (,. Si ha per ogni α ], 3[ lim f(x, y(x + y α. x +y Sappiamo (Esempio 4.5 che la funzione (x, y (x + y α è integrabile in R \ B 1 (,, dunque f(x, y dx dy R. R Esempio 4.8. Siano {(x, y R : < x + y 1} e f : R definita da 1 f(x, y sin(x + y. Per sapere se f è integrabile, calcoliamo il limite lim (x,y (, x + y sin(x + y 1.
33 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI 33 Dunque esiste c > t.c. per ogni (x, y c f(x, y x + y, e la seconda funzione ha integrale divergente in, come visto nell Esempio 4.6. Dunque f(x, y dx dy +. Osservazione 4.9. La teoria degli integrali generalizzati in R n (n 3 è analoga a quella in R. La differenza più importante da tenere a mente è che l esponente critico per la funzione campione f(x 1 (α > x α è n, ovvero f è integrabile in R 3 \ B 1 ( se e solo se α > n, mentre è integrabile in B 1 ( \ {} se e solo se α < n. Esercizio 4.1. Fare i calcoli dell Esempio 4.6. Esercizio Stabilire se convergono i seguenti integrali sull insieme sin(xy ln(x + y R x 4 + y 4 dx dy, dx dy + 1 R e x +y (attenzione ai cambiamenti di segno. Riferimenti bibliografici [1] M. Bramanti, C.D. Pagani, S. Salsa, nalisi matematica, Zanichelli (9. 1, 7, 19, 3 []. Iannizzotto, Insiemi numerici (15. 4 [3]. Iannizzotto, Calcolo integrale (15. 1,, 8, 3 [4]. Iannizzotto, Spazi euclidei (16. 15, 17, 3 [5]. Iannizzotto, Funzioni di più variabili reali (16. 3, 6, 9, 16 [6]. Iannizzotto, Calcolo differenziale in più variabili reali (16. 15, 17 [7]. Iannizzotto, Curve e superfici (16. 4, 7 [8] S. Salsa,. Squellati, Esercizi di analisi matematica, Zanichelli (11. 8 Dipartimento di Matematica e Informatica Università degli Studi di Cagliari Viale L. Merello 9, 913 Cagliari, Italy address: antonio.iannizzotto@unica.it
CALCOLO INTEGRALE IN PIÙ VARIABILI REALI
 CLCOLO INTEGRLE IN PIÙ VRIBILI RELI NTONIO INNIZZOTTO Sommario. Misura secondo Peano-Jordan in R n. Integrali doppi e tripli: funzioni integrabili secondo Riemann, formule di riduzione, domini normali,
CLCOLO INTEGRLE IN PIÙ VRIBILI RELI NTONIO INNIZZOTTO Sommario. Misura secondo Peano-Jordan in R n. Integrali doppi e tripli: funzioni integrabili secondo Riemann, formule di riduzione, domini normali,
Integrali doppi. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Misura e integrazione in più variabili
 Misura e integrazione in più variabili 15 novembre 2011 In queste note si vuole introdurre la nozione di insieme misurabile in R n e di integrale in più variabili secondo Riemann. 1 Rettangoli e plurirettangoli
Misura e integrazione in più variabili 15 novembre 2011 In queste note si vuole introdurre la nozione di insieme misurabile in R n e di integrale in più variabili secondo Riemann. 1 Rettangoli e plurirettangoli
R. Capone Analisi Matematica Integrali multipli
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Esercizi svolti e assegnati su integrali doppi e tripli
 Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
1. Cambiamenti di coordinate affini Esempio 1.1. Si debba calcolare l integrale doppio. (x + y) dx dy =
 . Cambiamenti di coordinate affini Esempio.. Si debba calcolare l integrale doppio (x + y) dx dy essendo il parallelogramma di vertici (, ), (, ), (3, 3), (, 3) nel quale é possibile riconoscere, vedi
. Cambiamenti di coordinate affini Esempio.. Si debba calcolare l integrale doppio (x + y) dx dy essendo il parallelogramma di vertici (, ), (, ), (3, 3), (, 3) nel quale é possibile riconoscere, vedi
Integrali doppi. Riccarda Rossi. Università di Brescia. Analisi Matematica B
 Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
quando il limite delle somme di Riemann esiste. In tal caso diciamo che la funzione è integrabile sul rettangolo.
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI. x x 2 + y 2 dxdy, tan(x + y) x + y. (x y) log (x + y) dxdy,
 PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
R = { (x, y) R 2 a x < b, c y < d } = [a, b[ [c, d[ è definita come
 5 Integrali La teoria dell integrazione in R 2 si costruisce a partire dalla nozione geometrica di area di un rettangolo Def 1 La misura (o area del rettangolo R è definita come R = (x, y R 2 a x < b,
5 Integrali La teoria dell integrazione in R 2 si costruisce a partire dalla nozione geometrica di area di un rettangolo Def 1 La misura (o area del rettangolo R è definita come R = (x, y R 2 a x < b,
Esercizi su integrali tripli: cambiamento di variabili
 Esercizi su integrali tripli: cambiamento di variabili Riccarda Rossi Università di Brescia Analisi II Riccarda Rossi (Università di Brescia) Integrali tripli Cambiamento di variabili Analisi II 1 / 51
Esercizi su integrali tripli: cambiamento di variabili Riccarda Rossi Università di Brescia Analisi II Riccarda Rossi (Università di Brescia) Integrali tripli Cambiamento di variabili Analisi II 1 / 51
Analisi Matematica 3 (Fisica) Prova scritta del 17 febbraio 2012 Un breve svolgimento delle versioni A
 Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Esercizio 1.1. Trovare il volume V della figura racchiusa tra il piano z = 8x + 6y e il rettangolo R = [0, 1] [0, 2]. (8x + 6y) dx dy. x=1. 4x 2.
![Esercizio 1.1. Trovare il volume V della figura racchiusa tra il piano z = 8x + 6y e il rettangolo R = [0, 1] [0, 2]. (8x + 6y) dx dy. x=1. 4x 2. Esercizio 1.1. Trovare il volume V della figura racchiusa tra il piano z = 8x + 6y e il rettangolo R = [0, 1] [0, 2]. (8x + 6y) dx dy. x=1. 4x 2.](/thumbs/94/119488836.jpg) Esercizi maurosaita@tiscalinet.it Versione provvisoria. Giugno 6. Indice Integrali doppi. isposte....................................... 6 Integrali doppi generalizzati 6. isposte.......................................
Esercizi maurosaita@tiscalinet.it Versione provvisoria. Giugno 6. Indice Integrali doppi. isposte....................................... 6 Integrali doppi generalizzati 6. isposte.......................................
Ω : 0 z x 2 y 2 + 5, x 2 + y 2 1. Soluzione: Tenuto conto che. 1 + f 2 x + f 2 y dx dy. riesce, servendosi delle coordinate polari,
 ANALISI VETTORIALE Soluzione scritto 19 settembre 11 4.1. Esercizio. Assegnata la superficie cartesiana S : z = x y + 5, x + y 1 calcolare l area di S calcolare il volume di Tenuto conto che Ω : z x y
ANALISI VETTORIALE Soluzione scritto 19 settembre 11 4.1. Esercizio. Assegnata la superficie cartesiana S : z = x y + 5, x + y 1 calcolare l area di S calcolare il volume di Tenuto conto che Ω : z x y
SPAZI EUCLIDEI ANTONIO IANNIZZOTTO
 SPAZI EUCLIDEI ANTONIO IANNIZZOTTO Sommario. L insieme R n : rappresentazione geometrica, struttura algebrica, sistemi di coordinate, trasformazioni, applicazioni lineari, matrici, determinanti, prodotto
SPAZI EUCLIDEI ANTONIO IANNIZZOTTO Sommario. L insieme R n : rappresentazione geometrica, struttura algebrica, sistemi di coordinate, trasformazioni, applicazioni lineari, matrici, determinanti, prodotto
Corso di Analisi Matematica 2. Corso di Laurea in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Soluzione della Prova Scritta di Analisi Matematica III - 28/02/02. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Analisi II, a.a Soluzioni 9. dx 1 + y 2 2xy
 Calcolare l integrale γ ω dove Analisi II, a.a. 7-8 Soluzioni 9 ω = + y xy ( + y mentre γ è la curva ( γ(t = e sin t cos t, + cos, t π/. t Non scriviamo neanche la complicata espresssione che si ottiene
Calcolare l integrale γ ω dove Analisi II, a.a. 7-8 Soluzioni 9 ω = + y xy ( + y mentre γ è la curva ( γ(t = e sin t cos t, + cos, t π/. t Non scriviamo neanche la complicata espresssione che si ottiene
I = 1 2. dtdx. (x 2 + t) 7/2 t=x 2 = 1 2 = 27/2 1. x 7 dx = 27/ b) Il segmento OP in figura. t=0. x=0
 X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Analisi Matematica T_2 (prof.g.cupini) A.A CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI
 Analisi Matematica T_2 (prof.g.cupini) A.A.2014-2015 - CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI Lu, 23 febbraio 2015 Presentazione del corso. Curve parametriche: definizione.
Analisi Matematica T_2 (prof.g.cupini) A.A.2014-2015 - CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI Lu, 23 febbraio 2015 Presentazione del corso. Curve parametriche: definizione.
Integrali doppi. f(x, y) dx dy, dove R = [0, 1] [0, 3] e. 2xy y x 2 x 3 + x 2 y y > x 2. (x + sin y) dx dy, dove Q = [ 1, 1] [ 1, 1].
![Integrali doppi. f(x, y) dx dy, dove R = [0, 1] [0, 3] e. 2xy y x 2 x 3 + x 2 y y > x 2. (x + sin y) dx dy, dove Q = [ 1, 1] [ 1, 1]. Integrali doppi. f(x, y) dx dy, dove R = [0, 1] [0, 3] e. 2xy y x 2 x 3 + x 2 y y > x 2. (x + sin y) dx dy, dove Q = [ 1, 1] [ 1, 1].](/thumbs/101/148528238.jpg) . Calcolare. Calcolare. Calcolare. Calcolare R T Integrali doppi f(, d d, dove R = [, ] [, ] e f(, = + > d d, dove T è il triangolo di vertici (,, (,, (,. ( + sin d d, dove = [, ] [, ]. di vertici (,,
. Calcolare. Calcolare. Calcolare. Calcolare R T Integrali doppi f(, d d, dove R = [, ] [, ] e f(, = + > d d, dove T è il triangolo di vertici (,, (,, (,. ( + sin d d, dove = [, ] [, ]. di vertici (,,
Analisi Matematica. Calcolo integrale
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Calcolo integrale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti. Parte
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Calcolo integrale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti. Parte
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
f(x, y, z) = xye z (x, y, z) R 3 : x > 0, y > 0, z 1 < x 2 + y 2 < z } 0 < z < 2 x < 1 y < 1
 ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
ANALISI MATEMATICA II Corso di Laurea in Fisica quadriennale Traccia di soluzione della prova scritta del 2 gennaio 24 Durata della prova scritta: 2 ore. Lo studente può svolgere fino a 3 esercizi tra
Soluzione della Prova Scritta di Analisi Matematica 4-25/06/13. C.L. in Matematica e Matematica per le Applicazioni. Proff. K. R. Payne e E.
 Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi Matematica 2 Funzioni di due o piú variabili
 Analisi Matematica 2 Funzioni di due o piú variabili Monica Marras - Universita di Cagliari mmarras@unica.it Monica Marras - Universita di Cagliari CCS Ingegneria Meccanica e Ingegneria Chimica mmarras@unica.it
Analisi Matematica 2 Funzioni di due o piú variabili Monica Marras - Universita di Cagliari mmarras@unica.it Monica Marras - Universita di Cagliari CCS Ingegneria Meccanica e Ingegneria Chimica mmarras@unica.it
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. ott. Franco Obersnel Esercizio 1 Sia R = [a 1, b 1 ] [a, b ] [a 3, b 3 ] IR 3 un parallelepipedo di IR 3. Si diano le
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo integrale in IR N. ott. Franco Obersnel Esercizio 1 Sia R = [a 1, b 1 ] [a, b ] [a 3, b 3 ] IR 3 un parallelepipedo di IR 3. Si diano le
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Analisi Matematica 2. Integrali doppi. Integrali doppi 1 / 24
 Analisi Matematica 2 Integrali doppi Integrali doppi 1 / 24 Integrali doppi su domini rettangolari. Sia f (x, y) una funzione limitata nel rettangolo Q = [a, b] [c, d] e sia D 1 = {x 0 = a, x 1,, x m =
Analisi Matematica 2 Integrali doppi Integrali doppi 1 / 24 Integrali doppi su domini rettangolari. Sia f (x, y) una funzione limitata nel rettangolo Q = [a, b] [c, d] e sia D 1 = {x 0 = a, x 1,, x m =
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Somme di Riemann. Il primo passo consiste nel dividere R in sottorettangoli, dividendo l intervallo
 Introduzione Se prendiamo una funzione non costante, la regione delimitata dal suo grafico ed il piano xy non è un parallelepipedo e dobbiamo definire il suo volume. Cominciamo con il caso in cui il dominio
Introduzione Se prendiamo una funzione non costante, la regione delimitata dal suo grafico ed il piano xy non è un parallelepipedo e dobbiamo definire il suo volume. Cominciamo con il caso in cui il dominio
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
FUNZIONI DI PIÙ VARIABILI REALI
 FUNZIONI DI PIÙ VARIABILI REALI ANTONIO IANNIZZOTTO Sommario. Funzioni reali definite in R n : dominio, immagine, grafico, insiemi di livello. Successioni in R n. Limite di una funzione in un punto o all
FUNZIONI DI PIÙ VARIABILI REALI ANTONIO IANNIZZOTTO Sommario. Funzioni reali definite in R n : dominio, immagine, grafico, insiemi di livello. Successioni in R n. Limite di una funzione in un punto o all
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
Analisi Matematica II.
 nalisi Matematica II. Integrazione secondo iemann Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PIS email: claudio.sacconchiocciolunipi.it sito web: http://pagine.dm.unipi.it/csblog1
nalisi Matematica II. Integrazione secondo iemann Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PIS email: claudio.sacconchiocciolunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2015/16 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
1. Calcolare, giustificandone l esistenza, il seguente integrale: y (1 + x) 2 dxdy, ydxdy. x 2 dxdy,
 . Calcolare, giustificandone l esistenza, il seguente integrale: ( + x dxd, = {(x, R :, x }.. isegnare il dominio = {(x, R : x, + x } e calcolare dxd. 3. Calcolare x dxd, è il triangolo di vertici ( 3,,
. Calcolare, giustificandone l esistenza, il seguente integrale: ( + x dxd, = {(x, R :, x }.. isegnare il dominio = {(x, R : x, + x } e calcolare dxd. 3. Calcolare x dxd, è il triangolo di vertici ( 3,,
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL 2/9/2011
 TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 7 gennaio 2010 Indichiamo con R n, Z n 1, l insieme delle n-uple ordinate di numeri reali R n 4 {(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16
 PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
5.3 Alcune classi di funzioni integrabili
 3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
Esercizi sull integrazione
 ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Il Principio di Piero della Francesca e il volume della volta a padiglione
 Il Principio di Piero della Francesca e il volume della volta a padiglione Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona La volta a padiglione è la regione
Il Principio di Piero della Francesca e il volume della volta a padiglione Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona La volta a padiglione è la regione
Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.
![Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e. Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.](/thumbs/96/129204172.jpg) 16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Esercizi 8 12 gennaio 2009
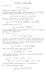 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Esercizi I : curve piane
 Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL COMPITO A. ( 1) k 2k + 1 e(2k+1)(x+y),
 1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari. (c) e5 e 4 e (2x 3y) dx + (1 + x)dx +
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
Esame di Analisi Matematica 2 18/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 18/9/13 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 1/13 A Esercizio 1. Sia C la regione aperta di R compresa tra le circonferenze di centro l origine e raggi
Esame di Analisi Matematica 18/9/13 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 1/13 A Esercizio 1. Sia C la regione aperta di R compresa tra le circonferenze di centro l origine e raggi
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II (Prof. Paolo Marcellini) 1 Esercizi tratti da temi d esame di anni precedenti
 Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
5.1. Esercizio. Sia D il cerchio di centro l origine e raggio R, calcolare, servendosi delle coordinate polari l integrale doppio x + y D
 ANALISI VTTORIAL Soluzione esercizi 26 novembre 2 5.. sercizio. Sia D il cerchio di centro l origine e raggio R, calcolare, servendosi delle coordinate polari l integrale doppio x + y dx dy D + x 2 + y2
ANALISI VTTORIAL Soluzione esercizi 26 novembre 2 5.. sercizio. Sia D il cerchio di centro l origine e raggio R, calcolare, servendosi delle coordinate polari l integrale doppio x + y dx dy D + x 2 + y2
Integrali doppi impropri per funzioni positive
 Integrali doppi impropri per funzioni positive Integrali doppi impropri su domini limitati Siano R 2 un insieme quadrabile (o misurabile) secondo Jordan e f(x, y) una funzione positiva a valori reali definita
Integrali doppi impropri per funzioni positive Integrali doppi impropri su domini limitati Siano R 2 un insieme quadrabile (o misurabile) secondo Jordan e f(x, y) una funzione positiva a valori reali definita
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Calcolo 2B - Analisi III dicembre 2004
 Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
ANALISI VETTORIALE COMPITO PER CASA DEL 6/12/ y x 2 + y 2 dxdy =
 ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Corso di Laurea in Matematica, A.A. 2013/2014 Analisi Reale e Complessa, Esame del y 2 x2 + y 2 2 R 2 ; 1 }
 NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
4. Calcolare il baricentro delle seguenti regioni del piano dotate di densità unitaria:
 INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
Geometria Differenziale 2017/18 Esercizi 3
 Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
Soluzione della Prova Parziale di Analisi Matematica III - 17/02/04. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Geometria iperbolica - Primo foglio Andrea Petracci
 Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Analisi Matematica 2. Superfici e integrali superficiali. Superfici e integrali superficiali 1 / 27
 Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
