Funzioni continue di una variabile
|
|
|
- Cesare Salvatore
- 4 anni fa
- Visualizzazioni
Transcript
1 Capitolo 7 Funzioni continue di una variabile 7.1 Definizioni e prime proprietà Sia f(x) definita nell insieme E e sia x DE. La definizione di limite per x x esprime una certa proprietà dei valori f(x) assunti dalla funzione in punti x E, diversi da x. Nel caso che sia x E, può darsi che il limite suddetto risulti uguale a f(x ). Il verificarsi di questa circostanza introduce il concetto di funzione continua, che formalizziamo come segue, utilizzando la frase x è un punto non isolato di E per esprimere che x E DE. Si hanno le due definizioni: a) Il punto x sia un punto non isolato di E. La funzione f(x) si dice continua nel punto x quando si ha lim f(x) = f(x ). (7.1) b) La funzione f(x) si dice continua nell insieme E quando è continua in ogni punto x non isolato di E. Dunque, per la continuità di f(x) nel punto x E DE debbono verificarsi questi due fatti: 1) deve essere finito il limite della funzione per x x ; 2) tale limite deve essere uguale a f(x ). Quindi non si ha continuità della f(x) nel punto x nelle seguenti due eventualità: 1) il limite della funzione per x x non esiste oppure è infinito; 2) il suddetto limite esiste finito ma non è uguale a f(x ). Osserviamo ancora che la definizione (7.1) di continuità si può ovviamente anche mettere nella forma ( ) lim f(x) = f lim x questa ci mostra che la continuità di una funzione esprime che il simbolo di funzione ed il simbolo di passaggio al limite sono permutabili fra loro (ovviamente, se hanno senso entrambi i termini di questa uguaglianza). Vediamo ora due immediate conseguenze della definizione di funzione continua, con l avvertenza che, da qui in avanti, parlando di continuità in un punto x, sarà sottinteso che x è un punto non isolato nell insieme E dove è definita la funzione. 7.1.I (Teorema della permanenza del segno) La funzione f(x) sia continua nel punto x e sia f(x ). Esiste allora un intorno I(x ) del punto x tale che, in tutti i punti x E I(x ), la f(x) ha lo stesso segno di f(x ). 7.1.II Se f(x) è continua nell insieme E essa è continua in ogni insieme G E. ; 57
2 Capitolo 7. Funzioni continue di una variabile Di quest ultimo risultato non è vero, in generale, il viceversa: la f(x) può essere continua in G, senza esserlo in E. Vediamo ora un modo alternativo di formulare la definizione di continuità; nel contempo introdurremo due locuzioni di cui faremo largo uso nel seguito. Sia E un insieme di punti sull asse reale e x E; diremo che il numero reale x è un incremento di x sull insieme E quando x + x E. Se y = f(x) è una funzione definita in E, la differenza f(x + x) f(x ) si chiamerà l incremento della funzione f(x) nel passaggio dal punto x al punto x + x e si indicherà col simbolo f oppure y. Con queste premesse, riformuliamo la definizione a) di continuità in un punto come segue: la f(x) è continua nel punto x quando, ε >, esiste in corrispondenza un numero δ ε > tale che per ogni incremento x di x su E che verifichi la x < δ ε, si abbia un incremento f della funzione che verifica la f < ε. Si vede immediatamente l equivalenza con la definizione precedente. x = x + x, la (7.1) si trasforma nella Infatti, ponendo lim f(x + x) = f(x ), x ossia nella che può anche scriversi lim [f(x + x) f(x )] =, x lim f =. (7.2) x Vediamo ora alcuni esempi di funzioni continue. Uno, di notevole generalità, è espresso come segue: 7.1.III La funzione f(x) sia definita in un dato intervallo [a, b]. Siano verificate le seguenti due ipotesi: α) f(x) è monotona in [a, b]; β) al variare di x in [a, b], la f(x) assume tutti i valori compresi fra f(a) e f(b). Allora la f(x) è continua in [a, b]. Consideriamo ora le funzioni elementari x α, a x, log a x, sin x, cos x, tan x, cot x, arcsin x, arccos x, arctan x. (7.3) Tenendo conto di quanto detto su di esse nel capitolo 4, è facile convincersi che, se x è un punto in cui una delle funzioni (7.3) è definita, tale punto si può sempre pensare contenuto in un intervallo [a, b] nel quale la funzione considerata gode delle due proprietà α), β) enunciate nel 7.1.III. Si ha pertanto: 58
3 7.2. Punti singolari di una funzione. Continuità a sinistra o a destra 7.1.IV Ciascuna delle funzioni (7.3) è continua in ogni punto dell insieme in cui essa è definita, ossia è continua nel suo insieme di definizione. Osserviamo che l insieme di definizione di ciascuna delle (7.3) è sempre costituito da uno o più intervalli (limitati o no, con o senza gli estremi). Mentre x descrive uno di questi intervalli I, la proprietà di continuità, pensata espressa dalla (7.2), ci dice che ad incrementi di x sufficientemente piccoli corrispondono incrementi arbitrariamente piccoli della funzione. Da ciò deriva che, in corrispondenza ai punti x I, il grafico della funzione può essere disegnato con moto continuo della punta scrivente, cioè senza mai sollevare tale punta dal foglio. Ciò non significa che tutto il grafico della funzione possa essere descritto in tal modo, ma che la cosa è possibile in corrispondenza ad ogni intervallo facente parte dell insieme E di definizione della funzione. Passando da un intervallo all altro si hanno salti bruschi del grafico; ciò avviene passando attraverso punti x che non appartengono ad E, ma che sono tuttavia punti di accumulazione di E. Quest ultimo fatto conduce al concetto generale di punto singolare di cui ci occuperemo nel seguito. 7.2 Punti singolari di una funzione. Continuità a sinistra o a destra Sia f(x) definita in un qualunque insieme E. Abbiamo già accennato in precedenza al fatto che possono esistere dei punti x (non isolati di E) in cui la funzione non è continua ed abbiamo sottolineato la particolare importanza che hanno i punti di accumulazione di E che non appartengono ad E. Tutti questi punti saranno chiamati punti singolari della f(x). La loro definizione precisa è la seguente: un punto x si dice singolare per la funzione f(x) definita nell insieme E quando si verifica uno di questi fatti: α) x E DE e la f(x) non è continua in x [sia perché non esiste il limite di f(x) per x x, sia perché tale limite è infinito, sia perché tale limite è finito e diverso da f(x )]; β) x DE E. Alcune volte ci sono dei punti singolari che sono del tutto artificiali e provengono soltanto da una non felice definizione della funzione Ciò avviene nei due casi seguenti: 1) x E DE, esiste finito, pari a l, il limite di f(x) per x x ma è l f(x ). 2) x DE E ed esiste finito il limite di f(x) per x x. In questi due casi la singolarità può essere eliminata: nel caso 1) basta ovviamente modificare il valore della funzione nel punto x ponendo f(x ) = l; nel caso 2) basta definire la funzione anche nel punto x, ponendo f(x ) = l, perché x non sia più punto singolare. In questo caso si parla di punti singolari (o singolarità) eliminabili. Un punto singolare x si dice punto di discontinuità di 1 a specie per la funzione f(x) quando esistono finiti entrambi i limiti lim f(x) = l x x 1, lim f(x) = l x x 2 con l 1 l
4 Capitolo 7. Funzioni continue di una variabile Un punto x si dice punto d infinito per la f(x) quando si ha oppure quando esistono entrambi i limiti lim f(x) = ± lim f(x), lim f(x) + ed uno almeno di essi è infinito. In ogni altro caso il punto singolare viene chiamato punto di discontinuità di 2 a specie. Una funzione si dice generalmente continua quando, in ogni intervallo limitato, essa ha un numero finito di punti singolari. sia Se x è un punto singolare di f(x) del tipo α) definito in precedenza, può accadere che lim f(x) = f(x ), ovvero lim f(x) = f(x ); + nel primo caso, nel punto x la funzione si dice continua a sinistra, nel secondo caso si dice continua a destra. 7.3 Operazioni sulle funzioni continue Siano f(x), g(x) due funzioni continue in un dato insieme E. Per ogni punto x E DE si ha lim f(x) = f(x ), lim g(x) = g(x ) e quindi, per il 6.4.VI: vale a dire: lim [f(x) + g(x)] = f(x ) + g(x ), lim f(x)g(x) = f(x )g(x ), 7.3.I La somma ed il prodotto di due funzioni continue sono funzioni continue. Supponiamo ora che la g(x) non sia identicamente nulla in E; allora, per ogni punto x E DE in cui sia g(x ), si ha e quindi: lim f(x) g(x) = f(x ) g(x ) 6
5 7.4. Teoremi fondamentali sulle funzioni continue 7.3.II Il quoziente di due funzioni f(x), g(x) continue in E (di cui la seconda non identicamente nulla) è una funzione continua nell insieme E ottenuto da E togliendogli i punti in cui si annulla il denominatore g(x). Analogamente, sempre sfruttando il 6.4.VI, si vede che: 7.3.III Se f(x) è continua nell insieme E, anche la funzione e f(x) è continua in E e, se è sempre f(x) >, sono anche continue le funzioni log f(x), [f(x)] α, qualunque sia il numero reale α. Da 7.3.I segue allora, per esempio, che ogni polinomio è una funzione continua su tutto l asse reale; da 7.3.II segue che ogni funzione razionale è una funzione continua nell insieme ottenuto dall asse reale togliendogli gli eventuali punti in cui si annulla il polinomio denominatore. Osserviamo anche che 7.3.III è un caso particolare di un risultato assai più generale. Infatti, utilizzando definizione e proprietà delle funzioni composte formulate nel capitolo 4, si vede facilmente che: 7.3.IV Ogni funzione composta mediante funzioni continue è una funzione continua. 7.4 Teoremi fondamentali sulle funzioni continue Daremo qui alcuni importanti risultati sulle funzioni continue. Il primo riguarda i concetti di minimo assoluto e di massimo assoluto di una funzione f(x) in un dato insieme E. 7.4.I (Teorema di Weierstrass) Ogni funzione f(x) continua in un insieme E chiuso e limitato è dotata in E di minimo e massimo assoluti. Il teorema di Weirstrass ha due immediate conseguenze: 7.4.II Ogni funzione f(x) continua in un insieme E chiuso e limitato è ivi limitata. 7.4.III Se f(x) continua nell insieme chiuso e limitato E è ivi sempre positiva, essa ha in E un minimo positivo. Diamo ora la seguente definizione. Una funzione f(x) definita in un insieme E, si dice uniformemente continua in E quando, comunque si fissi ε >, esiste un δ ε > tale che per due punti qualsiansi x, x E, per i quali sia x x < δ ε, risulti f(x ) f(x ) < ε. In sostanza, si possono trovare valori f(x ), f(x ) vicini quanto si vuole, giocando esclusivamente sulla distanza tra i due punti x, x. 61
6 Capitolo 7. Funzioni continue di una variabile Si vede immediatamente che se f(x) è uniformemente continua in E, essa è anche continua in E. Non è però vero il viceversa, cioè una funzione può essere continua in E senza essere uniformemente continua in E. Sorge quindi la questione di esaminare se, aggiungendo qualche ulteriore condizione, dalla continuità di f(x) in E si possa dedurre l uniforme continuità. A ciò risponde il seguente risultato. 7.4.IV (Teorema di Heine-Cantor) Se f(x) è continua in un insieme E chiuso e limitato, essa è uniformemente continua in E. Supponiamo ora che f(x) sia continua nell intervallo [a, b] (chiuso e limitato) e che negli estremi a, b essa assuma valori di segno opposto. Sussiste allora il seguente risultato. 7.4.V La funzione f(x) sia continua nell insieme chiuso e limitato [a, b] ed assuma, agli estremi di questo, valori di segno opposto. Esiste allora, nell interno di [a, b], almeno uno zero della f(x), cioè almeno un punto ξ in cui risulta f(ξ) =. Da questo risultato segue immediatamente l altro: 7.4.VI Se la funzione f(x) è continua in [a, b], essa non può assumere due valori distinti u, v senza assumere ogni valore w compreso fra u e v. Riunendo 7.4.VI e 7.4.I si può enunciare quanto segue. 7.4.VII Se f(x) è continua in un intervallo chiuso e limitato [a, b], essa è ivi dotata di minimo assoluto m e di massimo assoluto M ed assume come valori tutti e soli i valori dell intervallo [m, M]. 7.5 Funzioni inverse Consideriamo una funzione y = f(x) definita in un intervallo [a, b] e supponiamo che tale funzione sia continua. Ad ogni valore della x, preso in [a, b], corrisponde uno ed un solo valore della y. Sappiamo (7.4.VII) che l insieme dei valori assunti da y è un intervallo [m, M], ma non è detto che un valore y di [m, M] provenga da un solo valore x di [a, b] (in generale esso proverrà da più valori, anche infiniti, x, x,..., di x). Possiamo dire che in generale il grafico della funzione non è incontrato in un solo punto dalle parallele all asse x uscenti dai punti di [m, M]. Evidentemente, affinché tale grafico sia incontrato in un solo punto dalle predette parallele all asse x, occorre e basta che, mentre x descrive l intervallo [a, b], y descriva l intervallo [m, M] sempre nello stesso verso, vale a dire occorre e basta che la y = f(x) sia crescente oppure decrescente nell intervallo [a, b]. Si ha allora m = f(a), M = f(b), oppure m = f(b), M = f(a). Quindi ogni punto y di [m, M] proviene da uno ed un solo punto x di [a, b] e si ha pertanto una legge che ad ogni punto y di [m, M] associa un numero x di [a, b]. 62
7 7.5. Funzioni inverse Possiamo dunque guardare la x come funzione della y e scrivere x = g(y); questa funzione si chiama la funzione inversa della y = f(x). Si ha evidentemente f[g(y)] = y, g[f(x)] = x. (7.4) Si ha dunque il seguente risultato: 7.5.I Se la funzione y = f(x) è continua nell intervallo [a, b], ed ivi crescente (oppure decrescente), essa è dotata di funzione inversa x = g(y), anch essa continua, definita nell intervallo [m, M] descritto da y = f(x) al variare di x in [a, b]. Valgono le formule (7.4). Tutto quanto detto sopra può ovviamente estendersi al caso di una f(x) continua e crescente (oppure decrescente) in un intervallo A limitato ma non chiuso, ovvero illimitato, con la sola differenza che non è detto che esista il minimo m ed il massimo M della funzione. Rimane però il fatto che, al variare di x in A, il punto y descrive sempre nello stesso verso un intervallo B, onde ogni punto y B proviene da un solo punto x A. 63
8
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Funzioni continue di una variabile
 Università degli Studi di Palermo Facoltà di Economia Dip. di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica Generale Funzioni continue di una variabile Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia Dip. di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica Generale Funzioni continue di una variabile Anno Accademico 2013/2014
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 30-31 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezioni del 30-31/10/2008 1 / 26 Intervalli - Punti interni, ecc.
Lezioni di Matematica 1 - I modulo Luciano Battaia 30-31 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezioni del 30-31/10/2008 1 / 26 Intervalli - Punti interni, ecc.
Punti di discontinuità
 Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Limite Destro Finito
 Limite Destro Finito Quando la variabile assume valori via via più vicini ad a (ma sempre maggiori di a), i corrispondenti valori di f() si avvicinano sempre più al valore L. y scelta di ε y = f () y scelta
Limite Destro Finito Quando la variabile assume valori via via più vicini ad a (ma sempre maggiori di a), i corrispondenti valori di f() si avvicinano sempre più al valore L. y scelta di ε y = f () y scelta
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio. A. Figà Talamanca
 ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio.
 FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua Non è una funzione continua diciamo che
FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua Non è una funzione continua diciamo che
Avviso Importante. Le lezioni di matematica termineranno prima di Natale, pertanto saranno svolte 8 ore di lezione nelle seguenti giornate:
 Avviso Importante Le lezioni di matematica termineranno prima di Natale, pertanto saranno svolte 8 ore di lezione nelle seguenti giornate: martedì 19 novembre aula 1 ore 15.30-17 martedì 26 novembre aula
Avviso Importante Le lezioni di matematica termineranno prima di Natale, pertanto saranno svolte 8 ore di lezione nelle seguenti giornate: martedì 19 novembre aula 1 ore 15.30-17 martedì 26 novembre aula
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Funzioni continue. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Alcuni Teoremi sulle funzioni continue e uniforme continuità
 Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
FUNZIONI CONTINUE E FUNZIONI LIMITATE
 FUNZIONI CONTINUE E FUNZIONI LIMITATE FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua
FUNZIONI CONTINUE E FUNZIONI LIMITATE FUNZIONI CONTINUE Una funzione reale di variabile reale è continua se si può disegnare senza staccare la matita dal foglio. f x = x3 20 3 2 È una funzione continua
LIMITI. 1. Definizione di limite.
 LIMITI 1. Definizione di limite. Sia A un sottoinsieme di IR; se il numero reale x 0 è di accumulazione per A in ogni intorno di x 0 si trovano elementi di A distinti da x 0. Allora ha senso chiedersi
LIMITI 1. Definizione di limite. Sia A un sottoinsieme di IR; se il numero reale x 0 è di accumulazione per A in ogni intorno di x 0 si trovano elementi di A distinti da x 0. Allora ha senso chiedersi
Funzioni continue. quando. se è continua x I.
 Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Limiti di funzioni e continuità
 Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Esercizi. Soluzione: 1. Indicando con P il peso iniziale del materiale, si deve avere. . Il tempo richiesto è 800 log
 Esercizi Esercizio 4. Un materiale radioattivo è caratterizzato da un tempo di dimezzamento pari a 800 anni. Dopo quanto tempo un campione di tale materiale si sarà ridotto del 15%? Qual è il tempo di
Esercizi Esercizio 4. Un materiale radioattivo è caratterizzato da un tempo di dimezzamento pari a 800 anni. Dopo quanto tempo un campione di tale materiale si sarà ridotto del 15%? Qual è il tempo di
E, la successione di numeri {f n (x 0. n f n(x) (15.1)
 Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Funzioni reali continue
 E-school di Arrigo Amadori Analisi I Funzioni reali continue 01 Introduzione. Fra tutte le funzioni numeriche reali, le funzioni continue assumono una importanza particolare. Le funzioni continue rappresentano
E-school di Arrigo Amadori Analisi I Funzioni reali continue 01 Introduzione. Fra tutte le funzioni numeriche reali, le funzioni continue assumono una importanza particolare. Le funzioni continue rappresentano
Corsi di laurea in Fisica, Fisica ed Astrofisica Analisi A.A Foglio 4 1. Data la funzione
 Corsi di laurea in Fisica, Fisica ed Astrofisica Analisi A.A. 007-008 Foglio 4 1. Data la funzione x 6x + 8 x 0, 8 cos(x) x < 0, dire se è continua in 0. Affinché la funzione sia continua in zero, deve
Corsi di laurea in Fisica, Fisica ed Astrofisica Analisi A.A. 007-008 Foglio 4 1. Data la funzione x 6x + 8 x 0, 8 cos(x) x < 0, dire se è continua in 0. Affinché la funzione sia continua in zero, deve
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Analisi Matematica 1 Quattordicesima lezione
 Analisi Matematica 1 Quattordicesima lezione prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Analisi Matematica 1 Quattordicesima lezione prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
La derivata. variabile indipendente x. Definiamo f := f(x) f(x 0 ) l incremento (positivo o negativo) della variabile dipendente.
 La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
1.3. Se esistono i limiti sinistro e destro della funzione in un punto, allora esiste anche il limite della funzione nel punto stesso.
 Esercitazione 8 Novembre 018 1. Stabilire quali delle seguenti affermazioni sono vere e quali false. 1.1. Se una funzione f(x) è definita in un intervallo aperto (a, b), ha senso chiedersi se esistono
Esercitazione 8 Novembre 018 1. Stabilire quali delle seguenti affermazioni sono vere e quali false. 1.1. Se una funzione f(x) è definita in un intervallo aperto (a, b), ha senso chiedersi se esistono
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Matematica: Continuità e calcolo dei limiti (Cap.7)
 Matematica: Continuità e calcolo dei limiti (Cap.7) Marco Dall Aglio LUISS University mdallaglio@luiss.it A.A. 2016-17 Dall Aglio (LUISS) Guerraggio Cap.7 A.A. 2016-17 1 / 24 Continuità in un punto Definizione
Matematica: Continuità e calcolo dei limiti (Cap.7) Marco Dall Aglio LUISS University mdallaglio@luiss.it A.A. 2016-17 Dall Aglio (LUISS) Guerraggio Cap.7 A.A. 2016-17 1 / 24 Continuità in un punto Definizione
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
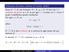 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Primi elementi di topologia dell asse reale. Intorni
 Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Primi elementi di topologia dell asse reale. Intorni R è uno spazio metrico: La distanza d(x, y) tra due numeri reali x, y è il valore assoluto della loro differenza: d(x, y) = x y Definizione (Intorno
Proprietà globali delle funzioni continue
 Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue
 ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/
ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/
Principali differenze tra la ristampa 2014 e l edizione 2008
 Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
Principali differenze tra la ristampa 214 e l edizione 28 Di seguito sono riportate le principali modifiche apportate al testo dell edizione 28 con la ristampa riveduta e corretta del 214. Si avverte il
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93
 Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Derivazione. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Prova Finale di Tipo B e Prova di Accesso alla Laura Special. Dip. Matematica - Università Roma Tre. 2 febbraio 2005
 Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
06 - Continuitá e discontinuitá
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 06 - Continuitá e discontinuitá Anno Accademico 2013/2014 D. Provenzano
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 06 - Continuitá e discontinuitá Anno Accademico 2013/2014 D. Provenzano
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
5.3 Alcune classi di funzioni integrabili
 3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti 1 A.A. 2009/2010
 ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti A.A. 2009/200 Limiti di funzione Calcolare i seguenti limiti ) 2) 3) 4) 5) 6) 6) lim 2 + 2 4 3 2 + 2 lim 2 + ( 3 2 ) lim log + 2 2 + ( 3 2 )
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti A.A. 2009/200 Limiti di funzione Calcolare i seguenti limiti ) 2) 3) 4) 5) 6) 6) lim 2 + 2 4 3 2 + 2 lim 2 + ( 3 2 ) lim log + 2 2 + ( 3 2 )
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Le funzioni con+nue (1)
 Le funzioni con+nue (1) Definizioni: - Sia I un intervallo, x 0 I. Una funzione f : I R è con$nua in x 0 se lim x x0 f(x) = f(x 0 ). La funzione f è con$nua nell'intervallo I se è con+nua in ogni punto
Le funzioni con+nue (1) Definizioni: - Sia I un intervallo, x 0 I. Una funzione f : I R è con$nua in x 0 se lim x x0 f(x) = f(x 0 ). La funzione f è con$nua nell'intervallo I se è con+nua in ogni punto
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
CORSO DI LAUREA IN FISICA
 CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
Confronto locale di funzioni
 Confronto locale di funzioni Equivalenza di funzioni in un punto Sia A R ed f, g due funzioni definite in A a valori in R. Sia x 0 R un punto di accumulazione per A. Definizione. Si dice che f è equivalente
Confronto locale di funzioni Equivalenza di funzioni in un punto Sia A R ed f, g due funzioni definite in A a valori in R. Sia x 0 R un punto di accumulazione per A. Definizione. Si dice che f è equivalente
7 Il Teorema di Bolzano - Weierstrass
 dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
Università degli Studi di Palermo Facoltà di Economia. CdS Statistica per l Analisi dei Dati. Appunti del corso di Matematica I Numeri Reali
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina, A.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 03 - I Numeri Reali Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina, A.
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
1 Limiti e continuità per funzioni di una variabile
 1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
Autore: Enrico Manfucci - 22/03/2012 LA CONTINUITA
 LA CONTINUITA CENNI STORICI Il concetto di continuità di una funzione viene elaborato tra il 7 e l 8 ed è contestuale allo sviluppo del concetto di funzione stesso. In particolare nello studio dei fenomeni
LA CONTINUITA CENNI STORICI Il concetto di continuità di una funzione viene elaborato tra il 7 e l 8 ed è contestuale allo sviluppo del concetto di funzione stesso. In particolare nello studio dei fenomeni
ESERCITAZIONE 7 : FUNZIONI
 ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
Limiti e continuità. Limiti di funzioni
 Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
Università degli Studi di Palermo Facoltà di Economia. CdS Sviluppo Economico e Cooperazione Internazionale. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 02 - I Numeri Reali Anno Accademico 2013/2014 D. Provenzano, M.
Calcolo differenziale II
 Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Lo studio di funzione. 18 febbraio 2013
 Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Corso di Analisi Matematica 1 - professore Alberto Valli
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 06/7 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - ottobre 06 iti.
Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 06/7 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - ottobre 06 iti.
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
APPUNTI SU FUNZIONI REALI DI VARIABILE REALE E LORO LIMITI
 APPUNTI SU FUNZIONI REALI DI VARIABILE REALE E LORO LIMITI 1. preliminari sulle funzioni Definizione 1. Una funzione è una legge che ad ogni elemento di un insieme D (detto dominio) associa un unico elemento
APPUNTI SU FUNZIONI REALI DI VARIABILE REALE E LORO LIMITI 1. preliminari sulle funzioni Definizione 1. Una funzione è una legge che ad ogni elemento di un insieme D (detto dominio) associa un unico elemento
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
Algebra dei limiti. quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha. lim. f (x)
 Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
CENNI SUL CONCETTO DI FUNZIONE
 CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
DERIVATE. 1.Definizione di derivata.
 DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
Limiti. Limite di una funzione per x che tende a +,.
 Limiti. Limite di una funzione per x che tende a +,. Altri esempi. considerate. Diamo un paio di esempi di funzioni un po diverse da quelle finora Ricordiamo che l approssimazione per difetto agli interi
Limiti. Limite di una funzione per x che tende a +,. Altri esempi. considerate. Diamo un paio di esempi di funzioni un po diverse da quelle finora Ricordiamo che l approssimazione per difetto agli interi
