Metodi Dinamici in Economia. Modulo 1
|
|
|
- Arianna Sole
- 7 anni fa
- Visualizzazioni
Transcript
1 Metodi Dinamici in Economia. Modulo 1 Professor Dipartimento di Scienze Statistiche, Università di Udine Anno Accademico
2 Statica Un semplice modello di equilibrio parziale D(p) = a bp: funzione di domanda S(p) = m + sp: funzione di offerta p: prezzo a, b, s > 0 m 0: costanti D(p) = S(p): condizione di equilibrio
3 Equilibrio p = a m b+s Si tratta di un problema statico: non cé riferimento al tempo La soluzione è data da uno o più valori della variabile che soddisfano un eqazione algebrica Esercizio 1 Trovare le condizioni sui parametri a, b, m, s affinchè: (i) p > 0; (ii) in equilibrio domanda e offerta siano positive.
4 Dinamica. Tempo Discreto Disequilibrio Cosa succede se p p? Bisogna sostituire la condizione di equilibrio D(p) = S(p) con un meccanismo di aggiustamento Meccanismo di Aggiustamento Adattivo p t+h = p t + hϑ[d(p t ) S(p t )] (1) p t : prezzo al tempo t, t Z! h : intervallo di tempo ϑ: coefficiente di reazione (con dimensione: quantità/tempo) D(p t ), S(p t ): funzioni di domanda e offerta come prima
5 L equazione dinamica di base Poniamo h = ϑ = 1 (una delle due puó sempre essere posta uguale a 1, scegliendo opportunamente l unitá di misura del tempo). p t+1 = p t + [D(p t ) S(p t )] (2) ovvero, usando (1) (2) e ponendo α = a m e β = 1 b s, p t+1 = α + βp t (3)
6 L equazione (3) dicesi equazione alle differenze finite. Essa pone una relazione funzionale fra il valore della variabile p al tempo t e quello della stessa variabile a un tempo diverso, t + 1 Nota che (3) è lineare, poiché f (p t ) = α + βp t lo è (a rigori, è affine ) una soluzione di (3) è una funzione del tempo p(t) che soddisfa (3), dato un valore iniziale non necessariamente di equilibrio
7 Soluzione dell equazione (3) 1 Passo. Soluzione della parte omogenea Consideriamo la parte omogenea di (3), cioè quella che non constiene funzioni del tempo o termini costanti: p t+1 = βp t (4) La soluzione di (4) è p(t) = Aβ t, A costante arbitraria. Esercizio 2 Provate che p(t) = Aβ t è una soluzione della (4).
8 2 Passo. Soluzione particolare Cercate una soluzione particolare di (3). Regola del pollice : tentate una forma funzionale simile alla parte non omogenea di (3) Poiché quest ultima é semplicemente una costante, α, ponete p(t) = K con K costante, da cui sostituendo ottenete K = α + βk, ovvero K = α 1 β = a m = p (5) b + s Quindi la soluzione particolare della (3) è stazionaria e altro non è che il valore di equilibrio del problema statico!
9 3 Passo. Soluzione generale Poiché l equazione é lineare, la somma di due soluzioni é ancora una soluzione, ovvero: p(t) = p + Aβ t (6) Esercizio 3 Provare che, nel presente caso lineare, la somma delle due soluzioni è ancora una soluzione.
10 4 Passo. Interpretazione del termine costante Poiché la soluzione vale per un valore qualsisi di t Z, poniamo t = 0, da cui abbiamo: p(0) = p + A (7) e quindi A = p(0) p (8) Interpretazione della soluzione p(t) = p }{{} + [p(0) p] }{{} equilibrio dev.iniz. β t }{{} coeff.diespansione (9)
11 Stabilitá e Instabilità Dipendenza dal parametro β = 1 (b + s) 1 Se β > 1, le deviazioni iniziali esplodono e p(t) ± 2 Se β < 1, le devizioni implodono e p(t) p Esercizio 4 Come possiamo interpretare le condizioni β 1, in termini dei parametri di base, b, s?
12 La tecnica della tela di ragno (cob web) Condizione iniziale / verticalmente fino alla curva / orizzontalmente fino alla bisettrice / verticalmente fino alla curva, e così via
13 Un caso particolare del modello di disequilibrio Il modello h = 1, ϑ = 1/b p t+1 = p t + 1 b [a bp t m sp t ] s b p t = a m b (10)
14 Il modello di equilibrio cob-web Il Modello D(p t ) = a bp t S(pt e) = m + spe t (11) D(p t ) = S(pt e) dove la notazione è come prima, eccetto che pt e denota il prezzo atteso anzichè quello effettivo.
15 Determinazione delle aspettative Aspettative ingenue Possiamo fare molte diverse ipotesi sulla determinazione del presso atteso. Scegliamo qui la più semplice, cioè pt e = p t 1, vale a dire, i produttori si aspettano che i prezzi oggi siano gli stessi di quelli di ieri. Sostituendo e spostando in avanti tutti gli indici temporali, otteniamo: p t+1 = a m s b b p t (12) Questa è la stessa equazione del caso particolare discussa sopra, con lo stesso stato stazionario p = a m b+s.
16 Dinamica di equilibrio e di disequilibrio L equazione del caso particolare h = 1, ϑ = 1/b descrive una dinamica di disequilibrio, mentre il modello cob-web descrive una dinamica di equilibrio (domanda=offerta per tutti i valori di t ma il prezzo di equilibrio e le corrispondenti domanda e offerta possono cambiare nel tempo. nel primo caso, il prezzo converge o meno verso l equilibrio, a seconda che β = 1 (b + s) 1 nel secondo caso l equilibrio converge verso lo stato stazionario ( p), o diverge da esso, a seconda che s/b 1 Esercizio 5 La dinamica (convergente o divergente) del modello cob web è oscillatoria?
17 Tempo Continuo 1 Riscrivete la (1), mantenendo ϑ = 1, ma rendendo esplicito h: p t+h = p t + h[d(p t ) S(p t )] (13) 2 Dividete per h (h 0!) e riarrangiate: p t+h p t h = [D(p t ) S(p t )] (14) 3 Prendete il limite per h 0 e omettete l indice temporale t: p t+h p t lim h 0 h = dp dt = [D(p) S(p)] = (a m) (b + s)p dove ora t R. La (15) si può anche scrivere: (15) ṗ = [D(p) S(p)] = (a m) (b + s)p (16)
18 Equazioni Differenziali Le equazioni(15) (16) sono equazioni differenziali (ordinarie), nelle quali il valore della variabile p rispetto alla (unica) variabile indipendente t è funzionalmente collegata alla sua derivata rispetto al tempo (velocità).
19 Soluzione dell equazione (15) 1 Passo. Soluzione della parte omogenea La parte omogenea della (15) si scrive: dp dt = (b + s)p (17) Separando le variabili si ottiene: dp (b + s)p = dt (18) Da cui si ottiene: ln p = (b + s)t + C (19) dove C è una costante di integrazione arbitraria.
20 Soluz. della parte omogenea (seguito) Dall equazione sopra, si ottiene la funzione del tempo desiderata, ovvero: dove A = e C. Esercizio 6 p(t) = e (b+s)t+c = Ae (b+s)t (20) Provate che la funzione p(t) sopra effettivamente è una soluzione della (15).
21 3 Passo. Soluzione Particolare Proviamo una soluzione costante come il termine non omogeneo, cioè poniamo p(t) = K Sostituendo nella (15), otteniamo: dk dt = 0 = (a m) (b + s)k K = a m b+s = p: la soluzione particolare è nientaltro che il valore di equilibrio, cioè a dire quello per cui ṗ = 0
22 4 Passo. Soluzione Generale Sommando le due soluzioni. abbiamo: p(t) = p + Ae (b+s)t (21) Ponendo t = 0, abbiamo p(0) = p + A, donde: A = p(0) p e sostituendo: p(t) = p + [p(0) p]e (b+s)t (22) Interpretazione p(t) = p }{{} + [p(0) p] }{{} equilibrio dev. iniz. e (b+s)t }{{} coeff. di espansione (23)
23 Il Diagramma di Fase
24 Tempo continuo. Un semplice modello di crescita Il Modello di Solow Swan Y = F(K, L): funzione di produzione, Y : output (=reddito) lordo, K :capitale, L: lavoro Ipotesi: F omogenea di grado 1 (=rendimenti costanti di scala) possiamo scrivere la funzione di produzione in termini pro capite, y = f (k) L(t) = L 0 e nt : la forza-lavoro cresce a un tasso proporzionale costante, n S = sy : il risparmio lordo, S, è una quota costante, s, del reddito lordo Y S = I G = K + mk : l investimento lordo I G è uguale al rispamio lordo S che, a sua volta è uguale all investimento netto, K più una quota costante m di deprezzamento del capitale
25 Derivazione dell equazione differenziale del modello k = d dt K L = sy L ( K L ) = L K K L L 2 m K L = K L kn = sy mk = sf (k) (n + m)k k = g(k) = sf (k) (n + m)k (24) un equazione differenziale nella variabile k, nonlineare se lo è la funzione f Caso particolare: funzione di produzione Cobb Douglas, F(K, L) = K α L 1 α, 0 < α < 1 (produttività marginale del capitale e del lavoro descresenti) quindi f (k) = k α e dunque: k = sk α (n + m)k (25)
26 Il diagramma di fase nel piano (k, k) Esercizio 7 Provate che, se la funzione di produzione F(K, L) è omogenea di grado 1, essa può essere espressa come f (k), dove k = K /L, cioè in termini pro capite
27 Tempo Discreto. Modello di Crescita Il Modello di Solow Swan Y t = F(K t, L t ): funzione di produzione (Y t : output (=reddito) lordo al tempo t Z, K t :capitale, L t : lavoro, al tempo t Ipotesi: F omognea di grado 1 (=rendimenti costanti di scala) possiamo scrivere la funzione di produzione in termini pro capite, y t = f (k t ) L t+1 = L t (1 + n): la forza-lavoro cresce a un tasso proporzionale costante, n S t = sy t : il risparmio lordo, S, è una quota costante, s, del reddito lordo Y t S t = IG t = K t+1 K t + mk t : l investimento lordo IG t è uguale al rispamio lordo S t che, a sua volta è uguale all investimento netto, K t+1 K t più una quota costante m < 1 di deprezzamento del capitale
28 Derivazione dell equazione alle differenze finite del modello Dividendo per L t 0 e utilizzando l ipotesi di rendimenti costanti, otteniamo sy t = sf (k t ) = K t+1 L t k t + mk t Consideriamo ora che K t+1 L t = K t+1 L t+1 (1 + n) = k t+1 (1 + n) L equazione alle differenze finite desiderata è dunque: k t+1 = G(k t ) = ( s 1 + n ) f (k t ) + ( 1 m 1 + n ) k t (26)
29 Il diagramma cob web Equilibrio Funzione di produzione Cobb Douglas : f (k) = k α, 0 < α < 1 Condizione di equilibrio: k = G( k) Soluzioni: k 1 = 0, k ( ) 1 2 = s 1 α n+m Esercizio 8 1. Provare che k 1 e k 2 sono i due valori di equilibrio del modello e discutere la loro stabilità. 2. Il fatto che k 1 e k 2 sono valori di equilibrio implica che per tali valori capitale e lavoro sono costanti?
30 Modello di crescita con effetti ambientali Tempo Discreto. Il Modello k t+1 = G(k t ) = ( ) s kt α Ak t (27) 1 + n Il termine Ak t < 0 denota la relazione negativa fra il livello dello stock di capitale e la crescita dello stesso, dovuta a una varietà di fattori, quali l eccessiva densità di strutture produttive, inquinamento, congestione del traffico, ecc. Notate che, per semplicità abbiamo assunto m = 1, cioé lo stock di capitale si deprezza interamente in un solo periodo Equilibri: [ k 2 = k 1 = 0 s (1+A)(1+n) ] 1 1 α (28)
31
32 Il punto massimo della curva G(k) (per il quale G (k) = 0) è uguale a: k 2 k se G( k 2 ) = 0 ( ) 1 ( ) 1 A(1 + n) k α 1 sα 1 α = = sα A(1 + n) A 1+A α E quindi la curva interseca l ascissa per k = k [ ] 1 1 α 2 = > k 2 > 0 s A(1+n)
33 Stabilitá locale dell equilibrio G ( k) 1 Equilibri della mappa G : k 1 = 0 instabile; k 2 stabile
34 lim k 0 G (k) = E dunque l equilibrio nullo k 1 = 0 è localmente instabile G ( k 2 ) = α(1 + A) A 0 se α A 1+A G ( k 2 ) 0 se k 2 k (29)
35 Due casi: 1.[ k 2 < k ] α(1 + A) A = α(1 + A) A < 1 per α < 1 2.[ k 2 > k ] α(1+a) A = A α(1+a) 1 se (A 1)/(1+A) α
36 Figura 3. Equilibri della mappa G: k 1 e k 2 entrambi instabili
37 e:/beamer/growthenv3 Figura 4. Diagramma di biforcazione della mappa G
38 Poiché d/da[a/(1 + A)] = [1/(1 + A) 2 ] > 0, tanto piú forte l effetto ambientale misurato da A, tanto maggiore é la probabilità che l equilibrio k 2 sia alto (maggiore di k ) Poichè d/da[(a 1)/(1 + A)] > 0, tanto piú forte é tale effetto, tanto maggiore é la probabilitá che l equilibrio sia instabile. Un equilibrio relativamente alto ( k 2 > k ) e stabile si ottiene per valori di α e A tali che (A 1)/(1 + A) < α < A/(1 + A) Infine, notate che affiché l intervallo I = [0, k 2 ] sia invariante (cioé, per qualsiasi k I, G(k) I), occorre che G(k ) k 2. Questo fatto é importante per escludere che k diventi negativo.
39 LA MAPPA LOGISTICA Insiemi invarianti. Stabilità x n+1 = G(x n ) = rx n (1 x n ) (30) L intervallo [0, 1] é invariante, cioé G([0, 1]) [0, 1] per 0 < r 4 Equilibrio: x 1 = 0, x 2 = 1 1/r dg dg dx = r(1 2x), dx x=0 = r, dg dx x=1 1/r = 2 r x 1 instabile se r > 1 x 2 { stabile se 1 < r < 3 instabile se r > 3 (31)
40 Orbite periodiche per r > 3, x 1, x 2 sono instabili Dove vanno a finire le orbite che non partono da uno di quei punti?
41 Orbite periodiche di periodo 2 cerchiamo i punti fissi di G 2 : G 2 ( x) = x G 2 è l iterata seconda di G : G 2 ( ) = G(G( )) Attenzione! x 1, x 2 sono punti fissi di G 2 in modo banale, nel senso che essi lo sono anche di G k per qualsiasi k i punti periodici di periodo 2 interessanti sono quelli che soddisfano G 2 (x) = x, ma non G(x) = x
42 Orbite Periodiche di G di periodo 2, non banali G 2 ( x) = G(G( x)) = x, da cui r 3 x 4 2r 3 x 3 + r 2 (1 + r) x 2 + (1 r 2 ) x = 0 Usando le due soluzioni note, abbiamo x 3,4 = 1 + r ± r 2 2r 3 2r (32) (discriminante 0 se r 3) Dalla (31) si ottiene G( x 3 ) = x 4, G( x 4 ) = x 3 Esercizio 9 Provare che x 3, x 4 sono effettivamente soluzioni di x = G 2 ( x)
43 Stabilitá delle orbite periodiche Stabilità dei punti fissi di G 2 = G G dg 2 dx = G (G( x 3 ))G ( x 3 ) = G ( x 4 )G (G( x 4 )) = dg dx x3 x4 (33)
44 dg dx = (1 2 x 3 )(1 2 x 4 ) x3, x 4 se 3 < r < , = r 2 [1 + 4 x 3 x 4 2( x 3 + x 4 )] = r 2 + 2r + 4 dg dx (34) < 1 e quindi il ciclo di x3, x 4 periodo 2 di G è stabile se r > 1 + 6, > 1 e quindi il ciclo-2 di G è x3, x 4 dg dx instabile. Nasce allora un ciclo-4 stabile di G, ovvero G 4 ha 4 punti fissi stabili
45 Raddoppio del periodo o Period doubling Aumentando r da 1 a r : ogni volta che un ciclo di periodo 2 k, k = 0, 1, 2,... della mappa G (convenzione: punto fisso = ciclo di periodo 2 0 = 1), perde la sua stabilitá, nasce un ciclo di periodo 2 k+1 (= nascono due punti fissi della mappa G k+1 ), inizialmente stabile. Per r = r 3.57 c é un infinitá di cicli con periodo 2 k tutti instabili L orbita tipica (escluso un insieme di punti iniziali di misura di Lebesgue zero) converge verso un insieme infinito di punti detto attrattore di Fegeinbaum. r < r 4: Regione Chaotica che include orbite periodiche, quasiperiodiche e chaotiche
46 Esponenti Caratteristici di Lyapunov Tasso di divergenza di orbite vicine. Caso Unidimensionale G : U R, U R x n+1 = G(x n ) (35) ˆx n x n = G n (ˆx 0 ) G n (x 0 ) = T (ˆx 0, x 0 ) (36) Poniamo: x 0 costante, e quindi T funzione di ˆx 0 soltanto; x i = G i (x 0 ) i 1.Espandendo in serie di Taylor attorno a ˆx 0 = x 0 e ignorando per il momento la funzione, otteniamo: ˆx n x n dt d ˆx 0 ˆx0 =x 0 (ˆx 0 x 0 ) = dgn d ˆx 0 ˆx0 =x 0 (ˆx 0 x 0 ) = [G (x 0 )G (x 1 ),, G (x n 1 )](ˆx 0 x 0 )] (37)
47 Divergenza di orbite vicine (continua) L approssimazione (37) può rendersi tanto accurata quanto si vuole prendendo ˆx 0 x 0 sufficientemente piccolo Considerando che: x = e ln x e xyz... = x y z..., possiamo scrivere ˆx 1 x 1 = e ln G (x 0 ) ˆx 0 x 0 ˆx 2 x 2 = e ln G (x 1 ) ˆx 1 x 1 ˆx n x n = e ln G (x n 1 ˆx n 1 x n 1 (38) Sostituendo: ˆx n x n = n 1 i=0( EXP(ln G (x i ) ) ˆx 0 x 0 n 1 ) = EXP i=0 ln G (x i ) ˆx 0 x 0 ( = EXP ln ) n 1 i=0 G (x i ) ˆx 0 x 0 (39)
48 Interpretazione Consideriamo dapprima il caso più semplice in cui G (x) sia costante in ( valore assoluto e ln G (x) = µ. Avremo n 1 ) allora che EXP i=0 ln G (x i ) = e nµ e quindi: ˆx n x n = e nµ ˆx 0 x 0 (40) Questo significa che, per valori di ˆx 0 vicini a x 0, la distanza fra due orbite che partono da ˆx 0 e x 0 diverge a un tasso esponenziale µ 0 se G (x) 1
49 Interpretazione (continua) Consideriamo ora il caso generale in cui G (x) non sia costante in valore assoluto. In tal caso, invece di una costante µ, prendiamo il valore atteso del tasso di espansione della distanza, calcolato lungo l orbita che parte da x 0, cioè: 1 n 1 λ(x 0 ) = lim ln G (x i ) (41) n n i=0 Se il limite esiste, possiamo scrivere ˆx n x n = e nλ(x 0) ˆx 0 x 0 (42)
50 Dipendenza sensibile dalle condizioni iniziali (DSCI) Definition Dipendenza Sensibile dalle Condizioni Iniziali (DSCI) Per una mappa G su uno spazio metrico M (uno spazio dotato di una funzione di distanza d), diciamo che vi é DSCI se un numero reale δ > 0 tale che x M e ɛ > 0, y M, y x e un intero k > 0 tali che d(x, y) < ɛ e d[(g k (x), G k (y)] > δ
51 ECL e DSCI λ(x 0 ) misura il tasso esponenziale di divergenza di orbite vicine, ovvero il tasso di amplificazione degli errori, calcolato in media lungo un orbita che parte da x 0. Esso é chiamato esponente caratteristico di Lyapunov (ECL) Quando λ > 0 c é una forma forte di DSCI (cioé le orbite divergono esponenzialmente) Per sistemi detti ergodici, esiste un valore tipico di λ che é lo stesso per quasi tutti i punti iniziali (nel senso di Lebesgue). Scrivere allora l ECL λ Per una mappa G sull intervallo, come quelle studiate, avremo: λ < 0 : orbita tipica periodica di per. 1 λ > 0 λ = 0 : orbita tipica caotica : caso particolare, ad esempio punti di biforcazione (43)
52 Un caso semplice La mappa a tenda" G Λ (y) = { 2y se 0 y 1/2 2 2y se 1/2 < y 1 (44) G (x) = 2 quasi dovunque. Quindi, per la mappa a tenda: 1 n 1 λ = lim ln G (x i ) = lim n n i=0 n 1 [n ln 2] = ln 2 > 0 (45) n
53 Coniugio Topologico Coniugio fra la mappa logistica e quella a tenda G 4 (x) = 4x(1 { x) 2y se 0 y 1/2 G Λ (y) = 2 2y se 1/2 < y 1 G Λ [0, 1] [0, 1] θ θ [0, 1] G4 [0, 1] (46) (47)
54 Due requisiti del coniugio topologico Le mappe G 4, G Λ si dicono topologicamente coniugate e sono dinamicamente equivalenti quando valgono le seguenti proprietà: 1 la mappa θ è un omeomorfismo (funzione continua con inversa continua) 2 per tutti i valori di y [0, 1], il diagramma (47) è commutativo, cioè a dire: θ[(g Λ (y)] θ G Λ = G 4 [θ(y)] ovvero, in termini di operatori = G 4 θ (48) Le suddette proprietà sono soddisfatte dalla mappa θ : [0, 1] [0, 1], θ(y) = sin 2 ( πy 2 )
55 Amplificazione degli errori e previsione Se lo stato iniziale é osservato che una precisione limitata e anziché un punto esso é un intervallo di lunghezza ɛ 0, dopo un numero di iterate k l incertezza sullo stato del sistema sará uguale a ɛ k = ɛ 0 e kλ Nel caso della mappa a tenda, dopo un numero di iterate k = ln ɛ 0 ln 2 ɛ k = 1 e dunque tutta l informazione contenuta nell osservazione dello stato iniziale sará perduta. Quando l esponente caratteristico di Lyapunov, λ, è maggiore di zero, la previsione possibile solo nel breve periodo
56 Modello a generazioni sovrapposte c 0 (t): consumo dell agente giovane al tempo t c 1 (t + 1): consumo dello stesso agente, vecchio al tempo t + 1 c 1 (t): consumo dell agente vecchio al tempo t w 0 : dotazione assegnata all agente giovane, costante w 1 : dotazione assegnata all agente vecchio, costante ρ t : fattore di interesse=tasso di cambio fra consumo presente e futuro al tempo t U(c 0 (t), c 1 (t + 1)): funzione di utilitá dell agente giovane
57 Problema dell agente giovane Vincoli: vincolo di bilancio max U(c 0(t), c 1 (t + 1)) c 0 (t),c 1 (t+1) c 1 (t + 1) = w 1 + ρ t [w 0 c 0 (t)] c 0 (t), c 1 (t + 1) 0 equilibrio di mercato, domanda = offerta del bene di consumo c 0 (t) + c 1 (t) = w 0 + w 1
58 Quindi ρ t = U( )/ c 0(t) U( )/ c 1 (t + 1) = F 1[c 0 (t), c 1 (t + 1)] (49) Da (1) + vincolo di bilancio abbiamo: F 1 [c 0 (t), c 1 (t + 1)] = w 1 c 1 (t + 1) c 0 (t) w 0 (50) Se possiamo invertire la (2) con rispetto a C t+1, abbiamo c 1 (t + 1) = F 2 [c 0 (t); w 0, w 1 ] (51)
59 Equilibrio del mercato Spostando il tempo in avanti di un unitá), abbiamo c 1 (t + 1) = w 0 + w 1 c 0 (t + 1) donde c 0 (t + 1) = G[c 0 (t)] = w 0 + w 1 F 2 [c 0 (t); w 0, w 1 ] un equazione alle differenze finite in c 0 (t)
60 Esempio da cui U(c 0 (t), c 1 (t + 1)) = ac 0 b/2c 2 0, c 1 0 c 0 a/b, a, b > 0 (w 0, w 1 ) = (0, w), w > a/b c 0 (t + 1) = ac 0 (t)(1 b/ac 0 (t)) (52) con un cambiamento di variabile, si ottiene c 0 = a b x e quindi e a b x t+1 = a2 b x t(1 x t ) x(t + 1) = rx(t)(1 x(t)) r = a la logistica
Crescita. Macroeconomia - a.a. 2017/2018
 Crescita Macroeconomia - a.a. 2017/2018 Contenuto Crescita e analisi di lungo periodo Il problema della crescita Il modello neoclassico di crescita (Solow) Produzione Accumulazione di capitale, progresso
Crescita Macroeconomia - a.a. 2017/2018 Contenuto Crescita e analisi di lungo periodo Il problema della crescita Il modello neoclassico di crescita (Solow) Produzione Accumulazione di capitale, progresso
ATTRATTORI CAOTICI. Attrattori. Classificazione degli attrattori: equilibri, cicli, tori, caos. Esponenti di Liapunov di attrattori
 ATTRATTORI CAOTICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di iapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 03/12/2009
ATTRATTORI CAOTICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di iapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 03/12/2009
IL MODELLO DI CRESCITA DI SOLOW [2.1], [2.2], [2.3]
![IL MODELLO DI CRESCITA DI SOLOW [2.1], [2.2], [2.3] IL MODELLO DI CRESCITA DI SOLOW [2.1], [2.2], [2.3]](/thumbs/97/132877476.jpg) IL MODELLO DI CRESCITA DI SOLOW Le ipotesi del modello Supponiamo piena occupazione. In Equilibrio: Y t = C t + I t [2.1] Gli investimenti lordi I t : sono la somma degli ammortamenti e della variazione
IL MODELLO DI CRESCITA DI SOLOW Le ipotesi del modello Supponiamo piena occupazione. In Equilibrio: Y t = C t + I t [2.1] Gli investimenti lordi I t : sono la somma degli ammortamenti e della variazione
CORSO DI POLITICA ECONOMICA AA
 CORSO DI POLITICA ECONOMICA AA 2016-2017 IL MODELLO SOLOW: FONDAMENTI DOCENTE PIERLUIGI MONTALBANO p.montalbano@dte.uniroma1.it Il modello Solow (1956) Funzione di produzione omogenea di primo grado (offerta):
CORSO DI POLITICA ECONOMICA AA 2016-2017 IL MODELLO SOLOW: FONDAMENTI DOCENTE PIERLUIGI MONTALBANO p.montalbano@dte.uniroma1.it Il modello Solow (1956) Funzione di produzione omogenea di primo grado (offerta):
Esercizi di macroeconomia (a.a. 2014/2015) Secondo modulo
 Esercizi di macroeconomia (a.a. 2014/2015) Secondo modulo Indice 1 Mercato del lavoro 1 2 Il modello AD - AS 3 3 Produzione, inflazione e moneta 7 4 Crescita 9 1 Mercato del lavoro Esercizio 1. Si consideri
Esercizi di macroeconomia (a.a. 2014/2015) Secondo modulo Indice 1 Mercato del lavoro 1 2 Il modello AD - AS 3 3 Produzione, inflazione e moneta 7 4 Crescita 9 1 Mercato del lavoro Esercizio 1. Si consideri
IL MODELLO DI CRESCITA DI SOLOW
 IL MODELLO DI CRESCITA DI SOLOW C. SARDONI Indice 1. Introduzione 1 2. La funzione di produzione well-behaved 1 3. La dinamica: il modello di solow 3 4. Il progresso tecnico 6 Appendice A. La distribuzione
IL MODELLO DI CRESCITA DI SOLOW C. SARDONI Indice 1. Introduzione 1 2. La funzione di produzione well-behaved 1 3. La dinamica: il modello di solow 3 4. Il progresso tecnico 6 Appendice A. La distribuzione
CAPITOLO 1 LA FUNZIONE DI PRODUZIONE E LA CRESCITA ECONOMICA
 CAPITOLO 1 LA FUZIOE DI PRODUZIOE E LA CRESCITA ECOOMICA 11 La funzione di produzione Data una funzione di produzione in cui la quantità prodotta () dipende dalla quantità di capitale () e di lavoro ()
CAPITOLO 1 LA FUZIOE DI PRODUZIOE E LA CRESCITA ECOOMICA 11 La funzione di produzione Data una funzione di produzione in cui la quantità prodotta () dipende dalla quantità di capitale () e di lavoro ()
La teoria neoclassica della crescita economica
 La teoria neoclassica della crescita economica La teoria neoclassica della crescita sostiene che la crescita economica è causata da: aumento della quantità di lavoro L utilizzata (crescita della popolazione)
La teoria neoclassica della crescita economica La teoria neoclassica della crescita sostiene che la crescita economica è causata da: aumento della quantità di lavoro L utilizzata (crescita della popolazione)
ATTRATTORI CAOTICI. Attrattori. Classificazione degli attrattori: equilibri, cicli, tori, caos. Esponenti di Liapunov di attrattori
 ARAORI CAOICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di Liapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 06/12/2012
ARAORI CAOICI Attrattori Classificazione degli attrattori: equilibri, cicli, tori, caos Esponenti di Liapunov di attrattori Sistemi dissipativi C. Piccardi e F. Dercole Politecnico di Milano - 06/12/2012
Metodi di Iterazione Funzionale
 Appunti di Matematica Computazionale Lezione Metodi di Iterazione Funzionale Il problema di calcolare il valore per cui F() = si può sempre trasformare in quello di trovare il punto fisso di una funzione
Appunti di Matematica Computazionale Lezione Metodi di Iterazione Funzionale Il problema di calcolare il valore per cui F() = si può sempre trasformare in quello di trovare il punto fisso di una funzione
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Soluzione del Compitino di Sistemi Dinamici del 21 dicembre 2016
 Soluzione del Compitino di Sistemi Dinamici del dicembre 06 Esercizio Si consideri il sistema newtoniano con dissipazione ẍ = x cosx γẋ, γ 0, ed il sistema dinamico continuo ad esso associato a Si trasformi
Soluzione del Compitino di Sistemi Dinamici del dicembre 06 Esercizio Si consideri il sistema newtoniano con dissipazione ẍ = x cosx γẋ, γ 0, ed il sistema dinamico continuo ad esso associato a Si trasformi
Politica Economica (5 CFU) Studio dell economia reale nel lungo periodo: accenni alla teoria della crescita
 Politica Economica (5 CFU) Il corso è suddiviso in due parti: Studio dell economia reale nel lungo periodo: accenni alla teoria della crescita Il materiale sarà fornito durante il corso Studio dell economia
Politica Economica (5 CFU) Il corso è suddiviso in due parti: Studio dell economia reale nel lungo periodo: accenni alla teoria della crescita Il materiale sarà fornito durante il corso Studio dell economia
In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali.
 Sistemi dinamici In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali. Le equazioni differenziali sono delle equazioni in cui le incognite rispetto
Sistemi dinamici In questa lezione ci occuperemo di sistemi dinamici in tempo continuo, rappresentati da equazioni differenziali. Le equazioni differenziali sono delle equazioni in cui le incognite rispetto
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
Analisi Matematica A e B Soluzioni prova scritta parziale n. 4
 Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
CORSO DI POLITICA ECONOMICA AA
 CORSO DI POLITICA ECONOMICA AA 2014-2015 IL MODELLO SOLOW: FONDAMENTI DOCENTE PIERLUIGI MONTALBANO p.montalbano@dte.uniroma1.it Dall analisi di breve a quella di lungo periodo La crescita di LP: Incremento
CORSO DI POLITICA ECONOMICA AA 2014-2015 IL MODELLO SOLOW: FONDAMENTI DOCENTE PIERLUIGI MONTALBANO p.montalbano@dte.uniroma1.it Dall analisi di breve a quella di lungo periodo La crescita di LP: Incremento
Esercizi 2: Curve dello spazio Soluzioni
 Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali
 Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali Argomenti trattati Introduzione ai modelli Equazioni differenziali del primo ordine Metodi risolutivi:integrazione diretta
Modelli matematici ambientali a.a. 2015/16 Introduzione alle equazioni differenziali Argomenti trattati Introduzione ai modelli Equazioni differenziali del primo ordine Metodi risolutivi:integrazione diretta
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
Matematica con elementi di Informatica
 Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Equazioni differenziali Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Equazioni
Calcolo delle Differenze
 Carla Guerrini 1 Calcolo delle Differenze Le differenze finite introdotte nel 17-esimo secolo per il calcolo delle funzioni, si prestano bene ad essere utilizzate in procedimenti e problemi discreti: da
Carla Guerrini 1 Calcolo delle Differenze Le differenze finite introdotte nel 17-esimo secolo per il calcolo delle funzioni, si prestano bene ad essere utilizzate in procedimenti e problemi discreti: da
L economia di lungo periodo 1 a p.
 L economia di lungo periodo 1 a p. La crescita: I modelli di Harrod e Domar; Il modello di Solow. Mario Sportelli Dipartimento di Matematica Università degli Studi di Bari Via E. Orabona, 4 I-70125 Bari
L economia di lungo periodo 1 a p. La crescita: I modelli di Harrod e Domar; Il modello di Solow. Mario Sportelli Dipartimento di Matematica Università degli Studi di Bari Via E. Orabona, 4 I-70125 Bari
Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:
![Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà: Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:](/thumbs/103/158017970.jpg) Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
SOLUZIONE PROBLEMA 1. Punto 1 Osserviamo anzitutto che la funzione
 SOLUZIONE PROBLEMA 1 Punto 1 Osserviamo anzitutto che la funzione g(x) = (ax b)e,-,. è continua e derivabile in R in quanto composizione di funzioni continue e derivabili. Per discutere la presenza di
SOLUZIONE PROBLEMA 1 Punto 1 Osserviamo anzitutto che la funzione g(x) = (ax b)e,-,. è continua e derivabile in R in quanto composizione di funzioni continue e derivabili. Per discutere la presenza di
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI. Lezione XI: Stabilità interna
 ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
ANALISI E SIMULAZIONE DI SISTEMI DINAMICI Lezione XI: Stabilità interna Stabilità interna e esterna Stabilità alla Lyapunov Stabilità asintotica I sistemi lineari Esempi 11-1 Tipi di Stabilità Idea intuitiva
Inflazione, disoccupazione e moneta
 Macroeconomia (Clamm) - a.a. 2011/2012 Contenuto Curva di Phillips e aspettative 1 Curva di Phillips e aspettative 2 3 4 Curva di Phillips Offerta aggregata: con: P t livello generale dei prezzi; P e t
Macroeconomia (Clamm) - a.a. 2011/2012 Contenuto Curva di Phillips e aspettative 1 Curva di Phillips e aspettative 2 3 4 Curva di Phillips Offerta aggregata: con: P t livello generale dei prezzi; P e t
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del ẋ = y y 2 + 2x
 Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Equazioni differenziali
 Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA. Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica
 NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica 9 Ottobre 13 Consideriamo un sistema dinamico unidimensionale con Hamiltoniana
NOTE SU VARIABILI AZIONE ANGOLO E TEORIA PERTURBATIVA Armando Bazzani Dipartimento di Fisica e Astranomia - Meccanica Analitica 9 Ottobre 13 Consideriamo un sistema dinamico unidimensionale con Hamiltoniana
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 5 febbraio 2018 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
STRADE AL CAOS. Sistemi parametrizzati. Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro. Caos alla Shilnikov.
 STRADE AL CAOS Sistemi parametrizzati Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro Caos alla Shilnikov Intermittenza Crisi C. Piccardi e F. Dercole Politecnico di Milano ver.
STRADE AL CAOS Sistemi parametrizzati Cascata di raddoppi di periodo (cascata di Feigenbaum) Rottura di toro Caos alla Shilnikov Intermittenza Crisi C. Piccardi e F. Dercole Politecnico di Milano ver.
Equazioni differenziali Problema di Cauchy
 Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
Equazioni differenziali Problema di Cauch Primo esempio - Risolvere l equazione '( ) = g( ) con g( ) :[ a, b] R continua Teor. fondamentale del calcolo integrale ( ) = + g ( t )dt Primo esempio - Osserviamo
PDE lineari primo ordine
 PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
Istituzioni di Analisi 2 (programma, domande ed esercizi)
 Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Introduciamo il sistema di riferimento indicato in figura b) con F 1 = ( f, 0) ed F 2 = (f, 0). Se P = (x, y) la condizione (1) fornisce
 1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
9. Test del χ 2 e test di Smirnov-Kolmogorov. 9.1 Stimatori di massima verosimiglianza per distribuzioni con densità finita
 9. Test del χ 2 e test di Smirnov-Kolmogorov 9. Stimatori di massima verosimiglianza per distribuzioni con densità finita Supponiamo di avere un campione statistico X,..., X n e di sapere che esso è relativo
9. Test del χ 2 e test di Smirnov-Kolmogorov 9. Stimatori di massima verosimiglianza per distribuzioni con densità finita Supponiamo di avere un campione statistico X,..., X n e di sapere che esso è relativo
CIRCUITI IN CORRENTE CONTINUA
 IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Corso di Matematica per la Chimica. Dott.ssa Maria Carmela De Bonis a.a
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni non lineari Sia F C 0 ([a, b]), cioé F è una funzione continua in un intervallo [a, b] R, tale che F(a)F(b) < 0 1.5 1 F(b) 0.5 0 a
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni non lineari Sia F C 0 ([a, b]), cioé F è una funzione continua in un intervallo [a, b] R, tale che F(a)F(b) < 0 1.5 1 F(b) 0.5 0 a
Il modello di Solow. Il modello di Solow. Economia Internazionale Economia dello Sviluppo Lezione 4 Il modello di Solow A.A Stefano Usai
 Economia Internazionale Economia dello Sviluppo Lezione 4 A.A 2007-2008 Stefano Usai La principale novità del modello di Solow rispetto a quello di Harrod-Domar è l enfasi sul concetto di rendimenti decrescenti
Economia Internazionale Economia dello Sviluppo Lezione 4 A.A 2007-2008 Stefano Usai La principale novità del modello di Solow rispetto a quello di Harrod-Domar è l enfasi sul concetto di rendimenti decrescenti
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Equaz. alle differenze - Equaz. differenziali
 1 Introduzione Problemi statici: Le quantità e le equazioni comportamentali (e di equilibrio) sono funzioni di un dato periodo. Il prezzo corrente di un bene dipende dalla domanda corrente dei consumatori.
1 Introduzione Problemi statici: Le quantità e le equazioni comportamentali (e di equilibrio) sono funzioni di un dato periodo. Il prezzo corrente di un bene dipende dalla domanda corrente dei consumatori.
6.3 Equazioni lineari del secondo ordine
 si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
Analisi Vettoriale - A.A Foglio di Esercizi n. 6 Soluzioni. 1. Esercizio Determinare l integrale generale dell equazione autonoma.
 Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
Fisica per Medicina. Lezione 2 - Matematica e Cinematica. Dr. Cristiano Fontana
 Fisica per Medicina Lezione - Matematica e Cinematica Dr. Cristiano Fontana Dipartimento di Fisica ed Astronomia Galileo Galilei Università degli Studi di Padova 17 ottobre 17 Indice Richiami di matematica
Fisica per Medicina Lezione - Matematica e Cinematica Dr. Cristiano Fontana Dipartimento di Fisica ed Astronomia Galileo Galilei Università degli Studi di Padova 17 ottobre 17 Indice Richiami di matematica
6. La convergenza del reddito e il capitale umano
 6. La convergenza del reddito e il capitale umano Se due economie hanno lo stesso tasso di risparmio, lo stessa cresctia della forza lavoro e la stessa tecnologia, nel lungo periodo hanno lo stesso livello
6. La convergenza del reddito e il capitale umano Se due economie hanno lo stesso tasso di risparmio, lo stessa cresctia della forza lavoro e la stessa tecnologia, nel lungo periodo hanno lo stesso livello
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017
 Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
La crescita economica
 La crescita economica Il percorso La crescita economica Il modello di Solow Costruzione Equilibrio di stato stazionario Il risparmio e la regola aurea La crescita della popolazione Obiettivi della teoria
La crescita economica Il percorso La crescita economica Il modello di Solow Costruzione Equilibrio di stato stazionario Il risparmio e la regola aurea La crescita della popolazione Obiettivi della teoria
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
INSIEMI FRATTALI. Dimensione di un insieme. Insiemi frattali elementari. Dimensioni frattali. Insiemi frattali e sistemi dinamici
 INSIEMI FRATTALI Dimensione di un insieme Insiemi frattali elementari Dimensioni frattali Insiemi frattali e sistemi dinamici C. Piccardi Politecnico di Milano - 03/01/2007 1/1 Caratteristiche tipiche
INSIEMI FRATTALI Dimensione di un insieme Insiemi frattali elementari Dimensioni frattali Insiemi frattali e sistemi dinamici C. Piccardi Politecnico di Milano - 03/01/2007 1/1 Caratteristiche tipiche
Lungo periodo. ! La curva di offerta aggregata è quindi verticale in corrispondenza della produzione di equilibrio (Y NAI )
 CRESCITA ECOOMICA Riferimento manuale: Fotocopie disponibili sul sito Elearning su vecchia edizione Dornbusch, Fischer, Startz (per maggiori dettagli si veda il sito Elearning) Lungo periodo! el lungo
CRESCITA ECOOMICA Riferimento manuale: Fotocopie disponibili sul sito Elearning su vecchia edizione Dornbusch, Fischer, Startz (per maggiori dettagli si veda il sito Elearning) Lungo periodo! el lungo
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Discretizzazione equazione del calore Per l equazione usiamo lo schema esplicito p tk+1 (x i ) p tk (x i ) h t p t = σ2 2 p 2 x 2 = σ2 2 p tk (x i+1 ) p tk
Probablità, Statistica e Processi Stocastici Discretizzazione equazione del calore Per l equazione usiamo lo schema esplicito p tk+1 (x i ) p tk (x i ) h t p t = σ2 2 p 2 x 2 = σ2 2 p tk (x i+1 ) p tk
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
n! n n. n=1 an = L [0, + ] Se L = 1 il criterio non dà una risposta e la serie potrebbe sia convergere che divergere. 2 n2. n 1
![n! n n. n=1 an = L [0, + ] Se L = 1 il criterio non dà una risposta e la serie potrebbe sia convergere che divergere. 2 n2. n 1 n! n n. n=1 an = L [0, + ] Se L = 1 il criterio non dà una risposta e la serie potrebbe sia convergere che divergere. 2 n2. n 1](/thumbs/100/146314498.jpg) 46 Roberto Tauraso - Analisi 2 Esempio 3.6 Determinare il carattere della serie Applichiamo il criterio del rapporto: n n. a n+ a n (n +! nn (n + nn (n + n+ (n + n n n+ (n + ( n + n e. n Dato che e
46 Roberto Tauraso - Analisi 2 Esempio 3.6 Determinare il carattere della serie Applichiamo il criterio del rapporto: n n. a n+ a n (n +! nn (n + nn (n + n+ (n + n n n+ (n + ( n + n e. n Dato che e
Q D = quantità domandata di un bene Q S = quantità offerta di un bene p = prezzo del bene
 La matematica che serve per Economia Politica CONCETTO DI FUNZIONE Il concetto di funzione viene utilizzato in analisi matematica per indicare la regola che associa tra loro due o più elementi secondo
La matematica che serve per Economia Politica CONCETTO DI FUNZIONE Il concetto di funzione viene utilizzato in analisi matematica per indicare la regola che associa tra loro due o più elementi secondo
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA COGNOME: NOME: MATR.:
 Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
Metodi di Ricerca Lineare
 Metodi di Ricerca Lineare Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com Metodi di Ottimizzazione
Metodi di Ricerca Lineare Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com Metodi di Ottimizzazione
Matematica con elementi di Informatica
 Limiti e Funzioni Continue Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologia Farmaceutiche Anno
Limiti e Funzioni Continue Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologia Farmaceutiche Anno
Argomento 8 Integrali indefiniti
 8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
Corso interno di Matematica compito scritto del n n+1
 Corso interno di Matematica compito scritto del 4.07.05 1. Dire se la serie converge e giustificare la risposta. n=1 1 n n+1 n Soluzione: Il criterio della radice o del rapporto falliscono; proviamo col
Corso interno di Matematica compito scritto del 4.07.05 1. Dire se la serie converge e giustificare la risposta. n=1 1 n n+1 n Soluzione: Il criterio della radice o del rapporto falliscono; proviamo col
Modelli discreti di due popolazioni
 Capitolo 7 Modelli discreti di due popolazioni Analogo del caso di un sistema di equazioni differenziali è un sistema di più successioni. Tale sistema descrive un sistema ecologico di due o più popolazioni
Capitolo 7 Modelli discreti di due popolazioni Analogo del caso di un sistema di equazioni differenziali è un sistema di più successioni. Tale sistema descrive un sistema ecologico di due o più popolazioni
Universita di Napoli Federico II Dipartimento di Scienze Economiche e Statistiche Anno Accademico Corso di Macroeconomia Lezione 12
 Universita di apoli Federico II Dipartimento di Scienze Economiche e Statistiche Anno Accademico 2016-2017 Corso di Macroeconomia Lezione 12 1 Interazioni tra produzione e capitale Il capitale determina
Universita di apoli Federico II Dipartimento di Scienze Economiche e Statistiche Anno Accademico 2016-2017 Corso di Macroeconomia Lezione 12 1 Interazioni tra produzione e capitale Il capitale determina
= 2 (64 1) = 42 > 28.
 9 LEZIONE 9 Esercizio 9.. Data una funzione y = f() = nell intervallo [, ], calcolare i valori e le aree dei rettangoli y = f(), y = f(), y = f() R = f(), R = f(), R = f(). Utilizzare il metodo dei rettangoli
9 LEZIONE 9 Esercizio 9.. Data una funzione y = f() = nell intervallo [, ], calcolare i valori e le aree dei rettangoli y = f(), y = f(), y = f() R = f(), R = f(), R = f(). Utilizzare il metodo dei rettangoli
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
26 - Funzioni di più Variabili Limiti e Derivate
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
1 n 1. n + 1. n=1 N+1. n=1. n=1 N N + 1.
 44 Roberto Tauraso - Analisi 2 e quindi la somma parziale s N è uguale a N N s N n(n + ( n n + n N n n N+ n n N +. n2 N n N n n + dove nell ultimo passaggio si sono annullati tutti i termini opposti tranne
44 Roberto Tauraso - Analisi 2 e quindi la somma parziale s N è uguale a N N s N n(n + ( n n + n N n n N+ n n N +. n2 N n N n n + dove nell ultimo passaggio si sono annullati tutti i termini opposti tranne
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Elementi di Teoria dei Sistemi
 Parte 2, 1 Elementi di Teoria dei Sistemi Parte 2, 2 Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Ingresso Uscita Parte 2, 4 Cosa significa Dinamico?? e` univocamente determinata?
Parte 2, 1 Elementi di Teoria dei Sistemi Parte 2, 2 Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Ingresso Uscita Parte 2, 4 Cosa significa Dinamico?? e` univocamente determinata?
Derivata di una funzione
 Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Teoria Economica della produzione e dei costi.
 Teoria Economica della produzione e dei costi. (1 a parte) Tecnologia e funzione di produzione. Mario Sportelli Dipartimento di Matematica Università degli Studi di Bari Via E. Orabona, 4 I-70125 Bari
Teoria Economica della produzione e dei costi. (1 a parte) Tecnologia e funzione di produzione. Mario Sportelli Dipartimento di Matematica Università degli Studi di Bari Via E. Orabona, 4 I-70125 Bari
Cognome:... Nome:... Matricola:
 Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni
Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni
Microeconomia - Problem set 4 - soluzione
 Microeconomia - Problem set 4 - soluzione (Prof Paolo Giordani - TA: Pierluigi Murro) 2 Maggio 2015 Esercizio 1 Calcolare i prodotti marginali di ciascun fattore produttivo (P M 1, P M 2 ) e il saggio
Microeconomia - Problem set 4 - soluzione (Prof Paolo Giordani - TA: Pierluigi Murro) 2 Maggio 2015 Esercizio 1 Calcolare i prodotti marginali di ciascun fattore produttivo (P M 1, P M 2 ) e il saggio
Vettori applicati. Capitolo Richiami teorici. Definizione 1.1 Un sistema di vettori applicati Σ è un insieme
 Capitolo 1 Vettori applicati 1.1 Richiami teorici Definizione 1.1 Un sistema di vettori applicati Σ è un insieme {(P i,v i ), P i E, v i V, i = 1,...,N}, (1.1) dove P i è detto punto di applicazione del
Capitolo 1 Vettori applicati 1.1 Richiami teorici Definizione 1.1 Un sistema di vettori applicati Σ è un insieme {(P i,v i ), P i E, v i V, i = 1,...,N}, (1.1) dove P i è detto punto di applicazione del
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
14 febbraio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP
 Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP Docente:Alessandra Cutrì Equazione delle onde unidimensionale non omogenea u tt (x, t = a 2 u xx (x,
Metodo di separazione di variabili e applicazione delle serie di Fourier alle soluzioni di alcune EDP Docente:Alessandra Cutrì Equazione delle onde unidimensionale non omogenea u tt (x, t = a 2 u xx (x,
Elementi di Teoria dei Sistemi. Definizione di sistema dinamico. Cosa significa Dinamico? Sistema dinamico a tempo continuo
 Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Corso di Modelli Matematici in Biologia Esame del 6 Luglio 2016
 Corso di Modelli Matematici in Biologia Esame del 6 Luglio 206 Scrivere chiaramente in testa all elaborato: Nome, Cognome, numero di matricola. Risolvere tutti gli esercizi. Tempo a disposizione: DUE ORE.
Corso di Modelli Matematici in Biologia Esame del 6 Luglio 206 Scrivere chiaramente in testa all elaborato: Nome, Cognome, numero di matricola. Risolvere tutti gli esercizi. Tempo a disposizione: DUE ORE.
Equazioni differenziali
 Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
Esame di Fisica Matematica 2, a.a (5/6/2012)
 Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
1.2.3 Lacrescitauniforme La regola d oro dell accumulazione del capitale e l inefficienzadinamica
 INDICE Presentazione dell edizione italiana... Premessa... Prefazione... vii xxi xxiii Introduzione.... 1 I.1 L importanzadellacrescita... 1 I.2 Fatti stilizzati riguardanti la crescita economica...........
INDICE Presentazione dell edizione italiana... Premessa... Prefazione... vii xxi xxiii Introduzione.... 1 I.1 L importanzadellacrescita... 1 I.2 Fatti stilizzati riguardanti la crescita economica...........
Il modello di Barro. Politica economica e crescita endogena
 Il modello di Barro Politica economica e crescita endogena 1 Spesa pubblica produttiva e crescita Il modello di Barro è un modello con tecnologia di tipo AK in cui A può essere visto come un coefficiente
Il modello di Barro Politica economica e crescita endogena 1 Spesa pubblica produttiva e crescita Il modello di Barro è un modello con tecnologia di tipo AK in cui A può essere visto come un coefficiente
Probabilità e Statistica per l Informatica Esercitazione 4
 Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
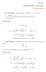 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Minimi quadrati vincolati e test F
 Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
