Problemi supplemetari
|
|
|
- Cristiano Colonna
- 9 anni fa
- Visualizzazioni
Transcript
1 Problemi supplemetari Problemi per Capitolo. Sistema a 3 stati Un sistema a tre stati è descritto dall Hamiltoniana H = H 0 + H = E E 0 0 ɛ E () (i) Determinare gli autovalori dell Hamiltoniana totale, H 0 +H, e gli autostati corrispondenti allo stato fondamentale ( ), al primo ( ) e al secondo stato di eccitazione 0 0 ( 3 ), in termini di = 0, =, e 3 = (Suggerimento: Diagonalizzare l operatore H. ) (ii) Come si verifica facilmente, l Hamiltoniana () commuta con l operatore 0 0 Π 0 0 ; Π =. () 0 0 Discutere, in concomitanza col risultato del punto i), le conseguenze di questo fatto. (iii) Esprimere gli stati, e 3 in termini dei tre autostati dell energia. (iv) Il sistema è nello stato = 0, all istante t = 0. Determinare la funzione 0 d onda all istante t, ψ(t), in termini degli stati, e 3. Determinare la probabilità P (t) che all istante t la particella si trovi nello stato e fare uno schizzo di P (t) come funzione di t.. Sistema a stati Si consideri un sistema a due stati descitto dall Hamiltoniana ( ) E0 η H = η E 0 (i) Rispondere se η può essere complesso (i.e., Im(η) 0); (ii) Determinare gli autovalori e gli autotati di H; (iii) All istante t = 0, il sistema si trova nello stato ψ(0) = (3) + i. (4) Si determinino le probabilità P (t), P (t), che all istante t il sistema si trovi o nello stato o nello stato. Fare uno schizzo di P (t) e P (t). 0 Si supponga che sia possibile fare una misura, corrispondente all operatore O A. Tale misura (filtro) darà o o 0 come risultato. La domanda può essere riformulata allora in maniera più precisa: qual è la probabilità che la misura di O eseguita all istante t, dia il risultato?
2 .3 Sistema a 3 stati, autostati e autovalori Si consideri un sistema a tre stati. Nella base di stati in cui l Hamiltoniana è diagonale (e con i livelli non degeneri), due operatori Hermitiani A e B sono dati da (a, b reali e positivi) A = 0 0 i a 0 0 0, B = b b. (5) i a b 0 i) Determinare gli autovalori e gli autostati dell operatore A. ii) Determinare gli autovalori e gli autostati dell operatore B. iii) All istante t = 0, la misura di A ha dato come risultato l autovalore massimo di A. Qual è la probabilità che la misura di B, eseguita immediatamente dopo la misura di A, dia l autovalore massimo di B? iv) Se la misura di B al punto iii) fosse fatta all istante t generico (t > 0), la probabilità di trovare l autovalore massimo di B sarebbe uguale al caso di iii)? Rispondere Sì o No, giustificando la risposta. 3 Problemi per Capitolo 3 3. Particella fra pareti Una particella di massa m è confinata in una buca { 0 0, x a, V (x) =, x < 0, x > a. (6) e si trova nello stato fondamentale. (i) Qual è la pressione che la particella esercita sul muro? (ii) A t = 0 il muro a destra della buca (a x = a ) si sposta all improvviso a x = a. Calcolare le probabilità che la particella si trovi in vari stati stazionari (della nuova buca). (iii) Se invece il muro viene adiabaticamente spostato da a fino a a, qual è lo stato finale? Calcolare il lavoro ricevuto (o dato) dal sistema legato. 3. Potenziale a delta Una particella di massa m si muove in un potenziale unidimensionale, { g δ(x) x < a, V (x) = (g > 0). (7) x a, (Fig. ). Si vogliono studiare le proprietà di un eventuale stato legato con energia negativa. (i) Trovare l equazione che implicitamente determina l energia di uno stato legato con E < 0. Dalla condizione di esistenza per una soluzione di questa equazione, trovare la condizione (sui parametri, m, g, a) affinché il sistema abbia uno stato legato di energia negativa; (ii) Discutere il limite a ; (iii) Dire se esistono degenerazioni per gli autovalori dell energia nello spettro continuo (E 0).
3 0 a Figura : 3.3 Potenziale a delta e pareti Consideriamo il moto di una particella in un potenziale unidimensionale (Fig. ): x < a V (x) = g δ(x) a x a x > a. Si vogliono studiare i primi due livelli energetici. Indichiamo con ψ (x) e ψ + (x) la funzione d onda nelle regioni x < 0 e x > 0, rispettivamente. Imponendo l annullamento della funzione d onda a x = a e a x = a, ψ (x) e ψ + (x) hanno la forma dove E = k m. ψ (x) = A sin k(x + a), ψ + (x) = B sin k(x a), (9) (i) Scrivere le equazioni che determinano i coefficienti A, B e il numero d onda k (cioè E), imponendo la condizione di raccordo a x = 0. (ii) Dimostrare che una delle soluzioni della condizione di cui sopra dà i risultati esatti per un gruppo di livelli, queli per i quali la funzione d onda si annulla a x = 0. (iii) Esiste un altro gruppo dei livelli, con la funzione d onda che non si annulla a x = 0. Le energie di questi livelli non possono essere calcolate analiticamente. Facendo uso di un grafico, dimostrare che lo stato fondamentale del sistema (8) appartiene a questo gruppo. Calcolare l energia di questo stato, nei limiti, g 0 e g. (iv) Discutere più in generale qual è la situazione fisica nei limiti g 0 e g. (8) 3.4 Potenziale con delta Una particella di massa m ed energia E < 0 si muove in una dimensione, nel potenziale V (x) = f δ(x) g δ(x a), g > 0. (0) (i) Nel caso di una singola buca delta (f = 0) dire qual è l energia dello stato legato, e scrivere la funzione d onda normalizzata. (ii) Nel caso f 0, g > 0, la funzione d onda di un autostato dell energia, prende la seguente forma nelle tre regioni (x < 0); (0 < x < a); 3 (x > a) m E A i e κ x + B i e κ x, κ = () (i =,, 3). Elencare tutte le relazioni o le condizioni per i coefficenti A i e B i. 3
4 -a 0 a x Figura : (iii) Trovare l equazione che determina implicitamente il livello (o i livelli) di energia, come condizione di esistenza di una soluzione non banale di {A i, B i } (iv) Analizzando tale equazione, dimostrare che per f sufficientemente piccolo, esiste un unico stato legato. Determinare approssimativamente l energia di questo stato. (Opzionale) Dimostrare che, se m g a <, per f positivo e sufficientemente grande non esiste alcun stato legato. 3.5 Buca asimmetrica Una particella di massa m si muove in un potenziale unidimensionale (V 0 > 0), x < 0, V (x) = 0 0 x a, V 0 x > a. () (i) Qual è la condizione per cui il sistema ha un solo stato legato? (ii) Determinare approssimativamente la funzione d onda e l energia dello stato fondamentale, nel limite di grande V 0. (iii) Supponiamo che una particella sia confinata nella buca di cui al punto ii), e si trovi nello stato fondamentale. All istante t = 0, il potenziale viene istantaneamente modificato ed acquista la forma x < 0, 0 0 x a, V (x) = V 0 a < x a, 0 x > a. Qual è la probabilità per unità di tempo che la particella scappi dal legame, i.e. che essa appaia come particella libera al di fuori della barriera, x > a? Suggerimento: paragonare i risultati per A /B ottenuti dalla condizione di continuità a x = 0 e a x = a. (3) 4
5 4 Problemi per Capitolo 4 4. Oscillatore Una particella di massa m si muove su una retta sotto l azione di una forza elastica con costante di richiamo κ. Al tempo t = 0, mentre la particella si trova nello stato fondamentale, il centro di richiamo viene istantaneamente spostato di un tratto x 0. (i) Calcolare il valore medio dell energia al tempo t > 0 generico; (ii) Calcolare la probabilità che il sistema si trovi per t > 0 nello stato fondamentale e nel primo stato eccitato della nuova Hamiltoniana. (iii) Calcolare le eventuali discontinuità a t = 0, per i valori medi degli operatori di Heisenberg, x H, p H, ẋ H e ṗ H. 5 Problemi per Capitolo 5 5. Spin in campo magnetico Una particella di spin S è sottoposta ad un campo magnetico esterno costante. L Hamiltoniana è H = µ B = β S z. (4) Supponiamo che all istante t = 0 lo spin sia orientato nella direzione i.e., Si vuole studiare l evoluzione temporale del sistema. (i) Calcolare i valori medi all istante t = 0. n = (sin θ cos φ, sin θ sin φ, cos θ), (5) S n 0 = S 0. (6) S x, S y, S z, (7) Per il calcolo, conviene considerare un sistema equivalente, composto da N = S particelle di spin, tutti nella stessa direzione a t = 0, n. E considerare l operatore S come N S = s i. (8) (ii) [Opzionale] Quali sono le probabilità, se si facesse una misura di S z a t = 0, di trovare i vari valori di S z? (Anche in questo problema, è utile considerare il sistema equivalente di cui al punto (i).) (iii) Si considerino gli operatori di Heisenberg, i= S (H) x (t), S (H) y (t), S (H) z (t). (9) Scrivere le equazioni di Heisenberg e risolverle. Utilizzando questo risultato, determinare t S x t, t S y t, t S z t, (0) dove t è la funzione d onda all istante t generico; S x, etc. Schrödinger. Dire qual è il valore minimo di t, per il quale riprende il valore iniziale. sono operatori di 0 S x 0 () 5
6 5. Oscillatore in campo magnetico Un oscillatore tridimensionale di massa m, carica elettrica q e di spin è sottoposto ad un campo magnetico esterno debole, omogeneo e statico, (0, 0, B). L Hamiltoniana è data da: H = (p q c A) m + m ω r µ B, µ = g s = g σ. () (i) Considerando prima il caso senza il campo magnetico (B = 0; A = 0), dire quali sono i livelli energetici, qual è la degenerazione di ciascun livello, e dare i valori possibili del momento angolare orbitale e del momento angolare totale. Rispondere solo per i primi tre livelli energetici. (ii) Considerate ora il caso con il campo magnetico non nullo, descritto dal potenziale vettore, A = ( B y, B x, 0). (3) Nell approssimazione in cui i termini quadratici in B sono trascurati (campo debole), dire quali sono gli operatori conservati. (iii) Sfruttando i risultati dei punti (i) e (ii), trovare gli autovalori esatti dell energia (sempre nell approssimazione di campo debole), per i livelli corrispondenti al primo livello eccitato del punto (i). 5.3 Moto in campo elettrico costante Una particella di massa m e carica q è soggetta all azione di un campo elettrico omogeneo e costante, diretto lungo l asse z, E = E 0 ẑ. (i) Scrivere le equazioni del moto di Heisenserg per la posizione r(t) e l impulso p(t); (ii) Risolvere le suddette equazioni di moto; (iii) Trovare gli operatori delle varie componenti del momento angolare L(t) al generico tempo t, usando le r(t) e p(t) del punto ii); (iv) Verificare che L(t), trovato al punto iii), è compatibile con le equazioni di moto di Heisenberg per L(t); (v) Calcolare i valori medi delle varie componenti del momento angolare al generico tempo t, sapendo che 5.4 Oscillatore e spin r t=0 = 0, p t=0 = p 0ˆx, L t=0 = 0. (4) Una particella di massa m e spin è descritta dall Hamiltoniana H = p m + V (x), V (x) = σ 3 + m ω x. (5) 4 (i) Qual è lo spettro dell energia e quali sono le autofunzioni dell energia? (ii) All istante t = 0, il sistema è descritto dalla funzione d onda (s z =, etc.) ψ(0, x) = ψ 0 (x), (6) 6
7 dove ψ 0 (x) è la funzione d onda dello stato fondamentale dell oscillatore armonico senza lo spin, H 0 = p m + mω x : ( mω ) /4 ψ 0 (x) = e mω x. (7) π Dire se lo stato (6) è un autostato dell Hamiltoniana H. Se lo è, qual è l autovalore? Altrimenti, determinare il valor medio dell energia H nello stato (6). (iii) Determinare la funzione d onda a tempo t. All istante t si misura la componente z dello spin, s z = σ 3, con un apparecchio à la Stern-Gerlach situato in x = 0. Calcolare la probabilità di trovare il risultato s z =. N.B.: La funzione d onda calcolata a x = 0, ψ(0, t), vista come funzione d onda di spin, non è normalizzata. Ri-normalizzare ψ(0, t) di modo che sia normalizzata come funzione d onda di spin. Potete usare la formula (Re(A) > 0). dz e A z +B z = 5.5 Decadimento e parità B A (z dz e A ) + B π 4 A = A e B 4 A (8) Una particella di spin J = e parità incognita decade a riposo in due particelle identiche di spin. (i) Determinare il momento angolare orbitale relativo delle due particelle finali e lo spin totale. (ii) Assumendo che il decadimento conservi la parità, determinare la parità della particella iniziale. (iii) Il sistema iniziale è nello stato di spin J, J z =, 0. Scrivere esplicitamente la funzione d onda in termini della funzione d onda radiale (incognita), delle armoniche sferiche del moto relativo, e delle funzioni d onda di spin delle due particelle finali. Si fanno una serie di misure dello spin delle due particelle finali con apparecchi à la Stern-Gerlach posti nelle direzioni (θ, φ) e (π θ, φ + π). (iv) Considerando le variabili (r, θ, φ) come parametri fissati, trovare la funzione d onda di spin normalizzata, associata alle particelle emesse nelle direzioni (θ, φ) e (π θ, φ + π). (v) Calcolare la probabilità che una particella venga emessa in direzione (θ, φ) con s z =. (vi) Calcolare la probabilità che la misura contemporanea di (s y (), s y ()) dia il risultato (, ). 6 Problemi per Capitolo 6 6. Interazione spin orbita Si consideri l Hamiltoniana dell atomo di un atomo di idrogeno, contenente, oltre all interazione Coulombiana, un interazione spin-orbita dell elettrone, H S O = A L s e, (9) 7
8 e l interazione fra lo spin dell elettrone e lo spin del protone (s e = s p = ), con A, B costanti. H S S = B s p s e, (30) (i) Dire qual è la degenerazione dei livelli n = e n =, tenendo conto anche dello spin dell elettrone e del protone, quando si trascurano del tutto le interazionni H S O e H S S di cui sopra. (ii) Trascurando, invece, solo l interazione H S S, si classifichino i livelli di n = e n = dell atomo mediante gli operatori: L, J, F, F z, (J = L + s e, F = J + s p ) (3) e si calcolino i relativi autovalori dell energia. (iii) Alcuni degli stati di cui al punto (ii) sono anche autostati dell Hamiltoniana totale. Dire quali e con quali autovalori. 6. Deutone Il deutone d è un nucleo di carica + (composto da un protone (p) e da un neutrone (n)), e ha spin parità +, J P = +. Il pione π di carica (di spin 0) e il deutone, possono formare una sorta di atomo di deuterio (il deuterio normale è un atomo di idrogeno con un deutone al posto del protone come nucleo). Supponiamo che tale sistema si formi, nell orbita più bassa di Bohr, per un breve intervallo di tempo. (Fig. 3). e π r r d p (a) (b) Figura 3: Il sistema considerato nel problema (Fig. (a)) e l atomo di idrogeno (Fig. (b)). Le grandezze non sono proporzionali. (i) Determinare il rapporto tra il raggio di Bohr di questo sistema, r B, e il raggio di Bohr standard (dell atomo di idrogeno); determinare l energia di legame di questo sistema. La massa del pione è di circa 39.6 MeV/c, quella dell elettrone circa 0.5 MeV/c, mentre la massa del deutone e la massa del protone sono rispettivamente MeV/c e MeV/c. (ii) A causa delle interazioni elettromagnetiche e forti, questo sistema non è stabile ma decade secondo la reazione π + d n + n. (3) 8
9 Nel sistema finale si hanno due neutroni (di spin /). Nel processo (3) sia il momento angolare totale che la parità sono conservati. Dalla conservazione di queste quantità nel sistema di riposo del centro di massa delle due particelle, e tenendo conto della statistica di Fermi-Dirac, determinare la parità intrinseca del pione π. (iii) Calcolare la distribuzione angolare dei due neutroni nel sistema di riferimento del centro di massa, sapendo che lo stato iniziale era nello stato J z = 0. Osservazione: È interessante chiedersi perché l atomo di idrogeno non decade tramite il processo un po analogo (permesso dalle cariche e dalle note leggi delle initerazioni elettrodeboli) e + p n + ν, (33) dove ν è il neutrino. L unico motivo per cui questo processo non avviene (e di conseguenza l atomo di idrogeno è stabile) è la conservazione dell energia relativistica. Dalle masse delle particelle coinvolte, m e 0.5 MeV, m p MeV, m n MeV, (m ν < O(eV) è ignoto ma comunque non negativo), segue che questo processo, partendo dallo stato legato (in cui l energia totale di riposo è minore della somma (m e + m p ) c, appunto di e r B ) è proibito cinematicamente. 6.3 Effetto Mössbauer Un nucleo atomico in uno stato eccitato (con energia di eccitazione G) emette un fotone e compie una transizione allo stato fondamentale. (i) Supponendo che il nucleo abbia massa infinita, si determini l energia del fotone emesso, E γ. (ii) Supponiamo che il nucleo, libero, di massa M, sia a riposo prima dell emissione del fotone. Tenendo conto del rinculo del nucleo, si determini approssimativamente l energia del fotone E γ (i.e., al primo ordine in O(G/Mc )). Si assuma Mc G. (iii) Supponiamo che, invece, il nucleo (sempre di massa M) sia legato ad un centro (fisso) di forza attrattiva. L Hamiltoniana è H = p M + M ω r (34) dove r è la posizione del centro di massa del nucleo. Il nucleo si trova inizialmente nello stato fondamentale ψ (0) della (34), mentre lo stato eccitato interno è come nei punti (i) e (ii). Quali sono i valori possibili per l energia del fotone emesso in questo caso? (iv) Giustificare un approssimazione secondo la quale lo stato finale del nucleo (sempre nello stato fondamentale del sistema interno) è dato da e i k z ψ (0), dopo l emissione di un fotone di impulso p = (0, 0, k ). Si chiede la formula per le probabilità P (E γ ) per i vari valori di E γ di cui al punto (iii). Opzionale: Calcolate esplicitamente P (E γ ) facendo uso degli operatori di creazione e di distruzione. 8 Problemi per Cap Effetto Zeeman Un atomo di idrogeno è in uno stato con n =. 9
10 (i) Dire quali sono l energia e la degenerazione degli stati di n =, tenendo conto anche dello spin dell elettrone (ma non del protone); (ii) Supponiamo che l Hamiltoniana sia modificata da un termine aggiuntivo del tipo spinorbita H = A L s, (35) dove A è una costante. Calcolare i livelli energetici, le degenerazioni e i numeri quantici conservati, corrispondenti agli stati del punto (i). (iii) Supponiamo, invece, che l atomo sia sottoposto ad un campo magnetico esterno debole, omogeneo e statico, B = (0, 0, B). È noto che l Hamiltoniana in questo caso è approssimativamente H = p m e r e (L + s) B (36) m c (effetto Zeeman). In quanti sottolivelli si divide il livello n =? Quali sono le energie, i numeri quantici e la degenerazione di ciascuno dei sottolivelli? (iv) Supponiamo che l atomo di idrogeno, senza il campo esterno, e senza l interazione (35), si trovi inizialmente nello stato, n =, (J, J z ) = (, ) e di parità negativa.3 All istante t = 0, si accende il campo magnetico di cui al punto (iii). Dire quali sono i valori possibili di (J, J z ) all istante t e calcolarne le relative probabilità. 8. Livelli di Landau Un elettrone, considerato qui come una particella carica (carica -e) e senza spin, si muove in un piano x y, in un campo magnetico costante e uniforme in direzione perpendicolare al piano, H = (0, 0, B). (i) Studiate lo spettro del sistema, assumendo come potenziale vettore (ii) Analizzate lo stesso sistema nella gauge simmetrica 9 Problemi per Cap Oscillatore Si consideri l Hamiltoniana H = H 0 + H, dove g è un parametro reale, g <. A = ( B y, 0, 0). (37) A = ( B y, B x, 0). (38) H = p m + m ω x, H = g ω ( x p + p x ) : (39) (i) Si calcoli esattamente lo spettro di H (Suggerimento: si scelga un appropriata trasformazione unitaria, o un semplice cambiamento delle variabili, per es. del tipo, p p + cost.x, x x). Facoltativo: confrontare il risultato quantistico con il caso classico. (ii) Trattando poi H come perturbazione rispetto a H 0, calcolare lo spostamento dei livelli energetici fino al secondo ordine in g. Confrontare questo risultato approssimato con quello esatto, discutendo quando ha senso trattare H come perturbazione. 3 Considerare la parità instrinseca dell elettrone positiva. 0
11 9. Oscillatore anarmonico Si valuti, usando il metodo variazionale, il livello fondamentale e il primo livello eccitato dell oscillatore anarmonico H = p m + α x4, α > 0. (40) (i) Per il livello fondamentale, si usi come funzione di prova ( σ ) /4 ψ 0 (x) = e σ x /4 π e si determini il parametro σ, minimizzando il valor medio dell energia sulla (4) al variare di σ. (ii) Per il primo livello eccitato procedere come prima, utilizzando però come funzione di prova ( ) σ 3 /4 ψ (x) = x e σ x /4. (4) π (iii) Fornire un criterio in base al quale la funzione d onda (4) è adatta al calcolo variazionale del fondamentale, mentre la (4) può descrivere il primo stato eccitato. Formula utile: dove ψ 0 (x) è la funzione d onda (4). dx x n ψ 0 (x) = (4) ( n)! n! n σ n, (43) 0 Problemi per Cap Interferenza gravitazionale Consideriamo un interferometro di neutrone, schematicamente mostrato nella figura Fig. 4. L Hamiltoniana per descrivere il moto del neutrone è H = p x + p z M + M g z, (44) dove M è la massa del neutrone, g = 980 cm/sec, ˆx la direzione orizzontale (che coincide con la direzione incidente) e ẑ la direzione verticale. Supponiamo che all inizio il piano BCED sia verticale (contiene l asse ẑ) mentre ABD coincida con l asse x. (i) Dire qual è la lunghezza d onda di de Broglie (λ) del neutrone incidente, in termini dell impulso incidente p (E = p M ). (ii) Assumendo p M M g z, determinare la differenza della fase Φ della funzione d onda corrispondente al cammino ABCEF e al cammino ABDEF, in termini di (λ, g, h 0, L,, M). (iii) Determinare la condizione per cui si ha massima interferenza; (iv) L apparato contenente il piano BCED è ruotato di un angolo φ attorno all asse incidente x, ABD. Quando φ varia, l intensità dei neutroni in arrivo al contatore F, I, varia con φ, mostrando dei massimi e dei minimi. Dire quanti massimi appaiono quando φ varia da 0 a π. Il neutrone incidente ha velocià v = 3 05 cm/sec, si consideri h 0 L = 0 cm. Ricordiamo che M = gr, = 0 7 erg sec.
12 C Ε F h h Α Β L D Figura 4: Interferometro del neutrone N.B. Questa interferenza dovuta alla fase gravitazionale è stata osservata da Colella, Overhauser e Werner (vedi Phys. Rev. Lett. (975) 47). La caduta gravitazionale del neutrone e la conseguente deviazione della traiettoria dalla retta durante i tragitti può essere trascurata per la considerazione dell interferenza.
13 Soluzioni [] Soluzioni per Capitolo.. Sistema a 3 stati (i) H = H 0 + H = E 0 Diagonalizzandola, si ottengono gli autovalori di H: con rispettivi autostati, = ɛ (45) E 0 ɛ, E 0, E 0 + ɛ (46) = + + 3, = 0 3 =, (47) 3 = = + 3. (48) (ii) I livelli non degeneri devono essere anche autostati di Π, con autovalori, ±. Infatti, lo stato fondamentale e il secondo stato eccitato sono pari rispetto a Π mentre il primo stato eccitato è dispari. (iii) (iv) = = + + 3, = 3 = 0 = 3, (49) = + 3. (50) ψ(t) = e ie0t/ eiɛt/ + + e iɛt/ 3 [ e iɛt/ ( ) + ( 3 ) 4 + e iɛt/ ( + 3 ) ] = e ie0t/ = e ie0t/ [( + cos ɛt ) + i sin ɛt ɛt + ( + cos ) 3. (5) 3
14 Un esempio fisico di un sistema del genere potrebbe essere un elettrone che si muove in un potenziale unidimensionale a tripla buca (Fig. 5). - un elettrone in una molecola triatomica lineare. Se le barriere tra e, e tra e 3 fossero infinitamente alte, lo stato fondamentale sarebbe tre volte degenere, con le funzioni d onda localizzate rispettivamente attorno a x, x e x 3, con l energia E 0, i.e., H 0 i = E 0 i, i =,, 3. (5) Tuttavia c è un ampiezza non nulla per penetrazione via l effetto tunnel tra due buche adiacenti. Questo sistema si riduce al modello considerato sopra. La probabilità (P i ) che l elettrone, inizialmente (a t = 0) localizzato all atomo, si trovi all istante t localizzato attorno agli atomi i =,, 3, sono ɛt ( + cos P = 4 ) ; P = sin ɛt ; ɛt P ( cos 3 = 4 ). (53) 3 Figura 5: Un potenziale a tripla-buca: i minimi sono a x, x e x 3. Figura 6: Grafici di P i.. Sistema a stati (i) No. Se η fosse complesso H non sarebbe Hermitiano. Si noti che non è possibile rendere reali gli elementi non diagonali con una ridefinizione dei vettori di base, poiché l elemento di matrice () e quello () acquisterebbero fasi opposte. Un altra nota ancora: gli autovalori di energia sarebbero complessi, con η complesso. (ii) Supponendo che η > 0, = + ; E = E 0 η, (54) 4
15 Figura 7: è lo stato fondamentale; è lo stato eccitato. + = ; E + = E 0 + η, (55) (iii) L inverso di = ; =. (56) ψ(0) = = + i i ( + ) = ( + i) + ( i) + ψ(t) = ( + i) e ie t/ + ( i) e ie+t/ + = e ie0t/ ( + i) eiηt/ + ( i) e iηt/ + = e ie0t/ ( + i) eiηt/ ( + ) + ( i) e iηt/ ( ) η t ie0t/ (cos = e sin η t η t ) + i (cos + sin η t ) (57) Perciò (Fig. 7) P (t) = (cos η t sin η t ) = sin η t P (t) = (cos η t + sin η t ) = + sin η t ; (58). (59).3.3 Sistema a 3 stati, autostati e autovalori (i) Gli autovalori di A sono ±a e 0. Gli autostati sono A : a = 0, A : a = 0 i i, A : 0 = 0 0, (60) 5
16 (ii) Gli autovalori di B = b b 0 b 0, (6) sono b, b e b, con autostati B : b, = 0, B : b, = 0, B : b = 0. 0 (iii) All istante t = 0 lo stato è A : a = 0 i = [ B : b, + i B : b, B : b ] (6) La probabilità che la misura di B in questo stato dia l autovalore massimo (b) è uguale alla somma delle probabilità che il sistema si trovi o in B : b, o in B : b, : Per completezza, la probabilità che la misura dia b è 4. (iv) Sì, perché lo stato a t generico è ψ(t) = P rimane uguale, e iet/ 0 i e ie3t/ [3] Soluzioni per Capitolo Particella fra pareti P = + 4 = 3 4. (63) = [ e iet/ ie3t/ B : b, B : b B : b, +i e ] : (64) P = + 4 = 3 4. (65) (i) La pressione è per definizione la forza (per unità di area) che la particella esercita sulla parete. Per comprimere la scatola di δa, occore un lavoro P δa. Questo è uguale alla variazione di energia, perciò (ii) La funzione d onda è inizialmente π m (a δa) π m a = π P = P (a) = π ψ = θ(x) θ(a x) m a 3 δa + O((δa) ), (66) m a 3. (67) a sin πx a, (68) Dopo l allargamento istantaneo della buca, rimane la stessa, ma non è più un autostato dell energia. La probablità che la particella si trovi in vari stati di energia definita 6
17 è P n = n ψ = a = a a = Visto che si ha 0 a dx cos ( n ) π x a dx sin π n x a sin π x cos ( n + ) π x a a a [ a π( n ) sin (n )π x a a π( n + ) sin (n + )π x a a ], per n =, P n = 0 per n = l, l =, 3, 4,..., 3 π (4 l 4l 3) per n = l, l =,, 3,.... l= 0 (69) (4 l 4l 3) = π 64, (70) P n =. (7) n= (iii) Nel caso adiabatico, non avvengono transizioni quantistiche: il sisitema resta nello stato fondamentale. Lo stato finale è πx ψ = θ(x) θ(a x) sin a a, (7) l energia decresce lentamente da π m a a π 8 m a. Il lavoro fatto dalla particella è: che è uguale a come ci si aspetta. π m a π 8 m a = 3 π 8 m a. (73) P dv = a a P (a) da, (74). 3. Potenziale a delta (i) La funzione d onda ha la forma ψ(x) = { A e κ x, x < 0, B e κ x + C e κ x, x > a. (75) dove κ = me/ > 0. La condizione di continuità a x = 0 è la condizione di continuità sulla derivata prima a x = 0 è B + C = A, (76) cioè, ψ + ψ = m g ψ(0), (77) B C = ( m g ) A. (78) κ 7
18 Combinando queste due si trova La condizione a x = a è B = ( m g κ ) A; C = m g A. (79) κ Sostituendo B e C dalla (79), si ha ψ(a) = B e κ a + C e κ a = 0. (80) e κ a = κ m g, (8) per avere una soluzione con A 0. Dai grafici delle curve y = e a x e y = x m g (Fig. 8) si vede che per m g < a esiste una soluzione della (8) con κ > 0, mentre per m g a l unica soluzione è κ = 0, che non corrisponde ad uno stato legato. La (8) può essere scritta alternativamente come: ξ ( + coth ξ) = m g a, ξ κ a, (8) da cui segue ugualmente la condizione m g a > per l esistenza di una soluzione non banale per κ > 0. (ii) Nel limite a, e κ a, perciò la soluzione è che è il ben noto risultato per una singola buca delta. (iii) Non esistono degenerazioni. κ = m g, (83) Per vedere questo fatto, osserviamo che la funzione d onda ha la forma (con k 0) A e i k x + B e i k x, x < 0, ψ(x) = C e i k x + D e i k x, 0 < x < a, (84) 0 x a. La condizione a x = a (ψ = 0) fissa la relazione tra C e D; le condizioni a x = 0 determinano A e B in termini di C, per cui per ogni k la soluzione è unica a parte la normalizzazione Figura 8: 8
19 Potenziale a delta e pareti (i) ψ (x) = A sin k (x + a); ψ + (x) = B sin k (x a). (85) (ii) La condizione sulla funzione d onda è: la condizione sulla derivata è: i.e., A sin ka = B sin ka; (86) ψ +(0) ψ (0) = m g A sin ka, (87) k [ B cos ka A cos ka ] = m g A sin ka. (88) Dalla prima condizione (86) segue che Una possibilità è sin ka = 0, sin ka (A + B cos ka) = 0. (89) k = π n a, E n = π n, n =,,.... (90) m a I coefficienti A, B sono determinati dalla condizione (88): (iii) Un altra possibilità che segue dalla (89) è B cos ka A cos ka = 0, B = ( ) n A. (9) A + B cos ka = 0, A = B cos ka. (9) Sostituendo questa relazione nella (88), si ha o definendo ξ k a, k cos ka + k cos ka = 4 m g cos ka sin ka, (93) ξ ( cos ξ + ) = Λ sin ξ, (vedi Fig.9). Dai grafici delle curve, Λ = 4 m g a > 0. (94) η = ξ ( cos ξ + ), η = Λ sin ξ, (95) si vede facilmente che il primo stato di questo gruppo corrisponde ad un valore di ξ = k a che sta nella regione π 3 < ξ < π, π 3 a < k < π a. (96) Paragonando questo con la (90), si vede che l intervallo (96) dà lo stato fondamentale, mentre lo stato più basso del gruppo (90) con n = è il primo stato eccitato del sistema. Nei due limit, g 0 e g, anche Λ tende a zero o a. A Λ 0, dal grafico si vede che la prima intersezione si avvicina al primo zero della curva η = ξ ( cos ξ + ) (cioè π 3 ), mentre a Λ essa si avvicina al primo zero della sin ξ, π. Di conseguenza k tende a π 3a e a π a, nei due limiti. 9
20 Figura 9: Potenziale con delta (i) (ii) E = mg ; ψ = κ [ θ(a x) e κ(x a) + θ(x a) e κ(x a) ], κ = mg. (97) ψ(x) = A e κ x θ( x)+[a e κx +B e κx ] θ(x) θ(a x)+b 3 e κx θ(x a) (98) A 3 = 0, B = 0, (99) A = A + B, (00) A e κa + B e κa = B 3 e κa (0) dalla continuità della funzione d onda e dalla normalizzabilità. Le condizioni sulla discontinuità corrispondenti ai potenziali delta sono: κ ( A + (A B )) = mf A ; (0) κ [ B 3 e κa + A e κa B e κa ] = mg B 3 e κa. (03) Ci sono quattro equazioni per quattro incognite, ma visto che le equazioni sono omogenee in A, A, B, B 3, M A A B B 3 = 0, (04) queste danno soluzioni non banali solo se i coefficienti soddisfano la condizione det M = 0. (05) 0
21 (iii) Invece di scrivere M e calcolare direttamente det M, conviene risolvere per A, B dalle eq. (00) e eq. (0), e per A e κa, B e κa dalle eq. (0) e eq. (03): A = ( + mf κ ) A ; B = mf κ A ; (06) A e κa = mg κ B 3 e κa ; Eliminando A i e B i, si ha B e κa = ( mg κ ) B 3 e κa. (07) oppure Ponendo κ m g x, la condizione è [ + mf κ ] [ mg κ ] eκa = mf κ mg κ (08) [ κ mg + f g ] [ κ mg ] eκa = f g. (09) (x + f g ) (x ) = f g e A x, A = m g a. (0) Si chiede se ci sono soluzioni con x > 0. Per f = 0, si ritrova la nota soluzione per una singola buca delta, x =, κ = m g. () Per f = g (doppia buca delta simmetrica) la condizione si riduce a come è noto. mg κ = ± mg κ e κa, () Per f sufficientemente piccolo, la soluzione è unica ed è approssimativamente x f g e A, κ = m g ( f g e A ). (3) E m g + m f g e m g a. (4) Dai grafici dei due membri della (0) segue che se la derivata prima del primo membro a x = 0 è più grande della derivata prima del secondo membro, i.e., se A = m g a < e per f g > f A, (5) g f > la (0) non ha alcuna soluzione. (Vedi Fig. 0). g m g a (6)
22 Figura 0: I due membri della (0) Buca asimmetrica (i) Nella regione interna della buca, mentre al di fuori ψ = A sin kx, k = me ; (7) ψ = Be κ x, κ = La condizione di continuità in a è Oppure, definendo ξ = k a; η = κ a, m(v0 E). (8) κ = k cot ka. (9) η = ξ cot ξ; ξ + η = mv 0a. (0) Risolvendo col metodo grafico, la condizione richiesta è π < mv0 a 3π. () (ii) Nel limite di grande V 0 ψ A sin kx, k = π n a,... E = π ma, ψ(0) (x) = a sin π x a. () (iii) Applicando il risultato del calcolo della penetrazione di barriera quadratica (Eq.(5.4)) si ha la probabilità di tunnelling, 4k 6 k D κ sinh κ a κ e κ a, k = π a, κ mv0. (3) Per la probabilità di decadimento per unità di intervallo di tempo dobbiamo moltiplicare questa probablità con la probabilità che la particella arrivi alla barriera di destra (x = a) in un intervallo unitario del tempo. Quest ultimo è dato da Notiamo anche che ψ (0) (x) = v a = k ma. (4) a sin π x a = e ika e ika a i (5)
23 per cui in accordo con la (4). Perciò j = v a = k ma, (6) P = j x>a = j D 4k3 3 m V 0 a e κ a = 4π3 3 3 [4] Soluzioni per Capitolo Oscillatore m V 0 a 4 e mv 0/ a. (7) (i) Il valor medio dell energia è una costante del moto, perciò basta calcolarlo al tempo t = 0 + : per t < 0 H = H 0 = p m + κ m ω x, ω = m ; (8) per t > 0, quindi H = p m + m ω (x x 0 ) = H 0 m ω x 0 x + m ω x 0, (9) H = ψ 0 H 0 m ω x 0 x + m ω x 0 ψ 0 = ω + m ω x 0. (30) poiché la funzione d onda a t = 0 + è quella dello stato fondamentale di H 0. (ii) Osserviamo che le probabilità richieste non dipendono dal tempo, essendo H costante del moto per t > 0. Infatti, esprimendo la funzione d onda a t = 0 + come ψ(x, 0) = a n ψ (n) (x), (3) k=0 dove ψ (n) (x) sono autostati di H, la funzione d onda per t generico è ψ(x, 0) = a n e i En t/ ψ (n) (x), (3) k=0 perciò le probabilità di trovare il sistema in uno degli autostati di H sono P n = a n e i En t/ = a n (33) e sono indipendenti dal tempo. Per calcolare a n = ψ (n) ψ 0 basta ricordare che a t = 0 la funzione d onda è data da: ( m ω ) /4 ψ(x, 0) = ψ 0 (x) = e m ω x ; (34) π mentre gli stati stazionari di H sono ψ () (x) = i ψ (0) (x) = ( m ω π ( m ω ) /4 e m ω (x x0) ; (35) π ) ( ) /4 / m ω e m ω (x x0) ; (36) 3
24 a 0 = a = dx ψ (0) (x) ψ(x, 0), (37) dx ψ () (x) ψ(x, 0). (38) Il calcolo è elementare, il risultato è P 0 = a 0 = e m ω x 0 ; (39) P = a = m ω x 0 e m ω x 0. (40) È interessante fare il calcolo di a n facendo uso degli operatori di creazione e di annichilazione. Siano a, a gli operatori definiti rispetto a H 0 in maniera standard, e ã, ã gli operatori corrispondenti a H: a = a = m ω x + i p; m ω m ω x i p, (4) m ω ã = ã = m ω (x x 0) + i p; m ω m ω (x x 0) i p. (4) m ω Evidentemente ã = a C, ã = a C, C = Ora scriviamo lo sviluppo (3) in notazione di Dirac, m ω x 0. (43) 0 = n a n n, (44) dove ã n = n n, n =,,..., (45) visto che n è l n-simo autostato di H. La condizione che 0 sia lo stato fondamentale di H 0 è a 0 = 0, [ ã + C ] n a n n = 0, (46) dal quale si ottengono (facendo uso di (45) ) delle relazioni di ricorrenza Dalla condizione di normalizzazione a n = ( C) n a n =... = ( C)n n! a 0. (47) = n a n = a 0 e C,... a 0 = e C. (48) 4
25 Si trova dunque che la probabilità di trovare il sistema nell n -simo stato della nuova Hamiltoniana è P n = a n = C n e C (49) n! che è una distribuzione Poissoniana. Per n = 0 e n = ovviamente il risultato è in accordo con quanto trovato prima, ma questo metodo è più adatto per calcolare le probabilità P n per n generico. (iii) I valor medi di x e di p non subiscono discontinuità, a causa dell accensione della perturbazione. Infatti la funzione d onda è uguale a t = 0 e a t = 0 +. Analogamente per d dtx che è uguale a p/m. Invece è discontinua a causa del cambiamento di V (x), d dt p = V (x), (50) x x V (x) = m ω x, t = 0 ; (5) x V (x) = m ω (x x 0 ), t = 0 +. (5) La dicontinuità richiesta è 4 [5] Soluzioni per Capitolo Spin in campo magnetico d dt p = m ω x 0. (53) (i) Consideriamo prima la funzione d onda di uno spin, nella direzione n: n = ( e iφ/ cos θ/ e iφ/ sin θ/ ). (54) Lo stato in questione, di spin S = N/ nella direzione n, può essere costruito da N particelle di spin paralleli: 0 = ( e iφ/ cos θ/ e iφ/ sin θ/ Il valor medio di S x = N i ) s i x è ( e iφ/ cos θ/ e iφ/ sin θ/ ) ( e iφ/ cos θ/ e iφ/ sin θ/ ) N. (55) S x = N n s x n = N (eiφ cos θ sin θ + e iφ cos θ sin θ ) = S cos φ sin θ. (56) Analogamente, (ii) Scrivendo la (55) come S y = S sin φ sin θ, S z = S cos θ. (57) 0 = (e iφ/ cos θ + e iφ/ sin θ ) (e iφ/ θ N + e iφ/ sin θ N) = N k= N c k S, S z = k (58) 5
26 S, S z = k è la combinazione simmetrica S, S z = k = ( N l ) / (59) dei termini con l spin up e N l spin down. Chiaramente, perciò e ( N c k = l La probabilità richiesta è ( N P k = l N k= N P k = N l=0 l N l = l N k = l N, = k, (60) l = N + k, (6) ) / (e iφ/ cos θ )l (e iφ/ sin θ )N l (6) ) (cos θ )l (sin θ )N l, l = N + k. (63) ( ) N (cos θ l )l (sin θ )N l = (cos θ + θ sin )N =. (64) (iii) S x (t) = e iht/ S x e iht/ = e i β Sz t/ S x e i β Sz t/, (65) etc. In particolare, S z (t) = S z (0) = S z. i d dt S x(t) = [S x, H] = β[s x, S z ] = i β S y ; (66) i d dt S y(t) = [S y, H] = β[s y, S z ] = i β S x ; (67) Prima di tutto si osserva che i d dt S z(t) = [S z, H] = 0. (68) S z (t) = S z (0) = S z. (69) S x = β S x, Sy = β S y ; (70) Queste si risolvono ponendo S x (t) = A cos β t + B sin β t. (7) Gli operatori A, B si determinano facendo uso della condizione al contorno a t = 0: S x (t) = S x cos β t + S y sin β t; (7) e analogamente, S y (t) = S y cos β t S x sin β t; (73) Allora t S x t = 0 S x (t) 0 = S( cos φ sin θ cos β t + sin φ sin θ sin β t) = S cos(φ β t) sin θ, (74) t S y t = 0 S y (t) 0 = S( sin φ sin θ cos β t cos φ sin θ sin β t) = S sin(φ β t) sin θ. (75) 6
27 4. 5. Oscillatore in campo magnetico (i) I livelli energetici dell oscillatore 3D sono E N = ω (N + 3 ), N = 0,,,.... (76) Si ha la degenerazione corrispondente ad un insieme di tre numeri interi non negativi (n, n, n 3 ) tali che N = n + n + n 3, n i = 0,,,... (77) oltre ad una doppia degenerazione di ogni livello dovuto allo spin. Il grado di degenerazione allora è data da, 6,, etc. ed in generale (N + )(N + ) per il livello N. Vista la parità del livello N, ( ) N, e la forma delle funzioni d onda, i possibili valori di L sono L = N, N,..., 0(). (78) Per i primi tre livelli,. N = 0, L = 0, J = ;. N =, L =, J = 3, ; 3. N =, L = e L = 0. Il momento angolare totale prende valori J = 5, 3,. (ii) In questa approssimazione, H = p m + m ω r e B m c L z g B σ z. (79) Gli operatori L, s, L z, s z e la parità commutano con l Hamiltoniana. (iii) Gli autostati di H sono gli stati di N, L z, s z definiti. Gli autovalori sono E N,Lz,s z = ω ( Moto in campo elettrico costante (i) + N) e B m c L z g B σ z. (80) H = p m q E 0z, (8) ṗ = i [H, p] = q E 0ẑ; (8) ṙ = i [H, r] = p m ; (83) (accellerazione costante.) r = q E 0 m ẑ (84) (ii) r(t) = r(0) + t m p(0) + q E 0 m t ẑ; (85) p(t) = p(0) + q E 0 t ẑ; (86) 7
28 (iii) L(t) = r(t) p(t): L z (t) = L z (0); (87) L x (t) = L x (0) + q E 0 t y(0) + q E 0 m t p y (0); (88) (iv) L y (t) = L y (0) q E 0 t x(0) q E 0 m t p x (0). (89) L = i [H, L], (90) L z (t) = 0, L z (t) = L z (0) (9) (costante del moto); L x (t) = q E 0 y(t), Ly (t) = q E 0 x(t); (9) t L x (t) = L x (0) + q E 0 dt y(t) = = L x (0) + q E 0 t y(0) + t L y (t) = L y (0) q E 0 dt x(t) = = L y (0) q E 0 t x(0) 0 0 q E 0 m t p y (0); (93) q E 0 m t p x (0). (94) v) L z (t) = 0, L x (t) = 0, L y (t) = Le condizioni iniziali erano: p 0 m q E 0 t (95) Oscillatore e spin r(0) = 0; p(0) = p 0 x; L(0) = 0. (96) (i) Visto che s z commuta con H possiamo prendere gli autostati di s z come base di autosati di H. Per gli stati di spin up, H descrive un oscillatore armonico H 0, con E n = ω (n + mω ), n = 0,,,..., ψ mωx n(x) = C n H n ( x) e ; (97) per stati di spin down, il systema descrive una particella libera H (free) = p m, per cui E p = p m, < p <, ψ p(x) = e i p x/. (98) π (ii) No, perché esso non è un autostato di s z. Il valor medio di H è ψ H ψ = [ ψ 0 H 0 ψ 0 + ψ 0 H (free) ψ 0 ] = (99) = [ ω + ψ 0 H 0 m ω x ψ 0 ] = [ ω + 4 ω ] = 3 8 ω. 8
29 (iii) La parte di spin up, essendo un autofunzione di H 0, evolve semplicemente ψ 0 (x) e ie0t/ ψ 0 (x), E 0 = ω. (00) L evoluzione della parte di spin down è ψ 0 (x) = Se scriviamo si ha, utilizzando la (8): dk a(k) e i k x ψ 0 = N e A x, N = a(k) = N π La funzione d onda a x = 0 al tempo t è Perciò dk a(k) e k t N π m = π A ψ(0, t) = N [e iωt/ dk a(k) e i k t m e i k x (0) ( mω ) /4 mω, A = π, (0) π A e k /4A. (03) dk e k /4A e i k t m = N + i ω t. (04) + i ω t ]. (05) La funzione d onda di spin normalizzata è + ω t ψ(0, t) = + + ω t [e iωt/ ]. (06) + i ω t la probabilità richiesta è P = + + ω t. (07) Decadimento e parità (i) S =, 0, l = 0,, (08) L unica combinazione consistente con la statistica di Fermi-Dirac (funzione d onda antisimmetrica) e con J = è S =, l =. (09) (ii) (iii) per cui P =. P = ( ) l (0) ψ = R(r) [ Y (θ, φ) χ, Y (θ, φ) χ, ] = R(r) i 3 8π [ sin θ eiφ + sin θ e iφ ] () 9
30 n L J F Energia Grad. Degener. (0) 0 0, E 4 (0) 0 0, E 4 0, E (0) A 4 3, E (0) + A 8 Tabella : (iv) ψ spin = [ e iφ + e iφ ] () v) / vi) L autostato con s y () = /, s y () = / è ψ = ( + i ) ( + i ) = ( + i + i ) (3) La probabilità richiesta è ψ ψ spin = sin φ (4) 5 [6] Soluzioni per Capitolo Interazione spin orbita (i) La degenerazione del livello n è 4 n, con energia (ii) (iii) E (0) n = m e4 n. (5) H S O = A L s e = A [ J L s e ] = A [ J(J +) L(L+) 3 ]. (6) 4 da cui segue il risultato in Tabella. H = H 0 + A L s e + B s p s e = H 0 + A [ J L s e ] + B [ S ] (7) Gli stati L, J, F, F z della Tabella. in generale non sono autostati di H totale, perché J non commuta con S, ma questo non esclude che lo siano alcuni di essi. Questo accade quando i valori di L e F determinano univocamente anche il valore di S, dove S = s e + s p ; F = L + S. (8) Dalla regola di composizione dei momenti angolari, si ha il risultato riportato nella Tabella. 30
31 n L J F S Energia Grad. Degener E (0) 3 B 4 0 E (0) + B E (0) 3 B 4 0 E (0) + B E (0) A + B 4 3 E (0) + A + B 4 5 Tabella : Deutone (i) µ = 9.9, L energia di legame è uguale a r B = m e r B µ = 0.5 = (9) 9.9 e r B = e r B r B r B = 3.6 = 3487 ev = 3.49 KeV. (0) (ii) Visto che l = 0, s π = 0, il momento angolare dello stato iniziale è. Gli stati possibili di momento angolare dello stato finale, permessi dalla statistica di Fermi-Dirac sono: (a) S = 0, L = 0,, 4,..., o (b) S =, L =, 3, 5,.... L unica combinazione compatibile con J tot = è [S =, L = ]. La parità dello stato finale è perciò, che deve essere uguale a P π ( ) 0 = P π () parità dello stato iniziale. La parità intrinseca di π è stata determinata storicamente così. (iii) Con J z = 0, lo stato iniziale è nello stato (J, J z ) = (, 0). In termini di stati di spin e del momento orbitale finale, ψ = (,,,, ) = [ Y, (θ, φ) χ, Y, (θ, φ) χ, ] La distribuzione angolare è () P dω = 3 8 π sin3 θ dθ dφ, (3) P dω =. (4) Effetto Mössbauer (i) E γ = G. (ii) Supponiamo che il fotone porti l impulso, p = k. Per rinculo, il nucleo acquista impulso, p = k. L energia cinetica del nucleo è allora k M, (5) e la conservazione di energia richiede (l energia del fotone essendo E γ = p c): k c + k M = G, (6) 3
32 oppure E γ E γ + = G. (7) M c Rislovendo approssimativamente questa equazione si trova che E γ G G M c +... (8) dove le correzioni di ordini più alti in G/Mc sono state trascurate. (iii) Per ipotesi il rinculo del centro di massa dell oscillatore è trascurabile. L unica maniera in cui l energia del fotone può essere diminuita è l eccitazione dell oscillatore, perciò G = E γ + E f E i, E γ = G ω N, N = 0,,,... (9) dove N è il livello di energia E osc = ω ( 3 + n + n + n 3 ) = ω ( 3 + N), (30) in cui si trova il nucleo dopo l emissione. (iv) e i kz è un operatore che trasla l impulso del nucleo di (0, 0, k ), che è l effetto della conservazione dell impulso. Perciò P N = ψ f e i k z ψ 0 = N e i k z 0, k c = G ω N. (3) Nel secondo termine l elemento di matrice si riferisce ad un oscillatore armonico unidimensionale H = p z M + M ω z. (3) Per calcolare l elemento di matrice, scriviamo N = 0 a N ; e i k z = e i C (a+a ) ; C = k N! M ω. (33) Facendo uso delle identità a e i C (a+a ) 0 = [a, e i C (a+a ) ] 0 = i C e i C (a+a ) 0, (34) a e i C (a+a ) 0 = i C a e i C (a+a ) 0 = (i C) e i C (a+a ) 0, (35) etc., si trova che N e i k z 0 = (i C)N 0 e i C (a+a ) (i C)N 0 = e C /. (36) N! N! Nell ultima uguaglianza è stata usata la formula di Haussdorff-Weyl (valida se [X, Y ] è proporzionale all operatore identità), La probabilità richiesta è dunque e X e Y = e X+Y + [X,Y ]. (37) P N = CN N! e C. (38) 3
33 6 [8] Soluzioni per Cap Effetto Zeeman (i) (ii) (iii) E = e 8 r B, d = 4 = 8. (39) L =, 0. In termini di stati di momento angolare totale, J = 3, (quattro stati), e due doppietti di J =. L s = J L s. (40) J, L, s commutano con H. Le degenerazione di ogni livello è dovuta a J z. I quattro stati di (J, L, s) = ( 3,, ) ha l energia E + A ; i due stati di (J, L, s) = (,, ) ha l energia E A; i due stati di (J, L, s) = (, 0, ) ha l energia E. H = e m c (L z + s z ) B. (4) Perciò in questo caso, i numeri quantici buoni sono L, L z, s e s z. L L z s z E (in unità di e B m c ) Tabella 3: Il livello n = si separa in cinque sottolivelli. Le energie sono (iv) E = E + e B m c E = E + e B m c (singolo), [L =, L z =, s z = ]; (doppio), [L =, L z = 0, s z = ] e [L = 0, L z = 0, s z = ]; E = E (doppio), [L =, L z =, s z = ] e [L =, L z =, s z = ]; E = E e B m c E = E e B m c (doppio), [L =, L z = 0, s z = ] e [L = 0, L z = 0, s z = ]; (singolo), [L =, L z =, s z = ]., = 3,, 0 3 t/, e i E 3, 0, (4) 3 33
34 nella seconda riga abbiamo trascurato la fase globale, e ie t/, e dal punto (iii). E = e B m c Riesprimendo (4) in termini di stati di momento angolare totale, si ha (43) = = 3 [ 3 3, + 3, ] e i e B t m c 3 [ 3 3, 3, ] 3 ( e i e B t 3 m c ), + ( e i e B t m c ),. (44) P 3, = 3 ( e i e B t m c ) = 8 e B t 9 sin 4 m c ; (45) P, = ( e i e B t m c ) = e B t (5 + 4 cos 9 m c ) = 8 e B t 9 sin 4 m c. (46) Livelli di Landau (i) L Hamiltoniana è H = (p + e c A) = (p x e B c y) + p y m m m. (47) Poiché H commuta con p x, è possibile costruire gli autosati di H ponendo ψ(y) soddisfa all equazione [ p y Ψ(x, y) = e i p x/ ψ(y). (48) m + ( eb c y p) ]ψ(y) = Eψ(y), (49) m che è l equazione di Schrödinger per un oscillatore armonico lineare, con la frequenza di Larmor ω = e B (50) m c e con il centro dell oscillatore a I livelli energetici sono y = p c e B. (5) E n = ω (n + ) : (5) e sono indipendenti da p. Questo significa che ogni livello n è infinitamente degenere, con valore di p compreso in < p <. La frequenza ω = e B m c corrisponde a quella di un moto circolare per un elettrone classico che entra nel campo magnetico uniforme B, d dt p = e v B. (53) c 34
35 (ii) L Hamiltoniana in questa gauge è H = (p + e c A) m = (p x e B c y) m Per semplificare la scrittura, poniamo = e B c + (py + e B c x). (54) m = m =. Allora H = ( i x y ) + ( i y + x ). (55) Un bel metodo per risolvere il problema è quello di introdurre le variabili complesse, z x + i y, z x i y, (56) Ovviamente, z = ( x i ), y z = ( x + i ). (57) y [z, z ] = [ z, z ] =, [ z, z ] = [z, z ] = 0. (58) ( z z, etc). Definiamo inoltre gli operatori di creazione e di distruzione, a ( z + z ), a ( 4 z + z ) : (59) 4 questi soddisfano alla solita regola di commutazione, [a, a ] =. (60) Un conto elementare dimostra che l Hamiltoniana è semplicemente (!) H = z z + 8 z z + z z z z = (a a + a a ) = a a +. (6) I livelli di Landau (5) seguono immediatamente da questa espressione. Per trovare le funzioni d onda e le degenerazioni, osserviamo che l equazione per lo stato fondamentale a ψ 0 = 0 (6) ha infinite soluzioni ψ 0, m = C m z m e 4 z z = C m (x iy) m e 4 (x +y ), m = 0,,,..., (63) tutte con E 0 = ω, distinte dall autovalore del momento angolare L = i (x y y x ), (64) L ψ 0, m = m ψ 0, m (la sola componente del momento angolare in un piano). L commuta con H. Infine, gli stati eccitati possono essere costruiti agendo a ripetutamente su ciascuna funzione ψ 0, m : ψ N, m = N! (a ) N ψ 0, m, m = 0,,,..., N = 0,,,.... (65) Nella gauge simmetrica l elettrone è localizzato sia in x che in y, mentre nella gauge, A = ( B y, 0, 0), esso è localizzato solo in y. Domanda: Qual è la gauge in cui l elettrone è localizzato attono ad un punto (x 0, y 0 )? 35
36 7 [9] Soluzioni per Cap Oscillatore Per eliminare il termine xp + px basta considerare la trasformazione unitaria p ˆp = p + γx; x ˆx = x, γ reale. (66) (Per un trattamento più generale vedi Nota.) Si noti che tale trasformazione conserva la relazione di commutazione canonica, ed è infatti generata dall operatore unitario, [x, ˆp] = [x, p] = i, (67) p ˆp = UpU ; x UxU, (68) con U = exp i(γ/ )x. (Alternativamente, la (66) può essere trattata come un semplice cambiamento delle variabili.) L Hamiltoniana si trasforma come i.e., H(x, p) Ĥ = UH(x, p)u = H(ˆx, ˆp) = H(x, p + γx), (69) (p + γx) Ĥ = m + m ω x + g ω (x(p + γx) + (p + γx)x) = p m + (g ω + γ m )(xp + px) + ( m ω + γ m + gωγ)x : (70) per risolvere il problema basta porre i.e., L Hamiltoniana diventa: Ĥ = g ω + γ m = 0 : (7) γ = gmω. (7) p m + m ω ( g )x. (73) Questa rappresenta un oscillatore armonico con la frequenza angolare ω = ω g, (74) (reale per g < ). Lo spettro esatto (che non dipende dalla rappresentazione) è dunque discreto, E n = g ω (n + ), n = 0,,,... ; (75) ogni livello è singolo. Si noti che per g > il sistema è instabile: non ci sono stati legati e lo spettro è continuo, < E <. Anche per g = lo spettro è continuo, ma in questo caso il sistema è equivalente ad una particella libera, perciò 0 E <. (Vedi Nota ). Confronto con il caso classico: Le equazioni canoniche per l Hamiltoniana classica H = p m + mω x + gωxp (76) 36
37 sono d dt x = H p = p + gωx (77) m d dt p = H x = mω x gωp, (78) da cui segue l equazione per un oscillatore armonico di pulsazione ω g d dt x + ω ( g )x = 0. (79) Per g > le soluzioni sono divergenti. Per g < H descrive un oscillatore armonico di pulsazione ω g. Per g = si ha l equazione di una particella libera. Questi risultati si ritrovano nel caso quantistico. Si noti che (sia nel caso classico sia in quello quantistico) il sistema non descrive un oscillatore armonico sottoposto ad una forza viscosa, come potrebbe far pensare il contributo proporzionale alla velocità nella espressione della forza F = V x = mω x gωp. (80) La forza viscosa, essendo non conservativa, non deriva da un potenziale Oscillatore anarmonico (i) Usando (ii) si ha x 4 0 = 3 x 0; p 0 = 4 x ; x 0 = σ, (8) 0 d E 0 dσ E 0 = 8m σ + 3α σ. (8) = 8m 6α σ 3 = 0,... σ = σ 0 = E 0 = 34/3 4 ( ) /3 48 m α (83) ( ) /3 α /3. (84) N.B. Per α = 5, m = =, si trova in questo modo E 0.65, da paragonare con il risultato esatto E 0 = ( %) m (iii) x 4 = x 6 0σ = 5 σ ; (85) p = ( ) dx dψ (86) dx ( ) dψ = σ ( + σ x 4 σx ) ψ0 (87) dx 4 p = σ ( + σ x σ x 0 ) = 3 4 σ. (88) E = 3 σ 4 m + 5 α σ. (89) 37
38 d E dσ = 3 8 m 30 α σ 3 = 0,... σ = σ = ( ) /3 80 m α (90) E = 9 ( ) /3 ( ) 4 5/3 α /3 / α /3. (9) m m N.B. Per α = 5, m = =, questo dà E 4.44, da paragonare con il risultato esatto E 0 = ( %) (iv) La (4) non ha nodi ed è pari; la (4) ha un nodo ed è dispari. 8 [0] Soluzioni per Cap Interferenza gravitazionale (i) λ = h p = π p. (ii) La funzione d onda del neutrone acquisterà fasi differenti lungo i cammini ABCEF e ABDEF, ciò non è dovuto alle diverse lunghezze dei percorsi (che sono identiche), ma alla della differenza della lunghezza d onda di de Broglie del neutrone. Infatti, a causa del potenziale gravitazionale, V = M g z, nei tratti orizzontali CE o BD il numero d onda (λ = π k ) è dato da M (E M g h) M E k CE = ; k BD = ; (9) (iii) la differenza è k = k k( M g h 0 E )/ M g h 0 k. (93) Questo induce la differenza di fase nella funzione d onda Φ = L k = M g h 0 L λ π (94) M g h 0 L λ π = π n, n = 0,,,.... (95) (iv ) Al variare di φ, l altezza del tragitto CE va da h 0 fino a h 0 cos π = 0. Usando la formula precedente, il numero di volte che i due percorsi danno le due componenti della funzione d onda in fase (interferenza massima e perciò l intensità massima) è N = M g h 0 L λ ( π) = M g (h 0 L) π v.7 98 π (96) 38
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Compitino 1 di Meccanica Quantistica I
 Compitino di Meccanica Quantistica I Facoltà di Scienze, M.F.N., Università degli Studi di Pisa, 5 dicembre 00 (A.A. 0/) (Tempo a disposizione: 3 ore ) Problema. Un sistema a due stati è caratterizzato
Compitino di Meccanica Quantistica I Facoltà di Scienze, M.F.N., Università degli Studi di Pisa, 5 dicembre 00 (A.A. 0/) (Tempo a disposizione: 3 ore ) Problema. Un sistema a due stati è caratterizzato
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. FISICA MODERNA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2013-2014 (1) Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2013-2014 (1) Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe ([email protected]) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe ([email protected]) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Lezioni di Meccanica Quantistica
 Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa [email protected] www.edizioniets.com
Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa [email protected] www.edizioniets.com
n(z) = n(0) e m gz/k B T ; (1)
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
Prova scritta del corso di Fisica con soluzioni. Prof. F. Ricci-Tersenghi 14/11/2014
 Prova scritta del corso di Fisica con soluzioni Prof. F. icci-tersenghi 14/11/214 Quesiti 1. Si deve trascinare una cassa di massa m = 25 kg, tirandola con una fune e facendola scorrere su un piano scabro
Prova scritta del corso di Fisica con soluzioni Prof. F. icci-tersenghi 14/11/214 Quesiti 1. Si deve trascinare una cassa di massa m = 25 kg, tirandola con una fune e facendola scorrere su un piano scabro
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
ATOMO. Legge della conservazione della massa Legge delle proporzioni definite Dalton
 Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
Democrito IV secolo A.C. ATOMO Lavoisier Proust Legge della conservazione della massa Legge delle proporzioni definite Dalton (808) Teoria atomica Gay-Lussac volumi di gas reagiscono secondo rapporti interi
5.4 Larghezza naturale di una riga
 5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
8.1 Problema della diffusione in meccanica quantistica
 8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton)
 Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
Atomi 16 Si arrivò a dimostrare l esistenza di una forma elementare della materia (atomo) solo nel 1803 (John Dalton) 17 Teoria atomica di Dalton Si basa sui seguenti postulati: 1. La materia è formata
Radioattività. 1. Massa dei nuclei. 2. Decadimenti nucleari. 3. Legge del decadimento XVI - 0. A. Contin - Fisica Generale Avanzata
 Radioattività 1. Massa dei nuclei 2. Decadimenti nucleari 3. Legge del decadimento XVI - 0 Nucleoni Protoni e neutroni sono chiamati, indifferentemente, nucleoni. Il numero di protoni (e quindi di elettroni
Radioattività 1. Massa dei nuclei 2. Decadimenti nucleari 3. Legge del decadimento XVI - 0 Nucleoni Protoni e neutroni sono chiamati, indifferentemente, nucleoni. Il numero di protoni (e quindi di elettroni
Compito di Meccanica Razionale M-Z
 Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
Diffusione dei raggi X da parte di un elettrone
 Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
e una frequenza = 0 /2 =1/T (misurata in Hertz). Infine è la fase, cioè un numero (radianti) che dipende dalla definizione dell istante t=0.
 8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
8. Oscillazioni Definizione di oscillatore armonico libero Si tratta di un sistema soggetto ad un moto descrivibile secondo una funzione armonica (seno o coseno) del tipo x(t) = Acos( 0 t + ) A è l ampiezza
Effetto Zeeman anomalo
 Effetto Zeeman anomalo Direzione del campo B esempio: : j=3/2 Direzione del campo B j=1+1/2 = 3/2 s m j =+3/2 m j =+1/2 l m j =-1/2 m j =-3/2 La separazione tra i livelli é diversa l e µ l antiparalleli
Effetto Zeeman anomalo Direzione del campo B esempio: : j=3/2 Direzione del campo B j=1+1/2 = 3/2 s m j =+3/2 m j =+1/2 l m j =-1/2 m j =-3/2 La separazione tra i livelli é diversa l e µ l antiparalleli
ẋ 1 = 2x 1 + (sen 2 (x 1 ) + 1)x 2 + 2u (1) y = x 1
 Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
Dottorato in Fisica XIV ciclo n.s. 21 gennaio 2013 Prova scritta n.1
 Dottorato in Fisica XIV ciclo n.s. 1 gennaio 013 Prova scritta n.1 Compito 1. I processi oscillatori in fisica. Conseguenze della corrente di spostamento nelle equazioni di Maxwell. Un cilindro di raggio
Dottorato in Fisica XIV ciclo n.s. 1 gennaio 013 Prova scritta n.1 Compito 1. I processi oscillatori in fisica. Conseguenze della corrente di spostamento nelle equazioni di Maxwell. Un cilindro di raggio
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Derivata materiale (Lagrangiana) e locale (Euleriana)
 ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
8. Energia e lavoro. 2 Teorema dell energia per un moto uniformemente
 1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
1 Definizione di lavoro 8. Energia e lavoro Consideriamo una forza applicata ad un corpo di massa m. Per semplicità ci limitiamo, inizialmente ad una forza costante, come ad esempio la gravità alla superficie
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale
 Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Fenomeni Oscillatori: Equazioni di Base della Meccanica del Punto Materiale Lezione del Corso di Esercitazioni di Laboratorio di Meccanica, Roma, 5 Maggio, 2014 Roberto Bonciani 1, Diparto di Fisica dell
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Interazione luce- atomo
 Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Generalità delle onde elettromagnetiche
 Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
Generalità delle onde elettromagnetiche Ampiezza massima: E max (B max ) Lunghezza d onda: (m) E max (B max ) Periodo: (s) Frequenza: = 1 (s-1 ) Numero d onda: = 1 (m-1 ) = v Velocità della luce nel vuoto
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
CORSO DI LAUREA IN OTTICA E OPTOMETRIA
 CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
CORSO DI LAUREA IN OTTICA E OPTOMETRIA Anno Accademico 007-008 CORSO di FISCA ED APPLICAZIONE DEI LASERS Questionario del Primo appello della Sessione Estiva NOME: COGNOME: MATRICOLA: VOTO: /30 COSTANTI
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Il gradino di potenziale.
 Il gradino di potenziale. Cerchiamo adesso di applicare quanto visto sull equazione di Schröedinger per gli stati stazionari ad alcuni casi semplici e particolarmente significativi. Per chiarezza e semplicità
Il gradino di potenziale. Cerchiamo adesso di applicare quanto visto sull equazione di Schröedinger per gli stati stazionari ad alcuni casi semplici e particolarmente significativi. Per chiarezza e semplicità
Esercitazione 2. Soluzione
 Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
Esercitazione 2 Esercizio 1 - Resistenza dell aria Un blocchetto di massa m = 0.01 Kg (10 grammi) viene appoggiato delicatamente con velocità iniziale zero su un piano inclinato rispetto all orizziontale
RETTE E PIANI. ove h R. Determinare i valori di h per cui (1) r h e α sono incidenti ed, in tal caso, determinare l angolo ϑ h da essi formato;
 RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
Risonanza magnetica nucleare
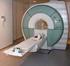 Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Grandezze angolari. Lineare Angolare Relazione x θ x = rθ. m I I = mr 2 F N N = rf sin θ 1 2 mv2 1
 Grandezze angolari Lineare Angolare Relazione x θ x = rθ v ω v = ωr a α a = αr m I I = mr 2 F N N = rf sin θ 1 2 mv2 1 2 Iω 2 Energia cinetica In forma vettoriale: v = ω r questa collega la velocità angolare
Grandezze angolari Lineare Angolare Relazione x θ x = rθ v ω v = ωr a α a = αr m I I = mr 2 F N N = rf sin θ 1 2 mv2 1 2 Iω 2 Energia cinetica In forma vettoriale: v = ω r questa collega la velocità angolare
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16)
 FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2015/16) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
Problema (tratto dal 7.42 del Mazzoldi 2)
 Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17)
 FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
FISICA QUANTISTICA CON ESERCITAZIONI - MOD. 2 (2016/17) Scopo del corso Il corso si propone di completare le conoscenze dello studente nell ambito della meccanica quantistica non relativistica, applicata
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 8. Generalizziamo, considerando due particelle interagenti.
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Potenziale elettrostatico
 Doppio strato piano Potenziale elettrostatico Consideriamo il lavoro compiuto dalla forza elettrica quando una particella di prova di carica q viene spostata in un campo elettrico E. Possiamo definire
Doppio strato piano Potenziale elettrostatico Consideriamo il lavoro compiuto dalla forza elettrica quando una particella di prova di carica q viene spostata in un campo elettrico E. Possiamo definire
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Capitolo 8 La struttura dell atomo
 Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
Problemi di Fisica per l ammissione alla Scuola Galileana Problema 1
 Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
Problemi di Fisica per l ammissione alla Scuola Galileana 014-015 Problema 1 Nella regione di spazio interna alla sfera S 1, centrata in O 1 e di raggio R 1, è presente una densità di carica di volume
CIRCUITI IN CORRENTE CONTINUA
 IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Misura del momento magnetico dell elettrone
 FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1
 FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
FISICA APPLICATA 2 FENOMENI ONDULATORI - 1 DOWNLOAD Il pdf di questa lezione (onde1.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/tsrm/ 08/10/2012 FENOMENI ONDULATORI Una classe di fenomeni
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
L atomo di Bohr. Argomenti. Al tempo di Bohr. Spettri atomici 19/03/2010
 Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Argomenti Spettri atomici Modelli atomici Effetto Zeeman Equazione di Schrödinger L atomo di Bohr Numeri quantici Atomi con più elettroni Al tempo di Bohr Lo spettroscopio è uno strumento utilizzato per
Richiami. Esercizio 1.1. La radiazione elettromagnetica del corpo nero ha la seguente densità di energia per unità di frequenza
 Parte I Problemi Richiami Esercizio 1.1. La radiazione elettromagnetica del corpo nero ha la seguente densità di energia per unità di frequenza u ν = 8π hν c 3 ν e βhν 1, dove c è la velocità della luce
Parte I Problemi Richiami Esercizio 1.1. La radiazione elettromagnetica del corpo nero ha la seguente densità di energia per unità di frequenza u ν = 8π hν c 3 ν e βhν 1, dove c è la velocità della luce
Geometria analitica del piano pag 12 Adolfo Scimone
 Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
REGISTRO DELLE LEZIONI 2005/2006. Tipologia
 Struttura formale della meccanica quantistica Rapprestazione matriciale Addì 03-10-2005 Addì 03-10-2005 15:00-16:00 Teorema della compatibilità Theorema dell'indeterminazione per operatori non commutanti
Struttura formale della meccanica quantistica Rapprestazione matriciale Addì 03-10-2005 Addì 03-10-2005 15:00-16:00 Teorema della compatibilità Theorema dell'indeterminazione per operatori non commutanti
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
Fenomeni quantistici
 Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
