Dispense del corso di Analisi II
|
|
|
- Cinzia Vacca
- 7 anni fa
- Visualizzazioni
Transcript
1 Dipene del coro di Analii II verione preliminare Paolo Tilli Diparimeno di Maemaica Poliecnico di Torino gennaio 25
2 Capiolo 5 Traformaa di Laplace 5. Inroduzione Sia x() una funzione coninua a rai e definia almeno ulla emirea [, + ). Scelo un numero reale, l inegrale improprio (5.) x()e d può eiere o non eiere, a econda del valore del paramero. L inieme D dei numeri per cui ale inegrale eie finio coiuice il dominio di una nuova funzione X(), dea raformaa di Laplace di x(), definia dall uguaglianza X() = x()e d, D. Chiaramene, il dominio D della raformaa di Laplace X() dipenderà dalla funzione x().! Eempio 5.. Se x() = e, l inegrale improprio X() = x()e d = e ( ) d eie finio olo per >, e quindi il dominio D della raformaa è dao dalla emirea apera (, ). Se invece x() = e 2 /( + 2 ), l inegrale X() = x()e d = e (2 ) + 2 d eie finio e e olo e 2, e quindi D è la emirea chiua [2, ). Ancora, per x() = e 2 l inegrale improprio X() = x()e d = e 2 d 5
3 eie finio per ogni, e perano i ha D = R. Infine, e x() = e 2, l inegrale improprio X() = x()e d = e 2 d non è finio per alcun valore di, e quindi il dominio D della raformaa i riduce all inieme vuoo. Negli eempi precedeni il dominio D della raformaa di Laplace era empre una emirea della forma (, ) oppure della forma [, ), coniderando l inera rea reale e l inieme vuoo come cai limie. In effei, queo accade in generale: in alre parole, e l inegrale improprio (5.2) x()e d eie finio per un cero, allora è poibile dimorare che eie finio anche l inegrale x()e d per ogni valore di ale che >, e quindi il dominio D della raformaa di Laplace è empre una emirea. Riaumiamo quano deo nella eguene definizione. Definizione 5..2 Daa una funzione x(), definia almeno per e coninua a rai, indichiamo con D la emirea (evenualmene degenere) definia da D eie finio l inegrale improprio x()e d. Si chiama raformaa di Laplace della funzione x(), e la i indica con uno dei imboli L [x() o X, la nuova funzione (5.3) L [x() () = X() = def x()e d, D avene l inieme D come dominio di definizione. Quando D è non vuoo, la funzione x() i dice raformabile econdo Laplace. Il ermine raformaa oolinea il fao che i coruice, a parire da una daa funzione x(), una nuova funzione X(), dea appuno raformaa di x(), econdo lo chema raformaa x(), X(), D La raformaa di Laplace rova numeroe applicazioni, ad eempio nella rioluzione eplicia di alcune equazioni differenziali. Il puno cruciale, a queo propoio, è la poibilià di ricoruire la funzione x(), conocendo la ua raformaa di Laplace X(). Quea pecie di operazione invera, dea aniraformaa di Laplace, opera econdo econdo lo chema x(), aniraformaa 6 X(), D
4 Se i inerprea x() come un egnale in funzione del empo, analizzao per empi poiivi, i vede dalla formula (5.3) che la variabile ha le dimenioni di una frequenza, dao che il prodoo (per poerne calcolare l eponenziale) deve eere adimenionale. Perano, i può penare alla raformaa di Laplace come a uno rumeno che permee di rappreenare un egnale nello pazio delle frequenze. Concludiamo quea inroduzione con il calcolo direo di alcune raformae di Laplace. Quei eempi elemenari, combinai con le proprieà generali della raformaa che udieremo nei paragrafi egueni, coneniranno di calcolare le raformae di Laplace di funzioni anche piuoo complee.! Eempio 5..3 (funzione a gradino) Conideriamo la coiddea funzione a gradino, definia da { e <, (5.4) U() = e. Quea funzione rivee un ruolo fondamenale nella eoria dei egnali, in quano rappreena un egnale di inenià uniaria, che inizia al empo zero e perie per un empo illimiao. Uando la definizione 5..2, calcoliamo la raformaa di Laplace di U(). Si ha U()e d = e d e l inegrale improprio eie finio e e olo e > : in queo cao, l inegrale vale /, come i verifica facilmene. Allora il dominio della raformaa L [U() è la emirea apera (, ), e i ha (5.5) L [U() () =, >.! Eempio 5..4 (eponenziale) Calcoliamo la raformaa di Laplace della funzione eponenziale x() = e a, dove a è un paramero reale. Si ha e a e d = e (a ) d = a > a, alrimeni l inegrale improprio non è convergene. Quindi il dominio della raformaa è la emirea apera (a, ) e (5.6) L [ e a () = a, > a. 7
5 ! Eempio 5..5 (funzioni rigonomeriche) Calcoliamo la raformaa di Laplace di x() = in. L inegrale improprio (in )e d è convergene e e olo e >, quindi il dominio della raformaa di Laplace di in è la emirea apera (, ). Per calcolare l inegrale improprio, calcoliamo prima di uo una primiiva (in )e d = e ( in co ). 2 + Quindi, per > i rova l (in )e d = lim (in )e e l ( in co ) d = lim l l 2 + ( ) e l ( in l co l) = lim e ( in co ) = l e la raformaa è quindi daa da (5.7) L [in () = 2 +, >. In maniera del uo analoga, i verifica che (5.8) L [co () = 2 +, >.! Eempio 5..6 Calcoliamo la raformaa di Laplace della funzione x() =. L inegrale improprio e d è convergene e e olo e >. Inolre, inegrando per pari i rova che la funzione e ( )/ 2 è una primiiva di e, quindi per > i ha l e d = lim e d = lim l = lim l La raformaa di Laplace è allora daa da e ( ) l 2 ( e l ( l ) e ( ) 2 2 (5.9) L [ () = 2, >. 8 l ) =. 2
6 Non empre è agevole deerminare eaamene il dominio della raformaa di Laplace di una daa funzione x(). In ogni cao, un crierio uile per abilire e x() è raformabile econdo Laplace conie nello udiare il uo ordine di crecia. Si dice che una funzione x() ha crecia eponenziale e eiono due coani M e α ali che valga la maggiorazione x() Me a. Inolre, l eremo inferiore degli eponeni α per cui è poibile avere una ima di queo ipo, viene deo ordine di crecia della funzione x(). Si può verificare facilmene che, e una funzione ha ordine di crecia, allora ea è raformabile econdo Laplace, almeno nella emirea apera (, ) (quea condizione è in generale olano ufficiene e non necearia ai fini della raformabilià). Eempio 5..7 Se x() è una funzione limiaa, cioè e eie una coane M ale che x() M, allora x() ha crecia eponenziale, e il uo ordine di crecia (come i verifica facilmene) è minore o uguale a zero. Quindi, qualiai funzione coninua a rai e limiaa, è raformabile econdo Laplace, almeno ulla emirea poiiva (, ).! Eempio 5..8 (ordine delle funzioni iperboliche) Le funzioni iperboliche inh def = e e, coh def = e + e 2 2 hanno enrambe crecia eponenziale e ordine di crecia. Infai, i ha per > inh = e e 2 2 e, e coh = e + e e, 2 e il numero in e = e non può eere oiuio da alcun faore più piccolo. Le funzioni iperboliche inh e coh, quindi, ono raformabili econdo Laplace nella emirea (, ): L [inh () = (inh )e d, L [coh () = (coh )e d, >. Il calcolo delle ripeive raformae verrà effeuao nel proimo paragrafo, uando la proprieà di linearià. Eercizi 5.. Calcolare, uilizzando la definizione, la raformaa di Laplace delle egueni funzioni, indicandone ogni vola il dominio di definizione: in 2, +, 2e 4 3 co 4, U( 3), Deerminare e le egueni funzioni hanno crecia eponenziale e, in cao affermaivo, deerminarne l ordine di crecia: e 5, 2e + 4, 2 +, ( + 3 )e 3, e 2 +2, e inh 2, in 9
7 5.2 Proprieà fondamenali La raformaa di Laplace gode di alcune proprieà fondamenali, che conenono di ridurre noevolmene il volume di calcolo che arebbe richieo e, per calcolarla, i facee ricoro unicamene alla definizione (5.3). La prima proprieà della raformaa di Laplace è quella di linearià. Linearià. Se x () e x 2 () ono due funzioni con raformae di Laplace X () e X 2 () nei ripeivi dominî D e D 2, allora una qualiai loro combinazione lineare ax () + bx 2 () è a ua vola raformabile, nel dominio dao dall inerezione dei due dominî, e vale: (5.) L [ax () + bx 2 () () = ax () + bx 2 (), D D 2. Eempio 5.2. Combinando la (5.6) e la (5.7), i ha L [ 2e in () = , > 3 (i noi che il dominio di raformabilià è dao dall inerezione dei due dominî (3, ) e (, )).! Eempio (funzioni iperboliche) Calcoliamo la raformaa di Laplace delle funzioni iperboliche inh a e coh a, dove a è un paramero reale. Si ha inh a = ea e a 2 = 2 ea 2 e a, quindi inh a è una combinazione lineare di due funzioni eponenziali, di cui abbiamo già calcolao la raformaa di Laplace. In paricolare, uando due vole la (5.6) (prima con a, poi con a) roviamo: L [ e a () = a, > a, e L [ e a () = + a, > a. I due dominî di raformabilià ono quindi le due emiree (a, ) e ( a, ), e la loro inerezione è la emirea ( a, ), indipendenemene dal egno di a. Applicando la proprieà di linearià (5.), i oiene quindi (5.) L [inh a () = 2 ( a ) + a = a 2 a 2, > a. In maniera del uo analoga, i rova (5.2) L [coh a () = ( 2 a + ) = + a 2 a 2, > a.
8 Paiamo ora in raegna alcune alre proprieà della raformaa di Laplace, con relaive dimorazioni ed eempi. Anche e quee non ono le ipoei oimali, upporremo empre che x() ia una funzione coninua a rai u [, ) con crecia eponenziale del ipo (5.3) x() Me per un cero numero. In queo modo, per > riula enz alro definia la ua raformaa di Laplace X() = x()e d, >. Ricalameno. Se a > è un paramero reale, allora (5.4) L [x(a) () = a X(/a), > a. Dimorazione. Baa effeuare il cambiameno di variabile z = a nella definizione di raformaa di Laplace. Infai, e > a, abbiamo L [x(a) () def = x(a)e d = a x(z)e z/a dz def = a X(/a).! Eempio (funzioni rigonomeriche) Vogliamo calcolare la raformaa di Laplace della funzione in a, dove a > è un paramero reale. Ponendo x() = in, dalla (5.7) appiamo che X() = 2 +, >. Applicando la proprieà di ricalameno (5.4), roviamo quindi (5.5) L [in a = a (/a) 2 + = Analogamene, parendo dalla (5.8) i rova (5.6) L [co a = a /a (/a) 2 + = a 2 + a 2, >. 2 + a 2, >. Proprieà di ralazione. Se a > è un paramero reale poiivo, allora (5.7) L [x( a)u( a) () = e a X(), >. Si noi che, ricordando la (5.4), i ha x( a)u( a) = { x( a) e a, e < a.
9 Il grafico della funzione x( a)u( a) u [, ), perano, i oiene ralando il grafico di x()u() di una quanià pari ad a vero dera (e quindi la funzione ralaa arà nulla u [, a)). In paricolare, e x()u() rappreena un egnale che inizia al empo =, la funzione x( a)u( a) rappreena un egnale idenico ma riardao nel empo (cioè, un egnale di forma idenica che inizia al empo a). Per queo moivo, la (5.7) è noa anche come formula del riardo. Dimorazione. È ufficiene noare che U( a) = per < a e U( a) = per a, e poi effeuare il cambiameno di variabile z = a nell inegrale: L [x( a)u( a) () def = = a = e a x( a)u( a)e d x( a)e d = x(z)e a z dz x(z)e z dz def = e a X(), >.! Eempio (gradino ralao) Fiao a, calcoliamo la raformaa di Laplace della funzione a gradino ralaa, ovvero { e < a, U( a) = e a. Noiamo che i ha U( a) = U( a)u( a), quindi poiamo uare la formula del riardo (5.7) con x() = U(), oenendo L [U( a) () = L [U( a)u( a) () = e a L [U() (). D alra pare, la raformaa L [U() () della funzione a gradino è già aa calcolaa nella (5.5), quindi i oiene (5.8) L [U( a) () = e a, >.! Eempio Calcoliamo la raformaa di Laplace della funzione { e <, x() = 2e 3 e. Per far queo, noiamo che i ha x() = 2e 3 U( ) = 2e 3 e 3( ) U( ). Applicando prima la linearià e poi la formula del riardo con a =, oeniamo L [x() () = 2e 3 L [ e 3( ) U( ) () = 2e 3 e L [ e 3 (), 2
10 e baa quindi calcolare la raformaa di Laplace di e 3. Del reo, fruando la (5.6) i rova L [ e 3 () = 3, > 3 e quindi e L [x() () = 2e 3 3, > 3. Modulazione. Se a è un paramero reale, allora (5.9) L [ e a x() () = X( a), > + a. Il ignificao della (5.9) è che la moliplicazione per una funzione di ipo eponenziale i riflee, nella raformaa di Laplace, in una ralazione nel dominio delle frequenze. Per queo moivo, la proprieà di modulazione è anche dea econda formula del iardo. Dimorazione. Si raa di una emplice verifica, uilizzando la definizione di raformaa di Laplace: L [ e a x() () def = e a x()e d = x()e ( a) d def = X( a), > + a.! Eempio Calcoliamo la raformaa di Laplace della funzione x() = e 2 in 3. Applicando prima la proprieà di modulazione (5.9) (con a = 2) e poi la formula (5.5) (con a = 3), i rova L [ e 2 in 3 () = L [in 3 ( 2) = 3 ( 2) = 3 ( 2) 2 + 9, > 2. Moliplicazione per. Si ha (5.2) L [x() () = X (), >. Applicando ripeuamene la (5.2), i oiene (5.2) L [ n x() () = ( ) n dn d n X(), >, n inero poiivo. Una dimorazione eauriene della proprieà (5.2) eula dai nori copi, in quano richiede rumeni piuoo avanzai di eoria dell inegrazione. Tuavia, è facile 3
11 fornire una giuificazione inuiiva della (5.2), oenua cambiando i imboli di derivaa e inegrale: X () def = d ( ) x()e d ( d = ) x()e d d d = x()e d def = L [x() (). Per rendere complea la dimorazione, arebbe neceario giuificare adeguaamene la econda uguaglianza, cioè il fao che la derivaa ripeo a dell inegrale in d (in cui compare come paramero), ia uguale all inegrale della funzione derivaa.! Eempio (poenze di ) Dao un inero poiivo n, calcoliamo la raformaa di Laplace della funzione n. È ufficiene applicare la (5.2), cegliendo x() = U(), cioè la funzione a gradino la cui raformaa è già aa calcolaa nella (5.5): ( ) L [ n () = L [ n U() () = ( ) n dn = n!, >. d n n+ Ad eempio, i ha cegliendo n =, 2, 3 L [ = ( ) = 2, L [ 2 = ( ) = 2 3, L [ 3 = ( ) = 6, >. 4! Eempio Calcoliamo la raformaa di Laplace di in 3. Dalla (5.5) con a = 3, i ha L [in 3 () = , > e quindi uando la (5.2) i rova L [ in 3 () = ( ) 3 = ( 2 + 9) 2, >. Coì come la moliplicazione per i raduce, nella raformaa di Laplace, in una derivazione e in un cambiameno di egno, la diviione per i raduce in una inegrazione: Diviione per. Se il limie dero eie finio, allora [ x() (5.22) L () = x( + x() ) def = lim + X(S) ds, >. 4
12 ! Eempio Calcoliamo la raformaa di laplace della funzione in()/. Il limie dero in lim + eie finio, quindi poiamo applicare la (5.22): [ in L () = L [in (S) ds. Ricordando la (5.7), oeniamo [ in L () = S 2 + ds = arcan(s) (5.23) = π arcan = arcan(/), >. 2 Oervazione 5.2. Se nella ima (5.3) i ha <, allora poiamo cegliere = nella (5.22), oenendo [ x() L () = X() d. Ma ricordando la definizione della raformaa di Laplace (5.3), poiamo crivere quea relazione nel modo eguene: (5.24) x() d = X() d. La (5.24) coninua a valere anche quando =, ma in queo cao biogna upporre che i due inegrali impropri iano convergeni.! Eempio 5.2. Per calcolare l inegrale improprio in che appiamo eere convergene, i può uare la (5.24). Infai, ponendo x() = in la (5.3) è verificaa con =, e i ha X() = /( 2 + ) per > grazie alla (5.7). Applicando la (5.24), i oiene d, in d = 2 + d = arcan = π 2. 5
13 Traformaa della derivaa. Se x() è coninua u [, ) ed è di clae C in (, + ), allora (5.25) L [x () () = X() x(), >. Dimorazione. Fiiamo un numero l >. Inegrando per pari, i ha l x ()e d = x()e l l l + x()e d = x(l)e l x() + x()e d. Per la (5.3), i ha lim l x(l)e l =, >, e quindi per definizione di raformaa di Laplace l ( l ) L [x () () def = lim x ()e d = lim x(l)e l x() + x()e d l l l = x() + lim x()e d def = x() + X(), >, l cioè la (5.25). Oervazione Ferme reando le alre ipoei, e x() è coninua in (, ) ed eie finio il limie dero allora la (5.25) rea valida nella forma x( + ) def = lim x(), + (5.26) L [x () () = X() x( + ), >. Inolre, e i fanno analoghe ipoei ulle derivae di ordine maggiore al primo, la (5.26) può eere applicaa ripeuamene, per calcolare la raformaa di Laplace delle derivae di ordine più alo. Ad eempio, e anche la derivaa x () oddifa le ee ipoei di x() i ha L [x () () = L [ (x ()) () = L [x () () x ( + ) = 2 X() x( + ) x ( + ) e quindi (5.27) L [x () = 2 X() x( + ) x ( + ), >. Faremo uo di quea relazione più avani, per la rioluzione eplicia di alcune equazioni differenziali. 6
14 ! Eempio Ricalcoliamo, in maniera divera, la raformaa di Laplace della funzione x() = in a, dove ora a è un paramero reale qualiai. Si ha x () = a 2 in a, x() =, x () = a. Per linearià, applicando la (5.27) quindi i ha a 2 L [in a () = L [x () () = 2 L [x() () a, e quindi riolvendo ripeo a L [x() () i oiene L [in a () = L [x() () = a 2 + a 2, >, in accordo con la (5.5) (che era aa dimoraa olano per a > ). Traformaa dell inegrale. Si ha [ (5.28) L x(r) dr () = X(), > max{, }. Dimorazione. Fiiamo un numero l > e poniamo g() = x(r) dr. Dao che g () = x() e g() =, inegrando per pari i ha l g()e d = g()e l + l g ()e d = g(l)e l l + l x()e d. Paando al limie per l i oiene la (5.28), dao che, in bae alla (5.3), l { l g(l) = x() d M e M/ e <, d Mle e, e quindi e > max{, } i ha g(l)e l lim l l Si noi che, nella (5.28), l ipoei che ia > max{, } non può eere oiuia dall ipoei più debole >. Infai, conideriamo ad eempio x() = e, che verifica la (5.3) con =. Allora i ha g() = e, e la raformaa di Laplace di g() ha dominio (, ) e non (, ). =. 7
15 ! Eempio (eno inegrale) Calcoliamo la raformaa di Laplace della funzione eno inegrale in r I() = dr,. r Ponendo x() = (in )/, la (5.3) è verificaa con = ; perano, applicando la (5.28) e ricordando la (5.23), oeniamo L [I() () = arcan(/), >. Funzioni periodiche. Se x() è periodica di periodo T u [, ), allora i ha (5.29) L [x() () = T x()e d e T, >. Dimorazione. Oerviamo anziuo che una funzione periodica e coninua a rai è limiaa, quindi raformabile econdo Laplace per >. Se n è un inero poiivo, col cambiameno di variabile = z + nt roviamo nt +T nt x()e d = T T x(z + nt )e (z+nt ) dz = e nt x(z)e z dz, avendo uao la periodicià. Sommando u N periodi conecuivi, i ha quindi NT x()e d = N n= nt +T nt ( T x()e d = ) N x(z)e z dz n= e nt, e la (5.29) egue ubio paando al limie per N, e ricordando la formula per la omma di una erie geomerica di ragione e T.! Eempio Calcoliamo la raformaa di Laplace dell onda quadra di periodo T e ampiezza A, definia ul periodo [, T ) come { A e < T/2, x() = A e T/2 < T. Per applicare la (5.29), calcoliamo T T x()e 2 d = A e quindi per la (5.29) T e d A e d = A 2e T/2 + e T T 2 = A ( e T/2 ) 2 ( ) e T/2 2 L [x() () = A ( e T ) = A e T/2 ( + e T/2 ), >. 8
16 Concludiamo quea raegna con due proprieà che meono in relazione i valori limie, nel puno zero e all infinio, di x() e della ua raformaa X(). Valore iniziale. Si ha (5.3) x( + ) def = lim x() = lim X(). + Dimorazione. Noiamo prima di uo che il primo limie eie finio, in quano x() è coninua a rai u [, ). Col cambiameno di variabile z =, i ha X() def = D alra pare, per qualiai z > i ha x()e d = lim x(z/) = lim x() = x(+ ). + Perano, cambiando il limie con l inegrale, i ha ( ) X() = lim x(z/)e z dz = lim = x( + )e z dz = x( + ) x(z/)e z dz. ( ) lim x(z/)e z dz e z dz = x( + ) e la (5.3) è dimoraa. Oerviamo però che, nella econda uguaglianza, biognerebbe giuificare adeguaamene la poibilià di cambiare ra loro l operazione di limie e quella di inegrale: una giuificazione rigoroa richiederebbe rumeni piuoo avanzai, e per queo moivo viene omea. Valore finale. Se, i ha (5.3) lim x() = lim + X() a pao che i limii in queione eiano. La proprieà del valore finale può eere giuificaa in maniera analoga a quano fao per la condizione iniziale; i noi uavia che qui biogna upporre che i limii eiano. Riaumiamo le proprieà della raformaa di Laplace nella Tabella 5.. Si enga però preene che alcune proprieà richiedono qualche ipoei aggiuniva olre la (5.3): per queo, i rimanda alla raazione più deagliaa epoa precedenemene. 5.3 Aniraformaa di Laplace La raformaa di Laplace arebbe di ben poca uilià e non foe poibile rialire alla funzione x(), conocendo la ua raformaa di Laplace X(). L operazione che permee di paare da X() a x() è dea aniraformaa di Laplace: una raazione deagliaa dell aniraformaa eula dai nori copi, in quano richiederebbe la eoria delle funzioni di variabile complea. Qui ci limieremo a fornire alcuni eempi ed alcune ecniche euriiche per il calcolo dell aniraformaa. 9
17 Linearià L [ax () + bx 2 () () = ax () + bx 2 () Ricalameno L [x(a) () = a X(/a), > a Tralazione L [x( a)u( a) () = e a X(), > Modulazione L [e a x() () = X( a), > + a Moliplicazione per L [x() () = X (), > [ x() Diviione per L () = X(S) ds, > Traformaa della derivaa L [x () () = X() x( + ), > Traformaa dell inegrale [ L x(r) dr () = X(), > max{, } Valore iniziale Valore finale lim x() = lim X() + lim x() = lim X() + Tabella 5.: Principali proprieà della raformaa di Laplace. Definizione 5.3. Sia X() una funzione definia almeno u una emirea apera del ipo (, ). Diciamo che x() è una aniraformaa di X() e criviamo x() = L [X() (), e x() è una funzione coninua a rai u [, ), raformabile econdo Laplace, e ale che X() = L [x() (), >. Va ubio noao che, quando eie, l aniraformaa di Laplace di X() non è mai univocamene deerminaa. Infai, dao che la raformaa di Laplace è definia ramie l inegrale (5.3), e x() è una aniraformaa di X(), allora qualiai funzione oenua modificando i valori di x() in un numero finio di puni è ancora una aniraformaa di X(). Tuavia, quea non è una evera limiazione, in quano i può dimorare che, e x() è una aniraformaa, allora la regolarizzaa di x() è univocamene deerminaa. Per queo moivo, parleremo peo della aniraformaa di Laplace, anziché di una aniraformaa. Si enga poi preene che, nella definizione di raformaa di Laplace (5.3), inervengono olano i valori di x() con : perano, conocendo la raformaa X(), 2
18 non i può avere alcuna informazione ull aniraformaa x() per valori negaivi di. Perciò, nel eguio, ue le aniraformae verranno coniderae, impliciamene, olano ulla emirea poiiva. Dao che l aniraformaa di Laplace è l operazione invera della raformaa, le proprieà fondamenali dell aniraformaa di Laplace i ricavano facilmene da quelle della raformaa. Per facilià di conulazione, le riporiamo in modo ineico nella Tabella 5.2: i noi però che quee proprieà vanno applicae cum grano ali, facendo paricolare aenzione alle ipoei e ai dominî di definizione. Linearià Ricalameno L [ax () + bx 2 () () = ax () + bx 2 () L [X(a) () = a x(/a) Tralazione L [e a X() () = x( a)u( a) Modulazione Aniraformaa della derivaa Aniraformaa dell inegrale Moliplicazione per Diviione per L [X( a) () = e a x() L [X () () = x() [ L X(S) ds () = x() L [X() x( + ) () = x () [ X() L () = x(r) dr Tabella 5.2: Principali proprieà dell aniraformaa di Laplace. Confronando le due abelle 5. e 5.2, va noao come la proprieà di moliplicazione per della raformaa diveni la proprieà di aniraformaa della derivaa, menre la proprieà di diviione per della raformaa divena la proprieà di aniraformaa dell inegrale (e, vicevera, relaivamene alla moliplicazione e alla diviione per ). Nel calcolare le aniraformae di Laplace, può eere uile fare riferimeno alla Tabella 5.3.! Eempio Deerminiamo l aniraformaa della funzione X() =
19 Funzione x() Traformaa di Laplace X() Dominio U() e α (a R) n (n N) in(a) (a R) co(a) (a R) inh(a) (a R) coh(a) (a R) e a in(b) (a, b R) e a co(b) (a, b R) in > a > a n! n+ > a 2 + a 2 > 2 + a 2 > a 2 a 2 > a a 2 a 2 > a b ( a) 2 + b 2 > a a ( a) 2 + b 2 > a arcan(/) > Tabella 5.3: Alcune funzioni e le loro raformae di Laplace Ricordando la (5.6) (i veda anche la Tabella 5.3), abbiamo per linearià [ [ 3 L () = 3L () = 3e ! Eempio Calcoliamo l aniraformaa di Laplace della funzione 2. Guardando la abella (5.3), i oiene ubio che [ L () = inh. 2 In alernaiva, i può decomporre la funzione in frai emplici: 2 = ( + )( ) = ( 2 ). + 22
20 Per linearià dell aniraformaa, i ha quindi [ [ ( L () = L = [ 2 L ) () () 2 L [ + (). Dao che /( ) è la raformaa di e menre /( + ) è la raformaa di e, i ricava L [ /( 2 ) () = 2 e 2 e = inh. Concludiamo queo paragrafo con una lunga erie di eempi di calcolo delle anriraformae di Laplace, meendo in luce le proprieà dell aniraformaa che vengono di vola in vola uilizzae. Inolre, i farà implicio riferimeno alla abella 5.3 per quano riguarda le raformae delle funzioni elemenari.! Eempio (linearià) Calcoliamo l aniraformaa della funzione Uando la linearià, i oiene [ 4 L () [ [ [ = 4L () 3L () + 5L () [ [ = 4L () 3L () + 52 [ L () = 4e 2 3 co in 2. 2! Eempio (ricalameno) Calcoliamo l aniraformaa della funzione Dao che [ [ L () = L () = co 4, per la proprieà di ricalameno dell aniraformaa roviamo [ [ L () = L () = 3 [ (3) L () = 3 ( ) 43 (3) co. 23
21 ! Eempio (ralazione) Calcoliamo l aniraformaa della funzione Dao che dalla proprieà di ricalameno i oiene L [ e π/3 + 2 e π/ [ L () = in, 2 + () = U( π/3) in( π/3) = { in( π/3) e π/3, e < π/3.! Eempio (modulazione) Calcoliamo l aniraformaa della funzione Per prima coa, compleiamo il quadrao a denominaore: Dao che = ( ) [ L () = in 2, dalla proprieà di modulazione oeniamo [ [ L () = L ( ) () = 2 e in 2.! Eempio (aniraformaa della derivaa) Calcoliamo l aniraformaa della funzione ( 2 + ) 2. Dao che i ha e quindi per linearià [ L () = in 2 + e ( ) d = 2 d 2 + ( 2 + ), 2 [ L 2 () = in ( 2 + ) 2 [ L () = in. ( 2 + )
22 ! Eempio (aniraformaa della derivaa) Calcoliamo l aniraformaa della funzione, a R, ed n inero poiivo. ( a) n+ Se n =, i ha chiaramene [ L () = e a. a Se invece n >, è imporane riconocere nella frazione /( a) n+ la derivaa (a meno di una coane moliplicaiva) di ordine n della funzione /( a). Più preciamene, i ha ( )n = ( a) n+ n! ( ) d n. d n a Quindi, applicando n vole la proprieà di aniraformaa della derivaa, oeniamo Ad eempio, per n = e n = 2 i rova [ L () = n ( a) n+ n! ea. [ [ (5.32) L () = e a, L ( a) 2 ( a) 3 () = 2 2 ea.! Eempio 5.3. (aniraformaa dell inegrale) Calcoliamo l aniraformaa della funzione ( ) + log. Noiamo che i ha ( ) + log = ( S ) ds S + e appiamo calcolare l aniraformaa della funzione inegranda, dao che [ L () = U() e. + Perano, per la proprieà dell aniraformaa dell inegrale, i oiene ( ) + L [log () = e. 25
23 ! Eempio 5.3. (moliplicazione per ) Calcoliamo l aniraformaa della funzione ( ) 2 +. Dao che, in bae alla abella 5.3, i ha [ L () = e in ( ) 2 + e x() = e in verifica x + () =, poiamo applicare la proprieà di moliplicazione per, oenendo [ L () = d ( e in ) = e (co + in ). ( ) 2 + d! Eempio (diviione per ) Calcoliamo l aniraformaa della funzione Dao che ( 2 + 4). [ L () = in 2, applicando la proprieà di diviione per oeneniamo [ L () = ( 2 + 4) 2 in 2r dr = 4 co 2. 4 Per calcolare l aniraformaa di 3 ( 2 + 4), baa applicare ancora due vole la proprieà di diviione: [ L ( () = 2 ( 2 + 4) 4 ) co 2r dr = 4 4 in 2, 8 e quindi [ L () = 3 ( 2 + 4) ( r 4 ) in 2r dr = co 2 6.! Eempio (frai emplici) Per calcolare l aniraformaa della funzione razionale = ( 3)( + ) 26
24 decomponiamola come omma di frai emplici, cioè deerminiamo A e B ali che (5.33) ( 3)( + ) = A 3 + B +. Per deerminare i numeri A e B, i può riolvere un iema lineare. In alernaiva, i può moliplicare la (5.33) per 3 e poi fare il limie per 3, oenendo lim 3 + = A + lim ( 3)B 3 + e quindi A = 4. Per oenere B, moliplichiamo la (5.33) per + e poi facciamo il limie per, oenendo lim 3 e quindi B =. Si ha allora L [ = 4L [ 3 ( 3)(2 + ) = lim 3A( + ) 3 () = L [ 4 () L [ + = A + B = B 3 + () = 4e 3 e. ()! Eempio (frai emplici) Per calcolare l aniraformaa della funzione razionale ( + )( 2) 3 decomponiamola come omma di frai emplici, cioè deerminiamo A, B, C e D ali che (5.34) ( + )( 2) = A B ( 2) + C 3 ( 2) + D 2 2. Per deerminare A, procediamo come nell eempio precedene: moliplichiamo per + e prendiamo il limie per, oenendo A = lim = ( 2) 3 3. Per deerminare B, analogamene, moliplichiamo per ( 2) 3 e poi paiamo al limie per 2, oenendo Trovai A e B, la (5.34) divena B = lim ( 2) 3 = ( + )( 2) = / ( 2) + C 3 ( 2) + D
25 Per deerminare C, occorre prima porare a primo membro la frazione 7/( 2) 3 e meere a faor comune, oenendo (5.35) ( + )( 2) = / C ( 2) + D 2 2. Ora i può moliplicare per ( 2) 2 e fare il limie per 2, oenendo C = lim 2 ( + )( 2) = lim 8 2 ( 2) + ( + ) = 4 (il limie è ao calcolao con la regola di De L Hôpial). La (5.35) divena quindi ( + )( 2) 3 = / ( 2) 2 + D 2 e per deerminare D occorre porare a primo membro la frazione 4/( 2) 2, oenendo ( + )( 2) = /3 ( + )( 2) D 2. Ora, moliplicando per 2 e paando al limie per 2, uando due vole la regola di De L Hôpial i oiene D = lim ( + )( 2) ( + )( 2) 2 8 4( + ) 4( 2) = lim 2 ( 2) 2 + 2( + )( 2) 4 4 = lim 2 2( 2) + 2( + ) + 2( 2) = 3. Perano, ricordando la (5.32) i ha [ 5 L 2 5 () ( + )( 2) [ 3 [ [ /3 =L () + L 7 () + L 4 + ( 2) 3 ( 2) 2 = [ [ [ 3 L () 7L () + 4L + ( 2) 3 = 3 e e 2 + 4e e2. [ /3 () + L 2 ( 2) 2 () () + 3 L [ 2 () Eercizi 5.3. Deerminare l aniraformaa di Laplace delle egueni funzioni (la ripoa è indicaa ra parenei): a) (3e 4 ) b) 2 5 ( 2 e5/2 ) c) (8 co 4) d) 5 ( 4 /24)
26 5.3.2 Verificare che le funzioni dell eercizio precedene ono le raformae di Laplace delle corripondeni funzioni indicae ra parenei Deerminare l aniraformaa di Laplace delle egueni funzioni (la ripoa è indicaa ra parenei): 6 a) (3 in 2) b) (3 co in 2 2) c) (2 coh inh 3) Verificare che le funzioni dell eercizio precedene ono le raformae di Laplace delle corripondeni funzioni indicae ra parenei Deerminare l aniraformaa di Laplace delle egueni funzioni (la ripoa è indicaa ra parenei): a) ( 3 4 co 5/2 4 5 in 5/2) b) ( 5 9 coh 4/ inh 4/3) Verificare che le funzioni dell eercizio precedene ono le raformae di Laplace delle corripondeni funzioni indicae ra parenei Deerminare l aniraformaa di Laplace delle egueni funzioni (la ripoa è indicaa ra parenei): a) (3 co 2 4 in 2 4 coh inh 4) b) ( 7 3 e 2/3 ) Verificare che le funzioni dell eercizio precedene ono le raformae di Laplace delle corripondeni funzioni indicae ra parenei Deerminare l aniraformaa di Laplace delle egueni funzioni (la ripoa è indicaa ra parenei): 3 4 a) (e (3 co 2 4 in 2)) b) (e 8 3e 4 ) 5.3. Verificare che le funzioni dell eercizio precedene ono le raformae di Laplace delle corripondeni funzioni indicae ra parenei. 29
Istituzioni di Probabilità Laurea magistrale in Matematica prova scritta del 20/6/2013
 Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
Applicazioni del Massimo flusso. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Applicazioni del Maimo fluo Progeazione di Algorimi a.a. 0-6 Maricole congrue a Docene: Annalia De Boni Maching bipario Problema del max maching. Inpu: grafo non direzionao G = (V, E). M E e` un maching
Applicazioni del Maimo fluo Progeazione di Algorimi a.a. 0-6 Maricole congrue a Docene: Annalia De Boni Maching bipario Problema del max maching. Inpu: grafo non direzionao G = (V, E). M E e` un maching
LABORATORIO di ELETTRONICA SEGNALI ELETTRICI PERIODICI
 LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
Basi di Elettronica (1 parte)
 Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
PREMESSA In questa lezione verranno esposte le regole per l analisi dei sistemi continui con il metodo della Trasformata di Laplace.
 ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
Università degli Studi di Napoli. Federico II. Appunti di METODI MATEMATICI PER L INGEGNERIA INDUSTRIALE
 Carlo Colella Davide Formiano Univerià degli Sudi di Napoli Federico II Diparimeno di Ingegneria Navale Appuni di METODI MATEMATICI PER INGEGNERIA INDUSTRIAE A.A. 8/9 INDICE Capiolo I A TRASFORMAZIONE
Carlo Colella Davide Formiano Univerià degli Sudi di Napoli Federico II Diparimeno di Ingegneria Navale Appuni di METODI MATEMATICI PER INGEGNERIA INDUSTRIAE A.A. 8/9 INDICE Capiolo I A TRASFORMAZIONE
3. MODELLI MATEMATICI
 3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
Esercizio 1. Sia L : R 3 R 2 l'applicazione lineare rappresentata, rispetto alle basi canoniche, dalla matrice : A =
 Tuoraggio di Algebra Lineare e Geomeria Eercii di ripao ulle applicaioni lineari Eerciio Sia L : R R 2 l'applicaione lineare rappreenaa, ripeo alle bai canoniche, dalla marice : A ( 2 2 Deerminare la marice
Tuoraggio di Algebra Lineare e Geomeria Eercii di ripao ulle applicaioni lineari Eerciio Sia L : R R 2 l'applicaione lineare rappreenaa, ripeo alle bai canoniche, dalla marice : A ( 2 2 Deerminare la marice
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
Calcolo di integrali - svolgimento degli esercizi
 Calcolo di inegrali - svolgimeno degli esercizi Calcoliamo una primiiva di cos(e 5. Inegriamo due vole per pari, scegliendo e 5 d come faore differenziale e cos( come faore finio. Si ha cos(e 5 d e5 5
Calcolo di inegrali - svolgimeno degli esercizi Calcoliamo una primiiva di cos(e 5. Inegriamo due vole per pari, scegliendo e 5 d come faore differenziale e cos( come faore finio. Si ha cos(e 5 d e5 5
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A )
 Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 25 Settembre y=x 2 =i L
 .9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
.9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
SOLUZIONI SCRITTO DI ANALISI MATEMATICA II - 24/06/08. C.L. in Matematica e Matematica per le Applicazioni
 SOLUZIONI SCRITTO DI ANALISI MATEMATICA II - 4/06/08 C.L. in Maemaica e Maemaica per le Applicazioni Prof. K. R. Payne e Do. M. Calanchi, C. Tarsi, L. Vesely Soluzione esercizio. (a) Sia f definia da f(x)
SOLUZIONI SCRITTO DI ANALISI MATEMATICA II - 4/06/08 C.L. in Maemaica e Maemaica per le Applicazioni Prof. K. R. Payne e Do. M. Calanchi, C. Tarsi, L. Vesely Soluzione esercizio. (a) Sia f definia da f(x)
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 21 Luglio 2008
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
Lezione 5. Calcolo dell antitrasformata di Laplace. F. Previdi - Automatica - Lez. 5 1
 Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Equazioni Differenziali (5)
 Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Soluzioni degli esercizi di Analisi Matematica I
 Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Outline. La trasformata di Laplace. (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi
 Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
Ricerca Operativa. Facoltà di Ingegneria dell Informazione, Informatica e Statistica. (Massimo Flusso) Giovanni Fasano.
 Facolà di Ingegneria dell Informazione, Informaica e Saiica Appuni dalle lezioni di Ricerca Operaiva (Maimo Fluo) ede di Laina Giovanni Faano faano@unive.i hp://venu.unive.i/ faano anno accademico 2013-2014
Facolà di Ingegneria dell Informazione, Informaica e Saiica Appuni dalle lezioni di Ricerca Operaiva (Maimo Fluo) ede di Laina Giovanni Faano faano@unive.i hp://venu.unive.i/ faano anno accademico 2013-2014
Note per la Lezione 29 Ugo Vaccaro
 Progeaione di Algorimi Anno Accademico 1 1 Noe per la Leione Ugo Vaccaro In quea leione coninueremo lo udio di cammini minimin grafi in cui vi poono eere archi di coo negaivo. Ricordiamo l algorimo baao
Progeaione di Algorimi Anno Accademico 1 1 Noe per la Leione Ugo Vaccaro In quea leione coninueremo lo udio di cammini minimin grafi in cui vi poono eere archi di coo negaivo. Ricordiamo l algorimo baao
Proprietà della Trasformata. Funzioni trasformabili (1/3) L {af(t) + bg(t)} (s) = (af(t) + bg(t))e st dt. Tabella 1. = a f(t)e st dt + b g(t)e st dt
 Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 27/28 (aggiornaa al 8//27) 2 Proprieà della rasformaa
Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 27/28 (aggiornaa al 8//27) 2 Proprieà della rasformaa
Rappresentazione del sistema. Classificazione dei sistemi di controllo
 Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Lezione 9. Calcolo dell antitrasformata di Laplace. F. Previdi - Fondamenti di Automatica - Lez. 9 1
 ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
campionatore - converte un segnale a tempo continuo in una sequenza sono quindi presenti sia variabili a tempo discreto sia variabili a tempo
 Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
27 DERIVATE DI ORDINI SUCCESSIVI
 27 DERIVATE DI ORDINI SUCCESSIVI Definizione Sia f derivabile sull inervallo I. Se esise la derivaa della funzione x f (x) in x, allora (f ) (x) si dice la derivaa seconda di f in x, e si denoa con f (x)
27 DERIVATE DI ORDINI SUCCESSIVI Definizione Sia f derivabile sull inervallo I. Se esise la derivaa della funzione x f (x) in x, allora (f ) (x) si dice la derivaa seconda di f in x, e si denoa con f (x)
Lezione 4. Risposte canoniche dei sistemi del primo e del secondo ordine
 Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Laboratorio di Algoritmi e Strutture Dati
 Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Laboraorio di Algorimi e Sruure Dai Aniello Murano hp://people.na.infn.i people.na.infn.i/~murano/ 1 Algorimi per il calcolo di percori minimi u un grafo 1 Un emplice problema Problema: Supponiamo che
Teoria dei Segnali. La Convoluzione (esercizi) parte prima
 Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
Note per la Lezione 33 Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 208 209 Noe per la Lezione 33 Ugo Vaccaro In quea lezione vedremo alcune applicazioni dei riulai ul calcolo del fluo maimo, derivai nelle lezioni precedeni. Prima
Progeazione di Algorimi Anno Accademico 208 209 Noe per la Lezione 33 Ugo Vaccaro In quea lezione vedremo alcune applicazioni dei riulai ul calcolo del fluo maimo, derivai nelle lezioni precedeni. Prima
SEGNALI E SISTEMI (a.a ) Prof. M. Pavon Esercizi risolti 6 Attenzione: u(t) = 1l(t)
 SEGNALI E SISTEMI (a.a. 9-) Prof. M. Pavon Esercizi risoli 6 Aenzione: u() = l(). Si deermini il periodo fondamenale T e i coefficieni di Fourier a k del segnale a empo coninuo sen + 4 cos + cos(6 π 4
SEGNALI E SISTEMI (a.a. 9-) Prof. M. Pavon Esercizi risoli 6 Aenzione: u() = l(). Si deermini il periodo fondamenale T e i coefficieni di Fourier a k del segnale a empo coninuo sen + 4 cos + cos(6 π 4
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del..9 TEMA Esercizio Si consideri la funzione f(x) = e x 6 x+, x D =], [. i) deerminare i ii di f agli esremi di D e gli evenuali asinoi;
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del..9 TEMA Esercizio Si consideri la funzione f(x) = e x 6 x+, x D =], [. i) deerminare i ii di f agli esremi di D e gli evenuali asinoi;
ANALISI VETTORIALE ESERCIZI SU EQUADIFF. y = y(y 1)t. = e C e t2 /2 y 1 y
 ANALISI VETTORIALE ESERCIZI SU EQUADIFF Esercizio Calcolare l inegrale generale dell equazione differenziale = ( ) e deerminare quali soluzioni sono definie su uo R. Risposa Fuori dagli equilibri = 0 e
ANALISI VETTORIALE ESERCIZI SU EQUADIFF Esercizio Calcolare l inegrale generale dell equazione differenziale = ( ) e deerminare quali soluzioni sono definie su uo R. Risposa Fuori dagli equilibri = 0 e
Note per la Lezione 28 Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 2017 2018 Noe per la Lezione 28 Ugo Vaccaro In quea lezione udieremo ancora problemi u cammini minimi, ma in grafi in cui vi poono eere archi di coo negaivo. Quindi,
Progeazione di Algorimi Anno Accademico 2017 2018 Noe per la Lezione 28 Ugo Vaccaro In quea lezione udieremo ancora problemi u cammini minimi, ma in grafi in cui vi poono eere archi di coo negaivo. Quindi,
RICERCA OPERATIVA GRUPPO A prova scritta del 5 luglio 2010
 RICERCA OPERATIVA GRUPPO A prova cria del luglio 00. Dao il problema di programmazione lineare P) min z = x +x +x max y + y x x x = y +y < x + x x y + y < x, x, x 0 y y < y > 0 a) coruirne il duale D;
RICERCA OPERATIVA GRUPPO A prova cria del luglio 00. Dao il problema di programmazione lineare P) min z = x +x +x max y + y x x x = y +y < x + x x y + y < x, x, x 0 y y < y > 0 a) coruirne il duale D;
Università degli Studi di Firenze Corso di Laurea triennale in Fisica e Astrofisica
 Universià degli Sudi di Firenze Corso di Laurea riennale in Fisica e Asrofisica Analisi Maemaica I (A.A. 5/6) Proff. F. Bucci & E. Paolini Seconda prova inercorso ( Dicembre 5). Dimosrare che per ogni
Universià degli Sudi di Firenze Corso di Laurea riennale in Fisica e Asrofisica Analisi Maemaica I (A.A. 5/6) Proff. F. Bucci & E. Paolini Seconda prova inercorso ( Dicembre 5). Dimosrare che per ogni
1) Determinare la soluzione massimale del problema di Cauchy. 2) Determinare la soluzione massimale del problema di Cauchy.
 Capiolo 3 Equazioni differenziali Esercizi ) Deerminare la soluzione massimale del problema di Cauchy y ()= y() 4 3 y()= ) Deerminare la soluzione massimale del problema di Cauchy y ()= 4 + 6 y()+ 8 (
Capiolo 3 Equazioni differenziali Esercizi ) Deerminare la soluzione massimale del problema di Cauchy y ()= y() 4 3 y()= ) Deerminare la soluzione massimale del problema di Cauchy y ()= 4 + 6 y()+ 8 (
ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA 1 SETTIMANA 27
 ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA SETTIMANA 27.. Convergenza di inegrali generalizzai. () Per ognuno dei segueni inegrali impropri deerminae qual è l insieme dei valori del paramero α > per
ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA SETTIMANA 27.. Convergenza di inegrali generalizzai. () Per ognuno dei segueni inegrali impropri deerminae qual è l insieme dei valori del paramero α > per
UNITA 3. LE EQUAZIONI GONIOMETRICHE.
 UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, eno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, eno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
INTRODUZIONE ALLE LEGGI FINANZIARIE
 Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Inroduzione alle leggi finanziarie Operazione finanziaria u due dae: S - S + I INTRODUZIONE ALLE LEGGI FINANZIARIE 0 1 anni Legge di equivalenza ineremporale inrodoa dal conrao finanziario: 0 S 1 S + I
Volume FISICA. Elementi di teoria ed applicazioni. Fisica 1
 Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Problema del flusso massimo
 Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
Ulteriori Esercizi su Grafi. Ugo Vaccaro
 Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Progeazione di Algorimi Anno Accademico 0 0 Uleriori Eercizi u Grafi. Ugo Vaccaro N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu e da un analii
Progettazione di Algoritmi Anno Accademico Esercizi su Grafi: Parte Seconda
 Progeazione di Algorimi Anno Accademico 0 09 Eercizi Ugo Vaccaro Eercizi u Grafi: Pare Seconda N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu
Progeazione di Algorimi Anno Accademico 0 09 Eercizi Ugo Vaccaro Eercizi u Grafi: Pare Seconda N.B. Si ricorda che ogni algorimo và accompagnao da una argomenazione ul perchè calcola correamene l oupu
Problema del flusso massimo
 Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
Rei di fluo Problema del fluo maimo Moivazione iniziale: problemi di raffico u rei di raporo Trapori ferroviari, auoradali, Traporo di liquidi in rei idriche Traporo di pacchei di dai in una ree di comunicazione.
La cicloide. Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche, Ancona
 La cicloide Flaviano Baelli Diparimeno di Scienze Maemaiche Universià Poliecnica delle Marche, Ancona In una circonferenza γ di raggio r che poggia su una rea fissiamo un puno P e facciamo roolare senza
La cicloide Flaviano Baelli Diparimeno di Scienze Maemaiche Universià Poliecnica delle Marche, Ancona In una circonferenza γ di raggio r che poggia su una rea fissiamo un puno P e facciamo roolare senza
Esercizi & Domande per il Compito di Elettrotecnica del 24 giugno 2002
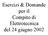 Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
PARTE 4: CINEMATICA DEL PUNTO MATERIALE
 PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
ALGEBRA DEGLI SCHEMI A BLOCCHI. La figura seguente rappresenta una relazione ingresso/uscita in forma grafica.
 Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
Analisi Matematica 3/Analisi 4 - SOLUZIONI (19/01/2015)
 Corso di Laurea in Maemaica Docene: Claudia Anedda Analisi Maemaica 3/Analisi 4 - SOLUZIONI (19/1/215) 1) Daa la serie x b e nx [(n + 1) 2 e x n 2 ], n1 b N +, b pari: i) dimosrare che essa è una serie
Corso di Laurea in Maemaica Docene: Claudia Anedda Analisi Maemaica 3/Analisi 4 - SOLUZIONI (19/1/215) 1) Daa la serie x b e nx [(n + 1) 2 e x n 2 ], n1 b N +, b pari: i) dimosrare che essa è una serie
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI
 DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine egnale i indica una funzione, generalmene del empo, che rappreena la legge di variazione di una grandezza fiica, (acuica, elerica, oica ec.) la preione
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine egnale i indica una funzione, generalmene del empo, che rappreena la legge di variazione di una grandezza fiica, (acuica, elerica, oica ec.) la preione
5. L integrale improprio x 2 : (a) diverge. (b) converge a 0 = lim. (c) converge a π 4 (d) è uguale al valore del limite
 INTEGRALI IMPROPRI Tes di auovaluazione. L inegrale improprio 5 d : (a) vale 4 5 (c) vale 5 4 (d) è negaivo.. L inegrale improprio 4 + 5 d : (a) vale 4 5 (c) vale 4 5 (d) ende a.. L inegrale improprio
INTEGRALI IMPROPRI Tes di auovaluazione. L inegrale improprio 5 d : (a) vale 4 5 (c) vale 5 4 (d) è negaivo.. L inegrale improprio 4 + 5 d : (a) vale 4 5 (c) vale 4 5 (d) ende a.. L inegrale improprio
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 1
 Universià Carlo Caaneo Ingegneria gesionale Analisi maemaica aa 06/07 EQUAZIONI DIFFERENZIALI ESERCIZI CON SOLUZIONE Trovare l inegrale generale dell equazione ' Si raa di un equazione differenziale lineare
Universià Carlo Caaneo Ingegneria gesionale Analisi maemaica aa 06/07 EQUAZIONI DIFFERENZIALI ESERCIZI CON SOLUZIONE Trovare l inegrale generale dell equazione ' Si raa di un equazione differenziale lineare
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Probabilià e Saisica 26-7 PBaldi, GTerenzi Tuorao 5, 2 aprile 27 Corso di Laurea in Maemaica Esercizio Dire se esisono delle cosani c ali che le funzioni a) f (x)
UNIVERSITÀ di ROMA TOR VERGATA Corso di Probabilià e Saisica 26-7 PBaldi, GTerenzi Tuorao 5, 2 aprile 27 Corso di Laurea in Maemaica Esercizio Dire se esisono delle cosani c ali che le funzioni a) f (x)
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 EQUAZIONI DIFFERENZIALI 1
 Universià Carlo Caaneo Ingegneria gesionale Analisi maemaica aa 07/08 EQUAZIONI DIFFERENZIALI ESERCIZI CON SOLUZIONE Trovare l inegrale generale dell equazione ' Si raa di un equazione differenziale lineare
Universià Carlo Caaneo Ingegneria gesionale Analisi maemaica aa 07/08 EQUAZIONI DIFFERENZIALI ESERCIZI CON SOLUZIONE Trovare l inegrale generale dell equazione ' Si raa di un equazione differenziale lineare
UNITA 3. LE EQUAZIONI GONIOMETRICHE.
 UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
TRASFORMATE DI LAPLACE
 CONTROLLI AUTOMATICI Ingegneria della Gesione Indusriale e della Inegrazione di Impresa hp://www.auomazione.ingre.unimore.i/pages/corsi/conrolliauomaicigesionale.hm Trasformae di Laplace Gli esempi visi
CONTROLLI AUTOMATICI Ingegneria della Gesione Indusriale e della Inegrazione di Impresa hp://www.auomazione.ingre.unimore.i/pages/corsi/conrolliauomaicigesionale.hm Trasformae di Laplace Gli esempi visi
e sostituendo il valore =6 si ottiene che:
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 011 CORSO DI ORDINAMENTO Quesionario Quesio 1 Poniamo = con i limii geomerici 0
ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 011 CORSO DI ORDINAMENTO Quesionario Quesio 1 Poniamo = con i limii geomerici 0
Claudio Arbib Università dell Aquila. Ricerca Operativa. Problemi di cammino ottimo
 Claudio Arbib Univerià dell Aquila Ricerca Operaiva Problemi di cammino oimo Sommario Il problema del cammino più breve Il problema del cammino più icuro Una formulazione come PL 0- Proprieà della formulazione
Claudio Arbib Univerià dell Aquila Ricerca Operaiva Problemi di cammino oimo Sommario Il problema del cammino più breve Il problema del cammino più icuro Una formulazione come PL 0- Proprieà della formulazione
TRASFORMATA DI FOURIER DI DISTRIBUZIONI
 TRASFORMATA DI FOURIER DI DISTRIBUZIONI Tue le proprieà vise per la rasformaa di Fourier sono applicabili alle funzioni dello spazio S. Queso permee di rasferire le sesse proprieà alle disribuzioni di
TRASFORMATA DI FOURIER DI DISTRIBUZIONI Tue le proprieà vise per la rasformaa di Fourier sono applicabili alle funzioni dello spazio S. Queso permee di rasferire le sesse proprieà alle disribuzioni di
Algebra vettoriale. risultante. B modulo, direzione e verso A punto di applicazione. Somma e differenza di vettori: a + b = c
 Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Algoritmi greedy III parte
 Algorimi greedy III pare Progeazione di Algorimi a.a. -1 Maricole congrue a 1 Docene: Annalia De Boni 1 Cammini minimi Si vuole andare da Napoli a Milano in auo percorrendo il minor numero di chilomeri
Algorimi greedy III pare Progeazione di Algorimi a.a. -1 Maricole congrue a 1 Docene: Annalia De Boni 1 Cammini minimi Si vuole andare da Napoli a Milano in auo percorrendo il minor numero di chilomeri
Svolgimento. Applicando la formula di Eulero. x(t) = e ( 1+j20)t 2j = 2je t ( cos 20t + j sin 20t) = 2e t (j cos 20t sin 20t) quindi
 SEGNALI E SISTEMI (a.a. 9-) Prof. M. Pavon Esercizi risoli. Si esprima la pare reale di x() = e ( +j) j, R nella forma Ae a cos(ω + ϕ) con A, a, ω, φ reali con A > e π < φ π. Svolgimeno. Applicando la
SEGNALI E SISTEMI (a.a. 9-) Prof. M. Pavon Esercizi risoli. Si esprima la pare reale di x() = e ( +j) j, R nella forma Ae a cos(ω + ϕ) con A, a, ω, φ reali con A > e π < φ π. Svolgimeno. Applicando la
Vediamo come si sviluppa la soluzione esplicita del problema. ( t)
 Analisi ransioria L'analisi dinamica ransioria (dea anche analisi emporale) è una ecnica che consene di deerminare la risposa dinamica di una sruura soggea ad una generica ecciazione emporale Gli effei
Analisi ransioria L'analisi dinamica ransioria (dea anche analisi emporale) è una ecnica che consene di deerminare la risposa dinamica di una sruura soggea ad una generica ecciazione emporale Gli effei
Calcolo della funzione di trasferimento P(s) Progetto del controllore in base alle specifiche
 Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
Metodo della Trasformata di Laplace (mtl)
 Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
2.4 Flussi di valore massimo
 .4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
.4 Flui di valore maimo I modelli di fluo hanno variae applicazioni in eori come elecomunicazioni informaica (muliproceori, proocolli inerne) rapori (aereo, radale, ferroviario, merci) Si raa di diribuire
TRASFORMAZIONE DEI SEGNALI. Lineari (tra cui il Filtraggio) Non Lineari
 TRASFORMAZIONE DEI SEGNALI SENZA MEMORIA: ZMNL (Zero-Memory Non Lineariy) g x( ) y = CON MEMORIA: Lineari (ra cui il Filraggio) Non Lineari L5/1 TRASFORMAZIONI SENZA MEMORIA (ISTANTANEE) y Limiazione dura
TRASFORMAZIONE DEI SEGNALI SENZA MEMORIA: ZMNL (Zero-Memory Non Lineariy) g x( ) y = CON MEMORIA: Lineari (ra cui il Filraggio) Non Lineari L5/1 TRASFORMAZIONI SENZA MEMORIA (ISTANTANEE) y Limiazione dura
Analisi Matematica II Corso di Ingegneria Gestionale Compito del log 1 + x2 y 2
 Analisi Maemaica II Corso di Ingegneria Gesionale Compio del 5-7-7 - È obbligaorio consegnare ui i fogli, anche la brua e il eso. - Le rispose senza giusificazione sono considerae nulle. Esercizio. puni
Analisi Maemaica II Corso di Ingegneria Gesionale Compio del 5-7-7 - È obbligaorio consegnare ui i fogli, anche la brua e il eso. - Le rispose senza giusificazione sono considerae nulle. Esercizio. puni
Controlli Automatici L
 Segnali e rasformae - Corso di Laurea in Ingegneria Meccanica Segnali e rasformae DEIS-Universià di Bologna el. 5 93 Email: crossi@deis.unibo.i URL: www-lar.deis.unibo.i/~crossi Segnali e rasformae - Segnali
Segnali e rasformae - Corso di Laurea in Ingegneria Meccanica Segnali e rasformae DEIS-Universià di Bologna el. 5 93 Email: crossi@deis.unibo.i URL: www-lar.deis.unibo.i/~crossi Segnali e rasformae - Segnali
Tema 3. Insiemi, elementi di logica, calcolo combinatorio, relazioni e funzioni
 Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
ESERCIZI di TEORIA dei SEGNALI. La Correlazione
 ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
Dispositivi e Sistemi Meccanici. 11 Esercizi. Politecnico di Torino CeTeM. Esercizio 11
 Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Soluzione. Le componenti del gradiente sono le derivate parziali della funzione: cos y 0 (x 0, y 0 ) domf =R 2. sin y 0 (x x 0 ) + e x 0
 Gradiene e piano angene Definizione 1 Sia f : A R 2 R, f derivabile in (x 0, y 0 ) A). Definiamo il veore gradiene di f in (x 0, y 0 ): f(x 0, y 0 ) = (f x (x 0, y 0 ), f y (x 0, y 0 )). Definiamo il piano
Gradiene e piano angene Definizione 1 Sia f : A R 2 R, f derivabile in (x 0, y 0 ) A). Definiamo il veore gradiene di f in (x 0, y 0 ): f(x 0, y 0 ) = (f x (x 0, y 0 ), f y (x 0, y 0 )). Definiamo il piano
Ci domandiamo allora se e sempre possibile rappresentare una funzione in questo modo.
 1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
f v, lim allora x, y x, y e analogamente se 0,1 Osserviamo che la derivata direzionale esiste per ogni punto x y e ogni vettore,2 0,0 cos 2 1
 DERIVATA DIREZIONALE La definizione di derivaa direzionale è y, lim,, f v y v f y v, v Se v, allora, y, y e analogamene se,, y, y f, y y Calcolare la derivaa direzionale della funzione dove v allora dom
DERIVATA DIREZIONALE La definizione di derivaa direzionale è y, lim,, f v y v f y v, v Se v, allora, y, y e analogamene se,, y, y f, y y Calcolare la derivaa direzionale della funzione dove v allora dom
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondameni di elecomunicazioni - SEGNALI E SPERI Prof. Mario Barbera [pare ] Sruura della lezione Proprieà dei segnali Valore medio, valore efficace, poenza, energia rasformaa di Fourier e speri
Corso di Fondameni di elecomunicazioni - SEGNALI E SPERI Prof. Mario Barbera [pare ] Sruura della lezione Proprieà dei segnali Valore medio, valore efficace, poenza, energia rasformaa di Fourier e speri
n 1 Un esempio di sistema rappresentabile con equazioni differenziali lineari del tipo (1) è illustrato in Appendice.
 RICHIAMI SULLE FUNZIONI DI TRASFERIMENTO, TRASFORMATE DI FOURIER E LAPLACE E DIAGRAMMI DI BODE Univerià di Padova Facolà di Ingegneria Coro di Fondameni di Eleronica A.A.4/5 Padova, 4//5 Le noe egueni
RICHIAMI SULLE FUNZIONI DI TRASFERIMENTO, TRASFORMATE DI FOURIER E LAPLACE E DIAGRAMMI DI BODE Univerià di Padova Facolà di Ingegneria Coro di Fondameni di Eleronica A.A.4/5 Padova, 4//5 Le noe egueni
EQUAZIONI GONIOMETRICHE
 EQUAZIONI GONIOMETRICHE ) risolvere: cos + cos 0 Si raa di un caso riconducibile ad un equazione algebrica di grado nell incognia cos, per cui si può scrivere: cos ± + 8 4 cos cos 80 + k60 ± 60 + k60 6)
EQUAZIONI GONIOMETRICHE ) risolvere: cos + cos 0 Si raa di un caso riconducibile ad un equazione algebrica di grado nell incognia cos, per cui si può scrivere: cos ± + 8 4 cos cos 80 + k60 ± 60 + k60 6)
Esercizi di Teoria dei Segnali. La Trasformata di Fourier
 Esercizi di Teoria dei Segnali La Trasformaa di Fourier 1 Esercizio 1 Calcolare la rasformaa di Fourier del segnale di fig. 1.1. x() A B - T/ T/ fig.1.1 Per calcolare la rasformaa di queso segnalesi può
Esercizi di Teoria dei Segnali La Trasformaa di Fourier 1 Esercizio 1 Calcolare la rasformaa di Fourier del segnale di fig. 1.1. x() A B - T/ T/ fig.1.1 Per calcolare la rasformaa di queso segnalesi può
REGISTRAZIONE DEL MOTO. Lo scopo è riempire una tabella t/s (istante di tempo/posizione occupata)
 REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
Teoria dei segnali terza edizione
 eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
CRESCITA. Modello di Solow
 CRESCITA Modello di Solow Modello di Solow (956) Idea: la crecia è dovua all accumulo di capiale. Capiale fiico () Y S I ecc. (idea di circolarià, ma aenzione a rendimeni decreceni di Ipoei: Economia chiua
CRESCITA Modello di Solow Modello di Solow (956) Idea: la crecia è dovua all accumulo di capiale. Capiale fiico () Y S I ecc. (idea di circolarià, ma aenzione a rendimeni decreceni di Ipoei: Economia chiua
Soluzione degli esercizi del Capitolo 3
 Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Ricordando dal Paragrafo A.6 dell Appendice A che è facile oenere ẋ () d d ( (e A e A x + Ae (e A A x + ( A e A( ) x + Ax () + Bu () d ( e
Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Ricordando dal Paragrafo A.6 dell Appendice A che è facile oenere ẋ () d d ( (e A e A x + Ae (e A A x + ( A e A( ) x + Ax () + Bu () d ( e
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel. e 5x dx.
 Universià di Triese Facolà d Ingegneria. Eserciazioni per la preparazione della prova scria di Maemaica 3 Do. Franco Obersnel Lezione 7: inegrali generalizzai; funzioni definie da inegrali. Esercizio.
Universià di Triese Facolà d Ingegneria. Eserciazioni per la preparazione della prova scria di Maemaica 3 Do. Franco Obersnel Lezione 7: inegrali generalizzai; funzioni definie da inegrali. Esercizio.
SESSIONE SUPPLETIVA PROBLEMA 2
 www.maefilia.i SESSIONE SUPPLETIVA - 26 PROBLEMA 2 Fissao k R, la funzione g k :R R è così definia: g k = e kx2. Si indica con Γ k il suo grafico, in un riferimeno caresiano Oxy. ) Descrivi, a seconda
www.maefilia.i SESSIONE SUPPLETIVA - 26 PROBLEMA 2 Fissao k R, la funzione g k :R R è così definia: g k = e kx2. Si indica con Γ k il suo grafico, in un riferimeno caresiano Oxy. ) Descrivi, a seconda
Regime di capitalizzazione: una famiglia di funzioni fattore di montante che dipende da uno o più parametri.
 5. Teoria generale Regimi finanziari Nel capiolo precedene abbiamo inrodoo alcuni parameri in grado di descrivere ualsiasi ipo di regime. Ciò ci permee di definire in generale i regimi finanziari. Regime
5. Teoria generale Regimi finanziari Nel capiolo precedene abbiamo inrodoo alcuni parameri in grado di descrivere ualsiasi ipo di regime. Ciò ci permee di definire in generale i regimi finanziari. Regime
Anno 4 Equazioni goniometriche lineari e omogenee
 Anno 4 Equazioni goniomeriche lineari e omogenee Inroduzione In quesa lezione descriveremo le equazioni goniomeriche lineari e omogenee. Esamineremo le definizioni e illusreremo i meodi risoluivi per ogni
Anno 4 Equazioni goniomeriche lineari e omogenee Inroduzione In quesa lezione descriveremo le equazioni goniomeriche lineari e omogenee. Esamineremo le definizioni e illusreremo i meodi risoluivi per ogni
SISTEMI LINEARI TEMPO INVARIANTI
 SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale x(, deo ingresso, generando
SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale x(, deo ingresso, generando
CONTROLLI AUTOMATICI Ingegneria Meccatronica
 CONTROLLI AUTOMATICI Ingegneria Meccaronica TRASFORMATE DI LAPLACE Prof. Cesare Fanuzzi Ing. Crisian Secchi e-mail: cesare.fanuzzi@unimore.i, crisian.secchi@unimore.i hp://www.auomazione.ingre.unimore.i
CONTROLLI AUTOMATICI Ingegneria Meccaronica TRASFORMATE DI LAPLACE Prof. Cesare Fanuzzi Ing. Crisian Secchi e-mail: cesare.fanuzzi@unimore.i, crisian.secchi@unimore.i hp://www.auomazione.ingre.unimore.i
Corso di laurea in Ingegneria Meccatronica CONTROLLI AUTOMATICI E CA - 03 FUNZIONE DI TRASFERIMENTO
 Auomaion Roboics and Sysem CONTROL Corso di laurea in Ingegneria Meccaronica CONTROLLI AUTOMATICI E AZIONAMENTI ELETTRICI CA - 03 FUNZIONE DI TRASFERIMENTO Universià degli Sudi di Modena e Reggio Emilia
Auomaion Roboics and Sysem CONTROL Corso di laurea in Ingegneria Meccaronica CONTROLLI AUTOMATICI E AZIONAMENTI ELETTRICI CA - 03 FUNZIONE DI TRASFERIMENTO Universià degli Sudi di Modena e Reggio Emilia
Esercizi & Domande per il Compito di Elettrotecnica del 1 giugno 2004
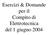 Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
Titolo unità. Dalla serie alla trasformata di Fourier Proprietà della trasformata di Fourier Uguaglianza di Parseval e principio di indeterminazione
 Inroduzione ai segnali deerminai iolo unià Dalla serie alla rasormaa di ourier Proprieà della rasormaa di ourier Uguaglianza di Parseval e principio di indeerminazione 005 Poliecnico di orino 1 Dalla serie
Inroduzione ai segnali deerminai iolo unià Dalla serie alla rasormaa di ourier Proprieà della rasormaa di ourier Uguaglianza di Parseval e principio di indeerminazione 005 Poliecnico di orino 1 Dalla serie
*5$1'(==(3(5,2',&+( W GW
 *51'((3(5'&+( 3UQFSDOGQ]RQ Una grandezza empodipendene D) si definisce SURGFD quando ad uguali inervalli T assume valori uguali cioè quando vale la relazione (con n inero qualsiasi): ( ) D( Q) D + (1)
*51'((3(5'&+( 3UQFSDOGQ]RQ Una grandezza empodipendene D) si definisce SURGFD quando ad uguali inervalli T assume valori uguali cioè quando vale la relazione (con n inero qualsiasi): ( ) D( Q) D + (1)
CM89sett.tex COMPLEMENTI DI MATEMATICA a.a Laurea magistrale in Ingegneria Elettrotecnica
 1 CM89se.ex COMPLEMENTI DI MATEMATICA a.a. 28-29 Laurea magisrale in Ingegneria Eleroecnica Nona seimana 24.11.28 - lunedì (2 ore) Commeno della prova parziale (vd. file CM8IcoA-B-C-D.pdf). Definizione
1 CM89se.ex COMPLEMENTI DI MATEMATICA a.a. 28-29 Laurea magisrale in Ingegneria Eleroecnica Nona seimana 24.11.28 - lunedì (2 ore) Commeno della prova parziale (vd. file CM8IcoA-B-C-D.pdf). Definizione
Progetto e Ottimizzazione di Reti A. A
 Progeo e Oimizzazione di Rei A. A. 006-007 Docene Fabrizio Roi roi@di.univaq.i Orario Maredi 15-17 aula.5 Mercoledi 11.30-13.30 aula.5 Giovedi 11.30-13.30 aula.5 Orario di ricevimeno Mercoledi 17-19 Progeo
Progeo e Oimizzazione di Rei A. A. 006-007 Docene Fabrizio Roi roi@di.univaq.i Orario Maredi 15-17 aula.5 Mercoledi 11.30-13.30 aula.5 Giovedi 11.30-13.30 aula.5 Orario di ricevimeno Mercoledi 17-19 Progeo
Problema 1: Una collisione tra meteoriti
 Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
