Diffrazione di raggi X
|
|
|
- Rossana Ricciardi
- 8 anni fa
- Просмотров:
Транскрипт
1 Diffrazione di raggi X Campione radiazione rivelatore tecnica monocromatica pellicole Oscillante Weissenberg Buerger Gandolfi Cristallo singolo Contatore (convenzionale, IP, CCD) Diffrattometro a 4-cerchi Metodi sperimentali bianca Pellicole, IP, CCD Laue pellicole Debye-Scherrer Polveri monocromatica contatore Diffrattometro di polveri Sfera di Ewald La costruzione geometrica della sfera di Ewald ci permette di visualizzare un esperimento di diffrazione La diffrazione avviene solo se un punto del r.r. interseca la sfera di Ewald Il raggio diffratto viaggerà dal centro della sfera di Ewald verso il punto in cui il punto di r.r. interseca la sfera. animazioni Legge di Bragg Sfera di Ewald Il raggio della sfera di Ewald è 1/λ 1
2 Metodo del cristallo rotante (I) informazioni: 1) parametri di cella: è possibile misurare il parametro reticolare lungo l asse di oscillazione 2) simmetria: è possibile ottenere informazioni su elementi di simmetria presenti nel cristallo? 3) indicizzazione: sì, ma Metodo del cristallo rotante (II) 1) misura di un parametro y1 tgα= R 1 1 y * = sinα= sin arctg λ λ R λ d( 010) = y1 sin arctg R nλ d (010) = y sin arctg n R d 1 2
3 Metodo del cristallo rotante (III) y 1 = 17 mm d 001 = 5.42 Å y 2 = 39.5 mm (d 002 = Å) d 001 = 5.43 Å Metodo del cristallo rotante (IV) A A RX A RX S S S S RX S S S S Vista lungo A A S S Vista lungo A A 3
4 Metodo del cristallo rotante (V) I diffrattogrammi di cristallo rotante (rotazione di 360 ) presentano sempre simmetria 2mm (punto di rotazione 2 con due linee di simmetria ortogonali), indipendentemente dalla simmetria del cristallo S S S S Metodo del cristallo oscillante (I) I diffrattogrammi di cristallo oscillante (rotazione di ) presentano in generale simmetria m solo se la simmetria della diffrazione del cristallo presenta effettivamente un piano di riflessione perpendicolarmente all asse di oscillazione 4
5 Metodo del cristallo oscillante (II) Cristallo rotante Simmetria del diffrattogramma = 2mm Simmetria del cristallo =? Cristallo oscillante Simmetria del diffrattogramma = m Simmetria di Laue del cristallo = un piano m all asse di rotazione Indicizzazione (I) In teoria, è anche possibile indicizzare un diffrattogramma di cristallo rotante. Infatti, conoscendo i parametri reticolari, è possibile ricostruire il reticolo reciproco e calcolare quale posizione avrà, per esempio, il riflesso 230 sulla stratolinea 0 di un rotante con asse di rotazione c b* b* a* a* 5
6 Indicizzazione (II) Il problema è che, in ogni piano di r.r., vettori aventi modulo assai simile incontrano la sfera di riflessione in punti assai vicini tra loro e danno quindi luogo ad effetti di diffrazione parzialmente o totalmente sovrapposti _ _ a* b* b* b* a* a* _ Indicizzazione (III) Il problema di una accurata indicizzazione dei riflessi può essere risolto con tecniche che permettano di separare spazialmente sulla pellicola riflessi che, pur corrispondendo a vettori reciproci di simile modulo, vengono prodotti in momenti diversi. Due tecniche principali: Metodo Weissenberg (vantaggio: semplice da un punto di vista operativo; svantaggio: immagine distorta del piano di r.r.) Metodo Buerger o di precessione (vantaggio: immagine non distorta del piano di r.r.; svantaggi: più complicato da ottenere; lo spazio di reticolo reciproco che si può esaminare è inferiore rispetto al metodo Weissenberg) 6
7 Metodo Weissenberg (I) Si utilizzano la stessa camera e la stessa disposizione sperimentale utilizzate per ottenere i diffrattogrammi di cristallo rotante/oscillante Si registrano solo i riflessi relativi ad un piano di reticolo reciproco (= una stratolinea nel diffr. di cristallo rotante/oscillante) Tutto il resto viene schermato (schermo che presenta una fenditura in corrispondenza del cono di diffrazione che ci interessa) Al movimento di rotazione del cristallo viene associato un movimento di traslazione della camera (e quindi della pellicola) Le macchie della stratolinea vengono quindi sparpagliate sull intera pellicola Metodo Weissenberg (II) Pellicola immobile Riflessi sovrapposti RX Pellicola che scorre parallelamente all asse Riflessi separati RX 7
8 Camera Weissenberg Tubo raggi X schermo (dx) collimatore schermo (sx) cristallo Camera Weissenberg 8
9 Weissenberg - Strato 0 (I) piano di r.r. hk0 a* b* Weissenberg - Strato 0 (II) (3) (2) (3) RX 1/λ (1) (1) (2) x 3 x 2 z 2 z 3 9
10 Weissenberg - Strato 0 (III) RX Y ω ω L altezza x alla quale la pellicola registra il fascio diffratto corrisponde all angolo Y (=2θ) Se ω è l angolo di rotazione del cristallo: Y = 2ω Inoltre: Y : 360 = x : 2πR da cui x = (2πR/360) Y = C 1 Y Per R = mm C 1 = 1/2 mm/grado D altra parte, l accoppiamento tra la rotazione ω del cristallo e la traslazione z della pellicola è scelto, normalmente, in modo che z = 1/2 ω = C 2 ω Poiché C 1 = C 2, dalla relazione Y = 2ω si ottiene che: x = 2z Weissenberg - Strato 0 (IV) x = 2z Ogni filare centrale si riprodurrà sulla pellicola come una retta con pendenza 2 T S OT OS ω O z = 1/2ω 10
11 Weissenberg - Strato 0 (V) I filari centrali non sono tutti uguali.. Alcuni sono più densamente popolati Alcuni coincidono con linee di simmetria Weissenberg - Strato 0 (VI) Cella nel reticolo diretto Piani atomici densamente popolati, e quindi con grandi distanze interplanari d Piani e filari atomici che coincidono con elementi di simmetria (100) Cella nel reticolo reciproco Vettori di reticolo reciproco più piccoli; filari di r.r. più fitti c e una relazione tra la simmetria della cella diretta e quella della cella reciproca (010)
12 Weissenberg - Strato 0 (VII) 45 mm Weissenberg - Strato 0 (VIII) x (in mm) = θ (in gradi) Eq. di Bragg 2 d sinθ = λ 2l x 2x Per ottenere il valore della distanza interplanare d 1) Si misura la distanza 2l (in mm) tra due riflessi eq. 2) Si calcola x = l * sin arctg2 3) Si applica l eq. di Bragg d = λ/2sinx 12
13 Weissenberg - Strato 0 (IX) Abbiamo visto come si presentano i filari centrali in un diffrattogramma Weissenberg. Vediamo ora che aspetto assumono i filari non centrali. piano di r.r. hk0 filare di r.r. 2k0 a* b* b* a* Indicizzazione
14 Weissenberg - Strati superiori Tranne nel caso di cristalli triclini, è possibile determinare tutte le costanti di cella mediante il solo diffrattogramma Weissenberg strato 0 ed il corrispondente diffrattogramma di cristallo rotante. Perché allora fare diffrattogrammi Weissenberg di strati superiori (1, 2, 3 )? 1) Per i cristalli triclini 2) Perché alcune serie di riflessi nello strato 0 potrebbero essere sistematicamente estinti (per la presenza di centrature di reticolo e/o slittopiani e/o elicogire), e potrei ottenere una cella più piccola di quella reale. Weissenberg - Strati superiori Esempio: Monoclino, gruppo spaziale C2/c 14
15 Metodo Buerger (precessione) (I) Il movimento del cristallo e della pellicola è tale da generare una immagine non distorta del piano di r.r. Angoli e distanze possono essere letti sulla pellicola più o meno direttamente (fattore di scala) Metodo Buerger (precessione) Condizioni di partenza: un asse del reticolo diretto del cristallo è parallelo alla direzione del fascio incidente (per esempio, l asse b) Il piano di reticolo reciproco h0l perpendicolare all asse b è allora tangente alla sfera di riflessione Piano h0l 15
16 Metodo Buerger (precessione) Adesso ruotiamo il vettore b di un angolo µ (solitamente = 30 ) rispetto alla direzione del fascio incidente Il piano di reticolo reciproco h0l adesso taglia la sfera di riflessione secondo una circonferenza di raggio sinµ/λ Metodo Buerger (precessione) Se all asse b viene fatto eseguire un movimento di precessione intorno alla direzione del fascio incidente, il piano di r.r. nel suo movimento solidale di precessione porterà a contatto della sfera di riflessione tutti i punti entro una circonferenza di raggio 2 (sinµ)/λ Una pellicola fotografica segue il moto di precessione del cristallo, mantenendosi sempre parallela al piano di r.r. 16
17 Camera Buerger (precessione) Camera Buerger (precessione) 17
18 esercizio 1 Misura dei parametri reticolari e riconoscimento della simmetria della diffrazione da pellicole di cristallo oscillante e Weissenberg strato zero. (Radiazione CuKα, λ = Å, raggio della camera R = mm) a) Quali informazioni sulla simmetria potete ottenere dallo spettro di cristallo oscillante? Verificate sulla vostra pellicola e annotate tali informazioni. Quanto misura il parametro reticolare nella direzione in cui il cristallo ruota? b) Quali informazioni sulla simmetria potete ottenere dallo spettro Weissenberg? Determinare i parametri reticolari su due filari principali e l angolo tra essi compreso. Tenendo conto anche delle informazioni ottenute in (a), provate a rispondere alle seguenti domande: A quale sistema appartiene il cristallo? Sono presenti piani di simmetria? Quali? Qual è la simmetria di Laue? Avete informazioni sufficienti per determinare il gruppo spaziale? Perché? Provate a dare gli indici ad alcuni riflessi dello strato zero. esercizio 2 Composto FIBC. Rotante [100]; Weissenberg (0kl), (1kl) e (2kl). Ottenere le stesse informazioni descritte nell esercizio 1. Inoltre, sulla base di spettri Weissenberg strato 0, 1 e 2, determinare le assenze sistematiche ed i possibili gruppi spaziali. E sufficiente lo strato zero per determinare correttamente i parametri reticolari? Perché? Completare la tabella: Simmetria di Laue Parametri di cella a b c α β γ Riflessi hkl presenti per 0kl h0l hk0 Gruppo/i spaziale/i 18
19 esercizio 3 β-nh 4 B 5 O 6 (OH) 4.2H 2 O. Manca lo spettro oscillante [010] (b = 8.66 Å); spettri Weissenberg (h0l), (h1l) e (h2l). Come l esercizio 2. Completare la tabella. Simmetria di Laue Parametri di cella a b 8.66 c α β γ Riflessi hkl presenti per 0kl h0l hk0 Gruppo/i spaziale/i 19
Diffrazione di Raggi X
 Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Interazione dei raggi X con la materia
 Interazione dei raggi X con la materia Emissione di fotoelettroni Fascio incidente (I 0 ) di raggi X Fluorescenza Scattering coerente e incoerente Assorbimento (I) calore Lo scattering coerente dei raggi
Interazione dei raggi X con la materia Emissione di fotoelettroni Fascio incidente (I 0 ) di raggi X Fluorescenza Scattering coerente e incoerente Assorbimento (I) calore Lo scattering coerente dei raggi
Diffrazione di Raggi-X da Monocristalli A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 Diffrazione di Raggi-X da Monocristalli A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Raccolta Dati di Diffrazione: Diffrazione di Raggi X Raccolta
Diffrazione di Raggi-X da Monocristalli A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Raccolta Dati di Diffrazione: Diffrazione di Raggi X Raccolta
DIFFRAZIONE DI ONDE NEI CRISTALLI
 DIFFRAZIONE DI ONDE NEI CRISTALLI Quando in cristallo si propaga un onda con λ a,b,c si verifica diffrazione dal suo studio è possibile ottenere informazioni su: Simmetria del cristallo (tipo di reticolo)
DIFFRAZIONE DI ONDE NEI CRISTALLI Quando in cristallo si propaga un onda con λ a,b,c si verifica diffrazione dal suo studio è possibile ottenere informazioni su: Simmetria del cristallo (tipo di reticolo)
Diffusione dei raggi X da parte di un elettrone
 Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
Diffusione dei raggi X da parte di un elettrone Consideriamo un onda elettro-magnetica piana polarizzata lungo x che si propaga lungo z L onda interagisce con un singolo elettrone (libero) inducendo un
Materiale didattico: dispense fornite durante il corso
 Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Struttura e geometria cristallina
 Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Simmetrie Cristallografiche A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE
 MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
MISURA DI LUNGHEZZE D ONDA CON UNO SPETTROSCOPIO A RETICOLO DI DIFFRAZIONE Il reticolo di diffrazione può essere utilizzato per determinare la lunghezza d onda di una radiazione monocromatica. Detto d
Reticoli di Bravais e sistemi cristallini
 Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Quando lungo il percorso della luce vi sono fenditure ed ostacoli con dimensioni dello stesso ordine di grandezza della lunghezza d'onda incidente
 OTTICA FISICA Quando lungo il percorso della luce vi sono fenditure ed ostacoli con dimensioni dello stesso ordine di grandezza della lunghezza d'onda incidente gli effetti sperimentali non sono spiegabili
OTTICA FISICA Quando lungo il percorso della luce vi sono fenditure ed ostacoli con dimensioni dello stesso ordine di grandezza della lunghezza d'onda incidente gli effetti sperimentali non sono spiegabili
Diffrazione di raggi X su polveri
 Diffrazione di raggi X su polveri Cenni di cristallochimica Generazione dei raggi X Diffrazione dei raggi X da parte dei cristalli Equazioni di Laue e Legge di Bragg Metodi diffrattometrici Motodo delle
Diffrazione di raggi X su polveri Cenni di cristallochimica Generazione dei raggi X Diffrazione dei raggi X da parte dei cristalli Equazioni di Laue e Legge di Bragg Metodi diffrattometrici Motodo delle
La diffrazione. Prof. F. Soramel Fisica Generale II - A.A. 2004/05 1
 La diffrazione Il fenomeno della diffrazione si incontra ogni volta che la luce incontra un ostacolo o un apertura di dimensioni paragonabili alla sua lunghezza d onda. L effetto della diffrazione è quello
La diffrazione Il fenomeno della diffrazione si incontra ogni volta che la luce incontra un ostacolo o un apertura di dimensioni paragonabili alla sua lunghezza d onda. L effetto della diffrazione è quello
Informazioni strutturali
 Informazioni strutturali Metodi spettroscopici (spettroscopia rotazionale, struttura rotazionale bande IR, NMR) Misure elettriche (momento di dipolo elettrico) Metodi diffrattometrici (raggi-x e neutroni;
Informazioni strutturali Metodi spettroscopici (spettroscopia rotazionale, struttura rotazionale bande IR, NMR) Misure elettriche (momento di dipolo elettrico) Metodi diffrattometrici (raggi-x e neutroni;
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 I raggi-x in mineralogia (pdf # 07) (2) - Mineralogia_2016/2017_Raggi X Raggi X: cosa sono e perché sono così importanti La scoperta dei RX ha rappresentato
Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 I raggi-x in mineralogia (pdf # 07) (2) - Mineralogia_2016/2017_Raggi X Raggi X: cosa sono e perché sono così importanti La scoperta dei RX ha rappresentato
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Spettrometro a reticolo e a prisma
 Spettrometro a reticolo e a prisma Marilena Teri, Valerio Toso & Ettore Zaffaroni (gruppo Lu4) 1 Introduzione 1.1 Introduzione ai feomeni in esame Quando la luce viene fatta incidere normalmente alla superficie
Spettrometro a reticolo e a prisma Marilena Teri, Valerio Toso & Ettore Zaffaroni (gruppo Lu4) 1 Introduzione 1.1 Introduzione ai feomeni in esame Quando la luce viene fatta incidere normalmente alla superficie
ESPERIMENTO DI YOUNG DOPPIA FENDITURA
 ESPERIMENTO DI YOUNG DOPPIA FENDITURA Larghezza fenditure a > d (L = distanza fenditure - schermo; d = distanza tra le fenditure) Evidenza della natura ondulatoria della luce Luce monocromatica
ESPERIMENTO DI YOUNG DOPPIA FENDITURA Larghezza fenditure a > d (L = distanza fenditure - schermo; d = distanza tra le fenditure) Evidenza della natura ondulatoria della luce Luce monocromatica
Apparati per uso industriale e ricerca Dott.ssa Alessandra Bernardini
 Apparati per uso industriale e ricerca Dott.ssa Alessandra Bernardini 1 Apparecchiature radiologiche per analisi industriali e ricerca Le apparecchiature a raggi X utilizzate nell industria utilizzano
Apparati per uso industriale e ricerca Dott.ssa Alessandra Bernardini 1 Apparecchiature radiologiche per analisi industriali e ricerca Le apparecchiature a raggi X utilizzate nell industria utilizzano
1 Distanza di un punto da una retta (nel piano)
 Esercizi 26/10/2007 1 Distanza di un punto da una retta (nel piano) Sia r = {ax + by + c = 0} una retta. Sia P = (p 1, p 2 ) R 2 un punto che non sta sulla retta r. Vogliamo vedere se si può parlare di
Esercizi 26/10/2007 1 Distanza di un punto da una retta (nel piano) Sia r = {ax + by + c = 0} una retta. Sia P = (p 1, p 2 ) R 2 un punto che non sta sulla retta r. Vogliamo vedere se si può parlare di
4.5 Polarizzazione Capitolo 4 Ottica
 4.5 Polarizzazione Esercizio 98 Un reticolo con N fenditure orizzontali, larghe a e con passo p, è posto perpendicolarmente a superficie di un liquido con n =.0. Il reticolo è colpito normalmente alla
4.5 Polarizzazione Esercizio 98 Un reticolo con N fenditure orizzontali, larghe a e con passo p, è posto perpendicolarmente a superficie di un liquido con n =.0. Il reticolo è colpito normalmente alla
RETTE E PIANI. ove h R. Determinare i valori di h per cui (1) r h e α sono incidenti ed, in tal caso, determinare l angolo ϑ h da essi formato;
 RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO
 I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO A differenza dei solidi amorfi, caratterizzati da disordine spaziale delle particelle (atomi o molecole) e isotropia delle proprietà fisiche, il solido cristallino
I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO A differenza dei solidi amorfi, caratterizzati da disordine spaziale delle particelle (atomi o molecole) e isotropia delle proprietà fisiche, il solido cristallino
Risposte ai quesiti D E H D
 Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Superfici e solidi di rotazione. Cilindri indefiniti
 Superfici e solidi di rotazione Consideriamo un semipiano α, delimitato da una retta a, e sul semipiano una curva g; facendo ruotare il semipiano in un giro completo attorno alla retta a, la curva g descrive
Superfici e solidi di rotazione Consideriamo un semipiano α, delimitato da una retta a, e sul semipiano una curva g; facendo ruotare il semipiano in un giro completo attorno alla retta a, la curva g descrive
Chimica Fisica dello Stato Solido 4 crediti lezioni frontali (32 ore) + 2 crediti (24 ore) di laboratorio/esercitazione
 Chimica Fisica dello Stato Solido 4 crediti lezioni frontali (3 ore) + crediti (4 ore) di laboratorio/esercitazione Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni
Chimica Fisica dello Stato Solido 4 crediti lezioni frontali (3 ore) + crediti (4 ore) di laboratorio/esercitazione Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni
SOLIDI. 10/05/2007 Chimica e Scienza e Tecnologia dei Materiali Elettrici L6 1
 SOLIDI Stato di aggregazione della materia caratterizzato da forma e volume proprio; gli atomi (ioni, molecole) si trovano in posizioni fisse e molto spesso ordinate nello spazio: Solido amorfo: ordine
SOLIDI Stato di aggregazione della materia caratterizzato da forma e volume proprio; gli atomi (ioni, molecole) si trovano in posizioni fisse e molto spesso ordinate nello spazio: Solido amorfo: ordine
Ottica fisica. Marcello Borromeo corso di Fisica per Farmacia - Anno Accademico
 Ottica fisica La natura ondulatoria della luce è stata evidenziata da Young ai primi dell 800 usando l interferenza e confutando l idea corpuscolare di Newton Le onde elettromagnetiche sono state previste
Ottica fisica La natura ondulatoria della luce è stata evidenziata da Young ai primi dell 800 usando l interferenza e confutando l idea corpuscolare di Newton Le onde elettromagnetiche sono state previste
Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi.
 Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi. (1) Sia A l insieme dei numeri dispari minori di 56 e divisibili per 3. Quale delle seguenti affermazioni
Domande di Analisi Matematica tratte dai Test di autovalutazione o di recupero dei debiti formativi. (1) Sia A l insieme dei numeri dispari minori di 56 e divisibili per 3. Quale delle seguenti affermazioni
Proprietà focali delle coniche.
 roprietà focali delle coniche. Mauro Saita e-mail: [email protected] Versione provvisoria, gennaio 2014 Indice 1 Coniche 1 1.1 arabola....................................... 1 1.1.1 roprietà focale
roprietà focali delle coniche. Mauro Saita e-mail: [email protected] Versione provvisoria, gennaio 2014 Indice 1 Coniche 1 1.1 arabola....................................... 1 1.1.1 roprietà focale
Diffrazione di raggi X da Polveri
 Corso di laurea triennale in Scienza dei Materiali a.a. 2016-2017 Diffrazione di raggi X da Polveri Docente: Ernesto Mesto e-mail: [email protected] Website: www.geo.uniba.it/mesto.html X-ray Powder
Corso di laurea triennale in Scienza dei Materiali a.a. 2016-2017 Diffrazione di raggi X da Polveri Docente: Ernesto Mesto e-mail: [email protected] Website: www.geo.uniba.it/mesto.html X-ray Powder
MECCANICA APPLICATA ALLE MACCHINE LS
 PROGRAMMA del CORSO TEORIA dei MECCANISMI Richiami di composizione dei meccanismi Richiami di cinematica I sistemi articolati piani (analisi e sintesi) e spaziali (cenni di analisi) Meccanismi con camme
PROGRAMMA del CORSO TEORIA dei MECCANISMI Richiami di composizione dei meccanismi Richiami di cinematica I sistemi articolati piani (analisi e sintesi) e spaziali (cenni di analisi) Meccanismi con camme
PNI 2014 SESSIONE STRAORDINARIA - QUESITI QUESITO 1
 www.matefilia.it PNI 0 SESSIONE STRAORDINARIA - QUESITI QUESITO Un gruppo di attivisti antinucleari ha organizzato una marcia di protesta verso un sito scelto per la costruzione di una centrale termonucleare.
www.matefilia.it PNI 0 SESSIONE STRAORDINARIA - QUESITI QUESITO Un gruppo di attivisti antinucleari ha organizzato una marcia di protesta verso un sito scelto per la costruzione di una centrale termonucleare.
L'intensità misurata per ogni segnale di diffrazione dipende:
 L'intensità misurata per ogni segnale di diffrazione dipende: dall'intensità incidente (I 0 ) da fattori strumentali e geometrici Fattore polarizzazione, se il raggio incidente non è polarizzato, la polarizzazione
L'intensità misurata per ogni segnale di diffrazione dipende: dall'intensità incidente (I 0 ) da fattori strumentali e geometrici Fattore polarizzazione, se il raggio incidente non è polarizzato, la polarizzazione
ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE
 ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE Scopo dell esperimento: studiare l ottica geometrica e i fenomeni di diffrazione MATERIALE A DISPOSIZIONE: 1 banco ottico 1 blocco di plexiglass 2 lenti con
ESPERIMENTO 6: OTTICA GEOMETRICA E DIFFRAZIONE Scopo dell esperimento: studiare l ottica geometrica e i fenomeni di diffrazione MATERIALE A DISPOSIZIONE: 1 banco ottico 1 blocco di plexiglass 2 lenti con
Capitolo 15. L interferenza e la natura ondulatoria della luce. Copyright 2009 Zanichelli editore
 Capitolo 15 L interferenza e la natura ondulatoria della luce 15.2 Il principio di sovrapposizione e l interferenza della luce Quando due onde luminose passano per uno stesso punto, i loro effetti si sommano
Capitolo 15 L interferenza e la natura ondulatoria della luce 15.2 Il principio di sovrapposizione e l interferenza della luce Quando due onde luminose passano per uno stesso punto, i loro effetti si sommano
POLARIZZAZIONE. I = < (E 0 cos ϕ) 2 > (1) dove < (E 0 cos ϕ) 2 > è il valore mediato nel tempo.
 POLARIZZAZIONE ESERCIZIO 1 Un fascio di luce naturale attraversa una serie di polarizzatori ognuno dei quali ha l asse di polarizzazione ruotato di 45 rispetto al precedente. Determinare quale frazione
POLARIZZAZIONE ESERCIZIO 1 Un fascio di luce naturale attraversa una serie di polarizzatori ognuno dei quali ha l asse di polarizzazione ruotato di 45 rispetto al precedente. Determinare quale frazione
Risolvere i seguenti esercizi (le soluzioni sono alla fine di tutti gli esercizi).
 La geometria analitica nello spazio: punti, vettori, rette e piani esercizi 1 prof D Benetti Risolvere i seguenti esercizi (le soluzioni sono alla fine di tutti gli esercizi) Esercizio 1 Determina due
La geometria analitica nello spazio: punti, vettori, rette e piani esercizi 1 prof D Benetti Risolvere i seguenti esercizi (le soluzioni sono alla fine di tutti gli esercizi) Esercizio 1 Determina due
Posizioni Atomiche nelle Celle Unitarie Cubiche
 Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
SOLIDI DI ROTAZIONE. Superficie cilindrica indefinita se la generatrice è una retta parallela all asse di rotazione
 SOLIDI DI ROTAZIONE Dato un semipiano α limitato dalla retta a, sia g una linea qualunque appartenente al semipiano α; ruotando il semipiano α di un angolo giro attorno alla retta a, la linea g genera
SOLIDI DI ROTAZIONE Dato un semipiano α limitato dalla retta a, sia g una linea qualunque appartenente al semipiano α; ruotando il semipiano α di un angolo giro attorno alla retta a, la linea g genera
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
C C B B. Fig. C4.1 Isometria.
 4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
Diffrazione di raggi X
 Diffrazione di raggi X Quando una radiazione X colpisce la faccia di un cristallo con un certo angolo di incidenza θ, essa in parte è diffusa dallo strato di atomi della superficie, in parte penetra verso
Diffrazione di raggi X Quando una radiazione X colpisce la faccia di un cristallo con un certo angolo di incidenza θ, essa in parte è diffusa dallo strato di atomi della superficie, in parte penetra verso
Principio di Huygens
 Ottica fisica La luce è stata considerata una particella da Newton fino a Young (inizi XIX secolo) Nell'800 si sono studiati i fenomeni ondulatori associati alla luce Nel secolo scorso alcuni effetti (fotoelettrico,
Ottica fisica La luce è stata considerata una particella da Newton fino a Young (inizi XIX secolo) Nell'800 si sono studiati i fenomeni ondulatori associati alla luce Nel secolo scorso alcuni effetti (fotoelettrico,
Un percorso di ottica parte III. Ottica ondulatoria
 Un percorso di ottica parte III Ottica ondulatoria Isabella Soletta Liceo Fermi Alghero Documento riadattato da MyZanichelli.it Questo simbolo significa che l esperimento si può realizzare con materiali
Un percorso di ottica parte III Ottica ondulatoria Isabella Soletta Liceo Fermi Alghero Documento riadattato da MyZanichelli.it Questo simbolo significa che l esperimento si può realizzare con materiali
Teoria generale delle coniche 1 / 17
 Teoria generale delle coniche 1 / 17 Introduzione 2 / 17 Una conica in R 2 è il luogo di punti γ definito da un equazione di secondo grado in x,y, cioè γ : a 11 x 2 + 2a 12 xy+a 22 y 2 + 2a 13 x+2a 23
Teoria generale delle coniche 1 / 17 Introduzione 2 / 17 Una conica in R 2 è il luogo di punti γ definito da un equazione di secondo grado in x,y, cioè γ : a 11 x 2 + 2a 12 xy+a 22 y 2 + 2a 13 x+2a 23
Geometria della diffrazione
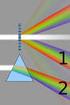 Geometria della diffrazione Diffrazione di solidi cristallini Max von Laue (1879-1960) Paul Peter Ewald (1888-1985) William Bragg (1862-1942) Lawrence Bragg (1890-1971) Equazioni di Laue Le equazioni di
Geometria della diffrazione Diffrazione di solidi cristallini Max von Laue (1879-1960) Paul Peter Ewald (1888-1985) William Bragg (1862-1942) Lawrence Bragg (1890-1971) Equazioni di Laue Le equazioni di
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
ESPERIMENTO SULL OTTICA. L ottica geometrica può essere considerata un metodo per la costruzione di immagini date
 ESPERIMENTO SULL OTTICA Introduzione L ottica geometrica può essere considerata un metodo per la costruzione di immagini date da sistemi ottici quali lenti e specchi. Essa costituisce una teoria approssimata,
ESPERIMENTO SULL OTTICA Introduzione L ottica geometrica può essere considerata un metodo per la costruzione di immagini date da sistemi ottici quali lenti e specchi. Essa costituisce una teoria approssimata,
La composizione di isometrie
 La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
GEOMETRIA B Esercizi
 GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
I FACOLTÀ DI INGEGNERIA - POLITECNICO DI BARI Corso di Laurea in Ingegneria Meccanica (corso A) A.A. 2009-2010, Esercizi di Geometria analitica
 I FACOLTÀ DI INGEGNERIA - POLITECNICO DI BARI Corso di Laurea in Ingegneria Meccanica (corso A) A.A. 2009-2010, Esercizi di Geometria analitica Negli esercizi che seguono si suppone fissato nello spazio
I FACOLTÀ DI INGEGNERIA - POLITECNICO DI BARI Corso di Laurea in Ingegneria Meccanica (corso A) A.A. 2009-2010, Esercizi di Geometria analitica Negli esercizi che seguono si suppone fissato nello spazio
Dipartimento di Matematica Corso di laurea in Fisica Compito di Geometria assegnato il 1 Febbraio 2002
 Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Laboratorio di Ottica e Spettroscopia
 Laboratorio di Ottica e Spettroscopia Quarta lezione Applicazione di tecniche di diffrazione (Laboratorio II) Antonio Maggio e Luigi Scelsi Istituto Nazionale di Astrofisica Osservatorio Astronomico di
Laboratorio di Ottica e Spettroscopia Quarta lezione Applicazione di tecniche di diffrazione (Laboratorio II) Antonio Maggio e Luigi Scelsi Istituto Nazionale di Astrofisica Osservatorio Astronomico di
1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta?
 Specchi piani MPZ 1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine
Specchi piani MPZ 1. Qual è la posizione dell immagine fornita da uno specchio piano? Di che tipo di immagine si tratta? Disponi il cilindro giallo dietro lo specchio, in modo che coincida con l immagine
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci [email protected] [email protected] Università di Napoli Parthenope Contenuti Coniche
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci [email protected] [email protected] Università di Napoli Parthenope Contenuti Coniche
Fisica Generale II (prima parte)
 Corso di Laurea in Ing. Medica Fisica Generale II (prima parte) Cognome Nome n. matricola Voto 4.2.2011 Esercizio n.1 Determinare il campo elettrico in modulo direzione e verso generato nel punto O dalle
Corso di Laurea in Ing. Medica Fisica Generale II (prima parte) Cognome Nome n. matricola Voto 4.2.2011 Esercizio n.1 Determinare il campo elettrico in modulo direzione e verso generato nel punto O dalle
MATRICI E SISTEMI LINEARI
 - - MATRICI E SISTEMI LINEARI ) Calcolare i seguenti determinanti: a - c - d - e - f - g - 8 7 8 h - ) Calcolare per quali valori di si annullano i seguenti determinanti: a - c - ) Calcolare il rango delle
- - MATRICI E SISTEMI LINEARI ) Calcolare i seguenti determinanti: a - c - d - e - f - g - 8 7 8 h - ) Calcolare per quali valori di si annullano i seguenti determinanti: a - c - ) Calcolare il rango delle
INTERFERENZA - DIFFRAZIONE
 INTERFERENZA - F. Due onde luminose in aria, di lunghezza d onda = 600 nm, sono inizialmente in fase. Si muovono poi attraverso degli strati di plastica trasparente di lunghezza L = 4 m, ma indice di rifrazione
INTERFERENZA - F. Due onde luminose in aria, di lunghezza d onda = 600 nm, sono inizialmente in fase. Si muovono poi attraverso degli strati di plastica trasparente di lunghezza L = 4 m, ma indice di rifrazione
La scoperta dei raggi X
 La scoperta dei raggi X 1 8 Novembre 1895 Wilhelm Konrad Röntgen (1845-1923) e il suo laboratorio all Università di Würzburg La sera dell 8 Novembre 1895 Röntgen scopre un nuovo tipo di radiazione, che
La scoperta dei raggi X 1 8 Novembre 1895 Wilhelm Konrad Röntgen (1845-1923) e il suo laboratorio all Università di Würzburg La sera dell 8 Novembre 1895 Röntgen scopre un nuovo tipo di radiazione, che
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Fononi e calori reticolari - Testi degli esercizi. Fisica della Materia Condensata
 Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata A.A. 015/016 Fononi e calori reticolari Esercizio 1 Si consideri una catena lineare biatomica. Calcolare le relazioni di
Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata A.A. 015/016 Fononi e calori reticolari Esercizio 1 Si consideri una catena lineare biatomica. Calcolare le relazioni di
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Cinematica Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale - a.a.
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Cinematica Maria Grazia Naso [email protected] Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica Razionale - a.a.
Esercizi Riepilogativi Svolti. = 1 = Or(v, w)
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia FORMULE DI GEOMETRIA IN R TRASFORMAZIONI DI R CIRCONFERENZE Docente: Prof F Flamini
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia FORMULE DI GEOMETRIA IN R TRASFORMAZIONI DI R CIRCONFERENZE Docente: Prof F Flamini
UNITÀ DIDATTICA 3 FUNZIONI GONIOMETRICHE
 UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
Algebra lineare Geometria 1 11 luglio 2008
 Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
Algebra lineare Geometria 1 11 luglio 2008 Esercizio 1. Si considerino la funzione: { R f : 3 R 3 (α, β, γ) ( 2β α γ, (k 1)β + (1 k)γ α, 3β + (k 2)γ ) dove k è un parametro reale, e il sottospazio U =
1. l induzione magnetica B in modulo, direzione e verso nel piano ortogonale al filo nel suo punto medio, a distanza r dal filo;
 Prova scritta di Elettromagnetismo e Ottica (CCS Fisica), 21 gennaio 2013 Nel piano x = 0 giace una lastra conduttrice collegata a terra. Nei punti di coordinate (a, a, 0) e (a, a, 0) si trovano due cariche,
Prova scritta di Elettromagnetismo e Ottica (CCS Fisica), 21 gennaio 2013 Nel piano x = 0 giace una lastra conduttrice collegata a terra. Nei punti di coordinate (a, a, 0) e (a, a, 0) si trovano due cariche,
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
4.4 Reticoli Capitolo 4 Ottica
 4.4 Reticoli Esercizio 92 Un fascio piano di onde e.m. con frequenza ν = 10 11 Hz incide su uno schermo conduttore piano su cui sono praticate 5 fenditure parallele e lunghe, di larghezza a = 6 mm e passo
4.4 Reticoli Esercizio 92 Un fascio piano di onde e.m. con frequenza ν = 10 11 Hz incide su uno schermo conduttore piano su cui sono praticate 5 fenditure parallele e lunghe, di larghezza a = 6 mm e passo
Compito di Meccanica Razionale M-Z
 Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Le coniche: circonferenza, parabola, ellisse e iperbole.
 Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Meccanica. 5. Cinematica del Corpo Rigido. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 5. Cinematica del Corpo Rigido http://campus.cib.unibo.it/252232/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. 2. 2 Si chiama numero dei gradi di libertà (GdL)
Meccanica 5. Cinematica del Corpo Rigido http://campus.cib.unibo.it/252232/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. 2. 2 Si chiama numero dei gradi di libertà (GdL)
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Coniche Quadriche. Coniche e quadriche. A. Bertapelle. 9 gennaio A. Bertapelle Coniche e quadriche
 .. Coniche e quadriche A. Bertapelle 9 gennaio 2013 Cenni storici Appollonio di Perga (III a. C.) in Le coniche fu il primo a dimostrare che era possibile ottenere tutte le coniche (ellisse, parabola,
.. Coniche e quadriche A. Bertapelle 9 gennaio 2013 Cenni storici Appollonio di Perga (III a. C.) in Le coniche fu il primo a dimostrare che era possibile ottenere tutte le coniche (ellisse, parabola,
Interpretazione di pattern di diffrazione da polveri
 Interpretazione di pattern di diffrazione da polveri Data la natura della tecnica di diffrazione da polveri, i dati sperimentali possono essere impiegati per ottenere e/o confermare le seguenti informazioni:
Interpretazione di pattern di diffrazione da polveri Data la natura della tecnica di diffrazione da polveri, i dati sperimentali possono essere impiegati per ottenere e/o confermare le seguenti informazioni:
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
CALENDARIO BOREALE 2 AMERICHE 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
Liceo Scientifico Cassini Esercizi di matematica, classe 5F, foglio3, soluzioni. normale parallelo a quello direzionale della retta sarà quindi
 Liceo Scientifico Cassini Esercizi di matematica, classe 5F, foglio3, soluzioni Problema1 x = y Dato il punto P(0,1,2), la retta r: y = z 2 ed il piano α: x 3y + z = 0 a) Trova il piano passante per P
Liceo Scientifico Cassini Esercizi di matematica, classe 5F, foglio3, soluzioni Problema1 x = y Dato il punto P(0,1,2), la retta r: y = z 2 ed il piano α: x 3y + z = 0 a) Trova il piano passante per P
ˆ b, si usa la convenzione di prendere. come verso positivo quello antiorario e come verso negativo quello orario.
 Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria II assegnati da dicembre 2000 a dicembre 2003
 Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
Dipartimento di Matematica Corso di laurea in Matematica Compiti di Geometria assegnati da dicembre 2000 a dicembre 2003 11/12/2000 n R 4 sono assegnati i punti A(3, 0, 1, 0), B(0, 0, 1, 0), C(2, 1, 0,
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
ESERCITAZIONI FISICA PER FARMACIA A.A. 2012/2013 ELETTROMAGNETISMO - OTTICA
 ESERCITAZIONI FISICA PER FARMACIA A.A. 2012/2013 ELETTROMAGNETISMO - OTTICA Esercizio 1 Due cariche q 1 e q 2 sono sull asse x, una nell origine e l altra nel punto x = 1 m. Si trovi il campo elettrico
ESERCITAZIONI FISICA PER FARMACIA A.A. 2012/2013 ELETTROMAGNETISMO - OTTICA Esercizio 1 Due cariche q 1 e q 2 sono sull asse x, una nell origine e l altra nel punto x = 1 m. Si trovi il campo elettrico
LA GEOMETRIA DELLO SPAZIO
 LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA. LEZIONE n 13
 METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
= E qz = 0. 1 d 3 = N
 Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
15 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
15 luglio 01 - Soluzione esame di geometria - Ing. gestionale - a.a. 01-01 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono
