Istituzione di Fisica Statistica
|
|
|
- Florindo Demetrio Antonelli
- 6 anni fa
- Visualizzazioni
Transcript
1 Istituzione di Fisica Statistica Comito e rova arziale (December 9, 004) Mattia Donega 8 dicembre 006 Esercizio Un gas classico di N articelle di massa m in equilibrio alla temeratura T è riartito fra due reciienti di volume V e V, che comunicano tramite un sottile tubo. Mostrare che il contributo massimo alla funzione di artizione canonica del sistema deriva dalle configurazioni in cui N articelle si trovano nel reciiente e N N N nel, con N tale da rendere uguali i otenziali chimici dei gas contenuti nel volume V e nel volume V searatamente. Risoluzione: Possiamo calcolare la funzione di artizione canonica dell intero sistema formato dai due volumi considerando i due gas searatamente nel suo interno. Per fare ciò dividiamo l hamiltoniana del sistema comleto in due arti, semlicemente valutandola rima er le coordinate e i momenti dele N articelle contenute in V e oi er le N articelle contenute in V. Otteniamo così H(, q, N) H(, q, N ) + H(, q, N N ) Tra tutti i termini che contribuiscono alla funzione di artizione canonica isoleremo quelli che derivano da differenti valori di N che saranno quindi sommati su quest indice. Q N (V, T ) h 3N N! d d N N 0 dq e β(h(,q,n)+h(,q,n)) V N d dq e h 3N N! V βh(,q,n) d dq e βh(,q,n) h 3N N! V N Q N (V, T )Q N N (V, T ) N 0 N 0 N! dq N!(N N )! V Suoniamo che ci sia un termine massimo che contribuisce a questa somma, diciamo er un numero N di articelle nel volume V. Per esso saranno valide le seguenti disuguaglianze:
2 Q N (V, T )Q N N (V, T ) N N 0 Q N (V, T )Q N N (V, T ) (N + )Q N (V, T )Q N N (V, T ) () Ricordiamo ora la relazione che lega la funzione di artizione canonica con la termodinamica: A(V, T ) kt logq N (V, T ) () Se quindi ora rendiamo il logaritmo di tutti i membri della () e moltilichiamo er kt otteniamo: kt log ( Q N (V, T )Q N N (V, T ) ) kt log ricordando la relazione () ( N N 0 Q N (V, T )Q N N (V, T ) kt log ( (N + )Q N (V, T )Q N N (V, T ) ) ) A N (V, T ) + A N (V, T ) A N (V, T ) A N (V, T ) + A N (V, T ) kt log(n + ) Da qui si vede che il massimo che abbiamo suosto dà quasi la totalità del contributo alla funzione di artizione, mentre le altre configurazione contribuiscono er termini roorzionali a log(n) che, data l estensività dell energia libera di Helmholtz, risultano trascurabili. Vediamo dunque a cosa orta la condizione di massimo, cioè l annularsi della derivata rima: ( kt log(q N (V, T )Q N N (V, T )) N 0 ( kt log(q N (V, T )) N (N N ) ( kt Q N N (V, T ) 0 Dunque otteniamo alla fine e ricordando che A N Esercizio A N (V, T ) A N N (V, T ) N (N N ) (3) µ è il otenziale chimico, giungiamo alla conclusione. Verificare che in contesto grancanonico l energia libera di Helmholtz uò essere esressa come: [ ] A kt log z log Z log Z (4) log z
3 Risoluzione Per rima cosa vediamo di eslicitare quel (log z) al denominatore saendo che d(log z) dz z er cui otteniamo A kt [(log z) z z ] log Z log Z in cui riconosciamo l esressione del numero di articelle del sistema considerato di artizione grancanonica Z, cioè N z z log Z Ricordando che β /kt, z e βµ e che in contesto grancanonico il logaritmo della funzione di artizione grancanonica vale log Z V/kT otteniamo: A [ ] V kt µn kt kt µn V che riconosciamo essere una esressione dell energia libera di Helmholtz dalla definizione di otenziale di Gibbs G µn. 3 Esercizio Un reciiente è diviso da un setto in due comarti non comunicanti di volumi V e V. In ciascun comarto è resente un gas erfetto classico. I gas in e sono inizialmente in equilibrio alla temeratura T e alla ressione. Imrovvisamente viene rimosso il setto e il sistema giunge ad una nuova situazione di equilibrio. Scrivere la variazione di energia libera di Helmholtz corrisondente allo stato finale e iniziale nei seguenti due casi: i) le molecole del gas hanno uguale massa m e sono identiche, ii) le molecole dei due gas, ur avendo uguale massa m, non sono identiche, ossono cioè essere distinte in base ad altre rorietà fisiche. Risoluzione In entrambi i casi l energia libera di Helmholtz dello stato iniziale, in cui cioè i due gas sono searati, si uò scrivere come somma delle energie libere di ognuno searatamente, er l estensività di A(V, T ), si ha cioè: (5) A(V, T ) A (V, T ) + A (V, T ) (6) Inoltre saiamo che l energia libera A(V, T ) è legata alla funzione di artizione canonica del sistema considerato, che er un gas erfetto classico saiamo essere uguale a: T. Q N (V, T ) Λ 3N (7) N! dove Λ è la lunghezza d onda termica relativa alla massa m e la temeratura V N 3
4 Nel caso i) le articelle sono comletamente indistinguibili doo che il setto è stato rimosso, quindi la funzione di artizione canonica dell intero sistema è esattamente (7). Possiamo quindi scrivere, con ovvio significato degli indici e, ricordando l arossimazione di Stirling er log N!: A kt N log V Λ 3 N + kt N A kt N log V Λ 3 N + kt N A kt N log V Λ 3 N + kt N quindi la variazione di energia libera di Helmholtz è: A(V, T ) A i (V, T ) A f (V, T ) kt log Λ 3 (N log V N + N + N log V N + N N log V N N) kt log Λ 3 (N log n + N log n N log n ) dove abbiamo inserito la densità n N/V. Essendo il gas in equilibrio alla stessa ressione e temeratura sia rima che doo di aver tolto il setto, la densità sarà costante e uguale nello stato iniziale e finale, cioè n n n. Quindi i logaritmi sono uguali e la arantesi diventa 0. Ci asettavamo questo risultato dal fatto che, essendo A U T S, non sono resenti fattori che aumentino l energia interna né l entroia, dunque l energia di Helmoltz anche deve rimanere costante. Nel caso ii) invece le articelle dei due gas hanno caratteristiche fisiche differenti che le rendono distinguibili quindi il combinatorio che comarirà nella funzione di artizione del sistema dei due gas mescolati sarà diverso: si dovrà tener conto che le N articelle del volume V sono indistinguibili tra loro, e lo stesso vale er quelle del volume V, ma searatamente, er cui si dovrà dividere er N!N!. Ora la variazione di A si scriverà: A(V, T ) A i (V, T ) A f (V, T ) V N N N V V kt log kt log + kt log Λ 3N N! Λ 3N N! Λ 3N N!N! kt log Λ 3 (N log V N + N + N log V N + N N log V N N N log V N N ) kt log Λ 3 (N log + N log N log n n n N log n ) dove n N /V e n N /V, mentre n N /V e n N /V. Dal fatto che i gas sono in equilibrio alla temeratura T e ressione abbiamo che n n, quindi il risultato è: 4
5 A(V, T ) kt log Λ 3 (N log n N log n N log n ) (8) Vediamo che in questo caso c è una variazione diversa da 0 che è dovuta al fatto che le due articelle sono di tio diverso e mescolandole imrovvisamente si crea un gradiente di densità che fa variare l entroia del sistema. 4 Esercizio Due gas di bosoni liberi hanno articelle con eguale massa m, ma con diverso sin, s e s. In quale relazione stanno le temerature di condensazione di BE, T c e T c, dei due gas a arità di v V N? Trovare anche in che relazione stanno le ressioni e nelle condizioni descritte. Risoluzione diventa: In resenza dello sin la funzione di artizione grancanonica Z(z, V, T ) z e βɛ,s,s ( z e βɛ ) g (9) dove g s + è la degenerazione dovuta allo sin, che nel nostro caso è g 3 er s e g 5 er s. Saiamo oi che er un gas di Bose ideale si ha condensazione di Bose-Einstein quando Λ 3 v g 3/() (0) con Λ la lunghezza d onda termica del sistema, v il volume secifico e g 3/ (z) n z n n 3/. Ciò che cambia risetto al caso di articelle senza sin è l esonente al denominatore della funzione di artizione grancanonica, che quando rendiamo il logaritmo di quest ultima, che saiamo essere l equazione di stato del gas, diventa una costante moltilicativa che non interferisce nel calcolo degli integrali che danno quindi gli stessi risultati a meno di g. Dunque le equazioni che definiscono il gas di bosoni sono: [ g kt Λ 3 g 5/(z) ] V log ( z) [ g v Λ 3 g 3/(z) z ] V z () () La condensazione di Bose-Einstein avviene quando la fugacità tende a, così che il termine che abbiamo isolato corrisondente a 0 diverge e fa sì che questo stato sia oolato da un numero finito di articelle. Per quello che 5
6 interessa il nostro esercizio è imortante saere che la linea di transizione ha equazione in v e T v g Λ 3 g 3/() (3) che estrendo la temeratura significa: T c h /πmk (4) g /3 [vg 3/ ()] /3 Dunque la relazione tra le temerature di condensazione dei due gas è la seguente: T ( c 5 ) /3 (5) T c 3 Secondo questo rinciio ossiamo trovare una relazione anche er le ressioni alla temeratura critica di condensazione che deriva dal fatto che la ressione del gas di Bose ideale è data dalla () e otteniamo così che 5 Esercizio c T c 3 ( 3 c 5 T c 5 ) /3 (6) Mostrare che er un gas di fermioni liberi vale semre: 0 N N N (7) Risoluzione esrimere Per un gas di fermioni liberi il valor medio di articelle si uò N z e βɛ + n (8) In base a queste relazioni ossiamo esrimere anche N e N : N n n q n n q q q ( ) N n n n q (9) q Saiamo oi anche che il valor medio del numero di occuazione del livello si uò esrimere come n β e che derivando un altra volta risetto a ɛ si ha n n ( β ɛ ɛ log Z(z, V, T ) (0) ) log Z(z, V, T ) n () β ɛ 6
7 Abbiamo quindi che n n q n n q β ɛ n q () in cui la arte destra è zero, oiché n diende solo da ɛ. Questo ci dice che n n q n n q er q. Da questo otteniamo er le (9) che ( n n q n n q ) ( n n ) q e oiché er un gas di fermioni n 0, si ha che la recedente è uguale a ( n n ) N n N (3) oiché sottraggo una quantità semre ositiva. Vediamo infine che è verificata anche la diseguaglianza di sinistra erché nell ultima equazione scritta, al rimo membro, abbiamo che la quantità dentro la arentesi è semre maggiore di 0, in quanto 0 n essendo un gas di fermioni, e quindi n n. 6 Esercizio Mostrare che er un gas di bosoni liberi di massa m in condizioni di temeratura e otenziale chimico tali che z /, vale N N N (4) Risoluzione Per un gas di bosoni vale una relazione simile a quella er i numeri di occuazione medi dei livelli energetici di un gas di fermioni, solo con un segno oosto: n n n + n (5) Questo si uò vedere dalle equazioni () rendendo l esressione eslicita del valor medio di occuazione del livello di energia ɛ e derivando: e oiché β ɛ n β ɛ ze βɛ ze βɛ ze βɛ ( ze βɛ ) n ze βɛ ze βɛ + βɛ ze ze βɛ si ottiene la relazione voluta. Da quanto aena fatto si ottiene che la arte destra della relazione che dobbiamo verificare è 7
8 N N ( n + n ) N + n (6) quindi tutto ciò che ci resta da verificare è che n N (7) Ora rendiamo le definizioni dei due membri e mettiamole a confronto (z e βɛ ) z e βɛ Questa è verificata se il denominatore del rimo membro è maggiore o uguale a, che ci orta a scrivere z e βɛ e βɛ (z /) La condizione su z ci ermette di concludere che la seconda relazione su scritta è verificata er ogni z e questa è verificata er valori ositivi dell esonente. Ma questo è semre ositivo essendo β /kt e ɛ /m dunque giungiamo alla nostra conclusione. 7 Esercizio Un gas di N fermioni liberi in una dimensione è descritto dalla hamiltoniana: H h ( ) 8π + α x i (8) m x i Trovare l energia del sistema a temeratura T 0. chimico nello stesso limite. i i Trovare il otenziale Risoluzione Si tratta di un gas di fermioni in un otenziale armonico, che diende cioè dal quadrato delle coordinate. Per rima cosa bisogna calcolare la funzione di artizione grancanonica e er fare questo abbiamo bisogno degli autovalori della hamiltoniana. Questi li conosciamo erché sono quelli di un oscillatore unidimensionale isotroo di frequenza ω α/m e valgono: Dunque la artizione grancanonica diventa: ɛ n ω(n + /) (9) Z(z, V, T ) n + ze βɛn n + ze β ω(n+/) (30) Saiamo oi che la relazione che lega la funzione di artizione grancanonica alla termodinamica è rorio quella che dà l energia interna del sistema e vale: U log Z(z, V, T ) β 8
9 β n n log( + ze β ω(n+/) ) n ze βɛn ω(n + /) + ze βɛn ω(n + /) z e βɛn + Ora nel limite T 0, cioè β, si ha che il termine frazionario che contiene gli esonenziali vale 0 o a seconda che ɛ n sia > o < di µ, il otenziale chimico. A noi ovviamente interessa il caso in cui esso vale, cioè sotto l energia di Fermi, che nel nostro caso sarà denotata da un indice n F, er il quale si ottiene la seguente esressione er l energia interna del sistema: U n n F n0 ω(n + /) e β(ɛn µ) + ω(n + /) In definitiva questa è la somma delle energie di n F oscillatori disaccoiati in cui ogni articella occua uno dei livelli di energia dell oscillatore armonico fino al livello n F in cui si trova l ultima articella. Vediamo ora di trovare quanto vale il otenziale chimico nello stesso limite con T 0. Il otenziale chimico µ è definito anche come: ( ) A µ (3) N e noi saiamo che A U T S, che nel limite termodinamico che stiamo considerando diventa sostanzialmente A U. Dunque ossiamo calcolarlo derivando risetto al numero di articelle che costituiscono il mio sistema, che ossiamo dire essere uguale a n F, quindi: µ n F n F n0 V,T ω(n + /) ω(n F + /) (3) il otenziale chimico è uguale all energia dell ultimo livello occuato. 9
Istituzioni di Fisica Statistica
 Istituzioni di Fisica Statistica Compito e proa parziale (December, 003) Mattia Donega 8 dicembre 006 Esercizio Mostrare che per un gas ideale classico all equilibrio in un olume V alla temperatura T nell
Istituzioni di Fisica Statistica Compito e proa parziale (December, 003) Mattia Donega 8 dicembre 006 Esercizio Mostrare che per un gas ideale classico all equilibrio in un olume V alla temperatura T nell
Tre tipi di Sistema Un richiamo
 Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Programma: a che unto siamo? Lezioni 25-26 2010 re tii di Sistema Un richiamo Un aio di riferimenti matematici Sistema isolato:
Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Programma: a che unto siamo? Lezioni 25-26 2010 re tii di Sistema Un richiamo Un aio di riferimenti matematici Sistema isolato:
Esercizi proposti - Gruppo 7
 Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
Argomenti di Matematica er l Ingegneria - Volume I - Esercizi roosti Esercizi roosti - Gruo 7 1) Verificare che ognuina delle seguenti coie di numeri razionali ( ) r + 1, r + 1, r Q {0} r ha la rorietà
IIASS International Institute for Advanced Scientific Studies
 IIASS International Institute for Advanced Scientific Studies Eduardo R. Caianiello Circolo di Matematica e Fisica Diartimento di Fisica E.R. Caianiello Università di Salerno Premio Eduardo R. Caianiello
IIASS International Institute for Advanced Scientific Studies Eduardo R. Caianiello Circolo di Matematica e Fisica Diartimento di Fisica E.R. Caianiello Università di Salerno Premio Eduardo R. Caianiello
Sistemi di particelle identiche
 Sistemi di articelle identiche 1. Princiio di indistinguibilità Due articelle si dicono identiche se hanno le stesse caratteristiche fisiche, quali massa, sin, carica elettrica, momento magnetico. Col
Sistemi di articelle identiche 1. Princiio di indistinguibilità Due articelle si dicono identiche se hanno le stesse caratteristiche fisiche, quali massa, sin, carica elettrica, momento magnetico. Col
ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA
 ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA Esercizio : Scelta ottimale di un monoolista e imoste Si consideri un monoolista con la seguente funzione di costo totale: C ( ) = 400 + + 0 0 La domanda
ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA Esercizio : Scelta ottimale di un monoolista e imoste Si consideri un monoolista con la seguente funzione di costo totale: C ( ) = 400 + + 0 0 La domanda
Esercizi sugli stati ed il diagramma entalpico dell'aria umida
 Esercizi sugli stati ed il diagramma entalico dell'aria umida CESARE MARIA JOPPOLO, STEFANO DE ANTONELLIS, LUCA MOLINAROLI DIPARTIMENTO DI ENERGIA POLITECNICO DI MILANO C. M. Joolo, S. De Antonellis, L.
Esercizi sugli stati ed il diagramma entalico dell'aria umida CESARE MARIA JOPPOLO, STEFANO DE ANTONELLIS, LUCA MOLINAROLI DIPARTIMENTO DI ENERGIA POLITECNICO DI MILANO C. M. Joolo, S. De Antonellis, L.
RELAZIONE DI MAYER. Per quanto riguarda l ultimo termine, esprimendo V in funzione di p e T si ha: dv dp. dv dt. nrt dt
 RELAZIONE DI MAYER La relazione di Mayer è: C C R IL rinciio della termodinamica si uò scrivere come du L () Consideriamo due trasformazioni, delle quali una sia un isocora e l altra una isobara, che ortino
RELAZIONE DI MAYER La relazione di Mayer è: C C R IL rinciio della termodinamica si uò scrivere come du L () Consideriamo due trasformazioni, delle quali una sia un isocora e l altra una isobara, che ortino
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Esercizi svolti di termodinamica applicata
 0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
Lezione 10 Termodinamica
 rgomenti della lezione: Lezione 0 ermodinamica relazione di Mayer trasformazioni adiabatiche trasformazioni isoterme macchine termiche ciclo di arnot secondo riiio della termodinamica cenni sull entroia
rgomenti della lezione: Lezione 0 ermodinamica relazione di Mayer trasformazioni adiabatiche trasformazioni isoterme macchine termiche ciclo di arnot secondo riiio della termodinamica cenni sull entroia
PALESTRA PER IL RECUPERO
 PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
RADICE QUADRATA ARITMETICA 2 IL CALCOLO DELLA RADICE QUADRATA. richiami della teoria MEDIANTE LE TAVOLE NUMERICHE COMPRENSIONE DELLA TEORIA
 RADICE QUADRATA ARITMETICA RADICE QUADRATA Q ISTITUTO ITALIANO EDIZIONI ATLAS IL CALCOLO DELLA RADICE QUADRATA MEDIANTE LE TAVOLE NUMERICHE richiami della teoria n L'oerazione di estrazione di radice o
RADICE QUADRATA ARITMETICA RADICE QUADRATA Q ISTITUTO ITALIANO EDIZIONI ATLAS IL CALCOLO DELLA RADICE QUADRATA MEDIANTE LE TAVOLE NUMERICHE richiami della teoria n L'oerazione di estrazione di radice o
ESERCITAZIONE 5: ESERCIZI DI RIPASSO
 Microeconomia CLEA A.A. 00-00 ESERCITAZIONE 5: ESERCIZI DI RIPASSO Esercizio 1: Scelte di consumo (beni comlementari) Un consumatore ha referenze raresentate dalla seguente funzione di utilità: U (, )
Microeconomia CLEA A.A. 00-00 ESERCITAZIONE 5: ESERCIZI DI RIPASSO Esercizio 1: Scelte di consumo (beni comlementari) Un consumatore ha referenze raresentate dalla seguente funzione di utilità: U (, )
MICROECONOMIA. Studiamo adesso la relazione tra variazioni dei ricavi e variazione della quantità venduta:
 Studiamo adesso la relazione tra variazioni dei ricavi e variazione della uantità venduta: In termini formali già saiamo che la variazione dei ricavi uò essere esressa come: R = + Seguendo una rassi ormai
Studiamo adesso la relazione tra variazioni dei ricavi e variazione della uantità venduta: In termini formali già saiamo che la variazione dei ricavi uò essere esressa come: R = + Seguendo una rassi ormai
A1. Soluzione. Ilcalore Q per unita di massa e negativo (ceduto all esterno) e vale:
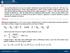 A. na maccina disosta su un asse orizzontale è alimentata da una ortata di 0 kg/s di aria (R = 87 J/kg K, c = 004 J/kg K) alla ressione P = 0 bar e alla temeratura T = 00 C, da un condotto circolare di
A. na maccina disosta su un asse orizzontale è alimentata da una ortata di 0 kg/s di aria (R = 87 J/kg K, c = 004 J/kg K) alla ressione P = 0 bar e alla temeratura T = 00 C, da un condotto circolare di
Sistema a tre stati L. P. 25 marzo 2014
 Sistema a tre stati L. P. 25 marzo 204 Consideriamo un sistema costituito da N particelle identiche, ognuna delle quali può trovarsi in uno di tre stati: i {0,, 2}, le cui energie valgono rispettivamente
Sistema a tre stati L. P. 25 marzo 204 Consideriamo un sistema costituito da N particelle identiche, ognuna delle quali può trovarsi in uno di tre stati: i {0,, 2}, le cui energie valgono rispettivamente
LE FUNZIONI ECONOMICHE
 M A R I O G A R G I U L O LE FUNZIONI EONOMIHE APPLIAZIONE DELL ANALISI MATEMATIA FUNZIONI EONOMIHE L economia è lo studio di come imiegare, con maggior convenienza, il denaro di cui si disone er raggiungere
M A R I O G A R G I U L O LE FUNZIONI EONOMIHE APPLIAZIONE DELL ANALISI MATEMATIA FUNZIONI EONOMIHE L economia è lo studio di come imiegare, con maggior convenienza, il denaro di cui si disone er raggiungere
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Per quanto detto prima il fenomeno di svuotamento termina quando la pressione di ristagno è pari a:
 Esercizi Si consideri il serbatoio schematicamente raresentato in Fig., in cui è contenuto un gas avente inizialmente (cioè al temo t=0) temeratura T o =0F e ressione oi =0si. Il serbatoio è collegato
Esercizi Si consideri il serbatoio schematicamente raresentato in Fig., in cui è contenuto un gas avente inizialmente (cioè al temo t=0) temeratura T o =0F e ressione oi =0si. Il serbatoio è collegato
CALCOLO DELLE PROBABILITÀ. 1. La probabilità che una candela accesa si spenga è p = 1, perché è assolutamente certo che si esaurirà.
 CALCOLO DELLE PROBABILITÀ -Definizione di robabilità -Legge additiva (eventi disgiunti) -Probabilità totale -Eventi comosti -Eventi indiendenti -Legge moltilicativa -Probabilità comoste - -Definizione
CALCOLO DELLE PROBABILITÀ -Definizione di robabilità -Legge additiva (eventi disgiunti) -Probabilità totale -Eventi comosti -Eventi indiendenti -Legge moltilicativa -Probabilità comoste - -Definizione
4 Interi somma di più di due quadrati
 4 Interi somma di iù di due quadrati Abbiamo già osservato, risolvendo l equazione diofantea X 2 + Y 2 = n, che non ogni intero ositivo si uò scrivere come somma di due quadrati di interi (ad esemio: 3
4 Interi somma di iù di due quadrati Abbiamo già osservato, risolvendo l equazione diofantea X 2 + Y 2 = n, che non ogni intero ositivo si uò scrivere come somma di due quadrati di interi (ad esemio: 3
Applicazione del principio di conservazione dell energia a sistemi aventi un gran numero di particelle.
 PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
non ha significato in R ¼
 MATEMATICAerTUTTI I radicai ESERCIZIO SVOLTO Potenze e radici. Saiamo che si uò estrarre a radice quadrata soo di numeri ositivi o nui e che i risutato è un numero ositivo o nuo. La radice cubica di un
MATEMATICAerTUTTI I radicai ESERCIZIO SVOLTO Potenze e radici. Saiamo che si uò estrarre a radice quadrata soo di numeri ositivi o nui e che i risutato è un numero ositivo o nuo. La radice cubica di un
DISUGUAGLIANZE. Umberto Marconi Dipartimento di Matematica Pura e Applicata Padova
 1. PREMESSA 1 DISUGUAGLIANZE Umberto Marconi Diartimento di Matematica Pura e Alicata Padova 1 Premessa Riassumiamo alcune disuguaglianze standard riguardanti somme e integrali (le dimostrazioni seguiranno
1. PREMESSA 1 DISUGUAGLIANZE Umberto Marconi Diartimento di Matematica Pura e Alicata Padova 1 Premessa Riassumiamo alcune disuguaglianze standard riguardanti somme e integrali (le dimostrazioni seguiranno
ESAME DI AMMISSIONE ALLA TERZA LICEO SCIENZE SPERIMENTALI: FISICA
 LICO CANTONAL DI LUGANO 2 SAM DI AMMISSION ALLA TRZA LICO SCINZ SRIMNTALI: FISICA COGNOM: NOM:...... RONINZA SCOLASTICA:. unti esercizi 1 2 3 TOT 18 4 3 25 unti fatti Nota SRCIZIO 1 Annerire o crociare
LICO CANTONAL DI LUGANO 2 SAM DI AMMISSION ALLA TRZA LICO SCINZ SRIMNTALI: FISICA COGNOM: NOM:...... RONINZA SCOLASTICA:. unti esercizi 1 2 3 TOT 18 4 3 25 unti fatti Nota SRCIZIO 1 Annerire o crociare
Lezione 24 IL TEOREMA DI BERNOULLI
 unti dei corsi di Idraulica e Idrodinamica Lezione 4 IL TEOREM DI ERNOULLI Nella LEZIONE 3 abbiamo dedotto il teorema di ernoulli er le correnti fluide, artendo dall equazione del moto valida in tali circostanze.
unti dei corsi di Idraulica e Idrodinamica Lezione 4 IL TEOREM DI ERNOULLI Nella LEZIONE 3 abbiamo dedotto il teorema di ernoulli er le correnti fluide, artendo dall equazione del moto valida in tali circostanze.
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1
 AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
Per determinare il dominio di f, occorre imporre x 6= 2,x>0elogx>0 di
 Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
1 TERMODINAMICA DELLE TURBINE A GAS 1.1 INTRODUZIONE
 TERMODINAMICA DELLE TURBINE A GAS. INTRODUZIONE Il ciclo termodinamico su cui è imostato il funzionamento delle turbine a gas è il ciclo Bryton, la cui analisi orta alla determinazione di due arametri
TERMODINAMICA DELLE TURBINE A GAS. INTRODUZIONE Il ciclo termodinamico su cui è imostato il funzionamento delle turbine a gas è il ciclo Bryton, la cui analisi orta alla determinazione di due arametri
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Comportamento asintotico delle Catene di Markov
 Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
Comortamento asintotico delle Catene di Markov In queste note analizzeremo il comortamento asintotico della catene di Markov a temo discreto omogenee, con sazio degli stati di dimensione finita. I risultati
TFA A048. Matematica applicata. Incontro del 28 aprile 2014, ore 15-17
 TFA A048. Matematica alicata Incontro del 8 arile 04, ore 5-7 Aunti di didattica della matematica alicata all economia e alla finanza. Alicazioni dell analisi (funzioni in iù variabili) a roblemi di Economia
TFA A048. Matematica alicata Incontro del 8 arile 04, ore 5-7 Aunti di didattica della matematica alicata all economia e alla finanza. Alicazioni dell analisi (funzioni in iù variabili) a roblemi di Economia
Esercitazioni 26/10/2016
 Esercitazioni 26/10/2016 Esercizio 1 Un anello sottile di raggio R = 12 cm disposto sul piano yz (asse x uscente dal foglio) è composto da due semicirconferenze uniformemente cariche con densità lineare
Esercitazioni 26/10/2016 Esercizio 1 Un anello sottile di raggio R = 12 cm disposto sul piano yz (asse x uscente dal foglio) è composto da due semicirconferenze uniformemente cariche con densità lineare
Fisica dell Atmosfera e del Clima
 Università degli studi di rento Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria er l Ambiente e il erritorio Prof. Dino Zardi Diartimento di Ingegneria Civile ed Ambientale Fisica dell Atmosfera
Università degli studi di rento Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria er l Ambiente e il erritorio Prof. Dino Zardi Diartimento di Ingegneria Civile ed Ambientale Fisica dell Atmosfera
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica,
 Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
LA PARABOLA E LE DISEQUAZIONI
 LA PARABOLA E LE DISEQUAZIONI DI SECONDO GRADO 6 Per ricordare H Una funzione di secondo grado la cui equazione assume la forma y ˆ a b c si chiama arabola. Le sue caratteristiche sono le seguenti (osserva
LA PARABOLA E LE DISEQUAZIONI DI SECONDO GRADO 6 Per ricordare H Una funzione di secondo grado la cui equazione assume la forma y ˆ a b c si chiama arabola. Le sue caratteristiche sono le seguenti (osserva
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
MOTI QUASI UNIDIMENSIONALI MOTI QUASI UNIDIMENSIONALI
 MOTI QUASI UNIDIMENSIONALI Nei moti quasi unidimensionali si iotizza la costanza del valore di tutte le grandezze termofluidodinamiche su ciascuna suerficie ermeabile aartenente alla suerficie esterna
MOTI QUASI UNIDIMENSIONALI Nei moti quasi unidimensionali si iotizza la costanza del valore di tutte le grandezze termofluidodinamiche su ciascuna suerficie ermeabile aartenente alla suerficie esterna
CONOSCENZE 1. gli elementi dell'estrazione della radice quadrata di un numero 2. le proprietaá delle radici quadrate
 ARITMETICA PREREQUISITI l conoscere le rorietaá delle quattro oerazioni e oerare con esse l conoscere le rorietaá delle otenze l fattorizzare un numero l oerare con le frazioni l arrotondare un numero
ARITMETICA PREREQUISITI l conoscere le rorietaá delle quattro oerazioni e oerare con esse l conoscere le rorietaá delle otenze l fattorizzare un numero l oerare con le frazioni l arrotondare un numero
CALORE E TERMODI NAMI CA - PRI MO PRI NCI PI O
 CALORE E ERMODI NAMI CA PRI MO PRI NCI PI O uanto calore è necessario er riscaldare, alla ressione di atm, una massa di kg di ghiaccio, inizialm ent e a 0 C, finchè t ut t o il ghiaccio non si è trasformato
CALORE E ERMODI NAMI CA PRI MO PRI NCI PI O uanto calore è necessario er riscaldare, alla ressione di atm, una massa di kg di ghiaccio, inizialm ent e a 0 C, finchè t ut t o il ghiaccio non si è trasformato
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
ESERCIZI SULLA DINAMICA DI CORPI RIGIDI.
 ESERCIZI SULL DINMIC DI CRPI RIIDI. Risoluzione mediante equazioni di Lagrange, equilibrio relativo (forze aarenti), stazionarietà del otenziale U; stabilità dell equilibrio e analisi delle iccole oscillazioni.
ESERCIZI SULL DINMIC DI CRPI RIIDI. Risoluzione mediante equazioni di Lagrange, equilibrio relativo (forze aarenti), stazionarietà del otenziale U; stabilità dell equilibrio e analisi delle iccole oscillazioni.
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Le quantità chimiche un modo per contare gli atomi...
 Secondo la teoria atomica di Dalton la è un elemento distintivo tra atomi Le quantità chimiche un modo er contare gli atomi... ATOMI DIVERSI HANNO MASSA DIVERSA Ma come ossiamo determinare la di un atomo?
Secondo la teoria atomica di Dalton la è un elemento distintivo tra atomi Le quantità chimiche un modo er contare gli atomi... ATOMI DIVERSI HANNO MASSA DIVERSA Ma come ossiamo determinare la di un atomo?
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Numeri primi e serie
 Numeri rimi e serie Fabio Durastante 5 ottobre 0 Sommario Dimostrazione dell infinità dei numeri rimi, divergenza serie degli inversi dei rimi e teorema di Mertens. Infinità dei numeri rimi Iniziamo dal
Numeri rimi e serie Fabio Durastante 5 ottobre 0 Sommario Dimostrazione dell infinità dei numeri rimi, divergenza serie degli inversi dei rimi e teorema di Mertens. Infinità dei numeri rimi Iniziamo dal
Il primo principio della termodinamica
 Il rimo rinciio della termodinamica 1) Concetti di variabile di stato e di trasformazione termodinamica Per studiare le relazioni fra calore Q, lavoro W e energia interna U Int nelle interazioni fra sistemi
Il rimo rinciio della termodinamica 1) Concetti di variabile di stato e di trasformazione termodinamica Per studiare le relazioni fra calore Q, lavoro W e energia interna U Int nelle interazioni fra sistemi
Funzioni di due variabili e rappresentazioni grafiche nello spazio
 Funzioni di due variabili e raresentazioni grafiche nello sazio Obiettivi l l l l comrendere il significato di derivata arziale calcolare derivate arziali comrendere il concetto di differenziale totale
Funzioni di due variabili e raresentazioni grafiche nello sazio Obiettivi l l l l comrendere il significato di derivata arziale calcolare derivate arziali comrendere il concetto di differenziale totale
tele limite è unico. Ciò significa che se non può accadere che una funzione abbia limiti diversi per x. Se per assurdo si avesse che lim f ( x)
 Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
ANALISI MATEMATICA I-A. Prova scritta del 1/9/2009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE
 ANALISI MATEMATICA I-A CORSO DI LAUREA IN FISICA Prova scritta del /9/009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE ESERCIZIO. Punti 8 Risolvere la seguente equazione nel campo complesso w 6 w 64 = 64 3
ANALISI MATEMATICA I-A CORSO DI LAUREA IN FISICA Prova scritta del /9/009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE ESERCIZIO. Punti 8 Risolvere la seguente equazione nel campo complesso w 6 w 64 = 64 3
Probabilità e tempi medi di assorbimento
 Probabilità e temi medi di assorbimento 6.1 Probabilità di assorbimento Consideriamo una catena con un numero finito di stati che indichiamo con S = {1, 2,... r}. Sia C una classe chiusa di S. Se la catena
Probabilità e temi medi di assorbimento 6.1 Probabilità di assorbimento Consideriamo una catena con un numero finito di stati che indichiamo con S = {1, 2,... r}. Sia C una classe chiusa di S. Se la catena
Procedura per la Risoluzione di Integrali Razionali Fratti
 Procedura er la Risoluzione di Integrali Razionali Fratti Matteo Tugnoli Marc, 0 Di seguito illustriamo una breve rocedura da alicare nel caso di integrazione di frazioni comoste da olinomi di differenti
Procedura er la Risoluzione di Integrali Razionali Fratti Matteo Tugnoli Marc, 0 Di seguito illustriamo una breve rocedura da alicare nel caso di integrazione di frazioni comoste da olinomi di differenti
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Termologia. Paolo Bagnaia - CTF Esercizi di termologia e termodinamica 1
 ermologia Paolo Bagnaia - CF - 3 - Esercizi di termologia e termodinamica 1 Esercizio Un cubetto di ghiaccio di 150 g alla temeratura di 0 C è gettato in unreciiente, i che contiene 300 g di acqua alla
ermologia Paolo Bagnaia - CF - 3 - Esercizi di termologia e termodinamica 1 Esercizio Un cubetto di ghiaccio di 150 g alla temeratura di 0 C è gettato in unreciiente, i che contiene 300 g di acqua alla
POLITECNICO DI MILANO ING. ENG AER MEC. Corso di FONDAMENTI DI CHIMICA ESAME del 09 Febbraio Compito A
 POLITECNICO DI MILANO ING. ENG AER MEC. Corso di FONDAMENTI DI CHIMICA ESAME del 09 Febbraio 01. Comito A Avvertenze: scrivere le soluzioni sull aosito foglio che va comletato con tutti i dati richiesti
POLITECNICO DI MILANO ING. ENG AER MEC. Corso di FONDAMENTI DI CHIMICA ESAME del 09 Febbraio 01. Comito A Avvertenze: scrivere le soluzioni sull aosito foglio che va comletato con tutti i dati richiesti
Esempio Le preferenze di un consumatore sono descritte dalla funzione di utilità U = x 1 x 2. Il suo reddito è pari a 400 con p 1 = 4 e p 2 = 10.
 4. Effetto reddito ed effetto sostituzione Esemio Le referenze di un consumatore sono descritte dalla funzione di utilità U. Il suo reddito è ari a 400 con 4 e 0. a) Determinare la scelta ottima e come
4. Effetto reddito ed effetto sostituzione Esemio Le referenze di un consumatore sono descritte dalla funzione di utilità U. Il suo reddito è ari a 400 con 4 e 0. a) Determinare la scelta ottima e come
È quella parte della termologia che studia le trasformazioni di calore in lavoro e viceversa.
 EMODINMI È quella arte della termologia che studia le trasformazioni di calore in lavoro e viceversa. PINIPIO DI EUIENZ OE - OO Grazie a questo imortante eserimento, Joule oté verificare che il calore
EMODINMI È quella arte della termologia che studia le trasformazioni di calore in lavoro e viceversa. PINIPIO DI EUIENZ OE - OO Grazie a questo imortante eserimento, Joule oté verificare che il calore
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
TEORIA DELLA PROBABILITÁ
 TEORIA DELLA PROBABILITÁ Cenni storici i rimi arocci alla teoria della robabilità sono della metà del XVII secolo (Pascal, Fermat, Bernoulli) gli ambiti di alicazione sono i giochi d azzardo e roblemi
TEORIA DELLA PROBABILITÁ Cenni storici i rimi arocci alla teoria della robabilità sono della metà del XVII secolo (Pascal, Fermat, Bernoulli) gli ambiti di alicazione sono i giochi d azzardo e roblemi
Sezione Prima Derivate di funzioni elementari: quadro riassuntivo e regole di derivazione. = ( n) lim x
 Capitolo USO DELLE DERIVATE IN ECONOMIA Sezione Prima Derivate di funzioni elementari: quadro riassuntivo e regole di derivazione Si definisce derivata della funzione y f() nel punto 0 del suo insieme
Capitolo USO DELLE DERIVATE IN ECONOMIA Sezione Prima Derivate di funzioni elementari: quadro riassuntivo e regole di derivazione Si definisce derivata della funzione y f() nel punto 0 del suo insieme
Lezione 14 Il mercato e il prezzo: Il meccanismo delle domanda e dell offerta
 Corso di Scienza Economica (Economia Politica) rof. G. Di Bartolomeo Lezione 14 Il mercato e il rezzo: Il meccanismo delle domanda e dell offerta Facoltà di Scienze della Comunicazione Università di Teramo
Corso di Scienza Economica (Economia Politica) rof. G. Di Bartolomeo Lezione 14 Il mercato e il rezzo: Il meccanismo delle domanda e dell offerta Facoltà di Scienze della Comunicazione Università di Teramo
Dal modellino dei Gas perfetti alla Tecnologia del vuoto
 Dal modellino dei Gas erfetti alla ecnologia del vuoto Il gas erfetto è un modellino teorico che ermette di rogettare e dimensionare i sistemi da vuoto, arte tutto da P= Nk () (*) P ressione del gas, olume
Dal modellino dei Gas erfetti alla ecnologia del vuoto Il gas erfetto è un modellino teorico che ermette di rogettare e dimensionare i sistemi da vuoto, arte tutto da P= Nk () (*) P ressione del gas, olume
Esercizi svolti. g(x) = sono una l inversa dell altra. Utilizzare la rappresentazione grafica di f e f 1 per risolvere l equazione f(x) = g(x).
 Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Esercizi svolti sugli integrali
 Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
Cinematica Relativistica
 Caitolo 1 Cinematica Relativistica Avvertenza: negli esercizi seguenti si e usata talvolta la convenzione = c = 1. Per esemio, il momento di una articella viene esresso indifferentemente in GeV o GeV/c.
Caitolo 1 Cinematica Relativistica Avvertenza: negli esercizi seguenti si e usata talvolta la convenzione = c = 1. Per esemio, il momento di una articella viene esresso indifferentemente in GeV o GeV/c.
MATEMATICA E STATISTICA CORSO A CORSO DI LAUREA IN SCIENZE BIOLOGICHE MOLECOLARI
 MATEMATICA E STATISTICA CORSO A CORSO DI LAUREA IN SCIENZE BIOLOGICHE MOLECOLARI ESERCITATI CON ME! I ESERCITAZIONE 1) Misure ripetute (materiale secco su vetrino) della lunghezza del diametro maggiore
MATEMATICA E STATISTICA CORSO A CORSO DI LAUREA IN SCIENZE BIOLOGICHE MOLECOLARI ESERCITATI CON ME! I ESERCITAZIONE 1) Misure ripetute (materiale secco su vetrino) della lunghezza del diametro maggiore
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
a 11 s 1 + a 12 s a 1n s n = b 1 a 21 s 1 + a 22 s a 2n s n = b 2..
 Matematica II 020304 Ogni sistema di m equazioni lineari in n incognite x 1 x 2 x n si uo raresentare nella forma a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1
Matematica II 020304 Ogni sistema di m equazioni lineari in n incognite x 1 x 2 x n si uo raresentare nella forma a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1
2 Le fluttuazioni economiche: domanda e offerta aggregata
 2 Le fluttuazioni economiche: domanda e offerta aggregata 2.1 Crescita economica e fluttuazioni È tradizione suddividere la Macroeconomia in due cami di studio distinti: la crescita e le fluttuazioni.
2 Le fluttuazioni economiche: domanda e offerta aggregata 2.1 Crescita economica e fluttuazioni È tradizione suddividere la Macroeconomia in due cami di studio distinti: la crescita e le fluttuazioni.
œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ Τ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ Τ œ Τ œ 2. Auf, auf! die rechte Zeit ist hier Auf,
 Rocco De Cia [9..01] Aunti di armonia () l basso cifrato J.S. Bach, Lieder und Arien (BW 9-18) Proseguiamo i nostri esercizi di armonia con i Lieder und Arien di J.S. Bach, una raccolta di canti con basso
Rocco De Cia [9..01] Aunti di armonia () l basso cifrato J.S. Bach, Lieder und Arien (BW 9-18) Proseguiamo i nostri esercizi di armonia con i Lieder und Arien di J.S. Bach, una raccolta di canti con basso
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008
 Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008 Soluzione: La risposta corretta è B. perché senza la parentesi l esponente si applica solo al numeratore:
Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008 Soluzione: La risposta corretta è B. perché senza la parentesi l esponente si applica solo al numeratore:
Capitolo 1 Esercizi svolti
 Caitolo 1 sercizi svolti sercizio 1.1 Il mercato del frumento oera in condizioni di concorrenza erfetta e le curve di domanda e offerta sono: = 1500-5 = 600 + 4 dove è esresso in /quintali e in milioni
Caitolo 1 sercizi svolti sercizio 1.1 Il mercato del frumento oera in condizioni di concorrenza erfetta e le curve di domanda e offerta sono: = 1500-5 = 600 + 4 dove è esresso in /quintali e in milioni
Liceo Scientifico Statale G. Stampacchia. Tricase
 Temo di lavoro Liceo Scientifico Statale G. Stamacchia 60 minuti Tricase Oggetto: Comito di Fisica Classe D Soluzione Pr1 Pr Pr3 Pr4 Tema: Dinamica: Alicazioni del secondo e del terzo rinciio Conservazione
Temo di lavoro Liceo Scientifico Statale G. Stamacchia 60 minuti Tricase Oggetto: Comito di Fisica Classe D Soluzione Pr1 Pr Pr3 Pr4 Tema: Dinamica: Alicazioni del secondo e del terzo rinciio Conservazione
LE TRASFORMAZIONI NON ISOMETRICHE
 GEOMETRIA 2 LE TRASFORMAZIONI NON ISOMETRICHE L'OMOTETIA richiami della teoria n Le trasformazioni non isometriche sono quelle trasformazioni in seguito alle quali le figure non restano congruenti; n l'omotetia
GEOMETRIA 2 LE TRASFORMAZIONI NON ISOMETRICHE L'OMOTETIA richiami della teoria n Le trasformazioni non isometriche sono quelle trasformazioni in seguito alle quali le figure non restano congruenti; n l'omotetia
ESERCIZIO 1. Dati due diodi a giunzione pn aventi le seguenti caratteristiche:
 ESERCIZIO 1 Dati due diodi a giunzione pn aventi le seguenti caratteristiche: DIODO A: Si, 10 18 cm 3,N D 10 15 cm 3 DIODO B: Ge, 10 18 cm 3,N D 10 15 cm 3 Valutare, giustificando quantitativamente le
ESERCIZIO 1 Dati due diodi a giunzione pn aventi le seguenti caratteristiche: DIODO A: Si, 10 18 cm 3,N D 10 15 cm 3 DIODO B: Ge, 10 18 cm 3,N D 10 15 cm 3 Valutare, giustificando quantitativamente le
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Strumenti di misura fluidodinamici
 Sonia Gherardini matricola n 4700 Lezione del 7/0/003, ore 8.30-0.30 Strumenti di misura fluidodinamici Per introdurre gli strumenti di misura della velocità di fluidi in condotti, ricordiamo intanto alcuni
Sonia Gherardini matricola n 4700 Lezione del 7/0/003, ore 8.30-0.30 Strumenti di misura fluidodinamici Per introdurre gli strumenti di misura della velocità di fluidi in condotti, ricordiamo intanto alcuni
UNIVERSITA` di ROMA TOR VERGATA
 UNIVERSITA` di ROMA TOR VERGATA Corso di PS2-Probabilità 2 P.Baldi appello, 7 giugno 200 Corso di Laurea in Matematica Esercizio Siano X, Y v.a. indipendenti di legge Ŵ(2, λ). Calcolare densità e la media
UNIVERSITA` di ROMA TOR VERGATA Corso di PS2-Probabilità 2 P.Baldi appello, 7 giugno 200 Corso di Laurea in Matematica Esercizio Siano X, Y v.a. indipendenti di legge Ŵ(2, λ). Calcolare densità e la media
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (24/06/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Tema A Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O,
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (24/06/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Tema A Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O,
Calore, lavoro e trasformazioni termodinamiche (1)
 Calore, lavoro e trasformazioni termodinamiche (1) Attraverso scambi di calore un sistema scambia energia con l ambiente. Tuttavia si scambia energia anche quando le forze (esterne e interne al sistema)
Calore, lavoro e trasformazioni termodinamiche (1) Attraverso scambi di calore un sistema scambia energia con l ambiente. Tuttavia si scambia energia anche quando le forze (esterne e interne al sistema)
Istituzioni di Matematiche, Integrali fratti. corso di laurea in Scienze geologiche. Mauro Costantini
 Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Breve formulario di matematica
 Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
Luciano Battaia a 2 = a ; lim sin = 1, se 0; sin(α + β) = sin α cos β + cos α sin β; f() = e 2 f () = 2e 2 ; sin d = cos + k; 1,2 = b± ; a m a n = 2a a n+m ; log a 2 = ; = a 2 + b + c; 2 + 2 = r 2 ; e
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
meccanica dei fluidi Problemi di Fisica
 Problemi di isica Meccanica dei luidi Equilibrio dei fluidi Comleta la seguente tabella: orza (N) 10 0 80 uerficie (m ) 1 5 4 Pressione (bar) 10 50 5 Tenendo resente la definizione di ressione: e le sue
Problemi di isica Meccanica dei luidi Equilibrio dei fluidi Comleta la seguente tabella: orza (N) 10 0 80 uerficie (m ) 1 5 4 Pressione (bar) 10 50 5 Tenendo resente la definizione di ressione: e le sue
Capitolo 2. Funzioni
 Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
1. Scrivere il termine generale a n delle seguenti successioni e calcolare lim n a n:
 Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
Corso di Progetto di Strutture. POTENZA, a.a Serbatoi e tubi
 Corso di Progetto di Strutture POTENZA, a.a. 01 013 Serbatoi e tubi Dott. Marco VONA Scuola di Ingegneria, Università di Basilicata marco.vona@unibas.it htt://www.unibas.it/utenti/vona/ CONSIDEAZIONI INTODUTTIVE
Corso di Progetto di Strutture POTENZA, a.a. 01 013 Serbatoi e tubi Dott. Marco VONA Scuola di Ingegneria, Università di Basilicata marco.vona@unibas.it htt://www.unibas.it/utenti/vona/ CONSIDEAZIONI INTODUTTIVE
Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008
 Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008 Soluzione: La risposta corretta è B. perché senza la parentesi l esponente si applica solo al numeratore:
Come risolvere i quesiti della Prova Nazionale di Terza Media (INVALSI) Anno Scolastico 2007/2008 Soluzione: La risposta corretta è B. perché senza la parentesi l esponente si applica solo al numeratore:
Dispensa del corso di FLUIDODINAMICA DELLE MACCHINE
 Disensa del corso di FLUIDODINAICA DELLE ACCHINE Argomento: Onde di ach e onde d'urto (flusso stazionario, non viscoso di un gas erfetto) Prof. Pier Ruggero Sina Diartimento di Ingegneria Prof. P. R. Sina
Disensa del corso di FLUIDODINAICA DELLE ACCHINE Argomento: Onde di ach e onde d'urto (flusso stazionario, non viscoso di un gas erfetto) Prof. Pier Ruggero Sina Diartimento di Ingegneria Prof. P. R. Sina
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
n L insieme dei numeri reali n La retta reale n Calcolo approssimato
 n L insieme dei numeri reali n La retta reale n Calcolo arossimato n L insieme dei numeri reali 1 Amliamento degli insiemi numerici Nelle recedenti unità, doo aver introdotto l insieme N dei numeri naturali,
n L insieme dei numeri reali n La retta reale n Calcolo arossimato n L insieme dei numeri reali 1 Amliamento degli insiemi numerici Nelle recedenti unità, doo aver introdotto l insieme N dei numeri naturali,
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 1 febbraio 2017 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Equazioni esponenziali e logaritmi
 Copyright c 2008 Pasquale Terrecuso Tutti i diritti sono riservati. Equazioni esponenziali e logaritmi 2 equazioni esponenziali..................................................... 3 casi particolari............................................................
Copyright c 2008 Pasquale Terrecuso Tutti i diritti sono riservati. Equazioni esponenziali e logaritmi 2 equazioni esponenziali..................................................... 3 casi particolari............................................................
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Soluzione del secondo Esonero di Meccanica Quantistica
 1 Soluzione del secondo Esonero di Meccanica Quantistica 1/3/007 Compito A Osserviamo che l hamiltoniana è separabile nella forma H = H x1 + H y1 + H x + H y dove si è posto H x1 = p x 1 m + U(x 1), H
1 Soluzione del secondo Esonero di Meccanica Quantistica 1/3/007 Compito A Osserviamo che l hamiltoniana è separabile nella forma H = H x1 + H y1 + H x + H y dove si è posto H x1 = p x 1 m + U(x 1), H
1) Si deve progettare un auto reattore per un missile che vola a M 1 := 1.8. Supponendo che
 Esercizi di Esame 1.mcd (1/9) 1) Si deve rogettare un auto reattore er un missile che vola a M 1 : 1.8. Suonendo che T 1 : 73.15 K, 1 : 0.7 atm, A : 0.0347 m, A 3 /A 1.34 e che la combustione roduce 196.7kJ/kg.
Esercizi di Esame 1.mcd (1/9) 1) Si deve rogettare un auto reattore er un missile che vola a M 1 : 1.8. Suonendo che T 1 : 73.15 K, 1 : 0.7 atm, A : 0.0347 m, A 3 /A 1.34 e che la combustione roduce 196.7kJ/kg.
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
