Corso di Metodi Matematici per la Finanza
|
|
|
- Tito Pieri
- 5 anni fa
- Visualizzazioni
Transcript
1 Corso di Metodi Matematici per la Finanza Soluzioni degli esercizi su EDO/ED lineari del secondo ordine a coecienti costanti Es. 1 a) x (t) 4x (t) + 4x(t) = 0, x(0) = 1, x (0) = 0 Equazione caratteristica: λ 4λ + 4 = (λ ) = 0; λ 1 = λ =. Soluzione generale: x(t) = c 1 e t + c te t, c 1, c R. Calcoliamo la derivata: x(t) = c 1 e t +c e t +c e t e imponiamo le condizioni iniziali, ottenendo un sistema lineare di equazioni nelle incognite c 1 e c : 1 = x(0) = c 1 + c 0 = x (0) = c 1 + c. Si ha: c 1 = 1, c =. Pertanto la soluzione particolare relativa ai dati iniziali assegnati è: x(t) = e t te t. b) x (t) + 4x (t) + 5x(t) = 0, x(0) = 1, x (0) = 0 Equazione caratteristica: λ + 4λ + 5 = 0; λ 1 = iλ = + i. Soluzione generale: x(t) = e t (c 1 cos t + c sin t), c 1, c R. Calcoliamo la derivata: x(t) = e t (c 1 cos t + c sin t) + e t ( c 1 sin t + c cos t) e imponiamo le condizioni iniziali, ottenendo un sistema lineare di equazioni nelle incognite c 1 e c : 1 = x(0) = c 1 0 = x (0) = c 1 + c. Si ha: c 1 = 1, c =. Pertanto la soluzione particolare relativa ai dati iniziali assegnati è: x(t) = e t (cos t + sin t). Es. a) x(t + ) 3x(t + 1) + x(t) = 0, x(0) = 1, x(1) = Equazione caratteristica: λ 3λ + 1 = 0; λ 1 = 1, λ = 1. Soluzione generale: x(t) = c 1 ( 1 ) t + c, c 1, c R. Imponiamo le condizioni iniziali, ottenendo un sistema lineare di equazioni nelle incognite c 1 e c : 1 = x(0) = c 1 + c = x(1) = c 1 + c. Si ha: c 1 =, c = 3. Pertanto la soluzione particolare relativa ai dati iniziali assegnati è: x(t) = ( 1 ) t
2 b) x(t + ) 4x(t + 1) + 4x(t) = 0, x(0) = x(1) = 1 Equazione caratteristica: λ 4λ + 4 = (λ ) = 0; λ 1 = λ =. Soluzione generale: x(t) = c 1 t + c t t, c 1, c R. Imponiamo le condizioni iniziali, ottenendo un sistema lineare di equazioni nelle incognite c 1 e c : 1 = x(0) = c 1 1 = x(1) = c 1 + c. Si ha: c 1 = 1, c = 1. Pertanto la soluzione particolare relativa ai dati iniziali assegnati è: x(t) = t 1 tt. c) x(t + ) + x(t + 1) + x(t) = 0, x(0) = 0, x(1) = 1 Equazione caratteristica: λ + λ + = 0; λ 1 = 1 i, λ = 1 + i. Si ha: ρ = a + b = pertanto la soluzione generale è x(t) = c 1 ρ t cos(θt) + c ρ t sin(θt) ( ) t ( ) 3 = c 1 cos 4 πt (, θ = arctan b ) + π = π a 4 + π, + c ( ) t ( ) 3 sin 4 πt, c 1, c R. Imponiamo le condizioni iniziali, ottenendo un sistema lineare di equazioni nelle incognite c 1 e c : 0 = x(0) = c 1 ( ) ( ) = x(1) = c 1 cos 4 π + c sin 4 π. Si ha: c 1 = 0, c =. Pertanto la soluzione particolare relativa ai dati iniziali assegnati è: ( ) t ( x(t) = sin 3 4 πt). Es. 3 a) x (t) + 5x (t) + 4x(t) = 3 t Equazione omogenea associata: z (t)+5z (t)+z(t) = 0; equazione caratteristica: λ +5λ+4 = 0; λ 1 = 4, λ = 1; soluzione generale equazione omogenea associata: z(t) = c 1 e 4t + c e t, c 1, c R. Quindi la soluzione generale sarà della forma: x(t) = c 1 e 4t + c e t + x(t), c 1, c R, dove x(t) è una soluzione particolare dell'equazione non omogenea. Dato che il termine noto dell'equazione è f(t) = 3 t = P 1 (t), i.e. un polinomio di grado 1 e il termine in x(t) dell'equazione è non degenere (il coeciente è diverso da 0), allora cerchiamo una soluzione particolare della forma x(t) = at + b, a, b R,
3 i.e. un polinomio di grado 1. Poiché x(t) è una soluzione particolare deve soddisfare l'equazione non omogenea. Allora, dopo aver calcolato le derivate (prima e seconda) di x(t) andiamo a sostituire nell'equazione e riordinando i termini otteniamo: 4at + (5a + 4b) = 3t + 3. Utilizzando il principio di identità dei polinomi, si ha: 4a = 5a + 4b = 3. Otteniamo a = 1, b = Quindi x(t) = 1 t e la soluzione generale è: b) x (t) x(t) = te t x(t) = c 1 e 4t + c e t 1 t , c 1, c R. Equazione omogenea associata: z (t) z(t) = 0; equazione caratteristica: λ 1 = 0; λ 1 = 1, λ = 1; soluzione generale equazione omogenea associata: z(t) = c 1 e t + c e t, c 1, c R. Quindi la soluzione generale sarà della forma: x(t) = c 1 e t + c e t + x(t), c 1, c R, f(t) = te t = P 1 (t)e αt, dove P 1 (t) denota un polinomio di primo grado e α = 1. Poiché α = 1 è radice di molteplicità 1 dell'equazione caratteristica, allora cerchiamo una soluzione particolare della forma x(t) = t 1 (at + b)e t = t(at + b)e t, a, b R. Poiché x(t) è una soluzione particolare deve soddisfare l'equazione non omogenea. calcoliamo le derivate (prima e seconda) di x(t): Allora, x (t) = (at + b)e t + ate t + t(at + b)e t x (t) = ae t + (at + b)e t + ae t + ate t + (at + b)e t + ate t + t(at + b)e t, andiamo a sostituire nell'equazione e semplicando e t e riordinando i termini otteniamo: 4at + a + b = t. Utilizzando il principio di identità dei polinomi, si ha: 4a = 1 a + b = 0. Otteniamo a = 1 4, b = 1 4. Quindi x(t) = t ( 1 4 t 4) 1 e t e la soluzione generale è: ( 1 x(t) = c 1 e t + c e t + t 4 t 1 ) e t, c 1, c R. 4 3
4 c) x (t) x(t) = 3e t cos t Equazione omogenea associata: z (t) z(t) = 0; equazione caratteristica: λ 1 = 0; λ 1 = 1, λ = 1; soluzione generale equazione omogenea associata: z(t) = c 1 e t + c e t, c 1, c R. Quindi la soluzione generale sarà della forma: x(t) = c 1 e t + c e t + x(t), c 1, c R, f(t) = 3e t cos t = P 0 (t)e αt cos (βt), dove P 0 (t) denota un polinomio di grado 0, ovvero una costante e α = e β = 1. Poiché α+iβ = +i non è radice dell'equazione caratteristica, allora cerchiamo una soluzione particolare della forma x(t) = e αt (k cos (βt) + h sin (βt)) = e t (k cos t + h sin t), k, h R. Poiché x(t) è una soluzione particolare deve soddisfare l'equazione non omogenea. calcoliamo le derivate (prima e seconda) di x(t): Allora, x (t) = e t (k cos t + h sin t) + e t ( k sin t + h cos t) x (t) = 4e t (k cos t + h sin t) + 4e t ( k sin t + h cos t) + e t ( k cos t h sin t), andiamo a sostituire nell'equazione e semplicando e t e riordinando i termini otteniamo: da cui (k + 4h) cos t + (k 4h) sin t = 3 cos t, k + 4h = 3 k 4h = 0 e in denitiva: k = 3 10 e h = 3 5. Soluzione particolare: x(t) = ( et 3 10 cos t sin t) Soluzione generale: ( 3 x(t) = c 1 e t + c e t + e t 10 cos t + 3 ) 5 sin t, c 1, c R. Es. 4 a) x(t + ) 3x(t + 1) + x(t) = 3 t Equazione omogenea associata: z (t) 3z (t)+z(t) = 0; equazione caratteristica: λ 3λ+ = 0; λ 1 = 1, λ = ; soluzione generale equazione omogenea associata: z(t) = c 1 1 t + c t = c 1 + c t, c 1, c R. Quindi la soluzione generale sarà della forma: x(t) = c 1 + c t + x(t), c 1, c R, 4
5 f(t) = 3 t = P 0 (t)σ t, dove P 0 (t) denota un polinomio di grado 0, ovvero una costante e σ = 3. Poiché σ = 3 non è radice dell'equazione caratteristica cerchiamo una soluzione particolare della forma x(t) = k3 t, k R. Calcoliamo x(t + 1) = k3 t+1 x(t + ) = k3 t+ e sostituiamo nell'equazione alle dierenze assegnata (essendo una soluzione particolare la deve soddisfare): k3 t+ 3k3 t+1 + k3 t = 3 t. Semplicando 3 t, otteniamo k = 1. Pertanto x(t) = 1 3t e la soluzione generale è: x(t) = c 1 1 t + c t = c 1 + c t + 1 3t, c 1, c R. b) x(t + ) 4x(t + 1) + 4x(t) = t Equazione omogenea associata: z (t) 4z (t)+4z(t) = 0; equazione caratteristica: λ 4λ+4 = 0; λ 1 = λ = ; soluzione generale equazione omogenea associata: z(t) = c 1 t + c t t, c 1, c R. Quindi la soluzione generale sarà della forma: x(t) = c 1 t + c t t + x(t), c 1, c R, f(t) = t = P 0 (t)σ t, dove P 0 (t) denota un polinomio di grado 0, ovvero una costante e σ =. Poiché σ = 3 è radice di molteplicità dell'equazione caratteristica cerchiamo una soluzione particolare della forma Calcoliamo x(t) = kt t, k R. x(t + 1) = k(t + 1) t+1 x(t + ) = k(t + ) t+ e sostituiamo nell'equazione alle dierenze assegnata: k(t + ) t+ 4k(t + 1) t+1 + 4kt t = t. Semplicando t, otteniamo k = 1 8. Pertanto x(t) = 1 8 t e la soluzione generale è: x(t) = c 1 t + c t t t, c 1, c R. 5
Corso di Laurea in Ingegneria dell Energia ANALISI MATEMATICA I. Prova scritta del 9 Giugno 2012 FILA 2
 Corso di Laurea in Ingegneria dell Energia ANALISI MATEMATICA I Prova scritta del 9 Giugno FILA Esporre il procedimento di risoluzione degli esercizi in maniera chiara e leggibile. Allegare il presente
Corso di Laurea in Ingegneria dell Energia ANALISI MATEMATICA I Prova scritta del 9 Giugno FILA Esporre il procedimento di risoluzione degli esercizi in maniera chiara e leggibile. Allegare il presente
Equazioni differenziali
 Equazioni differenziali Samuele MONGODI - 14/08/01 Un equazione differenziale è un equazione che coinvolge una funzione reale u : R R, le sue derivate e la variabile indipendente (u = u(t)). Esempi 1.
Equazioni differenziali Samuele MONGODI - 14/08/01 Un equazione differenziale è un equazione che coinvolge una funzione reale u : R R, le sue derivate e la variabile indipendente (u = u(t)). Esempi 1.
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Esercizi di riepilogo sulle curve. 1. Si fornisca una parametrizzazione per le seguenti curve:
 Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti:
 Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
ẋ + a 0 x = 0 (1) Dimostrazione. Risolvendo la (1) per separazione di variabili, troviamo x(t) = c 0 e a0t (2) φ :R S 1 ẍ + a 1 ẋ + a 0 x = 0 (3)
 Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Equazioni lineari secondo ordine a coefficienti continui. (Soluzione generale omogenea associata) + (Soluzione particolare).
 Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
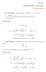 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio a) Studiare l esistenza e la natura degli estremi liberi della funzione.
 Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio 218 1) Data la funzione f(, ) = 4 + 4 4 2 7 a) Studiare l esistenza e la natura degli estremi liberi della funzione. b) Trovare il massimo
Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio 218 1) Data la funzione f(, ) = 4 + 4 4 2 7 a) Studiare l esistenza e la natura degli estremi liberi della funzione. b) Trovare il massimo
Equazioni differenziali del secondo ordine a coefficienti costanti Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo
 9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
EQUAZIONI DIFFERENZIALI CAPITOLO 4 EQUAZIONI DIFFERENZIALI LINEARI A COEFFICIENTI COSTANTI (III)
 EQUAZIONI DIFFERENZIALI LINEARI A COEFFICIENTI COSTANTI (III) EQUAZIONI NON OMOGENEE L'equazione, dove f y py qy f nome di equazione non omogenea è una funzione non identicamente nulla, prende il Dimostriamo
EQUAZIONI DIFFERENZIALI LINEARI A COEFFICIENTI COSTANTI (III) EQUAZIONI NON OMOGENEE L'equazione, dove f y py qy f nome di equazione non omogenea è una funzione non identicamente nulla, prende il Dimostriamo
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica. Pisa, 20 giugno (log x)x 1
 Università di Pisa - Corso di Laurea in Informatica Analisi Matematica Pisa, 0 giugno 019 e 1 se 0 Domanda 1 La funzione f : R R definita da 1 se = 0 A) ha minimo ma non ha massimo ) ha massimo ma non
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica Pisa, 0 giugno 019 e 1 se 0 Domanda 1 La funzione f : R R definita da 1 se = 0 A) ha minimo ma non ha massimo ) ha massimo ma non
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Analisi Matematica II - Ingegneria Meccanica/Energetica - 21 Giugno 2018
 Analisi Matematica II - Ingegneria Meccanica/Energetica - 21 Giugno 218 1 Data la funzione f, y y 2 + y 4 α, α >. a Determinare al variare del parametro α > il dominio di definizione di f. b tudiare al
Analisi Matematica II - Ingegneria Meccanica/Energetica - 21 Giugno 218 1 Data la funzione f, y y 2 + y 4 α, α >. a Determinare al variare del parametro α > il dominio di definizione di f. b tudiare al
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
7. Equazioni differenziali
 18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19
 Algebra Lineare Ingegneria Chimica Anno Accademico 08/9 Caboara Esercitazione guidata 5 ottobre 08 Esercizio. Trovare le soluzioni in C dell equazione (z 4 + )(z + iz + i) = 0 Soluzione: Le soluzioni dell
Algebra Lineare Ingegneria Chimica Anno Accademico 08/9 Caboara Esercitazione guidata 5 ottobre 08 Esercizio. Trovare le soluzioni in C dell equazione (z 4 + )(z + iz + i) = 0 Soluzione: Le soluzioni dell
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Traiettorie nello spazio degli stati
 . Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Equazioni differenziali lineari di ordine n
 Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Ist. di Fisica Matematica mod. A Quarta esercitazione
 Ist. di Fisica Matematica mod. A Quarta esercitazione Francesca Arici (farici@sissa.it Domenico Monaco (dmonaco@sissa.it 3 Novemre La numerazione seguita per gli Esercizi è quella delle note del corso.
Ist. di Fisica Matematica mod. A Quarta esercitazione Francesca Arici (farici@sissa.it Domenico Monaco (dmonaco@sissa.it 3 Novemre La numerazione seguita per gli Esercizi è quella delle note del corso.
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea in Fisica a.a.2001/02
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
Capitolo Quattordicesimo EQUAZIONI DIFFERENZIALI
 Capitolo Quattordicesimo EQUAZIONI DIFFERENZIALI. INTRODUZIONE DEFINIZIONE. Sono dette equazioni funzionali quelle equazioni in cui l'incognita è una funzione. ESEMPIO. ) Trovare una funzione f: Â Â tale
Capitolo Quattordicesimo EQUAZIONI DIFFERENZIALI. INTRODUZIONE DEFINIZIONE. Sono dette equazioni funzionali quelle equazioni in cui l'incognita è una funzione. ESEMPIO. ) Trovare una funzione f: Â Â tale
y 3y + 2y = 1 + x x 2.
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 16 gennaio 2018
 Università di Pisa - orso di Laurea in Informatica Analisi Matematica A Pisa, 6 gennaio 08 omanda La funzione f = e, nel suo insieme di definzione A ha minimo ma non ha massimo ha massimo ma non ha minimo
Università di Pisa - orso di Laurea in Informatica Analisi Matematica A Pisa, 6 gennaio 08 omanda La funzione f = e, nel suo insieme di definzione A ha minimo ma non ha massimo ha massimo ma non ha minimo
1. Equazioni differenziali del primo ordine. Si chiamano equazioni differenziali del primo ordine tutte quelle che si possono ricondurre alla forma
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2015-16 autore: Giovanni Alberti Equazioni differenziali [versione: 20 dicembre 2015] Richiamo delle nozioni
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
Michela Eleuteri ANALISI MATEMATICA. Equazioni differenziali ordinarie del secondo ordine
 Michela Eleuteri ANALISI MATEMATICA Equazioni differenziali ordinarie del secondo ordine A Giulia con la speranza che almeno nella matematica non assomigli al papà Indice 1 Equazioni dierenziali lineari
Michela Eleuteri ANALISI MATEMATICA Equazioni differenziali ordinarie del secondo ordine A Giulia con la speranza che almeno nella matematica non assomigli al papà Indice 1 Equazioni dierenziali lineari
Equazioni differenziali
 Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
Prova scritta di Algebra lineare e Geometria- 8 Settembre 2010
 CdL in Ingegneria d(el Recupero Edilizio ed Ambientale - - Ingegneria Edile-Architettura (A-L),(M-Z)- Ingegneria delle Telecomunicazioni - - Ingegneria Informatica (A-F), (R-Z) Prova scritta di Algebra
CdL in Ingegneria d(el Recupero Edilizio ed Ambientale - - Ingegneria Edile-Architettura (A-L),(M-Z)- Ingegneria delle Telecomunicazioni - - Ingegneria Informatica (A-F), (R-Z) Prova scritta di Algebra
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 2018 Parte B Tema B1
 Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 08 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
Università degli Studi di Bergamo Scuola di Ingegneria Corso di Geometria e Algebra Lineare Appello 5 settembre 08 Parte B Tema B Tempo a disposizione: due ore. Calcolatrici, libri e appunti non sono ammessi.
FM1 - Equazioni differenziali e meccanica. Il metodo di variazione delle costanti (Livia Corsi)
 Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 30 gennaio 2017
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 30 gennaio 2017 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. I soli risultati,
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 30 gennaio 2017 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. I soli risultati,
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 3 settembre 2018
 Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, settembre 208 ( cos x sin se x 0 Domanda Sia f : R R definita da f(x = x 0 se x = 0. non esiste la derivata di f in x = 0 f (0
Analisi Matematica 3 - Soluzioni Tutorato 8
 Analisi Matematica - Soluzioni Tutorato 8 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan 9 dicembre 07. Risolvere i seguenti problemi:
Analisi Matematica - Soluzioni Tutorato 8 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan 9 dicembre 07. Risolvere i seguenti problemi:
Matematica - Prova d esame (09/09/2004)
 Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA II - 27 Gennaio cos x
 COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
ESERCIZI SUI NUMERI COMPLESSI
 ESERCIZI SUI NUMERI COMPLESSI Esercizio Calcolare il modulo e l argomento principale del seguente numero complesso: z = ) 5 + i i) 7 Per risolvere l esercizio proposto applichiamo le formule per il calcolo
ESERCIZI SUI NUMERI COMPLESSI Esercizio Calcolare il modulo e l argomento principale del seguente numero complesso: z = ) 5 + i i) 7 Per risolvere l esercizio proposto applichiamo le formule per il calcolo
Analisi Matematica 2: Scritto Generale, Cognome e nome:...matricola:...
 Analisi Matematica : Scritto Generale, 300607 Cognome e nome: Matricola: es es es3 es4 es es6 es7 somma cr 6 6 6 6 6 - - 30 9cr/6cr 3 30 Determinare, nel punto ( 0, 0, z 0 ), l equazione del piano tangente
Analisi Matematica : Scritto Generale, 300607 Cognome e nome: Matricola: es es es3 es4 es es6 es7 somma cr 6 6 6 6 6 - - 30 9cr/6cr 3 30 Determinare, nel punto ( 0, 0, z 0 ), l equazione del piano tangente
Esercizi sulle funzioni f : R 2 R. Soluzioni
 Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Analisi dei Sistemi. Pre-esame 2 Novembre 2002
 Analisi dei Sistemi Pre-esame 2 Novembre 22 Esercizio Si consideri un sistema descritto dal seguente modello ingresso-uscita dove ϱ e η sono parametri reali costanti (4 punti) Individuare le proprietà
Analisi dei Sistemi Pre-esame 2 Novembre 22 Esercizio Si consideri un sistema descritto dal seguente modello ingresso-uscita dove ϱ e η sono parametri reali costanti (4 punti) Individuare le proprietà
TEMA 1. F (x, y) = e xy + x + y.
 FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
FONDAMENTI DI ANALII MATEMATICA 2 Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 23 gennaio 217 Primo appello Avvertenza: Nella prima
Elementi di Analisi dei Sistemi Soluzione esercizi prima prova intermedia
 Elementi di Analisi dei Sistemi Soluzione esercizi prima prova intermedia Gianluca Mereu, Alessandro Giua {gianluca.mereu,giua}@diee.unica.it 07/04/207 Soluzione Esercizio. Si risponda in modo chiaro ed
Elementi di Analisi dei Sistemi Soluzione esercizi prima prova intermedia Gianluca Mereu, Alessandro Giua {gianluca.mereu,giua}@diee.unica.it 07/04/207 Soluzione Esercizio. Si risponda in modo chiaro ed
SOLUZIONI COMPITO del 10/01/2019 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A
 SOLUZIONI COMPITO del 0/0/209 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Osserviamo che Pertanto, i = 2e iπ/, + i = 2e iπ/. e 7iπ/8, 2e iπ/ z = = e 2e 7iπ/2 = e 7iπ/8, iπ/ 2 8 2 e iπ/8, e
SOLUZIONI COMPITO del 0/0/209 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Osserviamo che Pertanto, i = 2e iπ/, + i = 2e iπ/. e 7iπ/8, 2e iπ/ z = = e 2e 7iπ/2 = e 7iπ/8, iπ/ 2 8 2 e iπ/8, e
Istituzioni di Matematica II 3 luglio 2014
 Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Esame scritto di fisica moderna
 Esame scritto di fisica moderna Traccia di soluzione 4 luglio 01 Esercizio 1. hamiltoniana data è quella di una buca di potenziale infinita, le cui autofunzioni sono date da due famiglie, dispari ψ n x
Esame scritto di fisica moderna Traccia di soluzione 4 luglio 01 Esercizio 1. hamiltoniana data è quella di una buca di potenziale infinita, le cui autofunzioni sono date da due famiglie, dispari ψ n x
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Addendum equazioni differenziali
 é Dispense per Matematica - AA 2015-2016 Addendum equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Soluzione
é Dispense per Matematica - AA 2015-2016 Addendum equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Soluzione
Analisi Matematica 3 - Soluzioni Tutorato 7
 Analisi Matematica 3 - Soluzioni Tutorato 7 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan dicembre 07 Equazioni lineari a coefficienti
Analisi Matematica 3 - Soluzioni Tutorato 7 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Jacopo Tenan dicembre 07 Equazioni lineari a coefficienti
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Alcuni esercizi sulle equazioni di erenziali
 Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Analisi Matematica 2
 Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
AM210 - Analisi Matematica 3: Soluzioni Tutorato 7
 AM10 - Analisi Matematica 3: Soluzioni Tutorato 7 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia Dobbiamo risolvere equazioni
AM10 - Analisi Matematica 3: Soluzioni Tutorato 7 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia Dobbiamo risolvere equazioni
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 21/211 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni dell'esame scritto del 1/6/211 1. Sia dato
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 21/211 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni dell'esame scritto del 1/6/211 1. Sia dato
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2018 Soluzioni Scritto. f(x) = ( ln 1 + x + 1 ) =
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018)
 Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
Equazioni differenziali ordinarie (ODE) lineari del secondo ordine a coefficienti costanti Fulvio Bisi Corso di Analisi Matematica A (ca) Università di Pavia Facoltà di Ingegneria 1 ODE lineari del secondo
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 2007 Tema A
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
NUMERI COMPLESSI Esercizi svolti. d) (1 i) 3. b) (1 + i)(1 i)(1 + 3 i) c) 1 i 1
 Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Soluzioni. 152 Roberto Tauraso - Analisi Risolvere il problema di Cauchy. { y (x) + 2y(x) = 3e 2x y(0) = 1
 5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
Equazioni differenziali lineari
 Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Analisi II. Foglio di esercizi n.2 10/10/2017 (Aggiornamento del 17/10/2017)
 Analisi II Foglio di esercizi n 10/10/017 (Aggiornamento del 17/10/017) Esercizi su massimi e minimi liberi con studi aggiuntivi 1 Siano K R n compatto e Ω R n un aperto contenente K Si consideri f C 1
Analisi II Foglio di esercizi n 10/10/017 (Aggiornamento del 17/10/017) Esercizi su massimi e minimi liberi con studi aggiuntivi 1 Siano K R n compatto e Ω R n un aperto contenente K Si consideri f C 1
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 00/0 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni all'esame scritto del 3/0/0 0 a 0 a. Dato
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 00/0 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni all'esame scritto del 3/0/0 0 a 0 a. Dato
5 Un applicazione: le matrici di rotazione
 5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
5 Un applicazione: le matrici di rotazione 51 Rotazioni nel piano di un angolo ϑ Si vuole considerare il caso della rotazione nel piano di un vettore di R di un angolo ϑ assegnato Chiaramente si tratta
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 15 gennaio 2018 Testi 1
 Secondo compitino e primo appello, 5 gennaio 8 Testi Prima parte, gruppo.. Calcolare la velocità (intesa come vettore) e il modulo della velocità di un punto che si muove nel piano con la seguente legge
Secondo compitino e primo appello, 5 gennaio 8 Testi Prima parte, gruppo.. Calcolare la velocità (intesa come vettore) e il modulo della velocità di un punto che si muove nel piano con la seguente legge
Corso di Laurea in Ingegneria Gestionale Anno Accademico 2013/2014 Calcolo Numerico
 1. Dato il problema ai valori iniziali f (t) = f(t) + cos t f(0) = 1, (ii) determinarne la soluzione numerica per 0 t 2π utilizzando il metodo di 2. Calcolare analiticamente e numericamente la media della
1. Dato il problema ai valori iniziali f (t) = f(t) + cos t f(0) = 1, (ii) determinarne la soluzione numerica per 0 t 2π utilizzando il metodo di 2. Calcolare analiticamente e numericamente la media della
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Soluzioni degli esercizi sulle equazioni alle differenze lineari
 Soluzioni degli esercizi sulle equazioni alle differenze lineari Bernardi Mauro Sapienza, University of Rome MEMOTEF Department April, 7th 2013 Mauro Bernardi (MEMOTEF) Soluzioni degli esercizi sulle equazioni
Soluzioni degli esercizi sulle equazioni alle differenze lineari Bernardi Mauro Sapienza, University of Rome MEMOTEF Department April, 7th 2013 Mauro Bernardi (MEMOTEF) Soluzioni degli esercizi sulle equazioni
Richiami sulle Equazioni Differenziali
 Richiami sulle Equazioni Differenziali Ing. Alessio Merola Laboratorio di Biomeccatronica Università degli Studi Magna Græcia di Catanzaro II anno I semestre CdL in Informatica e Biomedica Generalità sulle
Richiami sulle Equazioni Differenziali Ing. Alessio Merola Laboratorio di Biomeccatronica Università degli Studi Magna Græcia di Catanzaro II anno I semestre CdL in Informatica e Biomedica Generalità sulle
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
Modelli lineari del second ordine
 1 Peccati, Salsa, Squellati, Matematica per l economia e l azienda, EGEA 2004 Modelli lineari del second ordine Modelli discreti Partiamo da un esempio d interesse economico per capire come problemi di
1 Peccati, Salsa, Squellati, Matematica per l economia e l azienda, EGEA 2004 Modelli lineari del second ordine Modelli discreti Partiamo da un esempio d interesse economico per capire come problemi di
Alcune primitive. Francesco Leonetti (1) 5 giugno 2009
 Alcune primitive Francesco Leonetti ) 5 giugno 009 Introduzione La risoluzione di alcune equazioni differenziali ci ha mostrato come sia importante la capacità di trovare le primitive di funzioni assegnate.
Alcune primitive Francesco Leonetti ) 5 giugno 009 Introduzione La risoluzione di alcune equazioni differenziali ci ha mostrato come sia importante la capacità di trovare le primitive di funzioni assegnate.
Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/01/2015
 Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/0/205 (9 crediti) Esercizio. Si verifichi se nel punto (0, 0) la funzione 3 ye y 2 /x 4 se x 0 f (x, y) = 0 se x = 0, è
Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/0/205 (9 crediti) Esercizio. Si verifichi se nel punto (0, 0) la funzione 3 ye y 2 /x 4 se x 0 f (x, y) = 0 se x = 0, è
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Esercizi di ripasso. 17 Dicembre Federico Lastaria. Analisi e Geometria 1. Esercizi di ripasso (1) 1/10
 Esercizi di ripasso 17 Dicembre 2018 Federico Lastaria. Analisi e Geometria 1. Esercizi di ripasso (1) 1/10 1 Trovare l integrale generale dell equazione: y + 1 y = 0, x ( 1, + ) (1) x + 1 2 Verificare,
Esercizi di ripasso 17 Dicembre 2018 Federico Lastaria. Analisi e Geometria 1. Esercizi di ripasso (1) 1/10 1 Trovare l integrale generale dell equazione: y + 1 y = 0, x ( 1, + ) (1) x + 1 2 Verificare,
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a ) Homework assignment #2 Testo e Soluzione
 SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea (quadriennale) in Fisica a.a. 2002/03
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti
 Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
FONDAMENTI DI SISTEMI DINAMICI (prof. Vincenzo LIPPIELLO A.A ) Corso di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno
 Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI prof. Vincenzo LIPPIELLO A.A. 05 06 Corso di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 5 FEBBRAIO 06
Voto Cognome/Nome & No. Matricola FONDAMENTI DI SISTEMI DINAMICI prof. Vincenzo LIPPIELLO A.A. 05 06 Corso di Laurea in Ingegneria Elettronica e delle Telecomunicazioni - II anno PROVA DEL 5 FEBBRAIO 06
