Bande elettroniche nei cristalli - Esercizi con soluzioni. Fisica della Materia Condensata
|
|
|
- Leo Pasini
- 5 anni fa
- Visualizzazioni
Transcript
1 Bande elettroniche nei cristalli - Esercizi con soluzioni Fisica della Materia Condensata A.A. 2015/2016
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 Esercizio 10 - Prova di esonero 2014/2015 Un elemento cristallizza nella struttura cubica semplice con parametro reticolare a = 0.20 nm. L elemento è trivalente e di questi tre elettroni due occupano un orbitale p z ed uno occupa un orbitale s. Utilizzando l approssimazione del legame forte nella forma E i ( k) = E i α i R p.v. γ i ( R)exp i k R (i = p,s) dove γ i ( R) è l integrale di hopping, E p α p = 5.2 ev, E s α s = +2.0 ev, γ p = 0.6 ev, γ s = 0.5 ev, e limitando l interazione ai primi vicini: 1. scrivere l espressione esplicita di E i ( k) per le due bande di energia; 2. trovareivaloridellagapinterbandae g elamassaefficacedeglielettronidiconduzionealpuntoγ = (0,0,0) dello spazio k; 3. trovare lungo la direzione (1,0,0) il modulo della velocità di gruppo v g e calcolarne nel punto ( π a,0,0) il valore numerico; 4. utilizzando il modello dell elettrone quasi libero e assumendo una massa efficace isotropa e pari alla massa dell elettrone libero m 0, trovare il valore della velocità di Fermi v F. Soluzione 1. I primi vicini sono 6 e sono individuati dai vettori R = ( ± π a,0,0), ( 0,± π a,0), ( 0,0,± a) π. Per la banda p si ha γ p < 0 nella direzione ẑ e γ p > 0 nella direzione ˆx e ŷ, mentre per la banda s si ha γ s > 0 in tutte le direzioni. Per cui: E p ( k) = E p α p 2γ px cosk x a 2γ py cosk y a 2γ pz cosk z a = E p α p 2γ p (cosk x a+cosk y a cosk z a) = (cosk x a+cosk y a cosk z a) (ev) E s ( k) = E s α s 2γ sx cosk x a 2γ sy cosk y a 2γ sz cosk z a = E s α s 2γ s (cosk x a+cosk y a+cosk z a) = (cosk x a+cosk y a+cosk z a) (ev) 2. Il valore della gap al punto Γ è: E g (Γ) = E s (Γ) E p (Γ) = (1+1+1) ( (1+1 1)) ev = 5.4 ev Gli elettroni di conduzione sono quelli in banda s, che è parzialmente piena (la banda p è piena). Per questi elettroni le componenti del tensore di massa efficace sono: m ij = 2 [ 2 E s ( ] 1 k) k i k j Per la banda s il tensore è diagonale: m xx ( k) = 2 2a 2 γ s cosk x a ;m yy( k) = 2 2a 2 γ s cosk y a ;m zz( k) = 2 2a 2 γ s cosk z a ; 1
29 Al punto Γ i tre elementi sono uguali e valgono: m = m xx (Γ) = m yy (Γ) = m zz (Γ) = J s e Vs 2 ( m) 2 0.5eV 3. La velocità di gruppo è data da: ( v g ( k)) i = 1 E s ( k) = 1 k i 2aγ ssin(k i a) Lungo la direzione (1,0,0) si ha (k y = k z = 0), per cui: = Kg v g ( k) = 1 2aγ ssin(k i a)ˆx il cui modulo nel punto ( π a,0,0) vale, come prevedibile: v g (π/a,0,0) = 1 2aγ ssin(π) = 0 4. Calcoliamo il k F e la velocità di Fermi: v F = k F = ( )1 ( 3π 2N 3 3π 2 )1 3 = m 0 m 0 V m 0 a = m/s 2
30 Esercizio 11 - Esame I 2014/2015 Glistatielettronicidivalenzadiunacatenalinearemonoatomica conn= sitiedipassoreticolarea = 0.2 nm con condizioni periodiche al bordo sono ben descritti, in approssimazione ad elettroni indipendenti, da una base ortonormale di due diversi orbitali A> e B>, entrambi di simmetria s, su ciascun sito della catena. Gli elementi di matrice dell Hamiltoniana elettronica sono tutti nulli salvo quelli diagonali (stesso orbitale e stesso sito), che valgono rispettivamente ǫ A = 1 ev e ǫ B = 4 ev, e quelli fra orbitali dello stesso tipo centrati su siti primi vicini, che valgono rispettivamente t A = 3 ev e t B = 1 ev. Gli atomi della catena sono bivalenti ed il sistema si trova allo zero assoluto. Dopo aver scritto le espressioni delle due bande E A (k) e E B (k) ed averne tracciato un grafico approssimativo, 1. si determini l energia di Fermi E F del sistema; 2. si stabilisca se il modello ha comportamento metallico o isolante; 3. si calcolino le velocità di gruppo degli elettroni con energia E F ; 4. si calcoli il valore dell energia elettronica totale E TOT. Si fa presente che la densità degli stati per una generica banda ǫ(k) di una catena lineare di lunghezza L, senza molteplicità di spin, è data dall espressione: g(ǫ) = L ǫ(k) π k 1 Integrali utili: dx 1 x 2 = arcsin(x)+c x 1 x 2 dx = 1 x 2 +C Soluzione Le due bande sono: E A (k) = ǫ A 2t A cos(ka) = 1 6cos(ka) (ev) E B (k) = ǫ B 2t B cos(ka) = 4 2cos(ka) (ev) Per la banda A: il minimo vale ǫ A 2t A = 7 ev e il massimo ǫ A +2t A = 5 ev. Per la banda B: il minimo vale ǫ B 2t B = 2 ev e il massimo ǫ B +2t B = 6 ev. Le bande risultano quindu sovrapposte, come si vede anche dalla figura. 1. Poichè gli atomi sono bivalenti, nelle due bande vanno posizionati 2N elettroni. Le bande saranno dunque riempite dal rispettivo minimo al livello di Fermi. Indichiamo con k 1 il vettore d onda per il quale E B (k 1 ) = E F e con k 2 quello per cui E A (k 2 ) = E F. Sfruttiamo due condizioni: la prima è che ci devono essere 2N stati nei segmenti k 1 < k < k 1 e k 2 < k < k 2, quindi utilizzando la densità degli stati nello spazio k ed inserendo la degenerazione di spin si ha: 2N = 2 ( 2k1 2π L + 2k ) 2 2π L da questa risulta k 1 = π a k 2. La seconda condizione da sfruttare è che E A (k 2 ) = E B (k 1 ): 1 6cos(k 2 a) = 4 2cos(k 1 a) = 4 2cos(π k 2 a) = 4+2cos(k 1 a) = cos(k 2 a) = 5 8 =
31 6 4 E B (k) E A (k) E F 2 (ev) π/a -k 2 -k 1 0 k 1 k 2 π/a k E quindi possiamo calcolarci l energia di Fermi del sistema: E F = E A (k 2 ) = 1 6cos(k 2 a) ev = 1 6 ( 0.625) ev = 2.75 ev Controlliamo anche che E B (k 1 a) = E F : E F = E B (k 1 ) = 4 2cos(k 1 a) ev = 4 2 (+0.625) ev = 2.75 ev Soluzione alternativa: conteggio degli stati tramite la g(e): Calcoliamo la g(e) per la generica banda E(K) = ǫ 2tcos(ka) (dove va aggiunto il fattore 2 per la degenerazione di spin: g(e) = 2L π 1 2atsin(ka) = 2L π 1 2at 1 cos 2 (ka) = Il numero di elettroni con energia tra E 1 ed E 2, n(e 1,E 2 ) è dato da: 2πt 1 2N ( E(k) ǫ 2t ) 2 n(e 1,E 2 ) = E2 E 1 g(e)de Questi integrali si calcolano facendo il cambiamento di variabile x = E ǫ 2t, dx = de 2t : E2 E 1 2N ( 2πt 1 E ǫ 2t ) 2 de = E E 2 ǫ 2t 1 ǫ 2t 2N π dx 1 x 2 = 2N π [ arcsin ( ) E1 ǫ arcsin 2t ( )] E2 ǫ 2t a) 2N elettroni devono stare nelle due bande tra i rispettivi minimi e il livello di Fermi 2N = EF EF g A (E)dE + g B (E)dE ǫ A 2t A ǫ B 2t B 4
32 2N = 2N π = 2N π [ ( ) ( )] EF ǫ A EF ǫ B arcsin(1) arcsin + arcsin(1) arcsin 2t A 2t B [ ( ) ( )] EF ǫ A EF ǫ B π arcsin arcsin 2t A 2t B da cui: ( ( )) EF ǫ A sin arcsin 2t A E F ǫ A = E F ǫ B 2t A 2t B E F = ǫ At B +ǫ B t A t A +t B Questo è equivalente a: ( = sin arcsin = 1 (1) ( )) EF ǫ B ev = t B = 2.75 ev ( = sin arcsin ( )) EF ǫ B b) Gli elettroni con energie tra E F e il massimo della banda E A (5 ev) devono riempire la banda E B tra il suo minimo e E F, a causa del fatto che sono sovrapposte: 2t B ǫa+2t A E F g A (E)dE = EF ǫ B g B (E)dE 2N π [ ( EF ǫ A arcsin( 1) + arcsin 2t A )] = 2N π [ arcsin ( EF ǫ B 2t B ) ] +arcsin(1) da cui: ( ( )) EF ǫ A sin arcsin 2t A E F = ǫ At B +ǫ B t A t A +t B ( = sin 2π arcsin = 1 (1) ev = 11 4 ( )) EF ǫ B 2t B = 2.75 ev ( = sin arcsin ( )) EF ǫ B 2t B 2. Il sistema ha comportamento metallico a causa della sovrapposizione delle due bande. 3. Con energia pari a E F ci sono due gruppi di elettroni, quelli con momento ±k 1 e quelli con momento ±k 2. Elettroni sulla stessa banda avranno velocità di Fermi uguale in modulo e con verso opposto. Calcoliamo la velocità di gruppo di ciascuna banda: v A,B (k) = 1 de A,B (k) dk = 1 2at A,B sin(ka) = 1 2at A,B 1 cos2 (ka) I moduli delle due diverse velocità di Fermi sono: va F = va(k F 2 ) = 1 1 2at A 1 cos2 (k 2 a) = = m/s vb F = v F B (k 1 ) 1 1 = 2at B 1 cos2 (k 1 a) = = m/s 4. L energia totale è data da: E TOT = EF E g(e)de = EF ǫ A 2t A E g A (E)dE + EF ǫ B 2t B E g B (E)dE = E A +E B 5
33 I due integrali da calcolare sono uguali fra loro a patto di scambiare il pedice A con B: E A = 2N π = 2N π = 2N π = 2N π 1 E F ǫ A 2t A dx 1 x 2 ( 2t A x+ǫ A ) 1 ( EF ǫ A 2t A 2t A 1 ( EF ǫ A 2t A 2t A 6 ev 1 ) 2 +ǫ A ( arcsin ) 2 +ǫ A ( arcsin ( ) ev( arcsin 6 ( EF ǫ A 2t A ( EF ǫ A 2t A ( ) 2) π 6 ) +arcsin(1)) ) + π 2) = 2N ( 2.206) ev = ev E B = 2N π = 2N π 1 ( EF ǫ B 2t B 2t B ( ev 1 2 ) 2 +ǫ B ( arcsin ) 2 +4 ev( arcsin ( EF ǫ B 2t B ( ) + π 2) ) + π 2) = 2N (0.643) ev = ev E TOT = E A +E B = ev 6
34 Esercizio 12 - Esame II 2014/2015 Si consideri un ipotetico reticolo quadrato nel piano x-y, con distanza interatomica a ed un atomo monovalente di orbitale f 5 su ogni sito (l orbitale è mostrato in figura). Utilizzando il metodo del legame forte, l energia della banda risultante si può scrivere come: ǫ( k) = E 0 R 0 γ( R)exp(i k R) dove R indica un vettore appartenente al reticolo, e γ( R) è l integrale di trasferimento dato da: γ( R) = φ ( r) V( r)φ( r R)d r V è il potenziale cristallino, φ è la funzione d onda dell elettrone nell orbitale f. Per l orbitale considerato si ha E 0 =3 ev. Il valore in modulo dell integrale di trasferimento tra due siti primi vicini lungo ˆx è γ x =0.5 ev e lungo ŷ è γ y =0.3 ev. 1. Scrivere l espressione della banda risultante in approssimazione a primi vicini. 2. Disegnare l andamento delle bande di energia nelle direzioni (1,0) e (0,1) della prima zona di Brillouin e valutare la larghezza di banda in questo grafico; le direzioni sono fornite in unità di π/a. 3. Ricavare le componenti della massa efficace e calcolarne il valore numerico per un elettrone a centro zona. Sia il parametro reticolare a = 2.2 Å. 4. Si includa l interazione a secondi vicini, scrivere l espressione della nuova banda e rivalutarne la larghezza lungo le stesse direzioni. Sia l integrale di trasferimento tra due atomi secondi vicini γ= ev. Soluzione 1. La banda nell approssimazione a primi vicini ( R x = (±a,0), R y = (0,±a)) è: ǫ( k) = E 0 γ x ( e ik xa +e ikxa) γ y ( e ik ya +e ikya) = E 0 2γ x cos(k x a) 2γ y cos(k y a) Segni degli integrali di trasferimento (vedi figura): Lungo ˆx la sovrapposizione è negativa, per cui γ x < 0 e scriviamo γ x = γ x. Lungo ŷ la sovrapposizione è positiva, per cui γ y > 0 e scriviamo γ y = γ y. La banda la riscriviamo come: ǫ( k) = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) 7
35 2. Lungo la direzione (1,0), k x varia tra 0 e π/a e k y = 0, per cui la banda è: ǫ(k x,0) = E 0 +2 γ x cos(k x a) 2 γ y Lungo la direzione (0,1), k x = 0 e k y varia tra 0 e π/a, per cui la banda è: ǫ(0,k y ) = E 0 +2 γ x 2 γ y cos(k y a) Le bande lungo queste due direzioni sono mostrate in figura (linee continue). ǫ(0,0) = E 0 +2 γ x 2 γ y = ( ) ev = 3.4 ev ǫ( π a,0) = E 0 2 γ x 2 γ y = ( ) ev = 1.4 ev ǫ(0, π a ) = E 0 +2 γ x +2 γ y = ( ) ev = 4.6 ev (ev) ε(k x,0) ε(0,k y ) ε(k x,0) (secondi vicini) ε(0,k y ) (secondi vicini) π/a 0 π/a k y k x Dal grafico si valuta facilmente la larghezza della banda, il minimo è in ( π a,0) e il massimo in (0, π a ): Γ = ǫ(0, π a ) ǫ(π a,0) = ( ) ev = 3.2 ev. 8
36 3. Le componenti del tensore di massa sono definite da: m ij = 2 ( 2 ǫ( k) k i k j ) 1 dove i,j = x,y. Nella banda non compaiono termini misti in k x,k y, per cui il tensore possiede solamente gli elementi diagonali: m (k x,k y ) = Un elettrone nel centro zona (k x =0 e k y =0) ha dunque: ( ) 2 2a 2 γ x cos(k xa) a 2 γ y cos(k ya) m xx(0,0) = 2 2 γ x a 2 = Kg m yy(0,0) = 2 2 γ y a 2 = Kg 4. In un reticolo quadrato i secondi vicini sono 4 e sono individuati dai vettori R = (±a,±a). La nuova banda è dunque: ǫ ( k) = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) γ R e i k R = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) γ (e i(kxa+kya) +e i(kxa kya) +e i( kxa+kya) +e i( kxa kya)) = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) γ [ e ikxa( e ikya +e ikya) +e ikxa( e ikya +e ikya)] = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) γ ( e ikxa +e ikxa)( e ikya +e ikya) = E 0 +2 γ x cos(k x a) 2 γ y cos(k y a) 4 γcos(k x a)cos(k y a) Le nuove bande lungo le due direzioni (1,0) e (0,1) sono mostrate nella stessa figura (linee tratteggiate). ǫ (0,0) = (3.4 4( 0.1)) ev = 3.8 ev ǫ ( π a,0) = (1.4 4( 0.1)( 1)) ev = 1.0 ev ǫ (0, π a ) = (4.6 4( 0.1)( 1)) ev = 4.2 ev e la larghezza di banda rimane invariata: Γ = (4.2 1) ev = 3.2 ev 9
Bande elettroniche nei cristalli - Esercizi con soluzioni
 Bande elettroniche nei cristalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Bande elettroniche nei cristalli
Bande elettroniche nei cristalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Bande elettroniche nei cristalli
Scritto Appello IV, Materia Condensata. AA 2017/2018
 Scritto Appello IV, Materia Condensata AA 017/018 17/07/018 1 Esercizio 1 Un metallo monovalente cristallizza nella struttura cubica a corpo centrato La densità degli elettroni del metallo è n el = 65
Scritto Appello IV, Materia Condensata AA 017/018 17/07/018 1 Esercizio 1 Un metallo monovalente cristallizza nella struttura cubica a corpo centrato La densità degli elettroni del metallo è n el = 65
Solidi Es. 7. Esercizi Materia Condensata 2009/2010 Mario Capizzi
 Gli stati elettronici di valenza di una catena lineare monoatomica con N 10 23 siti e di passo reticolare a = 0,2 nm con condizioni periodiche al bordo sono ben descritti, in approssimazione a elettroni
Gli stati elettronici di valenza di una catena lineare monoatomica con N 10 23 siti e di passo reticolare a = 0,2 nm con condizioni periodiche al bordo sono ben descritti, in approssimazione a elettroni
Scritto Appello I, Materia Condensata. AA 2017/2018 (5/02/2018)
 Scritto Appello I, Materia Condensata. AA 017/018 5/0/018) Coloro che hanno superato il primo esonero dovranno svolgere gli esercizi 3 e 4 in un tempo massimo di due ore il punteggio sarà riportato in
Scritto Appello I, Materia Condensata. AA 017/018 5/0/018) Coloro che hanno superato il primo esonero dovranno svolgere gli esercizi 3 e 4 in un tempo massimo di due ore il punteggio sarà riportato in
Scritto Appello III, Materia Condensata. AA 2017/2018
 Scritto Appello III, Materia Condensata. AA 2017/2018 21/06/2018 1 Esercizio 1 Sia un A un solido monoatomico che cristallizza in una struttura cubica a facce centrate con lato del cubo a e velocità del
Scritto Appello III, Materia Condensata. AA 2017/2018 21/06/2018 1 Esercizio 1 Sia un A un solido monoatomico che cristallizza in una struttura cubica a facce centrate con lato del cubo a e velocità del
Scritto Appello II, Materia Condensata. AA 2017/2018
 Scritto Appello II, Materia Condensata. AA 017/018 19/0/018 Coloro che hanno superato il primo esonero dovranno svolgere gli esercizi 3 e 4 in un tempo massimo di due ore (il punteggio sarà riportato in
Scritto Appello II, Materia Condensata. AA 017/018 19/0/018 Coloro che hanno superato il primo esonero dovranno svolgere gli esercizi 3 e 4 in un tempo massimo di due ore (il punteggio sarà riportato in
Esercizio 1. CF 2 CS 2 CCl 4 ClF 3
 Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Fononi e calori reticolari - Testi degli esercizi. Fisica della Materia Condensata
 Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata A.A. 015/016 Fononi e calori reticolari Esercizio 1 Si consideri una catena lineare biatomica. Calcolare le relazioni di
Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata A.A. 015/016 Fononi e calori reticolari Esercizio 1 Si consideri una catena lineare biatomica. Calcolare le relazioni di
Fisica della Materia Condensata
 Fisica della Materia Condensata Prof. Paola Gallo Soluzioni della prova di esame del II appello - 13 Febbraio 2017 Esercizio 1 Considerare un cristallo con reticolo monoclino semplice con base monoatomica.
Fisica della Materia Condensata Prof. Paola Gallo Soluzioni della prova di esame del II appello - 13 Febbraio 2017 Esercizio 1 Considerare un cristallo con reticolo monoclino semplice con base monoatomica.
Fononi e calori reticolari - Testi degli esercizi
 Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Fononi e calori reticolari Esercizio
Fononi e calori reticolari - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Fononi e calori reticolari Esercizio
Fisica dello Stato Solido
 Corso di Fisica dello Stato Solido A.A. 2001/2002 Prof. Andrea Di Cicco INFM, Dipartimento di Fisica, via Madonna delle Carceri 62032 Camerino (MC), Italy http://www.unicam.it, http://gnxas.unicam.it LaTeX
Corso di Fisica dello Stato Solido A.A. 2001/2002 Prof. Andrea Di Cicco INFM, Dipartimento di Fisica, via Madonna delle Carceri 62032 Camerino (MC), Italy http://www.unicam.it, http://gnxas.unicam.it LaTeX
Fononi e calori reticolari - Soluzioni degli esercizi
 Fononi e calori reticolari - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Fononi e calori reticolari Esercizio
Fononi e calori reticolari - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Fononi e calori reticolari Esercizio
Raccolta Esami Scritti - Testi con soluzioni
 Raccolta Esami Scritti - Testi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Raccolta Esami Scritti - Testi con soluzioni
Raccolta Esami Scritti - Testi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Raccolta Esami Scritti - Testi con soluzioni
Sistemi cristallini - Soluzioni degli esercizi
 Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini - Soluzioni degli esercizi. Fisica della Materia Condensata
 Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata A.A. 05/06 Indice Esercizio Esercizio Esercizio 6 Esercizio 9 Esercizio 5 Esercizio 6 Esercizio 7 Esercizio 8 6 Esercizio
Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata A.A. 05/06 Indice Esercizio Esercizio Esercizio 6 Esercizio 9 Esercizio 5 Esercizio 6 Esercizio 7 Esercizio 8 6 Esercizio
Prova scritta di Materia Condensata del 5 Luglio 2011
 Proa scritta di Materia Condensata del Luglio 011 Prof. Paolo Calani Prof. Mario Capizzi Esercizio 1 Si assuma che un cristallo di litio metallico enga cresciuto mescolando in uguali proporzioni i due
Proa scritta di Materia Condensata del Luglio 011 Prof. Paolo Calani Prof. Mario Capizzi Esercizio 1 Si assuma che un cristallo di litio metallico enga cresciuto mescolando in uguali proporzioni i due
Elettronica dello Stato Solido Lezione 10: Strutture a bande in. Daniele Ielmini DEI Politecnico di Milano
 Elettronica dello Stato Solido Lezione 10: Strutture a bande in due e tre dimensioni Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it Outline Il reticolo reciproco Zone di Brillouin in
Elettronica dello Stato Solido Lezione 10: Strutture a bande in due e tre dimensioni Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it Outline Il reticolo reciproco Zone di Brillouin in
Reticoli e Diffrazione - Testi degli esercizi
 Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Reticoli e Diffrazione Esercizio 1....................................
Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Reticoli e Diffrazione Esercizio 1....................................
Elettronica dello Stato Solido Lezione 10: Strutture a bande in due e tre dimensioni
 Elettronica dello Stato Solido Lezione 10: Strutture a bande in due e tre dimensioni Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 10 2 Outline
Elettronica dello Stato Solido Lezione 10: Strutture a bande in due e tre dimensioni Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 10 2 Outline
Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni
 Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Trasporto in Semiconduttori
Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Trasporto in Semiconduttori
Reticoli e Diffrazione - Testi degli esercizi. Fisica della Materia Condensata
 Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata A.A. 2015/2016 Reticoli e Diffrazione Esercizio 1 Calcolare il fattore di struttura cristallino F( G) per il reticolo cubico
Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata A.A. 2015/2016 Reticoli e Diffrazione Esercizio 1 Calcolare il fattore di struttura cristallino F( G) per il reticolo cubico
Materia Condensata, Prova scritta del 01/07/2008 F. De Luca, [G. B. Bachelet], M. Capizzi, V. D. P. Servedio
![Materia Condensata, Prova scritta del 01/07/2008 F. De Luca, [G. B. Bachelet], M. Capizzi, V. D. P. Servedio Materia Condensata, Prova scritta del 01/07/2008 F. De Luca, [G. B. Bachelet], M. Capizzi, V. D. P. Servedio](/thumbs/97/133785056.jpg) Materia Condensata, Prova scritta del 01/07/2008 F. De Luca, [G. B. Bachelet], M. Capizzi, V. D. P. Servedio Esercizio 1 Nell atomo di elio gli stati eccitati 3 P = 1s2p e 1 P = 1s2p si osservano rispettivamente
Materia Condensata, Prova scritta del 01/07/2008 F. De Luca, [G. B. Bachelet], M. Capizzi, V. D. P. Servedio Esercizio 1 Nell atomo di elio gli stati eccitati 3 P = 1s2p e 1 P = 1s2p si osservano rispettivamente
Fisica Moderna: Corso di Laurea Scienze dei Materiali Prova scritta: 16/06/2017
 Fisica Moderna: Corso di aurea Scienze dei Materiali Prova scritta: 16/6/17 Problema 1 Una particella di spin 1/ è soggetta ad un campo magnetico uniforme B = B ẑ diretto lungo l asse delle z. operatore
Fisica Moderna: Corso di aurea Scienze dei Materiali Prova scritta: 16/6/17 Problema 1 Una particella di spin 1/ è soggetta ad un campo magnetico uniforme B = B ẑ diretto lungo l asse delle z. operatore
Effetto Stark (1) H 0 nlm > = E n nlm > (4) Ricordiamo che. E n = me4 2 h 2 n 2 = E 1
 Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
Effetto Stark Studiamo l equazione di Schrödinger per l atomo di idrogeno in presenza di un campo elettrico costante e diretto lungo l asse z, E = E k. La hamiltoniana di Schrödinger per l atomo di idrogeno
Corso di Laurea in Chimica e Tecnologie Chimiche - A.A Chimica Fisica II. Esame scritto del 25 Febbraio P = i.
 1 Corso di Laurea in Chimica e Tecnologie Chimiche - A.A. 212-213 Chimica Fisica II Esame scritto del 25 Febbraio 213 Quesiti d esame: 1. Definire gli operatori componente del momento cinetico P x e del
1 Corso di Laurea in Chimica e Tecnologie Chimiche - A.A. 212-213 Chimica Fisica II Esame scritto del 25 Febbraio 213 Quesiti d esame: 1. Definire gli operatori componente del momento cinetico P x e del
a/2+l/2 a/2-l/2 -a/2+l/2 -a/2-l/2
 Esame scritto di Elettromagnetismo del 17 Giugno 014 - a.a. 013-014 proff. F. Lacava, F. icci, D. Trevese Elettromagnetismo 10 o 1 crediti: esercizi 1,,3 tempo 3 h e 30 min; ecupero di un esonero: esercizi
Esame scritto di Elettromagnetismo del 17 Giugno 014 - a.a. 013-014 proff. F. Lacava, F. icci, D. Trevese Elettromagnetismo 10 o 1 crediti: esercizi 1,,3 tempo 3 h e 30 min; ecupero di un esonero: esercizi
S.I.C.S.I. Scuola Interuniversitaria Campana di Specializzazione all Insegnamento VIII ciclo - a.a. 2008/2009
 S.I.C.S.I. Scuola Interuniversitaria Campana di Specializzazione all Insegnamento VIII ciclo - a.a. 2008/2009 Conduzione elettrica nei metalli (conduttori e semiconduttori) Corso di Laboratorio di Didattica
S.I.C.S.I. Scuola Interuniversitaria Campana di Specializzazione all Insegnamento VIII ciclo - a.a. 2008/2009 Conduzione elettrica nei metalli (conduttori e semiconduttori) Corso di Laboratorio di Didattica
Matematica e Statistica
 Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Esercitazioni 26/10/2016
 Esercitazioni 26/10/2016 Esercizio 1 Un anello sottile di raggio R = 12 cm disposto sul piano yz (asse x uscente dal foglio) è composto da due semicirconferenze uniformemente cariche con densità lineare
Esercitazioni 26/10/2016 Esercizio 1 Un anello sottile di raggio R = 12 cm disposto sul piano yz (asse x uscente dal foglio) è composto da due semicirconferenze uniformemente cariche con densità lineare
Foglio Esercizi A (interpolazione, approssimazione, integrazione)
 Foglio Esercizi A (interpolazione, approssimazione, integrazione) Esercizio cos( ) +, [,π ] Costruire una approssimazione f ( ) di f () utilizzando elemento di ermite a nodi non equispaziati (, π, π )
Foglio Esercizi A (interpolazione, approssimazione, integrazione) Esercizio cos( ) +, [,π ] Costruire una approssimazione f ( ) di f () utilizzando elemento di ermite a nodi non equispaziati (, π, π )
Gli elettroni nei cristalli
 Gli elettroni nei cristalli esempio in una dimensione: V(x)=V(x+a) funzione d onda elettronica: deve risolvere l equazione di Schrödinger in presenza di un potenziale periodico come si risolve il problema
Gli elettroni nei cristalli esempio in una dimensione: V(x)=V(x+a) funzione d onda elettronica: deve risolvere l equazione di Schrödinger in presenza di un potenziale periodico come si risolve il problema
Esempi di struttura a bande: un isolante ionico, LIF
 Esempi di struttura a bande: un isolante ionico, LIF In figura, la struttura a bande di un isolante con un grosso gap (LiF, un materiale fortemente ionico), calcolata con due diversi metodi. Le 5 bande
Esempi di struttura a bande: un isolante ionico, LIF In figura, la struttura a bande di un isolante con un grosso gap (LiF, un materiale fortemente ionico), calcolata con due diversi metodi. Le 5 bande
ESAME DI FISICA II- Sessione 16/07/2013 Compito per l Ordinamento 270 e i VV.OO.
 ESAME DI FISICA II- Sessione 16/07/2013 Compito per l Ordinamento 270 e i VV.OO. PROBLEMA 1 Una lastra di dielettrico (a=b=1 cm; spessore 0.1 cm), in cui si misura un campo elettrico di 10 3 V.m -1, presenta
ESAME DI FISICA II- Sessione 16/07/2013 Compito per l Ordinamento 270 e i VV.OO. PROBLEMA 1 Una lastra di dielettrico (a=b=1 cm; spessore 0.1 cm), in cui si misura un campo elettrico di 10 3 V.m -1, presenta
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Concorso di ammissione al quarto anno, a.a. 2006/07 Prova scritta di fisica
 Concorso di ammissione al quarto anno, a.a. 2006/07 Prova scritta di fisica Corsi di laurea magistrale in Scienze Fisiche e Fisica Applicata 1) Una cometa si muove su una traiettoria parabolica intorno
Concorso di ammissione al quarto anno, a.a. 2006/07 Prova scritta di fisica Corsi di laurea magistrale in Scienze Fisiche e Fisica Applicata 1) Una cometa si muove su una traiettoria parabolica intorno
Semiconduttori. Bande di energia. Un cristallo è formato da atomi disposti in modo da costituire una struttura periodica regolare
 Semiconduttori Bande di energia Un cristallo è formato da atomi disposti in modo da costituire una struttura periodica regolare Quando gli atomi formano un cristallo, il moto degli elettroni dello strato
Semiconduttori Bande di energia Un cristallo è formato da atomi disposti in modo da costituire una struttura periodica regolare Quando gli atomi formano un cristallo, il moto degli elettroni dello strato
Uso del Calcolatore nella Scienza dei Materiali
 Uso del Calcolatore nella Scienza dei Materiali Introduzione alla Simulazione Quanto-Meccanica di Sistemi Molecolari Dalle molecole ai cristalli Bartolomeo Civalleri/Lorenzo Maschio Dip. Chimica Via P.
Uso del Calcolatore nella Scienza dei Materiali Introduzione alla Simulazione Quanto-Meccanica di Sistemi Molecolari Dalle molecole ai cristalli Bartolomeo Civalleri/Lorenzo Maschio Dip. Chimica Via P.
(2) cubico a facce centrate (3) esagonale compatto
 IL LEGAME METALLICO La maggior parte dei metalli cristallizza in strutture a massimo impacchettamento, ovvero in solidi in cui si può considerare che gli ioni metallici che occupano le posizioni reticolari,
IL LEGAME METALLICO La maggior parte dei metalli cristallizza in strutture a massimo impacchettamento, ovvero in solidi in cui si può considerare che gli ioni metallici che occupano le posizioni reticolari,
Terzo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/7. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/7. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Teorema di Cauchy. a) le azioni sono delle forze che ammettono densità rispetto alla lunghezza della linea ideale di taglio;
 Teorema di Cauchy Cosideriamo un corpo continuo in uno spazio bidimensionale. Esso può essere separato in due parti tracciando una linea (regolare) ideale. Queste parti si scambiano azioni dinamiche. L
Teorema di Cauchy Cosideriamo un corpo continuo in uno spazio bidimensionale. Esso può essere separato in due parti tracciando una linea (regolare) ideale. Queste parti si scambiano azioni dinamiche. L
Esame di stato 2014_2 2 M.Vincoli
 Esame di stato 0_ M.Vincoli . Per semplificare i calcoli, evitando altresì di introdurre immediatamente grandezze numeriche, è utile adottare una notazione semplificatrice, per cui poniamo:, 0 0,,0 0,60
Esame di stato 0_ M.Vincoli . Per semplificare i calcoli, evitando altresì di introdurre immediatamente grandezze numeriche, è utile adottare una notazione semplificatrice, per cui poniamo:, 0 0,,0 0,60
Elettronica dello Stato Solido Esercitazione di Laboratorio 3: Teoria a bande e statistica di portatori
 Elettronica dello Stato Solido Esercitazione di Laboratorio 3: Teoria a bande e statistica di portatori Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato
Elettronica dello Stato Solido Esercitazione di Laboratorio 3: Teoria a bande e statistica di portatori Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato
Compito di gennaio 2001
 Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
S.Barbarino - Esercizi svolti di Fisica generale II. Esercizi svolti di Fisica generale II - Anno 1996
 SBarbarino - Esercizi svolti di Fisica generale II Esercizi svolti di Fisica generale II - Anno 1996 96-1) Esercizio n 1 del 24/7/1996 Una regione di spazio é sede di un campo elettrico descrivibile dalla
SBarbarino - Esercizi svolti di Fisica generale II Esercizi svolti di Fisica generale II - Anno 1996 96-1) Esercizio n 1 del 24/7/1996 Una regione di spazio é sede di un campo elettrico descrivibile dalla
IL LEGAME METALLICO 1
 IL LEGAME METALLICO 1 Non metalli Metalli Metalloidi Proprietà dei metalli Elevata conducibilità elettrica; Elevata conducibilità termica; Effetto fotoelettrico; Elevata duttilità e malleabilità; Lucentezza;
IL LEGAME METALLICO 1 Non metalli Metalli Metalloidi Proprietà dei metalli Elevata conducibilità elettrica; Elevata conducibilità termica; Effetto fotoelettrico; Elevata duttilità e malleabilità; Lucentezza;
Elettroni negli Atomi
 Elettroni negli Atomi Solo alcune orbite sono stabili In realtànon sonoorbitema FUNZIONI D ONDA Ψ Ψ 2 è la DENSITA di probabilità di trovare l elettrone in una certa posizione rispetto al nucleo Le varie
Elettroni negli Atomi Solo alcune orbite sono stabili In realtànon sonoorbitema FUNZIONI D ONDA Ψ Ψ 2 è la DENSITA di probabilità di trovare l elettrone in una certa posizione rispetto al nucleo Le varie
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Elettrone fortemente legato
 Elettrone fortemente legato Introduzione Vogliamo studiare un altra strada, cioè un altra approssimazione per ottenere le bande elettroniche, e cioè quella del metodo dell elettrone fortemente legato.
Elettrone fortemente legato Introduzione Vogliamo studiare un altra strada, cioè un altra approssimazione per ottenere le bande elettroniche, e cioè quella del metodo dell elettrone fortemente legato.
LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI
 LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI Il legame covalente e la geometria delle molecole possono essere descritti dalla teoria del legame di valenza: i legami risultano dalla condivisione di
LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI Il legame covalente e la geometria delle molecole possono essere descritti dalla teoria del legame di valenza: i legami risultano dalla condivisione di
Diffrazione da reticolo.
 Reticolo della presente reciproco. opera. Diffrazione da reticolo. 1 Reticolo reciproco Sistema reticolare: periodico > ogni grandezza fisica sarà periodica con stesso periodo. Ogni grandezza Enrico Silva
Reticolo della presente reciproco. opera. Diffrazione da reticolo. 1 Reticolo reciproco Sistema reticolare: periodico > ogni grandezza fisica sarà periodica con stesso periodo. Ogni grandezza Enrico Silva
TECNOLOGIA DEI MATERIALI E CHIMICA APPLICATA- Appello scritto
 TCNOOGI DI MTRII CHIMIC PPICT- ppello scritto 0-6-05 sercizio.. Si abbia un materiale su cui agisce lo sforzo 00 MPa: calcolare lo sforzo di taglio risolto sul piano inclinato a 45 e la deformazione di
TCNOOGI DI MTRII CHIMIC PPICT- ppello scritto 0-6-05 sercizio.. Si abbia un materiale su cui agisce lo sforzo 00 MPa: calcolare lo sforzo di taglio risolto sul piano inclinato a 45 e la deformazione di
Prova Scritta di di Meccanica Analitica. 28 Giugno Problema 1. Si consideri un punto materiale di massa unitaria soggetto ad un potenziale
 Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = 1 x + x x > 0 determinare le frequenze delle piccole
Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = 1 x + x x > 0 determinare le frequenze delle piccole
Metalli come gas di elettroni liberi
 Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
Metalli come gas di elettroni liberi I metalli sono caratterizzati da elevata conducibilità elettrica e termica. La conducibilità elettrica in particolare (o il suo inverso, la resistività) è una delle
Terza prova di esonero di Elettromagnetismo a.a. 2012/ Giugno 2013 proff. F. Lacava, F. Ricci, D. Trevese
 Terza prova di esonero di Elettromagnetismo a.a. 2012/2013-7 Giugno 2013 proff. F. Lacava, F. icci, D. Trevese Esercizio 1 Un toroide di materiale ferromagnetico con sezione quadrata di lato a = 4 cm e
Terza prova di esonero di Elettromagnetismo a.a. 2012/2013-7 Giugno 2013 proff. F. Lacava, F. icci, D. Trevese Esercizio 1 Un toroide di materiale ferromagnetico con sezione quadrata di lato a = 4 cm e
Matematica e Statistica
 Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
Matematica - Prova d esame (09/09/2004)
 Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento
 Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 05: Trasformata di Laplace e funzione di trasferimento 28 marzo 208 (3h) Fondamenti di Automatica Prof. M. Farina Responsabile delle esercitazioni: Enrico Terzi Queste dispense sono state
Esercitazione 1: 09/03/2017
 Esercitazione 1: 09/03/017 Luigi Pilo a,b a Dipartimento di Fisica, Università di L Aquila, I-67010 L Aquila, Italy b INFN, Laboratori Nazionali del Gran Sasso, I-67010 Assergi, Italy luigi.pilo@aquila.infn.it
Esercitazione 1: 09/03/017 Luigi Pilo a,b a Dipartimento di Fisica, Università di L Aquila, I-67010 L Aquila, Italy b INFN, Laboratori Nazionali del Gran Sasso, I-67010 Assergi, Italy luigi.pilo@aquila.infn.it
Prova scritta di Probabilità e Statistica Appello unico, II sessione, a.a. 2015/ Settembre 2016
 Prova scritta di Probabilità e Statistica Appello unico, II sessione, a.a. 205/206 20 Settembre 206 Esercizio. Un dado equilibrato viene lanciato ripetutamente. Indichiamo con X n il risultato dell n-esimo
Prova scritta di Probabilità e Statistica Appello unico, II sessione, a.a. 205/206 20 Settembre 206 Esercizio. Un dado equilibrato viene lanciato ripetutamente. Indichiamo con X n il risultato dell n-esimo
Esercizio I Sia data una particella libera in tre dimensioni descritta a t = 0 dalla funzione d onda
 Compito I di MQ. Febbraio 0 Sia data una particella libera in tre dimensioni descritta a t = 0 dalla funzione d onda ψ( x = f(r (r + ix con Hamiltoniana H = µbl y determinare la funzione d onda al tempo
Compito I di MQ. Febbraio 0 Sia data una particella libera in tre dimensioni descritta a t = 0 dalla funzione d onda ψ( x = f(r (r + ix con Hamiltoniana H = µbl y determinare la funzione d onda al tempo
Limiti del modello a elettroni liberi
 Limiti del modello a elettroni liberi Il modello di elettroni liberi spiega in modo semi-quantitativo certi aspetti del comportamento dei metalli: contributo elettronico alla compressibilità e al calore
Limiti del modello a elettroni liberi Il modello di elettroni liberi spiega in modo semi-quantitativo certi aspetti del comportamento dei metalli: contributo elettronico alla compressibilità e al calore
Terzo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2018/2019. Prof. M. Bramanti. { y + y. 2 1 x 2 y (0) = 1.
 Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 5 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 5 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Le molecole ed il legame chimico
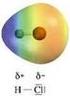 LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
Compito di recupero del giorno 27/11/2015
 Compito di recupero del giorno 27/11/2015 Esercizio n. 1 Una particella di massa m e spin 1/2 si muove in due dimensioni nel piano xy ed è soggetta alla seguente Hamiltoniana: H = 1 2m (p2 x + p 2 y) +
Compito di recupero del giorno 27/11/2015 Esercizio n. 1 Una particella di massa m e spin 1/2 si muove in due dimensioni nel piano xy ed è soggetta alla seguente Hamiltoniana: H = 1 2m (p2 x + p 2 y) +
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA) A.A. 2016/17 - Prova del
 Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (69AA) A.A. 06/7 - Prova del 07-07-07 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate. Problema
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (69AA) A.A. 06/7 - Prova del 07-07-07 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate. Problema
11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ
 11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ Sistemi irriducibili di operatori in uno spazio di Hilbert Un insieme o sistema di operatori {A, B,...} in uno spazio di Hilbert H si
11/3 IRRIDUCIBILITÀ NELLO SPAZIO DI HILBERT 10/11 1 IRRIDUCIBILITÀ Sistemi irriducibili di operatori in uno spazio di Hilbert Un insieme o sistema di operatori {A, B,...} in uno spazio di Hilbert H si
Esercizi di preparazione alla PFB
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari. (c) e5 e 4 e (2x 3y) dx + (1 + x)dx +
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 5.XI.7. Gli integrali richiesti valgono: (a) + ( e ) (b) (c) e5 e e + (d)
1 Sistemi di riferimento
 Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Formazione delle bande di energia. Fisica Dispositivi Elettronici CdL Informatica A.A. 2003/4
 Formazione delle bande di energia Calcolo formale: Equazione di Schröedinger L equazione di Schröedinger è una relazione matematica che descrive il comportamento ondulatorio di una particella (elettrone)
Formazione delle bande di energia Calcolo formale: Equazione di Schröedinger L equazione di Schröedinger è una relazione matematica che descrive il comportamento ondulatorio di una particella (elettrone)
Esercizi sui Solidi. Insegnamento di Chimica Generale CCS CHI e MAT. A.A. 2015/2016 (I Semestre)
 Insegnamento di Chimica Generale 083424 - CCS CHI e MAT A.A. 2015/2016 (I Semestre) Esercizi sui Solidi Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio Esercizio 1 Che composto
Insegnamento di Chimica Generale 083424 - CCS CHI e MAT A.A. 2015/2016 (I Semestre) Esercizi sui Solidi Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio Esercizio 1 Che composto
Prima prova d esonero del corso di Elettromagnetismo - a.a. 2012/13-12/4/2013 proff. F. Lacava, F. Ricci, D. Trevese
 Prima prova d esonero del corso di Elettromagnetismo - a.a. 212/13-12/4/213 proff. F. Lacava, F. Ricci, D. Trevese ESERCIZIO 1 Ad un sottile guscio sferico isolante di raggio R 1 cm è stata rimossa una
Prima prova d esonero del corso di Elettromagnetismo - a.a. 212/13-12/4/213 proff. F. Lacava, F. Ricci, D. Trevese ESERCIZIO 1 Ad un sottile guscio sferico isolante di raggio R 1 cm è stata rimossa una
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
= 0 Ciascuna frazione tende ad x x 4 2 cos x lim x = il secondo addendo del numeratore è una funzione x (cos sin x 3 1) cos(x π 2 )
 + sen x Es. lim x = il numeratore tende ad un numero positivo, il x 4 denominatore tende a zero. x 4 lim x = il denominatore ha grado maggiore del numeratore. x 8 + x sen x lim x +( + x) sen x = lim x
+ sen x Es. lim x = il numeratore tende ad un numero positivo, il x 4 denominatore tende a zero. x 4 lim x = il denominatore ha grado maggiore del numeratore. x 8 + x sen x lim x +( + x) sen x = lim x
1. Scrivere il termine generale a n delle seguenti successioni e calcolare lim n a n:
 Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
TEORIA DEGLI ORBITALI MOLECOLARI (MO).
 TEORIA DEGLI ORBITALI MOLECOLARI (MO). La teoria MO rappresenta l approccio quantomeccanico alle molecole in maniera analoga a quanto visto per la teoria atomica. Gli MO si considerano derivati da combinazioni
TEORIA DEGLI ORBITALI MOLECOLARI (MO). La teoria MO rappresenta l approccio quantomeccanico alle molecole in maniera analoga a quanto visto per la teoria atomica. Gli MO si considerano derivati da combinazioni
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2017/2018. Prof. M. Bramanti. Tema n 1.
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Metodo variazionale e applicazione all atomo di elio
 Metodo variazionale e applicazione all atomo di elio Descrizione del metodo Il metodo detto variazionale è un metodo approssimato che si usa per ottenere una stima dell energia dello stato fondamentale
Metodo variazionale e applicazione all atomo di elio Descrizione del metodo Il metodo detto variazionale è un metodo approssimato che si usa per ottenere una stima dell energia dello stato fondamentale
Anno Accademico Fisica I 12 CFU Esercitazione n.1 Operazioni con i vettori
 Anno Accademico 2018-2019 Fisica I 12 CFU Esercitazione n.1 Operazioni con i vettori Esercizio n.1 (28-11-2007, 8 CFU con soluz.) In un sistema di riferimento Oxyz, assegnati i punti A e B di coordinate
Anno Accademico 2018-2019 Fisica I 12 CFU Esercitazione n.1 Operazioni con i vettori Esercizio n.1 (28-11-2007, 8 CFU con soluz.) In un sistema di riferimento Oxyz, assegnati i punti A e B di coordinate
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
Legame nei cristalli. Cosa tiene insieme un cristallo?
 Legame nei cristalli Cosa tiene insieme un cristallo? L energia di coesione, dovuta all interazione elettrostatica attrattiva fra gli elettroni, carichi negativamente, e i nuclei, carichi positivamente
Legame nei cristalli Cosa tiene insieme un cristallo? L energia di coesione, dovuta all interazione elettrostatica attrattiva fra gli elettroni, carichi negativamente, e i nuclei, carichi positivamente
Foglio di Esercizi 5 Meccanica Razionale a.a. 2017/18 Canale A-L (P. Buttà)
 Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Foglio di Esercizi 5 Meccanica Razionale a.a. 017/18 Canale A-L (P. Buttà) Esercizio 1. Su un piano orizzontale sono poste due guide immateriali circolari di centri fissi O 1 e O e uguale raggio r; sia
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Prova Scritta Elettromagnetismo (a.a. 2017/18, S. Giagu/F. Lacava/F. Piacentini)
 Prova Scritta Elettromagnetismo - 2.6.208 (a.a. 207/8, S. Giagu/F. Lacava/F. Piacentini) recupero primo esonero: risolvere l esercizio : tempo massimo.5 ore. recupero secondo esonero: risolvere l esercizio
Prova Scritta Elettromagnetismo - 2.6.208 (a.a. 207/8, S. Giagu/F. Lacava/F. Piacentini) recupero primo esonero: risolvere l esercizio : tempo massimo.5 ore. recupero secondo esonero: risolvere l esercizio
La Teoria dell Atomo di Bohr Modello di Bohr dell atomo di idrogeno:
 La Teoria dell Atomo di Bohr Modello di Bohr dell atomo di idrogeno: Vedi documento Atomo di Bohr.pdf sul materiale didattico per la derivazione di queste equazioni Livelli Energetici dell Atomo di Idrogeno
La Teoria dell Atomo di Bohr Modello di Bohr dell atomo di idrogeno: Vedi documento Atomo di Bohr.pdf sul materiale didattico per la derivazione di queste equazioni Livelli Energetici dell Atomo di Idrogeno
Matematica e Statistica
 Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2018/2019. Prof. M. Bramanti
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
LA STRUTTURA ELETTRONICA DEGLI ATOMI
 LA STRUTTURA ELETTRONICA DEGLI ATOMI 127 Possiamo trattare insieme l atomo di idrogeno e gli atomi idrogenoidi He +, Li 2+, ecc., in quanto differiscono l uno dall altro solo per la carica nucleare. Protone
LA STRUTTURA ELETTRONICA DEGLI ATOMI 127 Possiamo trattare insieme l atomo di idrogeno e gli atomi idrogenoidi He +, Li 2+, ecc., in quanto differiscono l uno dall altro solo per la carica nucleare. Protone
Analisi Matematica II (Prof. Paolo Marcellini)
 Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 5//14 Michela Eleuteri 1 eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Cenni sulla teoria dell orbitale molecolare
 Cenni sulla teoria dell orbitale molecolare Legame chimico: teoria dell orbitale molecolare (MO) La formazione della molecola genera ORBITALI MOLECOLARI che derivano dalla combinazione degli ORBITALI ATOMICI.
Cenni sulla teoria dell orbitale molecolare Legame chimico: teoria dell orbitale molecolare (MO) La formazione della molecola genera ORBITALI MOLECOLARI che derivano dalla combinazione degli ORBITALI ATOMICI.
CONTROLLI AUTOMATICI LS Ingegneria Informatica. Analisi modale
 CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
Elementi di fisica dello stato solido
 Elementi di fisica dello stato solido Perché alcuni materiali sono buoni conduttori di elettroni ed altri no? Quali sono i meccanismi con cui la corrente fluisce nei solidi? Perché nei semiconduttori la
Elementi di fisica dello stato solido Perché alcuni materiali sono buoni conduttori di elettroni ed altri no? Quali sono i meccanismi con cui la corrente fluisce nei solidi? Perché nei semiconduttori la
Matematica e Statistica
 Matematica e Statistica Prova d esame (/07/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (/07/202) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (/07/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (/07/202) Università di Verona - Laurea in Biotecnologie
