Analisi dei sistemi nel dominio del tempo
|
|
|
- Alessandra Donato
- 4 anni fa
- Visualizzazioni
Transcript
1 Laboratorio di Telecomunicazioni - a.a. 2010/2011 Lezione n. 4 Analisi dei sistemi nel dominio del tempo L.Verdoliva In questa terza lezione ci occuperemo dell elaborazione di segnali tempo discreto mediante sistemi LTI (convoluzione) e della realizzazione in Matlab di sistemi descritti da equazioni alle differenze a coefficienti costanti (ARMA). 1 Sistemi LTI I sistemi lineari tempo invarianti (LTI) costituiscono la più importante classe di sistemi, sia perché modellano adeguatamente molte situazioni reali, sia perché risultano completamente caratterizzati dalla conoscenza della risposta impulsiva, h(n) = T [δ(n)]; in particolare l uscita di un sistema LTI è data dalla somma di convoluzione tra l ingresso x(n) e h(n): y(n) = x(n) h(n) = x(k)h(n k) Facendo un cambio di variabili, si può facilmente verificare che la convoluzione è commutativa, cioè x(n) h(n) = h(n) x(n). In Matlab esiste già un comando per il calcolo della convoluzione, la cui sintassi è la seguente: >> y=conv(x,h) Calcolate la convoluzione tra i seguenti segnali: x(n) = δ(n + 1) + δ(n) + δ(n 1) + δ(n 2) e h(n) = 1 2 δ(n) + 1 2δ(n 1) e verificate che scambiando i ruoli di x(n) e h(n) il risultato non cambia. Anche in questo caso (come per la correlazione) l uscita non dà indicazioni sull istante iniziale e finale della sequenza. Provate allora a scrivere una funzione con il seguente prototipo: function [y,ny]=convoluzione(x,nx,h,nh); tenendo presente che il risultato della convoluzione è compreso nell intervallo [n xi +n hi, n xf +n hf ], dove n xi, n hi, n xf e n hf sono gli istanti iniziali e finali di x(n) e h(n). 1.1 Esempi ed esperimenti proposti a) Convoluzione tra due finestre rettangolari 1
2 Siano x(n) e h(n) due finestre rettangolari di lunghezza N e M, rispettivamente, cioè x(n) = R N (n) e h(n) = R M (n). Per calcolare l uscita y(n) = x(n) h(n), per N = 4 e M = 4. Ripetete l esperimento aumentando la lunghezza del vettore di ingresso, e verificate che la convoluzione di due sequenze rettangolari di lunghezza N e M è una sequenza trapezoidale di durata L = M + N 1, cioè a causa della memoria del filtro la lunghezza del segnale in ingresso si allunga di M 1 campioni. Questo risultato è valido per due sequenze generiche purchè abbiano entrambe durata finita. b) Convoluzione tra un gradino e una sequenza esponenziale Si consideri adesso il calcolo della convoluzione tra x(n) = u(n) e h(n) = a n u(n), con 0 < a < 1. Analiticamente risulta: y(n) = h(k)x(n k) = a k u(k) u(n k) = n k=0 a k = 1 an+1 1 a n 0 Per a = 1/2 verificate col Matlab che l uscita tende a 1 1 a = 2 all aumentare di n. c) Convoluzione tra sequenze di durata finita Si consideri adesso il calcolo della convoluzione tra x(n) = R 5 (n) e h(n) = 2 n R 7 (n). Determinare la soluzione analitica e verificarne la correttezza con il Matlab. I sistemi LTI sono generalmente classificati in sistemi con risposta impulsiva a durata finita (FIR) e sistemi con risposta impulsiva a durata infinita (IIR). 1.2 Sistemi FIR Consideriamo per semplicità un filtro FIR causale e supponiamo che h(n) abbia durata M (filtro di ordine M), allora risulta: y(n) = h(m)x(n m) = b m x(n m) dove si è posto h(m) = b m per m = 0,, M. L uscita del sistema è semplicemente una combinazione lineare pesata dei campioni di ingresso del segnale; il sistema opera quindi come una finestra che vede solo i più recenti M campioni per determinare l uscita. Per questo motivo i sistemi FIR sono spesso chiamati filtri a media mobile (Moving-Average, MA). Essendo finita la memoria del sistema, sono facilmente realizzabili con un numero finito di locazioni di memoria, moltiplicatori e addizionatori. Realizzate in matlab la convoluzione tra il segnale x(n) = 4 R 11 (n) + 12 R 5 (n) e il filtro con coefficienti b 0 = 1/2 e b 1 = 1/2, l uscita risulta quindi in ogni istante la media aritmetica degli ultimi due valori della sequenza di ingresso x(n). Ripetete l operazione di filtraggio nel caso in cui b 0 = 1/2 e b 1 = 1/2. Come cambia l uscita? Che comportamento hanno questi due filtri? 2
3 1. Sistemi IIR I filtri IIR hanno risposta impulsiva a durata infinita pertanto non sono fisicamente realizzabili, tuttavia esiste una sottoclasse di tali sistemi (che include anche i filtri FIR) che ammette pratica realizzazione grazie all uso della ricorsione. Questi sistemi possono essere descritti da un equazione alle differenze a coefficienti costanti, del tipo: N a k y(n k) = k=0 b m x(n m), a 0 0 (1) Supporremo che il sistema evolva da una condizione iniziale di riposo (condizioni iniziali omogenee). Si può dimostrare allora che in questo caso l equazione alle differenze definisce un sistema lineare e tempo invariante (LTI), denominato sistema ARMA (Auto-Regressive Moving-Average, cioè auto-regressivo a media mobile). L equazione (1), assumendo per semplicità a 0 = 1, può essere riscritta nella forma: N y(n) = a k y(n k) + b m x(n m), (2) k=1 } {{ } AR } {{ } MA nella quale abbiamo evidenziato la parte ricorsiva o autoregressiva (AR) e la parte non ricorsiva o a media mobile (MA). Tale forma consente di calcolare l uscita y(n) in maniera esplicita, a partire dai valori dell ingresso (parte MA) e dai valori precedentemente calcolati dell uscita stessa (parte AR). Si possono considerare i seguenti casi particolari di sistema ARMA: M = 1, b 0 0 y(n) = N k=1 a k y(n k) + b 0 x(n) sistema AR N = 0, a 0 0 y(n) = M b m x(n m) sistema MA In Matlab, per risolvere equazioni alle differenze del tipo (1), è disponibile il comando filter, che può essere utilizzato per implementare filtri ARMA, AR o MA. La sintassi di tale comando è la seguente: >> y=filter(b,a,x); dove il vettore b contiene i coefficienti b 0, b 1,..., b M, il vettore a contiene, invece, i coefficienti a 0, a 1,..., a N, ed il segnale in ingresso è contenuto nel vettore x. Si noti che in questo modo si assume implicitamente che le condizioni iniziali da cui evolve il sistema siano nulle; in ogni caso, il comando filter prevede anche la possibilità di specificare le condizioni iniziali (ma noi non faremo uso di questa possibilità, si veda l help in linea per ulteriori dettagli). Richiamiamo l attenzione sul fatto che bisogna porre il filtro nella forma (1) per identificare correttamente i coefficienti b ed a; per intenderci, al primo membro della (1) compare solo l uscita, mentre al secondo membro compare solo l ingresso. Si noti che l uscita y calcolata dal comando filter è un vettore della stessa lunghezza di x (a rigore dovrebbe essere più lunga, per effetto della dispersione temporale introdotta dal sistema, cioè dalla convoluzione tra ingresso e risposta impulsiva). Come esempio provate a determinare
4 la convoluzione tra due sequenze rettangolari di durata 4 con il comando filter, osserverete che l uscita è stata troncata in modo da avere la stessa durata dell ingresso. Di conseguenza, se si vuole osservare l uscita anche per istanti di tempo successivi, bisogna allungare artificialmente l ingresso aggiungendo degli zeri in coda. Per filtri MA, per osservare correttamente tutto il segnale di uscita basta allungare il segnale d ingresso con M 1 zeri, pari alla lunghezza del filtro MA meno 1. Supponiamo, per esempio, che il legame ingresso/uscita sia del tipo: y(n) = x(n) + 2x(n 1) + x(n 2) e di porre in ingresso la sequenza [2, 1, 1, 0, 1, 4, ], i comandi >> a = [1]; b = [1 2 1]; y = filter(b,a,x); restituiscono in y solo 7 dei 9 valori dell uscita, mentre con la modifica >> x = [x zeros(1,length(b)-1)]; y = filter(b,a,x); viene generata l uscita completa. Chiaramente quest ultimo comando dà esattamente lo stesso risultato che si otterrebbe con il seguente codice: >> h = b; y = conv(x,h); Osserviamo inoltre che il comando filter non consente di specificare l asse dei tempi su cui è assegnato l ingresso: tuttavia, si può osservare che, data la natura tempo-invariante del filtro, l uscita è calcolata esattamente negli stessi istanti in cui è definito (implicitamente o esplicitamente) l ingresso. Consideriamo adesso un filtro AR in cui il legame ingresso/uscita è: y(n) y(n 1) y(n 2) = x(n) In questo caso, è semplice ricavare l uscita con i seguenti comandi: >> a = [1, -1, 0.9]; b = [1]; y = filter(b,a,x); Se volessimo determinare la risposta impulsiva (teoricamente di durata infinita) nell intervallo [ 20 : 120] dovremmo digitare il seguente codice: >> n = [-20:120]; x = [(n == 0)]; h = filter(b,a,x); >> subplot(211); stem(n,x); title( Ingresso x(n) ); >> subplot(212); stem(n,h); title( Risposta impulsiva ); E chiaro che se aumentiamo la durata del vettore dei tempi ci avviciniamo all espressione corretta della risposta impulsiva. Provate adesso a calcolare e diagrammare la risposta al gradino. 4
5 1.4 Esempi ed esperimenti proposti a) Sistema AR. Sia y(n) = 2 y(n 1) + x(n). Calcolate e diagrammate la risposta impulsiva h(n) per n = 5,..., 20 (ricordate di porre prima l equazione nella forma (1) per identificare correttamente i coefficienti da passare alla funzione filter); verificate che la risposta impulsiva si può esprimere come h(n) = ( 2 n ) u(n). b) Sistema ARMA. Sia Sia y(n) = 2 y(n 1) + x(n) + 1 2x(n 1). Calcolate e diagrammate la risposta impulsiva h(n) per 0 n 50; verificate che la risposta impulsiva si può esprimere come h(n) = ( 2 ) n u(n) ( 2 ) n 1 u(n 1). c) Filtraggio di un interferenza sinusoidale. Si consideri il seguente segnale per 0 n 40: y(n) = x(n) + i(n) dove x(n) è il segnale utile e i(n) = A cos(2πν 0 n + θ) è un segnale interferente sinusoidale. Se x(n) = V, A = 1, ν 0 = 1/2 e θ = 0, verificate che il filtro con risposta impulsiva h(n) = 1 2 δ(n) + 1 2δ(n 1) è in grado di rimuovere perfettamente l interferenza per ogni valore della costante V ; Se x(n) = (1.02) n, A = 1/2, ν 0 = 1/8 e θ = π/4, valutate l effetto di un filtro con risposta impulsiva h(n) = 1 M M k=1 δ(n k) all aumentare di M e commentate i risultati. 5
Analisi dei segnali nel dominio del tempo
 Laboratorio di Telecomunicazioni - a.a. 200/20 Lezione n. 3 Analisi dei segnali nel dominio del tempo L.Verdoliva In questa seconda lezione determiniamo, con l uso di Matlab, i parametri che caratterizzano
Laboratorio di Telecomunicazioni - a.a. 200/20 Lezione n. 3 Analisi dei segnali nel dominio del tempo L.Verdoliva In questa seconda lezione determiniamo, con l uso di Matlab, i parametri che caratterizzano
Rappresentazione dei segnali con sequenze di numeri e simboli
 Elaborazione numerica dei segnali Digital Signal Processing 1 Rappresentazione dei segnali con sequenze di numeri e simboli Elaborazione delle sequenze per stimare i parametri caratteristici di un segnale;
Elaborazione numerica dei segnali Digital Signal Processing 1 Rappresentazione dei segnali con sequenze di numeri e simboli Elaborazione delle sequenze per stimare i parametri caratteristici di un segnale;
Filtraggio Digitale. Alfredo Pironti. Ottobre Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20
 Filtraggio Digitale Alfredo Pironti Ottobre 2012 Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20 Filtri Analogici (1) Un filtro analogico è un sistema lineare tempo-invariante (LTI)
Filtraggio Digitale Alfredo Pironti Ottobre 2012 Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20 Filtri Analogici (1) Un filtro analogico è un sistema lineare tempo-invariante (LTI)
Lezione n.1 - Soluzioni
 Lezione n.1 - Soluzioni Laboratorio di Telecomunicazioni L.Verdoliva 1 Generazione di segnali a tempo discreto Di seguito trovate il codice che consente di generare un impulso triangolare compreso tra
Lezione n.1 - Soluzioni Laboratorio di Telecomunicazioni L.Verdoliva 1 Generazione di segnali a tempo discreto Di seguito trovate il codice che consente di generare un impulso triangolare compreso tra
( e j2! ft! 0.9 j) ( e j2! ft j)
 Esercitazione Filtri IIR Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
Esercitazione Filtri IIR Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
( e j2π ft 0.9 j) ( e j2π ft j)
 Esercitazione Filtri IIR Es. 1. Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
Esercitazione Filtri IIR Es. 1. Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
Elenco dei simboli 9. Prefazione 10
 Indice Elenco dei simboli 9 Prefazione 10 1 Analisi nel dominio del tempo 11 1.1 Segnali tempo discreto... 11 1.1.1 Segnali notevoli tempo discreto... 13 1.1.2 Alcuni criteri di classificazione di segnali
Indice Elenco dei simboli 9 Prefazione 10 1 Analisi nel dominio del tempo 11 1.1 Segnali tempo discreto... 11 1.1.1 Segnali notevoli tempo discreto... 13 1.1.2 Alcuni criteri di classificazione di segnali
Circuiti a tempo discreto Raffaele Parisi
 Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi Capitolo 3: Proprietà dei Circuiti nel dominio TD Proprietà e definizioni generali,
Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi Capitolo 3: Proprietà dei Circuiti nel dominio TD Proprietà e definizioni generali,
1 1, { x1 2x 2 + x 3 = 0 2x 2 8x 3 = 1 x 1 x 4 = = 0
 a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
Parte I Identificazione di modelli dinamici. 5: Analisi di sistemi dinamici alimentati da processi stazionari. Parte I 5, 1
 Parte I 5, 1 Parte I Identificazione di modelli dinamici 5: Analisi di sistemi dinamici alimentati da processi stazionari Parte I 5, 2 Consideriamo un sistema dinamico lineare tempo-invariante con funzione
Parte I 5, 1 Parte I Identificazione di modelli dinamici 5: Analisi di sistemi dinamici alimentati da processi stazionari Parte I 5, 2 Consideriamo un sistema dinamico lineare tempo-invariante con funzione
Prof. Carlo Rossi DEIS - Università di Bologna Tel:
 Prof. Carlo Rossi DEIS - Università di Bologna Tel: 051 2093020 email: carlo.rossi@unibo.it Sistemi Tempo-Discreti In questi sistemi i segnali hanno come base l insieme dei numeri interi: sono sequenze
Prof. Carlo Rossi DEIS - Università di Bologna Tel: 051 2093020 email: carlo.rossi@unibo.it Sistemi Tempo-Discreti In questi sistemi i segnali hanno come base l insieme dei numeri interi: sono sequenze
Esercizio 1 (12 punti) Si consideri il segnale s(t) in figura e se ne calcoli la Trasformata Continua di Fourier. A vale 2 V e T è paria a 1 s.
 ASB 17/01/12 (270) Esercizio 1 (12 punti) Si consideri il segnale s(t) in figura e se ne calcoli la Trasformata Continua di Fourier. A vale 2 V e T è paria a 1 s. A 0 T 2T 3T t - A Si consideri il segnale
ASB 17/01/12 (270) Esercizio 1 (12 punti) Si consideri il segnale s(t) in figura e se ne calcoli la Trasformata Continua di Fourier. A vale 2 V e T è paria a 1 s. A 0 T 2T 3T t - A Si consideri il segnale
Circuiti a Tempo Discreto Esercitazione 2 - Sequenze e Convoluzione in Matlab R
 Circuiti a Tempo Discreto Esercitazione 2 - Sequenze e Convoluzione in Matlab R Prof. Michele Scarpiniti Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università
Circuiti a Tempo Discreto Esercitazione 2 - Sequenze e Convoluzione in Matlab R Prof. Michele Scarpiniti Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università
Corso di Controllo Digitale Equazioni alle Differenze e Z-trasformate a
 Corso di Controllo Digitale Equazioni alle Differenze e Z-trasformate a Università degli Studi della Calabria Corso di Laurea in Ingegneria Elettronica. Ing. Domenico Famularo a Proprietà Letteraria Riservata
Corso di Controllo Digitale Equazioni alle Differenze e Z-trasformate a Università degli Studi della Calabria Corso di Laurea in Ingegneria Elettronica. Ing. Domenico Famularo a Proprietà Letteraria Riservata
Sistemi tempo-discreto - Complementi
 3 Sistemi tempo-discreto - Complementi 3.1 Risposta naturale e forzata di un sistema LTI Si consideri un sistema LTI caratterizzato dalla seguente funzione di trasferimento: M b k z k k=0 B(z) H(z) = =
3 Sistemi tempo-discreto - Complementi 3.1 Risposta naturale e forzata di un sistema LTI Si consideri un sistema LTI caratterizzato dalla seguente funzione di trasferimento: M b k z k k=0 B(z) H(z) = =
Problemi di base di Elaborazione Numerica dei Segnali
 Universita' di Roma TRE Corso di laurea in Ingegneria Elettronica Corso di laurea in Ingegneria Informatica Universita' di Roma "La Sapienza" Corso di laurea in Ingegneria delle Telecomunicazioni Problemi
Universita' di Roma TRE Corso di laurea in Ingegneria Elettronica Corso di laurea in Ingegneria Informatica Universita' di Roma "La Sapienza" Corso di laurea in Ingegneria delle Telecomunicazioni Problemi
Trasformata discreta di Fourier diunasequenzafinita: algoritmifft
 diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico Primo Appello 26/2/2015
 Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
Strutture di rete fondamentali per sistemi IIR
 Ad ogni funzione di trasferimento molteplicità di configurazioni di rete Scelta di una particolare realizzazione è dettata da compromessi tra: complessità di calcolo: preferenza per reti con minimo numero
Ad ogni funzione di trasferimento molteplicità di configurazioni di rete Scelta di una particolare realizzazione è dettata da compromessi tra: complessità di calcolo: preferenza per reti con minimo numero
Corso di Controllo DigitaleAntitrasformate Zeta e calcolo della risposta p.1/32
 Corso di Controllo Digitale Antitrasformate Zeta e calcolo della risposta Università degli Studi della Calabria Corso di Laurea in Ingegneria Elettronica. Ing. Domenico Famularo Istituto per la Sistemistica
Corso di Controllo Digitale Antitrasformate Zeta e calcolo della risposta Università degli Studi della Calabria Corso di Laurea in Ingegneria Elettronica. Ing. Domenico Famularo Istituto per la Sistemistica
ELABORAZIONE NUMERICA DEI SEGNALI 9CFU DIGITAL SIGNAL PROCESSING Prof. Marina Ruggieri. Ing. Tommaso Rossi
 Università di Roma Tor Vergata Facolta di Ingegneria Benvenuti al al modulo di: di: ELABORAZIONE NUMERICA DEI SEGNALI 9CFU DIGITAL SIGNAL PROCESSING Prof. Marina Ruggieri ruggieri@uniroma2.it Ing. Tommaso
Università di Roma Tor Vergata Facolta di Ingegneria Benvenuti al al modulo di: di: ELABORAZIONE NUMERICA DEI SEGNALI 9CFU DIGITAL SIGNAL PROCESSING Prof. Marina Ruggieri ruggieri@uniroma2.it Ing. Tommaso
Corso di Teoria dei Circuiti 1 - II modulo
 Università di Roma La Sapienza - Sede di Latina - Laurea in Ingegneria dell Informazione Corso di Teoria dei Circuiti 1 - II modulo Docente: Fabio Massimo Frattale Mascioli : Proprietà dei Circuiti nel
Università di Roma La Sapienza - Sede di Latina - Laurea in Ingegneria dell Informazione Corso di Teoria dei Circuiti 1 - II modulo Docente: Fabio Massimo Frattale Mascioli : Proprietà dei Circuiti nel
Analisi armonica su dati campionati
 Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Circuiti a tempo discreto Raffaele Parisi
 Università di Roma La Sapienza Laurea Specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Cenni alla sintesi di Circuiti TD Generalità sulle tecniche di progetto. Filtri
Università di Roma La Sapienza Laurea Specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Cenni alla sintesi di Circuiti TD Generalità sulle tecniche di progetto. Filtri
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a ) Homework assignment #2 Testo e Soluzione
 SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
MASB AA10/11 21/01/11 test #1 1
 MASB 0/06/11 AA010011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 0/06/11 AA010011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
Elementi di Teoria dei Sistemi. Sistemi dinamici a tempo discreto
 Parte 2, 1 Elementi di Teoria dei Sistemi Sistemi dinamici a tempo discreto Introduzione e motivazione Parte 2, 2 Necessità di introdurre una nuova classe di sistemi dinamici: i sistemi dinamici a tempo
Parte 2, 1 Elementi di Teoria dei Sistemi Sistemi dinamici a tempo discreto Introduzione e motivazione Parte 2, 2 Necessità di introdurre una nuova classe di sistemi dinamici: i sistemi dinamici a tempo
ESAME DI ELAB. NUM. DEL SEGNALE (0/0) (21/07/2015) Cognome e Nome: Matricola: Lab: Convoluzione veloce tramite overlap-and-save
 Convoluzione veloce tramite overlap-and-save Si consideri il filtro IIR stabile avente funzione di trasferimento H(z) = 1 1 1.2z 1 0.45z 2 e sia h : Z C la sua risposta impulsiva. Sia h N : Z C la versione
Convoluzione veloce tramite overlap-and-save Si consideri il filtro IIR stabile avente funzione di trasferimento H(z) = 1 1 1.2z 1 0.45z 2 e sia h : Z C la sua risposta impulsiva. Sia h N : Z C la versione
Teoria dei segnali terza edizione
 Teoria dei segnali Capitolo 7 Progetto di filtri digitali SOLUZIONI DEGLI ESERCIZI Soluione dell eserciio 7. La risposta in frequena del filtro può essere riscritta come π f f H( f) cos rect + B B Antitrasformando
Teoria dei segnali Capitolo 7 Progetto di filtri digitali SOLUZIONI DEGLI ESERCIZI Soluione dell eserciio 7. La risposta in frequena del filtro può essere riscritta come π f f H( f) cos rect + B B Antitrasformando
MASB AA10/11 21/01/11 test #1 1
 MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
Geometria per Fisica e Astrofisica
 Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Sistemi e segnali a tempo discreto
 Sistemi e segnali a tempo discreto Segnali Per segnale si intende una grandezza fisica qualsiasi a cui è associata informazione. L informazione che trasporta il segnale, lo caratterizza. I segnali possono
Sistemi e segnali a tempo discreto Segnali Per segnale si intende una grandezza fisica qualsiasi a cui è associata informazione. L informazione che trasporta il segnale, lo caratterizza. I segnali possono
ESERCIZI sui VETTORI
 ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
Funzioni continue. quando. se è continua x I.
 Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui
 Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it
Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it
SECONDO COMPITINO DI SEGNALI E SISTEMI 3 Dicembre 2003
 SECONDO COMPIINO DI SEGNALI E SISEMI 3 Dicembre 003 Esercizio. Si consideri il modello ingresso/uscita a tempo discreto e causale descritto dalla seguente equazione alle differenze: vk) con a parametro
SECONDO COMPIINO DI SEGNALI E SISEMI 3 Dicembre 003 Esercizio. Si consideri il modello ingresso/uscita a tempo discreto e causale descritto dalla seguente equazione alle differenze: vk) con a parametro
Teoria dei Segnali Richiami di analisi matematica; alcune funzioni notevoli
 Teoria dei Segnali Richiami di analisi matematica; alcune funzioni notevoli Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Richiami
Teoria dei Segnali Richiami di analisi matematica; alcune funzioni notevoli Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Richiami
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
FA-es Parte 1Z, 1 Fondamenti di Automatica Prof. Thomas Parisini Fondamenti di Automatica
 FA-es Parte 1Z, 1 e Prof. Gianfranco Fenu DIA-Università di Trieste Tel. (Parisini) 334 6936615 Email: parisini@units.it, fenu@units.it URL: http://control.units.it FA-es Parte 1Z, 2 Trasformata Zeta Segnali
FA-es Parte 1Z, 1 e Prof. Gianfranco Fenu DIA-Università di Trieste Tel. (Parisini) 334 6936615 Email: parisini@units.it, fenu@units.it URL: http://control.units.it FA-es Parte 1Z, 2 Trasformata Zeta Segnali
PRIMA PROVA PARZIALE DI CONTROLLO DIGITALE A.A. 2005/ aprile 2006 TESTO E SOLUZIONE
 PRIMA PROVA PARZIALE DI CONTROLLO DIGITALE A.A. 2005/2006 2 aprile 2006 TESTO E SOLUZIONE Esercizio Assegnato il sistema dinamico, non lineare, tempo invariante x (k + ) = x (k) + x 2 (k) 2 + u(k) x 2
PRIMA PROVA PARZIALE DI CONTROLLO DIGITALE A.A. 2005/2006 2 aprile 2006 TESTO E SOLUZIONE Esercizio Assegnato il sistema dinamico, non lineare, tempo invariante x (k + ) = x (k) + x 2 (k) 2 + u(k) x 2
Circuiti per la multimedialità
 Università di Roma La Sapienza Laurea in Ingegneria delle Comunicazioni Circuiti per la multimedialità Raffaele Parisi Capitolo 2. Sintesi di circuiti a tempo discreto a partire da circuiti analogici.
Università di Roma La Sapienza Laurea in Ingegneria delle Comunicazioni Circuiti per la multimedialità Raffaele Parisi Capitolo 2. Sintesi di circuiti a tempo discreto a partire da circuiti analogici.
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 4 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 4 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 5.2, 5.3
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 4 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 5.2, 5.3
Strutture realizzative per sistemi tempo-discreto: soluzione dei problemi proposti
 4 Strutture realizzative per sistemi tempo-discreto: soluzione dei problemi proposti P-4.1: Dopo aver diviso per 0.5, cioè il coefficiente di, l equazione alle differenze finite data, si ottengono le strutture
4 Strutture realizzative per sistemi tempo-discreto: soluzione dei problemi proposti P-4.1: Dopo aver diviso per 0.5, cioè il coefficiente di, l equazione alle differenze finite data, si ottengono le strutture
Esercitazione di laboratorio per il corso di SISTEMI DI TELECOMUNICAZIONI 1 Ritardo Frazionario
 Esercitazione di laboratorio per il corso di SISTEMI DI TELECOMUNICAZIONI Ritardo Frazionario 8 marzo 2009 Indice Scopo dell esercitazione A La struttura di Farrow B Norme per la consegna dell esercitazione
Esercitazione di laboratorio per il corso di SISTEMI DI TELECOMUNICAZIONI Ritardo Frazionario 8 marzo 2009 Indice Scopo dell esercitazione A La struttura di Farrow B Norme per la consegna dell esercitazione
COMPITO DI SEGNALI E SISTEMI 23 Luglio 2003
 COMPITO DI SEGNALI E SISTEMI 3 Luglio 003 Esercizio. Si consideri il sistema a tempo discreto, LTI e causale, descritto dalla seguente equazione alle differenze ( v(k) a + ) v(k ) + a v(k ) = bu(k) + cu(k
COMPITO DI SEGNALI E SISTEMI 3 Luglio 003 Esercizio. Si consideri il sistema a tempo discreto, LTI e causale, descritto dalla seguente equazione alle differenze ( v(k) a + ) v(k ) + a v(k ) = bu(k) + cu(k
Circuiti a tempo discreto Raffaele Parisi
 Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Risposta in frequenza dei circuiti TD Rappresentazione nel dominio della frequenza,
Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Risposta in frequenza dei circuiti TD Rappresentazione nel dominio della frequenza,
Elaborazione numerica dei segnali: si occupa della
 Introduzione al corso Elaborazione numerica dei segnali: si occupa della Rappresentazione dei segnali con sequenze di numeri e simboli Elaborazione delle sequenze per stimare i parametri caratteristici
Introduzione al corso Elaborazione numerica dei segnali: si occupa della Rappresentazione dei segnali con sequenze di numeri e simboli Elaborazione delle sequenze per stimare i parametri caratteristici
1 = Processi Autoregressivi AR(1) Filtro IIR di ordine 1. (WGN White Gaussian Noise) Eq. alle differenze ricorsiva. w=randn(n,1) MATLAB:
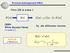 Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio 2004
 Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio TOTALE PUNTI: L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione
Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio TOTALE PUNTI: L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione
MASB AA10/11 21/01/11 test #1 1
 MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico Seconda Prova Intermedia 4/2/2013
 Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 0-0 Seconda Prova Intermedia 4//0 Quesiti relativi alla seconda prova in itinere (tempo max. h). (6 punti) Calcolare la H(z) Y (z)/x(z) associata
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 0-0 Seconda Prova Intermedia 4//0 Quesiti relativi alla seconda prova in itinere (tempo max. h). (6 punti) Calcolare la H(z) Y (z)/x(z) associata
Cenni sulla Serie di Fourier
 Cenni sulla Serie di Fourier Note per le lezioni del corso di Controlli Automatici Prof.ssa Maria Elena Valcher 1 Serie di Fourier Osserviamo preliminarmente che la somma di segnali periodici non è necessariamente
Cenni sulla Serie di Fourier Note per le lezioni del corso di Controlli Automatici Prof.ssa Maria Elena Valcher 1 Serie di Fourier Osserviamo preliminarmente che la somma di segnali periodici non è necessariamente
Università degli Studi di Ferrara Corso di Laurea in Chimica - A.A
 Università degli Studi di Ferrara Corso di Laurea in Chimica - A.A. 2018-2019 Programmazione Lezione 12A Esercizi in MATLAB Docente: Lorenzo Caruso lorenzo.caruso@unife.it Nelle lezioni precedenti Matlab:
Università degli Studi di Ferrara Corso di Laurea in Chimica - A.A. 2018-2019 Programmazione Lezione 12A Esercizi in MATLAB Docente: Lorenzo Caruso lorenzo.caruso@unife.it Nelle lezioni precedenti Matlab:
Teoria dei Segnali Quantizzazione dei segnali; trasformata zeta
 Teoria dei Segnali Quantizzazione dei segnali; trasformata zeta Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Quantizzazione;
Teoria dei Segnali Quantizzazione dei segnali; trasformata zeta Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Quantizzazione;
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
1 Esercizi di Matlab. L operatore : permette di estrarre sottomatrici da una matrice assegnata. Vediamo alcuni esempi.
 Esercizi di Matlab L operatore : permette di estrarre sottomatrici da una matrice assegnata. Vediamo alcuni esempi. Esempio Consideriamo la matrice A formata da n = righe e m = colonne M = 5 6 7 8. 9 0
Esercizi di Matlab L operatore : permette di estrarre sottomatrici da una matrice assegnata. Vediamo alcuni esempi. Esempio Consideriamo la matrice A formata da n = righe e m = colonne M = 5 6 7 8. 9 0
SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X
 CATENE DI MARKOV SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X X X 0 T 0 T! Δ 0, 1,, 0 Δ 1 Δ Δ 1Δ Δ Δ ESEMPIO: I GUASTI (Ipotesi
CATENE DI MARKOV SISTEMI CASUALI DINAMICI (PROCESSI) ESEMPIO: I GUASTI (Ipotesi Markoviana) Frequenza dei guasti: N Guasti = N/T X X X X X X X X X 0 T 0 T! Δ 0, 1,, 0 Δ 1 Δ Δ 1Δ Δ Δ ESEMPIO: I GUASTI (Ipotesi
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
Università di Roma Tor Vergata Corso di Teoria dei Fenomeni Aleatori, AA 2012/13. Catene di Markov
 Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando
In realtà i segnali con i quali dobbiamo confrontarci più frequentemente sono limitati nel tempo
 Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Esame di FONDAMENTI DI AUTOMATICA (9 crediti) SOLUZIONE
 Esame di FONDAMENTI DI AUTOMATICA (9 crediti) Prova scritta 16 luglio 2014 SOLUZIONE ESERCIZIO 1. Dato il sistema con: si determinino gli autovalori della forma minima. Per determinare la forma minima
Esame di FONDAMENTI DI AUTOMATICA (9 crediti) Prova scritta 16 luglio 2014 SOLUZIONE ESERCIZIO 1. Dato il sistema con: si determinino gli autovalori della forma minima. Per determinare la forma minima
SEGNALI E SISTEMI (a.a ) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 2003 Testo e Soluzione
 Esercizio 1 [punti 4] SEGNALI E SISTEMI (a.a. 003-004) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 003 Testo e Soluzione Per ciascuno dei seguenti segnali dire se è periodico e,
Esercizio 1 [punti 4] SEGNALI E SISTEMI (a.a. 003-004) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 003 Testo e Soluzione Per ciascuno dei seguenti segnali dire se è periodico e,
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Circuiti a tempo discreto Raffaele Parisi
 Circuiti a tempo discreto Raffaele Parisi Università di Roma La Sapienza Laurea Specialistica in Ingegneria Elettronica : Architetture di Circuiti TD Grafo di un circuito TD, validità di un circuito TD,
Circuiti a tempo discreto Raffaele Parisi Università di Roma La Sapienza Laurea Specialistica in Ingegneria Elettronica : Architetture di Circuiti TD Grafo di un circuito TD, validità di un circuito TD,
FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (n r,n c ) composta da
FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (n r,n c ) composta da
Note su filtri digitali
 Progettazione nell'ambiente LPCXpresso Introduzione alla progettazione di sistemi embedded a microcontrollore Note su filtri digitali S. Salvatori - Microelettronica aprile 2016 (1 di 42) Sommario Perché
Progettazione nell'ambiente LPCXpresso Introduzione alla progettazione di sistemi embedded a microcontrollore Note su filtri digitali S. Salvatori - Microelettronica aprile 2016 (1 di 42) Sommario Perché
1) Codici convoluzionali. 2) Circuito codificatore. 3) Diagramma a stati e a traliccio. 4) Distanza libera. 5) Algoritmo di Viterbi
 Argomenti della Lezione 1) Codici convoluzionali 2) Circuito codificatore 3) Diagramma a stati e a traliccio 4) Distanza libera 5) Algoritmo di Viterbi 1 Codici convoluzionali I codici convoluzionali sono
Argomenti della Lezione 1) Codici convoluzionali 2) Circuito codificatore 3) Diagramma a stati e a traliccio 4) Distanza libera 5) Algoritmo di Viterbi 1 Codici convoluzionali I codici convoluzionali sono
Prova di AUTOVALUTAZIONE (novembre 2009). nota: l esame ha validità solo se incluso nel piano degli studi per l anno accademico corrente.
 UNIVERSITA DEGLI STUDI ROMA TRE CdS in Ingegneria Informatica corso di FONDAMENTI DI TELECOMUNICAZIONI Prova di AUTOVALUTAZIONE (novembre 2009). COMPITO A nota: l esame ha validità solo se incluso nel
UNIVERSITA DEGLI STUDI ROMA TRE CdS in Ingegneria Informatica corso di FONDAMENTI DI TELECOMUNICAZIONI Prova di AUTOVALUTAZIONE (novembre 2009). COMPITO A nota: l esame ha validità solo se incluso nel
Correzione dell Esercitazione 3
 Correzione dell Esercitazione Stefano Angioni novembre 005 Esercizio Il testo dell esercizio fornisce il modello di un sistema lineare e stazionario in termini di relazione ingresso uscita d y(t) dt +
Correzione dell Esercitazione Stefano Angioni novembre 005 Esercizio Il testo dell esercizio fornisce il modello di un sistema lineare e stazionario in termini di relazione ingresso uscita d y(t) dt +
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA
 RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
SISTEMI LINEARI. (a) Il segnale x(t) in ingresso passa attraverso la trasformazione F{ } e produce l uscita y(t)
 SISTEMI LINEARI F F (a) Il segnale x(t) in ingresso passa attraverso la trasformazione F{ } e produce l uscita y(t) SCHEMA A BLOCCHI DI UN SISTEMA (LINEARE) (b) L uscita y(t) è rappresentata dalla convoluzione
SISTEMI LINEARI F F (a) Il segnale x(t) in ingresso passa attraverso la trasformazione F{ } e produce l uscita y(t) SCHEMA A BLOCCHI DI UN SISTEMA (LINEARE) (b) L uscita y(t) è rappresentata dalla convoluzione
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
ANALISI DI FOURIER. Segnali a Tempo Discreto:
 ANALISI DI FOURIER Segnali a Tempo Discreto: - - Sequenza periodica - Taratura degli assi frequenziali - TDF di una sequenza finita - Campionamento in Frequenza Serie discreta di Fourier Consideriamo una
ANALISI DI FOURIER Segnali a Tempo Discreto: - - Sequenza periodica - Taratura degli assi frequenziali - TDF di una sequenza finita - Campionamento in Frequenza Serie discreta di Fourier Consideriamo una
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
1 Schemi alle differenze finite per funzioni di una variabile
 Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Studio di funzione. Studio di funzione: i passi iniziali
 Studio di funzioni Studio di funzione Si dice che una variabile dipendente y è funzione di una variabile indipendente x quando esiste un legame di natura qualsiasi che ad ogni valore di x faccia corrispondere
Studio di funzioni Studio di funzione Si dice che una variabile dipendente y è funzione di una variabile indipendente x quando esiste un legame di natura qualsiasi che ad ogni valore di x faccia corrispondere
SEGNALI E SISTEMI Ripasso per Io Compitino
 SEGNALI E SISTEMI Ripasso per Io Compitino Esercizio 1 Si consideri il segnale a tempo continuo x(t) = 2 ( 1) k 1 1 sin(kt), t R. k=1 k a. Trovare il periodo fondamentale T p di x(t) e dire se il segnale
SEGNALI E SISTEMI Ripasso per Io Compitino Esercizio 1 Si consideri il segnale a tempo continuo x(t) = 2 ( 1) k 1 1 sin(kt), t R. k=1 k a. Trovare il periodo fondamentale T p di x(t) e dire se il segnale
Geometria analitica del piano pag 12 Adolfo Scimone
 Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Geometria analitica del piano pag 12 Adolfo Scimone Fasci di rette Siano r e r' due rette distinte di equazioni r: ax + by + c r': a' x + b' y + c' Consideriamo la retta combinazione lineare delle due
Circuiti a Tempo Discreto DFT - La Trasformata di Fourier Discreta
 Circuiti a Tempo Discreto - La Trasformata di Fourier Discreta Prof. Michele Scarpiniti Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università di Roma http://ispac.ing.uniroma1.it/scarpiniti/index.htm
Circuiti a Tempo Discreto - La Trasformata di Fourier Discreta Prof. Michele Scarpiniti Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università di Roma http://ispac.ing.uniroma1.it/scarpiniti/index.htm
Calcolo delle Differenze
 Carla Guerrini 1 Calcolo delle Differenze Le differenze finite introdotte nel 17-esimo secolo per il calcolo delle funzioni, si prestano bene ad essere utilizzate in procedimenti e problemi discreti: da
Carla Guerrini 1 Calcolo delle Differenze Le differenze finite introdotte nel 17-esimo secolo per il calcolo delle funzioni, si prestano bene ad essere utilizzate in procedimenti e problemi discreti: da
Laboratorio di Programmazione Esercitazione 10
 Laboratorio di Programmazione Esercitazione 10 Prof. Michele Scarpiniti Prof. Danilo Comminiello Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università di Roma
Laboratorio di Programmazione Esercitazione 10 Prof. Michele Scarpiniti Prof. Danilo Comminiello Dipartimento di Ingegneria dell Informazione, Elettronica e Telecomunicazioni Sapienza Università di Roma
Lo sviluppo di un semplice programma e la dimostrazione della sua correttezza
 Il principio di induzione Consideriamo inizialmente solo il principio di induzione per i numeri non-negativi, detti anche numeri naturali. Sia P una proprietà (espressa da una frase o una formula che contiene
Il principio di induzione Consideriamo inizialmente solo il principio di induzione per i numeri non-negativi, detti anche numeri naturali. Sia P una proprietà (espressa da una frase o una formula che contiene
(E) x > 0 (F) x < 1/2 (E) (1/ 2) 1. (E) f 1 (x) = 2x 2 (F) f 1 (x) = x. (E) x = 2 ln 3 (F) x = 3 ln 2 (F) 1/2
 1 Esercizi 8 di Calcolo e Biostatistica Es. 1. Rispondere alle seguenti sette domande nel tempo massimo di 30 minuti, senza usare strumenti elettronici (a) sapendo che log 10 0.3 e log 10 3 0.8, i valori
1 Esercizi 8 di Calcolo e Biostatistica Es. 1. Rispondere alle seguenti sette domande nel tempo massimo di 30 minuti, senza usare strumenti elettronici (a) sapendo che log 10 0.3 e log 10 3 0.8, i valori
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
Osservatore di Luenberger
 1 Osservatore di Luenberger In queste note verrà presentato l osservatore di Luenberger, uno stimatore dello stato per sistemi lineari. Si farà il caso di sistemi dinamici tempo-continui e tempo-discreti.
1 Osservatore di Luenberger In queste note verrà presentato l osservatore di Luenberger, uno stimatore dello stato per sistemi lineari. Si farà il caso di sistemi dinamici tempo-continui e tempo-discreti.
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 5 febbraio 2018 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Elaborazione numerica dei segnali
 POLITECNICO DI TORINO Elaborazione numerica dei segnali Progetto di un filtro FIR Fiandrino Claudio Matricola: 138436 18 giugno 21 Relazione sul progetto di un filtro FIR Descrizione del progetto L obbiettivo
POLITECNICO DI TORINO Elaborazione numerica dei segnali Progetto di un filtro FIR Fiandrino Claudio Matricola: 138436 18 giugno 21 Relazione sul progetto di un filtro FIR Descrizione del progetto L obbiettivo
CONTROLLI AUTOMATICI LS Ingegneria Informatica. Analisi modale
 CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
CONTROLLI AUTOMATICI LS Ingegneria Informatica Analisi modale Prof. Claudio Melchiorri DEIS-Università di Bologna Tel. 5 9334 e-mail: claudio.melchiorri@unibo.it http://www-lar.deis.unibo.it/~cmelchiorri
La Trasformata di Fourier: basi matematiche ed applicazioni. Parte II
 Metodi di Calcolo per la Chimica A.A. 2016-2017 Marco Ruzzi La Trasformata di Fourier: basi matematiche ed applicazioni Parte II Showing a Fourier transform to a physics student generally produces the
Metodi di Calcolo per la Chimica A.A. 2016-2017 Marco Ruzzi La Trasformata di Fourier: basi matematiche ed applicazioni Parte II Showing a Fourier transform to a physics student generally produces the
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
Elaborazione numerica dei segnali
 Massimiliano Laddomada Marina Mondin Elaborazione numerica dei segnali 0)+)2(% %VKSQIRXSXVEXXEXSEPI^MSRI %VKSQIRXSXVEXXEXSEPI^MSRIMRQSHSTEV^MEPIS HMJJIVIRXIVMJIVMVWMEKPMETTYRXM %VKSQIRXSEGGIRREXSEPI^MSRIVMJIVMVWMEKPMETTYRXM
Massimiliano Laddomada Marina Mondin Elaborazione numerica dei segnali 0)+)2(% %VKSQIRXSXVEXXEXSEPI^MSRI %VKSQIRXSXVEXXEXSEPI^MSRIMRQSHSTEV^MEPIS HMJJIVIRXIVMJIVMVWMEKPMETTYRXM %VKSQIRXSEGGIRREXSEPI^MSRIVMJIVMVWMEKPMETTYRXM
FILTRI NUMERICI. Sistema LTI H (z)
 x [n] FILTRI UMERICI Sistema LTI H (z) y [n] Un sistema numerico LTI è in molti casi descritto con un equazione alle differenze lineare a coefficienti costanti: M [ ] = [ ] a y n k b x n r k k= r= Z {}
x [n] FILTRI UMERICI Sistema LTI H (z) y [n] Un sistema numerico LTI è in molti casi descritto con un equazione alle differenze lineare a coefficienti costanti: M [ ] = [ ] a y n k b x n r k k= r= Z {}
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
