Esercizi. Alberto Saracco. December 11, Esercizio 1.1 Calcola il prodotto tra z = 1 + 2i e il suo coniugato z.
|
|
|
- Martino Bellini
- 4 anni fa
- Visualizzazioni
Transcript
1 1
2 Esercizi Alberto Saracco December 11, Numeri complessi 1.1 Esercizi Esercizio 1.1 Calcola il prodotto tra z = 1 + 2i e il suo coniugato z. Esercizio 1.2 Calcola il prodotto tra z = 1 i e il suo coniugato z. Esercizio 1.3 Calcola il prodotto (1 i) ( 1 i). Esercizio 1.4 Calcola il prodotto (1 + i) (2 i). Esercizio 1.5 Calcola il prodotto (3i) (1 i). Esercizio 1.6 Calcola il prodotto (3 i) 2. Esercizio 1.7 Metti in forma trigonometrica il numero z = i. Esercizio 1.8 Metti in forma trigonometrica il numero z = 3 3i. Esercizio 1.9 Metti in forma trigonometrica il numero z = 3i. Esercizio 1.10 Metti in forma trigonometrica il numero z = i. Esercizio 1.11 Scomponi in fattori di primo grado il polinomio z 2 + 2z + 1. Esercizio 1.12 Scomponi in fattori di primo grado il polinomio z 2 + 2iz + i. Esercizio 1.13 Scomponi in fattori di primo grado il polinomio z 3 + 2z 2 + z. Esercizio 1.14 Scomponi in fattori di primo grado il polinomio z 2 + 2iz + 1. Esercizio 1.15 Calcola le radici quarte di 1. Esercizio 1.16 Calcola le radici quarte di 1. Esercizio 1.17 Calcola le radici quarte di i. Esercizio 1.18 Calcola le radici quarte di i. 2
3 1.2 Soluzioni (degli esercizi dispari) Esercizio 1.1. Il prodotto tra un numero complesso e il suo coniugato è il quadrato del suo modulo. Pertanto z z = = 5. Esercizio Esercizio i. Esercizio 1.7. z = 10 2(cos(π/4) + i sin(π/4)). Esercizio 1.9. z = 3(cos(π/2) + i sin(π/2)). Esercizio (z + 1) 2. Esercizio z (z + 1) 2. Esercizio , i, 1, i. Esercizio Sono i numeri complessi di modulo 1 e argomento θ = π/8, 5π/8, 9π/8, 13π/8. 2 Curve 2.1 Esercizi Esercizio 2.1 Quali tra le seguenti sono curve piane? Quelle che non lo sono, perchè non lo sono? 1. ϕ : [0, 1] R, ϕ(t) = t 3 ; 2. ϕ : [0, 1] R 2, ϕ(t) = (t, t 3 ); 3. ϕ : [0, 2π] R 2, ϕ(t) = (3 cos t, 2 sin t); 4. ϕ = {(x, y) R 2 x 2 + y 2 = 2}; 5. ϕ : { 10} [ 3, 1] R 2, ϕ(t) = (t, t 5); 6. ϕ : [ 2, 2] R 2 : 7. ϕ : [ 2, 3] R 2 : ϕ(t) = { ( t, t 2 1)se t 1(t, t 1)se t > 1 ϕ(t) = { ( t, t 2 1)se t 2(3t 2, (t 1) 2 )se t > 2 Esercizio 2.2 Quali tra le seguenti sono curve? Quelle che non lo sono, perchè non lo sono? 1. ϕ : [ 5, 4] [ 3, 1] R 2, ϕ(t) = (t, t + t 5 ); 2. ϕ : [0, 2] R 3, ϕ(t) = (t, t 2, t 3 ); 3. ϕ : [ 2, 2] R 2 : ϕ(t) = { ( t 2 1, t ) se t 1(t, t 1)se t > 1 3
4 4. ϕ : [ 2, 3] R 2 : ϕ(t) = { ( t, t 2 1) se t 2(3t 2, (t 1) 2 + 3)se t > 2 5. ϕ : [0, 1] R 2, ϕ(t) = (t, t 2 t 3 ); 6. ϕ : [0, 2π] R 2, ϕ(t) = (3 cos t 2, 2t 2 + sin t); 7. ϕ = {(x, y) R 2 x 2 + y 2 = 0}; 8. ϕ : [ 100, 2] R 2, ϕ(z) = (0, 0). Esercizio 2.3 Quali delle curve dell esercizio 1 sono regolari? Esercizio 2.4 Quali delle curve dell esercizio 2 sono regolari? Esercizio 2.5 Calcola il vettore tangente quando il parametro assume valore 1 2, in tutte le curve dell esercizio 1 in cui è possibile. Esercizio 2.6 Calcola il vettore tangente quando il parametro assume valore 1 2, in tutte le curve dell esercizio 2 in cui è possibile. Esercizio 2.7 Quali delle curve dell esercizio 1 sono chiuse? Quali sono semplici? Esercizio 2.8 Quali delle curve dell esercizio 2 sono chiuse? Quali sono semplici? Esercizio 2.9 Qual è il supporto delle seguenti curve? 1. ϕ : [0, π] R 2, ϕ(t) = (cos t, 2 sin t); 2. ϕ : [ 3, 3] R 2, ϕ(t) = (t 3, t 1); 3. delle curve dell esercizio 1; 4. delle curve dell esercizio 2. Esercizio 2.10 Trova delle curve con il seguente supporto: 1. S = {(x, y) R 2 x 2 + 2x + y 2 = 0}; 2. S = {(x, y) R 2 y = x 3 1, 1 y 1}; 3. una curva semplice e chiusa con supporto che contiene l origine; 4. S = {(x, y) R 2 x = 0, 5 y 100}. Esercizio 2.11 Trova la lunghezza delle seguenti curve: 1. ϕ : [π, 4π] R 2, ϕ(t) = (3 + 2 cos(2t), 1 2 sin(2t)); 2. ϕ : [π, 4π] R 2, ϕ(t) = (3π, 2t 3 ); 4
5 3. ϕ : [ 1, 1] R 2, ϕ(t) = (e t + e t, 2t). Esercizio 2.12 Disegna il supporto e il verso di percorrenza della seguente curva definita a pezzi: per 0 t 1, ϕ(t) = (t, t 2 ); per 1 t 3, ϕ(t) = (t 2, t); per 3 t 9, ϕ(t) = (12 t, 3); per 9 t π, ϕ(t) = (3 cos(t 9), sin(t 9)). ϕ è una curva chiusa? È una curva semplice? 2.2 Soluzioni (degli esercizi dispari) Esercizio 2.1. Sono curve quelle definite in (2), (3), (6). In (1) ϕ non è una funzione a valori nel piano R 2. In (4) ϕ è un sottoinsieme, non una funzione. In (5) il dominio di ϕ non è un intervallo. In (7) ϕ non è continua. Esercizio 2.3. Sono regolari la (2) e la (3). La (6) non è derivabile in t = 0 e in t = 1. Esercizio 2.5. (2) ϕ ( 1 2 ) = (1, 3 4 ). (3) ϕ ( 1 2 ) = ( 3 sin( 1 2 ), 2 cos( 1 2 )). (6) ϕ ( 1 2 ) = (1, 1) Esercizio 2.7. Solo la (3) è chiusa. La (2) e la (3) sono semplici. Esercizio Il supporto è un semi-ellisse: 2. Il supporto è: S = {(x, y) R 2 4x 2 + y 2 = 4, y 0}. S = {(x, y) R 2 x = (y + 1) 3, 4 y 2}. Esercizio La lunghezza è 12π. 2. La lunghezza è 126π La lunghezza è 2e 2 e. 3 Equazioni differenziali 3.1 Esercizi Esercizio 3.1 Risolvi il seguente problema di Chauchy: u(0) = 0, u (0) = 1. u (t) 2u (t) + u(t) = t 2, 5
6 Esercizio 3.2 Risolvi il seguente problema di Chauchy: u (t) + u (t) u(t) = t2, u(0) = 1, u (0) = 1. Esercizio 3.3 Risolvi il seguente problema di Chauchy: 4u (t) 4u (t) + u(t) = e 1 2 t, u(0) = 0, u (0) = 0. Esercizio 3.4 Risolvi il seguente problema di Chauchy: u (t) + 6u (t) + 9u(t) = te t, u(0) = 0, u (0) = 0. Esercizio 3.5 Risolvi il seguente problema di Chauchy: u (t) + u(t) = t 2, u(0) = 1. Esercizio 3.6 Risolvi il seguente problema di Chauchy: u (t) + 2tu(t) = e t2, u(0) = 1. Esercizio 3.7 Risolvi il seguente problema di Chauchy: tu (t) + u(t) = t 3, u(1) = 2. Esercizio 3.8 Risolvi il seguente problema di Chauchy: tu (t) + 2u(t) = t, u(1) = 1. Esercizio 3.9 Risolvi il seguente problema di Chauchy: u (t) = (t 2 + t)u, u(0) = 1. Esercizio 3.10 Risolvi il seguente problema di Chauchy: u (t) = (t 2 t)u, u(0) = 1. 6
7 Esercizio 3.11 Risolvi il seguente problema di Chauchy: u(0) = 1. u (t) = (t 2 t)u 2, Esercizio 3.12 Risolvi il seguente problema di Chauchy: u(0) = 1. u (t) = (t 2 t)(u 2 u), Esercizio 3.13 Risolvi il seguente problema di Chauchy: u(0) = 1. u (t) = (t 2 t)(u 2 + u), 3.2 Soluzioni (degli esercizi dispari) Esercizio 3.1. u(t) = (t 6)e t + t 2 + 4t + 6. Esercizio 3.3. u(t) = 1 8 t2 e 1 2 t. Esercizio 3.5. u(t) = e t + t 2 2t + 2. Esercizio 3.7. u(t) = t t3. Esercizio 3.9. u(t) = e t3 /3 e t2 /2 Esercizio Esercizio u(t) = 6 6 3t 2 + 2t 3 e t 3 3 t2 2 u(t) = 2 e t3 3 t2 2 4 Funzioni di due variabili: gradienti e differenziali 4.1 Esercizi Esercizio 4.1 Sia f : R 2 R la funzione definita da f(x, y) = 3x 5 y 10x 3 y + 15xy 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); 7
8 Esercizio 4.2 Sia f : R 2 R la funzione definita da f(x, y) = xy 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); Esercizio 4.3 Sia f : R 2 R la funzione definita da f(x, y) = 3x 5 y 2 10x 3 y xy 2 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); Esercizio 4.4 Sia f : R 2 R la funzione definita da f(x, y) = x 2 10xy + y 2 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (0, 2); Esercizio 4.5 Sia f : R 2 R la funzione definita da f(x, y) = x 3 + y 3 12xy 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 0); 8
9 Esercizio 4.6 Sia f : R 2 R la funzione definita da f(x, y) = x 6 + y 6 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (0, 0); Esercizio 4.7 Sia f : R 2 R la funzione definita da f(x, y) = x 2 + y xy trova l equazione del piano tangente nel punto (x 0, y 0 ) = (10, 10); Esercizio 4.8 Sia f : R 2 R la funzione definita da f(x, y) = e x2 xy 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); Esercizio 4.9 Sia f : R 2 R la funzione definita da f(x, y) = e x2 y 2 9
10 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); Esercizio 4.10 Sia f : R 2 R la funzione definita da f(x, y) = x 2 y trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); Esercizio 4.11 Sia f : R 2 \ {(0, 0)} R la funzione definita da f(x, y) = x x 2 + y 2 2. trova l equazione del piano tangente nel punto (x 0, y 0 ) = (1, 1); 4.2 Soluzioni (degli esercizi dispari) Esercizio f è differenziabile. 2. z = 8y; 3. (0, 0) è l unico punto stazionario. 4. Non ci sono punti di massimo o minimo relativo. (0, 0) è punto di sella. 5. Non ci sono punti di massimo o minimo assoluto. Esercizio f è differenziabile. 10
11 2. z = 16y 8; 3. (0, 0) e (1, 0). 4. Il test del determinante hessiano fallisce. Con un analisi più approfondita si scopre che non ci sono minimi e massimi relativi. 5. Non ci sono punti di massimo o minimo assoluto. Esercizio f è differenziabile. 2. z = 3x 12y + 10; 3. (0, 0) e (4, 4). 4. (4, 4) è punto di minimo relativo. (0, 0) è punto di sella. 5. Non ci sono punti di massimo o minimo assoluto. Esercizio f è differenziabile. 2. z = 170x + 170y 1400; 3. (0, 0) è l unico punto stazionario. 4. Non ci sono punti di massimo o minimo relativo. (0, 0) è punto di sella. 5. Non ci sono punti di massimo o minimo assoluto. Esercizio f è differenziabile. 2. z = 2x + 2y 3; 3. (0, 0) è l unico punto stazionario. 4. Non ci sono punti di massimo o minimo relativo. (0, 0) è punto di sella. 5. Non ci sono punti di massimo o minimo assoluto. Esercizio f è differenziabile. 2. 2z = y; 3. Non ci sono punti stazionari. 4. Non ci sono punti di massimo o minimo relativo. 5. Non ci sono punti di massimo o minimo assoluto. 11
12 5 Integrali in due variabili 5.1 Esercizi Esercizio 5.1 Sia f : R 2 R la funzione definita da f(x, y) = e x+y 1. La funzione f è integrabile sul rettangolo Q = [0, 2] [0, 1]? 2. Calcola l integrale di f su Q riducendo per verticali; 3. Calcola l integrale di f su Q riducendo per orizzontali. Esercizio 5.2 Sia f : R 2 R la funzione definita da f(x, y) = 3x 5 y 2 10x 3 y xy 2 1. La funzione f è integrabile sul quadrato Q = [0, 1] [0, 1]? 2. Calcola l integrale di f su Q riducendo per verticali; 3. Calcola l integrale di f su Q riducendo per orizzontali. Esercizio 5.3 Sia f : R 2 R la funzione definita da f(x, y) = y log(1 + x) 1. La funzione f è integrabile sul rettangolo Q = [0, 2] [0, 3]? 2. Calcola l integrale di f su Q riducendo per verticali; 3. Calcola l integrale di f su Q riducendo per orizzontali. Esercizio 5.4 Sia f : R 2 R la funzione definita da f(x, y) = x2 1 + y 1. La funzione f è integrabile sul rettangolo Q = [0, 2] [0, 1]? 2. Calcola l integrale di f su Q riducendo per verticali; 3. Calcola l integrale di f su Q riducendo per orizzontali. Esercizio 5.5 Sia f : R 2 R la funzione definita da f(x, y) = x + y 1 + xy 1. La funzione f è integrabile sul rettangolo Q = [0, 1] [0, 1]? 2. Calcola l integrale di f su Q riducendo per verticali; 12
13 3. Calcola l integrale di f su Q riducendo per orizzontali. Esercizio 5.6 Sia f : R 2 R la funzione definita da f(x, y) = xy 1. La funzione f è integrabile sul triangolo T di vertici (0, 1), (1, 1), (2, 1)? 2. Calcola l integrale di f su T riducendo per verticali; 3. Calcola l integrale di f su T riducendo per orizzontali. Esercizio 5.7 Sia f : R 2 R la funzione definita da f(x, y) = x 1. La funzione f è integrabile sul disco D di centro l origine e raggio 1? 2. Calcola l integrale di f su D; 3. C è un modo immediato per dire quanto fa l integrale di f su D? Esercizio 5.8 Sia f : R 2 R la funzione definita da f(x, y) = y 1. La funzione f è integrabile sul quarto di disco (nel primo quadrante) D di centro l origine e raggio 1? 2. Calcola l integrale di f su D. Esercizio 5.9 Sia f : R 2 R la funzione definita da f(x, y) = x + y 1. La funzione f è integrabile sul quadrato Q di vertici (1, 1), (1, 1), ( 1, 1), ( 1, 1)? 2. Calcola l integrale di f su Q. 3. C è un modo immediato per dire quanto fa l integrale di f su D? Esercizio 5.10 Sia f : R 2 R la funzione definita da f(x, y) = x 2 + y 1. La funzione f è integrabile sul quadrato Q di vertici (1, 1), (1, 1), ( 1, 1), ( 1, 1)? 2. Calcola l integrale di f su Q. 13
14 Esercizio 5.11 Sia f : R 2 R la funzione definita da f(x, y) = x 2 y 1. La funzione f è integrabile sul quadrato Q di vertici (1, 1), (1, 1), ( 1, 1), ( 1, 1)? 2. Calcola l integrale di f su Q. 3. C è un modo immediato per dire quanto fa l integrale di f su D? Esercizio 5.12 Sia f : R 2 R la funzione definita da f(x, y) = x y 2 1. La funzione f è integrabile sul quadrilatero Q di vertici (1, 1), (2, 1), (3, 1), (2, 0)? 2. Calcola l integrale di f su Q. 5.2 Soluzioni degli esercizi dispari Esercizio 5.1. L integrale di f su Q è e 3 e 2 e + 1. Esercizio 5.3. L integrale di f su Q è 9 2 (3 log 3 2). Esercizio 5.5. L integrale di f su Q è 4 log 2 2. Esercizio 5.7. L integrale di f su D è 0... infatti D è simmetrico rispetto ad {x = 0} e f è dispari rispetto ad x, quindi... Esercizio 5.9. L integrale di f su Q è 0. Esercizio L integrale di f su Q è 0. 14
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = (x 2 2y 2 ) e x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Esercizi di Matematica A.A. 2017/2018
 C.d.L. in Produzioni Animali - Scuola di Agraria e Medicina Veterinaria - Università di Bologna Cod. corso 65965 Esercizi di Matematica A.A. 2017/2018 Insiemistica Dati: A = {1, 2,, 4, 5} B = {1, 5, 7,
C.d.L. in Produzioni Animali - Scuola di Agraria e Medicina Veterinaria - Università di Bologna Cod. corso 65965 Esercizi di Matematica A.A. 2017/2018 Insiemistica Dati: A = {1, 2,, 4, 5} B = {1, 5, 7,
SOLUZIONI COMPITO A. Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo:
 SOLUZIONI COMPITO A Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo: z = i + i + i 3 In forma algebrica, otteniamo: = i + 1 +
SOLUZIONI COMPITO A Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo: z = i + i + i 3 In forma algebrica, otteniamo: = i + 1 +
1) Sia f(x) la funzione di periodo 1 tale che. f(x) = 4x 3 x + 3
 X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
Analisi Matematica T-2 Ingegneria Edile Ravenna 2015/16
 Analisi Matematica T-2 Ingegneria Edile Ravenna 2015/16 Fausto Ferrari, Daniele Morbidelli Aggiornato al 2 giugno 2016 Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica
Analisi Matematica T-2 Ingegneria Edile Ravenna 2015/16 Fausto Ferrari, Daniele Morbidelli Aggiornato al 2 giugno 2016 Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
NUMERI COMPLESSI. = 2 + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9 = 0
 NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica 2: Scritto Generale, , Fuori corso. Cognome e nome:...matricola:...
 Analisi Matematica 2: Scritto Generale, 26.11.216, Fuori corso Cognome e nome:....................................matricola:......... es.1 es.2 es. es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 6/9cr. 5 5 5 5
Analisi Matematica 2: Scritto Generale, 26.11.216, Fuori corso Cognome e nome:....................................matricola:......... es.1 es.2 es. es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 6/9cr. 5 5 5 5
Esercizi su Funzioni di più variabili. - Parte II. Derivate parziali, derivate direzionali, piano tangente
 Esercizi su Funzioni di più variabili. - Parte II Derivate parziali, derivate direzionali, piano tangente 1. Data la funzione f(x, y, z) = e x2 y 3 sin(x + z) calcolarne il gradiente e la derivata direzionale
Esercizi su Funzioni di più variabili. - Parte II Derivate parziali, derivate direzionali, piano tangente 1. Data la funzione f(x, y, z) = e x2 y 3 sin(x + z) calcolarne il gradiente e la derivata direzionale
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 12 giugno 2000
 assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
assegnato il 1 giugno 1 Risolvere il sistema di disequazioni ( ) 1 x 1 3 9 3 log (13 x) > 3 x 9 x 4 + 1 < Scrivere le equazioni delle circonferenze che passano per il punto A = (, ) e sono tangenti alle
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Geometria Differenziale 2017/18 Esercizi I
 Geometria Differenziale 17/18 Esercizi I 1 Esercizi sulle curve piane 1.1 Esercizio Si consideri la curva parametrizzata sin t, t [, π]. cos(t) a) Stabilire per quali valori di t la parametrizzazione è
Geometria Differenziale 17/18 Esercizi I 1 Esercizi sulle curve piane 1.1 Esercizio Si consideri la curva parametrizzata sin t, t [, π]. cos(t) a) Stabilire per quali valori di t la parametrizzazione è
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo differenziale in IR N. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione x del versore v
Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione x del versore v
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. 2
 Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f:
![ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f: ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f:](/thumbs/103/158892828.jpg) ANALISI MATEMATICA Prova scritta /7/1 COGNOME e Nome firma 1. [15 pt] Data la funzione f : dom f R R, fx, y) 1 4 logx + 3y ) ) [1 pt] calcolare f: [ pt] Disegnare l insieme dei punti stazionari di f [
ANALISI MATEMATICA Prova scritta /7/1 COGNOME e Nome firma 1. [15 pt] Data la funzione f : dom f R R, fx, y) 1 4 logx + 3y ) ) [1 pt] calcolare f: [ pt] Disegnare l insieme dei punti stazionari di f [
Matematica e Statistica
 Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo Appello 8 Settembre 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (3/09/011) Università di Verona - Laurea in Biotecnologie - A.A. 010/11 1 Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (3/09/011) Università di Verona - Laurea in Biotecnologie - A.A. 010/11 1 Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z)
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
1) i) Rappresentare sia attraverso disequazioni, sia attraverso un disegno, il dominio della funzione
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni
 Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Matematica e Statistica
 Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Funzioni a valori vettoriali Differenziabilità e regola della catena
 e regola della catena Analisi Matematica A Secondo modulo Corso di Laurea in Matematica Università di Trento 4 aprile 2019 o: le curve o: F : R 2 R 2 Sia E R n. Una funzione a valori vettoriali f : E R
e regola della catena Analisi Matematica A Secondo modulo Corso di Laurea in Matematica Università di Trento 4 aprile 2019 o: le curve o: F : R 2 R 2 Sia E R n. Una funzione a valori vettoriali f : E R
Esempio di grafico di una funzione reale di due variabili reali
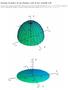 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
b) Dimostrare che se f(x) è differenziabile in x 0, allora è continua in x 0.
 Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Scritto d esame di Analisi Matematica II
 Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14
 Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, MATEMATICA, Seconda edizione, Zanichelli
Analisi Matematica T-2 Ingegneria Edile Ravenna 2013/14 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, MATEMATICA, Seconda edizione, Zanichelli
Analisi Matematica 2: Scritto Generale, Cognome e nome:...matricola:...
 Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA 8 DERIVATE DI FUNZIONI A VALORI VETTORIALI
 DRIVAT DI FUNZIONI A VALORI VTTORIALI MATRIC JACOBIANA n m Una funzione f : A definita su un aperto di uno spazio n-dimensionale a m componenti, è derivabile parzialmente in A se ogni componente di f è
DRIVAT DI FUNZIONI A VALORI VTTORIALI MATRIC JACOBIANA n m Una funzione f : A definita su un aperto di uno spazio n-dimensionale a m componenti, è derivabile parzialmente in A se ogni componente di f è
Esercizio 2 SI NO Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente
 GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
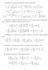 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
MMAC - Lauree Magistrali Scienze Chimiche - 12 Maggio sol
 MMAC - Lauree Magistrali Scienze Chimiche - 1 Maggio 011- sol Esercizi I - Soluzioni (1) Il grafico è una curva, ma in R 4, era implicito nell esercizio che graficamente si voleva il sostegno della curva
MMAC - Lauree Magistrali Scienze Chimiche - 1 Maggio 011- sol Esercizi I - Soluzioni (1) Il grafico è una curva, ma in R 4, era implicito nell esercizio che graficamente si voleva il sostegno della curva
Funzioni di due o più variabili reali
 5 Funzioni di due o più variabili reali 5.. Esempi ed esercizi svolti e/o proposti 5... Domini ed insiemi di livello Esercizio 5... Disegnare sul piano Oxy il dominio delle seguenti funzioni. ln y x, ln
5 Funzioni di due o più variabili reali 5.. Esempi ed esercizi svolti e/o proposti 5... Domini ed insiemi di livello Esercizio 5... Disegnare sul piano Oxy il dominio delle seguenti funzioni. ln y x, ln
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A)
 Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = 3x 2 x 2 y + y + 1
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II. Padova, 19.9.
 Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 19.9.2016 Si svolgano i seguenti esercizi facendo attenzione a giustificare
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 19.9.2016 Si svolgano i seguenti esercizi facendo attenzione a giustificare
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini.
 Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Corso di Analisi Matematica 2. Corso di Laurea in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16
 PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
PROGRAMMA DI ANALISI MATEMATICA 2 Corsi di Laurea in Ing. Informatica (Prof. Ravaglia) Anno Accademico 2015/16 Simboli: I= introduzione intuitiva, D = definizione, T = teorema C = criterio deduttivo, d
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2017 2018 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Sia K un campo. Si dimostri che un polinomio f(x) K[x] di grado d, dove 2 d 3, è riducibile se
Geometria 3 A.A. 2017 2018 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Sia K un campo. Si dimostri che un polinomio f(x) K[x] di grado d, dove 2 d 3, è riducibile se
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria 2 Primo Appello 13 Luglio 2017
 Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Politecnico di Milano Ingegneria Industriale e dell Informazione Analisi e Geometria Primo Appello 13 Luglio 017 Cognome: Nome: Matricola: Es.1: 11 punti Es.: 6 punti Es.3: 7 punti Es.: 8 punti Totale
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Massimi e minimi assoluti vincolati: esercizi svolti
 Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 2013/14 scheda 1
 Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Analisi Matematica 2: Scritto Generale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Scritto Generale, 7.9.16, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 3 9cr. 5 5 5 5 5 /3
Analisi Matematica : Scritto Generale, 7.9.16, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es.4 es.5 es.6/7 somma 5cr. 6 6 6 6 6 3 9cr. 5 5 5 5 5 /3
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 II compitino 29/05/09 (fila A) valutazione
 Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 II compitino 29/05/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 II compitino 29/05/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Esprimendo il vettore (u, v) in coordinate polari (u = r cos θ, v = r sin θ), si ha. = u2 v 0 0 u 0 v
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Matematica e Statistica
 Matematica e Statistica Prova d esame (06/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (06/0/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (06/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (06/0/03) Università di Verona - Laurea in Biotecnologie
Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3.4, 3.9. Esercizi 3.4, 3.9.
 Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Appunti sul corso di Complementi di Matematica - mod Analisi prof. B.Baccelli 200/ 07 - Funzioni vettoriali, derivata della funzione composta, formula di Taylor. Riferimenti: R.Adams, Calcolo Differenziale
Il NUMERO della FILA è contenuto nel testo dell esercizio 8 ed è il valore assegnato di y (0) f(x) =,
 Analisi Matematica 1 14 gennaio 2019 Il NUMERO della FILA è contenuto nel testo dell esercizio 8 ed è il valore assegnato di y (0) Fila 1 1. dom f =], 2[ ] 2, 2[ ]2, + [; f non è pari né dispari; x 2 f(x)
Analisi Matematica 1 14 gennaio 2019 Il NUMERO della FILA è contenuto nel testo dell esercizio 8 ed è il valore assegnato di y (0) Fila 1 1. dom f =], 2[ ] 2, 2[ ]2, + [; f non è pari né dispari; x 2 f(x)
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018)
 Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Esame di Analisi Matematica 2 24/9/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013 Esercizio 1. Sia A il cerchio aperto del piano di centro l origine e raggio 1. Sia f(x, y) una
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo Appello 9 Luglio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 9 Luglio Cognome: Nome: Matricola: Compito A Es: punti Es: 6 punti Es: 8 punti Es: 8 punti Totale Data la funzione f : D
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 9 Luglio Cognome: Nome: Matricola: Compito A Es: punti Es: 6 punti Es: 8 punti Es: 8 punti Totale Data la funzione f : D
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Matematica e Statistica
 Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (05/09/202) Università di Verona - Laurea in Biotecnologie - A.A. 20/2 Matematica e Statistica Prova di MATEMATICA (05/09/202) Università di Verona - Laurea in Biotecnologie
IV Scientifico - 24 Novembre 2014
 SOLUZIONI IV Scientifico - 24 Novembre 204 0 02 03 04 05 06 07 08 09 0 20 D C C C C E E E E C 202 E C C A C D E A A C 203 E A C E C C A C E C 204 D C B E A B A A A A 205 E E D C D B C C E A 206 D D B C
SOLUZIONI IV Scientifico - 24 Novembre 204 0 02 03 04 05 06 07 08 09 0 20 D C C C C E E E E C 202 E C C A C D E A A C 203 E A C E C C A C E C 204 D C B E A B A A A A 205 E E D C D B C C E A 206 D D B C
Esercizi proposti. 1 Numeri complessi. 1.1 Forma cartesiana. Esercizio 1.1 Dato il numero complesso. z = 7 3 7i,
 Numeri complessi Esercizi proposti 1 Numeri complessi 1.1 Forma cartesiana Esercizio 1.1 Dato il numero complesso z = 7 3 7i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria
Numeri complessi Esercizi proposti 1 Numeri complessi 1.1 Forma cartesiana Esercizio 1.1 Dato il numero complesso z = 7 3 7i, a) determinare la parte reale x di z: x = Re z, b) determinare la parte immaginaria
Corso di laurea in Chimica. Matematica
 Corso di laurea in Chimica Matematica Esercizi di ricapitolazione per la prova in itinere (tratti dalle prove in itinere degli anni precedenti) (Gli esercizi segnati con una crocetta sono di livello più
Corso di laurea in Chimica Matematica Esercizi di ricapitolazione per la prova in itinere (tratti dalle prove in itinere degli anni precedenti) (Gli esercizi segnati con una crocetta sono di livello più
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Esercizi sui numeri complessi. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. 1. Trovare parte reale e immaginaria dei numeri complessi:
 Esercizi sui numeri complessi Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1 Esercitazione 1. Trovare parte reale e immaginaria dei numeri complessi: 3 + i 5 4i e Soluzione: 3 + i
Esercizi sui numeri complessi Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1 Esercitazione 1. Trovare parte reale e immaginaria dei numeri complessi: 3 + i 5 4i e Soluzione: 3 + i
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
COMPLEMENTI DI ANALISI MATEMATICA 19 GENNAIO 2010
 COMPLEMENTI DI ANALISI MATEMATICA 19 GENNAIO 2010 Esercizio 1. Data la funzione f : R 2 R, (x, y) y log(1 + x 2 ), i) determinare la natura degli eventuali punti stazionari di f in R 2 (N.B. anche se lo
COMPLEMENTI DI ANALISI MATEMATICA 19 GENNAIO 2010 Esercizio 1. Data la funzione f : R 2 R, (x, y) y log(1 + x 2 ), i) determinare la natura degli eventuali punti stazionari di f in R 2 (N.B. anche se lo
Syllabus per la seconda prova intermedia e per le prove scritte di esame. Esercizi di preparazione.
 Università di Trento - Corsi di Laurea in Ingegneria Civile e in Ingegneria Ambientale Analisi matematica 2 - a.a. 2013-14 - Prof. Gabriele Anzellotti Syllabus per la seconda prova intermedia e per le
Università di Trento - Corsi di Laurea in Ingegneria Civile e in Ingegneria Ambientale Analisi matematica 2 - a.a. 2013-14 - Prof. Gabriele Anzellotti Syllabus per la seconda prova intermedia e per le
