Breve guida all uso di AMPL
|
|
|
- Marilena Romagnoli
- 9 anni fa
- Visualizzazioni
Transcript
1 Breve guida all uso di AMPL Renato Bruni AMPL (A Modeling Language for Mathematical Programming) è un linguaggio di modellazione per la programmazione matematica. Serve ad esprimere un problema di ottimizzazione in una forma che sia comprensibile dal solutore. È un linguaggio algebrico, cioè contiene primitive per esprimere la notazione matematica normalmente utilizzata nello scrivere i modelli. Tutto viene espresso attraverso normali file di testo. Gli spazi e gli a capo sono generalmente liberi, nel senso che possono essere inseriti senza provocare errori, ma conviene rispettare un formato preciso per rendere agevole lettura ed interpretazione di questi file. Occorre scrivere un file di modello, in cui è descritta la struttura logica del modello del problema in esame. I valori numerici del problema in esame possono essere inseriti nello stesso file di modello o in uno o più file di dati. Inserendo la struttura logica nel file di modello ed i dati nel file di dati è possibile cambiare i dati in modo semplice e senza pericolo di introdurre errori nel modello. Il file di modello ha obbligatoriamente estensione.mod, quello di dati estensione.dat. I dati possono anche essere letti, tramite opportuni comandi in altri file di testo. Possono essere inoltre creati file di comandi (analoghi ai file batch del DOS) che hanno estensione.run. Dichiarazione di parametri ed insiemi I parametri sono i dati (non variabili) che compaiono nel modello che descrive il nostro problema di ottimizzazione. Un parametro può essere utilizzato solo dopo la sua dichiarazione. Si usa la parola chiave param, seguita dal nome del parametro. La più semplice dichiarazione di parametro è: param t; AMPL è case sensitive, cioè le lettere maiuscole vengono considerate differenti da quelle minuscole. Un parametro va chiamato sempre nello stesso modo ogni volta che si fa riferimento ad esso. Ogni istruzione termina con ;. Si possono inserire commenti preceduti dal simbolo #. Se un parametro è composto da un insieme di valori (ad esempio un vettore), serve un indice per distinguere i diversi valori. Nella dichiarazione, la dimensione del parametro viene indicata tra parentesi graffe. param C; param costi{1..c}; # indice numerico che va da 1 a C Quanto sopra serve a dichiarare un parametro C, ed un insieme di parametri costi identificati da un indice numerico che varia da 1 fino a C. Un insieme è semplicemente una lista degli elementi che lo costituiscono. Serve ad esempio per dichiarare un parametro indicizzato su un insieme, ma anche per varie altre cose. Un insieme si dichiara con la parola chiave set. set VAR; set VINC; parm a{vinc,var}; # insieme delle variabili # insieme dei vincoli # matrice Quanto sopra ha l effetto di dichiarare un insieme VAR (i cui elementi non sono ancora stati specificati), un insieme VINC (i cui elementi non sono ancora stati specificati), ed un parametro bidimensionale a (cioè una matrice) con elementi identificati da coppie di valori, il primo appartenente all insieme VINC ad il secondo all insieme VAR.
2 Per fare riferimento ad una specifica componente di un parametro si scrive l indice che individua quella componente tra parentesi quadre....costi[10]......a[i,j]... a[i,j] è il valore della matrice a corrispondente all i-esimo elemento dell insieme VINC e al j-esimo elemento dell insieme VAR. Il primo indice è quello di riga, il secondo quello di colonna. Gli elementi di un insieme possono essere numeri o stringhe. Se poi quell insieme serve ad indicizzare un parametro, bisogna ricordarsi che gli indici sono gli elementi dell insieme, e quindi rispettivamente numeri o stringhe. Scegliendo numeri si ha il vantaggio di poter individuare tramite operazioni matematiche i vari elementi del parametro, cosa che in molti casi è necessaria. Scegliendo stringhe, al contrario, questo non è possibile, e le istruzioni risulteranno spesso più lunghe e macchinose, mentre si ha il vantaggio di poter usare nomi autoesplicativi. Per accorgersi di eventuali errori nei dati, si possono imporre restrizioni sui parametri. Ad esempio, se sappiamo che un certo parametro T deve essere un intero maggiore di 1, possiamo scriverlo come limitazione nel modo seguente, in modo che ci venga segnalato subito quando ciò non è verificato. param T >1 integer; Alcuni parametri possono avere valori calcolati in base ad altri parametri param costi{a}; param sommacosti := sum{i in A} costi[i]; Il parametro sommacosti ha come valore la somma dei parametri costi. Assegnazione di parametri ed insiemi I valori dei parametri vengono assegnati (e non possono più essere cambiati) sempre attraverso la parola chiave param, seguita dal nome del parametro (come dichiarato nel file di modello), da := e da un valore param T:= 1; param C := 20; Gli elementi di un insieme si assegnano con la parola chiave set, seguita dal nome del insieme, da := e da una sequenza di valori separati da spazi set vinc := A B ; set var := X Y ; Dopo l assegnazione degli insiemi è possibile assegnare i valori ai parametri indicizzati con tali insiemi. Per un parametro monodimensionale, occorre specificare gli indici seguiti dai valori che assume in corrispondenza dei vari indici. Per aumentare la leggibilità conviene scriverlo nel seguente modo. Notare che il punto e virgola che conclude l istruzione è solo alla fine dell ultima riga. param vettore:= A 1 B 3; Per un parametro bidimensionale occorre specificare le coppie di indici seguite dai corrispondenti valori. param a:= X A 6 Y A 2 X B 8
3 Y B 0; Eventuali valori non presenti nell elenco si intendono con valore non specificato. Parametri bidimensionali possono essere anche rappresentati nella più leggibile forma tabellare: il nome del parametro è seguito da :, da un elenco di indici che costituiscono una dimensione del parametro, da :=, e dagli elementi dell altro indice seguiti dalle sequenze di valori del parametro corrispondenti. param a: X Y:= A 6 2 B 8 0; Se una matrice è molto larga e poco alta, e quindi non è agevolmente visibile nella schermata, conviene scriverne la trasposta, facendo seguire al nome della matrice la parola (tr). Il formato con cui sono scritti i parametri indicizzati serve solo ad aumentare la leggibilità. Il solutore avrebbe letto correttamente la matrice a anche se fosse stata scritta param a: X Y := A 6 2 B 8 0; Per un parametro avente più di due dimensioni, basta indicare le n-ple dei valori degli indici seguite dal valore del parametro corrispondente a quella n-pla di indici. Esempio: param cost:= X A ST 2 X A DL 3 X B ST 2 X B DL 1 Y A ST 2 Y A DL 2 Y B ST 2 Y B DL 2; I valori di un insieme numerico si possono assegnare enumerandoli set NUMERI:={1,2,5,10}; O, se possibile, semplicemente indicando gli estremi. set NUMERI:= ; È possibile indicare anche il passo tra numeri consecutivi. Ad esempio, i numeri pari fino a 100 sono set PARI := by 2; Se si vuole imporre che un parametro e abbia un valore all interno di un certo insieme S si può specificare tramite il comando seguente param e symbolic in S; Se un parametro deve essere modificabile, anziché assegnarlo con := occorre inizializzarlo con il comando default e poi modificarlo col comando let param peso default 100; # peso inizializzato a let peso := 200; # peso aggiornato a 200 Infine, i valori dei parametri possono anche essere letti con il comando read sia da un qualsiasi file di testo sia immettendoli da tastiera. In questo caso il file di testo deve semplicemente riportare, separati da spazi, tutti i valori che volgiamo leggere, senza bisogno di indicare gli indici come nel file.dat read r < valore.txt; # legge r nel file valore.txt
4 Le seguenti istruzioni invece scrivono il valore del parametro peso e ne leggono il nuovo valore da tastiera printf"peso valeva %d", peso; printf"\ndimmi il nuovo valore di peso ; read peso; Ovviamente leggere valori da file di testo conviene prevalentemente per paramentri di grande dimensione. Ad esempio, per leggere uno dopo l altro tutti gli elementi di una matrice occorre fare così (usando anche l istruzione for) for{j in T, i in S} { read r[j,i] < matrice_r.txt; }; Espressioni aritmetiche I numeri vengono rappresentati con un eventuale segno, ed il separatore per le cifre decimali è il punto. La notazione esponenziale viene accettata e3 # -4.8 per 10 alla 3, cioè 4800 Le funzioni aritmetiche che è possibile utilizzare sono: Significato Valore assoluto di x Arcoseno(x) Arcoseno iperbolico(x) Arcocoseno(x) Arcocoseno iperbolico(x) Arcotangente iperbolico(x) Seno(x) Coseno(x) Tangente(x) Tangente iperbolica(x) Parte intera inferiore di x Parte intera superiore di x Logaritmo naturale loge x Logaritmo decimale log10 x Esponenziale e x Radice quadrata di x Minimo tra 2 o più numeri (x, y, z, ) Massimo tra 2 o più numeri (x, y, z, ) indicato con abs(x) acos(x) acosh(x) asin(x) asinh(x) atanh(x) sin(x) cos(x) tan(x) tanh(x) ceil(x) floor(x) log(x) log10(x) exp(x) sqrt(x) min(x,y,z, ) max(x,y,z, ) Gli operatori che è possibile utilizzare, in ordine di precedenza decrescente, sono: Significato Tipo indicato con o anche con Potenza Aritmetico ^ ** Numero negativo Aritmetico - Somma Aritmetico +
5 Sottrazione Aritmetico - Moltiplicazione Aritmetico * Divisione Aritmetico / Divisione intera Aritmetico div Modulo Aritmetico mod Differenza non negativa: max(a-b,0) Aritmetico less Sommatoria Aritmetico sum Produttoria Aritmetico prod Minimo Aritmetico min Massimo Aritmetico max Unione di insiemi Insiemistica union Intersezione di insiemi Insiemistica inter Differenza tra insiemi Insiemistica diff Differenza simmetrica tra insiemi Insiemistica symdiff Prodotto cartesiano tra insiemi Insiemistica cross Appartenenza ad un insieme Insiemistica in Non appartenenza ad un insieme Insiemistica not in Maggiore, maggiore o uguale Aritmetico >, >= Minore, minore o uguale Aritmetico <, <= Uguale Aritmetico = == Diverso Aritmetico <>!= Negazione logica Logico not! And logico Logico and && Quantificatore esistenziale logico Logico exists Quantificatore universale logico Logico forall Or logico Logico or If then else Aritmetico if then else Esempi: abs(sum {i in ORIG} offerta[i] sum{j in DEST} domanda[j]) è il valore assoluto della somma delle offerte meno la somma delle domande sum{i in A} d[i] + (if t=10 then a[i] else -a[i]) è la somma dei d più gli a se t=10, e meno gli a altrimenti. Variabili A differenza dei parametri, sono dei simboli il cui valore numerico deve essere calcolato dal solutore, e non indicato da noi. Rappresentano le grandezze incognite che vogliamo conoscere risolvendo il problema di ottimizzazione. Si dichiarano con la parola chiave var, ed appaiono solo nel file di modello. Le variabili devono essere dichiarate prima di poter essere utilizzate. La più semplice dichiarazione di variabile è var x; normalmente le variabili sono un insieme di valori indicizzato su in insieme, eventualmente con delle restrizioni. var x{p in VAR} >=0, <=LIMIT;
6 indica un insieme di variabili con indice che varia nell insieme VAR, che devono essere tutte >=0 e <= del parametro LIMIT. Altre possibili restrizioni sono integer per specificare variabili intere e binary per specificare variabili binarie. È possibile, anche se inusuale, specificare restrizioni di uguaglianza sulle variabili. var Buy{j in FOOD} = f_min[j]; questo vuol dire che siamo interessati solo alle soluzioni in cui le variabili hanno il valore dei corrispondenti parametri f_min. È possibile, inoltre, specificare valori iniziali sulle variabili. var Buy{j in FOOD} := f_min[j]; questo vuol dire che le variabili vengono inizializzate ai valori dei corrispondenti parametri f_min, ma il solutore le può poi modificare. Questo serve nel caso si voglia far lavorare il solutore a partire da una soluzione data. Si noti che il significato è completamente diverso dal caso precedente. Obiettivo È ciò che vogliamo massimizzare o minimizzare nel nostro problema di ottimizzazione. Può essere uno solo. È dichiarato con la parola chiave maximize o minimize, seguita obbligatoriamente da un qualsiasi nome per questo obiettivo, dai due punti, e da una espressione in cui possono comparire solo gli insiemi, i parametri e le variabili già definiti. È conclusa, al solito, da ;. La più semplice dichiarazione di obiettivo è minimize obiettivo: x; Significa che vogliamo che il solutore trovi un valore per le variabili tale da rendere minimo il valore di x. minimize total_cost: sum{j in VAR} cost[j]*x[j]; Vuol dire minimizzare la somma dei prodotti delle variabili per i rispettivi costi. Di regola, nell obiettivo compaiono sempre le variabili. L espressione può essere complicata, come nel caso di minimize obj: sum{i in N_H, j in N_W} (z[i,j] - sum{r in N_H, s in N_W} x[r,s] * vdef[i-r] * hdef[j-s])^2 + q[1]*( sum{k in N_H1, h in N_H} (x[k+1,h] - x[k,h] - vgap[k,h])^2 ) + q[2]*( sum{l in N_H, m in N_W1} (x[l,m+1] - x[l,m] - hgap[l,m])^2 ); Conviene, per quanto possibile, evitare espressioni complicate, in quanto rendono il processo di soluzione molto più lento. Vincoli Sono delle specifiche che dobbiamo soddisfare nel nostro problema di ottimizzazione. Sono dichiarati con la parola chiave subject to. Questa parola chiave può essere abbreviata in s.t. ed è opzionale, dato che ogni dichiarazione che non comincia con una parola chiave viene considerata vincolo. Devono avere un nome, seguito dai due punti, e una espressione in cui possono comparire solo gli insiemi, i parametri e le variabili già definiti. Deve ovviamente comparire un operatore di relazione (<, <=, >, >=, =) Sono conclusi, al solito, da ;. La più semplice dichiarazione di vincolo è
7 subject to vinc: x <=4; Vuol dire che vogliamo che il solutore trovi una soluzione in cui la variabile x valga al più 4 (questo tipo di semplice vincolo poteva anche essere specificato come restrizione nella dichiarazione della variabile x). subject to time: sum {p in PROD} rate[p]*make[p] <= disp; Vuol dire che la somma dei prodotti delle componenti di stesso indice di rate e make deve essere minore di disp. I vincoli possono essere indicizzati: s. t. limiti{s in VINC}: sum{i in VAR} a[s,i]*x[i] <= b[s]; Se l insieme VINC è formato dai quattro elementi A, B, C, D, equivale ai quattro vincoli s. t. limite_a: sum{i in VAR} a[a,i]*x[i] <= b[a]; s. t. limite_b: sum{i in VAR} a[b,i]*x[i] <= b[b]; s. t. limite_c: sum{i in VAR} a[c,i]*x[i] <= b[c]; s. t. limite_d: sum{i in VAR} a[d,i]*x[i] <= b[d]; Con gli strumenti sintattici visti è possibile esprimere direttamente una grande varietà di modelli. File di comandi Avviando l eseguibile ampl.exe si ha una finestra in cui è possibile lavorare da riga di comando, cioè scrivendo le istruzioni da tastiera. Ad esempio, per scegliere come solutore cplex si scrive option solver cplex; Per usare un file di modello pian.mod ed un file di dati pian.dat si scrive model pian.mod; data pian.dat; Infine, per risolvere il modello corrente si usa il comando solve; e per vedere i valori dei vari elementi del modello (ad esempio le variabili x) si usa display x; Tutti questi comandi possono essere anche scritti in un file di comandi, cioè un file di testo con estensione.run, dove è possibile usare anche istruzioni di controllo del flusso come for o repeat per eseguire in sequenza diverse operazioni. Tale file va poi lanciato con l istruzione commands esegui.run;
1 Breve introduzione ad AMPL
 1 Breve introduzione ad AMPL Il primo passo per risolvere un problema reale attraverso strumenti matematici consiste nel passare dalla descrizione a parole del problema al modello matematico dello stesso.
1 Breve introduzione ad AMPL Il primo passo per risolvere un problema reale attraverso strumenti matematici consiste nel passare dalla descrizione a parole del problema al modello matematico dello stesso.
Introduzione. AMPL Introduzione. F. Rinaldi. Dipartimento di Matematica Università di Padova. Corso di Laurea Matematica. F. Rinaldi AMPL Introduzione
 Dipartimento di Matematica Università di Padova Corso di Laurea Matematica Outline Introduzione Utilizzo di un Solver Definizione Un solver (o risolutore) è un software che riceve in input una descrizione
Dipartimento di Matematica Università di Padova Corso di Laurea Matematica Outline Introduzione Utilizzo di un Solver Definizione Un solver (o risolutore) è un software che riceve in input una descrizione
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Funzioni in C. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Funzioni - in breve: Funzioni Definizione di funzioni
Progetto e ottimizzazione di reti 2
 Progetto e ottimizzazione di reti 2 Esercitazione AMPL A.A. 29-2 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma.it Università di Roma La Sapienza Dipartimento di Informatica
Progetto e ottimizzazione di reti 2 Esercitazione AMPL A.A. 29-2 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma.it Università di Roma La Sapienza Dipartimento di Informatica
RISOLUTORE AUTOMATICO PER SUDOKU
 RISOLUTORE AUTOMATICO PER SUDOKU Progetto Prolog - Pierluigi Tresoldi 609618 INDICE 1.STORIA DEL SUDOKU 2.REGOLE DEL GIOCO 3.PROGRAMMAZIONE CON VINCOLI 4.COMANDI DEL PROGRAMMA 5.ESEMPI 1. STORIA DEL SUDOKU
RISOLUTORE AUTOMATICO PER SUDOKU Progetto Prolog - Pierluigi Tresoldi 609618 INDICE 1.STORIA DEL SUDOKU 2.REGOLE DEL GIOCO 3.PROGRAMMAZIONE CON VINCOLI 4.COMANDI DEL PROGRAMMA 5.ESEMPI 1. STORIA DEL SUDOKU
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c
![MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c MATLAB. Caratteristiche. Dati. Esempio di programma MATLAB. a = [1 2 3; 4 5 6; 7 8 9]; b = [1 2 3] ; c = a*b; c](/thumbs/25/4541811.jpg) Caratteristiche MATLAB Linguaggio di programmazione orientato all elaborazione di matrici (MATLAB=MATrix LABoratory) Le variabili sono matrici (una variabile scalare equivale ad una matrice di dimensione
Caratteristiche MATLAB Linguaggio di programmazione orientato all elaborazione di matrici (MATLAB=MATrix LABoratory) Le variabili sono matrici (una variabile scalare equivale ad una matrice di dimensione
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari
 Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Introduzione allo Scilab Parte 1: numeri, variabili ed operatori elementari Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro 6 Giugno 2007 Felice Iavernaro (Univ.
Linguaggi di modellizzazione
 p. 1/5 Linguaggi di modellizzazione Come visto, il primo passo per risolvere un problema di decisione consiste nel formularne il modello matematico. Una volta definito il modello matematico lo dobbiamo
p. 1/5 Linguaggi di modellizzazione Come visto, il primo passo per risolvere un problema di decisione consiste nel formularne il modello matematico. Una volta definito il modello matematico lo dobbiamo
Ottimizzazione Combinatoria
 Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2010-20112011 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma1.it Università i di Roma La Sapienza Dipartimento di Informatica
Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2010-20112011 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma1.it Università i di Roma La Sapienza Dipartimento di Informatica
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
Uso di base delle funzioni in Microsoft Excel
 Uso di base delle funzioni in Microsoft Excel Le funzioni Una funzione è un operatore che applicato a uno o più argomenti (valori, siano essi numeri con virgola, numeri interi, stringhe di caratteri) restituisce
Uso di base delle funzioni in Microsoft Excel Le funzioni Una funzione è un operatore che applicato a uno o più argomenti (valori, siano essi numeri con virgola, numeri interi, stringhe di caratteri) restituisce
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Ottimizzazione Combinatoria
 Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2009-2010 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma1.it Università di Roma La Sapienza Dipartimento di Informatica e
Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2009-2010 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma1.it Università di Roma La Sapienza Dipartimento di Informatica e
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
EXCEL PER WINDOWS95. sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area di lavoro, detta foglio di lavoro,
 EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri
 Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Microsoft Excel. Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle. Numeri, date, formule, testo, funzioni
 Microsoft Excel Sommario Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle Numeri, date, formule, testo, funzioni Formattazione dei dati Creazione di serie di
Microsoft Excel Sommario Il foglio elettronico Microsoft Excel Cartelle, Fogli di lavoro e celle Contenuto delle celle Numeri, date, formule, testo, funzioni Formattazione dei dati Creazione di serie di
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
Richiesta pagina PHP (es: index.php)
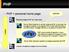 PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
PHP PHP = personal home page SERVER Richiesta pagina PHP (es: index.php) Server Web (Apache) in ascolto sulla porta 80, si accorge che la pagina richiesta è una pagina PHP in base all'estensione o con
Matematica in laboratorio
 Unità 1 Attività guidate Attività 1 Foglio elettronico Divisibilità tra numeri naturali Costruisci un foglio di lavoro per determinare se a è divisibile per b, essendo a e b due numeri naturali, con a
Unità 1 Attività guidate Attività 1 Foglio elettronico Divisibilità tra numeri naturali Costruisci un foglio di lavoro per determinare se a è divisibile per b, essendo a e b due numeri naturali, con a
4. Operazioni aritmetiche con i numeri binari
 I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
IL CONCETTO DI FUNZIONE
 IL CONCETTO DI FUNZIONE Il concetto di funzione è forse il concetto più importante per la matematica: infatti la matematica e' cercare le cause, le implicazioni, le conseguenze e l'utilità di una funzione
IL CONCETTO DI FUNZIONE Il concetto di funzione è forse il concetto più importante per la matematica: infatti la matematica e' cercare le cause, le implicazioni, le conseguenze e l'utilità di una funzione
(anno accademico 2008-09)
 Calcolo relazionale Prof Alberto Belussi Prof. Alberto Belussi (anno accademico 2008-09) Calcolo relazionale E un linguaggio di interrogazione o e dichiarativo: at specifica le proprietà del risultato
Calcolo relazionale Prof Alberto Belussi Prof. Alberto Belussi (anno accademico 2008-09) Calcolo relazionale E un linguaggio di interrogazione o e dichiarativo: at specifica le proprietà del risultato
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo
 Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL
 LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
Introduzione al Foglio Elettronico
 Microsoft Excel Introduzione al Foglio Elettronico Il Foglio Elettronico Si presenta come una grande tabella su un foglio di carta Le celle contengono differenti dati Numeri Testo Date Ecc I dati possono
Microsoft Excel Introduzione al Foglio Elettronico Il Foglio Elettronico Si presenta come una grande tabella su un foglio di carta Le celle contengono differenti dati Numeri Testo Date Ecc I dati possono
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Algebra Booleana ed Espressioni Booleane
 Algebra Booleana ed Espressioni Booleane Che cosa è un Algebra? Dato un insieme E di elementi (qualsiasi, non necessariamente numerico) ed una o più operazioni definite sugli elementi appartenenti a tale
Algebra Booleana ed Espressioni Booleane Che cosa è un Algebra? Dato un insieme E di elementi (qualsiasi, non necessariamente numerico) ed una o più operazioni definite sugli elementi appartenenti a tale
Alcune regole di base per scrivere un programma in linguaggio C
 Alcune regole di base per scrivere un programma in linguaggio C Un programma il linguaggio C (listato) viene scritto in formato testo ed archiviato in un file: *.c Per scrivere un listato C si utilizza
Alcune regole di base per scrivere un programma in linguaggio C Un programma il linguaggio C (listato) viene scritto in formato testo ed archiviato in un file: *.c Per scrivere un listato C si utilizza
Metodologie di programmazione in Fortran 90
 Metodologie di programmazione in Fortran 90 Ing. Luca De Santis DIS - Dipartimento di informatica e sistemistica Anno accademico 2007/2008 Fortran 90: Metodologie di programmazione DIS - Dipartimento di
Metodologie di programmazione in Fortran 90 Ing. Luca De Santis DIS - Dipartimento di informatica e sistemistica Anno accademico 2007/2008 Fortran 90: Metodologie di programmazione DIS - Dipartimento di
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Modelli di Programmazione Lineare e Programmazione Lineare Intera
 Modelli di Programmazione Lineare e Programmazione Lineare Intera 1 Azienda Dolciaria Un azienda di cioccolatini deve pianificare la produzione per i prossimi m mesi. In ogni mese l azienda ha a disposizione
Modelli di Programmazione Lineare e Programmazione Lineare Intera 1 Azienda Dolciaria Un azienda di cioccolatini deve pianificare la produzione per i prossimi m mesi. In ogni mese l azienda ha a disposizione
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Comparatori. Comparatori di uguaglianza
 Comparatori Scopo di un circuito comparatore é il confronto tra due codifiche binarie. Il confronto può essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo "maggiore",
Comparatori Scopo di un circuito comparatore é il confronto tra due codifiche binarie. Il confronto può essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo "maggiore",
Javascript: il browser
 Javascript: il browser Un browser è un programma Un browser interpreta il linguaggio HTML e visualizza le pagine sullo schermo Per la visualizzazione delle pagine un browser si appoggia al software di
Javascript: il browser Un browser è un programma Un browser interpreta il linguaggio HTML e visualizza le pagine sullo schermo Per la visualizzazione delle pagine un browser si appoggia al software di
MODULO 4: FOGLIO ELETTRONICO (EXCEL)
 MODULO 4: FOGLIO ELETTRONICO (EXCEL) 1. Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei Personal computer. Essi
MODULO 4: FOGLIO ELETTRONICO (EXCEL) 1. Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei Personal computer. Essi
APPUNTI SUL LINGUAGGIO DI PROGRAMMAZIONE PASCAL
 APPUNTI SUL LINGUAGGIO DI PROGRAMMAZIONE PASCAL In informatica il Pascal è un linguaggio di programmazione creato da Niklaus Wirth ed é un linguaggio di programmazione strutturata. I linguaggi di programmazione
APPUNTI SUL LINGUAGGIO DI PROGRAMMAZIONE PASCAL In informatica il Pascal è un linguaggio di programmazione creato da Niklaus Wirth ed é un linguaggio di programmazione strutturata. I linguaggi di programmazione
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Algoritmo. I dati su cui opera un'istruzione sono forniti all'algoritmo dall'esterno oppure sono il risultato di istruzioni eseguite precedentemente.
 Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Pre Test 2008... Matematica
 Pre Test 2008... Matematica INSIEMI NUMERICI Gli insiemi numerici (di numeri) sono: numeri naturali N: insieme dei numeri interi e positivi {1; 2; 3; 4;...} numeri interi relativi Z: insieme dei numeri
Pre Test 2008... Matematica INSIEMI NUMERICI Gli insiemi numerici (di numeri) sono: numeri naturali N: insieme dei numeri interi e positivi {1; 2; 3; 4;...} numeri interi relativi Z: insieme dei numeri
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT.
 NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT. Con l utilizzo delle procedure di iscrizione on line la società organizzatrice ha a disposizione tutti
NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT. Con l utilizzo delle procedure di iscrizione on line la società organizzatrice ha a disposizione tutti
Anno 3. Funzioni: dominio, codominio e campo di esistenza
 Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Funzioni. Funzioni /2
 Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
CREAZIONE DI UN DATABASE E DI TABELLE IN ACCESS
 CONTENUTI: CREAZIONE DI UN DATABASE E DI TABELLE IN ACCESS Creazione database vuoto Creazione tabella Inserimento dati A) Creazione di un database vuoto Avviamo il programma Microsoft Access. Dal menu
CONTENUTI: CREAZIONE DI UN DATABASE E DI TABELLE IN ACCESS Creazione database vuoto Creazione tabella Inserimento dati A) Creazione di un database vuoto Avviamo il programma Microsoft Access. Dal menu
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO
 SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
Pianificazione di Produzione in DEC
 Pianificazione di Produzione in DEC L esempio considerato qui è un problema reale che la Digital Equipment Corporation (DEC) ha dovuto affrontare nell autunno del 1988 per preparare la pianificazione di
Pianificazione di Produzione in DEC L esempio considerato qui è un problema reale che la Digital Equipment Corporation (DEC) ha dovuto affrontare nell autunno del 1988 per preparare la pianificazione di
Automatizzare i compiti ripetitivi. I file batch. File batch (1) File batch (2) Visualizzazione (2) Visualizzazione
 Automatizzare i compiti ripetitivi I file batch Anno accademico 2000-01 1 Spesso capita di dover eseguire ripetutatmente una data sequenza di comandi Introdurli uno a uno da tastiera è un processo lento
Automatizzare i compiti ripetitivi I file batch Anno accademico 2000-01 1 Spesso capita di dover eseguire ripetutatmente una data sequenza di comandi Introdurli uno a uno da tastiera è un processo lento
Grafico qualitativo di una funzione reale di variabile reale
 Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
2 Rappresentazioni grafiche
 asi di matematica per la MPT 2 Rappresentazioni grafiche I numeri possono essere rappresentati utilizzando i seguenti metodi: la retta dei numeri; gli insiemi. 2.1 La retta numerica Domanda introduttiva
asi di matematica per la MPT 2 Rappresentazioni grafiche I numeri possono essere rappresentati utilizzando i seguenti metodi: la retta dei numeri; gli insiemi. 2.1 La retta numerica Domanda introduttiva
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda
 Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
Informatica B. Sezione D. Scuola di Ingegneria Industriale Laurea in Ingegneria Energetica Laurea in Ingegneria Meccanica
 Scuola di Ingegneria Industriale Laurea in Ingegneria Energetica Laurea in Ingegneria Meccanica Dipartimento di Elettronica, Informazione e Bioingegneria Informatica B Sezione D Franchi Alessio Mauro,
Scuola di Ingegneria Industriale Laurea in Ingegneria Energetica Laurea in Ingegneria Meccanica Dipartimento di Elettronica, Informazione e Bioingegneria Informatica B Sezione D Franchi Alessio Mauro,
A destra è delimitata dalla barra di scorrimento verticale, mentre in basso troviamo una riga complessa.
 La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
Google AdWords. Corrispondenze Parole Chiave
 Google AdWords Corrispondenze Parole Chiave Una mini guida sulle varie tipologie di corrispondenze per le parole chiave di Google AdWords, la scelta su quali usare può far cambiare di molto il punteggio
Google AdWords Corrispondenze Parole Chiave Una mini guida sulle varie tipologie di corrispondenze per le parole chiave di Google AdWords, la scelta su quali usare può far cambiare di molto il punteggio
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
ESERCIZI DI PROBLEM SOLVING E COMPOSIZIONE DEI DIAGRAMMI DI FLUSSO per le classi terza
 ESERCIZI DI PROBLEM SOLVING E COMPOSIZIONE DEI DIAGRAMMI DI FLUSSO per le classi terza vers.3 in lavorazione Docente SAFFI FABIO Contenuti 01.Esercizi generici sul diagramma di flusso - flow chart... 2
ESERCIZI DI PROBLEM SOLVING E COMPOSIZIONE DEI DIAGRAMMI DI FLUSSO per le classi terza vers.3 in lavorazione Docente SAFFI FABIO Contenuti 01.Esercizi generici sul diagramma di flusso - flow chart... 2
MATEMATICA CLASSE PRIMA
 CLASSE PRIMA L alunno/a si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l opportunità di ricorrere a una calcolatrice. Contare oggetti o eventi, a voce e mentalmente,
CLASSE PRIMA L alunno/a si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l opportunità di ricorrere a una calcolatrice. Contare oggetti o eventi, a voce e mentalmente,
Operazioni sui database
 Operazioni sui database Le operazioni nel modello relazionale sono essenzialmente di due tipi: Operazioni di modifica della base di dati (update) Interrogazioni della base di dati per il recupero delle
Operazioni sui database Le operazioni nel modello relazionale sono essenzialmente di due tipi: Operazioni di modifica della base di dati (update) Interrogazioni della base di dati per il recupero delle
Laboratorio di Informatica
 Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
Laboratorio di Informatica Introduzione a Python Dottore Paolo Parisen Toldin - parisent@cs.unibo.it Argomenti trattati Che cosa è python Variabili Assegnazione Condizionale Iterazione in una lista di
Arduino: Programmazione
 Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Programmazione formalmente ispirata al linguaggio C da cui deriva. I programmi in ARDUINO sono chiamati Sketch. Un programma è una serie di istruzioni che vengono lette dall alto verso il basso e convertite
Ricerca Operativa e Logistica
 Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 2011/2012 Lezione 10: Variabili e vincoli logici Variabili logiche Spesso nei problemi reali che dobbiamo affrontare ci sono dei
Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 2011/2012 Lezione 10: Variabili e vincoli logici Variabili logiche Spesso nei problemi reali che dobbiamo affrontare ci sono dei
EXCEL FUNZIONI PRINCIPALI
 EXCEL FUNZIONI PRINCIPALI Funzione SE() Sintassi: SE(VERIFICA, VALORE SE VERO, VALORE SE FALSO): verifica un valore e ritorna una risposta in base al risultato vero/falso Esempio: =SE(A2=15; "OK"; "NO")
EXCEL FUNZIONI PRINCIPALI Funzione SE() Sintassi: SE(VERIFICA, VALORE SE VERO, VALORE SE FALSO): verifica un valore e ritorna una risposta in base al risultato vero/falso Esempio: =SE(A2=15; "OK"; "NO")
Le query. Lezione 6 a cura di Maria Novella Mosciatti
 Lezione 6 a cura di Maria Novella Mosciatti Le query Le query sono oggetti del DB che consentono di visualizzare, modificare e analizzare i dati in modi diversi. Si possono utilizzare query come origine
Lezione 6 a cura di Maria Novella Mosciatti Le query Le query sono oggetti del DB che consentono di visualizzare, modificare e analizzare i dati in modi diversi. Si possono utilizzare query come origine
Ottimizzazione Multi Obiettivo
 Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA D ISTITUTO COMPETENZA CHIAVE EUROPEA DISCIPLINA
 ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0)
 PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0) (Da effettuare non prima del 01/01/2011) Le istruzioni si basano su un azienda che ha circa 1000 articoli, che utilizza l ultimo
PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0) (Da effettuare non prima del 01/01/2011) Le istruzioni si basano su un azienda che ha circa 1000 articoli, che utilizza l ultimo
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Gian Luca Marcialis studio degli algoritmi programma linguaggi LINGUAGGIO C
 Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
1 Principali funzioni e loro domini
 Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE
 Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Tutte le interrogazioni possono essere condotte su qualsiasi campo della banca dati (ad esempio, Forma, Frequenza, Lunghezza, ecc...).
 ESEMPIO DI QUERY SUL FILE Formario_minuscolo Tutte le interrogazioni possono essere condotte su qualsiasi campo della banca dati (ad esempio, Forma, Frequenza, Lunghezza, ecc...). Durante l interrogazione,
ESEMPIO DI QUERY SUL FILE Formario_minuscolo Tutte le interrogazioni possono essere condotte su qualsiasi campo della banca dati (ad esempio, Forma, Frequenza, Lunghezza, ecc...). Durante l interrogazione,
Ricerca Operativa e Logistica
 Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 20/202 Lezione 6-8 Rappresentazione di funzioni non lineari: - Costi fissi - Funzioni lineari a tratti Funzioni obiettivo non lineari:
Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 20/202 Lezione 6-8 Rappresentazione di funzioni non lineari: - Costi fissi - Funzioni lineari a tratti Funzioni obiettivo non lineari:
Parte II Indice. Operazioni aritmetiche tra valori rappresentati in binario puro. Rappresentazione di numeri con segno
 Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013
 Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Introduzione a Visual Basic Lezione 1 Concetti base e istruzioni condizionali
 a Visual Basic Lezione 1 Concetti base e istruzioni condizionali Mario Alviano Introduzione all informatica Università della Calabria http://alviano.net/introinfo A.A. 2008/09 Introduzione Un esempio:
a Visual Basic Lezione 1 Concetti base e istruzioni condizionali Mario Alviano Introduzione all informatica Università della Calabria http://alviano.net/introinfo A.A. 2008/09 Introduzione Un esempio:
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
L analisi dei dati. Capitolo 4. 4.1 Il foglio elettronico
 Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
USO DI EXCEL CLASSE PRIMAI
 USO DI EXCEL CLASSE PRIMAI In queste lezioni impareremo ad usare i fogli di calcolo EXCEL per l elaborazione statistica dei dati, per esempio, di un esperienza di laboratorio. Verrà nel seguito spiegato:
USO DI EXCEL CLASSE PRIMAI In queste lezioni impareremo ad usare i fogli di calcolo EXCEL per l elaborazione statistica dei dati, per esempio, di un esperienza di laboratorio. Verrà nel seguito spiegato:
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
