Elementi di Informatica e Programmazione
|
|
|
- Anna Maria Vitale
- 8 anni fa
- Visualizzazioni
Transcript
1 Elementi di Informatica e Programmazione La Codifica dell informazione (parte ) Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Premessa Nella prima lezione è stato presentato il concetto astratto di calcolatore: non com è fatto o come funziona, ma che cos è in sé Concetto di problema (classe di domande omogenee, alle quali si possa dare risposta con una procedura uniforme), istanza, soluzione Concetto di algoritmo (specifica attraverso una sequenza di istruzioni come produrre una soluzione per ogni istanza) Il calcolatore come esecutore universale di algoritmi Ora cominciamo a esaminare come in pratica i calcolatori attuali sono costruiti, quali sono le loro componenti e le rispettive funzioni Cominciamo da un sistema di elaborazione elementare Docente: Daniela Fogli Daniela Fogli Elementi di Informatica e Programmazione 2 Architettura di Von Neumann Funzionamento dell architettura di Von Neumann Si basa sui seguenti principi: ambiente NOTE: CPU = Central Processing Unit (Unità centrale) detta oggi Microprocessore o processore Dispositivi di I/O Bus di sistema CPU Memoria Dati e istruzioni del programma da eseguire sono memorizzati nella memoria centrale Il processore (CPU) legge e scrive in memoria per acquisire le istruzioni da eseguire e i relativi dati e per memorizzare i risultati delle istruzioni eseguite Le istruzioni vengono acquisite ed eseguite dalla CPU in modo sequenziale. Reperimento dell istruzione da eseguire 2. Interpretazione dell istruzione 3. Esecuzione dell istruzione Le singole operazioni necessarie per l esecuzione delle istruzioni sono scandite da un orologio di sistema (clock) che definisce l evolvere del tempo all interno della macchina Daniela Fogli Elementi di Informatica e Programmazione 3 Daniela Fogli Elementi di Informatica e Programmazione 4
2 Programma e dati in memoria Bus Indirizzo In memoria viene caricata la forma binaria del programma zona della memoria che contiene le istruzioni zona della memoria che contiene i dati Insieme di collegamenti (linee) che permettono di trasferire dati da più sorgenti a più destinazioni (componenti del calcolatore) Il bus può essere suddiviso funzionalmente in: Bus dati (trasferisce i dati scambiati tra componenti) Bus indirizzi (trasferisce gli indirizzi della memoria o delle interfacce di ingresso-uscita coinvolte nel trasferimento) Bus comandi o di controllo (trasferisce segnali di controllo che regolano le operazioni del sistema di elaborazione) zona libera MEMORIA NB: non distinguibili in sé, è il programma che ne stabilisce il significato fine della premessa Daniela Fogli Elementi di Informatica e Programmazione 5 Daniela Fogli Elementi di Informatica e Programmazione 6 Il concetto di informazione e supporto Informazione: entità che può essere comunicata Non può esistere informazione senza supporto fisico: mezzo su cui l informazione può essere memorizzata e attraverso cui può essere trasmessa... Programmi, dati, risultati, indirizzi sono informazioni Ora vediamo come si RAPPRESENTANO nel calcolatore Un brano musicale Il CD in cui è memorizzato L aria attraverso cui viene trasmesso Daniela Fogli Elementi di Informatica e Programmazione 7 Daniela Fogli Elementi di Informatica e Programmazione 8
3 Proprietà di un supporto Codice Il supporto deve poter assumere configurazioni differenti altrimenti non è in grado di portare informazione Ad ogni configurazione viene associata una differente entità di informazione Il caso più semplice: 2 configurazioni possibili Esempi: interruttore acceso/spento, tensione sì/no, circuito aperto/chiuso Elemento di informazione rappresentato dalla configurazione del supporto (es. soccorso sanitario: ) Associazione simboli-significati: convenzione semantica Es. di convenzione semantica alternativa: soccorso sanitario: Successione di simboli Attività di interpretazione E necessario un codice: un insieme di regole che stabiliscono le associazioni fra configurazioni e entità di informazione Entità di informazione Daniela Fogli Elementi di Informatica e Programmazione 9 Daniela Fogli Elementi di Informatica e Programmazione Esempio di codice Codifica e Decodifica Attraverso il codice si attribuisce un significato convenzionale a ciascuna configurazione che il supporto può assumere Codifica = operazione con cui l informazione viene scritta (su un supporto fisico) Decodifica = operazione con cui l informazione viene letta (da un supporto fisico) ES., 2 dadi lettera A codifica Il numero dieci Informazione lettera B. decodifica Supporto fisico Daniela Fogli Elementi di Informatica e Programmazione Daniela Fogli Elementi di Informatica e Programmazione 2
4 Codifica dei dati e delle istruzioni Codifica binaria Programma = istruzioni che operano su dati Istruzioni e dati devono essere rappresentate (codificate) secondo il linguaggio noto all esecutore L esecutore deve essere infatti in grado di memorizzare e manipolare istruzioni e dati Nel caso del calcolatore, istruzioni e dati vengono codificati come sequenze di e Poiché il nostro esecutore utilizza componenti a 2 soli stati, è in grado di riconoscere solamente sequenze di e Alfabeto binario = {, } dove e sono dette cifre binarie o BIT (Binary digit) Importanza tecnologica: Dispositivi a due stati (livelli di tensione, magnetizzazione, ) Semplicità di realizzazione Affidabilità Tutti i calcolatori elettronici e i dispositivi magnetici di memorizzazione utilizzano tale corrispondenza Daniela Fogli Elementi di Informatica e Programmazione 3 Daniela Fogli Elementi di Informatica e Programmazione 4 Bit, Byte, KiloByte, MegaByte,... Il problema della rappresentazione Bit = oppure Byte = 8 bit = 2 3 KiloByte (KB) = 2 byte =.24 byte MegaByte (MB) = 2 2 byte = byte GigaByte (GB) = 2 3 byte = byte TeraByte (TB) = 2 4 byte = PetaByte (PB) = 2 5 byte = ExaByte (EB) = 2 6 byte = Insieme di oggetti che vogliamo rappresentare Problema: assegnare un codice univoco a tutti gli oggetti compresi in un insieme Insieme di simboli disponibili nel calcolatore = {, } Ho n oggetti da codificare e 2 soli simboli, quanto è la lunghezza k delle sequenze di simboli? Oppure: dispongo di sequenze di lunghezza k di simboli e, quanto è il numero n di oggetti che posso codificare? Daniela Fogli Elementi di Informatica e Programmazione 5 Daniela Fogli Elementi di Informatica e Programmazione 6
5 Codice binario a n bit Funzione: - dominio (insieme di oggetti da rappresentare) - codominio: insieme di tutte le possibili sequenze di n bit Funzione biunivoca tra il dominio e la sua immagine, detta insieme delle codifiche Esempio di codice binario a 3 bit: O O 2 O 3 insieme delle codifiche Codifica binaria Se k = Posso codificare due oggetti (n=2): al primo assegno il codice e al secondo assegno il codice Se k = 2 Posso codificare n=4 oggetti:,,, Se k = 3 Posso codificare n=8 oggetti:,,,,,,, Qual è la regola???? (Ipotesi implicita: i codici hanno tutti la stessa lunghezza) dominio codominio Daniela Fogli Elementi di Informatica e Programmazione 7 Daniela Fogli Elementi di Informatica e Programmazione 8 n = 2 k k = log 2 n Esempio: i mesi dell anno Se ho a disposizione sequenze di k = 5 bit, quanti elementi posso codificare? n = 2 5 = 32 elementi Se n = 28, di quanti bit ho bisogno (k) per codificarli tutti? k = log 2 28 = 7 e se n = 29??? Allora ho bisogno di bit in più! Ottengo uno spreco di configurazioni, perché con 8 bit posso codificare fino a 256 elementi Gennaio Febbraio Marzo Aprile Maggio Giugno Luglio Agosto Settembre Ottobre Novembre Dicembre bit 2 gruppi Gennaio Febbraio Marzo Aprile Maggio Giugno Luglio Agosto Settembre Ottobre Novembre Dicembre Gennaio Febbraio Marzo Aprile Maggio Giugno Luglio Agosto Settembre Ottobre Novembre Dicembre 3 bit 8 gruppi 2 bit 4 gruppi Gennaio Febbraio Marzo Aprile Maggio Giugno Luglio Agosto Settembre Ottobre Novembre Dicembre Gennaio Febbraio Marzo Aprile Maggio Giugno Luglio Agosto Settembre Ottobre Novembre Dicembre 4 bit 6 gruppi mancano 4 configurazioni! Daniela Fogli Elementi di Informatica e Programmazione 9 Daniela Fogli Elementi di Informatica e Programmazione 2
6 Esempio: codifica BCD Tipologie di codici Cifra Codifica binaria decimale rappresentata b 3 b 2 b b codifiche non usate Nel seguito vedremo tipologie di rappresentazioni diverse: Senza assumere limitazioni sul numero di bit a disposizione: per numeri [notazione binaria, ovvero posizionale con base 2] Disponendo di un numero di bit limitato: numeri naturali interi relativi [valore assoluto e segno, compl. a, compl. a 2] reali [virgola fissa e virgola mobile] valori logici, caratteri alfabetici, testi suoni, immagini e sequenze video codici per la rilevazione e correzione di errori Codici di compressione (senza con perdita) Daniela Fogli Elementi di Informatica e Programmazione 2 Daniela Fogli Elementi di Informatica e Programmazione 22 Tipologie di codici Sistema di numerazione posizionale Nel seguito vedremo tipologie di rappresentazioni diverse: Senza assumere limitazioni sul numero di bit a disposizione: per numeri [notazione binaria, ovvero posizionale con base 2] Disponendo di un numero di bit limitato: numeri naturali interi relativi [valore assoluto e segno, compl. a, compl. a 2] reali [virgola fissa e virgola mobile] valori logici, caratteri alfabetici, testi suoni, immagini e sequenze video codici per la rilevazione e correzione di errori Codici di compressione (senza con perdita) Daniela Fogli Elementi di Informatica e Programmazione 23 Ad ogni cifra del numero è attribuito un peso a seconda della sua posizione all interno del numero Sistema di numerazione posizionale in base b: Numero N b = c k c k- c k-2 c.c - c -2 c c -h Dove c k è la cifra più significativa mentre c è la cifra meno significativa (prima della virgola) (c - è quella più significativa della parte frazionaria, c -h quella meno significativa) N b è il numero ottenuto facendo: c k xb k +c k- xb k- +c k-2 xb k-2 +c xb +c - xb - + +c -h xb -h Esempio: b=, il numero dove c 3 = 3, c 2 = 2, c = 5, c = 6, c - =2, c -2 =3, c -3 =4 rappresenta 3x 3 + 2x 2 + 5x + 6x + 2x - + 3x x -3 = = Daniela Fogli Elementi di Informatica e Programmazione 24
7 Le basi più comuni Notazione Binaria Base = 2 Cifre:, Se la base è b, allora le cifre che possono essere utilizzate per comporre un numero vanno da a b- Esempio: b =, cifre possibili: [,,2,3,4,5,6,7,8,9] Esempio: b = 2, cifre possibili: [,] Esempio: b = 8, cifre possibili: [,,2,3,4,5,6,7] Esempio: b = 6, cifre possibili: [,,2,3,4,5,6,7,8,9,A, B,C,D,E,F] Numeri espressi nella forma (a n a n- a a. a - a -2 ) due [a i {,}] il cui valore è (a n *2 n + a n- *2 n- + + a *2 + a - * a -2 *2-2 ) ESEMPIO N =. due N = = = dieci Daniela Fogli Elementi di Informatica e Programmazione 25 Daniela Fogli Elementi di Informatica e Programmazione 26 Conversione binario decimale Domande Come visto, la conversione si ottiene direttamente dalla definizione stessa di numero binario Scriviamo i numeri denotando la base attraverso il pedice: es.. due E facile convertirlo in un numero decimale facendo:. due = x2 3 + x2 2 + x2 + x2 + x2 - = 8 dieci + 4 dieci + dieci + + dieci +.5 dieci = 3.5 dieci Altri esempi:. due = x2 4 + x2 3 + x2 2 + x2 + x2 + x2 - + x2-2 = = 2.25 dieci. due = x2 5 + x2 4 + x2 3 + x2 2 + x2 + x2 + + x2-3 = = = 5.25 dieci due = x2 6 + x2 5 + x2 4 + x2 3 + x2 2 + x2 + x2 = 64 + = 65 dieci Il numero binario due è pari o dispari? A quale numero decimale corrisponde? due = (x2 8 + x2 7 + x2 6 + x2 5 + x2 4 + x2 3 + x2 2 + x2 + x2 ) dieci = ( ) dieci = 33 dieci Daniela Fogli Elementi di Informatica e Programmazione 27 Daniela Fogli Elementi di Informatica e Programmazione 28
8 Conversione decimale binario Conversione decimale binario metodo pratico Usare lo stesso metodo visto prima è complesso! 3 dieci dieci 2 dieci Esempio: 345 dieci = x + x + x = e poi bisogna fare le moltiplicazioni e l elevamento a potenza in base 2 e sommarne i risultati in base 2 Useremo un metodo pratico Dato un numero decimale N, innanzitutto distinguiamo parte intera e la parte frazionaria: N = I.F (ES: dato 56.5 dieci, convertiamo separatamente 56 e.5) Regola pratica per convertire la parte intera Si noti che: c k c k- c k-2 c si può scrivere anche come c k c k- c k-2 c xb+c Ad esempio: 3256 = 325x + 6 (in base b = dieci) 325 = 32x = 3x + 2 3=x + 3 In pratica, per isolare le cifre del numero, basta fare una serie di divisioni per la base e tenere il resto Alla fine, quando il numero è diventato, si leggono i resti dall ultimo al primo e si ottiene di nuovo il numero Daniela Fogli Elementi di Informatica e Programmazione 29 Daniela Fogli Elementi di Informatica e Programmazione 3 Conversione decimale binario metodo pratico Esempio di conversione da decimale a binario Allo stesso modo, per convertire un numero decimale in un numero binario basta fare una sequenza di divisioni (operazione div) per la base 2 e prendere il resto (operazione mod) Esempio: 56 div 2 = 28 & 56 mod 2 = (cifra meno significativa del numero bin) 28 div 2 = 4 & 28 mod 2 = 4 div 2 = 7 & 4 mod 2 = 7 div 2 = 3 & 7 mod 2 = 3 div 2 = & 3 mod 2 = div 2 = & mod 2 = (cifra più significativa del numero bin) 37 dieci =? due 37 div 2 = 68 & 37 mod 2 = 68 div 2 = 34 & 68 mod 2 = 34 div 2 = 7 & 34 mod 2 = 7 div 2 = 8 & 7 mod 2 = 8 div 2 = 4 & 8 mod 2 = 4 div 2 = 2 & 4 mod 2 = 2 div 2 = & 2 mod 2 = div 2 = & mod 2 = Si legge dal basso verso l alto!!! Si ottiene due = 32 dieci + 6 dieci + 8 dieci = 56 dieci Risultato = due Esercizio: riconvertire il risultato in decimale Daniela Fogli Elementi di Informatica e Programmazione 3 Daniela Fogli Elementi di Informatica e Programmazione 32
9 Errore Tipico () Errore Tipico (2) E un errore considerare la prima cifra ottenuta come la più significativa 5 2 otterrei che vale 69! E un errore fermarsi quando si ottiene come dividendo otterrei (24) anziché (64+24) NB: se si è colti dal dubbio, ragionare: se continuassi il procedimento di divisioni successive aggiungerei zeri; questi non pesano solo se corrispondono alle posizioni più significative ( xyz )! NB: se si è colti dal dubbio, ricordare che la prima cifra significativa in questo caso vale sempre Daniela Fogli Elementi di Informatica e Programmazione 33 Daniela Fogli Elementi di Informatica e Programmazione 34 Regola pratica per convertire la parte frazionaria Conversione da decimale a binario della parte frazionaria F = a - *b - + a -2 *b a -n *b -n (dove b è la base) F * b = a - + a -2 *b a -n *b -(n-) la parte intera è a - (F*b - a - ) * b = a a -n *b -(n-2) la parte intera è a Es. con b =, sia F= x = la parte intera è 5.3 x = 3 +. la parte intera è 3. x = la parte intera è Le 3 cifre che costituiscono il numero Ma a noi interessa che la base di arrivo sia la base 2 Basta fare una sequenza di moltiplicazioni per 2 e prendere la parte intera di ciascun prodotto dalla cifra più significativa a quella meno significativa Esempio:.587 dieci binario?.587 x 2 =.74: p.f..74, parte intera (cifra più significativa).74 x 2 =.348: p.f..348, parte intera.348 x 2 =.696: p.f..696, parte intera.696 x 2 =.392: p.f..392, parte intera.392 x 2 =.784: p.f..784, parte intera.784 x 2 =.568: p.f..568, parte intera. Si ottiene. due con 5 cifre binarie dopo la virgola, oppure. due con 6 cifre binarie dopo la virgola, oppure In ogni caso c è un approssimazione Daniela Fogli Elementi di Informatica e Programmazione 35 Daniela Fogli Elementi di Informatica e Programmazione 36
10 Esempio: convertire dieci in binario Operazioni aritmetiche x 2 p.i. Operazioni +, -, *, / su numeri in base x 2 p.i..748 x 2 p.i. Valgono le stesse regole e proprietà delle operazioni in base x 2 p.i x 2 p.i dieci =. due (fermandosi al quinto bit per la parte frazionaria) Daniela Fogli Elementi di Informatica e Programmazione 37 Daniela Fogli Elementi di Informatica e Programmazione 38 Aritmetica binaria: addizione Aritmetica binaria: sottrazione + () Riporto: + = 2 dieci = due Esempio: + 6 = 2 - () Prestito (borrow): 2 2 (= 2 ) = 2 Esempio: 4 = 3 Daniela Fogli Elementi di Informatica e Programmazione 39 Daniela Fogli Elementi di Informatica e Programmazione 4
11 Aritmetica binaria: moltiplicazione Altri esempi di operazioni aritmetiche in base 2 * Esempio: * 58 = 638 addizione + = sottrazione - = moltiplicazione = Esercizio: controllare se i risultati sono corretti convertendo in decimale Daniela Fogli Elementi di Informatica e Programmazione 4 Daniela Fogli Elementi di Informatica e Programmazione 42 Numeri in base 8 (ottali) Numeri in base 6 (esadecimali) Le cifre: [,, 2, 3, 4, 5, 6, 7] 7 otto =? dieci otto = dieci 7 otto = 7 dieci 7 otto = ( x x 8 ) dieci = (8 + 7) dieci = 5 dieci 372 otto =? dieci 372 otto = (3 x x x 8 ) dieci = (3 x ) dieci = 25 dieci Le cifre: [,, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F] 7D2 sedici =? dieci 7 sedici = 7 dieci D sedici = 3 dieci 2 sedici = 2 dieci 7D2 sedici = (7 x x x 6 ) dieci = (7 x ) dieci = ( ) dieci = 22 dieci FA sedici =? dieci F sedici = 5 dieci A sedici = dieci FA sedici = (5 x 6 + x 6 ) dieci = (24 + ) dieci = 25 dieci Daniela Fogli Elementi di Informatica e Programmazione 43 Daniela Fogli Elementi di Informatica e Programmazione 44
12 I primi 6 numeri in base, 2, 8, e 6 Perché le basi 2, 8 e 6? Sistema di numerazione decimale binario ottale esadecimale A 3 B 2 4 C 3 5 D 4 6 E 5 7 F La rappresentazione binaria ha motivazioni di tipo tecnologico Le rappresentazioni ottali ed esadecimali sono utili per rappresentare sinteticamente i valori binari E facile convertire un numero in base 2 in un numero in base 8 o 6 Le cifre binarie si possono raggruppare a 3 a 3 e poi codificare con numeri ottali Le cifre binarie si possono raggruppare a 4 a 4 e poi codificare con numeri esadecimali Daniela Fogli Elementi di Informatica e Programmazione 45 Daniela Fogli Elementi di Informatica e Programmazione 46 Conversione binario ottale Conversione binario esadecimale Tabella di conversione due otto due otto due 2 otto due 3 otto due 4 otto due 5 otto due 6 otto due 7 otto. due = otto Separazione a gruppi di tre cifre binarie a partire dalla meno significativa per la parte intera, e dalla più significativa per la parte frazionaria (dalla virgola!) Nel gruppo più significativo della parte intera si possono aggiungere degli zeri a sinistra, nel meno significativo della frazionaria zeri a destra Tabella di conversione due sedici due sedici due 2 sedici due 3 sedici due 4 sedici due 5 sedici due 6 sedici due 7 sedici due 8 sedici due 9 sedici due A sedici due B sedici due C sedici due D sedici due E sedici due F sedici due = 7 B 4 sedici Si procede nello stesso modo, ma separando le cifre a gruppi di 4 anziché di 3 Daniela Fogli Elementi di Informatica e Programmazione 47 Daniela Fogli Elementi di Informatica e Programmazione 48
13 Errore Tipico Esecuzione corretta Convertire in notazione ottale il numero binario. L esercizio quindi va risolto così: Invece = 5*64 + 6* /8 = che sicuramente non può essere rappresentato con una parte intera di soli 8 bit!!! PARTIRE SEMPRE DAL PUNTO DI RADICE, EVENTUALMENTE COMPLETANDO LE CIFRE CON DEGLI ZERI PER OTTENERE LE TERNE: xxx xxx. yyy yyy infatti risulta = 2*64 + 7* /8 = e. 2 = = Daniela Fogli Elementi di Informatica e Programmazione 49 Daniela Fogli Elementi di Informatica e Programmazione 5 Un altro esempio Esempi di conversione esadecimale-binario Convertire in binario il numero in notazione ottale ). 3 A ) E ERRORE TIPICO: CONVERTIRE IN. infatti. 8 = /8 =.25 mentre. 2 = /2 =.5 ATTENZIONE!!! PARTIRE SEMPRE DAL PUNTO DI RADICE!!! xxxx. xxxx xxxx Daniela Fogli Elementi di Informatica e Programmazione 5 Daniela Fogli Elementi di Informatica e Programmazione 52
14 Esercizio (in aula) Esercizio (in aula) Dato il numero binario due convertirlo in un numero ottale e poi in un numero esadecimale Convertire il numero ottale in numero decimale Numero ottale: 267 otto Numero esadecimale: 2B7 6 Numero decimale: 267 otto = (x x x8 + 7x8 ) dieci = ( ) dieci = 695 dieci Se la base considerata è b = 4, quali sono le cifre utilizzate per comporre i numeri? [,,2,3] Convertire il numero (32) quattro nel corrispondente numero in base 32 quattro = (x x x4 + x4 ) dieci = ( ) dieci = 2 dieci Qual è il numero massimo rappresentabile in base 3 con quattro cifre (espresso in base 3)? 2222 tre Daniela Fogli Elementi di Informatica e Programmazione 53 Daniela Fogli Elementi di Informatica e Programmazione 54 Esercizi. Convertire in formato decimale i seguenti numeri binari:,,,, 2. Convertire in decimale i seguenti numeri frazionari binari :.,.,. 3. Convertire in formato decimale i seguenti numeri ottali: 2, 23, 345, 333.4, Convertire in formato decimale i seguenti numeri esadecimali: 2.5, DAB, 5D, FFFF, 5A 5. Convertire in binario i seguenti numeri decimali (considerando 6 bit per la parte frazionaria): , , 67.72, Convertire in ottale e in esadecimale i numeri binari ottenuti dalla conversione dei numeri decimali di cui al punto precedente Daniela Fogli Elementi di Informatica e Programmazione 55
15 Elementi di Informatica e Programmazione La Codifica dell informazione (parte 2) Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Docente: Daniela Fogli Tipologie di codici Nel seguito vedremo tipologie di rappresentazioni diverse: Senza assumere limitazioni sul numero di bit a disposizione: per numeri [notazione binaria, ovvero posizionale con base 2] Disponendo di un numero di bit limitato: numeri naturali interi relativi [valore assoluto e segno, compl. a, compl. a 2] reali [virgola fissa e virgola mobile] valori logici, caratteri alfabetici, testi suoni, immagini e sequenze video codici per la rilevazione e correzione di errori Codici di compressione (senza con perdita) Daniela Fogli Elementi di Informatica e Programmazione 2 Codifica dei numeri naturali Nota I numeri naturali si rappresentano normalmente, ma con n cifre binarie possiamo rappresentare solo i numeri da a N max Esempio: con 8 cifre (n=8) Con n cifre binarie si possono rappresentare i numeri da a 2 n - Esempio precedente n = 8 N max = 2 n - = 256- = N max = 255 Daniela Fogli Elementi di Informatica e Programmazione 3 Daniela Fogli Elementi di Informatica e Programmazione 4
16 Viceversa In generale Voglio rappresentare i numeri naturali da a N max. Di quante cifre binarie ho bisogno? Esempio Voglio rappresentare numeri da a 35 con n = 7 N max = 27 con n = 8 N max = 255 con n = 9 N max = 5 n = 9 Per poter rappresentare numeri naturali fino a N, serve un numero di cifre n tali che: N max N ovvero (2 n ) N Quindi deve essere Esempio precedente N = 35 n log 2 (N + ) n log 2 (35) = 8,. quindi n 9 Daniela Fogli Elementi di Informatica e Programmazione 5 Daniela Fogli Elementi di Informatica e Programmazione 6 Operazioni aritmetiche Tipologie di codici Nel caso di addizione, ho traboccamento (overflow) quando ho un riporto dal bit più significativo che non può essere rappresentato con le cifre a disposizione + 4 = 2 ()? Nel caso di sottrazione, un prestito dal bit più significativo indica un risultato negativo (non rappresentabile) 2 = 3 () 5? Nel seguito vedremo tipologie di rappresentazioni diverse: Senza assumere limitazioni sul numero di bit a disposizione: per numeri [notazione binaria, ovvero posizionale con base 2] Disponendo di un numero di bit limitato: numeri naturali interi relativi [valore assoluto e segno, compl. a, compl. a 2] reali [virgola fissa e virgola mobile] valori logici, caratteri alfabetici, testi suoni, immagini e sequenze video codici per la rilevazione e correzione di errori Codici di compressione (senza con perdita) Daniela Fogli Elementi di Informatica e Programmazione 7 Daniela Fogli Elementi di Informatica e Programmazione 8
17 Codifica in valore assoluto e segno Codifica in valore assoluto e segno con 4 bit Il modo più semplice: indicare il segno seguito dal valore assoluto Se i bit disponibili per la codifica sono n si utilizza il primo bit della sequenza per indicare il segno ( per positivo e per negativo), e i restanti bit rappresentano il valore assoluto del numero Esempio: n = 8 (8 bit a disposizione) Rappresentazione di - segno - Numeri positivi Numeri negativi Daniela Fogli Elementi di Informatica e Programmazione 9 Daniela Fogli Elementi di Informatica e Programmazione Due note importanti Che problemi ha questa codifica? Esistono due codifiche per il valore + - I valori rappresentabili vanno: da - (2 n- - ) a + (2 n- - ) segno * * * * * * * n- bit: da a 2 n- - Questa tecnica non viene usata nel calcolatore Difficoltà nel fare le operazioni aritmetiche (es. la sottrazione) Es. (sottrazione di numeri entrambi positivi) a: b: - Dato che b > a, il segno del risultato è negativo, il valore assoluto è a-b: - = b a Daniela Fogli Elementi di Informatica e Programmazione Daniela Fogli Elementi di Informatica e Programmazione 2
18 Un altro esempio In generale Es. 2: Sottrazione di numeri entrambi positivi ma con a > b a: b: - Dato che a > b, il segno del risultato è positivo, il valore assoluto è - a = b Segno a Segno b segno(a-b) a-b + + a > b + a - b + + b > a - b - a a + b a + b - - a > b - a - b - - b > a + b - a Per il calcolatore le operazioni di somma e sottrazione sono complesse Si vuole una rappresentazione per la quale esista un unico semplice metodo per l addizione e la sottrazione a-b: +6 Daniela Fogli Elementi di Informatica e Programmazione 3 Daniela Fogli Elementi di Informatica e Programmazione 4 Codifica in complemento a Esempi Si ottiene facendo il complemento di tutti i bit (ovvero si sostituiscono gli con e gli con ) Es.: 5 dieci = due e 5 dieci = due Il bit più significativo indica se positivo o negativo I numeri positivi si rappresentano come nella rappresentazione in valore assoluto e segno I numeri negativi si rappresentano come complemento a del numero positivo corrispondente Ad esempio: n = 8 +2 dieci = due 2 dieci = due Anche questa volta il numero dieci ha due rappresentazioni: e Esercizio: n = dieci = due - 36 dieci =???????? due Daniela Fogli Elementi di Informatica e Programmazione 5 Daniela Fogli Elementi di Informatica e Programmazione 6
19 Operazioni aritmetiche Codifica in complemento a 2 La somma si ottiene facendo la somma degli addendi e poi sommando l eventuale riporto Esempi: dieci dieci = -28 dieci = -54 dieci () + () + = = -27 dieci +2 dieci Risultato OK Risultato ERRATO! (overflow) Sia n è il numero di bit utilizzati per la codifica I numeri positivi sono rappresentati normalmente (rappresentazione binaria dei numeri positivi) con il bit più significativo pari a I numeri negativi si ottengono come complemento a due del numero positivo x corrispondente, ovvero come 2 n x, e il bit più significativo è pari a Esempi (con n = 4): +6 dieci = (rappresentato normalmente) - 6 dieci = -6 dieci = c2 +3 dieci (rappresentato normalmente) - 3 dieci = 3-3 dieci = c2 E complicato? Somma più semplice ma con il problema di sommare il riporto Daniela Fogli Elementi di Informatica e Programmazione 7 Daniela Fogli Elementi di Informatica e Programmazione 8 Codifica in complemento a 2 con n=4 bit Due metodi pratici Bit di segno Numeri positivi Bit di segno Numeri negativi Unica rappresentazione del numero zero Esistono due metodi pratici equivalenti per calcolare il complemento a due di un numero x Metodo :. Effettuare il complemento a di x 2. Aggiungere Metodo 2:. Partendo da destra e andando verso sinistra, lasciare invariati tutti i bit fino al primo compreso 2. Complementare (invertire) tutti i bit successivi al primo NB: i numeri rappresentabili vanno da -2 n- (-8) a +(2 n- -) (+7) NB: il Metodo è quello utilizzato nei dispositivi elettronici Daniela Fogli Elementi di Informatica e Programmazione 9 Daniela Fogli Elementi di Informatica e Programmazione 2
20 Esempio di uso del metodo Esempio di uso dell algoritmo 2 Dato +6 dieci codificato su 4 bit Dato +6 dieci codificato su 4 bit Facendo il complemento a si ottiene Sommando al risultato si ottiene + = rimane invariato rimane invariato viene invertito viene invertito Risultato Daniela Fogli Elementi di Informatica e Programmazione 2 Daniela Fogli Elementi di Informatica e Programmazione 22 Altro esempio Errore Tipico A partire dalla codifica binaria di 5 dieci troviamo la codifica binaria di 5 dieci 5 dieci = nota 5 bit! Usando il primo metodo: complemento Aggiungo a Usando il secondo metodo: lascio invariato il primo a destra e complemento tutti gli altri ERRORE TIPICO: dimenticarsi che la rappresentazione in C.a 2 è relativa ad un numero di bit fissati!!! Es. Rappresentare in C. a 2 con 8 bit il numero decimale 3. 3 dieci = due quindi 3 dieci = due ma questo risulta un numero positivo!!! Svolgimento corretto: 3 dieci = due -3 dieci = Daniela Fogli Elementi di Informatica e Programmazione 23 Daniela Fogli Elementi di Informatica e Programmazione 24
21 Una visione globale Intervalli di rappresentazione: esempio Con n cifre si possono rappresentare 2 n numeri. Metà per i positivi e metà per i negativi, come in figura Rapp."normale n- - 2 n- (2 n- -) 2 3 C. A 2: 2 n - N Numeri positivi Numeri negativi NB: i numeri rappresentabili vanno da -2 n- a +(2 n- -) Supponiamo di avere una codifica con n=6 bit Rappresentazione in valore assoluto e segno: numeri compresi fra (2 5 -) e 2 5 -, ovvero fra e lo ha due rappresentazioni Rappresentazione in complemento a : numeri compresi fra (2 5 - ) e 2 5 -, ovvero fra e lo ha due rappresentazioni Rappresentazione in complemento a 2: numeri compresi fra 2 5 e 2 5 -, ovvero fra e lo ha una sola rappresentazione (in pratica, però, tipicamente si utilizzano i valori fra e per simmetria, così dato un qualsiasi numero anche il suo opposto è rappresentabile) Daniela Fogli Elementi di Informatica e Programmazione 25 Daniela Fogli Elementi di Informatica e Programmazione 26 Conversione da numero binario in complemento a 2 a numero decimale Altri esempi Si può usare la simmetria dell operazione in compl. a 2 Esempio: due è un numero negativo, pari a = -63 dieci Oppure si può usare la seguente regola: il valore di un numero c k c k- c c rappresentato in complemento a due è dato dalla seguente espressione -c k x2 k + c k- x2 k- + + c x2 + c x2 = -x2 4 + x2 = -6 + = -5 dieci = -x2 3 + x2 = = -6 dieci = -x2 7 + x2 5 + x2 3 + x2 = = -86 Esercizio proposto: ricavare il valore decimale col metodo della simmetria Esempio: due = (-)x2 6 + x2 = = - 63 dieci Daniela Fogli Elementi di Informatica e Programmazione 27 Daniela Fogli Elementi di Informatica e Programmazione 28
Elementi di Informatica e Programmazione
 Elementi di Informatica e Programmazione La Codifica dell informazione (parte 1) Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Docente:
Elementi di Informatica e Programmazione La Codifica dell informazione (parte 1) Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Docente:
Informazione analogica e digitale
 L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
Sistemi di Numerazione Binaria NB.1
 Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
Sistemi di Numerazione Binaria NB.1 Numeri e numerali Numero: entità astratta Numerale : stringa di caratteri che rappresenta un numero in un dato sistema di numerazione Lo stesso numero è rappresentato
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
CODIFICA DELL INFORMAZIONE E CODICI BINARI
 Codifica dell informazione 1 CODIFICA DELL INFORMAZIONE E CODICI BINARI Andrea Bobbio Anno Accademico 2001-2002 Codifica dell informazione 2 La codifica dell informazione I sistemi di elaborazione operano
Codifica dell informazione 1 CODIFICA DELL INFORMAZIONE E CODICI BINARI Andrea Bobbio Anno Accademico 2001-2002 Codifica dell informazione 2 La codifica dell informazione I sistemi di elaborazione operano
Informatica B a.a 2005/06 (Meccanici 4 squadra) PhD. Ing. Michele Folgheraiter
 Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
RAPPRESENTAZIONE BINARIA DEI NUMERI. Andrea Bobbio Anno Accademico 1996-1997
 1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
L'informazione e la sua codifica
 L'informazione e la sua codifica Corso di Informatica CdL: Chimica Claudia d'amato claudia.damato@di.uniba.it Informatica e telecomunicazione Cos è l informatica informatica? lo studio sistematico degli
L'informazione e la sua codifica Corso di Informatica CdL: Chimica Claudia d'amato claudia.damato@di.uniba.it Informatica e telecomunicazione Cos è l informatica informatica? lo studio sistematico degli
Codifica binaria dei numeri
 Codifica binaria dei numeri Caso più semplice: in modo posizionale (spesso detto codifica binaria tout court) Esempio con numero naturale: con 8 bit 39 = Codifica in virgola fissa dei numeri float: si
Codifica binaria dei numeri Caso più semplice: in modo posizionale (spesso detto codifica binaria tout court) Esempio con numero naturale: con 8 bit 39 = Codifica in virgola fissa dei numeri float: si
Sistemi di Numerazione
 Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione
 Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione Fondamenti di Informatica Michele Ceccarelli Università del Sannio ceccarelli@unisannio.it Angelo Ciaramella DMI-Università degli
Esempi ed esercizi Aritmetica degli elaboratori e algebra di commutazione Fondamenti di Informatica Michele Ceccarelli Università del Sannio ceccarelli@unisannio.it Angelo Ciaramella DMI-Università degli
(71,1), (35,1), (17,1), (8,1), (4,0), (2,0), (1,0), (0,1) 0, 7155 2 = 1, 431 0, 431 2 = 0, 862 0, 896 2 = 1, 792 0, 724 2 = 1, 448 0, 448 2 = 0, 896
 2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
2. Codifica dell informazione
 2. Codifica dell informazione Codifica Una codifica è una regola per associare in modo univoco i valori di un dato da codificare con sequenze di simboli. La corrispondenza definita dalla codifica è arbitraria,
2. Codifica dell informazione Codifica Una codifica è una regola per associare in modo univoco i valori di un dato da codificare con sequenze di simboli. La corrispondenza definita dalla codifica è arbitraria,
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Logica e codifica binaria dell informazione
 Politecnico di Milano Corsi di Laurea in Ingegneria Matematica e Ingegneria Fisica Dipartimento di Elettronica ed Informazione Logica e codifica binaria dell informazione Anno Accademico 2002 2003 L. Muttoni
Politecnico di Milano Corsi di Laurea in Ingegneria Matematica e Ingegneria Fisica Dipartimento di Elettronica ed Informazione Logica e codifica binaria dell informazione Anno Accademico 2002 2003 L. Muttoni
Rappresentazione dei numeri in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
CODIFICA BINARIA. ... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità.
 I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
Laboratorio di Informatica
 per chimica industriale e chimica applicata e ambientale LEZIONE 2 Rappresentazione delle informazioni: numeri e caratteri 1 Codice La relazione che associa ad ogni successione ben formata di simboli di
per chimica industriale e chimica applicata e ambientale LEZIONE 2 Rappresentazione delle informazioni: numeri e caratteri 1 Codice La relazione che associa ad ogni successione ben formata di simboli di
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri
 Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Obiettivi dell Analisi Numerica. Avviso. Risoluzione numerica di un modello. Analisi Numerica e Calcolo Scientifico
 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Appunti di informatica. Lezione 2 anno accademico 2015-2016 Mario Verdicchio
 Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Appunti di informatica Lezione 2 anno accademico 2015-2016 Mario Verdicchio Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento
Rappresentazione binaria
 Rappresentazione binaria DOTT. ING. LEONARDO RIGUTINI RICERCATORE ASSOCIATO DIPARTIMENTO INGEGNERIA DELL INFORMAZIONE UNIVERSITÀ DI SIENA VIA ROMA 56 53100 SIENA UFF. 0577234850-7102 RIGUTINI@DII.UNISI.IT
Rappresentazione binaria DOTT. ING. LEONARDO RIGUTINI RICERCATORE ASSOCIATO DIPARTIMENTO INGEGNERIA DELL INFORMAZIONE UNIVERSITÀ DI SIENA VIA ROMA 56 53100 SIENA UFF. 0577234850-7102 RIGUTINI@DII.UNISI.IT
Codifica binaria e algebra di Boole
 Codifica binaria e algebra di Boole Corso di Programmazione A.A. 2008/09 G. Cibinetto Contenuti della lezione Codifica binaria dell informazione Numeri naturali, interi, frazionari, in virgola mobile Base
Codifica binaria e algebra di Boole Corso di Programmazione A.A. 2008/09 G. Cibinetto Contenuti della lezione Codifica binaria dell informazione Numeri naturali, interi, frazionari, in virgola mobile Base
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Informatica. Rappresentazione binaria Per esempio +101010000 diventa +0.10101 10 18/10/2007. Introduzione ai sistemi informatici 1
 Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
Informatica Pietro Storniolo storniolo@csai.unipa.it http://www.pa.icar.cnr.it/storniolo/info200708 Numeri razionali Cifre più significative: : sono le cifre associate ai pesi maggiori per i numeri maggiori
Rappresentazione dell informazione Codifica Binaria
 Fondamenti di Informatica Rappresentazione dell informazione Codifica Binaria Fondamenti di Informatica - D. Talia - UNICAL 1 Rappresentazione dell informazione Tutta l'informazione in un calcolatore è
Fondamenti di Informatica Rappresentazione dell informazione Codifica Binaria Fondamenti di Informatica - D. Talia - UNICAL 1 Rappresentazione dell informazione Tutta l'informazione in un calcolatore è
Codifica dei numeri negativi
 E. Calabrese: Fondamenti di Informatica Rappresentazione numerica-1 Rappresentazione in complemento a 2 Codifica dei numeri negativi Per rappresentare numeri interi negativi si usa la cosiddetta rappresentazione
E. Calabrese: Fondamenti di Informatica Rappresentazione numerica-1 Rappresentazione in complemento a 2 Codifica dei numeri negativi Per rappresentare numeri interi negativi si usa la cosiddetta rappresentazione
la scienza della rappresentazione e della elaborazione dell informazione
 Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013
 Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
2.12 Esercizi risolti
 Codifica dell'informazione 55 Lo standard IEEE prevede cinque cause di eccezione aritmetica: underflow, overflow, divisione per zero, eccezione per inesattezza, e eccezione di invalidità. Le eccezioni
Codifica dell'informazione 55 Lo standard IEEE prevede cinque cause di eccezione aritmetica: underflow, overflow, divisione per zero, eccezione per inesattezza, e eccezione di invalidità. Le eccezioni
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE. Lez2 Informatica Sc. Giuridiche Op. aritmetiche/logiche arch.
 Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
Rappresentazione di informazioni con un alfabeto finito
 Rappresentazione di informazioni con un alfabeto finito Sia A = { a 1,, a k } un insieme (alfabeto) di k simboli, detti anche lettere. Quante sono le sequenze composte da n simboli (anche ripetuti) di
Rappresentazione di informazioni con un alfabeto finito Sia A = { a 1,, a k } un insieme (alfabeto) di k simboli, detti anche lettere. Quante sono le sequenze composte da n simboli (anche ripetuti) di
Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2
 Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2 1 Dott. Pasquale De Michele Dipartimento di Matematica e Applicazioni Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via
Lez. 3 L elaborazione (II parte) Prof. Pasquale De Michele Gruppo 2 1 Dott. Pasquale De Michele Dipartimento di Matematica e Applicazioni Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio
 Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio Rappresentazione dell Informazione
Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio Rappresentazione dell Informazione
Informatica Generale 02 - Rappresentazione numeri razionali
 Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
Informatica Generale 02 - Rappresentazione numeri razionali Cosa vedremo: Rappresentazione binaria dei numeri razionali Rappresentazione in virgola fissa Rappresentazione in virgola mobile La rappresentazione
APPUNTI DI ELETTRONICA DIGITALE
 APPUNTI DI ELETTRONICA DIGITALE ITIS MARCONI-GORGONZOLA docente :dott.ing. Paolo Beghelli pag.1/24 Indice 1.ELETTRONICA DIGITALE 4 1.1 Generalità 4 1.2 Sistema di numerazione binario 4 1.3 Operazioni con
APPUNTI DI ELETTRONICA DIGITALE ITIS MARCONI-GORGONZOLA docente :dott.ing. Paolo Beghelli pag.1/24 Indice 1.ELETTRONICA DIGITALE 4 1.1 Generalità 4 1.2 Sistema di numerazione binario 4 1.3 Operazioni con
la scienza della rappresentazione e della elaborazione dell informazione
 Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri.
 Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri. A partire da questa lezione, ci occuperemo di come si riescono a codificare con sequenze binarie, quindi con sequenze di 0 e 1,
Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri. A partire da questa lezione, ci occuperemo di come si riescono a codificare con sequenze binarie, quindi con sequenze di 0 e 1,
Rappresentazione delle informazioni
 Rappresentazione delle informazioni Abbiamo informazioni (numeri, caratteri, immagini, suoni, video... ) che vogliamo rappresentare (e poter elaborare) in un calcolatore. Per motivi tecnologici un calcolatore
Rappresentazione delle informazioni Abbiamo informazioni (numeri, caratteri, immagini, suoni, video... ) che vogliamo rappresentare (e poter elaborare) in un calcolatore. Per motivi tecnologici un calcolatore
Un ripasso di aritmetica: Rappresentazione binaria - operazioni. riporti
 Un ripasso di aritmetica: Rappresentazione binaria - operazioni A queste rappresentazioni si possono applicare le operazioni aritmetiche: riporti 1 1 0 + 1 0 = 1 0 0 24 Un ripasso di aritmetica: Rappresentazione
Un ripasso di aritmetica: Rappresentazione binaria - operazioni A queste rappresentazioni si possono applicare le operazioni aritmetiche: riporti 1 1 0 + 1 0 = 1 0 0 24 Un ripasso di aritmetica: Rappresentazione
Parte II Indice. Operazioni aritmetiche tra valori rappresentati in binario puro. Rappresentazione di numeri con segno
 Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Parte II Indice Operazioni aritmetiche tra valori rappresentati in binario puro somma sottrazione Rappresentazione di numeri con segno modulo e segno complemento a 2 esercizi Operazioni aritmetiche tra
Codifica binaria dei numeri relativi
 Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
11010010 = 1*2^7 + 1*2^6 + 0*2^5 + 1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 210
 Il sistema BINARIO e quello ESADECIMALE. Il sistema di numerazione binario è particolarmente legato ai calcolatori in quanto essi possono riconoscere solo segnali aventi due valori: uno alto e uno basso;
Il sistema BINARIO e quello ESADECIMALE. Il sistema di numerazione binario è particolarmente legato ai calcolatori in quanto essi possono riconoscere solo segnali aventi due valori: uno alto e uno basso;
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica Dispensa 05 La rappresentazione dell informazione Carla Limongelli Ottobre 2011 http://www.dia.uniroma3.it/~java/fondinf/ La rappresentazione
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica Dispensa 05 La rappresentazione dell informazione Carla Limongelli Ottobre 2011 http://www.dia.uniroma3.it/~java/fondinf/ La rappresentazione
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Esercitazioni su rappresentazione dei numeri e aritmetica dei calcolatori"
 Esercitazioni su rappresentazione dei numeri e aritmetica dei calcolatori" slide a cura di Salvatore Orlando & Marta Simeoni " Architettura degli Elaboratori 1 Interi unsigned in base 2" Si utilizza un
Esercitazioni su rappresentazione dei numeri e aritmetica dei calcolatori" slide a cura di Salvatore Orlando & Marta Simeoni " Architettura degli Elaboratori 1 Interi unsigned in base 2" Si utilizza un
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
Elementi di Informatica. ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale
 Elementi di Informatica ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale Il sistema di numerazione posizionale decimale Nella numerazione posizionale ogni cifra del numero
Elementi di Informatica ( Lezione II, parte I ) Sistemi di numerazione: binario, ottale ed esadecimale Il sistema di numerazione posizionale decimale Nella numerazione posizionale ogni cifra del numero
PROVA INTRACORSO TRACCIA A Pagina 1 di 6
 PROVA INTRACORSO DI ELEMENTI DI INFORMATICA MATRICOLA COGNOME E NOME TRACCIA A DOMANDA 1 Calcolare il risultato delle seguenti operazioni binarie tra numeri interi con segno rappresentati in complemento
PROVA INTRACORSO DI ELEMENTI DI INFORMATICA MATRICOLA COGNOME E NOME TRACCIA A DOMANDA 1 Calcolare il risultato delle seguenti operazioni binarie tra numeri interi con segno rappresentati in complemento
Calcolatori: Algebra Booleana e Reti Logiche
 Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
La codifica delle informazioni
 La codifica delle informazioni Bit e byte Come già visto l elaboratore è in grado di rappresentare informazioni al proprio interno solo utilizzando cifre binarie (bit) che solitamente vengono manipolate
La codifica delle informazioni Bit e byte Come già visto l elaboratore è in grado di rappresentare informazioni al proprio interno solo utilizzando cifre binarie (bit) che solitamente vengono manipolate
Esercitazione Informatica I AA 2012-2013. Nicola Paoletti
 Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Esercitazione Informatica I AA 2012-2013 Nicola Paoletti 4 Gigno 2013 2 Conversioni Effettuare le seguenti conversioni, tenendo conto del numero di bit con cui si rappresenta il numero da convertire/convertito.
Esercizi. Esercizi sulla codifica (Parte 1) Elementi di Informatica e Programmazione. Soluzioni degli esercizi Esercizio 2
 Esercizi sulla codifica (Parte 1) Elementi di Informatica e Programmazione Docente: Dr. Daniela Fogli Esercizi 1. Convertire in formato decimale i seguenti numeri binari: 11, 101011, 1100, 111111, 10101010
Esercizi sulla codifica (Parte 1) Elementi di Informatica e Programmazione Docente: Dr. Daniela Fogli Esercizi 1. Convertire in formato decimale i seguenti numeri binari: 11, 101011, 1100, 111111, 10101010
Un ripasso di aritmetica: Conversione dalla base 10 alla base 16
 Un ripasso di aritmetica: Conversione dalla base 1 alla base 16 Dato un numero N rappresentato in base dieci, la sua rappresentazione in base sedici sarà del tipo: c m c m-1... c 1 c (le c i sono cifre
Un ripasso di aritmetica: Conversione dalla base 1 alla base 16 Dato un numero N rappresentato in base dieci, la sua rappresentazione in base sedici sarà del tipo: c m c m-1... c 1 c (le c i sono cifre
 Andrea Bobbio CODIFICA DELL'INFORMAZIONE E CODICI BINARI Anno Accademico 1996-1997 1 Codiæca dell'informazione 2 La codiæca dell'informazione sistemi di elaborazione operano al loro interno soltanto I
Andrea Bobbio CODIFICA DELL'INFORMAZIONE E CODICI BINARI Anno Accademico 1996-1997 1 Codiæca dell'informazione 2 La codiæca dell'informazione sistemi di elaborazione operano al loro interno soltanto I
Parte 1. Vettori di bit - AA. 2012/13 1.1
 1.1 Parte 1 Vettori di bit 1.2 Notazione posizionale Ogni cifra assume un significato diverso a seconda della posizione in cui si trova Rappresentazione di un numero su n cifre in base b: Posizioni a n
1.1 Parte 1 Vettori di bit 1.2 Notazione posizionale Ogni cifra assume un significato diverso a seconda della posizione in cui si trova Rappresentazione di un numero su n cifre in base b: Posizioni a n
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione dell informazione negli elaboratori
 Informazione e computer Si può rappresentare l informazione attraverso varie forme: Numeri Testi Suoni Immagini 0001010010100101010 Computer Cerchiamo di capire come tutte queste informazioni possano essere
Informazione e computer Si può rappresentare l informazione attraverso varie forme: Numeri Testi Suoni Immagini 0001010010100101010 Computer Cerchiamo di capire come tutte queste informazioni possano essere
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE
 Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
La codifica dell informazione
 La codifica dell informazione Parte I Sui testi di approfondimento: leggere dal Cap. del testo C (Console, Ribaudo):.,. fino a pg.6 La codifica delle informazioni Un calcolatore memorizza ed elabora informazioni
La codifica dell informazione Parte I Sui testi di approfondimento: leggere dal Cap. del testo C (Console, Ribaudo):.,. fino a pg.6 La codifica delle informazioni Un calcolatore memorizza ed elabora informazioni
4. Operazioni aritmetiche con i numeri binari
 I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
Sistemi di numerazione: generalità
 Sistemi di numerazione: generalità Nel corso della storia sono stati introdotti diversi sistemi di numerazione, dettati di volta in volta dalle specifiche esigenze dei vari popoli. Poiché ogni numero maggiore
Sistemi di numerazione: generalità Nel corso della storia sono stati introdotti diversi sistemi di numerazione, dettati di volta in volta dalle specifiche esigenze dei vari popoli. Poiché ogni numero maggiore
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO
 SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
SISTEMI DI NUMERAZIONE DECIMALE E BINARIO Il sistema di numerazione decimale (o base dieci) possiede dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) utili a rappresentare i numeri. Le cifre possiedono
Fondamenti di Informatica
 Università degli Studi di Messina Facolta di Ingegneria - 98100 Messina Tel. (090) 393229 - Fax (090) 393502 Fondamenti di Informatica Ing. delle Tecnologie Industriali Docente: Ing. Mirko Guarnera 1 Sistemi
Università degli Studi di Messina Facolta di Ingegneria - 98100 Messina Tel. (090) 393229 - Fax (090) 393502 Fondamenti di Informatica Ing. delle Tecnologie Industriali Docente: Ing. Mirko Guarnera 1 Sistemi
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Tipi di dato-prima parte
 Corso di Fondamenti di Informatica Corso di Laurea in Ingegneria Meccanica (A-K) Tipi di dato-prima parte Ing. Agnese Pinto 1 di 15 Tipi di dato Sommario Tipi di dato Classificazione dei tipi di dato Tipi
Corso di Fondamenti di Informatica Corso di Laurea in Ingegneria Meccanica (A-K) Tipi di dato-prima parte Ing. Agnese Pinto 1 di 15 Tipi di dato Sommario Tipi di dato Classificazione dei tipi di dato Tipi
Informazione binaria: caratteri e testi suoni, immagini, sequenze video
 Informazione binaria: caratteri e testi suoni, immagini, sequenze video Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Tipologie di codici
Informazione binaria: caratteri e testi suoni, immagini, sequenze video Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Tipologie di codici
SISTEMI DI NUMERAZIONE IL SISTEMA DECIMALE
 SISTEMI DI NUMERAZIONE IL SISTEMA DECIMALE La base del sistema decimale è 10 I simboli del sistema decimale sono: 0 1 2 3 4 5 6 7 8 9 Il sistema di numerazione decimale è un sistema posizionale. L aggettivo
SISTEMI DI NUMERAZIONE IL SISTEMA DECIMALE La base del sistema decimale è 10 I simboli del sistema decimale sono: 0 1 2 3 4 5 6 7 8 9 Il sistema di numerazione decimale è un sistema posizionale. L aggettivo
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Variabili e tipi di dato
 Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
ESERCIZI di FONDAMENTI DI INFORMATICA RAPPRESENTAZIONE DEI NUMERI
 ESERCIZI di FONDAMENTI DI INFORMATICA RAPPRESENTAZIONE DEI NUMERI Esercizio 1 Indicare come un elaboratore effettua la seguente operazione, supponendo di operare con numeri interi rappresentati in complemento
ESERCIZI di FONDAMENTI DI INFORMATICA RAPPRESENTAZIONE DEI NUMERI Esercizio 1 Indicare come un elaboratore effettua la seguente operazione, supponendo di operare con numeri interi rappresentati in complemento
Sommario. Addizione naturale
 Sommario Introduzione Rappresentazione dei numeri interi positivi Rappresentazione dei numeri interi Operazioni aritmetiche Modulo e segno Addizione e sottrazione urale Addizione e sottrazione in complemento
Sommario Introduzione Rappresentazione dei numeri interi positivi Rappresentazione dei numeri interi Operazioni aritmetiche Modulo e segno Addizione e sottrazione urale Addizione e sottrazione in complemento
Codifica delle Informazioni
 Codifica delle Informazioni Luca Bortolussi Dipartimento di Matematica e Informatica Università degli studi di Trieste Panoramica Le informazioni gestite dai sistemi di elaborazione devono essere codificate
Codifica delle Informazioni Luca Bortolussi Dipartimento di Matematica e Informatica Università degli studi di Trieste Panoramica Le informazioni gestite dai sistemi di elaborazione devono essere codificate
Memorie ROM (Read Only Memory)
 Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
Definizioni iniziali
 Fondamenti di Informatica: Codifica Binaria dell Informazione 1 Definizioni iniziali BIT: unita elementare di informazione Due soli valori: 0 e 1 Byte: sequenza di 8 bit Fondamenti di Informatica: Codifica
Fondamenti di Informatica: Codifica Binaria dell Informazione 1 Definizioni iniziali BIT: unita elementare di informazione Due soli valori: 0 e 1 Byte: sequenza di 8 bit Fondamenti di Informatica: Codifica
Aritmetica dei Calcolatori 1
 Architettura degli Elaboratori e Laboratorio 1 Marzo 2013 1 Sistema di numerazione sistema posizionale 2 rappresentazione binaria cambio di base basi potenze di 2 3 Rappresentazione binaria con segno Sistema
Architettura degli Elaboratori e Laboratorio 1 Marzo 2013 1 Sistema di numerazione sistema posizionale 2 rappresentazione binaria cambio di base basi potenze di 2 3 Rappresentazione binaria con segno Sistema
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
IL CODICE BINARIO. Il codice binario. Codifica posizionale. Aritmetica binaria
 IL CODICE BINARIO Il codice binario Codifica posizionale Aritmetica binaria www.stoianov.it 1 CODIFICA DI BASE La voce si distribuisce con onde di frequenze 20-20.000 Hz La luce sta nel ordine di 500.000.000.000.000
IL CODICE BINARIO Il codice binario Codifica posizionale Aritmetica binaria www.stoianov.it 1 CODIFICA DI BASE La voce si distribuisce con onde di frequenze 20-20.000 Hz La luce sta nel ordine di 500.000.000.000.000
Fondamenti di Informatica 2. Le operazioni binarie
 Corso di per il corso di Laurea di Ingegneria Gestionale Le operazioni binarie Università degli Studi di Udine - A.A. 2010-2011 Docente Ing. Sandro Di Giusto Ph.D. 1 L'algebra binaria Il fatto di aver
Corso di per il corso di Laurea di Ingegneria Gestionale Le operazioni binarie Università degli Studi di Udine - A.A. 2010-2011 Docente Ing. Sandro Di Giusto Ph.D. 1 L'algebra binaria Il fatto di aver
Appunti sulla rappresentazione dell informazione
 Appunti sulla rappresentazione dell informazione Roberto Beraldi DISPENSA PER IL CORSO DI FONDAMENTI DI INFORMATICA CORSI DI LAUREA IN INGEGNERIA CHIMICA, DEI MATERIALI,NUCLEARE (vecchi ordinamenti) Anno
Appunti sulla rappresentazione dell informazione Roberto Beraldi DISPENSA PER IL CORSO DI FONDAMENTI DI INFORMATICA CORSI DI LAUREA IN INGEGNERIA CHIMICA, DEI MATERIALI,NUCLEARE (vecchi ordinamenti) Anno
Architettura (10/9/2003) Pag. 1/6. Cognome e Nome (in stampatello):
 Architettura (10/9003) Pag. 1/6 Esame di Architettura (matr.0-1) del 10/9003 Per Fondamenti di Architettura NON rispondere Per le domande a risposta multipla cerchiare la risposta scelta. Non alle domande
Architettura (10/9003) Pag. 1/6 Esame di Architettura (matr.0-1) del 10/9003 Per Fondamenti di Architettura NON rispondere Per le domande a risposta multipla cerchiare la risposta scelta. Non alle domande
C. P. U. MEMORIA CENTRALE
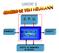 C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
LA NUMERAZIONE BINARIA
 LA NUMERAZIONE BINARIA 5 I SISTEMI DI NUMERAZIONE Fin dalla preistoria l uomo ha avuto la necessità di fare calcoli, utilizzando svariati tipi di dispositivi: manuali (mani, bastoncini, sassi, abaco),
LA NUMERAZIONE BINARIA 5 I SISTEMI DI NUMERAZIONE Fin dalla preistoria l uomo ha avuto la necessità di fare calcoli, utilizzando svariati tipi di dispositivi: manuali (mani, bastoncini, sassi, abaco),
Base generica: B A = {... }, con A = B, sequenze di n simboli (cifre) c n
 Rappresentare le informazioni con un insieme limitato di simboli (detto alfabeto A) in modo non ambiguo (algoritmi di traduzione tra codifiche) Esempio: numeri interi assoluti Codifica decimale (in base
Rappresentare le informazioni con un insieme limitato di simboli (detto alfabeto A) in modo non ambiguo (algoritmi di traduzione tra codifiche) Esempio: numeri interi assoluti Codifica decimale (in base
ALGEBRA BOOLEANA FONDAMENTI DI INFORMATICA 1. Algebra di Boole. Definizione NOT, AND, OR
 Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica, Chimica, Elettrica e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011 Docente: Gian
Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica, Chimica, Elettrica e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011 Docente: Gian
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Numerazione binaria e rappresentazione delle informazioni
 Numerazione binaria e rappresentazione delle informazioni Info Sito del corso: http://home.dei.polimi.it/amigoni/informaticab.html Nicola Basilico, nicola.basilico@gmail.com Problema Abbiamo informazioni
Numerazione binaria e rappresentazione delle informazioni Info Sito del corso: http://home.dei.polimi.it/amigoni/informaticab.html Nicola Basilico, nicola.basilico@gmail.com Problema Abbiamo informazioni
Università degli Studi di Ferrara Corso di Laurea in Informatica A.A. 2007/2008
 Università degli Studi di Ferrara Corso di Laurea in Informatica A.A. 2007/2008 Tutorato di Architettura degli Elaboratori e Laboratorio Cambio di base Operazioni binarie Dott.ssa Ambra Giovannini 15 Aprile
Università degli Studi di Ferrara Corso di Laurea in Informatica A.A. 2007/2008 Tutorato di Architettura degli Elaboratori e Laboratorio Cambio di base Operazioni binarie Dott.ssa Ambra Giovannini 15 Aprile
Materiale di approfondimento: numeri interi relativi in complemento a uno
 Materiale di approfondimento: numeri interi relativi in complemento a uno Federico Cerutti AA. 2011/2012 Modulo di Elementi di Informatica e Programmazione http://apollo.ing.unibs.it/fip/ 2011 Federico
Materiale di approfondimento: numeri interi relativi in complemento a uno Federico Cerutti AA. 2011/2012 Modulo di Elementi di Informatica e Programmazione http://apollo.ing.unibs.it/fip/ 2011 Federico
Fondamenti di Informatica Ingegneria Clinica Lezione 19/11/2009. Prof. Raffaele Nicolussi
 Fondamenti di Informatica Ingegneria Clinica Lezione 19/11/2009 Prof. Raffaele Nicolussi FUB - Fondazione Ugo Bordoni Via B. Castiglione 59-00142 Roma Docente Raffaele Nicolussi rnicolussi@fub.it Lezioni
Fondamenti di Informatica Ingegneria Clinica Lezione 19/11/2009 Prof. Raffaele Nicolussi FUB - Fondazione Ugo Bordoni Via B. Castiglione 59-00142 Roma Docente Raffaele Nicolussi rnicolussi@fub.it Lezioni
Modulo 8. Elettronica Digitale. Contenuti: Obiettivi:
 Modulo 8 Elettronica Digitale Contenuti: Introduzione Sistemi di numerazione posizionali Sistema binario Porte logiche fondamentali Porte logiche universali Metodo della forma canonica della somma per
Modulo 8 Elettronica Digitale Contenuti: Introduzione Sistemi di numerazione posizionali Sistema binario Porte logiche fondamentali Porte logiche universali Metodo della forma canonica della somma per
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
