e n (x) = e(x) n = e iωnx e, naturalmente,
|
|
|
- Lelio Nigro
- 7 anni fa
- Visualizzazioni
Transcript
1 8.. Analisi armonica nel discreto e in un intervallo infinito. L analisi di Fourier che abbiamo visto finora può essere trasformata in due direzioni opposte: ristretta verso il discreto, cioè rivolta alle funzioni ottenute per discretizzazione finita dell intervallo [ L/2, L/2], oppure estesa al caso in cui il periodo L aumenta a dismisura fino a che [ L/2, L/2] diventa l intera retta reale. aturalmente, si potrà parlare ancora di analisi di Fourier, seppure in un senso generalizzato, se queste trasformazioni preservano in qualche modo la struttura fondamentale dell analisi di Fourier. Ma qual è la struttura fondamentale dell analisi di Fourier? 8... Qual è la struttura fondamentale dell analisi di Fourier? L essenza dell analisi di Fourier classica è quella di decomporre un segnale periodico in una somma pesata di armoniche, dove ciascun armonica ha una frequenza che è un multiplo intero della frequenza fondamentale. In effetti, l analisi di Fourier è comunemente chiamata anche analisi armonica. È importante sottolineare che tutte le armoniche sono generate dall armonica fondamentale e(x) = e iωx, di frequenza angolare ω, nel seguente modo e (x) = e(x), e 2 (x) = e(x) 2 = e iω2x,..., e n (x) = e(x) n = e iωnx,... Le potenze negative danno le frequenze negative (cioè moti circolari nella direzione opposta), e, naturalmente, e n (x) = e(x) n = e iωnx e n (x)e n (x) = cioè il modo zero. In breve, l insieme delle armoniche e n (x) = e inx forma una rappresentazione moltiplicativa del gruppo additivo degli interi Z, nel senso che e n+m (x) = e n (x)e m (x) e n (x) = e n (x) L armonica fondamentale e iωx è chiamata generatore del gruppo. È questa proprietà di gruppo, tutto sommato abbastanza astratta, che rende conto matematicamente del significato concreto dell analisi di Fourier. Quando combiniamo questa proprietà con l altro aspetto fondamentale delll analisi di Fourier, che è la decomposizione di un vettore rispetto ad una base ortonormale, otteniamo tutto quello che c è da dire sull analisi di Fourier. E tutto questo può essere riassunto in 6 punti: (I) Ad ogni funzione f : T C è associata una successione {c n } = { f(n)} di numeri complessi. Questi numeri sono noti come coordinate (o coefficienti) di Fourier di f. Quando, per semplicità, lavoriamo in T, come torneremo a fare tra poco, ω =.
2 (II) La coordinate di Fourier sono date dalla formula c n = f(n) = 2π π π f(x)e inx dx per n Z (III) I mattoni di base delle serie di Fourier sono le funzioni trigonometriche e n : T C date da e n (x) = e inx, dove n Z e x T (sono chiamate trigonometriche piuttosto che esponenziali per sottolineare il legame con seni e coseni dato dalla formula di Eulero). L n-esima coordinata di Fourier può essere scritta in termini di prodotto scalare L 2 come c n = f(n) = e n f. (IV) L insieme delle funzioni trigonometriche e n (x) = e inx forma una rappresentazione moltiplicativa del gruppo additivo degli interi Z, nel senso che (V) La serie associata a f è e n+m (x) = e n (x)e m (x) e n (x) = e n (x) f(x) n= c n e inx Usiamo il simbolo invece del simbolo = per mettere in evidenza che per un dato punto x, la serie di Fourier non necessariamente si somma al valore f(x), in verità, nel punto x, la serie di Fourier può non convergere del tutto. (VI) L insieme {e inx } n Z forma una base ortonormale per lo spazio vettoriale L 2 (T) delle funzioni a quadrato integrabile su T. In particolare, questo significa che per f L 2 (T), le somme parziali di f convergono a f nel senso L 2, cioè f f(n)e inx L 2 per n e vale l identità di Parseval (cioè il teorema di Pitagora infinito-dimensionale) f L 2 = 2π π π f(x) 2 dx = n Z f(n) 2 = f l Analisi armonica nel discreto. Consideriamo la seguente situazione: nel suo intervallo fondamentale, il segnale è un vettore v con un numero finito di componenti complesse, diciamo. Quindi è un vettore in C. Poi è ripetuto con periodicità a destra e a sinistra. Quale analisi armonica è appropriata per una situazione come questa? 2
3 Incominciamo col fissare le notazioni. Si consideri la base standard in C, che conveniamo di denotare con dei ket, =..., =,..., = (La ragione di questa notazione non convenzionale, sia per i ket sia per partire da anziché da, apparirà chiara tra poco.) Denotiamo un generico vettore di questa base con Il prodotto scalare in C è e, =,,..., v u = v()u() = v u β = δ β dove δ β è la delta di Kronecker. Allora, per un vettore v C possiamo scrivere v = v sottintendendo che tutte le somme d ora in avanti corrono da a. Si osservi che v è la -esima componente del vettore. Possiamo, per comodità, pensare a v come ad una funzione definita sull insieme finito di punti =,,...,, e a valori in C, e scrivere v() = v Adesso torniamo al problema di partenza. Vogliamo analizzare il segnale discreto v() in termine di armoniche: è chiaro che non possiamo aspettarcene più di. Se vogliamo mantenere la struttura fondamentale dell analisi di Fourier, dobbiamo cercare un analogo della proprietà (IV) per un insieme discreto. L esercizio 3 della prima esercitazione in classe ha quello che fa per noi. Allora avevamo visto (si veda il foglio con le soluzioni) che l insieme C delle radici n-esime dell unità, C = {z C z = } è un gruppo abeliano rispetto all operazione di moltiplicazione con elementi ed è il gruppo ciclico di ordine. In effetti, è una rappresentazione del gruppo additivo modulo. Per esempio, per = il 3
4 4 gruppo additivo si rappresenta con i vertici di un pentagono regolare 2 3 e le addizioni sono costruite per ciclicità, per esempio: + 2 = 3, + 4 =, = etc.. La sua rappresentazione moltiplicativa è data dalle radici quinte complesse:, e i2π/, e i4π/, e i6π/, e i8π/ e si verifica facilmente che si tratta proprio di una rappresentazione: si consideri, per esempio, +2 = 3, questo è rappresentato in e i2π/ e i4π/ = e i6π/, oppure + 4 = e i2π/ e i8π/ =, cioè l elemento neutro rispetto all addizione () è trasformato nell elemento neutro rispetto alla moltiplicazione. E così via. Per l analisi armonica in uno spazio a dimensioni, considereremo allora 4 e(x) = e i2π/ come armonica fondamentale. Il sistema di armoniche generato da e(x) consiste dunque negli vettori ẽ n, con componenti e(x) n rispetto alla base, n =,,... (per n = si ritorna a n = ), cioè ẽ n = e(x) = e i2πn/, dove =,,..., e n =,,... Si verifica facilmente che i vettori ẽ n sono ortogonali tra loro e hanno tutti norma uguale a (esercizio): ẽ n ẽ m = δ nm. È quindi conveniente passare alla base ortonormale e n = ẽ n, e n = e i2πn/ = e n () La trasformata di Fourier discreta del segnale discreto v() è definita come v(n) = e n v = v()e n () ovvero v(n) = v()e i2πn/ Poichè {e n } è una base ortornormale, la trasformata di Fourier discreta è una trasformazione unitaria e si ha v() = v = e n e n v = v(n)e n () = v(n)e i2πn/ n n n e vale l analogo finito dell identità di Parseval (che è proprio il teorema di Pitagora finito-dimensionale).
5 Si osservi che avremmo potuto convenire di assorbire il fattore di normalizzazione nel prodotto scalare e definire in C il nuovo prodotto scalare v u = f()u() = f u (che, con abuso di notazione, denotiamo nello stesso modo di prima) e utilizzare come armoniche le ẽ n e i2πn/, che nel nuovo prodotto scalare sono automaticamente normalizzate. Allora, con questo nuovo prodotto scalare, le formule per la trasformata di Fourier discreta e la sua inversa diventano v(n) = ẽ n v = v() = v = n v()e i2πn/ v(n)e i2πn/ ( analisi ) ( sintesi ) Esempio. =. Posto e i2π/ = ε, si ha (rispetto al prodotto scalare usuale) la seguente base ortonormale di Fourier: e =, e = ε ε 2 ε 3, e 2 = ε 2 ε 4 ε, e 3 = ε 3 ε ε 4, e 4 = ε 4 ε 3 ε 2 ε 4 ε 3 ε 2 ε La matrice della trasformata di Fourier discreta è ottenuta come la matrice le cui colonne sono i vettori testé trovati (che è la regola generale per la matrice di cambiamento di base). A questo punto, ecco una domanda su cui riflettere: in che modo i sei punti indicati all inizio della lezione come caratterizzanti dell analisi di Fourier si sono trasformati nel passaggio dal continuo al discreto? Chiaramente, tutti i problemi di convergenza sono evaporati, ma che dire del resto? È ragionevole dire che la struttura di base è preservata? Comunque si risponda a questa domanda, c è un senso preciso in cui l analisi di Fourier discreta approssima quella continua, che è quello di cui ci vogliamo occupare adesso. Prima un osservazione di cosmetica. L analisi di Fourier nel discreto può essere resa ancora più simile a quella nel continuo se consideriamo un numero dispari. Se è dispari è naturale scegliere una numerazione simmetrica dello spazio delle : ( )/2, ( 2)/2,..., 2,,, 2,... ( 2)/2, ( )/2
6 e analogamente per i vettori e i vettori e n. Le formule per la trasformata di Fourier e la sua inversa (le ultime che abbiamo ricavato), restano inalterate v(n) = v() = n v()e i2πn/ v(n)e i2πn/ ( analisi ) ( sintesi ) 6 ma le somme adesso sono da ( )/2 a ( )/2. Adesso mostriamo che l analisi di Fourier nel discreto è in effetti un approssimazione di quella nel continuo. Poiché consideriamo, trascureremo la differenza tra e. Siamo interessati al caso in cui i valori discreti del segnale v() sono stati ottenuti campionando un segnale continuo f(x) di periodo L, ad intervalli di ampiezza ɛ. Dunque, = L/ɛ e v() = f(x) per x = ɛ, al variare di da /2 a /2. Abbiamo cioè la discretizzazione dell intervallo reale [ L/2, L/2] in blocchi di ampiezza ɛ = L/ come mostrato in figura: L/2 L/2 Consideriamo la formula per le coordinate di Fourier discrete v(n) = v()e i2πn/ = ɛ f(ɛ)e i2πnɛ/l = ɛ f(x)e i 2π L nx L L el limite ɛ riconosciamo a secondo membro il limite della somma di Riemann dell integrale L/2 f(x)e i 2π L nx dx, L L/2 cioè v(n) f(n). Quando ɛ si ha e quindi la formula per la sintesi diventa x f(x) = lim n= v(n)e i 2π L nx = lim n= f(n)e i 2π L nx = n= f(n)e i 2π L nx In breve, abbiamo mostrato euristicamente (cioè senza preoccuparci troppo dell esistenza dei limiti) che nel limite continuo l analisi di Fourier discreta diventa
7 7 l usuale analisi di Fourier, basata sulle relazioni () f(n) = L (2) f(x) = lim L/2 L/2 n= f(x)e i 2π L nx dx f(n)e i 2π L nx = n= f(n)e i 2π L nx Analisi armonica in un intervallo infinito. Vogliamo adesso capire che cosa succede alle relazioni () e (2) quando l intervallo [ L/2, L/2] aumenta a dismisura fino a ricoprire l intera retta reale. Se assumiamo che la funzione f(x) sia buona, l integrale a secondo membro della () convergerà nel limite di grandi L, ma il fattore /L davanti farà tendere a zero le coordinate di Fourier. È dunque utile passare a coordinate dimensionate per le coordinate e riscalarle con un fattore L in modo da garantire che si abbia un limite finito non nullo. A tal fine, definiamo (3) (4) () δ def = L y def = n L = δn f δ (y) def = δ f(n) = δ f ( y δ ) e sostituiamo nella (). Si ottiene f δ (y) = δ f ( y ) = δ L/2 L/2 f(x)e i2πyx dx Consideriamo un possibile grafico delle coordinate di Fourier riscalate f δ (asumendole per semplicità reali). Il grafico mostra chiaramente che nel limite, quando la distanza tra due punti sulle ascisse si avvicina sempre più, si dovrebbe ottenere, almeno euristicamente, una funzione limite f(y) definita su tutti i punti dell asse delle y. f δ (ξ) δ =/L ξ = δn
8 Possiamo aspettarci un limite finito e non nullo per δ arbitrariamente piccolo o, equivalentemente, per L arbitrariamente grande, se f(x) è buona : deve essere non solo regolare, ma anche con decrescenza abbastanza rapida al crescere di x in modo tale che l integrale improprio f(y) = f(x)e i2πyx dx, che si ottiene nel limite δ = /L, sia finito. Consideriamo adesso la somma parziale della serie di Fourier in (2): f(n)e i 2π L nx n= Tenuto conto della (), possiamo riscrivere la somma parziale come (6) S = δ f δ (y)e i2πiyx n= Se adesso facciamo crescere come /δ = L, riconosciamo in S la somma di Riemann che nel limite diventa l integrale (improprio) f(y)e i2πiyx dy = lim S È difficile trasformare le argomentazioni euristiche precedenti in una dimostrazione rigorosa. Possiamo però dire che abbiamo buone ragioni per ritenere che se f(x) è buona, nel limite del periodo L che va all infinito e tenuto conto del riscalamento () i processi di analisi e sintesi dell analisi di Fourier diventano f(y) = f(x) = f(x)e i2πyx dx f(y)e i2πiyx dy Ci aspettiamo cioè che valga un teorema analogo al seguente (che è corretto chiamare teorema di Fourier, visto che il passaggio al limite di periodo infinito era già stato considerato da Fourier con argomentazioni analoghe a quelle che abbiamo esposto). Teorema (di Fourier). Sia (7) f(y) def = f(x)e i2πyx dx Allora, se f(x) appartiene ad una certa classe di funzioni, si ha (8) f(x) = f(y)e i2πiyx dy 8
9 Prima di procedere, due parole su notazioni e terminologia. La funzione ˆf(y) è detta trasformata di Fourier di f. L interpretazione fisica della y è di una frequenza temporale, se x è un tempo, o spaziale, se x è uno spazio (in quest ultimo caso, se k è il numero d onda, ν = k/2π). La notazione standard per la trasformata inversa di una funzione g = g(y) è g (x) = g(y)e i2πiyx dy, Il teorema di Fourier è dunque riassunto dalla formula ˆf = f. Infine, si osservi che f(x) = ˆf( x). aturalmente, il teorema di Fourier è vuoto, se non si chiarisce quale sia la certa classe di funzioni di cui si parla. Ad essere generici, si potrebbe dire che, se le funzioni sono buone, il teorema di Fourier vale. Questa affermazione è in effetti molto meno vaga di quanto possa sembrare. Infatti, nella prossima lezione mostreremo che se le funzioni sono buone, nel senso tecnico del termine specificato nella lezione 9.2, vale il teorema di Fourier. 9
f(n)r n e inx lim Se f(x) C(T) allora f S (r) f(x) = lim e inx
 17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx
![Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx Serie di Fourier. Tra queste funzioni definiamo un prodotto scalare nel seguente modo: date f, g V poniamo f (x) g (x) dx. f (x) [g (x) + h (x)] dx](/thumbs/96/128133073.jpg) Serie di Fourier Indichiamo con V l insieme delle funzioni f : R R che siano periodiche di periodo π, si abbia cioè f ( + π) = f (), e che risultino integrabili nell intervallo [, π]. Tra queste funzioni
Serie di Fourier Indichiamo con V l insieme delle funzioni f : R R che siano periodiche di periodo π, si abbia cioè f ( + π) = f (), e che risultino integrabili nell intervallo [, π]. Tra queste funzioni
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
Analisi di segnali variabili nel tempo: la trasformata di Fourier
 Analisi di segnali variabili nel tempo: la trasformata di Fourier Aniello (a.k.a. Daniele) Mennella Università degli Studi di Milano Dipartimento di Fisica 13 ottobre 2015 Laboratorio di strumentazione
Analisi di segnali variabili nel tempo: la trasformata di Fourier Aniello (a.k.a. Daniele) Mennella Università degli Studi di Milano Dipartimento di Fisica 13 ottobre 2015 Laboratorio di strumentazione
Limitiamoci dapprima a considerare una funzione f di periodo 2π. Cercheremo di approssimarla con polinomi trigonometrici di ordine n della forma
 Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Registro delle lezioni
 Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
Il problema della migliore approssimazione. Teorema 3.2 Il problema 3.1 ammette sempre almeno una soluzione.
 3. Spazi di Hilbert Wir müssen wissen. Wir werden wissen. Noi abbiamo il dovere di conoscere. Alla fine conosceremo.) David Hilbert 1862-1943) Il problema della migliore approssimazione Problema 3.1 Migliore
3. Spazi di Hilbert Wir müssen wissen. Wir werden wissen. Noi abbiamo il dovere di conoscere. Alla fine conosceremo.) David Hilbert 1862-1943) Il problema della migliore approssimazione Problema 3.1 Migliore
Serie di Fourier Richiami di teoria. Funzioni periodiche. Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R
 Serie di Fourier Richiami di teoria Funzioni periodiche Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R 2π-periodiche. Esempio 1. Consideriamo il prolungamento 2π-periodico
Serie di Fourier Richiami di teoria Funzioni periodiche Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R 2π-periodiche. Esempio 1. Consideriamo il prolungamento 2π-periodico
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
ANALISI DI FOURIER. 2πk. è periodica di periodo T. Più precisamente, essendo. T x + 2π = cos. s(x) = s x + T ) T +α. f(x) dx
 ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
Segnali e trasformate
 Segnali e trasformate - 1 Corso di Laurea in Ingegneria dell Automazione Segnali e trasformate DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
Segnali e trasformate - 1 Corso di Laurea in Ingegneria dell Automazione Segnali e trasformate DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
Serie e Trasformata di Fourier
 Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
Controlli Automatici LA Segnali e trasformate
 - 1 Corso di Laurea in Ingegneria dell Automazione DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Controlli Automatici L - 2 Segnali tempo continui
- 1 Corso di Laurea in Ingegneria dell Automazione DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Controlli Automatici L - 2 Segnali tempo continui
La Trasformata di Fourier
 La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
La Trasformata di Fourier Preliminari: Spazi di Hilbert Da Wikipedia In matematica uno spazio di Hilbert è uno spazio vettoriale che generalizza la nozione di spazio euclideo. Gli spazi di Hilbert sono
1. Martedì 1/10/2013, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2013/2014 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 18 dicembre 2013 1. Martedì 1/10/2013, 12 14. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2013/2014 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 18 dicembre 2013 1. Martedì 1/10/2013, 12 14. ore:
E, la successione di numeri {f n (x 0. n f n(x) (15.1)
 Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
esiste. Esempio 3. La successione e x2 /n 2 è regolare. In questo caso il limite è
 9.2. Funzioni generalizzate e integrali regolarizzati. 9.2.. Funzioni generalizzate. Lasciamo per un momento da parte l analisi complessa e occupiamoci di un argomento che prima o poi spunta fuori in un
9.2. Funzioni generalizzate e integrali regolarizzati. 9.2.. Funzioni generalizzate. Lasciamo per un momento da parte l analisi complessa e occupiamoci di un argomento che prima o poi spunta fuori in un
Convergenza puntuale ed uniforme delle serie di Fourier
 Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
R 2 e i numeri complessi
 L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
Argomento della lezione N. 1. Argomento della lezione N. 2. Argomento della lezione N. 12. Argomento della lezione N. 11
 C. Presilla Modelli e Metodi Matemacici della Fisica a.a. 2011/2012 2 Argomento della lezione N. 1 Fondamenti assiomatici. L unità immaginaria Argomento della lezione N. 2 Moduli e coniugati. Disuguaglianza
C. Presilla Modelli e Metodi Matemacici della Fisica a.a. 2011/2012 2 Argomento della lezione N. 1 Fondamenti assiomatici. L unità immaginaria Argomento della lezione N. 2 Moduli e coniugati. Disuguaglianza
Esponenziale complesso
 Esponenziale complesso Paola Rubbioni Analisi Matematica II - CdL in Ingegneria Informatica ed Elettronica a.a. 2016/2017 1 Serie nel campo complesso Per fornire il concetto di serie nel campo complesso
Esponenziale complesso Paola Rubbioni Analisi Matematica II - CdL in Ingegneria Informatica ed Elettronica a.a. 2016/2017 1 Serie nel campo complesso Per fornire il concetto di serie nel campo complesso
( 1 π. (a n cos nt + b n sin nt) t R (3)
 7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
f(x) := lim f n (x) Se introduciamo la norma uniforme di una funzione f (sull insieme A) mediante := sup f(x)
 Capitolo 2 Successioni e serie di funzioni 2. Convergenza puntuale e orme Supponiamo che sia un sottoinsieme di R N e supponiamo che per ogni intero n sia data una funzione f n : R M. Diremo in questo
Capitolo 2 Successioni e serie di funzioni 2. Convergenza puntuale e orme Supponiamo che sia un sottoinsieme di R N e supponiamo che per ogni intero n sia data una funzione f n : R M. Diremo in questo
1. Mercoledì 1/10/2014, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2014/2015 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 16 dicembre 2014 1. Mercoledì 1/10/2014, 15 17. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2014/2015 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 16 dicembre 2014 1. Mercoledì 1/10/2014, 15 17. ore:
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Analisi Matematica per i corsi di Laurea in Ingegneria Energetica e Meccanica N-Z dell Università di Bologna. Anno Accademico 2003/2004.
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Analisi Matematica per i corsi di Laurea in Ingegneria Energetica e Meccanica N-Z dell Università di Bologna. Anno Accademico 2003/2004.
ANALISI DI FOURIER E APPLICAZIONI
 ANALISI DI FOURIER E APPLICAZIONI Dipartimento di Matematica e Informatica Università di Catania ORIGINE DELLE SERIE DI FOURIER Problema della propagazione del calore in una sbarra. Fourier - 1822 (caso
ANALISI DI FOURIER E APPLICAZIONI Dipartimento di Matematica e Informatica Università di Catania ORIGINE DELLE SERIE DI FOURIER Problema della propagazione del calore in una sbarra. Fourier - 1822 (caso
Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 2018 A.A. 2017/2018. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 18 A.A. 17/18. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 18 A.A. 17/18. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
VERSIONE PRELIMINARE Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a
 Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a. 2005-06 G. Molteni, M. Vignati Notazioni I vettori di R n e le funzioni a valori in R n sono indicate in grassetto, per cui si dirà v R n
Lezioni di Analisi Matematica 3 corso di Laurea in Fisica a.a. 2005-06 G. Molteni, M. Vignati Notazioni I vettori di R n e le funzioni a valori in R n sono indicate in grassetto, per cui si dirà v R n
Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Determinare quali sei seguenti insiemi è uno spazio vettoriale rispetto alle usuali operazioni
Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Determinare quali sei seguenti insiemi è uno spazio vettoriale rispetto alle usuali operazioni
Registro di Matematica Applicata /18 - Dott.ssa L. Fermo 2
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2018/2019 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 19 dicembre 2018 1. Mercoledì 26/09/2018, 15 17. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2018/2019 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 19 dicembre 2018 1. Mercoledì 26/09/2018, 15 17. ore:
Sviluppo in Serie di Fourier
 Capitolo Sviluppo in Serie di Fourier. Proprietà della Serie di Fourier Un segnale reale tempo continuo e periodico di periodo, per il quale sono valide le condizioni di Dirichlet vedi pag. 4 [], può essere
Capitolo Sviluppo in Serie di Fourier. Proprietà della Serie di Fourier Un segnale reale tempo continuo e periodico di periodo, per il quale sono valide le condizioni di Dirichlet vedi pag. 4 [], può essere
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame
 Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
Complemento 10 Numeri complessi
 Analisi Matematica I CL Fisica, Università Roma Tre AA 2008/09 L. Chierchia Complemento 0 Numeri complessi. Il campo complesso Il campo complesso C è, per definizione, la terna R 2, +,, cioè R 2 equipaggiato
Analisi Matematica I CL Fisica, Università Roma Tre AA 2008/09 L. Chierchia Complemento 0 Numeri complessi. Il campo complesso Il campo complesso C è, per definizione, la terna R 2, +,, cioè R 2 equipaggiato
Serie di Fourier. 1. Introduzione Le funzioni somme di funzioni trigonometriche
 Serie di Fourier. Introduzione Le funzioni somme di funzioni trigonometriche, sin(x), cos(x), sin(2x), cos(2x),...ecc. P (x) = 2 a + a cos(x) + b sin(x) +... + b n sin(x) si dicono polinomi trigonometrici:
Serie di Fourier. Introduzione Le funzioni somme di funzioni trigonometriche, sin(x), cos(x), sin(2x), cos(2x),...ecc. P (x) = 2 a + a cos(x) + b sin(x) +... + b n sin(x) si dicono polinomi trigonometrici:
Analisi di Fourier e alcune equazioni della fisica matematica 1. SESTA e SETTIMA Lezione Serie di Fourier
 Analisi di Fourier e alcune equazioni della fisica matematica 1 SESTA e SETTIMA Lezione Serie di Fourier 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it
Analisi di Fourier e alcune equazioni della fisica matematica 1 SESTA e SETTIMA Lezione Serie di Fourier 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
i) la somma e il prodotto godano delle proprietà associativa, commutativa e distributiva;
 1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
MODELLI e METODI MATEMATICI della FISICA. Programma dettagliato del corso - A.A
 MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2017-18 Lezione 1, 28 febbraio 2018: Introduzione ai numeri complessi. Rappresentazione cartesiana e polare. Radice n-esima
MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2017-18 Lezione 1, 28 febbraio 2018: Introduzione ai numeri complessi. Rappresentazione cartesiana e polare. Radice n-esima
Introduzione ai segnali determinati
 Teoria dei segnali Unità 1 Introduzione ai segnali determinati Introduzione ai segnali determinati Sviluppo in serie di Fourier Trasformata di Fourier 005 Politecnico di Torino 1 Introduzione ai segnali
Teoria dei segnali Unità 1 Introduzione ai segnali determinati Introduzione ai segnali determinati Sviluppo in serie di Fourier Trasformata di Fourier 005 Politecnico di Torino 1 Introduzione ai segnali
1. Martedì 29/09/2015, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2015/2016 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 18 dicembre 2015 1. Martedì 29/09/2015, 12 14. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2015/2016 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 18 dicembre 2015 1. Martedì 29/09/2015, 12 14. ore:
Analisi Reale e Complessa - a.a. 2008/2009
 Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
1. Lunedì 26/09/2016, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2016/2017 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 13 dicembre 2016 1. Lunedì 26/09/2016, 11 13. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2016/2017 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 13 dicembre 2016 1. Lunedì 26/09/2016, 11 13. ore:
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei.
 Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
La Trasformata di Fourier: basi matematiche ed applicazioni. Parte II
 Metodi di Calcolo per la Chimica A.A. 2016-2017 Marco Ruzzi La Trasformata di Fourier: basi matematiche ed applicazioni Parte II Showing a Fourier transform to a physics student generally produces the
Metodi di Calcolo per la Chimica A.A. 2016-2017 Marco Ruzzi La Trasformata di Fourier: basi matematiche ed applicazioni Parte II Showing a Fourier transform to a physics student generally produces the
3.2 Funzioni periodiche e sviluppi in Serie di Fourier
 3. Funzioni periodiche e sviluppi in Serie di Fourier Una prima classe di funzioni per cui si può effettuare l analisi armonica (3.5 contiene le funzioni periodiche (di periodo, tali cioè che f(t + = f(t,
3. Funzioni periodiche e sviluppi in Serie di Fourier Una prima classe di funzioni per cui si può effettuare l analisi armonica (3.5 contiene le funzioni periodiche (di periodo, tali cioè che f(t + = f(t,
5.2 Sistemi ONC in L 2
 5.2 Sistemi ONC in L 2 Passiamo ora a considerare alcuni esempi di spazi L 2 e di relativi sistemi ONC al loro interno. Le funzioni trigonometriche Il sistema delle funzioni esponenziali { e ikx 2π },
5.2 Sistemi ONC in L 2 Passiamo ora a considerare alcuni esempi di spazi L 2 e di relativi sistemi ONC al loro interno. Le funzioni trigonometriche Il sistema delle funzioni esponenziali { e ikx 2π },
1. Martedì 27/09/2016, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Chimica e Meccanica 6 CFU - A.A. 2016/2017 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2016 1. Martedì 27/09/2016,
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Chimica e Meccanica 6 CFU - A.A. 2016/2017 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2016 1. Martedì 27/09/2016,
Serie di Fourier. prof. Sergio Zoccante 27 gennaio 2011
 Serie di Fourier prof. Sergio Zoccante 27 gennaio 2011 1 Le serie di Fourier Gli sviluppi in serie di Taylor hanno applicazioni numerosissime. Tuttavia, le condizioni alle quali una funzione deve soddisfare
Serie di Fourier prof. Sergio Zoccante 27 gennaio 2011 1 Le serie di Fourier Gli sviluppi in serie di Taylor hanno applicazioni numerosissime. Tuttavia, le condizioni alle quali una funzione deve soddisfare
Segnali e trasformate
 Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano
 Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
1. Mercoledì 27/09/2017, ore: 2(2) Introduzione al corso: problemi ben posti, condizionamento, stabilità, complessità
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Chimica e Meccanica 6 CFU - A.A. 2017/2018 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2017 1. Mercoledì 27/09/2017,
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Chimica e Meccanica 6 CFU - A.A. 2017/2018 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2017 1. Mercoledì 27/09/2017,
2. la ricerca di funzioni che hanno una derivata assegnata.
 INTEGRALI PER FUNZIONI DI UNA VARIABILE Il calcolo integrale per funzioni reali di una variabile reale si occupa di risolvere due problemi:. il calcolo dell area di parti di piano qualsiasi, 2. la ricerca
INTEGRALI PER FUNZIONI DI UNA VARIABILE Il calcolo integrale per funzioni reali di una variabile reale si occupa di risolvere due problemi:. il calcolo dell area di parti di piano qualsiasi, 2. la ricerca
AL220 - Gruppi, Anelli e Campi
 AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
2.1 Numeri naturali, interi relativi, razionali
 2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
Analisi Matematica 1
 Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Foglio 1 Lunedì 3 ottobre. f(x) = log x 2 6x + 5.
 Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Analisi Matematica Foglio Lunedì 3 ottobre Esercizio. Trovare il dominio naturale della funzione f data da ( ) f(x) = log x 2 6x + 5. Esercizio 2. Dire quali tra le seguenti funzioni sono iniettive :.
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 10 gennaio 2007
 Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 0 gennaio 007 Primo esercizio. È assegnato il numero complesso z = + i. (a) Posto z = + i, determinare la forma trigonometrica
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 0 gennaio 007 Primo esercizio. È assegnato il numero complesso z = + i. (a) Posto z = + i, determinare la forma trigonometrica
dx dy = 2r vediamo che l effetto dello Jacobiano su (dx, dy) è semplicemente la moltiplicazione per il numero complesso 2z, cioè dw = (2z)dz
 4.1. Funzioni analitiche. 4.1.1. Un fenomeno strano. Le funzioni viste finora hanno la proprietà quadratini quadratini. Abbiamo detto che questo è un segno che le funzioni sono conformi, ma per il momento
4.1. Funzioni analitiche. 4.1.1. Un fenomeno strano. Le funzioni viste finora hanno la proprietà quadratini quadratini. Abbiamo detto che questo è un segno che le funzioni sono conformi, ma per il momento
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier p. 2
 Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
Elettronica II Segnali periodici; serie di Fourier; trasformata di Fourier Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Registro di Matematica Applicata /18 - Dott.ssa L. Fermo 2
 Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2017/2018 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2017 1. Lunedì 25/09/2017, 11 13. ore:
Registro delle lezioni di MATEMATICA APPLICATA Corsi di Laurea in Biomedica 6 CFU - A.A. 2017/2018 docente: Dott.ssa Luisa Fermo ultimo aggiornamento: 15 dicembre 2017 1. Lunedì 25/09/2017, 11 13. ore:
La lunghezza dei vettori e legata alle operazioni sui vettori nel modo seguente: Consideriamo due vettori v, w e il vettore v + w loro somma.
 Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Dispense sulle serie di potenze, funzioni esponenziali e trigonometriche
 Dispense sulle serie di potenze, funzioni esponenziali e trigonometriche Luca Biasco 1 27 dicembre 2015 1 Queste dispense sono prese, quasi verbatim, da alcune pagine del libro di Analisi Matematica 2
Dispense sulle serie di potenze, funzioni esponenziali e trigonometriche Luca Biasco 1 27 dicembre 2015 1 Queste dispense sono prese, quasi verbatim, da alcune pagine del libro di Analisi Matematica 2
Qualche informazione su gruppi e anelli
 Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
ossia può anche essere localizzato univocamente sul piano complesso con la sua forma polare.
 ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
ALGEBRA COMPLESSA Nel corso dei secoli gli insiemi dei numeri sono andati man mano allargandosi per rispondere all esigenza di dare soluzione a equazioni e problemi sempre nuovi I numeri complessi sono
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 2018
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 18 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: 1 la correttezza del risultato ottenuto e della procedura utilizzata;
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 4 DICEMBRE 18 Si risolvano cortesemente i seguenti problemi, sapendo che verranno valutati: 1 la correttezza del risultato ottenuto e della procedura utilizzata;
Diario delle lezioni di Calcolo e Biostatistica (O-Z) - a.a. 2013/14 A. Teta
 Diario delle lezioni di Calcolo e Biostatistica (O-Z) - a.a. 2013/14 A. Teta 1. (1/10 Lu.) Generalità sugli insiemi, operazioni di unione, intersezione e prodotto cartesiano. Insiemi numerici: naturali,
Diario delle lezioni di Calcolo e Biostatistica (O-Z) - a.a. 2013/14 A. Teta 1. (1/10 Lu.) Generalità sugli insiemi, operazioni di unione, intersezione e prodotto cartesiano. Insiemi numerici: naturali,
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini.
 Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
f(x)e 2πixy dx g(y)e 2πixy dy
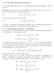 18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA RADICALI Dr. Erasmo Modica erasmo@galois.it LE RADICI Abbiamo visto che l insieme dei numeri reali è costituito da tutti
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA RADICALI Dr. Erasmo Modica erasmo@galois.it LE RADICI Abbiamo visto che l insieme dei numeri reali è costituito da tutti
MATEMATICA. a.a. 2014/ LIMITI (I parte): Definizione, proprietà e calcolo. Limiti di funzioni, continuità e asintoti.
 MATEMATICA a.a. 2014/15 2. LIMITI (I parte): Definizione, proprietà e calcolo. Limiti di funzioni, continuità e asintoti. Definizione Il campo di esistenza è l insieme di tutti i punti nei quali la funzione
MATEMATICA a.a. 2014/15 2. LIMITI (I parte): Definizione, proprietà e calcolo. Limiti di funzioni, continuità e asintoti. Definizione Il campo di esistenza è l insieme di tutti i punti nei quali la funzione
CALCOLO DEI COEFFICIENTI DI FOURIER CON SOLI SENI O COSENI nell intervallo [-π ; π ]
![CALCOLO DEI COEFFICIENTI DI FOURIER CON SOLI SENI O COSENI nell intervallo [-π ; π ] CALCOLO DEI COEFFICIENTI DI FOURIER CON SOLI SENI O COSENI nell intervallo [-π ; π ]](/thumbs/104/162476443.jpg) CALCOLO DEI COEFFICIENTI DI FOURIER CON SOLI SENI O COSENI nell intervallo [-π ; π ] La costruzione di una qualunque oscillazione complessa a partire dalla sovrapposizione di oscillazioni armoniche semplici
CALCOLO DEI COEFFICIENTI DI FOURIER CON SOLI SENI O COSENI nell intervallo [-π ; π ] La costruzione di una qualunque oscillazione complessa a partire dalla sovrapposizione di oscillazioni armoniche semplici
Sol. Sia P = (x, y) un punto che soddisfa l equazione Y 2 = X 3 + ax + b. Ricordiamo che per definizione P = (x, y) è un punto regolare di E se
 Teoria Elementare dei Numeri. Soluzioni Esercizi 5. Curve ellittiche. 1. Sia E una curva su R di equazione Y 2 = X 3 + ax + b. Verificare che è una curva regolare di R 2 (senza punti singolari) se e solo
Teoria Elementare dei Numeri. Soluzioni Esercizi 5. Curve ellittiche. 1. Sia E una curva su R di equazione Y 2 = X 3 + ax + b. Verificare che è una curva regolare di R 2 (senza punti singolari) se e solo
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
L ANALISI ARMONICA DI UN SEGNALE PERIODICO
 L ANALISI ARMONICA DI UN SEGNALE PERIODICO Il segnale elettrico è una grandezza fisica (in genere una tensione) che varia in funzione del tempo e che trasmette un'informazione. Quasi tutti i segnali che
L ANALISI ARMONICA DI UN SEGNALE PERIODICO Il segnale elettrico è una grandezza fisica (in genere una tensione) che varia in funzione del tempo e che trasmette un'informazione. Quasi tutti i segnali che
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 2014 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 24 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 luglio 24 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Successioni e serie di funzioni
 Capitolo 2 Successioni e serie di funzioni In questo capitolo studiamo le successioni e le serie di funzioni. quindi particolari metodi per approssimare una data funzione Studiamo CAPITOLO 2. SUCCESSIONI
Capitolo 2 Successioni e serie di funzioni In questo capitolo studiamo le successioni e le serie di funzioni. quindi particolari metodi per approssimare una data funzione Studiamo CAPITOLO 2. SUCCESSIONI
Analisi Matematica 2
 Analisi Matematica Appunti delle lezioni tenute dal Prof. A. Fonda Università di Trieste CdL Matematica a.a. 07/08 La derivata direzionale In questa sezione E sarà un sottoinsieme aperto di R N x 0 un
Analisi Matematica Appunti delle lezioni tenute dal Prof. A. Fonda Università di Trieste CdL Matematica a.a. 07/08 La derivata direzionale In questa sezione E sarà un sottoinsieme aperto di R N x 0 un
f(x) = E chiaro che in questo caso, l integrale di f si puo fare ed e finito: f(x)dx = dx = b a
 1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
