LA GEOMETRIA CON GEOGEBRA
|
|
|
- Leonardo Maggi
- 8 anni fa
- Visualizzazioni
Transcript
1 La geometria con Geogebra Introduzione 1 SERGIO BALSIMELLI LA GEOMETRIA CON GEOGEBRA (seconda edizione) Esercizi per la scuola secondaria di primo grado e di secondo grado
2 La geometria con Geogebra Introduzione 2 EDITING NICOLA CHIRIANO Matematicamente.it Corso Umberto 27c San Donato di Lecce libri@matematicamente.it Stampa Universal Book Via Botticelli, Rende (CS) Tel. Fax ISBN:
3 La geometria con Geogebra Introduzione 3 Indice Introduzione La barra degli strumenti di disegno La barra di inserimento La barra dei menu Esercizi per la prima media Esercizi per la seconda media Esercizi per la terza media Geometria analitica Figure ottenute con la riga di inserimento Esercizi per la prima superiore Operazioni con i polinomi Equazioni di primo grado e retta Sistemi di equazioni di primo grado Equazioni di secondo grado e parabola Sistemi di equazioni di secondo grado Equazioni di secondo grado e parabola Disequazioni di primo grado Disequazioni di secondo grado Isometrie Esercizi per la seconda superiore Geometria analitica Le rette Luoghi geometrici Fasci di rette La parabola Esercizi per la terza superiore Iperbole Circonferenza Ellisse Intersezioni e posizioni reciproche Disegno di coniche come luoghi geometrici Esercizi per la quarta superiore Curve deducibili Goniometria Disegno di una funzione goniometrica come luogo Semplici disequazioni goniometriche Funzioni goniometriche inverse Curve goniometriche deducibili
4 La geometria con Geogebra Introduzione 4 Risoluzione dei triangoli rettangoli Risoluzione di un triangolo generico Esercizi per la quinta superiore Tangenti a una funzione Punti di flesso di una funzione Funzione crescente, decrescente e punti stazionari Funzioni condizionate Integrali definiti Due funzioni delimitano una superficie chiusa Valore medio di una funzione Teorema di Rolle Teorema di Lagrange Calcolo del volume dei solidi di rotazione Area di una superficie di rotazione Area del trapezoide Geogebra e formule
5 La geometria con Geogebra Introduzione 5 A mia moglie, Donella, e ai miei figli Benedetta, Marco e Tommaso
6 La geometria con Geogebra Introduzione 6 INTRODUZIONE Geogebra è un software didattico per l'insegnamento della geometria, ma non solo, che fa parte del gruppo di software detti di geometria dinamica. È un software open-source rilasciato sotto licenza GNU GPL (General Public Licence), ossia può essere scaricato e usato gratuitamente ed essere copiato e distribuito liberamente, purché non a scopo di lucro. Si può scaricare dal sito del progetto Ideatore e principale sviluppatore è Markus Hohenwarter della Florida Atlantic University (USA). Esiste un forum, in più lingue, italiano compreso, dove è possibile scambiare consigli e informazioni. Esistono poi aree Wiki in diverse lingue dove è possibile pubblicare i propri lavori oppure scaricare quelli degli altri. In questo manuale saranno utilizzate le seguenti convenzioni: > Il simbolo > conduce a voci di menu nidificate. Ad es. la sequenza File> Esporta> Foglio da disegno indica che bisogna aprire la voce di menu File, selezionare da questo menu la voce Esporta e selezionare la voce Foglio da disegno dalla finestra di dialogo. grassetto Il testo in grassetto indica le voci del software da selezionare: voci di menu e opzioni delle finestre di dialogo. monospazio Questo tipo di carattere indica il testo o i caratteri che devono essere digitati da tastiera. monospazio grassetto Questo tipo di carattere indica i messaggi e le risposte che il software visualizza sullo schermo. Per scaricare Geogebra nella versione offline, che funziona cioè anche se non si è connessi ad Internet, accedere al sito: e cliccare sull icona del sistema operativo che si usa (Windows o altro). Dopo aver cliccato due volte sul file scaricato, scegliere Italiano, poi cliccare su Avanti più volte fino al tipo di installazione, qui scegliere Tipica. Come cartella di destinazione si può lasciare quella indicata e
7 La geometria con Geogebra Introduzione 7 infine cliccare sul pulsante Installa.. Ad installazione completata cliccare sul pulsante Eseguito per far avviare il programma. A questo punto appare la schermata iniziale, nella quale si possono distinguere quattro parti fondamentali: a sinistra la Finestra Algebra; al centro il Foglio da Disegno; in basso la Barra Inserimento; in alto la Barra dei Menu e la Barra dei Comandi
8 La geometria con Geogebra Introduzione 8 La barra degli strumenti di disegno Cliccando sulla freccetta in basso a destra di ogni icona si apre un menu a tendina con gli altri comandi presenti. Nel seguito indicheremo le icone con un numero come segue: Icona1 Icona2 Icona3 Icona4 Icona5 Icona6 Icona7 Icona8 Icona9 Icona10 Icona11 Icona 1 Muovi. Permette di spostare un oggetto libero con il mouse, cliccando su di esso e trascinandolo. Premendo il tasto Canc si cancella l oggetto selezionato. Tenendo premuto Ctrl si selezionano più oggetti che possono così essere gestiti assieme. Ruota intorno a un punto. Scelto un punto come centro di rotazione, si possono ruotare gli oggetti liberi attorno a questo punto, cliccando prima sul centro di rotazione e poi trascinando il punto. Registra sul foglio di calcolo. Con questo strumento è possibile memorizzare la sequenza dei valori assunti da un oggetto in movimento. Icona 2 Nuovo punto. Cliccando sul foglio da disegno, su un segmento, retta o conica, si crea un nuovo punto. Intersezione di due oggetti. Per trovare l intersezione di due oggetti si può cliccare successivamente su di essi, o direttamente nel punto di intersezione. Punto medio o centro. Permette di trovare il punto medio tra due punti cliccando su ciascuno di essi; di un segmento cliccandoci su, o il centro di una conica cliccando sulla conica.
9 La geometria con Geogebra Introduzione 9 Icona 3 Retta per due punti. Cliccare per fissare il primo punto, poi spostarsi e cliccare di nuovo. Segmento tra due punti. Permette di tracciare il segmento che unisce due punti cliccando prima su uno poi sull altro. Segmento di data lunghezza da un punto. Cliccare per fissare il primo punto, poi nella finestra che si apre digitare il valore della sua lunghezza e cliccare sul pulsante Applica. Semiretta per due punti. Cliccare per fissare il primo punto poi spostarsi e cliccare di nuovo per ottenere la semiretta. Vettore tra due punti. Cliccare sul primo punto, poi spostarsi sul secondo e cliccare di nuovo. Vettore da un punto. Prendere un punto A ed un vettore tra due punti B e C. Dopo aver preso lo strumento vettore da un punto, cliccare su A e sul vettore BC. Si ottiene il vettore AD avente stesso modulo, direzione e verso di BC. Icona 4 Retta perpendicolare. Dati un punto ed una retta, clic-care sul punto e sulla retta per ottenere la perpendicolare. Retta parallela. Dati un punto ed una retta, cliccare sul punto e sulla retta per ottenere la parallela. Asse di un segmento. Dato un segmento, cliccare sullo stesso per ottenere il suo asse (perpendicolare passante per il punto medio). Bisettrice. Cliccando sui tre punti che formano un angolo (quello centrale è il vertice) si ottiene la bisettrice. Cliccando sulle due semirette che formano un angolo si ottengono le due bisettrici (angolo interno ed esterno). Tangenti. Cliccando su un punto A e poi sulla conica c si formano tutte le tangenti alla conica c passanti per A. Cliccando su una retta r ed una conica c, si generano tutte le tangenti alla conica c parallele alla retta r. Polare o diametro. Cliccando su un punto A e su una conica c si ottiene la polare. Cliccando su una retta (o vettore e poi sulla conica si ottiene la retta passante per il centro. Retta di regressione. Per generare la retta, selezione una lista o un gruppo di punti e cliccare sullo strumento. Luogo. Dopo aver cliccato sul punto A il cui luogo deve essere disegnato, cliccare sul punto B da cui A dipende. B deve essere un punto su un oggetto (segmento, conica...)
10 La geometria con Geogebra Introduzione 10 Icona 5 Poligono. Si ottiene un poligono del numero di lati voluto (se si parte dal punto A alla fine cliccare di nuovo su A). Poligono regolare. Selezionare due punti A e B, si aprirà una finestra con il campo di inserimento testo, dove andrà inserito il numero di lati del poligono. Icona 6 Circonferenza di dato centro. Cliccare su un punto per definire il centro, spostarsi e cliccare di nuovo fino alla grandezza desiderata. Circonferenza dati centro e raggio. Cliccare su un punto per definire il centro e nella finestra che si apre digitare il valore del raggio. Compasso. Selezionare un segmento (o due punti) per fissare il raggio e poi cliccare sul punto che farà da centro. Circonferenza per tre punti. Cliccare successiva-mente su tre punti dati e si ottiene la circonferenza passante per i tre punti. Semicirconferenza per due punti. Cliccare su due punti per otte-nere la semicirconferenza di diametro i due punti. Arco di circonferenza di dato centro per due punti. Si fa clic sul centro della circonferenza e poi sui due punti estremi dell arco. Arco di circonferenza per tre punti. Si fa clic su tre punti, il primo e l ultimo saranno gli estremi dell arco. Settore circolare di dato centro per due punti. Dati tre punti A, B e C, cliccare in A, centro del settore, poi in B e infine in C (C non deve necessariamente giacere sull arco). Settore circolare per tre punti. Si fa clic su tre punti e si ottiene il settore circolare che ha per estremi il primo e l ultimo punto, il punto intermedio giace sull arco
11 La geometria con Geogebra Introduzione 21 Circonferenza: x 2 +y 2 =1 Prova a disegnare le circonferenze Equazione testo da digitare x 2 +y 2 =16 x^2+y^2=16 (x-3) 2 + (y-1) 2 = 9 (x-3)^2+(y-1)^2=9 x 2 +y 2-4x+2y+1=0 1 Si possono disegnare le coniche anche utilizzando l apposito strumento Conica della Icona7.
12 La geometria con Geogebra Introduzione 22 Funzione generica: f(x) = x 3 + 2x Prova a disegnare le seguenti funzioni: funzioni f(x)=x 3 -x 2 testo da digitare x^3-x^2 f(x)=x 4 -x 3 f(x)=x 3 -x 2-4x+4 1 (x+1)/(x-1) sqrt(x-1) abs(x)
13 La geometria con Geogebra Introduzione 23 La Barra dei Menu Menu File A parte i consueti comandi Apri, Salva, Salva con nome abbiamo: Esporta> Foglio di lavoro dinamico come pagina web viene richiesto l inserimento del Titolo, dell Autore, della Data e si generano più file con estensione.html (da lanciare per visualizzare il lavoro nel browser).ggb e.jar Esporta> Protocollo di costruzione come pagina web dopo aver inserito Titolo, Data, Autore vengono generati due file, uno.html (da lanciare per vedere l immagine della pagina di lavoro con sotto il protocollo di costruzione) e l altro.png (immagine). Esporta> Foglio da disegno come immagine si può scegliere la risoluzione (da 72 a 600 d.p.i.) e la scala. Esporta> Esporta il foglio da disegno negli appunti come immagine.png l immagine viene copiata negli appunti da dove può essere incollata in altre applicazioni tipo Word. Menu Modifica A parte i consueti comandi Annulla e Ripristina (per annullare e ripristinare un operazione eseguita) abbiamo Proprietà> visualizza le proprietà di tutti gli oggetti presenti nel lavoro fatto Menu Visualizza Assi per visualizzare o meno gli assi cartesiani. Griglia per visualizzare una griglia quadrettata che agevola la ricerca di un punto attraverso le sue coordinate. Finestra Algebra visualizza tutti gli oggetti nella finestra apposita posta nella parte sinistra della schermata.
14 La geometria con Geogebra Esercizi per la prima media 26 ESERCIZI PER LA PRIMA MEDIA [Esercizio 1] Punti nel piano Usando Icona2> Nuovo punto, individuare i punti A(1,2), B(3,4), C(4,2), D(3,2). Dopo aver scelto Icona1> Muovi, spostare il punto A in (5,4), B in (5,5) e C in (4,0). Individuare poi i punti E(-2,3) ed F(-4,5). Spostare E in (0,3) ed F in (0,4). Cancellare tutti i punti (cliccare su ciascuno di essi e premere il tasto Canc) ed inserire i seguenti: A(-4,-2), B(-3,2), C(-1,4), D(4,-5), E(6,3), F(4,2), G(3,0), H(0,5). Scegliere File> Nuovo, non salvare e riportare i seguenti punti: A(-2,-4), B(-2,3), C(2,4),, D(4,-3), E(-4, -1), F(0,3) e G(-3,0). [Esercizio 2] Segmenti Dopo aver scelto File> Nuovo, senza salvare quanto fatto, prendere Icona3> Segmento tra due punti e individuare il segmento AB con A(1,2) e B(5,2). Quanto misura il segmento? Come viene indicato? (Vedere sulla sinistra nella Finestra Algebra). Ripetere con i segmenti CD con C(1,4) e D(1,7), EF con E(6,2) ed F(5,4), GH con G(-2,4) ed H(4,-2), IL con I(-2,-4) ed L(4,-3). Con lo strumento Icona8> Distanza misurare la distanza dei vari segmenti cliccando su ciascuno di essi. Scegliere File> nuovo senza salvare il lavoro. Prendere quindi lo strumento Icona3> Segmento di data lunghezza da un punto, cliccare in A(2,2) e poi, nella finestra che si apre, digitare il valore 6. Cliccare sul punto B col tasto destro e scegliere Traccia on, poi selezionarlo e spostarlo. Quale curva descrive? Ripetere con il punto C(3,3) disegnando un segmento di lunghezza 4.
15 La geometria con Geogebra Esercizi per la prima media 27 [Esercizio 3] Semirette Dopo aver scelto Icona3> Semiretta per due punti disegnare la semiretta con origine A in (2,2) e passante per B(4,4). Come viene indicata la semiretta? Con lo strumento Muovi, cliccare sulla semiretta e cambiare la sua posizione. Con lo stesso strumento cliccare su B e far ruotare la semiretta attorno ad A; ripetere poi cliccando su A. Cliccare infine sulla semiretta e cancellarla premendo il tasto Canc; ripetere con i punti A e B. [Esercizio 4] Rette Scegliere Icona3> Retta per due punti e disegnare la retta cliccando su A(2,2) e B(6,6). Come viene indicata la retta? Con lo strumento Muovi spostare la retta, poi cliccare sul punto B e ruotare la retta attorno ad A, infine cliccare su A e ruotarla attorno a B. Selezionare la retta, cancellarla ed eliminare anche i punti A e B. Tracciare un altra retta passante per due punti a piacere. [Esercizio 5] Intersezione tra rette Disegnare la retta passante per A(1,1) e B(4,4) e quella passante per C(1,5) e D(4,1). Con lo strumento Icona2> Intersezione di due oggetti, individuare il punto d incontro delle rette (avvicinarsi allo stesso e cliccare quando le rette diventano più spesse, oppure cliccare successivamente su ciascuna retta). Con lo strumento Muovi spostare il punto B, il punto A, il punto C ed infine D. Prendere Icona10> Testo e digitare, nella finestra che si apre: E è il punto d incontro delle rette AB e CD. Cliccare poi sul pulsante Applica. Cliccare quindi col tasto destro sulla scritta e scegliere Proprietà> Testo> 16 punti, Colore> rosso cliccando su OK e infine su Applica. Dopo aver scelto File> Nuovo, senza salvare quanto fatto ripetere l esercizio precedente considerando le rette AB e CD passanti per A(2,2) e B(4,6) ; C(1,5) e D(6,1).
16 La geometria con Geogebra Esercizi per la prima media 28 [Esercizio 6] Rette e triangolo Disegnare le retta AB con A(1,1) e B(6,6) la retta CD con C(1,8) e D(7,2) ed infine la retta EF con E(1,2) e F(7,3). Individuare i tre punti di intersezione G,H ed I poi con lo strumento Icona5> Poligono disegnare il triangolo con i vertici trovati. Cliccare all interno del triangolo con il tasto destro, scegliere proprietà e cambiare il colore in azzurro. Con lo strumento Icona11> Mostra nascondi oggetto, cliccare sulle tre rette iniziali e poi sullo strumento Muovi. È possibile spostare i punti G, H o I? Provare a spostare invece i punti che individuano le tre rette. Cancellare il tutto. [Esercizio 7] Triangolo Con Icona5> Poligono, disegnare il triangolo di vertici A(2,2) B(7,5) e C(4,6) ricordandosi di chiudere il poligono cliccando su A. Con lo strumento Muovi spostare le lettere dei vertici del triangolo in modo che restino tutte all esterno dello stesso, poi spostare il punto B in (5,4) e C in (2,4). Colorare il triangolo di rosso. Con lo strumento Icona10> Testo digitare L area del triangolo è= +poly1 + cm 2 e cliccare sul pulsante Applica.. Con lo strumento Muovi spostare il vertice B e osservare cosa accade alla misura dell area. Calcolare il perimetro del triangolo prendendo lo strumento Testo e digitando Il perimetro del triangolo è = +(a+b+c) + cm. Con lo strumento Muovi spostare il vertice B e osservare cosa accade alla misura del perimetro; ripetere con i vertici A e C. Selezionare il triangolo, cliccando al suo interno, e cancellarlo. Ripetere l esercizio disegnando il triangolo di vertici A(-2,4) B(6,2) C(4,-1) colorandolo di blu e calcolando perimetro ed area. NOTA: per calcolare il valore di un area, di un perimetro il testo va racchiuso tra virgolette, poi va inserito il simbolo + davanti al valore che si vuole determinare.
17 La geometria con Geogebra Esercizi per la prima media 29 [Esercizio 8] Triangoli Disegnare il triangolo di vertici A(1,1) B(7,2) e C(2,4) ricordandosi di chiudere il poligono cliccando su A. Con lo strumento Icona2> Punto medio o centro, cliccare su ciascun lato del triangolo individuando i punti medi D, E ed F e spostando le etichette all esterno del triangolo. Disegnare il triangolo DEF e colorarlo di blu. Calcolare il perimetro del triangolo ABC e del triangolo DEF. Quale relazione c è tra il perimetro dei due triangoli? [Esercizio 9] Rette parallele e perpendicolari Disegnare la retta passante per A(1,2) e B(3,4) poi prendere con Icona2> Nuovo punto il punto C(4,2). Con Icona4> Retta parallela, tracciare la parallela alla retta AB passante per C (cliccare su C e poi sulla retta o viceversa). Con lo strumento Muovi spostare B o A. Cosa accade? Con lo strumento Icona4> Retta perpendicolare tracciare la perpendicolare alla retta AB passante per C individuando il punto d intersezione D. Con lo strumento Icona3> Segmento tra due punti tracciare il segmento DC e calcolare la sua lunghezza (distanza tra le due rette parallele) usando lo strumento Testo e digitando Distanza tra le due parallele = +d + cm. [Esercizio 10] Rette parallele e perpendicolari Disegnare la retta AB esattamente orizzontale e la parallela condotta da un punto C. Usando lo strumento Icona5> Poligono e le rette parallele e perpendicolari ad AB, costruire le seguenti figure: rettangolo, parallelogramma, trapezio isoscele, trapezio rettangolo e trapezio scaleno prendendo punti a piacere. Colorare i poligoni con colori diversi.
18 La geometria con Geogebra Esercizi per la prima media 30 [Esercizio 11] Rette parallele e perpendicolari Disegnare le lettere dell alfabeto H, E, F e T, così come si vedono nel disegno, a partire dal segmento AB, con A(2,7) e B(2,1). Per determinare il punto medio usare lo strumento Icona2 > Punto medio o centro. [Esercizio 12] Asse di un segmento Tracciare il segmento AB di estremi A(2;6) e B(5;3) con Icona3> Segmento tra due punti. Trovare quindi il suo punto medio C scegliendo Icona2> Punto medio o centro cliccare sul segmento AB; tracciare la perpendicolare al segmento AB passante per C, scegliendo Icona4> Retta perpendicolare e cliccando sul segmento AB e poi sul punto C, individuando l asse di AB. Prendere quindi un punto D sull asse e tracciare i segmenti AD e DB. Nella Finestra Algebra osservare che i due segmenti hanno la stessa misura e ciò avviene anche spostando D sull asse. Con lo strumento Icona8> Distanza cliccare sui segmenti c e d, e osservare che i valori rimangono uguali anche spostando D. Cliccare sul punto D e premere il tasto + o del tastierino numerico per farlo scorrere sull asse e osservare l uguaglianza dei due segmenti (anche nella finestra algebra). Usando lo strumento Icona10> Testo, digitare <L asse di un segmento è la perpendicolare re passante per il punto medio del segmento stesso, ma è anche il luogo dei punti equidistanti dagli estremi del segmento>. Cliccare ancora sul punto D col tasto destro e scegliere Proprietà> Algebra> Incremento e dare valore 0,01 all incremento, cliccando infine su Chiudi. Provare di nuovo a spostare il punto D dopo averlo selezionato e agendo sul tastierino numerico.
19 La geometria con Geogebra Esercizi per la seconda media 47 ESERCIZI PER LA SECONDA MEDIA [Esercizio 40] Costruzione del quadrato dato il lato Disegnare il segmento AB con A(1,1) e B(6,4). Tracciare da A e da B le perpendicolari al segmento AB. Con Icona6> Circonferenza di dato centro, cliccare in A e aprire fino a B, cliccare poi in B ed aprire fino ad A. Individuare le intersezioni C e D su queste rette ed unire i punti ABCD con lo strumento Icona5> Poligono. Nascondere le rette e le circonferenze. Nella Finestra Algebra come risultano i lati AB, BC, CD e DA? [Esercizio 41] Costruzione del quadrato di diagonale assegnata Disegnare un segmento AB inclinato a piacere e determinare con Icona2> Punto medio o centro il suo punto medio. Tracciare per esso la perpendicolare al lato AB. Con Icona6> Circonferenza di dato centro disegnare la circonferenza di centro C e raggio AC. Individuare le intersezioni D ed E della stessa con la retta. Con lo strumento Icona5> Poligono tracciare il poligono AEBD, che è un quadrato. Nella Finestra Algebra come risultano i lati AE, EB, BD e DA?
20 La geometria con Geogebra Esercizi per la seconda media 48 [Esercizio 42] Costruzione del parallelogramma Tracciare una retta AB passante per due punti, poi prendere un punto C esterno alla retta e tracciare per esso la parallela alla retta AB. Disegnare la retta passante per i punti A e C, tracciare la parallela a quest ultima condotta da B individuando l intersezione D. Con lo strumento Icona5> Poligono disegnare il poligono ABDC e colorarlo di rosso. Il poligono ABCD è un parallelogramma? Verifica con lo strumento Icona10> Relazione tra due oggetti che i lati opposti sono paralleli: dopo aver selezionato lo strumento fai clic su due lati opposti del parallelogramma. [Esercizio 43] Costruzione del rombo Disegnare un segmento AB ed individuare il suo punto medio C. Tracciare per esso la perpendicolare ad AB e prendere sulla perpendicolare stessa un punto D. Con Icona5> Circonferenza di dato centro, tracciare la circonferenza di centro C e passante per D, individuando l ulteriore intersezione E. Disegnare il poligono ADBE, nascondere circonferenza e retta e tracciare la diagonale DE con lo strumento Icona3> Segmento tra due punti. Il poligono ADBE è un rombo? Verifica che ha i lati congruenti e le diagonali perpendicolari.
21 La geometria con Geogebra Esercizi per la seconda media 49 [Esercizio 44] Disegno del trapezio Disegnare un segmento AB e prendere un punto C esterno ad esso. Per C disegnare la parallela ad AB con Icona4> Retta parallela, unire C con A e B con un punto D qualsiasi preso sulla retta passante per C. Si ottiene così un trapezio scaleno. Come si può fare per disegnare un trapezio isoscele? Cancellare il punto D e trovare il punto medio di AB, per esso far passare la perpendicolare ad AB, determinando il punto E di intersezione con la retta passante per C. Con Icona6> Circonferenza di dato centro,, tracciare la circonferenza di centro E e raggio EC che interseca la retta in F. Unire B con F e nascondere la circonferenza. Per ottenere un trapezio rettangolo cancellare il punto F e da B condurre la perpendicolare, con Icona4> Retta perpendicolare,, alla retta passante per C, individuando l intersezione F. Dopo aver tracciato il segmento BF nascondere le rette e ed f con Icona11> Mostra/Nascondi oggetto. [Esercizio 45] Costruzione di un poligono regolare Prendere due punti A e B, la cui distanza sarà il raggio del cerchio circoscritto al poligono. Scegliere Icona9> Ruota intorno ad un punto di un angolo, cliccare sul punto A, poi su B e nella finestra che si apre inserire il valore dell angolo di rotazione (360 : numero dei lati): pentagono 72 esagono 60 ottagono 45 Quindi cliccare in C e in B, D e in B, E e B... fino a chiudere la figura. Disegnare un pentagono, un esagono, un ottagono, un decagono ed un poligono a 18 lati.
22 La geometria con Geogebra Esercizi per la seconda media 50 [Esercizio 46] Disegno dell esagono regolare (metodo 1) Disegnare il segmento AB, lato dell esagono regolare con A(2,1) e B(5,1). Disegnare la circonferenza di centro A e raggio AB e quella di centro B e raggio BA con Icona6> Circonferenza di dato centro. Determinando l intersezione superiore C. Con centro C e raggio CA disegnare la circonferenza e trovare le intersezioni D ed E con le due precedenti circonferenze. Con centro in E e raggio EB, centro in D e raggio DA trovare le intersezioni F e G con la circonferenza di centro C. Con lo strumento Icona5> Poligono unire in ordine i punti FGEBADF e nascondere le circonferenze. [Esercizio 47] Costruzione dell esagono regolare (metodo 2) Disegnare il segmento AB esattamente verticale di 6 quadretti e determinare il punto medio C. Disegnare con Icona6> Circonferenza di dato centro la circonferenza di centro C e raggio AC e le circonferenze di centro A e raggio AB e quella di centro B e raggio BA, individuare le loro intersezioni D ed E. Prendere ere sul segmento AC i punti F e G distanti rispettivamente 2 e 4 quadretti da B e tracciare le semirette DG e DF individuando i punti di intersezione H ed I con la prima circonferenza e le semirette EG ed EF individuando i punti di intersezione K e J ancora a con la prima circonferenza. Disegnare l esagono AHIBJKA con Icona5> Poligono.
23 La geometria con Geogebra Esercizi per la seconda media 60 quadrato ABIH= +Poly4 Somma aree quadrati ACDE e BGFC= +(Poly2+Poly3). Spostare quindi il punto C, cosa si osserva? [Esercizio 64] Mediane di un triangolo, proprietà 1 Disegnare con lo strumento Icona5> Poligono il triangolo di vertici A(2,2), B(8,4), C(4,9), trovare i punti medi dei lati AB e BC con Icona2> Punto medio o centro. Tracciare con lo strumento segmento tra due punti le mediane AE e CD; individuare la loro intersezione F. Tracciare i segmenti AF, EF, CF e DF e calcolare la misura di ciascuno con lo strumento Testo (ad esempio Il segmento AF misura = +f + cm ). Quale relazione c è tra
24 La geometria con Geogebra Esercizi per la seconda media 61 AF e EF e tra CF ed FD? Provare a spostare uno dei vertici. Cosa accade? Con lo strumento Testo scrivere <Il baricentro di un triangolo divide le mediane in due parti delle quali una è doppia dell altra>. [Esercizio 65] Mediane di un triangolo, proprietà 2 Disegnare il segmento AB (a), per l estremo B tracciare la perpendicolare ad AB (retta b). Prendere su questa retta un punto C a piacere e disegnare il segmento AC. Che tipo di triangolo è ABC? Trovare il punto medio D di AC e disegnare il segmento BD (mediana di AC). Con lo strumento Icona8> Distanza cliccare su AC e BD per calcolarne la misura. Quale relazione c è tra i due segmenti? Con lo strumento Testo digitare <In un triangolo rettangolo la mediana relativa all ipotenusa è la metà dell ipotenusa stessa.> [Esercizio 66] Punti notevoli del triangolo isoscele Disegnare il segmento di estremi A(2,2) e B(10,2) trovare il punto medio C e tracciare la perpendicolare ad AB passante per C (retta b). Su questa retta prendere il punto D (6,7) e disegnare con lo strumento Icona5> Poligono il triangolo ABD. Tracciare la perpendicolare al lato DB condotta da A e trovare l intersezione tra le due altezze (ortocentro). Nascondere le due rette. Tracciare gli assi dei lati AD e DB (Icona4> asse di un segmento) e determinare l intersezione F (circocentro) poi nascondere gli assi. Determinare i punti medi dei lati AD (G) e DB (H) e tracciare i segmenti AH e BG trovando la loro intersezione I (baricentro) nascondendo poi i due segmenti. Disegnare le bisettrici (Icona4> Bisettrice) degli angoli DBA e BAD (cliccare in DB e AB poi in AB e AD) e determinare l intersezione J. Nascondere le bisettrici e tracciare il segmento DC.
25 La geometria con Geogebra Esercizi per la seconda media 62 Come risultano Ortocentro, Baricentro, Incentro e Circocentro rispetto a questo segmento? Con lo strumento Testo misurare i lati AB, AD e DB (a, b_1 e a_1) poi cliccare col tasto destro sul punto D nella finestra algebra e scegliere Proprietà> Algebra> Incremento> 0,01> Chiudi.. Cliccare di nuovo sul punto D col tasto sinistro e agire sul + e del tastierino numerico. Cosa si può osservare? In quale tipo di triangolo i 4 punti notevoli vanno a coincidere in un punto solo? [Esercizio 67] Punti notevoli del triangolo equilatero Disegnare il segmento di estremi A(2,2) e B(6,2) poi con lo strumento Icona5> Circonferenza di dato centro costruire il triangolo equilatero ABC e ripassarlo con lo strumento Icona5> Poligono. Misurare gli angoli interni (cliccare dentro al triangolo dopo aver preso lo strumento Icona8> Angolo e nella Finestra Algebra osservare la misura dei lati e degli angoli. Cosa si può dedurre? Determinare l ortocentro e nascondere le rette, il baricentro e nascondere le rette, il circocentro e nascondere le rette ed infine l incentro e nascondere le rette. Cosa si può dire riguardo al punto d incontro delle altezze, delle mediane, degli assi e delle bisettrici?
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
DISPENSA DI GEOMETRIA
 Il software di geometria dinamica Geogebra GeoGebra è un programma matematico che comprende geometria, algebra e analisi. È sviluppato da Markus Hohenwarter presso la Florida Atlantic University per la
Il software di geometria dinamica Geogebra GeoGebra è un programma matematico che comprende geometria, algebra e analisi. È sviluppato da Markus Hohenwarter presso la Florida Atlantic University per la
Geogebra. Numero lati: Numero angoli: Numero diagonali:
 TRIANGOLI Geogebra IL TRIANGOLO 1. Fai clic sull icona Ic2 e nel menu a discesa scegli Nuovo punto : fai clic all interno della zona geometria e individua il punto A. Fai di nuovo clic per individuare
TRIANGOLI Geogebra IL TRIANGOLO 1. Fai clic sull icona Ic2 e nel menu a discesa scegli Nuovo punto : fai clic all interno della zona geometria e individua il punto A. Fai di nuovo clic per individuare
Quickstart. Cos è GeoGebra? Notizie in pillole
 Quickstart Cos è GeoGebra? Un software di Matematica Dinamica in un pacchetto semplice da usare Per l apprendimento e la didattica a tutti i livelli scolastici Comprende geometria, algebra, tabelle, grafici,
Quickstart Cos è GeoGebra? Un software di Matematica Dinamica in un pacchetto semplice da usare Per l apprendimento e la didattica a tutti i livelli scolastici Comprende geometria, algebra, tabelle, grafici,
Guida rapida - versione Web e Tablet
 Guida rapida - versione Web e Tablet Cos è GeoGebra? Un pacchetto completo di software di matematica dinamica Dedicato all apprendimento e all insegnamento a qualsiasi livello scolastico Gestisce interattivamente
Guida rapida - versione Web e Tablet Cos è GeoGebra? Un pacchetto completo di software di matematica dinamica Dedicato all apprendimento e all insegnamento a qualsiasi livello scolastico Gestisce interattivamente
r.berardi COSTRUZIONI GEOMETRICHE
 r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti. Equazioni e Disequazioni
 Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti Equazioni e Disequazioni Ripasso generale relativo alla risoluzione di equazioni, disequazioni,
Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti Equazioni e Disequazioni Ripasso generale relativo alla risoluzione di equazioni, disequazioni,
Punti notevoli di un triangolo
 Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
CONTROLLO ORTOGRAFICO E GRAMMATICALE
 CONTROLLO ORTOGRAFICO E GRAMMATICALE Quando una parola non è presente nel dizionario di Word, oppure nello scrivere una frase si commettono errori grammaticali, allora si può eseguire una delle seguenti
CONTROLLO ORTOGRAFICO E GRAMMATICALE Quando una parola non è presente nel dizionario di Word, oppure nello scrivere una frase si commettono errori grammaticali, allora si può eseguire una delle seguenti
LA FINESTRA DI OPEN OFFICE CALC
 LA FINESTRA DI OPEN OFFICE CALC Barra di Formattazione Barra Standard Barra del Menu Intestazione di colonna Barra di Calcolo Contenuto della cella attiva Indirizzo della cella attiva Cella attiva Intestazione
LA FINESTRA DI OPEN OFFICE CALC Barra di Formattazione Barra Standard Barra del Menu Intestazione di colonna Barra di Calcolo Contenuto della cella attiva Indirizzo della cella attiva Cella attiva Intestazione
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
A destra è delimitata dalla barra di scorrimento verticale, mentre in basso troviamo una riga complessa.
 La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
Guida all uso di Java Diagrammi ER
 Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Il programma CONFELMOD CAD creazione e modifica
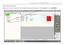 CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry
 LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
DIAGRAMMA CARTESIANO
 DIAGRAMMA CARTESIANO Imparerai ora a costruire con excel un diagramma cartesiano. Inizialmente andremo a porre sul grafico un solo punto, lo vedremo cambiare di posizione cambiando i valori nelle celle
DIAGRAMMA CARTESIANO Imparerai ora a costruire con excel un diagramma cartesiano. Inizialmente andremo a porre sul grafico un solo punto, lo vedremo cambiare di posizione cambiando i valori nelle celle
4. Fondamenti per la produttività informatica
 Pagina 36 di 47 4. Fondamenti per la produttività informatica In questo modulo saranno compiuti i primi passi con i software applicativi più diffusi (elaboratore testi, elaboratore presentazioni ed elaboratore
Pagina 36 di 47 4. Fondamenti per la produttività informatica In questo modulo saranno compiuti i primi passi con i software applicativi più diffusi (elaboratore testi, elaboratore presentazioni ed elaboratore
Liceo G.B. Vico Corsico
 Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Windows 8 App per tablet
 Windows 8 App per tablet GeoGebra Settembre 2013 Cosa è GeoGebra? GeoGebra è un software di matematica dinamica per tutti i livelli educativi, dedicato alla didattica e alla valutazione. Dispone di molte
Windows 8 App per tablet GeoGebra Settembre 2013 Cosa è GeoGebra? GeoGebra è un software di matematica dinamica per tutti i livelli educativi, dedicato alla didattica e alla valutazione. Dispone di molte
Introduzione al Cabri
 Lo schermo di Cabri II Introduzione al Cabri All avvio lo schermo di Cabri II presenta due barre: La barra dei menu classica; La barra delle icone, che contiene tutti gli strumenti necessari per le costruzioni
Lo schermo di Cabri II Introduzione al Cabri All avvio lo schermo di Cabri II presenta due barre: La barra dei menu classica; La barra delle icone, che contiene tutti gli strumenti necessari per le costruzioni
Capitolo 3. L applicazione Java Diagrammi ER. 3.1 La finestra iniziale, il menu e la barra pulsanti
 Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Piano Lauree Scientifiche Progetto MATEMATICA e STATISTICA Sapienza Università di Roma a.a. 2010/11
 Piano Lauree Scientifiche Progetto MATEMATICA e STATISTICA Sapienza Università di Roma a.a. 2010/11 Corso di formazione rivolto a insegnanti delle Superiori Giuseppe Accascina accascina@dmmm.uniroma1.it
Piano Lauree Scientifiche Progetto MATEMATICA e STATISTICA Sapienza Università di Roma a.a. 2010/11 Corso di formazione rivolto a insegnanti delle Superiori Giuseppe Accascina accascina@dmmm.uniroma1.it
Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente.
 Linee Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente. a. curva spezzata retta mista aperta chiusa b. curva spezzata
Linee Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente. a. curva spezzata retta mista aperta chiusa b. curva spezzata
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Gestione Rapporti (Calcolo Aree)
 Gestione Rapporti (Calcolo Aree) L interfaccia dello strumento generale «Gestione Rapporti»...3 Accedere all interfaccia (toolbar)...3 Comandi associati alle icone della toolbar...4 La finestra di dialogo
Gestione Rapporti (Calcolo Aree) L interfaccia dello strumento generale «Gestione Rapporti»...3 Accedere all interfaccia (toolbar)...3 Comandi associati alle icone della toolbar...4 La finestra di dialogo
Guida rapida. Cos è GeoGebra? Notizie in pillole
 Guida rapida Cos è GeoGebra? Un pacchetto completo di software di matematica dinamica Dedicato all apprendimento e all insegnamento a qualsiasi livello scolastico Riunisce geometria, algebra, tabelle,
Guida rapida Cos è GeoGebra? Un pacchetto completo di software di matematica dinamica Dedicato all apprendimento e all insegnamento a qualsiasi livello scolastico Riunisce geometria, algebra, tabelle,
Personalizza. Page 1 of 33
 Personalizza Aprendo la scheda Personalizza, puoi aggiungere, riposizionare e regolare la grandezza del testo, inserire immagini e forme, creare una stampa unione e molto altro. Page 1 of 33 Clicca su
Personalizza Aprendo la scheda Personalizza, puoi aggiungere, riposizionare e regolare la grandezza del testo, inserire immagini e forme, creare una stampa unione e molto altro. Page 1 of 33 Clicca su
EasyPrint v4.15. Gadget e calendari. Manuale Utente
 EasyPrint v4.15 Gadget e calendari Manuale Utente Lo strumento di impaginazione gadget e calendari consiste in una nuova funzione del software da banco EasyPrint 4 che permette di ordinare in maniera semplice
EasyPrint v4.15 Gadget e calendari Manuale Utente Lo strumento di impaginazione gadget e calendari consiste in una nuova funzione del software da banco EasyPrint 4 che permette di ordinare in maniera semplice
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
Patente Europea di Informatica ECDL Modulo 4. Lezione 3: Grafici Impostazione e verifica del foglio Opzioni di stampa. Anno 2011/2012 Syllabus 5.
 Patente Europea di Informatica ECDL Modulo 4 Lezione 3: Grafici Impostazione e verifica del foglio Opzioni di stampa Anno 2011/2012 Syllabus 5.0 Una delle funzioni più importanti di un foglio elettronico
Patente Europea di Informatica ECDL Modulo 4 Lezione 3: Grafici Impostazione e verifica del foglio Opzioni di stampa Anno 2011/2012 Syllabus 5.0 Una delle funzioni più importanti di un foglio elettronico
progetti guidati EXCEL Dalla tabella statistica al relativo grafico
 EXCEL progetti guidati Dalla tabella statistica al relativo grafico L interpretazione di dati relativi all andamento di un particolare fenomeno risulta più agevole se tali dati sono rappresentati in forma
EXCEL progetti guidati Dalla tabella statistica al relativo grafico L interpretazione di dati relativi all andamento di un particolare fenomeno risulta più agevole se tali dati sono rappresentati in forma
LA FINESTRA DI EXCEL
 1 LA FINESTRA DI EXCEL Barra di formattazione Barra degli strumenti standard Barra del titolo Barra del menu Intestazione di colonna Contenuto della cella attiva Barra della formula Indirizzo della cella
1 LA FINESTRA DI EXCEL Barra di formattazione Barra degli strumenti standard Barra del titolo Barra del menu Intestazione di colonna Contenuto della cella attiva Barra della formula Indirizzo della cella
2.2.2.1 Identificare le diverse parti di una finestra: barra del titolo, barra dei menu, barra degli strumenti, barra di stato, barra di scorrimento.
 Uso del computer e gestione dei file 57 2.2.2.1 Identificare le diverse parti di una finestra: barra del titolo, barra dei menu, barra degli strumenti, barra di stato, barra di scorrimento. All interno
Uso del computer e gestione dei file 57 2.2.2.1 Identificare le diverse parti di una finestra: barra del titolo, barra dei menu, barra degli strumenti, barra di stato, barra di scorrimento. All interno
EXCEL ESERCIZIO DELLE SETTIMANE
 EXCEL ESERCIZIO DELLE SETTIMANE 1. PREPARAZIONE 1. Aprire Microsoft Office Excel 2007. 2. Creare una nuova cartella di lavoro. 3. Aggiungere due fogli di lavoro come mostrato in figura: 4. Rinominare i
EXCEL ESERCIZIO DELLE SETTIMANE 1. PREPARAZIONE 1. Aprire Microsoft Office Excel 2007. 2. Creare una nuova cartella di lavoro. 3. Aggiungere due fogli di lavoro come mostrato in figura: 4. Rinominare i
Operazioni fondamentali
 Elaborazione testi Le seguenti indicazioni valgono per Word 2007, ma le procedure per Word 2010 sono molto simile. In alcuni casi (per esempio, Pulsante Office /File) ci sono indicazioni entrambe le versioni.
Elaborazione testi Le seguenti indicazioni valgono per Word 2007, ma le procedure per Word 2010 sono molto simile. In alcuni casi (per esempio, Pulsante Office /File) ci sono indicazioni entrambe le versioni.
IMPOSTARE UNA MASCHERA CHE SI APRE AUTOMATICAMENTE
 IMPOSTARE UNA MASCHERA CHE SI APRE AUTOMATICAMENTE Access permette di specificare una maschera che deve essere visualizzata automaticamente all'apertura di un file. Vediamo come creare una maschera di
IMPOSTARE UNA MASCHERA CHE SI APRE AUTOMATICAMENTE Access permette di specificare una maschera che deve essere visualizzata automaticamente all'apertura di un file. Vediamo come creare una maschera di
CREARE PRESENTAZIONI CON POWERPOINT
 CREARE PRESENTAZIONI CON POWERPOINT Creare presentazioni per proiettare album fotografici su PC, presentare tesi di laurea, o esporre prodotti e servizi. Tutto questo lo puoi fare usando un programma di
CREARE PRESENTAZIONI CON POWERPOINT Creare presentazioni per proiettare album fotografici su PC, presentare tesi di laurea, o esporre prodotti e servizi. Tutto questo lo puoi fare usando un programma di
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
[Tutoriale] Realizzare un cruciverba con Excel
![[Tutoriale] Realizzare un cruciverba con Excel [Tutoriale] Realizzare un cruciverba con Excel](/thumbs/30/14141462.jpg) [Tutoriale] Realizzare un cruciverba con Excel Aperta in Excel una nuova cartella (un nuovo file), salviamo con nome in una precisa nostra cartella. Cominciamo con la Formattazione del foglio di lavoro.
[Tutoriale] Realizzare un cruciverba con Excel Aperta in Excel una nuova cartella (un nuovo file), salviamo con nome in una precisa nostra cartella. Cominciamo con la Formattazione del foglio di lavoro.
Concetti Fondamentali
 EXCEL Modulo 1 Concetti Fondamentali Excel è un applicazione che si può utilizzare per: Creare un foglio elettronico; costruire database; Disegnare grafici; Cos è un Foglio Elettronico? Un enorme foglio
EXCEL Modulo 1 Concetti Fondamentali Excel è un applicazione che si può utilizzare per: Creare un foglio elettronico; costruire database; Disegnare grafici; Cos è un Foglio Elettronico? Un enorme foglio
Tutorial 3DRoom. 3DRoom
 Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
EXCEL PER WINDOWS95. sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area di lavoro, detta foglio di lavoro,
 EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
EXCEL PER WINDOWS95 1.Introduzione ai fogli elettronici I fogli elettronici sono delle applicazioni che permettono di sfruttare le potenzialità di calcolo dei personal computer. Essi si basano su un area
Il controllo della visualizzazione
 Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Word Libre Office. Barra degli strumenti standard Area di testo Barra di formattazione
 SK 1 Word Libre Office Se sul video non compare la barra degli strumenti di formattazione o la barra standard Aprite il menu Visualizza Barre degli strumenti e selezionate le barre che volete visualizzare
SK 1 Word Libre Office Se sul video non compare la barra degli strumenti di formattazione o la barra standard Aprite il menu Visualizza Barre degli strumenti e selezionate le barre che volete visualizzare
PROGRAMMA SVOLTO NELLA CLASSE I E A.S. 2012/2013 DISCIPLINA : MATEMATICA DOCENTI : CECILIA SAMPIERI, TAMARA CECCONI
 PROGRAMMA SVOLTO NELLA CLASSE I E A.S. 2012/2013 LIBRO DI TESTO:L. Sasso Nuova Matematica a colori Algebra e Geometria 1 edizione Azzurra ed. Petrini TEMA A I numeri e linguaggio della Matemati Unità 1
PROGRAMMA SVOLTO NELLA CLASSE I E A.S. 2012/2013 LIBRO DI TESTO:L. Sasso Nuova Matematica a colori Algebra e Geometria 1 edizione Azzurra ed. Petrini TEMA A I numeri e linguaggio della Matemati Unità 1
L analisi dei dati. Capitolo 4. 4.1 Il foglio elettronico
 Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Scuola di Wrenn, Dipartimento di Matematica. Investigare cerchi. Questo pacchetto di fogli di lavoro vi fornisce alcune attività per aiutarvi
 Scuola di Wrenn, Dipartimento di Matematica Investigare cerchi Questo pacchetto di fogli di lavoro vi fornisce alcune attività per aiutarvi a scoprire alcune proprietà di cerchi usando The Geometer s Sketchpad.
Scuola di Wrenn, Dipartimento di Matematica Investigare cerchi Questo pacchetto di fogli di lavoro vi fornisce alcune attività per aiutarvi a scoprire alcune proprietà di cerchi usando The Geometer s Sketchpad.
Operazioni fondamentali
 Foglio elettronico Le seguenti indicazioni valgono per Excel 2007, ma le procedure per Excel 2010 sono molto simile. In alcuni casi (per esempio, Pulsante Office /File) ci sono indicazioni entrambe le
Foglio elettronico Le seguenti indicazioni valgono per Excel 2007, ma le procedure per Excel 2010 sono molto simile. In alcuni casi (per esempio, Pulsante Office /File) ci sono indicazioni entrambe le
TEST: Word & Excel. 2014 Tutti i diritti riservati. Computer Facile - www.computerfacile.webnode.it
 TEST: Word & Excel 1. Come viene detta la barra contenente il nome del documento? A. barra del titolo B. barra di stato C. barra del nome D. barra dei menu 2. A cosa serve la barra degli strumenti? A.
TEST: Word & Excel 1. Come viene detta la barra contenente il nome del documento? A. barra del titolo B. barra di stato C. barra del nome D. barra dei menu 2. A cosa serve la barra degli strumenti? A.
CORSO DI INFORMATICA 2
 CORSO DI INFORMATICA 2 RINOMINARE FILE E CARTELLE Metodo 1 1 - clicca con il tasto destro del mouse sul file o cartella che vuoi rinominare (nell esempio Mio primo file ) 2 - dal menu contestuale clicca
CORSO DI INFORMATICA 2 RINOMINARE FILE E CARTELLE Metodo 1 1 - clicca con il tasto destro del mouse sul file o cartella che vuoi rinominare (nell esempio Mio primo file ) 2 - dal menu contestuale clicca
Syllabus (estratto) Foglio elettronico. Excel. Open office - Office. Principio e funzionamento 26/11/2012. A. Ferrari
 Foglio elettronico A. Ferrari Syllabus (estratto) Lavorare con i fogli elettronici e salvarli in diversi formati. Inserire dati nelle celle e applicare modalità appropriate per creare elenchi. Selezionare,
Foglio elettronico A. Ferrari Syllabus (estratto) Lavorare con i fogli elettronici e salvarli in diversi formati. Inserire dati nelle celle e applicare modalità appropriate per creare elenchi. Selezionare,
Prof.ssa Paola Vicard
 DISTRIBUZIONE DI FREQUENZE PER CARATTERI QUALITATIVI Questa nota consiste per la maggior parte nella traduzione (con alcune integrazioni) da Descriptive statistics di J. Shalliker e C. Ricketts, 2000,
DISTRIBUZIONE DI FREQUENZE PER CARATTERI QUALITATIVI Questa nota consiste per la maggior parte nella traduzione (con alcune integrazioni) da Descriptive statistics di J. Shalliker e C. Ricketts, 2000,
On-line Corsi d Informatica sul Web
 On-line Corsi d Informatica sul Web Corso base di Excel Università degli Studi della Repubblica di San Marino Capitolo 1 ELEMENTI DELLO SCHERMO DI LAVORO Aprire Microsoft Excel facendo clic su Start/Avvio
On-line Corsi d Informatica sul Web Corso base di Excel Università degli Studi della Repubblica di San Marino Capitolo 1 ELEMENTI DELLO SCHERMO DI LAVORO Aprire Microsoft Excel facendo clic su Start/Avvio
Foglio elettronico. OpenOffice.org Calc 1.1.3
 Foglio elettronico OpenOffice.org Calc 1.1.3 PRIMI PASSI CON IL FOGLIO ELETTRONICO Aprire il programma Menu Avvio applicazioni Office OpenOffice.org Calc. Chiudere il programma Menu File Esci. Pulsanti
Foglio elettronico OpenOffice.org Calc 1.1.3 PRIMI PASSI CON IL FOGLIO ELETTRONICO Aprire il programma Menu Avvio applicazioni Office OpenOffice.org Calc. Chiudere il programma Menu File Esci. Pulsanti
TRASFORMAZIONI GEOMETRICHE NEL PIANO. Parte 1
 TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
Elementi di Geometria. Lezione 03
 Elementi di Geometria Lezione 03 I triangoli I triangoli sono i poligoni con tre lati e tre angoli. Nelle rappresentazioni grafiche (Figura 32) i vertici di un triangolo sono normalmente contrassegnati
Elementi di Geometria Lezione 03 I triangoli I triangoli sono i poligoni con tre lati e tre angoli. Nelle rappresentazioni grafiche (Figura 32) i vertici di un triangolo sono normalmente contrassegnati
MODULO 3. Microsoft Excel. TEST ED ESERCIZI SU: http://www.informarsi.net/ecdl/excel/index.php
 MODULO 3 Microsoft Excel TEST ED ESERCIZI SU: http:///ecdl/excel/index.php Foglio Elettronico - SpreadSheet Un foglio elettronico (in inglese spreadsheet) è un programma applicativo usato per memorizzare
MODULO 3 Microsoft Excel TEST ED ESERCIZI SU: http:///ecdl/excel/index.php Foglio Elettronico - SpreadSheet Un foglio elettronico (in inglese spreadsheet) è un programma applicativo usato per memorizzare
DISPENSA PER MICROSOFT WORD 2010
 DISPENSA PER MICROSOFT WORD 2010 Esistono molte versioni di Microsoft Word, dalle più vecchie ( Word 97, Word 2000, Word 2003 e infine Word 2010 ). Creazione di documenti Avvio di Word 1. Fare clic sul
DISPENSA PER MICROSOFT WORD 2010 Esistono molte versioni di Microsoft Word, dalle più vecchie ( Word 97, Word 2000, Word 2003 e infine Word 2010 ). Creazione di documenti Avvio di Word 1. Fare clic sul
Il foglio elettronico: Excel
 Il foglio elettronico: Excel Laboratorio di Informatica Corso di Laurea triennale in Biologia Dott. Fabio Aiolli (aiolli@math.unipd.it) Dott.ssa Elisa Caniato (ecaniato@gmail.com) Anno accademico 2007-2008
Il foglio elettronico: Excel Laboratorio di Informatica Corso di Laurea triennale in Biologia Dott. Fabio Aiolli (aiolli@math.unipd.it) Dott.ssa Elisa Caniato (ecaniato@gmail.com) Anno accademico 2007-2008
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
LA FINESTRA DI GOAL (SCHERMATA PRINCIPALE E PANNELLO DEI COMANDI)
 FUNZIONI DEL PROGRAMMA GOAL Il programma GOAL consente all utilizzatore di creare animazioni grafiche rappresentanti schemi, esercitazioni e contrapposizioni tattiche. Le animazioni create possono essere
FUNZIONI DEL PROGRAMMA GOAL Il programma GOAL consente all utilizzatore di creare animazioni grafiche rappresentanti schemi, esercitazioni e contrapposizioni tattiche. Le animazioni create possono essere
Università di L Aquila Facoltà di Biotecnologie Agro-alimentari
 RIFERIMENTI Università di L Aquila Facoltà di Biotecnologie Agro-alimentari Esame di Laboratorio di informatica e statistica Parte 3 (versione 1.0) Il riferimento permette di identificare univocamente
RIFERIMENTI Università di L Aquila Facoltà di Biotecnologie Agro-alimentari Esame di Laboratorio di informatica e statistica Parte 3 (versione 1.0) Il riferimento permette di identificare univocamente
Stampa Unione per lettere tipo
 per lettere tipo Con Stampa Unione è possibile creare lettere tipo, etichette per indirizzi, buste, elenchi indirizzi e liste per la distribuzione via posta elettronica e fax in grandi quantitativi. Lo
per lettere tipo Con Stampa Unione è possibile creare lettere tipo, etichette per indirizzi, buste, elenchi indirizzi e liste per la distribuzione via posta elettronica e fax in grandi quantitativi. Lo
Capitolo 9. Figura 104. Tabella grafico. Si evidenzia l intera tabella A1-D4 e dal menù Inserisci si seleziona Grafico. Si apre la seguente finestra:
 Capitolo 9 I GRAFICI Si apra il Foglio3 e lo si rinomini Grafici. Si crei la tabella seguente: Figura 104. Tabella grafico Si evidenzia l intera tabella A1-D4 e dal menù Inserisci si seleziona Grafico.
Capitolo 9 I GRAFICI Si apra il Foglio3 e lo si rinomini Grafici. Si crei la tabella seguente: Figura 104. Tabella grafico Si evidenzia l intera tabella A1-D4 e dal menù Inserisci si seleziona Grafico.
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
Geogebra matematica dinamica per tutti. Tiziana Segalini liceo Ariosto-Spallanzani Reggio Emilia a.s.2012-2013
 Geogebra matematica dinamica per tutti Tiziana Segalini liceo Ariosto-Spallanzani Reggio Emilia a.s.2012-2013 Geogebra può servire ad un insegnante e ad un allievo: Disegnare grafici di funzioni e non
Geogebra matematica dinamica per tutti Tiziana Segalini liceo Ariosto-Spallanzani Reggio Emilia a.s.2012-2013 Geogebra può servire ad un insegnante e ad un allievo: Disegnare grafici di funzioni e non
INTRODUZIONE A WINDOWS
 INTRODUZIONE A WINDOWS Introduzione a Windows Il Desktop Desktop, icone e finestre Il desktop è una scrivania virtuale in cui si trovano: Icone: piccole immagini su cui cliccare per eseguire comandi o
INTRODUZIONE A WINDOWS Introduzione a Windows Il Desktop Desktop, icone e finestre Il desktop è una scrivania virtuale in cui si trovano: Icone: piccole immagini su cui cliccare per eseguire comandi o
Creazione di percorsi su Colline Veronesi
 Creazione di percorsi su Colline Veronesi Per inserire i dati nel portale Colline Veronesi accedere all indirizzo: http://66.71.191.169/collineveronesi/index.php/admin/users/login Una volta inserito username
Creazione di percorsi su Colline Veronesi Per inserire i dati nel portale Colline Veronesi accedere all indirizzo: http://66.71.191.169/collineveronesi/index.php/admin/users/login Una volta inserito username
E possibile modificare la lingua dei testi dell interfaccia utente, se in inglese o in italiano, dal menu [Tools
 Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli.
 I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli. In ogni triangolo un lato è sempre minore della somma degli altri due e sempre maggiore della loro differenza. Relazione fra i lati di
I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli. In ogni triangolo un lato è sempre minore della somma degli altri due e sempre maggiore della loro differenza. Relazione fra i lati di
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
MAUALE PIATTAFORMA MOODLE
 MAUALE PIATTAFORMA MOODLE La piattaforma moodle ci permette di salvare e creare contenuti didattici. Dal menù principale è possibile: inviare dei messaggi agli altri docenti che utilizzano la piattaforma:
MAUALE PIATTAFORMA MOODLE La piattaforma moodle ci permette di salvare e creare contenuti didattici. Dal menù principale è possibile: inviare dei messaggi agli altri docenti che utilizzano la piattaforma:
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Corso di ordinamento Sessione straordinaria - a.s. 2009-2010 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA
 Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Esame di Informatica CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO CHE COS È UN FOGLIO ELETTRONICO. Facoltà di Scienze Motorie
 Facoltà di Scienze Motorie CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche e funzioni statistiche. Esame di Informatica
Facoltà di Scienze Motorie CHE COS È UN FOGLIO ELETTRONICO Una tabella che contiene parole e numeri che possono essere elaborati applicando formule matematiche e funzioni statistiche. Esame di Informatica
GESTIONE DI FINESTRE, FILE E CARTELLE con Windows XP
 GESTIONE DI FINESTRE, FILE E CARTELLE con Windows XP Desktop (scrivania) Il Desktop è la prima schermata che appare all accensione del computer. icone Barra delle applicazioni Le piccole immagini che appaiono
GESTIONE DI FINESTRE, FILE E CARTELLE con Windows XP Desktop (scrivania) Il Desktop è la prima schermata che appare all accensione del computer. icone Barra delle applicazioni Le piccole immagini che appaiono
geometriche. Parte Sesta Trasformazioni isometriche
 Parte Sesta Trasformazioni isometriche In questa sezione di programma di matematica parliamo della geometria delle trasformazioni che studia le figure geometriche soggette a movimenti. Tali movimenti,
Parte Sesta Trasformazioni isometriche In questa sezione di programma di matematica parliamo della geometria delle trasformazioni che studia le figure geometriche soggette a movimenti. Tali movimenti,
Prof.ssa Paola Vicard
 Questa nota consiste perlopiù nella traduzione da Descriptive statistics di J. Shalliker e C. Ricketts, 2000, University of Plymouth Consideriamo come esempio il data set contenuto nel foglio excel esercizio1_dati.xls.
Questa nota consiste perlopiù nella traduzione da Descriptive statistics di J. Shalliker e C. Ricketts, 2000, University of Plymouth Consideriamo come esempio il data set contenuto nel foglio excel esercizio1_dati.xls.
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
PROCEDURA PER L UTILIZZO DELLO SPAZIO CARTA. Preparazione dello SPAZIO CARTA nel file dove inserire la mascherina.
 PROCEDURA PER L UTILIZZO DELLO SPAZIO CARTA. ing. g. mongiello Versione aggiornata AA 2012-2013 SI CONSIGLIA DI STAMPARE QUESTE ISTRUZIONI. ATTENZIONE: NON USARE IL FILE DEL LAYOUT PER CREARE IL NUOVO
PROCEDURA PER L UTILIZZO DELLO SPAZIO CARTA. ing. g. mongiello Versione aggiornata AA 2012-2013 SI CONSIGLIA DI STAMPARE QUESTE ISTRUZIONI. ATTENZIONE: NON USARE IL FILE DEL LAYOUT PER CREARE IL NUOVO
9 tecniche di selezione testi formattazione, copiare e incollare testi
 9 tecniche di selezione testi formattazione, copiare e incollare testi Creare un file (OpenOffice.org Writer) dentro ad una cartella e digitare un breve testo Per prima cosa occorre creare un file di testo
9 tecniche di selezione testi formattazione, copiare e incollare testi Creare un file (OpenOffice.org Writer) dentro ad una cartella e digitare un breve testo Per prima cosa occorre creare un file di testo
Software standard Alpi Label Ver. 2.2.0.0
 Pag. 1 di 16 Manuale utente Software standard Alpi Label Ver. 2.2.0.0 Pag. 2 di 16 1 SOMMARIO Sommario 1 Sommario... 2 2 Specifiche Tecniche... 3 3 Maschera Principale... 4 4 Funzioni menù... 7 Pag. 3
Pag. 1 di 16 Manuale utente Software standard Alpi Label Ver. 2.2.0.0 Pag. 2 di 16 1 SOMMARIO Sommario 1 Sommario... 2 2 Specifiche Tecniche... 3 3 Maschera Principale... 4 4 Funzioni menù... 7 Pag. 3
Tabelle 3.4. Unità didattica. Copyright 2009 Apogeo. Obiettivi. Prerequisiti
 Unità didattica 3.4 In questa unità realizzerai un annuncio da appendere in una bacheca per la vendita del tuo lettore MP3. Il tuo annuncio deve essere gradevole e armonioso in modo che, tra tanti altri
Unità didattica 3.4 In questa unità realizzerai un annuncio da appendere in una bacheca per la vendita del tuo lettore MP3. Il tuo annuncio deve essere gradevole e armonioso in modo che, tra tanti altri
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida. 4 x
 UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
Come costruire una presentazione. PowerPoint 1. ! PowerPoint permette la realizzazione di presentazioni video ipertestuali, animate e multimediali
 PowerPoint Come costruire una presentazione PowerPoint 1 Introduzione! PowerPoint è uno degli strumenti presenti nella suite Office di Microsoft! PowerPoint permette la realizzazione di presentazioni video
PowerPoint Come costruire una presentazione PowerPoint 1 Introduzione! PowerPoint è uno degli strumenti presenti nella suite Office di Microsoft! PowerPoint permette la realizzazione di presentazioni video
. A primi passi con microsoft a.ccepss SommarIo: i S 1. aprire e chiudere microsoft access Start (o avvio) l i b tutti i pro- grammi
 Capitolo Terzo Primi passi con Microsoft Access Sommario: 1. Aprire e chiudere Microsoft Access. - 2. Aprire un database esistente. - 3. La barra multifunzione di Microsoft Access 2007. - 4. Creare e salvare
Capitolo Terzo Primi passi con Microsoft Access Sommario: 1. Aprire e chiudere Microsoft Access. - 2. Aprire un database esistente. - 3. La barra multifunzione di Microsoft Access 2007. - 4. Creare e salvare
On-line Corsi d Informatica sul web
 On-line Corsi d Informatica sul web Corso base di FrontPage Università degli Studi della Repubblica di San Marino Capitolo1 CREARE UN NUOVO SITO INTERNET Aprire Microsoft FrontPage facendo clic su Start/Avvio
On-line Corsi d Informatica sul web Corso base di FrontPage Università degli Studi della Repubblica di San Marino Capitolo1 CREARE UN NUOVO SITO INTERNET Aprire Microsoft FrontPage facendo clic su Start/Avvio
Laboratorio Informatico di base A.A. 2013/2014 Dipartimento di Scienze Aziendali e Giuridiche Università della Calabria Dott.
 Strumenti di presentazione (Microsoft PowerPoint) Laboratorio Informatico di base A.A. 2013/2014 Dipartimento di Scienze Aziendali e Giuridiche Università della Calabria Dott. Pierluigi Muoio (pierluigi.muoio@unical.it)
Strumenti di presentazione (Microsoft PowerPoint) Laboratorio Informatico di base A.A. 2013/2014 Dipartimento di Scienze Aziendali e Giuridiche Università della Calabria Dott. Pierluigi Muoio (pierluigi.muoio@unical.it)
