Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
|
|
|
- Casimiro Vigano
- 5 anni fa
- Visualizzazioni
Transcript
1 Inggnri Sinz Informtih - Csn A.A. 3- iln@s.unio.it, pitro.iln@unio.it
2 : psuooi Clol il osto l mmino minimo un vrti sorgnt s tutti i rstnti vrtii nl grfo. Clol un lro i oprtur i mmini minimi (shortst pth tr) on ri s. I psi gli rhi possono ssr ngtivi. Può ssr utilizzto pr trminr s il grfo ontin un ilo on pso ngtivo. In tl so, non sist uno shortst pth tr l lgoritmo trmin on FALSE. In so ontrrio, trmin on TRUE i punttori nl vttor p[] prmttono i riostruir l lro i oprtur. I: pr V itrzioni visit tutti gli rhi (u, v) in E ppli l Rlx(u, v). Costo omputzionl: O( V E )
3 : psuooi Inizilizzzion on sorgnt. []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=nil
4 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=nil
5 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=nil
6 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=nil
7 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=
8 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]=nil 3 []= p[]=nil []= p[]=
9 : psuooi Roun, ro (, ). []= p[]=nil []= p[]=nil []= p[]= 3 []= p[]=nil []= p[]=
10 : psuooi Roun, ro (, ). []= p[]=5 []= p[]=nil []= p[]= 3 []= p[]=nil []= p[]=
11 : psuooi Roun, ro (, ). []= p[]=5 []=6 p[]= []= p[]= 3 []= p[]=nil []= p[]=
12 : psuooi Fin roun. Non i sono ultriori moifih pr i roun,.., 5. []= p[]=5 []=6 p[]= []= p[]= 3 []= p[]=nil []= p[]=
13 : psuooi Shortst pth tr sorgnt. []= p[]=nil []= p[]= []= p[]= []= p[]=6 []= p[]=5
14 : psuooi : psuooi : funtion BllmnFor(G, s) : InitSinglSour(G, s) 3: for i to VrtxSiz(G) o : for h g (u, v) in G o 5: Rlx(u, v) 6: n for 7: n for 8: for h g (u, v) in G o 9: if [v] > [u] + w(u, v) thn : rturn FALSE : n if : n for 3: rturn TRUE : n funtion : prour InitSinglSour(G, s) : for h vrtx v in G o 3: [v] : p[v] NIL 5: n for 6: [s] 7: n prour : prour Rlx(u, v) : if [v] > [u] + w(u, v) thn 3: [v] [u] + w(u, v) : p[v] u 5: n if 6: n prour Qul implmntzion è mggiormnt ffiint: on list o mtrii i inz?
15 Soisfiilità ooln: finizioni Soisfiilità ooln SAT SAT: smpio SAT: psuooi Un formul norml ongiuntiv (CNF) è un ongiunzion i lusol, ov l lusol sono un isgiunzion i lttrli (vriili ooln). Ex. x, y, z vriili ooln Φ = (x y z) ( x z) x y z () Un CNF l ui lusol ino k vriili vin himt kcnf. Ex. CNF Φ = (x y) (x z) ( x z) (y z) () Un CNF si i soisfiil s sist un ssgnmnto ll vriili h l rn vr. Ex. L formul Φ in Eq. () non è soisfiil L formul Φ in Eq. () è soisfiil pr x =, y =, z = ( =FALSE, =TRUE)
16 Soisfiilità ooln: prolm Soisfiilità ooln SAT SAT: smpio SAT: psuooi Prolm (SAT). Dt in input un formul ooln Φ in CNF, trminr s Φ è soisfiil. Prolm (ksat). Dt in input un formul ooln Φ in kcnf, trminr s Φ è soisfiil. Complssità omputzionl: SAT è un prolm NP-omplto ksat è un prolm NP-omplto pr k 3 SAT è un prolm risolviil in tmpo polinomil
17 SAT Algoritmi vnzti su grfi: mmini minimi sorgnt singol Soisfiilità ooln SAT SAT: smpio SAT: psuooi I pr SAT. Costruimo il grfo ll implizioni G(Φ) pr l formul Φ. Vrifihimo h nssun omponnt fortmnt onnss i G(Φ) ontng un oppi i vrtii x, x (ov x è un vriil ooln nll formul Φ) Costruzion l grfo ll implizioni pr SAT. E vrifit l sgunt proprità pr un lusol (x y) : s (x y) è vr llor x = y y Costruimo il grfo G(F ) nl sgunt moo: = x pr ogni vriil x in Φ, il grfo G(Φ) ontin i vrtii x x pr ogni lusol (x y) in Φ, il grfo G(Φ) ontin gli rhi x y y x. Lmm S il grfo G(Φ) ontin un prorso x x... x n x n llor ontin nh il prorso x n x n... x x. Proof. E suffiint notr h s sist in G(Φ) un ro x i x j llor, pr finizion, sist in Φ un lusol ( x i x j ) quini sist in G(Φ) nh l ro x j x i.
18 SAT Algoritmi vnzti su grfi: mmini minimi sorgnt singol Soisfiilità ooln SAT SAT: smpio SAT: psuooi Thorm Un formul Φ in CNF non è soisfiil s solo s sist un lttrl x in Φ tl h: sist in G(Φ) un mmino x x, sist in G(Φ) un mmino x x. Proof. Pr ipotsi in G(Φ) sistono u mmini x... x x.. x. S x =TRUE tru llor l tn i implizioni x.. x i port vr x =TRUE. Simmtrimnt, s x =TRUE ottnimo x=true. In ntrmi in si, imo un ontrizion quini x non può ssr nè TRUE nè FALSE. Pr ipotsi G(Φ) non è soisfiil. Assumimo pr ssuro h pr ogni lttrl x non sist un mmino x x oppur x x. Esguimo il sgunt lgoritmo (trsurno luni ttgli i onsistnz): Sglimo un x non nor visitto pr ui non sist un prorso vrso x. Assgnmo TRUE x tutti i vrtii rggiungiili x. 3 Assgnmo FALSE l prorso omplmntr/ngto h sist pr il Lmm prnt. Riptimo fino quno tutti i vrtii sono stti ssgnti. Qusto lgoritmo prou un ssgnmnto h soisf Φ, ontrino l ipotsi.
19 SAT: smpio Soisfiilità ooln SAT SAT: smpio SAT: psuooi Consirimo l sgunt formul in CNF. Φ = (x y) (x z) ( x z) (y z) Tll i possiili ssgnmnti oolni pr l vriili x, y, z x y z FALSE TRUE FALSE FALSE FALSE TRUE FALSE TRUE Not. Pr un formul ontnnt n vriili sistono n ssgnmnti / possiili. Qunto tmpo è nssrio pr lnr tutti gli ssgnmnti possiili in un formul ontnnt n = vriili? Assumimo i vr isposizion un prossor h poss lolr/vrifir 9 ssgnmnti l sono. Elnr tutti gli ssgnmnti in un formul on n = vriili ost quini 9.3 soni 3 nni > nni ( tà ll univrso)
20 SAT: smpio Soisfiilità ooln SAT SAT: smpio SAT: psuooi Costruzion l grfo ll implizioni. Φ = (x y) (x z) ( x z) (y z) x y j x y x y y x z j x z x z z x j x z x x z x y x z j y z y z z y Notimo h: Il grfo G(Φ) ontin un prorso z z m non z z. Il grfo G(Φ) non ontin nssun prorso x x y y. Il grfo G(Φ) non possi nssun omponnt fortmnt onnss. Pr il Torm prnt, onluimo h l formul Φ è soisfiil.
21 SAT: psuooi Soisfiilità ooln SAT SAT: smpio SAT: psuooi : funtion SAT(Φ) : G ImplitionGrph(Φ) 3: for h vrtx v in G o : if thr xist pths v.. v n v... v in G thn 5: rturn FALSE 6: n if 7: n for 8: rturn TRUE 9: n funtion Com possimo vrifir l onizion sull rig utilizzno uno gli lgoritmi visti urnt il lortorio?
Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
 Inggnri Sinz Informtih - Csn A.A. - iln@s.unio.it, pitro.iln@unio.it Algoritmo i Floy-Wrshll Algoritmo Floy-Wrshll Algoritmo i Floy-Wrshll: psuooi Clol il osto l mmino minimo tr tutt l oppi i vrtii in
Inggnri Sinz Informtih - Csn A.A. - iln@s.unio.it, pitro.iln@unio.it Algoritmo i Floy-Wrshll Algoritmo Floy-Wrshll Algoritmo i Floy-Wrshll: psuooi Clol il osto l mmino minimo tr tutt l oppi i vrtii in
Informatica 3. Informatica 3. LEZIONE 25: Algoritmi sui grafi. Lezione 25 - Modulo 1. Problema. Notazioni per il percorso più breve
 Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Esempio 1 Consideriamo un grafo G con insieme di nodi. mentre l insieme di archi é il seguente sottinsieme di coppie di nodi in V
 1 Tori i grfi Pr prim os imo l finizion i grfo. Dfinizion 1 Un grfo G é ostituito un oppi i insimi (V, A) ov V é tto insim i noi A é tto insim i rhi é un sottinsim i tutt l possiili oppi i noi in V. S
1 Tori i grfi Pr prim os imo l finizion i grfo. Dfinizion 1 Un grfo G é ostituito un oppi i insimi (V, A) ov V é tto insim i noi A é tto insim i rhi é un sottinsim i tutt l possiili oppi i noi in V. S
Algoritmi e Strutture Dati. Grafi
 Algoritmi Struttur Dti Grfi Alrto Montrsor Univrsità i Trnto 08//7 This work is lins unr Crtiv Commons Attriution-ShrAlik 4.0 Intrntionl Lins. Sommrio Introuzion Dfinizioni Spifi Mmorizzzion Visit i grfi
Algoritmi Struttur Dti Grfi Alrto Montrsor Univrsità i Trnto 08//7 This work is lins unr Crtiv Commons Attriution-ShrAlik 4.0 Intrntionl Lins. Sommrio Introuzion Dfinizioni Spifi Mmorizzzion Visit i grfi
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Sistemi lineari COGNOME... NOME... Classe... Data...
 Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
Circuiti Nel progettare un circuito destinato a svolgere una certa funzione normalmente si hanno a disposizione i seguenti elementi:
 Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica
 Modlli di Sistmi di Produzion Modlli Algoritmi dll Logisti 000- Prolm dl ommsso viggitor: EURISTICHE CARLO MANNINO Spinz Univrsità di Rom Diprtimnto di Informti Sistmisti Euristih pr il TSP simmtrio Considrimo
Modlli di Sistmi di Produzion Modlli Algoritmi dll Logisti 000- Prolm dl ommsso viggitor: EURISTICHE CARLO MANNINO Spinz Univrsità di Rom Diprtimnto di Informti Sistmisti Euristih pr il TSP simmtrio Considrimo
1 a. 1 b. Rappresenta i seguenti numeri su una retta orientata, scegliendo autonomamente una opportuna unità di misura. b 1
 Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Corso di Automi e Linguaggi Formali Parte 3
 Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Cammini minimi in un grafo orientato pesato. Un problema di percorso. Problemi di ottimizzazione
 Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
+ poligoni e l equivalenza di figure piane + triangoli + quadrilateri
 + poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
+ poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
Il problema da un milione di dollari
 Il prolem un milione i ollri SienzOrient: Informti Ginlu Rossi www.informti.unirom2.it (www.informti.unirom2.it) Prolem $ 000 000 / 9 Algoritmi Requisiti i un uon lgoritmo: Correttezz; Effiienz ovvero
Il prolem un milione i ollri SienzOrient: Informti Ginlu Rossi www.informti.unirom2.it (www.informti.unirom2.it) Prolem $ 000 000 / 9 Algoritmi Requisiti i un uon lgoritmo: Correttezz; Effiienz ovvero
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
a b }. L insieme Q è pertanto l insieme delle frazioni.
 I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
Grandezze, funzioni empiriche e matematiche. 1 Stabilisci se le seguenti affermazioni sono vere o false.
 Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
6) Nel 1991 Carl Lewis ha stabilito il record del mondo dei 100 m percorrendoli in 9,86 s. Qual è la velocità media in km/h?
 1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
Strutture dati per insiemi disgiunti
 Sopo Struttur ati pr insimi isiunti Gstir in moo iint una ollzion S = {S 1, S 2,..., S k } i insimi isiunti qualora l sol oprazioni onsntit siano: 1) rar un nuovo insim ontnnt un solo lmnto (tal lmnto
Sopo Struttur ati pr insimi isiunti Gstir in moo iint una ollzion S = {S 1, S 2,..., S k } i insimi isiunti qualora l sol oprazioni onsntit siano: 1) rar un nuovo insim ontnnt un solo lmnto (tal lmnto
e una funzione g ε S f tali che = sup g : g S f tale che h ε f < ε/2; analogamente, per
 C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
Sintesi: Assegnamento degli stati. Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone. Sintesi: Scelta del codice
 Sintsi: Assgnmnto gli stti Sintsi Squnzil Sinron Sintsi Comportmntl i rti Squnzili Sinron L riuzion l numro gli stti minimizz il numro i lmnti i mmori quini i vriili i stto h srivono l mhin sinttizzr A
Sintsi: Assgnmnto gli stti Sintsi Squnzil Sinron Sintsi Comportmntl i rti Squnzili Sinron L riuzion l numro gli stti minimizz il numro i lmnti i mmori quini i vriili i stto h srivono l mhin sinttizzr A
Minimizzazione degli Stati in una macchina a stati finiti
 Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
INTEGRALI. 1. Integrali indefiniti
 INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
Corso di Laurea in Ingegneria Informatica. Corso di Reti di Calcolatori (a.a. 2010/11)
 orso di Laura in Inggnria Informatica orso di Rti di alcolatori (a.a. /) Robrto anonico (robrto.canonico@unina.it) Giorgio Vntr (giorgio.vntr@unina.it) lgoritmo di ijkstra novmbr I lucidi prsntati al corso
orso di Laura in Inggnria Informatica orso di Rti di alcolatori (a.a. /) Robrto anonico (robrto.canonico@unina.it) Giorgio Vntr (giorgio.vntr@unina.it) lgoritmo di ijkstra novmbr I lucidi prsntati al corso
Che cosa c è nella lezione. Questa lezione si occupa di tecniche avanzate di risoluzione dei problemi: il backtracking. il paradigma greedy.
 Algoritmi Progrmmzion Avnzt - tori /9 Ch cos c è nll lzion Qust lzion si occup i tcnich vnzt i risoluzion i problmi: il bcktrcking il prigm gry. 2/9 Algoritmi Progrmmzion Avnzt - tori 3/9 Tipologi i problmi
Algoritmi Progrmmzion Avnzt - tori /9 Ch cos c è nll lzion Qust lzion si occup i tcnich vnzt i risoluzion i problmi: il bcktrcking il prigm gry. 2/9 Algoritmi Progrmmzion Avnzt - tori 3/9 Tipologi i problmi
Aquadue Duplo. Guida all utilizzo. click! NEW! ON! c. Collegare il programmatore al rubinetto.
 Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
ALGORITMI E COMPLESSITÀ CORSO DI LAUREA MAGISTRALE IN INFORMATICA UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
S kx. e che è dispari in quanto
 imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
Informatica II. Capitolo 5. Alberi. E' una generalizzazione della struttura sequenza
 Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
j Verso la scuola superiore Geometria euclidea e analitica
 j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
j Verso la scuola superiore Gli insiemi N, Z, Q, R
 j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
Euristiche per il Problema del Commesso Viaggiatore
 Spinz Univrsità di Rom - Diprtimnto di Inggnri Informti, Automti Gstionl Euristih pr il Problm dl Commsso Viggitor Rnto Bruni bruni@dis.unirom.it Il mtril prsntto è drivto d qullo di proff. A. Sssno C.
Spinz Univrsità di Rom - Diprtimnto di Inggnri Informti, Automti Gstionl Euristih pr il Problm dl Commsso Viggitor Rnto Bruni bruni@dis.unirom.it Il mtril prsntto è drivto d qullo di proff. A. Sssno C.
The cost of the material maintenance is averaged over the last 3 years.
 Anlisi i osti i un Diprtimnto 11 TABLE 4 Dprition n mintnn osts (unit: ITL) Ctgory Y Prio Inrs vlu Annul vlu 1 Furnitur 5 1.1.90{31.12.95 219 311 127 43 862 225 2 Lirry 5 1.1.90{31.12.95 542 832 793 108
Anlisi i osti i un Diprtimnto 11 TABLE 4 Dprition n mintnn osts (unit: ITL) Ctgory Y Prio Inrs vlu Annul vlu 1 Furnitur 5 1.1.90{31.12.95 219 311 127 43 862 225 2 Lirry 5 1.1.90{31.12.95 542 832 793 108
Alberi di copertura minimi
 Albri di coprtura minimi Albro di coprtura (spanning tr) Dato un grafo G=(V, E, w) non orintato, connsso psato, un albro di coprtura di G è un sottografo X=(V, T) tal ch X è un albro (quindi connsso) T
Albri di coprtura minimi Albro di coprtura (spanning tr) Dato un grafo G=(V, E, w) non orintato, connsso psato, un albro di coprtura di G è un sottografo X=(V, T) tal ch X è un albro (quindi connsso) T
Matematica 15 settembre 2009
 Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Elettronica dei Sistemi Digitali Sintesi di porte logiche combinatorie fully CMOS
 Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Algebra + numeri relativi +l calcolo letterale Equazioni, disequazioni, problemi
 Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR
 ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR Tizin Rprlli 5/5/8 RICHIAMI DI TEORIA Proposizion.. Si f C ([, b]) g C ([, b]), llor f(x)g(x)dx = [F (x)g(x)] b F (x)g (x)dx. dov F (x) è un
ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR Tizin Rprlli 5/5/8 RICHIAMI DI TEORIA Proposizion.. Si f C ([, b]) g C ([, b]), llor f(x)g(x)dx = [F (x)g(x)] b F (x)g (x)dx. dov F (x) è un
α = α λ e Essendo ( ) , sostituendo nella (81) si ottiene: (83) 3 (86) Possiamo adesso scrivere la soluzione generale della (81): ~ 2
 Appunti dll lzion dl Prof Stfno D Mrchi dl //6 cur dl Prof Frnndo D Anglo Soluzion di un srcizio ssgnto nll scors lzion (srcizio h) (8) L soluzion gnrl dll quzion ssocit è dt d: (8) ( ) o Ossrvto ch il
Appunti dll lzion dl Prof Stfno D Mrchi dl //6 cur dl Prof Frnndo D Anglo Soluzion di un srcizio ssgnto nll scors lzion (srcizio h) (8) L soluzion gnrl dll quzion ssocit è dt d: (8) ( ) o Ossrvto ch il
Matematica. Indice lezione. (Esercitazioni) dott. Francesco Giannino dott. Valeria Monetti. Funzione esponenziale
 Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Corso di ordinamento - Sessione suppletiva - a.s. 2009-2010
 Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
ISTRUZIONI DI MONTAGGIO per controtelai SP
 ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
Aquauno Video 2 Plus
 Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
Funzione esponenziale e logaritmo. Proprietà di esponenziale e logaritmo.
 Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Sintesi. Sintesi Sequenziale Sincrona Sintesi comportamentale di reti sequenziali sincrone. Riduzione del numero degli stati
 Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 5/12/02 Sintsi La sintsi si svol
Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 5/12/02 Sintsi La sintsi si svol
ISTRUZIONI DI MONTAGGIO - ARCATE MRL 1:1 ASSEMBLY INSTRUCTION - CAR FRAMES MRL 1:1
 ISTRUZIONI I MONTIO - RT 0-0 MRL : SSMLY INSTRUTION - R RMS 0-0 MRL : LIMITTOR OVRSP OVRNOR ONTRPPSO OUNTRWIHT ONTRPPSO OUNTRWIHT RT-R RM // RT-R RM // RT-R RM 0// RT-R RM // OSS > 00 LV TTO UN LIMITTOR
ISTRUZIONI I MONTIO - RT 0-0 MRL : SSMLY INSTRUTION - R RMS 0-0 MRL : LIMITTOR OVRSP OVRNOR ONTRPPSO OUNTRWIHT ONTRPPSO OUNTRWIHT RT-R RM // RT-R RM // RT-R RM 0// RT-R RM // OSS > 00 LV TTO UN LIMITTOR
Trasformazioni geometriche +sometrie Omotetia e similitudine Teoremi di Euclide e teorema di Talete
 Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Elettronica dei Sistemi Digitali Disegno del layout di porte logiche combinatorie CMOS
 Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
tx P ty P 1 + t(z P 1)
 Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
GT Definizione di grafo orientato e non
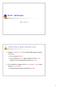 Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Da cartesiano geocentrico a cartesiano locale
 Trsformzion tr sistmi di rifrimnto D crtsino gocntrico crtsino locl Si considri un punto l cui posizion è not risptto d un llissoid di rifrimnto. Si ssoci tl punto un sistm crtsino locl, ch h: origin nl
Trsformzion tr sistmi di rifrimnto D crtsino gocntrico crtsino locl Si considri un punto l cui posizion è not risptto d un llissoid di rifrimnto. Si ssoci tl punto un sistm crtsino locl, ch h: origin nl
Esercizi di Algebra Lineare - Fogli 1-2 Corso di Laurea in Matematica 2 ottobre 2016
 Esrizi i Algr Linr - Fogli 1-2 Corso i Lur in Mtmti 2 ottor 2016 1. Logi tori lmntr gli insimi Esrizio 1.1 Ngr un ssrzion. Espliitr l ngzion ll sgunti ssrzioni: (P ) ogni stunt i qust ul minornn, oppur
Esrizi i Algr Linr - Fogli 1-2 Corso i Lur in Mtmti 2 ottor 2016 1. Logi tori lmntr gli insimi Esrizio 1.1 Ngr un ssrzion. Espliitr l ngzion ll sgunti ssrzioni: (P ) ogni stunt i qust ul minornn, oppur
La rappresentazione per elencazione consiste nell elencare tutte le coppie ordinate che verificano la relazione
 RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
Lezione 2: tanti tipi di problemi, anche insolubili
 Lzion : tnti tipi i prolmi, nh insoluili Mirim Di Inni 5 nnio 011 1 Tnti tipi i prolmi Aimo inizito l sors lzion inno, più o mno ormlmnt, qullo h trizionlmnt vin onsirto un prolm: un insim i ti prtir i
Lzion : tnti tipi i prolmi, nh insoluili Mirim Di Inni 5 nnio 011 1 Tnti tipi i prolmi Aimo inizito l sors lzion inno, più o mno ormlmnt, qullo h trizionlmnt vin onsirto un prolm: un insim i ti prtir i
Sintesi. Sintesi Sequenziale Sincrona Sintesi comportamentale di reti sequenziali sincrone. Riduzione del numero degli stati
 Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 12/12/2004 Sintsi La sintsi si
Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 12/12/2004 Sintsi La sintsi si
Ellisse. L ellisse è il luogo geometrico dei punti del piano tali che la somma delle distanze da due punti fissi. definizione. P semidistanza focale
 Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
Algoritmi e Strutture Dati
 Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno A.A. 00/0 Dnzon l prolm Prt I Mnmo Alro Roprnt Dnzon l prolm Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso
Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno A.A. 00/0 Dnzon l prolm Prt I Mnmo Alro Roprnt Dnzon l prolm Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso
A.A.2009/10 Fisica 1 1
 Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Aniello Murano NP- Completezza (seconda parte)
 Aniello Murno NP- Completezz (second prte) 15 Lezione n. Prole chive: Np-completezz Corso di Lure: Informtic Codice: Emil Docente: murno@ n.infn.it A.A. 2008-2009 Definizione di NP- COMPLETEZZA Si ricordi
Aniello Murno NP- Completezz (second prte) 15 Lezione n. Prole chive: Np-completezz Corso di Lure: Informtic Codice: Emil Docente: murno@ n.infn.it A.A. 2008-2009 Definizione di NP- COMPLETEZZA Si ricordi
PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO
 ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
Soluzioni dei Problemi di controllo
 Soluioni i roblmi i ontrollo Si v raliar un sistma i ontrollo i tipo on transitorio h si annulli in tmpo finito minimo Dato h la ha già un polo in non è nssario introurn altri pr mo l ontrollor G r ottnr
Soluioni i roblmi i ontrollo Si v raliar un sistma i ontrollo i tipo on transitorio h si annulli in tmpo finito minimo Dato h la ha già un polo in non è nssario introurn altri pr mo l ontrollor G r ottnr
SPOSTAMENTO E RETTIFICA DI CONFINE
 SPOSEO E REIFI I OFIE Lo SPOSEO si qundo un confin ià rttilino vin sostituito con un ltro smpr rttilino L REIFI si qundo un confin polionl o curvilino vin sostituito con un ltro rttilino. SPOSEO REIFI
SPOSEO E REIFI I OFIE Lo SPOSEO si qundo un confin ià rttilino vin sostituito con un ltro smpr rttilino L REIFI si qundo un confin polionl o curvilino vin sostituito con un ltro rttilino. SPOSEO REIFI
Elettra Evolution 1 OK! OK! Guida all utilizzo
 lttr volution ui ll utilizzo Pg. ISTALLAZIO LL LTTROVALVOLA. L lttrovlvol progrmmil è prftt tnut stgn funzion nh immrs prmnntmnt in qu fino un mtro i profonità (gro i protzion IP8). Può ssr instllt ll
lttr volution ui ll utilizzo Pg. ISTALLAZIO LL LTTROVALVOLA. L lttrovlvol progrmmil è prftt tnut stgn funzion nh immrs prmnntmnt in qu fino un mtro i profonità (gro i protzion IP8). Può ssr instllt ll
Esercizi di matematica
 Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
Algebra astratta +nsiemi Relazioni e funzioni Operazioni binarie e strutture algebriche Logica
 lr strtt +nsimi Rlzioni unzioni Oprzioni inri struttur lrih Loi +nsimi Quli ll sunti sprssioni iniviuno un insim? SEZ. S h i l Gli otti sul mio tvolo. Tr iori proumti. L onn h vivono s tu. Cinqu rzz ll.
lr strtt +nsimi Rlzioni unzioni Oprzioni inri struttur lrih Loi +nsimi Quli ll sunti sprssioni iniviuno un insim? SEZ. S h i l Gli otti sul mio tvolo. Tr iori proumti. L onn h vivono s tu. Cinqu rzz ll.
Esercitazione di AM120
 Univrsità dgli Studi Roma Tr - Corso di Laura in Matmatica Esrcitazion di AM0 A.A. 07 08 - Esrcitator: Luca Battaglia Soluzioni dll srcitazion dl 6 7 Marzo 08 Argomnto: Drivat. Dimostrar, utilizzando la
Univrsità dgli Studi Roma Tr - Corso di Laura in Matmatica Esrcitazion di AM0 A.A. 07 08 - Esrcitator: Luca Battaglia Soluzioni dll srcitazion dl 6 7 Marzo 08 Argomnto: Drivat. Dimostrar, utilizzando la
Esame di Fisica 2. Corso Interateneo di Ing. Informatica e Biomedica 22/07/2011
 sam i Fisica orso ntratno i ng. nformatica Biomica 7 Problma Sia ato un filo conuttor tituito a u lunghi fili rttilini raccorati a un tratto smicircolar i raggio, com rapprsntato in figura. l filo è prcorso
sam i Fisica orso ntratno i ng. nformatica Biomica 7 Problma Sia ato un filo conuttor tituito a u lunghi fili rttilini raccorati a un tratto smicircolar i raggio, com rapprsntato in figura. l filo è prcorso
Tecniche di Progettazione Digitale Progettazione e layout di porte logiche combinatorie CMOS p. 2
 Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Metodologie informatiche per la chimica
 Metodologie informtihe per l himi Dr. Sergio Brutti Mtrii Prodotto tr mtrii d Dte mtrii x Il prodotto delle due mtrii produe un nuov mtrie on un numero di righe pri l numero di righe dell mtrie e numero
Metodologie informtihe per l himi Dr. Sergio Brutti Mtrii Prodotto tr mtrii d Dte mtrii x Il prodotto delle due mtrii produe un nuov mtrie on un numero di righe pri l numero di righe dell mtrie e numero
Albero di supporto di costo minimo
 Algortm Struttur Dat II Alro supporto osto mnmo Nl prolma lla struzon ll nrga lttra sono vrs as h vono rvr nrga a una ntral lttra. Pr rvr nrga, ogn asa v ssr ollgata alla ntral attravrso un ammno fatto
Algortm Struttur Dat II Alro supporto osto mnmo Nl prolma lla struzon ll nrga lttra sono vrs as h vono rvr nrga a una ntral lttra. Pr rvr nrga, ogn asa v ssr ollgata alla ntral attravrso un ammno fatto
Test di autovalutazione
 UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
Studio di funzione. Pertanto nello studio di tali funzioni si esamino:
 Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Esercizi per il corso di Calcolatori Elettronici
 Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Test di autovalutazione
 Tst i autovalutazion Tst 0 0 0 30 0 50 60 70 80 90 00 n Il mio puntggio, in ntsimi, è n Risponi a ogni qusito sgnano una sola ll 5 altrnativ. n Confronta l tu rispost on l soluzioni. n Colora, partno a
Tst i autovalutazion Tst 0 0 0 30 0 50 60 70 80 90 00 n Il mio puntggio, in ntsimi, è n Risponi a ogni qusito sgnano una sola ll 5 altrnativ. n Confronta l tu rispost on l soluzioni. n Colora, partno a
Teoria. Tale retta limite non sempre esiste. Si veda il grafico sottostante. Matematica 1
 LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI
 RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
Modi dominanti. L evoluzione libera del sistema lineare. x(k + 1) = Ax(k) a partire dalla condizione iniziale x(0) = x 0 è:
 Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
Nome Cognome classe 5D 16 Dicembre VERIFICA di MATEMATICA PROBLEMA
 Nom Cognom cls D 6 Dicmr 8 VERIFICA di MATEMATICA PROBLEMA Considr l unzion, studin l ndmnto trccin il grico proil punti: Di l dinizion di unzion inittiv Sull dl grico proil ch hi trccito, l unzion è inittiv?
Nom Cognom cls D 6 Dicmr 8 VERIFICA di MATEMATICA PROBLEMA Considr l unzion, studin l ndmnto trccin il grico proil punti: Di l dinizion di unzion inittiv Sull dl grico proil ch hi trccito, l unzion è inittiv?
Esercizi Circuiti Resistivi
 srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
SICUREZZA SUL LAVORO SAFETY AT WORK SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31
 SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
RSA e PARIGP: POSSIBILI ATTACCHI
 RSA PARIGP: POSSIBILI ATTACCHI Di Cristiano Armllini, cristiano.armllini@alic.it Supponiamo i consirar un problma RSA : p 7, q, n 87 ϕ( n) (7 )( ) 60 7, MCD(, ϕ( n)), mo( ϕ( n)) C M M C,mo( n),mo( n) ov
RSA PARIGP: POSSIBILI ATTACCHI Di Cristiano Armllini, cristiano.armllini@alic.it Supponiamo i consirar un problma RSA : p 7, q, n 87 ϕ( n) (7 )( ) 60 7, MCD(, ϕ( n)), mo( ϕ( n)) C M M C,mo( n),mo( n) ov
Test di autovalutazione
 Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
ANALISI 2 ESERCITAZIONE DEL 06/12/2010 PUNTI CRITICI
 ANALISI ESERCITAZIONE DEL 06//00 PUNTI CRITICI Un punto critico è un punto in cui la funzion è diffrnziabil il piano tangnt al grafico è orizzontal Riconosciamo qusti punti prché il gradint è il vttor
ANALISI ESERCITAZIONE DEL 06//00 PUNTI CRITICI Un punto critico è un punto in cui la funzion è diffrnziabil il piano tangnt al grafico è orizzontal Riconosciamo qusti punti prché il gradint è il vttor
Fondamenti di Algebra Lineare e Geometria TEMA A
 Fondamnti di Algbra Linar Gomtria Inggnria Arospazial d Inggnria dll Enrgia - Canal B Quarto Appllo - 3 fbbraio 5 TEMA A Risolvr i sgunti srcizi motivando adguatamnt ogni risposta. () Sia data la matric
Fondamnti di Algbra Linar Gomtria Inggnria Arospazial d Inggnria dll Enrgia - Canal B Quarto Appllo - 3 fbbraio 5 TEMA A Risolvr i sgunti srcizi motivando adguatamnt ogni risposta. () Sia data la matric
Algoritmi e Strutture Dati
 Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno novmr 00 Prt I Mnmo Alro Roprnt Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso psto (w : E R è l unzon pso,
Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno novmr 00 Prt I Mnmo Alro Roprnt Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso psto (w : E R è l unzon pso,
Calcolo delle Probabilità e Statistica. Prova scritta del III appello - 7/6/2006
 Corso di Laura in Informatica - a.a. 25/6 Calcolo dll Probabilità Statistica Prova scritta dl III appllo - 7/6/26 Il candidato risolva i problmi proposti, motivando opportunamnt l propri rispost.. Sia
Corso di Laura in Informatica - a.a. 25/6 Calcolo dll Probabilità Statistica Prova scritta dl III appllo - 7/6/26 Il candidato risolva i problmi proposti, motivando opportunamnt l propri rispost.. Sia
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
 Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
Utilizzo della funzione Adesivo stampabile. Utilizzo della schermata di modifica. Computer. Tablet. ScanNCutCanvas
 SnNCutCnvs Utilizzo ll unzion Asivo stmpil È possiil rr in moo molto smpli sivi unii utilizzno un stmpnt gtto inhiostro l unzion Tglio irtto ll mhin SnNCut. Pr inormzioni sull oprzioni i s i SnNCutCnvs,
SnNCutCnvs Utilizzo ll unzion Asivo stmpil È possiil rr in moo molto smpli sivi unii utilizzno un stmpnt gtto inhiostro l unzion Tglio irtto ll mhin SnNCut. Pr inormzioni sull oprzioni i s i SnNCutCnvs,
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Corso di Automi e Linguaggi Formali Parte 4 Linguaggi liberi dal contesto
 Grmmtich Rgol pr spcificr frsi corrtt in itlino Un frs un soggtto sguito d un vrbo sguito d un complmnto oggtto Un soggtto un nom o un rticolo sguito d un nom Uso dll rgol: pr gnrr frsi corrtt Esmpio:
Grmmtich Rgol pr spcificr frsi corrtt in itlino Un frs un soggtto sguito d un vrbo sguito d un complmnto oggtto Un soggtto un nom o un rticolo sguito d un nom Uso dll rgol: pr gnrr frsi corrtt Esmpio:
Totti, 37 anni da leggenda. Un monumento vivente. Scritto da Redazione Venerdì 27 Settembre 2013 08:39 - VALERIA META
 37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
Ordina per: orario di partenza tempo di percorrenza numero di cambi Staz. Partenza: Latina Staz. Arrivo: Roma ( Tutte Le Stazioni ) Data: 16/12/2010
 http://orario.trenitalia.com/b2c/npppricetravelsolutions.do?car=0&stazin=latina&stazout=roma&dat... 1 di 1 08/12/2010 23.20 04:50 05:08 05:25 05:45 06:13 05:35 06:00 06:05 06:23 06:58 00:45 12282 ND ND
http://orario.trenitalia.com/b2c/npppricetravelsolutions.do?car=0&stazin=latina&stazout=roma&dat... 1 di 1 08/12/2010 23.20 04:50 05:08 05:25 05:45 06:13 05:35 06:00 06:05 06:23 06:58 00:45 12282 ND ND
Ordina per: orario di partenza tempo di percorrenza numero di cambi Staz. Partenza: Roma ( Tutte Le Stazioni ) Staz. Arrivo: Latina Data: 16/12/2010
 http://orario.trenitalia.com/b2c/npppricetravelsolutions.do?car=0&stazin=roma&stazout=latina&dat... 1 di 1 08/12/2010 23.15 04:52 04:59 RO TIB 05:41 06:12 06:27 05:29 05:38 06:17 06:48 06:56 00:37 12293
http://orario.trenitalia.com/b2c/npppricetravelsolutions.do?car=0&stazin=roma&stazout=latina&dat... 1 di 1 08/12/2010 23.15 04:52 04:59 RO TIB 05:41 06:12 06:27 05:29 05:38 06:17 06:48 06:56 00:37 12293
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 2004/ gennaio 2005 TESTO E SOLUZIONE
 PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
ESERCIZIO DI ASD DEL 27 APRILE 2009
 ESERCIZIO DI ASD DEL 27 APRILE 2009 Dimetro Algoritmi. Ricordimo che un grfo non orientto, ciclico e connesso è un lero. Un lero può essere pensto come lero rdicto un volt che si si fissto un nodo come
ESERCIZIO DI ASD DEL 27 APRILE 2009 Dimetro Algoritmi. Ricordimo che un grfo non orientto, ciclico e connesso è un lero. Un lero può essere pensto come lero rdicto un volt che si si fissto un nodo come
