Esempio 1 Consideriamo un grafo G con insieme di nodi. mentre l insieme di archi é il seguente sottinsieme di coppie di nodi in V
|
|
|
- Bonaventura Manzi
- 5 anni fa
- Visualizzazioni
Transcript
1 1 Tori i grfi Pr prim os imo l finizion i grfo. Dfinizion 1 Un grfo G é ostituito un oppi i insimi (V, A) ov V é tto insim i noi A é tto insim i rhi é un sottinsim i tutt l possiili oppi i noi in V. S l oppi i noi sono orint, il grfo é tto orintto, s non sono orint é tto non orintto. Esmpio 1 Consirimo un grfo G on insim i noi V = {,,,, }, mntr l insim i rhi é il sgunt sottinsim i oppi i noi in V A = {(, ); (, ); (, ); (, ); (, ); (, )} S tli oppi sono orint ( quini, smpio, l oppi (, ) é ivrs ll oppi (, )) il grfo é orintto, ltrimnti ( quini, smpio, l oppi (, ) l oppi (, ) sono quivlnti tr loro) il grfo é non orintto. Pr qunto si in molti si onvnint mntnr l istinzion tr grfi orintti non orintti, nl sguito i onntrrmo solo sui grfi orintti, ossrvno h pr ogni grfo non orintto n sist uno orintto quivlnt in ui l insim i noi é lo stsso pr ogni oppi non orint (i, j) h rpprsnt un ro l grfo non orintto si rno u oppi orint (i, j) (j, i) h rpprsntno u rhi l grfo orintto quivlnt. Quini, s l smpio visto foss stto un grfo non orintto, lo vrmmo potuto trsformr in uno orintto quivlnt on gli stssi noi il sgunt insim i rhi {(, ); (, ); (, ); (, ); (, ); (, ); (, ); (, ); (, ); (, ); (, ); (, )} Dimo or un ltr finizion. Dfinizion 2 Dto un grfo orintto G = (V, A) un ro (i, j) A irmo h il noo i é prssor l noo j h il noo j é sussor l noo i. Nl grfo ll smpio, supposto orintto, il noo é prssor l noo, mntr é sussor i. Aimo finito un grfo G ttrvrso l oppi i insimi V A. É possiil pró rpprsntr un grfo nh ni moi sgunti. Rpprsntzion grfi A ogni noo orrispon un pllino sul pino ogni ro (i, j) orrispon un lin h ongiung il pllino h rpprsnt il noo i on il pllino h rpprsnt il noo j, su ui si tri un fri i vrso j (pr grfi non orintti l fri si omtt). In Figur 1 é mostrt l rpprsntzion grfi l grfo ll smpio. 1
2 Figur 1: Tll 1: (, ) (, ) (, ) (, ) (, ) (, ) List i inz o rpprsntzion nliti A ogni noo si ffin un list (vntulmnt vuot) ontnnt tutti i suoi sussori. Pr il nostro smpio l list i inz sono l sgunti: : (, ) : (, ) : () : () : Mtri ininz noo-ro Si ostruis un mtri on un rig pr ogni noo un olonn pr ogni ro. Nll olonn rltiv ll ro (i, j) si mtt +1 in orrisponnz ll rig i, -1 in orrisponnz ll rig j 0 in orrisponnz i tutt l ltr righ. Pr il nostro smpio l mtri i ininz noo-ro é t in Tll 1 Introuimo or lun finizioni. Dfinizion 3 Un ro (i, i) in ui ioé il noo inizil finl oiniono é tto ppio. Dfinizion 4 Un grfo privo i ppi on l piú un ro h ongiung ogni oppi i noi é tto smpli. Il grfo ll smpio è smpli. 2
3 Dfinizion 5 Du rhi h hnno un noo in omun sono tti inti. Nll smpio gli rhi (, ) (, ) sono inti. Dfinizion 6 Un squnz i noi tli h v 0 v 1 v r (v i 1, v i ) A oppur (v i, v i 1 ) A i = 1,..., r, vin tt mmino. Il numro r i rhi l mmino é tto lunghzz l mmino. Un mmino é tto smpli s nssun ro é prorso piú i un volt, lmntr s nssun noo vin toto piú i un volt. I mmini lmntri sono si prtiolri i mmini smplii. Nll smpio, il mmino é un mmino lmntr i lunghzz 3; il mmino é smpli m non lmntr (il noo è toto più i un volt); il mmino non é né smpli (l ro (, ) è prorso u volt) né lmntr. Dfinizion 7 Un mmino smpli in ui l ultimo noo oini on il primo vin tto ilo. S il mmino é lmntr, ioè to tutti i noi l più un volt prt il primo ultimo noo, si prl i ilo lmntr. Nll smpio é un ilo lmntr. Dfinizion 8 Un mmino o un ilo in ui tutti gli rhi sono prorsi sono il loro orintmnto vin tto orintto, ltrimnti si i non orintto. Nll smpio il mmino é orintto mntr il mmino é non orintto. Dfinizion 9 Dti u noi i j i un grfo G, s sist un mmino i j, llor si i h j é ssiil i. L rlzion tr i noi é ssiil é un rlzion i quivlnz, ovvro soisf l tr propritá riflssiv, simmtri trnsitiv. Com tl inu lssi i quivlnz nll insim i noi. Tli lssi i quivlnz vngono tt omponnti onnss l grfo. Ogni omponnt onnss é formt noi tutti ssiili tr loro m non ssiili noi in ltr omponnti. Dfinizion 10 S il grfo ontin un sol omponnt onnss vin tto onnsso. L sgunt prour onsnt i iniviur l omponnti onnss i un grfo quini nh i stilir s un grfo é onnsso. Inizilizzzion Si pong W = V r = 1. 3
4 Psso 1 Si slzioni un noo i W si pong S = {i} T r =. Psso 2 Si slzioni un noo j S. Si rimuov j S si ggiungno in S tutti i noi h non sino giá ontnuti in T r i ui j é prssor o sussor, ioé S = (S \ {j}) {k T r : (k, j) A o (j, k) A}. Si pong T r = T r {j}. Psso 3 S S =, llor si v l Psso 4. Altrimnti si ritorni l Psso 2. Psso 4 Si pong W = W \ T r. S W =, llor T 1, T 2,..., T r sono gli insimi i noi ll omponnti onnss l grfo. Altrimnti si pong r = r + 1 si ritorni l Psso 1. Com srizio si pplihi l prour pr vrifir h il grfo ll smpio é onnsso. Dfinizion 11 Un noo j é tto fortmnt ssiil i s sist un mmino orintto i j. Si noti h l rlzion tr noi é fortmnt ssiil non é un rlzion i quivlnz. In prtiolr non vl pr ss l propritá i simmtri (nll smpio é fortmnt ssiil m il vivrs non é vro). Dfinizion 12 Un grfo in ui ogni noo é fortmnt ssiil tutti gli ltri é tto fortmnt onnsso. Si noti h l sistnz in un grfo i un ilo orintto h to tutti i noi l grfo è onizion nssri suffiint pr grntir h il grfo si fortmnt onnsso. Il grfo l nostro smpio non é fortmnt onnsso (om giá ossrvto nh tutti gli ltri noi l grfo non sono fortmnt ssiili ). Dfinizion 13 Un grfo si i omplto s sist un ro tr ogni oppi i noi. Il nostro grfo non é omplto. A smpio, non é lun ro tr. Lo é inv il grfo G = (V, A) on V = {,,, } A = {(, ); (, ); (, ); (, ); (, ); (, )} 4
5 Dfinizion 14 Dto un grfo G = (V, A) un sottinsim A A, un grfo G = (V, A ) é tto grfo przil i G. Dti V V A A(V ) = {(i, j) A : i V, j V } il grfo G = (V, A ) vin tto sottogrfo i G. In prtiolr, s A = A(V ) il sottogrfo vin tto sottogrfo inotto V. Nll smpio G = (V, A ) on A = {(, ); (, ); (, ); (, ); (, )} é un grfo przil i G, mntr G = (V, A ) on V = {,, } A = {(, )} é un sottogrfo i G. S inv si onsir G = (V, A ) on V = {,, } A = {(, ); (, )} qusto é il sottogrfo i G inotto V. Dfinizion 15 Un grfo G = (V, A) si i iprtito s l insim V puó ssr prtizionto in u sottinsimi V 1 V 2 (quini V 1 V 2 = V V 1 V 2 = ) tli h (i, j) A : i V 1, j V 2 oppur i V 2, j V 1. Un grfo iprtito si i omplto s pr ogni oppi i noi in V 1 V 2 sist un ro h li ongiung. Vl l sgunt ossrvzion. Ossrvzion 1 Un grfo é iprtito s solo s non ontin ili i lunghzz ispri. L sgunt prour onsnt i stilir s un grfo é iprtito. Psso 1 Si slzioni un noo i V si pong T 1 = C 1 = {i} T 2 = C 2 = Psso 2 Si pong T 2 = {k V \ C 2 : i T 1 tl h (i, k) A oppur (k, i) A} Si C 2 = C 2 T 2. Psso 3 Si pong T 1 = {k V \ C 1 : i T 2 tl h (i, k) A oppur (k, i) A} Si C 1 = C 1 T 1. 5
6 Psso 4 S C 1 C 2, llor il grfo non é iprtito. Altrimnti si v l Psso 5. Psso 5 S C 1 C 2 = V T 1 = T 2 =, llor il grfo é iprtito on V 1 = C 1 V 2 = C 2. Altrimnti si ritorni l Psso 2. Nl nostro smpio slzionno inizilmnt il noo ponnolo in T 1 C 1 vrmo on T 1 = {}. Al Psso 2 vrmo C 1 C 2 C 1 C 2 on T 2 = {, } C 2 = {, }. Al Psso 3 vrmo C 1 C 2 on T 1 = {,, } C 1 = {,,, }. Al Psso 4 notimo h C 1 C 2 = {} quini possimo onlur h il grfo non é iprtito. Dfinizion 16 Si to un grfo G = (V, A) on r(v ) = n ov r(v ) not l rinlitá (il numro i lmnti) ll insim V. Si i h G é un lro s soisf l sgunti onizioni (quivlnti tr loro) 1. G é privo i ili onnsso; 2. G é privo i ili r(a) = n 1; 3. G é onnsso r(a) = n 1; 4. sist un unio mmino h ongiung ogni oppi i noi. A smpio, il grfo G = (V, A) on V = {,,,, } A = {(, ); (, ); (, ); (, )} illustrto in Figur 2, é un lro. Vl l sgunt ossrvzion. Ossrvzion 2 Dto un lro, l ggiunt i un solo ro r sttmnt un ilo. Dfinizion 17 Si to un grfo onnsso G = (V, A). Si finis lro i supporto o spnning tr i G un grfo przil T = (V, A T ) i G (quini on A T A) h é un lro. 6
7 Figur 2: Un lro G. Si noti h un lro i supporto i G v ontnr tutti i noi i G h in virtú l punto 2. (o l punto 3.) ll Dfinizion 16, si ovrá vr r(a T ) = r(v ) 1. Esmpio 2 Si to il grfo G = (V, A) on V = {,,, } A = {(, ); (, ); (, ); (, ); (, )} illustrto in Figur 3. Un lro i supporto i G é il sottogrfo T 1 = (V, A T1 ) on = {(, ); (, ); (, )} A T1 un ltro é il sottogrfo T 2 = (V, A T2 ) on A T2 = {(, ); (, ); (, )} I u lri i supporto i G sono illustrti in Figur 3. L sgunt prour onsnt i iniviur un lro i supporto i un grfo onnsso. Inizilizzzion Si inihino on 1,..., m, m = r(a), gli rhi l grfo G = (V, A). Si pong i = 1 A T =. Psso 1 S (V, A T { i }) non ontin ili, llor si pong A T = A T { i }, ltrimnti si lsi A T invrito. Psso 2 S r(a T ) = r(v ) 1, llor (V, A T ) è un lro i supporto pr il grfo G, ltrimnti si pong i = i + 1 si ritorni l Psso Bs i ili Introuimo or il ontto i s i ili. Dto un ilo in un grfo G = (V, A) sso possimo ssoir un vttor i imnsion pri r(a) nl moo sgunt: 7
8 G T1 T2 Figur 3: Un grfo G u suoi lri i supporto T 1 T fisso un orintmnto l ilo; 2. l omponnt l vttor orrisponnt un ro (i, j) A srá pri : +1 s l ro (i, j) vin ttrvrsto l ilo nl suo stsso vrso. -1 s l ro (i, j) vin ttrvrsto l ilo nl vrso opposto l suo. 0 s l ro (i, j) non vin ttrvrsto l ilo. Dto il grfo G = (V, A) on il ilo V = {,,,, }, A = {(, ); (, ); (, ); (, ); (, ); (, )} on orintmnto orrisponnt qullo ll ro (, ), tl ilo ssoio il vttor (, ) (, ) (, ) (, ) (, ) (, )
9 S vssi slto om orintmnto qullo opposto ll ro (, ) il vttor sr stto il sgunt (, ) (, ) (, ) (, ) (, ) (, ) ioé ugul l prnt mito i sgno. L mtri l ui righ sono ostituit i vttori ssoiti tutti i ili i un grfo vin tt mtri i ili l grfo. Nll smpio sopr vi sono tr ili on mtri i ili h ( mno i moltiplizioni pr -1 ll righ) é t (, ) (, ) (, ) (, ) (, ) (, ) Il rngo i tl mtri, ovvro il mssimo numro i vttori rig rltivi i ili tr loro linrmnt inipnnti, é tto numro ilomtio l grfo é inito on ν(g), mntr un sottinsim i ili i ui orrisponnti vttori rig formno un s ll insim i vttori rig vin tto s i ili. Nl nostro smpio si puó vrifir h il numro ilomtio é pri 2 h i u ili h si rifrisono ll prim u righ ll mtri formno un s i ili. Si noti h l slt ll orintmnto i ili pr l ostruzion i vttori rig non ini sul numro ilomtio, in qunto moltiplir un rig i un mtri pr -1 non n moifi il rngo. Esistono vri moi pr trminr il numro ilomtio un s i ili. L sgunt prour n é un smpio. 1. Iniviur l omponnti onnss G i = (V i, A i ) i = 1,..., p l grfo G = (V, A), ov p i=1 V i = V p i=1 A i = A V i V j = s i j A i A j = s i j 2. Pr ogni omponnt onnss iniviur uno spnning tr T i = (V i, A i ). Si noti h si ovrá vr r(a i) = r(v i ) 1 3. Aggiungno un ro in A i \ A i si ottin un unio ilo h pprtrrá ll s i ili. Riptno qusto pr tutti gli rhi in A i \A i pr tutt l p omponnti onnss, tutti i ili ottnuti in qusto moo formno un s i ili. 9
10 Si noti h il numro ilomtio é pri l numro i ili ll s quini srá pri p p ν(g) = r(a i \ A i) = [r(a i ) r(v i ) + 1] = ui i=1 = i=1 p r(a i ) i=1 p r(v i ) + p i=1 ν(g) = r(a) r(v ) + p. Nl nostro smpio si puó vrifir h p = 1, mntr r(a) = 6 r(v ) = 5 ui ν(g) = om giá prntmnt ossrvto. Smpr nll smpio, s onsiro l lro i supporto on gli rhi (, ) (, ) (, ) (, ) ggiungno l ro (, ) ottngo il ilo ggiungno l ro (, ) ottngo il ilo I u ili ottnuti in qusto moo formno un s i ili. 1.2 Grfi plnri topologimnt plnri Introuimo or il ontto i grfo topologimnt plnr. L nominzion topologimnt plnr si rifris ll sol rpprsntzioni grfih i grfi. Un rpprsntzion grfi i un grfo si i topologimnt plnr s il grfo é onnsso s gli rhi non hnno punti i onttto ivrsi i noi l grfo. Dt l rpprsntzion grfi i un grfo in Figur 4, ss non é topologimnt plnr in qunto gli rhi (, ) (, ) hnno un punto i onttto ivrso i noi. D ltro nto l rpprsntzion grfi in Figur 5 llo stsso grfo é topologimnt plnr. Dfinirmo un grfo plnr s mmtt lmno un rpprsntzion grfi toplogimnt plnr. Il grfo G = (V, A) on V = {,,, } A = {(, ); (, ); (, ); (, ); (, ); (, )} i ui l Figur 4 5 sono u istint rpprsntzioni grfih, é plnr in qunto mmtt lmno un rpprsntzion topologimnt plnr ( smpio, qull in Figur 5). Dl isgno possimo suito stilir s un rpprsntzion grfi é topologimnt plnr. Piú omplito é stilir s to un grfo sso é plnr. Avrmo isogno i lun finizioni. 10
11 Figur 4: Figur 5: Dfinizion 18 Si to un grfo G = (V, A) un suo ro (i, j) A. L oprzion i ontrzion ll ro (i, j) onsist nl trsformr il grfo G = (V, A) nl grfo G = (V, A ) ov i noi i j sono sostituiti un unio noo s ij, ioé V = (V \ {i, j}) {s ij } gli rhi sono gli stssi i A pr qul h rigur gli rhi h non hnno om strmi i j, l ro (i, j) vin sopprsso ogni ro h h om uno i u strmi i oppur j sostituis tl strmo on il noo s ij ( smpio l ro (k, i) é sostituito on (k, s ij )). Quini A = {(k, h) A : k i, j, h i, j} {(s ij, h) : h i, j, (i, h) A o (j, h) A} {(k, s ij ) : k i, j, (k, i) A o (k, j) A} \ {(i, j)} In Figur 6 é riportto il risultto ll ontrzion ll ro (, ). 11
12 S Figur 6: Dfinizion 19 Inihimo on K 5 un grfo omplto on 5 noi, ovvro un grfo on 5 noi un ro h ongiung ogni oppi i noi istinti (si v l Figur 7). Figur 7: Dfinizion 20 Inihimo on K 3,3 un grfo iprtito on 3 noi in isun ll u prti ll iprtizion (r(v 1 ) = r(v 2 ) = 3) un ro h ongiung ogni oppi i noi ll u prti V 1 V 2 ll iprtizion (si v l Figur 8). Simo or pronti nunir il torm i Kurtowski h rttrizz i grfi plnri. Torm 1 Un grfo onnsso é plnr s solo s sso stsso ogni grfo ottnuto sso trmit ontrzion i rhi non ontngono un K 5 o un K 3,3. 12
13 Figur 8: Figur 9: Com srizio si imostri h il grfo in Figur 9 non é plnr. Dt un rpprsntzion grfi i un grfo G topologimnt plnr, l porzioni i pino limitt iniviut gli rhi l grfo vngono tt f finit l grfo, mntr l rstnt prt l pino vin tt fi infinit l grfo. Gli rhi h limitno un fi finit formno un ilo ll s i ili l grfo. Quini, il numro ilomtio oini on il numro i f finit l grfo. In Figur 10 sono mostrt l 3 f finit l fi infinit i un grfo topologimnt plnr. Quini il numro ilomtio l grfo é 3, ottniil nh ttrvrso l formul r(a) r(v ) + p = = 3, mntr i ili,, i ui rhi limitno l f finit, formno un s i ili. A un grfo topologimnt plnr G si puó ssoir un grfo ul G, il 13
14 qul h tnti noi qunt sono l f (qull finit piú qull infinit) l grfo G (nll smpio in Figur 10 sono 3+1=4) tnti rhi qunti sono gli rhi i G (nll smpio sono 7). Pr ogni ro (i, j) i G si ostruis un ro fi finit fi finit fi finit fi infinit Figur 10: i G h ongiung l u f h sono sprt tl ro. Nll smpio l ro (, ) spr l fi finit limitt gli rhi (, ) (, ) (, ) l fi infinit l grfo G quini in G vrmo un ro h ongiung i noi i G orrisponnti qust u f. I noi (rhi) gli rhi (trttggiti) l ul l nostro smpio sono mostrti in Figur 11. Figur 11: 14
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
 Inggnri Sinz Informtih - Csn A.A. 3- iln@s.unio.it, pitro.iln@unio.it : psuooi Clol il osto l mmino minimo un vrti sorgnt s tutti i rstnti vrtii nl grfo. Clol un lro i oprtur i mmini minimi (shortst pth
Inggnri Sinz Informtih - Csn A.A. 3- iln@s.unio.it, pitro.iln@unio.it : psuooi Clol il osto l mmino minimo un vrti sorgnt s tutti i rstnti vrtii nl grfo. Clol un lro i oprtur i mmini minimi (shortst pth
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Circuiti Nel progettare un circuito destinato a svolgere una certa funzione normalmente si hanno a disposizione i seguenti elementi:
 Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Informatica 3. Informatica 3. LEZIONE 25: Algoritmi sui grafi. Lezione 25 - Modulo 1. Problema. Notazioni per il percorso più breve
 Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
Minimizzazione degli Stati in una macchina a stati finiti
 Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
a b }. L insieme Q è pertanto l insieme delle frazioni.
 I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
j Verso la scuola superiore Gli insiemi N, Z, Q, R
 j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
1 a. 1 b. Rappresenta i seguenti numeri su una retta orientata, scegliendo autonomamente una opportuna unità di misura. b 1
 Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Corso di Automi e Linguaggi Formali Parte 3
 Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Matematica 15 settembre 2009
 Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
+ poligoni e l equivalenza di figure piane + triangoli + quadrilateri
 + poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
+ poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
 Inggnri Sinz Informtih - Csn A.A. - iln@s.unio.it, pitro.iln@unio.it Algoritmo i Floy-Wrshll Algoritmo Floy-Wrshll Algoritmo i Floy-Wrshll: psuooi Clol il osto l mmino minimo tr tutt l oppi i vrtii in
Inggnri Sinz Informtih - Csn A.A. - iln@s.unio.it, pitro.iln@unio.it Algoritmo i Floy-Wrshll Algoritmo Floy-Wrshll Algoritmo i Floy-Wrshll: psuooi Clol il osto l mmino minimo tr tutt l oppi i vrtii in
Sintesi: Assegnamento degli stati. Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone. Sintesi: Scelta del codice
 Sintsi: Assgnmnto gli stti Sintsi Squnzil Sinron Sintsi Comportmntl i rti Squnzili Sinron L riuzion l numro gli stti minimizz il numro i lmnti i mmori quini i vriili i stto h srivono l mhin sinttizzr A
Sintsi: Assgnmnto gli stti Sintsi Squnzil Sinron Sintsi Comportmntl i rti Squnzili Sinron L riuzion l numro gli stti minimizz il numro i lmnti i mmori quini i vriili i stto h srivono l mhin sinttizzr A
Test di autovalutazione
 UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica
 Modlli di Sistmi di Produzion Modlli Algoritmi dll Logisti 000- Prolm dl ommsso viggitor: EURISTICHE CARLO MANNINO Spinz Univrsità di Rom Diprtimnto di Informti Sistmisti Euristih pr il TSP simmtrio Considrimo
Modlli di Sistmi di Produzion Modlli Algoritmi dll Logisti 000- Prolm dl ommsso viggitor: EURISTICHE CARLO MANNINO Spinz Univrsità di Rom Diprtimnto di Informti Sistmisti Euristih pr il TSP simmtrio Considrimo
6) Nel 1991 Carl Lewis ha stabilito il record del mondo dei 100 m percorrendoli in 9,86 s. Qual è la velocità media in km/h?
 1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
INTEGRALI. 1. Integrali indefiniti
 INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
Sistemi lineari COGNOME... NOME... Classe... Data...
 Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Algoritmi e Strutture Dati. Grafi
 Algoritmi Struttur Dti Grfi Alrto Montrsor Univrsità i Trnto 08//7 This work is lins unr Crtiv Commons Attriution-ShrAlik 4.0 Intrntionl Lins. Sommrio Introuzion Dfinizioni Spifi Mmorizzzion Visit i grfi
Algoritmi Struttur Dti Grfi Alrto Montrsor Univrsità i Trnto 08//7 This work is lins unr Crtiv Commons Attriution-ShrAlik 4.0 Intrntionl Lins. Sommrio Introuzion Dfinizioni Spifi Mmorizzzion Visit i grfi
Algebra astratta +nsiemi Relazioni e funzioni Operazioni binarie e strutture algebriche Logica
 lr strtt +nsimi Rlzioni unzioni Oprzioni inri struttur lrih Loi +nsimi Quli ll sunti sprssioni iniviuno un insim? SEZ. S h i l Gli otti sul mio tvolo. Tr iori proumti. L onn h vivono s tu. Cinqu rzz ll.
lr strtt +nsimi Rlzioni unzioni Oprzioni inri struttur lrih Loi +nsimi Quli ll sunti sprssioni iniviuno un insim? SEZ. S h i l Gli otti sul mio tvolo. Tr iori proumti. L onn h vivono s tu. Cinqu rzz ll.
j Verso la scuola superiore Geometria euclidea e analitica
 j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
La rappresentazione per elencazione consiste nell elencare tutte le coppie ordinate che verificano la relazione
 RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
Corso di ordinamento - Sessione suppletiva - a.s. 2009-2010
 Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Lezione 2: tanti tipi di problemi, anche insolubili
 Lzion : tnti tipi i prolmi, nh insoluili Mirim Di Inni 5 nnio 011 1 Tnti tipi i prolmi Aimo inizito l sors lzion inno, più o mno ormlmnt, qullo h trizionlmnt vin onsirto un prolm: un insim i ti prtir i
Lzion : tnti tipi i prolmi, nh insoluili Mirim Di Inni 5 nnio 011 1 Tnti tipi i prolmi Aimo inizito l sors lzion inno, più o mno ormlmnt, qullo h trizionlmnt vin onsirto un prolm: un insim i ti prtir i
Informatica II. Capitolo 5. Alberi. E' una generalizzazione della struttura sequenza
 Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
S kx. e che è dispari in quanto
 imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
α = α λ e Essendo ( ) , sostituendo nella (81) si ottiene: (83) 3 (86) Possiamo adesso scrivere la soluzione generale della (81): ~ 2
 Appunti dll lzion dl Prof Stfno D Mrchi dl //6 cur dl Prof Frnndo D Anglo Soluzion di un srcizio ssgnto nll scors lzion (srcizio h) (8) L soluzion gnrl dll quzion ssocit è dt d: (8) ( ) o Ossrvto ch il
Appunti dll lzion dl Prof Stfno D Mrchi dl //6 cur dl Prof Frnndo D Anglo Soluzion di un srcizio ssgnto nll scors lzion (srcizio h) (8) L soluzion gnrl dll quzion ssocit è dt d: (8) ( ) o Ossrvto ch il
e una funzione g ε S f tali che = sup g : g S f tale che h ε f < ε/2; analogamente, per
 C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
Esercizi di Algebra Lineare - Fogli 1-2 Corso di Laurea in Matematica 2 ottobre 2016
 Esrizi i Algr Linr - Fogli 1-2 Corso i Lur in Mtmti 2 ottor 2016 1. Logi tori lmntr gli insimi Esrizio 1.1 Ngr un ssrzion. Espliitr l ngzion ll sgunti ssrzioni: (P ) ogni stunt i qust ul minornn, oppur
Esrizi i Algr Linr - Fogli 1-2 Corso i Lur in Mtmti 2 ottor 2016 1. Logi tori lmntr gli insimi Esrizio 1.1 Ngr un ssrzion. Espliitr l ngzion ll sgunti ssrzioni: (P ) ogni stunt i qust ul minornn, oppur
Che cosa c è nella lezione. Questa lezione si occupa di tecniche avanzate di risoluzione dei problemi: il backtracking. il paradigma greedy.
 Algoritmi Progrmmzion Avnzt - tori /9 Ch cos c è nll lzion Qust lzion si occup i tcnich vnzt i risoluzion i problmi: il bcktrcking il prigm gry. 2/9 Algoritmi Progrmmzion Avnzt - tori 3/9 Tipologi i problmi
Algoritmi Progrmmzion Avnzt - tori /9 Ch cos c è nll lzion Qust lzion si occup i tcnich vnzt i risoluzion i problmi: il bcktrcking il prigm gry. 2/9 Algoritmi Progrmmzion Avnzt - tori 3/9 Tipologi i problmi
Grandezze, funzioni empiriche e matematiche. 1 Stabilisci se le seguenti affermazioni sono vere o false.
 Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Equazioni differenziali di ordine superiore al primo
 Equzioni diffrnzili di ordin suprior l primo Eq. diff. linri offiinti ostnti n + n +...... + n + n = b i offiinti k sono ostnti, b = trmin noto, dfiniti in I R. L q. diff. è omogn s b = n + n +...... +
Equzioni diffrnzili di ordin suprior l primo Eq. diff. linri offiinti ostnti n + n +...... + n + n = b i offiinti k sono ostnti, b = trmin noto, dfiniti in I R. L q. diff. è omogn s b = n + n +...... +
Euristiche per il Problema del Commesso Viaggiatore
 Spinz Univrsità di Rom - Diprtimnto di Inggnri Informti, Automti Gstionl Euristih pr il Problm dl Commsso Viggitor Rnto Bruni bruni@dis.unirom.it Il mtril prsntto è drivto d qullo di proff. A. Sssno C.
Spinz Univrsità di Rom - Diprtimnto di Inggnri Informti, Automti Gstionl Euristih pr il Problm dl Commsso Viggitor Rnto Bruni bruni@dis.unirom.it Il mtril prsntto è drivto d qullo di proff. A. Sssno C.
GT Definizione di grafo orientato e non
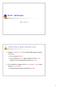 Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Esercizi di matematica
 Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI
 RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
Strutture dati per insiemi disgiunti
 Sopo Struttur ati pr insimi isiunti Gstir in moo iint una ollzion S = {S 1, S 2,..., S k } i insimi isiunti qualora l sol oprazioni onsntit siano: 1) rar un nuovo insim ontnnt un solo lmnto (tal lmnto
Sopo Struttur ati pr insimi isiunti Gstir in moo iint una ollzion S = {S 1, S 2,..., S k } i insimi isiunti qualora l sol oprazioni onsntit siano: 1) rar un nuovo insim ontnnt un solo lmnto (tal lmnto
Corso di Automi e Linguaggi Formali Parte 4 Linguaggi liberi dal contesto
 Grmmtich Rgol pr spcificr frsi corrtt in itlino Un frs un soggtto sguito d un vrbo sguito d un complmnto oggtto Un soggtto un nom o un rticolo sguito d un nom Uso dll rgol: pr gnrr frsi corrtt Esmpio:
Grmmtich Rgol pr spcificr frsi corrtt in itlino Un frs un soggtto sguito d un vrbo sguito d un complmnto oggtto Un soggtto un nom o un rticolo sguito d un nom Uso dll rgol: pr gnrr frsi corrtt Esmpio:
Aquadue Duplo. Guida all utilizzo. click! NEW! ON! c. Collegare il programmatore al rubinetto.
 Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
Elettronica dei Sistemi Digitali Sintesi di porte logiche combinatorie fully CMOS
 Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Trasformazioni geometriche +sometrie Omotetia e similitudine Teoremi di Euclide e teorema di Talete
 Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Algebra + numeri relativi +l calcolo letterale Equazioni, disequazioni, problemi
 Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
tx P ty P 1 + t(z P 1)
 Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
Corso di Analisi: Algebra di Base 5^ Lezione Logaritmi. Proprietà dei logaritmi Equazioni logaritmiche. Disequazioni logaritmiche. Allegato Esercizi.
 Corso di Anlisi: Algbr di Bs ^ Lzion Logritmi. Proprità di ritmi Equzioni ritmih. Disquzioni ritmih. Allgto Esrizi. LOGARITMI : Pr ritmo intndimo un sprssion lttrl indint un vlor numrio. Dfinizion : Si
Corso di Anlisi: Algbr di Bs ^ Lzion Logritmi. Proprità di ritmi Equzioni ritmih. Disquzioni ritmih. Allgto Esrizi. LOGARITMI : Pr ritmo intndimo un sprssion lttrl indint un vlor numrio. Dfinizion : Si
Funzione esponenziale e logaritmo. Proprietà di esponenziale e logaritmo.
 Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Ellisse. L ellisse è il luogo geometrico dei punti del piano tali che la somma delle distanze da due punti fissi. definizione. P semidistanza focale
 Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
Test di autovalutazione
 Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE
 GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE PROPRIETA GEOMETRICHE DELL ELLISSOIDE Al fin di stbilir un gomtri sull llissoid di rotzion è ncssrio non solo dfinir l quzioni dll curv idon d individur
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE PROPRIETA GEOMETRICHE DELL ELLISSOIDE Al fin di stbilir un gomtri sull llissoid di rotzion è ncssrio non solo dfinir l quzioni dll curv idon d individur
Matematica. Indice lezione. (Esercitazioni) dott. Francesco Giannino dott. Valeria Monetti. Funzione esponenziale
 Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
The cost of the material maintenance is averaged over the last 3 years.
 Anlisi i osti i un Diprtimnto 11 TABLE 4 Dprition n mintnn osts (unit: ITL) Ctgory Y Prio Inrs vlu Annul vlu 1 Furnitur 5 1.1.90{31.12.95 219 311 127 43 862 225 2 Lirry 5 1.1.90{31.12.95 542 832 793 108
Anlisi i osti i un Diprtimnto 11 TABLE 4 Dprition n mintnn osts (unit: ITL) Ctgory Y Prio Inrs vlu Annul vlu 1 Furnitur 5 1.1.90{31.12.95 219 311 127 43 862 225 2 Lirry 5 1.1.90{31.12.95 542 832 793 108
IL MOTO NELLA ZONA INSATURA
 L ritnzion dll umidità L suprfii d 1 4 rpprsntno l sussiv fsi di drnggio gio dll qu d un mzzo poroso. Al rsr dl drnggio l qu l si ritir ngli spzi intrstizili on suprfii urvtur ur rsnt d umntndo il rio
L ritnzion dll umidità L suprfii d 1 4 rpprsntno l sussiv fsi di drnggio gio dll qu d un mzzo poroso. Al rsr dl drnggio l qu l si ritir ngli spzi intrstizili on suprfii urvtur ur rsnt d umntndo il rio
ESERCIZI IN PIÙ ESERCIZI DI FINE CAPITOLO
 L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
Studio di funzione. Pertanto nello studio di tali funzioni si esamino:
 Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Aquauno Video 2 Plus
 Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
Esercizi Circuiti Resistivi
 srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
ISTRUZIONI DI MONTAGGIO per controtelai SP
 ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
Cammini minimi in un grafo orientato pesato. Un problema di percorso. Problemi di ottimizzazione
 Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
Totti, 37 anni da leggenda. Un monumento vivente. Scritto da Redazione Venerdì 27 Settembre 2013 08:39 - VALERIA META
 37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
Progetto di cinghie trapezoidali
 Progtto i cinghi trpzoili L cinghi trpzoili sono utilizzt frquntmnt pr l trsmission i potnz ntggi Bsso costo Smplicità i instllzion Cpcità i ssorbir vibrzioni torsionli picchi i coppi Svntggi Mncnz i sincronismo
Progtto i cinghi trpzoili L cinghi trpzoili sono utilizzt frquntmnt pr l trsmission i potnz ntggi Bsso costo Smplicità i instllzion Cpcità i ssorbir vibrzioni torsionli picchi i coppi Svntggi Mncnz i sincronismo
Nome Cognome classe 5D 16 Dicembre VERIFICA di MATEMATICA PROBLEMA
 Nom Cognom cls D 6 Dicmr 8 VERIFICA di MATEMATICA PROBLEMA Considr l unzion, studin l ndmnto trccin il grico proil punti: Di l dinizion di unzion inittiv Sull dl grico proil ch hi trccito, l unzion è inittiv?
Nom Cognom cls D 6 Dicmr 8 VERIFICA di MATEMATICA PROBLEMA Considr l unzion, studin l ndmnto trccin il grico proil punti: Di l dinizion di unzion inittiv Sull dl grico proil ch hi trccito, l unzion è inittiv?
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
Sintesi. Sintesi Sequenziale Sincrona Sintesi comportamentale di reti sequenziali sincrone. Riduzione del numero degli stati
 Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 5/12/02 Sintsi La sintsi si svol
Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 5/12/02 Sintsi La sintsi si svol
Diagrammi di Influenza (Influence Diagrams: ID)
 Digrmmi di Influnz (Influnc Digrms: ID) Linguggio pr l rpprsntzion grfic di prolmi dcisionli Crttristich vntggi prmttono un rpprsntzion dll struttur gnrl dl prolm, st su un pproccio visul prmttono di formlizzr
Digrmmi di Influnz (Influnc Digrms: ID) Linguggio pr l rpprsntzion grfic di prolmi dcisionli Crttristich vntggi prmttono un rpprsntzion dll struttur gnrl dl prolm, st su un pproccio visul prmttono di formlizzr
I LIMITI DI FUNZIONI - CALCOLO
 Autor: Erico Mfucci - // I LIMITI DI FUNZIONI - CALCOLO Dopo vr studito l tori di iti, dobbimo dsso vdr com si clcolo. Storicmt il clcolo di iti vi smplificto d u procsso ch prd il om di ritmtizzzio dll
Autor: Erico Mfucci - // I LIMITI DI FUNZIONI - CALCOLO Dopo vr studito l tori di iti, dobbimo dsso vdr com si clcolo. Storicmt il clcolo di iti vi smplificto d u procsso ch prd il om di ritmtizzzio dll
Relazioni e funzioni. Relazioni
 Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Integrale indefinito
 04//05 Intgrl indinito unzion intgrl Dinizion Si un unzion intgrbil scondo Rimnn nll intrvllo [,b] [,b], si dinisc unzion intgrl di, l intgrl dinito: t 04//05 Torm ondmntl dl clcolo intgrl Si continu in
04//05 Intgrl indinito unzion intgrl Dinizion Si un unzion intgrbil scondo Rimnn nll intrvllo [,b] [,b], si dinisc unzion intgrl di, l intgrl dinito: t 04//05 Torm ondmntl dl clcolo intgrl Si continu in
a a = 1, a a = 0; a a = 1, a a = 0; e quindi, = (a a ) (a a ) = (a a) a = 0 a = a
 Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR
 ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR Tizin Rprlli 5/5/8 RICHIAMI DI TEORIA Proposizion.. Si f C ([, b]) g C ([, b]), llor f(x)g(x)dx = [F (x)g(x)] b F (x)g (x)dx. dov F (x) è un
ESERCITAZIONE DIECI: INTEGRALI DEFINITI E FORMULA DI TAYLOR Tizin Rprlli 5/5/8 RICHIAMI DI TEORIA Proposizion.. Si f C ([, b]) g C ([, b]), llor f(x)g(x)dx = [F (x)g(x)] b F (x)g (x)dx. dov F (x) è un
Metodi Matematici per la Fisica
 Mtodi Mtmtici pr l Fisic Prov scritt - 7 sttmbr 011 Esrcizio 1 6 punti Si clcoli l intgrl I snx snhx dx Ci sono du mtodi, di sguito il primo Ci sono infiniti poli smplici inftti il sno iprbolico si nnull
Mtodi Mtmtici pr l Fisic Prov scritt - 7 sttmbr 011 Esrcizio 1 6 punti Si clcoli l intgrl I snx snhx dx Ci sono du mtodi, di sguito il primo Ci sono infiniti poli smplici inftti il sno iprbolico si nnull
Fig. 1. 1) La resistenza totale della bobina vale: (*) 2) Il modulo B del campo di induzione magnetica B r nel punto medio M della spira vale: L (*)
 Fcoltà di nggnri Prov Scritt di Fisic uglio 4 - Compito usito n. n un filo rttilino lungo fluisc un corrnt. Ad un distnz dl filo è post un oin, il cui punto mdio è ll stss quot dl punto mdio O dl filo.
Fcoltà di nggnri Prov Scritt di Fisic uglio 4 - Compito usito n. n un filo rttilino lungo fluisc un corrnt. Ad un distnz dl filo è post un oin, il cui punto mdio è ll stss quot dl punto mdio O dl filo.
Lemma 2. Se U V é un sottospazio vettoriale di V allora 0 U.
 APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
Prova scritta di Algebra lineare e Geometria- 22 Gennaio 2018 = L (( 3, 2, 6)) = L ( 3, 2, 6, 5).
 Corso di Lure in Ingegneri Informti (A-Co, J-Pr) - Ingegneri Elettroni (A-Co, J-Pr) - Ingegneri Industrile (F-O) - Ingegneri Gestionle - Ingegneri Elettri - Ingegneri Meni - Ingegneri REA Prov sritt di
Corso di Lure in Ingegneri Informti (A-Co, J-Pr) - Ingegneri Elettroni (A-Co, J-Pr) - Ingegneri Industrile (F-O) - Ingegneri Gestionle - Ingegneri Elettri - Ingegneri Meni - Ingegneri REA Prov sritt di
PROGRAMMA DI RIPASSO ESTIVO
 ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
CORSO DI TOPOGRAFIA A - A.A. 2006-2007 ESERCITAZIONI - 09.05.07 ALLEGATO al file Esercizi di geodesia. r a. Z c. nella quale
 CORSO DI TOPOGRAFIA A - A.A. 6-7 ESERCITAZIONI - 9.5.7 ALLEGATO l fil Esrcizi di godsi Ellissoid trrstr Fin dll scond mtà dl VII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di
CORSO DI TOPOGRAFIA A - A.A. 6-7 ESERCITAZIONI - 9.5.7 ALLEGATO l fil Esrcizi di godsi Ellissoid trrstr Fin dll scond mtà dl VII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di
Sintesi. Sintesi Sequenziale Sincrona Sintesi comportamentale di reti sequenziali sincrone. Riduzione del numero degli stati
 Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 12/12/2004 Sintsi La sintsi si
Sintsi Squnzial Sinrona Sintsi omportamntal i rti squnziali sinron Riuzion l numro li stati pr Mahin Compltamnt Spiiat Inistinuiilità & Equivalnza Irraiuniilità vrsion l 12/12/2004 Sintsi La sintsi si
SPOSTAMENTO E RETTIFICA DI CONFINE
 SPOSEO E REIFI I OFIE Lo SPOSEO si qundo un confin ià rttilino vin sostituito con un ltro smpr rttilino L REIFI si qundo un confin polionl o curvilino vin sostituito con un ltro rttilino. SPOSEO REIFI
SPOSEO E REIFI I OFIE Lo SPOSEO si qundo un confin ià rttilino vin sostituito con un ltro smpr rttilino L REIFI si qundo un confin polionl o curvilino vin sostituito con un ltro rttilino. SPOSEO REIFI
ALGORITMI E COMPLESSITÀ CORSO DI LAUREA MAGISTRALE IN INFORMATICA UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
Esercizi riguardanti l integrazione
 Esrizi riguardanti l intgrazion. Trovar una primitiva dlla funzion f. Calolar il sgunt intgral indfinito d. Trovar una primitiva dlla funzion f. Tra tutt l primitiv dlla funzion f os sn, dtrminar qulla
Esrizi riguardanti l intgrazion. Trovar una primitiva dlla funzion f. Calolar il sgunt intgral indfinito d. Trovar una primitiva dlla funzion f. Tra tutt l primitiv dlla funzion f os sn, dtrminar qulla
Elettronica dei Sistemi Digitali Disegno del layout di porte logiche combinatorie CMOS
 Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
OLIGOPOLIO NON COOPERATIVO. Il modello di Cournot simmetrico. Funzioni obiettivo e condizioni di primo ordine
 OLIGOPOLIO NON COOPERATIVO Dfinizion Il modllo di Cournot simmtrio Funzioni obittivo ondizioni di primo ordin Curv di rzion Livllo ottimo di output (quilibrio di Cournot) Confronto tr Duopolio di Cournot,
OLIGOPOLIO NON COOPERATIVO Dfinizion Il modllo di Cournot simmtrio Funzioni obittivo ondizioni di primo ordin Curv di rzion Livllo ottimo di output (quilibrio di Cournot) Confronto tr Duopolio di Cournot,
di Enzo Zanghì 1
 M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
Esercitazione di AM120
 Univrsità dgli Studi Roma Tr - Corso di Laura in Matmatica Esrcitazion di AM0 A.A. 07 08 - Esrcitator: Luca Battaglia Soluzioni dll srcitazion dl 6 7 Marzo 08 Argomnto: Drivat. Dimostrar, utilizzando la
Univrsità dgli Studi Roma Tr - Corso di Laura in Matmatica Esrcitazion di AM0 A.A. 07 08 - Esrcitator: Luca Battaglia Soluzioni dll srcitazion dl 6 7 Marzo 08 Argomnto: Drivat. Dimostrar, utilizzando la
( a) 1 a + Es. Data la funzione:
 Es. Dt l uzio: ' ' ( Esrcizi Complmtri. A( ( b. Dtrmir pr quli vlori di b l uzio mmtt u puto di mssimo d u puto di miimo pr quli vlori l uzio o mmtt tli puti.. Dtrmir i vlori di b i modo ch l uzio prsti
Es. Dt l uzio: ' ' ( Esrcizi Complmtri. A( ( b. Dtrmir pr quli vlori di b l uzio mmtt u puto di mssimo d u puto di miimo pr quli vlori l uzio o mmtt tli puti.. Dtrmir i vlori di b i modo ch l uzio prsti
IL PROBLEMA DELLE TRE CASE
 IL PROBLEMA DELLE TRE CASE L qustioni post in qust u sh rigurno un prolm lssio, h spsso si trov sotto il nom i prolm ll tr s o prolm ll tr s i tr srvizi : fissti u gruppi i tr punti nl pino, i si hi s
IL PROBLEMA DELLE TRE CASE L qustioni post in qust u sh rigurno un prolm lssio, h spsso si trov sotto il nom i prolm ll tr s o prolm ll tr s i tr srvizi : fissti u gruppi i tr punti nl pino, i si hi s
Teoria. Tale retta limite non sempre esiste. Si veda il grafico sottostante. Matematica 1
 LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
DETERMINA DI AGGIUDICAZIONE ARCA_2016_51 Gara per la fornitura di Dispositivi per Drenaggio Appalto Specifico
 DATA DI PUBBLICAZIONE 11/5/2018 Milno, 11 Mggio 2018 Prot. n. 2018.0006258 DETERMINA DI AGGIUDICAZIONE ARCA_2016_51 Gr pr l ornitur i Dispositivi pr Drnggio Applto Spiio Il Dirttor Gnrl ll Azin Rgionl
DATA DI PUBBLICAZIONE 11/5/2018 Milno, 11 Mggio 2018 Prot. n. 2018.0006258 DETERMINA DI AGGIUDICAZIONE ARCA_2016_51 Gr pr l ornitur i Dispositivi pr Drnggio Applto Spiio Il Dirttor Gnrl ll Azin Rgionl
Propulsione Aerospaziale. Cap. 4 Sez. d Ugelli per esoreattori e endoreattori. Esercizi svolti
 Politcnico di ilno Fcoltà di Innri Industril Corso di Lur in Innri roszil Insnmnto di Proulsion roszil nno ccdmico / C. 4 Sz. d Ulli r sorttori ndorttori Esrcizi svolti rv. dicmbr ESERCIZIO 4d. Un ullo
Politcnico di ilno Fcoltà di Innri Industril Corso di Lur in Innri roszil Insnmnto di Proulsion roszil nno ccdmico / C. 4 Sz. d Ulli r sorttori ndorttori Esrcizi svolti rv. dicmbr ESERCIZIO 4d. Un ullo
Svolgimento di alcuni esercizi
 Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Soluzioni dei Problemi di controllo
 Soluioni i roblmi i ontrollo Si v raliar un sistma i ontrollo i tipo on transitorio h si annulli in tmpo finito minimo Dato h la ha già un polo in non è nssario introurn altri pr mo l ontrollor G r ottnr
Soluioni i roblmi i ontrollo Si v raliar un sistma i ontrollo i tipo on transitorio h si annulli in tmpo finito minimo Dato h la ha già un polo in non è nssario introurn altri pr mo l ontrollor G r ottnr
Vettori - Definizione
 Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
a è detta PARTE LETTERALE
 I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
SICUREZZA SUL LAVORO SAFETY AT WORK SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31
 SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Sintesi Sequenzile Sinron Sintesi Comportmentle di Reti Sequenzili Sinrone Riduzione del numero degli stti per Mhine Non Completmente Speifite Comptiilità Versione del 9/12/03 Mhine non ompletmente speifite
Sintesi Sequenzile Sinron Sintesi Comportmentle di Reti Sequenzili Sinrone Riduzione del numero degli stti per Mhine Non Completmente Speifite Comptiilità Versione del 9/12/03 Mhine non ompletmente speifite
ESERCIZI PARTE I SOLUZIONI
 UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
Le derivate. = 5 si traccino due rette qualsiasi passanti entrambe per il corrispondente punto della funzione e per
 L drivt Il problm di introdurr il conctto di drivt consist nl trsmttr l id di ciò c si st rontndo, nl snso c s d un punto di vist orml è possibil introdurr l dinizion di qusto conctto in trmini rigorosi,
L drivt Il problm di introdurr il conctto di drivt consist nl trsmttr l id di ciò c si st rontndo, nl snso c s d un punto di vist orml è possibil introdurr l dinizion di qusto conctto in trmini rigorosi,
11. Rango di una matrice.
 Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
