Alcuni esempi di equazioni differenziali ordinarie lineari del primo e del secondo ordine
|
|
|
- Dario Angelini
- 5 anni fa
- Visualizzazioni
Transcript
1 Alcuni esempi di equazioni differenziali ordinarie lineari del primo e del secondo ordine Esempio 1 : il decadimento del neutrone. Il neutrone non é una particella stabile:si disintegra in un protone, un elettrone ed un neutrino. Se indichiamo con N(t) il numero dei neutroni presenti al tempo t e con p la probabilitá che un neutrone si disintegri in un secondo,il processo di decadimento si descrive con un equazione differenziale lineare del primo ordine del tipo: N (t) = pn(t). Ció significa che la variazione di neutroni in un secondo é proporzionale al numero di neutroni presenti. Il segno indica che i neutroni diminuiscono perche si disintegrano. Supponiamo N(t) diverso da zero e dividiamo i due membri dell equazione di sopra per N(t),l equazione che si ottiene,integrata rispetto a t,fornisce log N(t) = pt + c da cui si ricava la soluzione: N(t) =e pt e c = Ce pt. Non deve sorprendere la presenza della costante C : infatti non é possibile conoscere il numero dei neutroni all istante t se non si conosce il numero dei neutroni all istante iniziale del processo t 0. Se, nella formula della soluzione, poniamo t = t 0 =0, avremo N(0) = C, quindi la costante C rappresenta il numero di neutroni presenti all istante t = t 0 =0. In definitiva la funzione N(t) =Ce pt risolve il problema di Cauchy che si ottiene associando all equazione N (t) = pn(t) la condizione iniziale N(0) = C. Esempio 2 : modello di Malthus per la dinamica delle popolazioni. Si considera una popolazione che evolve isolata e i cui fattori di evoluzione sono soltanto la fertilitá e la mortalitá. Sia N(t) il numero degli individui presenti al tempo t; indichiamo con λ e µ rispettivamente il numero di nuovi nati e di morti per individuo nell unitá di tempo t. In un intervallo temporale di durata h il numero di nuovi nati sará λhn(t) e il numero di morti sará µhn(t). Ne segue che la variazione del numero degli individui in un tempo h sara : N(t + h) N(t) =λhn(t) µhn(t). 1
2 Dividendo per h e calcolando il limite per h che tende a zero, si perviene all equazione: N (t) =(λ µ)n(t) che é evidentemente dello stesso tipo di quella considerata sopra e si risolve come gia visto. Esempio 3: le vibrazioni lineari. Consideriamo una particella di massa m che si muove lungo una retta ed é soggetta ad una forza di richiamo elastica,proporzionale allo spostamento, e ad una resistenza viscosa,proporzionale alla velocitá. In base alla legge di Newton il moto della particella verifica l equazione differenziale mx = µx kx. dove x = x(t) é lo spostamento al tempo t rispetto alla posizione di equilibrio, mentre k e µ sono costanti positive che caratterizzano la forza elastica e la resistenza viscosa e che si chiamano costante elastica e costante di smorzamento del sistema.supponiamo che all istante t = 0 la particella occupi la posizione x 0 ed abbia velocitá v 0, allora il moto é descritto dal problema di Cauchy: mx = µx kx, x(0) = x 0 e x (0) = v 0. Questa equazione descrive molti modelli di sistemi lineari di natura assai diversa. Si tratta di un equazione omogenea e a coefficienti costanti che si risolve considerando l equazione caratteristica: mλ 2 + µλ + k =0, e le sue radici: λ = µ ± µ 2 4km. 2m Esaminiamo il caso in cui non c é resistenza viscosa, cioé µ =0. La soluzione generale dell equazione é: x(t) =A cos ω 0 t + B sin ω 0 t 2
3 dove si é posto ω 0 =( k m ) 1 2. Imponendo le condizioni iniziali si ricava A = x 0 e B = v 0 ω 0, quindi la soluzione del problema di Cauchy é data da: x(t) =x 0 cos ω 0 t + v 0 ω 0 sin ω 0 t. Da note formule trigonometriche,si puó anche scrivere: x(t) =R sin(ω 0 t + φ) dove R = x 02 + v 0 2 ω 2 0, sin φ = x 0 R e cos φ = v 0 ω 0 R La particella si muove dunque di moto armonico; il numero R individua l ampiezza, 2π ω 0 è il periodo e φ è lo spostamento di fase. Si noti che il periodo è indipendente dalla condizioni iniziali. Se µ 0 esaminiamo solo il caso seguente 0 <µ<2 mk. Le radici dell equazione caratteristica sono complesse coniugate e quindi la soluzione dell equazione differenziale è del tipo x(t) =e αt (A cos ω 0 t + B sin ω 0 t) dove α = µ 2m,ω 0 = 4mk mu 2 2m. Imponendo le condizioni iniziali si trova ( x(t) =e αt x 0 cos ω 0 t + ν ) 0 + αx 0 sin ω 0 t. ω 0 Il moto della particella è anche in questo caso oscillatorio, ma l ampiezza delle oscillazioni tende rapidamente a zero al crescere di t (oscillazioni smorzate). La soluzione si può scrivere in modo sintetico nella forma: x(t) =Re αt sin(ω 0 t + φ) con opportuni parametri R e φ. Cenni sulle equazioni differenziali ordinarie lineari di ordine n Sia I un intervallo della retta reale e siano p h (x),h =0, 1, 2,..., n e q(x) funzioni continue su I. L equazione differenziale: p o (x)y (n) + p 1 (x)y (n 1) p n 1 (x)y + p n (x)y = q(x) 3
4 si dice equazione differenziale lineare. Se p o (x) non è nulla,l equazione è di ordine n e,dividendo per p o (x), dopo aver posto a h (x) = p h(x) p o (x) semplificata: dove q(x) e f(x) = p o (x),si ottiene in forma L(y) =f(x), (1) L(y) =y (n) + a 1 (x)y (n 1) a n 1 (x)y + a n (x)y. (2) L operatore L è l operatore differenziale che ad ogni funzione y C n (I), cioe dotata di derivate continue fino all ordine n,associa la combinazione di y e delle sue derivate fino all ordine n rappresentata da (2). L equazione (1),nel caso f(x) = 0, si dice omogenea e L(y) =0, (3) rappresenta l equazione omogenea associata alla (1). L operatore L soddisfa la relazione L(µy + λz) =µl(y)+λl(z) per ogni coppia di numeri µ e λ e per ogni coppia di funzioni y e z. Ne segue che, per ogni numero finito di funzioni y 1,...y p di funzioni di classe C n (I) e di costanti c 1,..., c p, risulta L(c 1 y c p y p )=c 1 L(y 1 ) c p L(y p ). Si conclude che se y 1,...y p sono soluzioni dell equazione lineare omogenea (3), ogni combinazione lineare del tipo c 1 y c p y p è ancora soluzione della stessa equazione. Sussiste inoltre il seguente teorema: Teorema 1.Se y 0 è soluzione dell eq.(1) (non omogenea) e y(x)è soluzione di (3) (eq.omogenea associata),la loro somma è soluzione dell equazione (1). Viceversa ogni soluzione z dell eq. (1) si può ottenere come somma di una soluzione particolare di (1) e una qualunque soluzione di (3). Prova. Dalle ipotesi L(y 0 )=f(x) el(y) = 0,dunque,sommando membro a membro e sfruttando la proprietà di linearità dell operatore L si ottiene: L(y 0 + y) =L(y 0 )+L(y) =f(x). 4
5 Viceversa sia z una qualunque soluzione di (1).Se y 0 è soluzione di (1), dalla linearità dell operatore risulta: L(z y o )=L(z) L(y 0 )=f(x) f(x) =0, dunque y = z y o è soluzione dell equazione omogenea (3) e z = y 0 + y. Osservazione. Questo teorema prova che tutte le soluzioni dell equazione non omogenea (1) si possono ottenere sommando una sua particolare soluzione a tutte le possibili soluzioni dell equazione omogenea (3). Ci proponiamo ora di risolvere le equazioni di tipo omogeneo. Vogliamo individuare l integrale generale di (3),cioè una espressione dalla quale si possano ricavare tutte le possibili soluzioni di (3). Si è visto che ogni combinazione lineare di un numero finito di soluzioni o integrali di (3) è ancora soluzione di (3), quindi l espressione richiesta è del tipo c 1 y c p y p, (4) dove y 1,..., y p sono integrali di (3). Si è pure visto che nel caso di un equazione lineare del primo ordine,l integrale generale dipende da una costante arbitraria e nel caso dell equazione del secondo ordine dipende da due costanti arbitrarie,ciò potrebbe indurre all errata conclusione che la combinazione lineare (4),con p = n, fornisca l integrale generale dell equazione (3).In effetti l integrale generale di (3) è del tipo c 1 y c n y n, ma gli integrali y 1,..., y n devono essere scelti in modo opportuno;a tale scopo introduciamo la definizione seguente: Definizione. Si dice che le funzioni y 1,..., y n sono linearmente indipendenti se l uguaglianza c 1 y c n y n = 0 implica necessariamente che le costanti c 1,..., c n, sono tutte nulle. Non entriamo nel merito delle motivazioni di questa definizione per ragioni di brevitá, ma concludiamo dicendo che l integrale generale dell equazione differenziale lineare omogenea (3), cioé la formula che fornisce tutte le possibili soluzioni di tale equazione,é dato da y = c 1 y c n y n, dove y 1,..., y n sono n soluzioni linearmente indipendenti di (3) e c 1,..., c n, sono n costanti arbitrarie. 5
6 Equazioni differenziali ordinarie lineari di ordine n a coefficienti costanti omogenee. Per alcune classi di equazioni é facile individuare l integrale generale, cioé esprimere in un unica formula tutte le possibili soluzioni. E il caso delle equazioni a coefficienti costanti: L(y) =y (n) + a 1 y (n 1) a n 1 y + a n y =0, (5) dove a 1,..., a n sono costanti reali. Osserviamo che,se y(x) =e αx risolve la (5), poiché y (h) (x) =α h e αx per ogni h =1,...n,il numero α risolve l equazione algebrica α n + a 1 α (n 1) a n 1 α + a n = 0 (6) e viceversa.l equazione (6) prende il nome di equazione caratteristica associata alla (5). Il problema si riconduce quindi alla determinazione di n integrali linearmente indipendenti di (5) utilizzando le soluzioni dell equazione (6). Distinguiamo due casi: il caso in cui l equazione (6) ammette solo radici semplici e quello in cui l equazione (6) ammette anche radici multiple. Nel primo caso, denotate con α 1,..., α n le n radici semplici dell equazione caratteristica,prendiamo come integrali linearmente indipendenti della (5) le funzioni e α1x,..., e αnx. Infatti se α i α j risulta: c i e αix + c j e αjx =0= c i = c j =0. Ció si vede facilmente perché,supposto c i 0, dividendo per c i e α jx, si ottiene: che non puó essere vera per ogni x. e (α i α j )x = c j c i Analogamente si ragiona scambiando il ruolo di i con j e si conclude che devono essere nulle entrambe le costanti. In questo primo caso l integrale generale di (5) sará dato da y(x) =c 1 e α 1x c n e α nx. Nel secondo caso l equazione caratteristica presenta radici multiple. Sia α i una di queste radici multiple e sia ν i la sua molteplicitá. Si puó provare che i ν i integrali 6
7 linearmente indipendenti relativi a tale radice sono : e α ix,xe α ix,..., x ν i 1 e α ix e che l integrale generale di (5) é una combinazione lineare di funzioni del tipo e αx per ogni radice semplice α dell equazione caratteristica e di funzioni del tipo e αx,xe αx,..., x ν 1 e αx per ogni radice α di molteplicitá ν dell equazione caratteristica. Esempi Risolviamo le equazioni seguenti: 1) y +3y +2y =0. L equazione caratteristica associata α 2 +3α +2=0 ha soluzioni α 1 = 1 eα 2 = 2, dunque due integrali linearmente indipendenti di 1) sono e x e e 2x e l integrale generale di 1) é y(x) =c 1 e x + c 2 e 2x 2) y +6y +9y =0. L equazione caratteristica associata α 2 +6α +9=0 ha soluzione α = 3 di molteplicitá due; ne segue che due integrali linearmente indipendenti di 1) sono e 3x e xe 3x e l integrale generale di 2) é y(x) =c 1 e 3x + c 2 xe 3x 3) y 3y +2y =0. L equazione caratteristica associata α 3 3α +2=0 7
8 ha soluzione α = 1 e, dividendo α 3 3α +2 per α 1, si ottiene α 2 + α 2 che ha radici α =1eα = 2. In definitiva l equazione caratteristica di 3) ha una radice semplice α = 2. e una radice doppia α =1. L integrale generale di 3) é y(x) =c 1 e x + c 2 xe x + c 3 e 2x Finora si sono trattati esempi di equazioni la cui caratteristica presenta radici reali. In generale un equazione algebrica a coefficienti reali puó presentare radici complesse.la teoria precedentemente esposta non distingue fra soluzioni reali e soluzioni complesse della caratteristica quindi proviamo a trattare in modo analogo l equazione differenziale: 4) y +2y +3y =0. L equazione caratteristica associata α 2 +2α +3=0 ha soluzioni complesse coniugate semplici α 1 = 1 + 2i e α 2 = 1 2i e quindi l integrale generale di 4) é dato da y(x) =c 1 e ( 1 2i)x + c 2 e ( 1+ 2i)x. Volendo una rappresentazione dell integrale generale in termini di funzioni reali,osserviamo che due integrali linearmente indipendenti dell equazione 4) si possono ottenere dalle formule di Eulero e sono: e x cos 2x e e x sin 2x e quindi l integrale generale di 4) é y(x) =c 1 e x cos 2x + c 2 e x sin 2x. Risolvere l equazione 8
9 5) y IV +2y + y =0. L equazione caratteristica associata α 4 +2α 2 +1=0 equivalente alla equazione (α 2 +1) 2 =0 ha soluzioni complesse coniugate doppie α 1 = i e α 2 =+i, quindi quattro integrali linearmente indipendenti sono: e l integrale generale di 5) é cosx, xcosx, sinx, xsinx y(x) =(c 1 + c 2 x)cosx +(c 3 + c 4 x)sinx. Risolvere l equazione 6) y VI y IV y + y =0. L equazione caratteristica associata, α 6 α 4 α 2 +1=0 equivalente alla equazione (α 2 1) 2 (α 2 +1)=0, ha soluzioni complesse coniugate semplici α 1 = i e α 2 =+i, e due soluzioni reali doppie α 3 = 1 eα 4 =1, quindi sei integrali linearmente indipendenti sono: e l integrale generale di 5) é e x,xe x,e x,xe x, cosx, sinx y(x) =(c 1 + c 2 x)e x +(c 3 + c 4 x)e x + c 5 cosx + c 6 sinx. 9
10 Equazioni differenziali ordinarie lineari del primo ordine Consideriamo ora l equazione L(y) =y + a(x)y = f(x). (6) Dalla teoria precedentemente esposta,l integrale generale di (6) si ottiene aggiungendo all integrale generale dell equazione omogenea associata un integrale particolare dell equazione completa. Ció sipuó fare in modo standard, seguendo il metodo della variazione delle costanti arbitrarie oppure, nel caso di equazioni differenziali a coefficienti costanti, osservando che per alcune funzioni f(x) di tipo particolare si puó cercare un integrale della stessa forma di f(x). Il metodo della variazione delle costanti arbitrarie sará esposto ed applicato, per semplicitá, solo ad equazioni del primo e del secondo ordine e si basa sulla conoscenza dell integrale generale dell equazione omogenea associata. Per l equazione del primo ordine, se y(x) =cy 1 (x) é l integrale generale dell equazione omogenea associata, si cerca l integrale particolare nella forma y 0 (x) =c(x)y 1 (x) dove c(x) é una funzione incognita da determinare in modo che sia soddisfatta l equazione completa. Poiché y 0(x) =c (x)y 1 (x)+c(x)y 1(x), sostituendo nell equazione y + ay = f, si ottiene : c (x)y 1 (x)+c(x)y 1(x)+ac(x)y 1 (x) =f(x), da cui, ricordando che y 1 risolve l omogenea associata, segue c (x)y 1 (x) =f(x). A questo punto si puó determinare c (x) e,per integrazione,la funzione incognita c(x). In definitiva l integrale generale dell equazione completa é y(x) =cy 1 (x)+y 0 (x). 10
11 Equazioni differenziali ordinarie lineari del secondo ordine a coefficienti costanti non omogenee. Ci occupiamo del problema di determinare un integrale particolare dell equazione completa associata ad un equazione lineare a coefficienti costanti: ay (x)+by (x)+cy(x) =f(x) (a, b costanti.) (7) Illustriamo prima il metodo di somiglianza, che per una certa classe di casi particolari permette di determinare tale integrale particolare con brevi calcoli; vedremo poi il metodo di variazione delle costanti, che può essere impiegato sempre, ma in compenso porta solitamente a calcoli più pesanti (perciò, quando possibile, è meglio applicare il primo metodo). Metodo di somiglianza Quando il termine noto f(x) ha un aspetto particolarmente semplice si può cercare una soluzione pure abbastanza semplice e simile ad f in un senso che ora preciseremo. f(x) =p r (x) (polinomio di grado r). Si cerca una soluzione di tipo polinomiale: y(x) =q r (x) se c 0 y(x) =xq r (x) se c =0,b 0 y(x) =x 2 q r (x) se c =0,b=0. Esercizi. Trovare una soluzione particolare delle equazioni y y =1+x 2,y + 2y = x. f(x) =Ae λx, λ C. Si cerca una soluzione del tipo y(x) =γ(x)e λx. Basterà trovare una qualsiasi γ che soddisfi l equazione: aγ + γ (2aλ + b)+γ(aλ 2 + bλ + c) =A. Se aλ 2 + bλ + c 0 (cioè λ non è radice dell equazione caratteristica), basterà prendere γ(x) =A/(aλ 2 + bλ + c). Se aλ 2 + bλ + c = 0 ma 2aλ + b 0, basterà prendere γ (x) =A/(2aλ + b), da cui γ(x) =Ax/(2aλ + b). 11
12 Se infine aλ 2 + bλ + c =0e2aλ + b =0, allora aγ (x) =A, da cui γ(x) = A 2a x2. Nella classe di termini noti del tipo e λx con λ C rientrano anche i casi cos ωx, sin ωx, e λx cos ωx, e λx sin ωx con λ R. Esercizi. Trovare una soluzione particolare delle equazioni y +2y +3y =2e 3x, y +2y 3y =2e 3x,y +2y y =2e x cos 3x, 2y + y +2y = 3 sin 2x, y +3y = x + 2 cos x. Metodo di variazione delle costanti Illustriamo ora un metodo generale che consente di determinare una soluzione particolare dell equazione completa, qualunque sia la forma del termine noto f(x). Il metodo è applicabile purchè si conoscano già due soluzioni indipendenti dell equazione omogenea. Siano dunque y 1 (x) ey 2 (x) due soluzioni indipendenti dell equazione omogenea associata. L idea è cercare una soluzione particolare della forma y 0 (x) =c 1 (x)y 1 (x)+c 2 (x)y 2 (x). (8) Ricordiamo che le funzioni y 1 (x) ey 2 (x) sono note, mentre le funzioni c 1 (x) ec 2 (x) sono incognite e vanno determinate in modo che y 0 soddisfi l equazione (7). Questa equazione fornirà una condizione sulle due funzioni c 1 e c 2. Poichè le funzioni da determinare sono due, potremo imporre una seconda condizione su c 1 e c 2 che sceglieremo come ci fa più comodo. Cominciamo a calcolare dalla (8) y 0 = c 1y 1 + c 2y 2 + c 1 y 1 + c 2 y 2. Imponiamo come condizione su c 1 e c 2 la seguente c 1y 1 + c 2y 2 =0. Questa fa sì che risulti e di conseguenza y 0 = c 1 y 1 + c 2 y 2. (9) y 0 = c 1y 1 + c 2y 2 + c 1 y 1 + c 2 y 2. (10) 12
13 Sostituendo la (9) e la (10) nella (7) si ottiene a(c 1y 1 + c 2y 2 + c 1 y 1 + c 2 y 2 )+b(c 1 y 1 + c 2 y 2)+c(c 1 y 1 + c 2 y 2 )=f che si può riscrivere come c 1 (ay 1 + by 1 + cy 1 )+c 2 (ay 2 + by 2 + cy 2 )+(c 1y 1 + c 2y 2)=f che a sua volta, ricordando che per ipotesi y 1 e y 2 soddisfano l equazione omogenea, si riduce a c 1y 1 + c 2y 2 = f. In definitiva siamo arrivati a scrivere il sistema lineare di due equazioni nelle due funzioni incognite c 1 e c 2 c 1y 1 + c 2y 2 =0 c 1y 1 + c 2y 2 = f. Il determinante del sistema è y 1 y 2 y 1 y 2 ed è diverso da zero per l ipotesi di indipendenza delle due soluzioni y 1 e y 2. Perciò il sistema può essere risolto in c 1 e c 2. Si trova c 1 = y 2 f y 2 y 1 y 2 y 1, c 2 = y 1 f y 2 y 1 y 2 y 1. Da queste relazioni, integrando si ottengono c 1 (x) ec 2 (x) che sostituite nella (8) forniscono un integrale particolare dell equazione completa. Esercizi Trovare una soluzione particolare delle equazioni y y = 1+e x,y + y = 1 1+e 2x. 13
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159
 4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
6.3 Equazioni lineari del secondo ordine
 si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti:
 Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Risolvere i problemi di Cauchy o trovare l integrale generale delle seguenti equazioni differenziali del II ordine lineari a coefficienti costanti: 1. y 5y + 6y = 0 y(0) = 0 y (0) = 1 2. y 6y + 9y = 0
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Matematica II. Risolvere o integrare una e.d. significa trovarne tutte le soluzione, che costituiscono il cosidetto integrale generale.
 Definizione Si dice equazione differenziale di ordine n nella funzione incognita y = y (x) una relazione fra y, le sue derivate y,..., y (n), e la variabila indipendente x Risolvere o integrare una e.d.
Definizione Si dice equazione differenziale di ordine n nella funzione incognita y = y (x) una relazione fra y, le sue derivate y,..., y (n), e la variabila indipendente x Risolvere o integrare una e.d.
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0
![Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0 Analisi Vettoriale - A.A Foglio di Esercizi n Esercizio. y [17] + y [15] = 0. z + z = 0](/thumbs/98/136376494.jpg) Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 5 Determinare l integrale generale di 1. Esercizio y [17] + y [15] = Posto y [15] = z l equazione proposta diventa Il cui integrale generale é z +
Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 5 Determinare l integrale generale di 1. Esercizio y [17] + y [15] = Posto y [15] = z l equazione proposta diventa Il cui integrale generale é z +
Soluzioni. 152 Roberto Tauraso - Analisi Risolvere il problema di Cauchy. { y (x) + 2y(x) = 3e 2x y(0) = 1
 5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
1 Note sulle equazioni differenziali ordinarie
 1 Note sulle equazioni differenziali ordinarie La ricerca di una primitiva su un intervallo, y = f(x), è l esempio più semplice di equazione differenziale cioè la ricerca di una funzione con assegnata
1 Note sulle equazioni differenziali ordinarie La ricerca di una primitiva su un intervallo, y = f(x), è l esempio più semplice di equazione differenziale cioè la ricerca di una funzione con assegnata
Equazioni differenziali lineari di ordine n
 Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali
 1 Equazioni differenziali Definizioni introduttive Una equazione differenziale è una uguaglianza che contiene come incognita una funzione f x, insieme con le sue derivate rispetto alla variabile indipendente
1 Equazioni differenziali Definizioni introduttive Una equazione differenziale è una uguaglianza che contiene come incognita una funzione f x, insieme con le sue derivate rispetto alla variabile indipendente
Indice slides. 1 Oscillatore semplice 5. 2 Equazione caratteristica 6. 3 Radici complesse 7. 4 Integrale generale 8. 5 Forza Peso 9.
 Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
Moto di Oscillatori Pietro Pantano Dipartimento di Matematica Università della Calabria Slides 1 di 27 Slides 2 di 27 1 Oscillatore semplice 5 2 Equazione caratteristica 6 3 Radici complesse 7 4 Integrale
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine
 9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
9.2 Il problema di Cauchy per le equazioni differenziali del primo ordine 349 y = f(y, x), (9.23) allora la sostituzione z = y conduce all equazione del primo ordine z = f(z, x) nell incognita z = z(x).
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Un equazione differenziale ordinaria di ordine n è una relazione tra: 1. una variabile indipendente x R, 2. una funzione incognita y = y(x) a valori reali 3. le derivate
Equazioni differenziali ordinarie Un equazione differenziale ordinaria di ordine n è una relazione tra: 1. una variabile indipendente x R, 2. una funzione incognita y = y(x) a valori reali 3. le derivate
Esercizio Determinare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (i) y = 3y cos(x);
 134 Capitolo 4. Equazioni differenziali ordinarie del problema di Cauchy (4.28) bisogna risolvere il sistema lineare (nelle incognite c 1,..., c n )) c 1 y 1 (x 0 ) +... + c n y n (x 0 ) = y 0, c 1 y 1
134 Capitolo 4. Equazioni differenziali ordinarie del problema di Cauchy (4.28) bisogna risolvere il sistema lineare (nelle incognite c 1,..., c n )) c 1 y 1 (x 0 ) +... + c n y n (x 0 ) = y 0, c 1 y 1
LEZIONI DI ANALISI MATEMATICA I. Equazioni Differenziali Ordinarie. Sergio Lancelotti
 LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
LEZIONI DI ANALISI MATEMATICA I Equazioni Differenziali Ordinarie Sergio Lancelotti Anno Accademico 2006-2007 2 Equazioni differenziali ordinarie 1 Equazioni differenziali ordinarie di ordine n.................
1 Equazioni Differenziali
 Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Lezione 3 Equazioni del secondo ordine
 Lezione 3 Equazioni del secondo ordine Vogliamo ora prendere in esame equazioni differenziali del secondo ordine del tipo: y (x) + p(x)y (x) + q(x)y(x) = g(x) Diremo che un equazione differenziale della
Lezione 3 Equazioni del secondo ordine Vogliamo ora prendere in esame equazioni differenziali del secondo ordine del tipo: y (x) + p(x)y (x) + q(x)y(x) = g(x) Diremo che un equazione differenziale della
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Equazioni differenziali
 Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
Equazioni differenziali Versione da non divulgare. Scritta per comodità degli studenti. Può contenere errori. 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Dicembre 2013 Generalità
ESERCIZI sui VETTORI
 ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
ESERCIZI sui VETTORI 1. Calcolare la somma di v 1 (2, 3) e v 2 (1, 4). 2. Calcolare la somma di v 1 (1, 5, 4) e v 2 (6, 8, 2). 3. Calcolare il prodotto di α = 2 e v 1 (1, 4). 4. Calcolare il prodotto di
7. Equazioni differenziali
 18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
Per determinare una soluzione particolare descriveremo un metodo che vale solo nel caso in cui la funzione f(x) abbia una forma particolare:
 42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008. Dott.ssa G. Bellomonte
 Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Equazioni differenziali
 Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Appunti sulle equazioni differenziali lineari a coefficienti costanti del secondo ordine
 Appunti sulle equazioni differenziali lineari a coefficienti costanti del secondo ordine A. Figà-Talamanca 22 maggio 2005 L equazione differenziale y + ay + by = 0, (1) dove a e b sono costanti, si chiama
Appunti sulle equazioni differenziali lineari a coefficienti costanti del secondo ordine A. Figà-Talamanca 22 maggio 2005 L equazione differenziale y + ay + by = 0, (1) dove a e b sono costanti, si chiama
CIRCUITI IN CORRENTE CONTINUA
 IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Addendum equazioni differenziali
 é Dispense per Matematica - AA 2015-2016 Addendum equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Soluzione
é Dispense per Matematica - AA 2015-2016 Addendum equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Soluzione
Equazioni differenziali del secondo ordine a coefficienti costanti Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo
 9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
9 Lezione Equazioni differenziali del secondo ordine a coefficienti costanti Def. (C) Un equazioni differenziale del secondo ordine a coefficienti costanti è del tipo u + au + bu = f(t), dove a e b sono
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Corso interno di Matematica compito scritto del n n+1
 Corso interno di Matematica compito scritto del 4.07.05 1. Dire se la serie converge e giustificare la risposta. n=1 1 n n+1 n Soluzione: Il criterio della radice o del rapporto falliscono; proviamo col
Corso interno di Matematica compito scritto del 4.07.05 1. Dire se la serie converge e giustificare la risposta. n=1 1 n n+1 n Soluzione: Il criterio della radice o del rapporto falliscono; proviamo col
Introduzione alle equazioni differenziali attraverso esempi. 20 Novembre 2018
 Introduzione alle equazioni differenziali attraverso esempi 20 Novembre 2018 Indice: Equazioni separabili. Esistenza e unicità locale della soluzione di un Problemi di Cauchy. Equazioni differenziali lineari
Introduzione alle equazioni differenziali attraverso esempi 20 Novembre 2018 Indice: Equazioni separabili. Esistenza e unicità locale della soluzione di un Problemi di Cauchy. Equazioni differenziali lineari
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
Equazioni separabili. Un esempio importante
 Equazioni separabili. Un esempio importante Esempio La soluzione generale dell equazione y = αy, α R (1) è data da y(x) = Ke αx, K R (2) C è un unica soluzione costante: y = 0: cioè y(x) = 0 per ogni x.
Equazioni separabili. Un esempio importante Esempio La soluzione generale dell equazione y = αy, α R (1) è data da y(x) = Ke αx, K R (2) C è un unica soluzione costante: y = 0: cioè y(x) = 0 per ogni x.
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
y 3y + 2y = 1 + x x 2.
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Equazioni differenziali ordinarie di ordine n
 Equazioni differenziali ordinarie di ordine n Indice Indice 1 1 ODE 1 Equazioni differenziali ordinarie del primo ordine 1 Equazioni differenziali a variabili separabili Equazioni differenziali del primo
Equazioni differenziali ordinarie di ordine n Indice Indice 1 1 ODE 1 Equazioni differenziali ordinarie del primo ordine 1 Equazioni differenziali a variabili separabili Equazioni differenziali del primo
EQUAZIONI LINEARI DEL SECONDO ORDINE
 EQUAZIONI LINEARI DEL SECONDO ORDINE Umberto Marconi Dipartimento di Matematica Università di Padova 1 Considerazioni generali Nel seguito le funzioni sono continue (e derivabili quanto basta) su un intervallo
EQUAZIONI LINEARI DEL SECONDO ORDINE Umberto Marconi Dipartimento di Matematica Università di Padova 1 Considerazioni generali Nel seguito le funzioni sono continue (e derivabili quanto basta) su un intervallo
Moti oscillatori. Parte I Oscillatore armonico
 1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
1 10.1-10.2 OSCILLATORE ARMONICO Parte I Moti oscillatori 1 10.1-10.2 Oscillatore armonico Abbiamo visto che una situazione che si riconduce a soddisfare l equazione differenziale d 2 x(t) dt 2 +ω 2 x(t)
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA
 ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 6-7 Settimana : Equazioni Differenziali Esempio. L esempio più familiare di equazione differenziale proviene dalla legge di Newton. Se t y(t)
ANALISI MATEMATICA A CORSO DI LAUREA TRIENNALE IN MATEMATICA 6-7 Settimana : Equazioni Differenziali Esempio. L esempio più familiare di equazione differenziale proviene dalla legge di Newton. Se t y(t)
Argomento 14 Esercizi: suggerimenti
 Argomento 4 Esercizi: suggerimenti Ex.. Equazione differenziale lineare del primo ordine, cioè del tipo: y + a(x) y = f(x) il cui integrale generale è dato dalla formula: ] y(x, C) = e [C A(x) + f(x)e
Argomento 4 Esercizi: suggerimenti Ex.. Equazione differenziale lineare del primo ordine, cioè del tipo: y + a(x) y = f(x) il cui integrale generale è dato dalla formula: ] y(x, C) = e [C A(x) + f(x)e
Appunti sulle equazioni differenziali lineari del secondo ordine
 Appunti sulle equazioni differenziali lineari del secondo ordine 10 maggio 2009 Dopo aver trattato delle equazioni differenziali lineari del primo ordine (cioè quelle in cui interviene la sola derivata
Appunti sulle equazioni differenziali lineari del secondo ordine 10 maggio 2009 Dopo aver trattato delle equazioni differenziali lineari del primo ordine (cioè quelle in cui interviene la sola derivata
1 Equazioni differenziali
 1 Equazioni differenziali Iniziamo adesso lo studio di alcuni tipi di equazioni differenziali. Questo argomento è uno dei più importanti, se non il più importante dal punto di vista applicativo. Basti
1 Equazioni differenziali Iniziamo adesso lo studio di alcuni tipi di equazioni differenziali. Questo argomento è uno dei più importanti, se non il più importante dal punto di vista applicativo. Basti
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
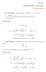 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Corso di Analisi Matematica 1 - professore Alberto Valli
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 8/9 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - dicembre 8 Integrali
Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 8/9 Corso di Analisi Matematica - professore Alberto Valli foglio di esercizi - dicembre 8 Integrali
Equazioni differenziali. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2018-2019, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff. 1 2 Un equazione differenziale e un equazione che
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2018-2019, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff. 1 2 Un equazione differenziale e un equazione che
FABIO SCARABOTTI Note sulle equazioni differenziali ordinarie Ingegneria Meccanica - Corso di Analisi Matematica I - Canale L-Z. y(x) = f(x)dx + C (2)
 FABIO SCARABOTTI Note sulle equazioni differenziali ordinarie Ingegneria Meccanica - Corso di Analisi Matematica I - Canale L-Z Introduzione. L esempio più semplice di equazione differenziale è dato dal
FABIO SCARABOTTI Note sulle equazioni differenziali ordinarie Ingegneria Meccanica - Corso di Analisi Matematica I - Canale L-Z Introduzione. L esempio più semplice di equazione differenziale è dato dal
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
Analisi Matematica A e B Soluzioni prova scritta parziale n. 4
 Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Correzione del quarto compitino di Analisi 1 e 2 A.A. 2014/2015
 Correzione del quarto compitino di Analisi e A.A. 04/05 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo 4 maggio 05 Esercizio Testo. Risolvere il seguente problema di Cauchy: y = 3x e 8y y( ) = 0. Prima
Correzione del quarto compitino di Analisi e A.A. 04/05 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo 4 maggio 05 Esercizio Testo. Risolvere il seguente problema di Cauchy: y = 3x e 8y y( ) = 0. Prima
Equazioni differenziali. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html Inversa Eq. diff. 1 Un equazione differenziale e un equazione
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html Inversa Eq. diff. 1 Un equazione differenziale e un equazione
c.l. Matematica Analisi 3 prof. Molteni/Cavaterra 17 Giugno 2019 IV Appello d esame versione A
 c.l. Matematica Analisi 3 prof. Molteni/Cavaterra 17 Giugno 2019 IV Appello d esame versione A 1A](8 p.ti) L obiettivo del seguente esercizio è tracciare le curve del piano che sono grafici delle soluzioni
c.l. Matematica Analisi 3 prof. Molteni/Cavaterra 17 Giugno 2019 IV Appello d esame versione A 1A](8 p.ti) L obiettivo del seguente esercizio è tracciare le curve del piano che sono grafici delle soluzioni
Calcolo integrale. Regole di integrazione
 Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
Corso di FISICA-MATEMATICA
 Fisica-Matematica p. 1/48 Università Politecnica delle Marche Facoltà di Ingegneria Scuola di Dottorato Curriculum in Architettura, Costruzioni e Strutture Corso di FISICA-MATEMATICA Docente: Prof. Lucio
Fisica-Matematica p. 1/48 Università Politecnica delle Marche Facoltà di Ingegneria Scuola di Dottorato Curriculum in Architettura, Costruzioni e Strutture Corso di FISICA-MATEMATICA Docente: Prof. Lucio
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzioni degli esercizi
 Equazioni differenziali Soluzioni degli esercizi Premessa: in tutti gli esercizi x denota la variabile indipendente, y la funzione (di x) incognita dell equazione differenziale. Un equazione differenziale
Equazioni differenziali Soluzioni degli esercizi Premessa: in tutti gli esercizi x denota la variabile indipendente, y la funzione (di x) incognita dell equazione differenziale. Un equazione differenziale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Equazioni differenziali
 é Dispense per Matematica - AA 2015-2016 Equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Nozioni preliminari
é Dispense per Matematica - AA 2015-2016 Equazioni differenziali Decio Levi, Valentino Lacquaniti levi@roma3.infn.it Corso di Laurea in Ottica ed Optometria Dipartimento di Scienze 1 Nozioni preliminari
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2014-15 autore: Giovanni Alberti Equazioni differenziali [versione: 2 gennaio 2015] Richiamo delle nozioni fondamentali
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Un equazione differenziale è un equazione in cui l incognita è una funzione, anziché un semplice numero, e tale funzione può apparire con diversi ordini di derivazione.
Equazioni differenziali ordinarie Un equazione differenziale è un equazione in cui l incognita è una funzione, anziché un semplice numero, e tale funzione può apparire con diversi ordini di derivazione.
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi.
 Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Sistemi vibranti ad 1 gdl
 Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura
Equazioni Differenziali (4)
 Equazioni Differenziali (4) Esercizio 1 Risolvere il problema di Cauchy y = e y x + y x, y(1) = 1. Esercizio 2 Risolvere il problema di Cauchy y = 2y 1 x 2 + 1 x, y(0) = 0. Esercizio 3 Risolvere il problema
Equazioni Differenziali (4) Esercizio 1 Risolvere il problema di Cauchy y = e y x + y x, y(1) = 1. Esercizio 2 Risolvere il problema di Cauchy y = 2y 1 x 2 + 1 x, y(0) = 0. Esercizio 3 Risolvere il problema
Analisi e Modelli Matematici
 Analisi e Modelli Matematici Marzo - Aprile 04 Lezione 3 Equazioni differenziali del primo ordine Una equazione differenziale del primo ordine si scrive nella forma: F (x, y, y )=0 oppure, isolando la
Analisi e Modelli Matematici Marzo - Aprile 04 Lezione 3 Equazioni differenziali del primo ordine Una equazione differenziale del primo ordine si scrive nella forma: F (x, y, y )=0 oppure, isolando la
Alcuni esercizi sulle equazioni di erenziali
 Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Equazioni differenziali
 Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
Equazioni differenziali Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ.
Equazioni differenziali lineari a coefficienti costanti
 Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
Equazioni differenziali lineari a coefficienti costanti Generalità Il modello matematico di un qualsiasi sistema fisico in regime variabile conduce alla scrittura di una o più equazioni differenziali.
Integrazione di funzioni razionali
 Esercitazione n Integrazione di funzioni razionali Consideriamo il rapporto P (x) di due polinomi di gradi n e m rispettivamente. Per determinare una primitiva della funzione f(x) P (x) possiamo procedere
Esercitazione n Integrazione di funzioni razionali Consideriamo il rapporto P (x) di due polinomi di gradi n e m rispettivamente. Per determinare una primitiva della funzione f(x) P (x) possiamo procedere
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Fondamenti di Meccanica Quantistica (Prof. Tarantelli)
 Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
Fondamenti di Meccanica Quantistica (Prof. Tarantelli) 1 MOTO LINEARE E L OSCILLATORE ARMONICO 2 EQUAZIONE DI SCHRODINGER Equazione di Schrödinger: descrive il comportamento di un insieme di particelle:
Esercizi svolti sugli integrali
 Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
Esercizio. Calcolare il seguente integrale indefinito x dx. Soluzione. Poniamo da cui x = t derivando rispetto a t abbiamo t = x x = t dx dt = quindi ( t x dx = ) poiché t = t, abbiamo t dt = = in definitiva:
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio Soluzioni
 Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio 2006. Soluzioni In questo documento sono contenuti gli svolgimenti del tema d esame del 05/06/2006. Alcuni esercizi
Esame di Complementi di Matematica (STC) e Parziale di Matematica II (SMat). 3 Maggio 2006. Soluzioni In questo documento sono contenuti gli svolgimenti del tema d esame del 05/06/2006. Alcuni esercizi
Analisi Vettoriale - A.A Foglio di Esercizi n. 6 Soluzioni. 1. Esercizio Determinare l integrale generale dell equazione autonoma.
 Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
Analisi Vettoriale - A.A. 23-24 Foglio di Esercizi n. 6 Soluzioni. Esercizio Determinare l integrale generale dell equazione autonoma.. Soluzione. y = y(y )(y 2) y(y )(y 2) dy = Tenuto conto che y(y )(y
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Matematica per le scienze sociali Equazioni e disequazioni. Domenico Cucina
 Matematica per le scienze sociali Equazioni e disequazioni Domenico Cucina University of Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Matematica per le scienze sociali Equazioni e disequazioni Domenico Cucina University of Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
