Inferenza Statistica (3 crediti) per la Laurea Magistrale in Informatica
|
|
|
- Albino Serafino Bernardini
- 7 anni fa
- Visualizzazioni
Transcript
1 Uiversità di Roma Tor Vergata Facoltà di Scieze Matematiche Fisiche e Naturali Dipartimeto di Matematica Apputi di Ifereza Statistica 3 crediti) per la Laurea Magistrale i Iformatica Claudio Macci Ao Accademico 3-4 Cotatti e iformazioi alla pagia web macci
2 Premessa Questo materiale rappreseta ciò che ho preparato per teere le lezioi dei primi tre crediti di Ifereza Statistica e Teoria dell Iformazioe, isegameto per la Laurea Magistrale i Iformatica, per l a.a Le variazioi rispetto alla versioe per l a.a. -3 riguardao ua correzioe di u sego ell Esempio.., u commeto subito dopo la codizioe F), e la dimostrazioe del Teorema.3.. Il materiale è abbodate e, i base a quato verrà spiegato i aula di ao i ao, alcue parti di questo materiale o sarao el programma d esame. Nella scelta degli argometi ho teuto coto di quato abitualmete isego elle lezioi di Calcolo delle Probabilità e Statistica per la Laurea Trieale i Iformatica) e delle esigeze segalate da altri doceti che tegoo altri isegameti del Corso di Laurea Magistrale i Iformatica. Nei Capitoli e 3 di questi apputi ho tratto sputo da quato imparato da studete dell esame di Statistica Matematica teuto dal Prof. Fabio Spizzichio Laurea i Matematica presso l Uiversità di Roma La Sapieza, Ao Accademico 99-99) e dal materiale preparato per le lezioi che ho teuto i ai passati per i segueti isegameti: Statistica II Laurea i Matematica presso l Uiversità di Torio, Ai Accademici -, -3 e 3-4); esercitazioi di Statistica Laurea i Matematica presso l Uiversità di Roma Tor Vergata, Ai Accademici 5-6, 6-7 e 7-8). Mi scuso fi da ora per gli errori e refusi di varia atura che troverete ad esempio o mi soo preoccupato di cotrollare se le parole soo correttamete divise i sillabe quado si va a capo...). Ovviamete qualsiasi segalazioe i proposito è beveuta e rigrazio fi da ora chi provvederà e chi ha provveduto) i tal seso. Roma, Aprile 4 Claudio Macci
3 Idice Risultati di Calcolo delle Probabilità. Variabili aleatorie reali discrete e cotiue Variabili aleatorie reali discrete: defiizioi ed esempi Variabili aleatorie reali cotiue: defiizioi ed esempi Variabili aleatorie -dimesioali Variabili aleatorie -dimesioali discrete Variabili aleatorie -dimesioali cotiue Casi co desità cogiuta mista Il teorema del cambio di variabile per desità cogiute cotiue Variabili aleatorie -dimesioali o cotiue, co margiali cotiue Distribuzioe Normale -dimesioale Statistica Classica e Statistica Bayesiaa. Itroduzioe Statistica Classica Sufficieza Stimatori Statistica Bayesiaa Sufficieza Stimatori Predizioe Ua proprietà delle statistiche sufficieti Modelli statistici di uso comue 3 3. Osservazioi Beroulliae Osservazioi a valori i u isieme fiito Osservazioi Poissoiae Osservazioi Espoeziali Osservazioi Normali co sola media icogita) Osservazioi Normali co sola variaza icogita) Osservazioi Normali co media e variaza icogite) Osservazioi Uiformi Bibliografia 46
4 Capitolo Risultati di Calcolo delle Probabilità. Variabili aleatorie reali discrete e cotiue Ua variabile aleatoria reale X assume valori i R. La sua fuzioe di distribuzioe F X è defiita come segue: F X x) P X x), per ogi x R... Variabili aleatorie reali discrete: defiizioi ed esempi Ua variabile aleatoria reale X è discreta, co desità discreta f X, se P X A) x A f X x) per ogi A R. La desità discreta f X è defiita come segue: f X x) P X x), per ogi x R. Ioltre si dice che X ha speraza matematica fiita se x X x f Xx) < e, i tal caso, la speraza matematica è E[X] x X xf Xx). Ifie, se X ha speraza matematica fiita, allora X ha speraza matematica fiita e si defiisce variaza la seguete quatità fiita): Var[X] E[X E[X]) ]. I particolare si verifica che Var[X] E[X ] E [X]. Cocludiamo co u eleco di distribuzioi di variabili aleatorie discrete reali. Distribuzioi Beroulliaa. Ua variabile aleatoria X ha distribuzioe Beroulliaa di parametro p [, ] i simboli X Bp)) se si ha f X ) p e f X ) p; quidi f X k) p k p) k per k, }. I corrispodeza si ha E[X] p e Var[X] p p). Distribuzioi Biomiale. Ua variabile aleatoria X ha distribuzioe Biomiale di parametri e p i simboli X Bi, p)) se si ha Y X + + X, dove X,..., X } soo idipedeti e co distribuzioe Bp); quidi f X k) k )pk p) k per k,,..., } perché ogua delle k ) sequeze ordiate di elemeti i, } co esattamete k volte ha probabilità pk p) k. I particolare si ha Bi, p) Bp). I corrispodeza si ha E[X] p e Var[X] p p). La variabile aleatoria X viee itrodotta per cotare il umero di successi su prove idipedeti e tutte co probabilità di successo p.
5 Distribuzioe di Poisso. Ua variabile aleatoria X ha distribuzioe di Poisso di parametro λ > i simboli X P oissoλ)) se si ha f X k) λk k! e λ per ogi k itero. I corrispodeza si verifica che E[X] λ e Var[X] λ. Distribuzioe Geometrica. Ua variabile aleatoria X ha distribuzioe Geometrica di parametro p, ) i simboli X Geop)) se si ha f X k) p) k p per ogi k itero. I corrispodeza si verifica che E[X] p p e Var[X]. La variabile aleatoria X viee itrodotta p per cotare il umero di prove ecessarie per avere il primo successo el caso i cui si abbiao prove idipedeti e tutte co probabilità di successo p... Variabili aleatorie reali cotiue: defiizioi ed esempi Ua variabile aleatoria reale X è cotiua, co desità cotiua f X, se P X A) f X x)dx per ogi A B R, dove B R è la più piccola σ-algebra su R coteete gli isiemi aperti di R. A A differeza della desità discreta, esistoo diverse versioi della desità cotiua f X ; ad esempio la defiizioe della desità cotiua è arbitraria su isiemi fiiti o umerabili di puti. Tutte le fuzioi che coicidoo co F X ei puti dove F X è derivabile foriscoo versioi della desità cotiua. Ioltre si dice che X ha speraza matematica fiita se x f Xx)dx < e, i tal caso, la speraza matematica è E[X] xf Xx)dx. La defiizioe di variaza si ottiee adattado a questo cotesto la defiizioe vista per il caso discreto. I quel che segue faremo riferimeto alla seguete proposizioe che forisce la desità cotiua di ua variabile aleatoria X otteuta come trasformazioe affie o costate di ua variabile cotiua X. Proposizioe.. Trasformazioe affie di ua variabile aleatoria cotiua). Sia X ua variabile aleatoria reale cotiua co desità f X e sia X ax + b per a, b R tali che) a. Allora la variabile aleatoria X è cotiua co desità f X, e si ha f X x ) a f x b X a. Cocludiamo co u eleco di distribuzioi di variabili aleatorie cotiue reali; i corrispodeza richiamiamo ache alcui risultati Proposizioi.. e..3). I vista di quel che segue, dato u qualsiasi A R, useremo la otazioe A per la fuzioe A : R, } defiita come segue: se x A A x) se x A c, dove A c R\A è il complemetare dell isieme A. Ioltre faremo riferimeto alla fuzioe Gamma defiita come segue: Γα) x α e x dx per ogi α >. Si osservi che si ha Γα + ) αγα) per ogi α > ; quidi, se α è itero, si ha Γα) α )!. Distribuzioe Espoeziale. Ua variabile aleatoria X ha distribuzioe Espoeziale di parametro λ > i simboli X Expλ)) se si ha f X x) λe λx, ) x). I corrispodeza si ha E[X] λ e Var[X] λ. 3
6 Distribuzioe Gamma. Ua variabile aleatoria X ha distribuzioe Gamma di parametri α, β > i simboli X Gammaα, β)) se si ha f X x) βα Γα) xα e βx, ) x). Ua variabile aleatoria X ha distribuzioe chi-quadro co gradi di libertà i simboli X χ )) se X Gamma, ). I particolare si ha Gamma, β) Expβ). I corrispodeza si ha E[X] α β e Var[X] α β. Ifie richiamiamo i segueti risultati. Proposizioe... i) Se X,..., X } soo idipedeti e, per ogi i,..., }, X i Gammaα i, β), allora X + + X Gammaα + + α, β). ii) Se X Gammaα, β) e c >, allora cx Gammaα, β c ). Distribuzioe Uiforme. Ua variabile aleatoria X ha distribuzioe Uiforme su [a, b] i simboli X U[a, b]) se si ha f X x) b a [a,b]x). I corrispodeza si ha E[X] a+b puto medio dell itervallo) e Var[X] b a). Distribuzioe Beta. Ua variabile aleatoria X ha distribuzioe Beta di parametri α, β > i Γα+β) simboli X Betaα, β)) se si ha f X x) Γα)Γβ) xα x) β [,] x). I particolare si ha Beta, ) U[, ]. I corrispodeza si ha E[X] α α+β e Var[X] Distribuzioe di Pareto. αβ α+β) α+β+). Ua variabile aleatoria X ha distribuzioe di Pareto di parametri α, β > i simboli X P aretoα, β)) se si ha f X x) αβ α x α+) [β, ) x). Osserviamo che E[X k ] x k αβ α x α+) [β, ) x)dx β αβ α x α k+) dx per ogi k e quidi E[X k ] < se e solo se α k + >, che equivale a dire k < α; ioltre, se k < α, si ha E[X k ] αβk αβ α k. Quidi i corrispodeza si ha E[X] α se α > e Var[X] αβ α ) α ) se α >. Distribuzioe Normale o Gaussiaa). Ua variabile aleatoria X ha distribuzioe Normale di parametri µ R e σ > i simboli X Nµ, σ x µ) )) se si ha f X x) e σ. I πσ corrispodeza si ha E[X] µ e Var[X] σ ; quidi talvolta si parla di distribuzioe Normale di media µ e variaza σ. È oto che, se X Nµ, σ ), X µ σ N, ); la distribuzioe N, ) è detta distribuzioe Normale stadard. I alcui casi è utile fare riferimeto al reciproco della variaza σ ; quidi si cosidera r e tale σ parametro r viee detto precisioe; i corrispodeza la desità assume la seguete espressioe: f X x) r π e rx µ). Spiegazioe della termiologia. Si usa questo termie perché, quado si ha ua piccola variaza, i valori soo cocetrati attoro alla media µ co alta probabilità e quidi è ragioevole pesare al fatto che si ha u alta precisioe. Lo stesso tipo di discorso si può fare el caso di variaza grade a cui corrispode ua piccola precisioe. Talvolta questo viee utile quado si fa riferimeto alla estesioe -dimesioale) ua variabile aleatoria costate c quidi discreta) viee cosiderata come ua variabile aleatoria co distribuzioe Nc, ). Cocludiamo richiamado i segueti risultati. 4
7 Proposizioe..3. Se X,..., X } soo idipedeti e, per ogi i,..., }, X i Nµ i, σi ), allora i Gamma, ) χ ). X i µ i ) σ i Dimostrazioe. Noi siamo iteressati alla distribuzioe di i Z i dove, per ogi i,..., }, Z i X i µ i σ i. Le variabili aleatorie Z,..., Z } soo idipedeti e Normali stadard. Le variabili aleatorie Z,..., Z } soo ovviamete idipedeti. Ioltre ciascua delle variabili aleatorie Z,..., Z } ha distribuzioe Gamma, ); ifatti, per ogi i,..., }, se usiamo il simbolo Φ per la fuzioe di distribuzioe delle variabili aleatorie co distribuzioe Normale stadard si ha P t Z i t) Φ t) Φ t) P Zi t) Φ t) Φ t)) Φ t) se t se t <, e la corrispodete desità cotiua che si ottiee derivado è f Zi t) e t) π t, )t) t e t, ) t) βα π Γα) tα e βt, ) t) αβ, perché Γ ) y e y dy x e x dx π ) e x xdx π } } Φ) e x dx x e x xdx π π si è cosiderato il cambio di variabile y x, da cui segue che dy xdx e gli estremi di itegrazioe o cambiao). I coclusioe possiamo dire che i Z i Gamma, ) come cosegueza della Proposizioe..i) co α α β.. Variabili aleatorie -dimesioali Ua variabile aleatoria -dimesioale X X,..., X ) assume valori i R... Variabili aleatorie -dimesioali discrete Ua variabile aleatoria -dimesioale X X,..., X ) è discreta, co desità discreta f X, se P X A) f X x ) per ogi A R. x A La desità discreta f X è defiita come segue: f X x ) P X x ), per ogi x x,..., x ) R. I corrispodeza possiamo cosiderare le desità margiali discrete) per u sottoisieme di variabili aleatorie. Ad esempio, per i,..., } arbitrariamete fissato, la desità margiale discreta f Xi della variabile aleatoria reale X i si ottiee come segue: f Xi x i ) f X y ). y :y i x i 5
8 Si verifica che le compoeti di X X,..., X ) soo idipedeti, cioè P X A,..., X A ) P X A ) P X A ) per ogi A..., A R, se e solo se f X x ) f X x ) f X x ), per ogi x x,..., x ) R. Esempio.. Geometriche Idipedeti). Cosideriamo X, X ) dove X e X soo idipedeti e, per i, }, X i Geop i ). Calcoliamo le segueti probabilità: P X X ) f X x )f X x ) f X,X x, x ) x x x p ) x p p ) x p p p p ) p )) x x x p p p ) p ) p p ; p + p p p P X > X ) f X,X x, x ) f X x ) f X x ) x >x x x >x p ) x p p ) x p p p p ) x p ) x + p x x >x ) x p p ) p )) x p p ) p ) p p p ) p ) x p p ) p + p p p p p p p + p p p e P X < X ) p p p p +p p p si calcola i maiera aaloga a quato fatto per P X > X ); si ottiee lo stesso valore scambiado il ruolo di p e p ). Si osservi che la somma delle tre probabilità calcolate è uguale a come deve essere. Desità codizioate e speraze matematiche codizioate. Per fissare le idee cosideriamo il caso e il codizioameto di X rispetto a X x. Nel caso i cui f X x ) >, possiamo cosiderare la desità di X codizioata a X x, defiita come segue f X X x x ) f X,X x, x ). f X x ) Si verifica facilmete che f X X x ) è ua desità di ua variabile aleatoria reale discreta. I riferimeto a tale desità si può fare riferimeto al cocetto di speraza matematica e di variaza come visto i precedeza; i corrispodeza abbiamo la speraza matematica di X codizioata a X x che idicheremo co E[X X x ] e, aalogamete, la variaza di X codizioata a X x che idicheremo co Var[X X x ]. Esempio.. Schema di Beroulli: tempi di primo e secodo successo). Cosideriamo X, X ) co la seguete desità cogiuta: p) x p p) x x ) p p p) x se x > x, x e x iteri) f X,X x, x ) altrimeti. 6
9 Allora si ha f X x ) x f X,X x, x ) da cui segue f X X x x ) f X,X x, x ) f X x ) x x p p) x x )p p) x per x itero, p p) x x )p p) x x per x,..., x } quidi X X x ha distribuzioe Uiforme Discreta sull isieme,..., x }) e E[X X x ] x x x x x )x x x. Si osservi che le variabili aleatorie i questo esempio hao la seguete iterpretazioe: X k è il umero di prove ecessarie per avere il k-simo successo i prove idipedeti co probabilità di successo p i ogi prova. I riferimeto a tale iterpretazioe è oto che, per ogi k itero, la desità discreta di X k è f Xk x k ) x k k )pk p) x k k per x k k itero, e i tal caso si dice che X k ha distribuzioe Biomiale Negativa di parametri k e p... Variabili aleatorie -dimesioali cotiue Ua variabile aleatoria -dimesioale X X,..., X ) è cotiua, co desità cotiua f X, se P X A) dove B R A f X x )dx dx per ogi A B R, è la più piccola σ-algebra su R coteete gli isiemi aperti di R. I corrispodeza possiamo cosiderare le desità margiali cotiue) per u sottoisieme di variabili aleatorie. Ad esempio, per i,..., } arbitrariamete fissato, la desità margiale discreta f Xi della variabile aleatoria reale X i si ottiee come segue: f Xi x i ) f X y,..., y i, x i, y i+,..., y )dy dy i dy i+ dy. R Si verifica che le compoeti di X X,..., X ) soo idipedeti, cioè P a X b,..., a X b ) P a X b ) P a X b ) per ogi a, b..., a, b R, se e solo se f X x ) f X x ) f X x ), per ogi x x,..., x ) R. Esempio..3 Espoeziali Idipedeti). Cosideriamo X, X ) dove X e X soo idipedeti e, per i, }, la variabile aleatoria X i Expλ i ). Calcoliamo le segueti probabilità: P X X ) perché l eveto fa riferimeto ad u sottoisieme del piao di area ulla; P X > X ) f X,X x, x ) x >x dx dx dx λ e λ x dx λ e λ x R x λ λ + λ dx λ e λ x [ e λ x ] x x x dx λ e λ x e λ x dx λ + λ )e λ +λ )x λ λ + λ λ λ + λ 7
10 e P X < X ) λ λ +λ si calcola i maiera aaloga a quato fatto per P X > X ); si ottiee lo stesso valore scambiado il ruolo di λ e λ ). Si osservi che la somma delle tre probabilità calcolate è uguale a come deve essere. Desità codizioate e speraze matematiche codizioate. Per fissare le idee cosideriamo il caso e il codizioameto di X rispetto a X x. Nel caso i cui f X x ) >, possiamo cosiderare la desità di X codizioata a X x, defiita come segue f X X x x ) f X,X x, x ). f X x ) Si verifica facilmete che f X X x ) è ua desità di ua variabile aleatoria reale cotiua. I riferimeto a tale desità si può fare riferimeto al cocetto di speraza matematica e di variaza come visto i precedeza el caso discreto e i corrispodeza useremo le stesse otazioi. Esempio..4 Processo di Poisso: tempi del primo e secodo eveto). Cosideriamo X, X ) co la seguete desità cogiuta: λe λx λe λx x ) λ e λx se x > x > f X,X x, x ) altrimeti. Allora si ha f X x ) da cui, per x >, segue R f X,X x, x )dx quidi X X x U[, x ]) e x λ e λx dx, ) x ) λ x e λx, ) x ), f X X x x ) λ e λx λ x e λx x per x, x ) E[X X x ] x x x dx [ ] x x x x x x. Si osservi che E[X X x ] coicide co il puto medio dell itervallo [, x ] i accordo co quato avevamo detto sulla distribuzioe Uiforme. Si osservi che le variabili aleatorie i questo esempio hao la seguete iterpretazioe: X k è l istate del k-simo eveto di u Processo di Poisso di itesità λ. I riferimeto a tale iterpretazioe è oto che, per ogi k itero, la desità cotiua di X k è cioè X k Gammak, λ). f Xk x k )..3 Casi co desità cogiuta mista λk Γk) xk k e λx k, ) x k ), Esistoo casi co desità cogiuta mista. Per fissare le idee cosideriamo il caso ; ioltre supporremo che X sia ua variabile aleatoria discreta e che X sia ua variabile aleatoria cotiua. La variabile aleatoria X, X ) ha desità cogiuta mista f X,X, discreta su X e cotiua su X, se P X, X ) A A ) x A A f X,X x, x )dx per ogi A R e A B R. 8
11 I corrispodeza si le desità margiali soo defiite come segue: la desità discreta di X è f X x ) f X,X x, x )dx ; R la desità cotiua di X è f X x ) f X,X x, x ). x R Come egli altri casi visti i precedeza possiamo dire che le variabili aleatorie X e X soo idipedeti, cioè P X A, a X b) P X A)P a X b) per ogi A R e a, b R, se e solo se f X,X x, x ) f X x )f X x ), per ogi x x, x ) R. Ioltre possiamo defiire le desità codizioate, le speraze matematiche codizioate e le variaze codizioate. Ovviamete f X X x ) è ua desità discreta come f X e f X X x ) è ua desità cotiua come f X. Ora presetiamo due esempi. Esempio..5 Geometrica co parametro uiforme). Cosideriamo la seguete desità cogiuta mista co, X discreta e X cotiua): x ) x x se x, x ),, 3,...}, ) f X,X x, x ) altrimeti. Allora si ha f X x ) f X,X x, x ) x ) x x x x,) x ),) x ) da cui, per x, ), segue f X X x x ) x ) x x quidi X X x Geox )) e x ) x x per x itero E[X X x ] x x x ) x x x i accordo co quato avevamo detto sulla distribuzioe Geometrica. Ioltre si ha f X x ) R f X,X x, x )dx x ) x x dx x x ) x dx Γ)Γx ) Γ + x ) per x itero l ultima uguagliaza tiee coto dell espressioe della desità cotiua della distribuzioe Beta, x )) da cui segue f X X x x ) x ) x x,) x ) Γ)Γx ) Γ+x ) quidi X X x Beta, x )) e E[X X x ] Γ + x ) Γ)Γx ) x x ) x,) x ) x Γ + x ) Γ)Γx ) x x ) x dx + x i accordo co quato avevamo detto sulla distribuzioe Beta. 9
12 Esempio..6 Dati cesurati). Cosideriamo ua variabile aleatoria -dimesioale cotiua Y, Y ) dove Y e Y soo idipedeti e, per ogi i, }, Y i Expλ i ). I corrispodeza cosideriamo la variabile aleatoria X, X ) Y Y, miy, Y }). Le distribuzioi margiali della variabili aleatoria X, X ) si deducoo facilmete come segue. λ Si ha X B λ +λ ) per quato visto ell Esempio..3; quidi si ha la desità discreta ) x ) f X x ) λ λ +λ λ x λ +λ per x, }; ifatti P X ) P Y Y ) P Y < Y ) λ λ +λ P X ) P Y > Y ) λ λ +λ λ λ +λ. Si ha X Expλ + λ ) perché, per ogi t, miy, Y } > t} Y > t} Y > t} da cui segue per le ipotesi su Y e Y - idipedeza e distribuzioe espoeziale per etrambe le variabili aleatorie) P miy, Y } > t) P Y > t)p Y > t) e λ t e λ t e λ +λ )t. Ora studiamo la distribuzioe cogiuta di X, X ). Per ogi t, si ha e P X, X > t) P Y Y, Y > t) P t < Y Y ) ) λ e λ y λ e λ y dy dy t y λ λ + λ t t λ e λ y e λ y dy λ + λ )e λ +λ )y dy P X )P X > t) P X, X > t) P Y > Y, Y > t) P t < Y < Y ) ) λ e λ y λ e λ y dy dy t y λ λ + λ t t λ e λ y e λ y dy λ + λ )e λ +λ )y dy P X )P X > t). Quidi le variabili aleatorie X e X soo idipedeti, e questo è u caso particolare co desità cogiuta mista. I coclusioe diamo ua spiegazioe della termiologia dati cesurati usata ei casi i cui si hao tempi aleatori da studiare o completamete osservabili. Per fissare le idee suppoiamo di avere a che fare co u qualsiasi cotesto i survival aalysis e parleremo di tempo di fuzioameto. Ad esempio suppoiamo di essere iteressati ad u tempo di fuzioameto Y e di avere u tempo massimo di osservazioe Y, il quale a sua volta potrebbe essere aleatorio come accade sopra) o meo e idipedete come accade sopra) o meo da Y. Allora il tempo di fuzioameto osservato sarà X miy, Y } e abbiamo due casi idividuati dai valori della variabile aleatoria variabile aleatoria X Y Y : se X, siamo riusciti ad osservare tutto il tempo di fuzioameto e l iterruzioe del fuzioameto; se X, siamo riusciti ad osservare ua parte del tempo di fuzioameto i questo seso si parla di tempo di fuzioameto cesurato), che coicide co il massimo tempo di osservazioe; quidi o osserveremo l iterruzioe del fuzioameto che accadrà dopo la fie del tempo di osservazioe.
13 ..4 Il teorema del cambio di variabile per desità cogiute cotiue Iiziamo co l euciato. Teorema..7 Teorema del cambio di variabile). Siao U e V aperti di R e sia ψ : U V ua fuzioe biuivoca tale che ψ e ψ hao derivate parziali cotiue. Ioltre siao X X,..., X ) e Y Y,..., Y ) due variabili aleatorie -dimesioali tali che P Y U) e X ψy ). Allora, se Y ha desità cotiua f Y, X ha desità cotiua dove J ψ x ) f X x ) f Y ψ x )) det J ψ x ) V x ), ψ ) i x j x ) è la matrice Jacobiaa associata a i,j,...,} ψ. Ora vediamo alcui esempi co l uso di questo risultato. Esempio..8 Esempio co Espoeziali). Cosideriamo ua variabile aleatoria -dimesioale cotiua Y, Y ) dove Y e Y soo idipedeti e, per ogi i, }, Y i Expλ) è la stessa situazioe dell Esempio..6 co λ λ λ). I corrispodeza cosideriamo la variabile Y aleatoria X, X ) Y +Y, Y + Y ). Le distribuzioi margiali della variabili aleatoria X, X ) si deducoo facilmete come segue. La variabile aleatoria X ha la seguete fuzioe di distribuzioe ) Y se x F X x ) P X x ) P x ) se x Y + Y, ) se x, dove ) P Y x Y + Y )) P x Y x )Y ) P ) λe λy λe λy dy x dy y x ) λe λ + x y x dy Y x ) Y x λe λy e λ x x y dy λe λ y x λ dy x e λ y x dy x, x e quidi X ha desità cotiua f X x ) [,] x ). I coclusioe X U[, ]. Si ha X Gamma, λ) per la Proposizioe..i) co α α e β λ. Ora studiamo la distribuzioe cogiuta di X, X ). Teorema..7) co U, ), ), V ), ), ) ψy, y ) y y +y, y + y f Y,Y y, y ) λe λy, ) y )λe λy, ) y ). Si usa il teorema del cambio di variabile I corrispodeza si ha ψ x, x ) x x, x x )) perché x y y +y x x y y x x x y + y, x y + y, y x x x x x );
14 ioltre si ha det J ψ x, x ) det e si verifica che x x x x ) x x ) + x x x, ) y ), ) y ), ) x x ), ) x x )) V x, x ). Quidi otteiamo la seguete desità cogiuta f X,X x, x ) λe λx x λe λx x ) x V x, x ),) x ) λ x e λx, ) x ), } } } } f X x ) f X x ) dove l ultima uguagliaza mette i evideza il fatto che X e X soo idipedeti co le desità margiali che già calcolate ifatti,) x ) è ua diversa versioe della desità cotiua della distribuzioe U[, ], e λ x e λx, ) x ) coicide co λ Γ) x e λx, ) x )). Esempio..9 Esempio co Normali). Cosideriamo ua variabile aleatoria -dimesioale cotiua Y, Y ) dove Y e Y soo idipedeti e, per ogi i, }, Y i N, ). I corrispodeza cosideriamo la variabile aleatoria X, X ) costituita dalle coordiate polari associate al puto di coordiate cartesiae Y, Y ), cioè X, X ) Y + Y, ÂOA Y,Y )), dove A è il puto del piao co coordiate, ), A Y,Y ) è il puto del piao co coordiate Y, Y ) e O, ) è l origie. Si usa il teorema del cambio di variabile Teorema..7) co U R \ y, y ) : y, y }, V, ) π, π) ψy, y ) y + y, ÂOA y,y )) f Y,Y y, y ) π e y π e y +y. y π e Vale la pea osservare che, per avere ua fuzioe biuivoca tra isiemi aperti, per le coordiate cartesiae cosideriamo il piao privato del semiasse egativo, cioè l isieme U; quidi osservado che per la desità cogiuta si può trascurare il semiasse egativo perché ha area ulla) si pesa di avere f Y,Y y, y ) y π e +y U y, y ). È oto che ψ x, x ) x cos x, x si x ); ioltre si ha ) det J ψ x, x ) det cos x x si x si x x cos x x cos x + x si x x e si verifica che U y, y ) U x cos x, x si x ) V x, x ). Quidi otteiamo la seguete desità cogiuta f X,X x, x ) x π e x V x, x ) x e x, ) x ) π π,π)x ). } } f X x ) } } f X x ) I corrispodeza possiamo dire che X e X soo idipedeti co le desità margiali f X idicate; i particolare X U[ π, π]. e f X
15 Esempio.. Proseguimeto dell Esempio..9). Cosideriamo la stessa situazioe dell Esempio..9 e defiiamo la variabile aleatoria W Y Y. Allora per ogi t R si ha ) } ) } ) Y Y Y F W t) P W t) P t P t Y } + P t Y < } Y Y Y P Y ty } Y > }) + P Y ty } Y < }) π e y ty π e y dy ) dy + π e y ) e y dy dy. π ty A questo puto possiamo otteere la desità cotiua di W derivado rispetto a t. Prima di tutto, teedo presete che si può derivare sotto il sego di itegrale, si ha f W t) e y e ty ) y dy π π π e +t )y y dy π π e y π e ty ) y dy e +t )y y dy ; ioltre, poiché il secodo itegrale coicide co l opposto del primo basta cosiderare u semplice cambio di variabile), otteiamo la seguete espressioe: f W t) π π + t ) e +t )y y dy [ e +t )y ] y y π + t ) π + t ). e +t )y + t )y dy Possiamo otteere lo stesso risultato i u altro modo osservado che W ta X, dove X è la variabile aleatoria ell Esempio..9 e quidi X U[ π, π]. A tal proposito si ricorda che x ta x è ivertibile co iversa y arcta y per x π, π ). Quidi si ha arcta t F W t) P W t) P ta X t) ) π π dx arcta t + π ) π si osservi che l uguagliaza ) si motiva i maiera diversa distiguedo i casi t e t > ) da cui, derivado rispetto a t, si ottiee acora la desità f W t). I coclusioe possiamo π+t ) dire che la variabile aleatoria W ha distribuzioe di Cauchy, e tale distribuzioe costituisce u esempio di distribuzioe cotiua per cui o si ha ua speraza matematica fiita. Esempio.. Esempio co Uiformi). Cosideriamo ua variabile aleatoria -dimesioale cotiua Y, Y ) dove Y e Y soo idipedeti e ciascua delle due ha distribuzioe Uiforme su [, ]. I corrispodeza cosideriamo la variabile aleatoria X, X ) Y + Y, Y Y ). Si usa il teorema del cambio di variabile Teorema..7) co U, ), ), V x, x ) : < x + x <, < x x < } ψy, y ) y + y, y y ) f Y,Y y, y ),) y ),) y ) stiamo cosiderado le versioi,) y ) e,) y ) al posto di [,] y ) e [,] y ) rispettivamete). I corrispodeza si ha ψ x, x ) x +x, x ) x perché x y + y y x +x x y y, y x x ; 3
16 ioltre si ha e si verifica che det J ψ x, x ) det,) y ),) y ),) x + x Quidi otteiamo la seguete desità cogiuta f X,X x, x ) V x, x ). ) 4 4 ) ) x x,) V x, x ). I corrispodeza possiamo dire che X, X ) ha distribuzioe uiforme sull isieme V che è il quadrato di vertici, ),, ),, ),, ); l area di tale quadrato è uguale a e i effetti si vede che il lato del quadrato ha lughezza ) e questo spiega perchè appare il deomiatore ell espressioe della desità. Osserviamo che X e X o soo idipedeti perché V o è u isieme esprimibile come prodotto cartesiao tra due isiemi...5 Variabili aleatorie -dimesioali o cotiue, co margiali cotiue I geerale, date variabili aleatorie reali X,..., X defiite su uo stesso spazio di probabilità, o è possibile cooscere la distribuzioe della variabile aleatoria -dimesioale X X,..., X ). Però la distribuzioe della variabile aleatoria -dimesioale è ota se le compoeti soo idipedeti. I particolare abbiamo già illustrato il caso di compoeti idipedeti el caso di variabile aleatoria -dimesioale X X,..., X ) discreta e cotiua e ache il caso co desità mista). È opportuo osservare la seguete differeza tra variabili aleatorie -dimesioali discrete e cotiue. I geerale, date variabili aleatorie reali discrete X,..., X defiite su uo stesso spazio di probabilità, è sempre possibile pesarle come le compoeti di ua variabile aleatoria discreta - dimesioale X X,..., X ). Al cotrario, date variabili aleatorie reali cotiue X,..., X defiite su uo stesso spazio di probabilità, o è garatito che queste siao le compoeti di ua variabile aleatoria cotiua -dimesioale X X,..., X ). I quel che segue costruiremo alcui esempi e, per fare questo, è opportuo fare riferimeto a casi i cui si ha P X S), dove S R e il R -volume di S è ullo. I quel che segue cosideriamo alcui esempi -dimesioali co per fissare le idee) i cui l isieme S è ua retta, o l uioe di due semirette e u segmeto, o l uioe di due rette. Esempio.. Trasformazioe affie). Sia. Poiamo X ax +b dove a, b R e a si esclude a perché altrimeti si avrebbe X b, e quidi si avrebbe u caso co X discreta). Allora X, X ) o può essere cotiua perché o è possibile trovare ua desità cotiua f X,X. Ifatti, se cosideriamo l isieme S x, x ) R : x ax + b}, si ha P X, X ) S) per costruzioe e S ha area ulla el piao essedo ua retta). Però possiamo avere le margiali cotiue. Ifatti, se X è ua variabile aleatoria cotiua co desità f X, allora ache X è cotiua co desità f X data dalla Proposizioe... Si osservi che si ha P X, X ) A) x R:x,ax +b) A} Ad esempio il R -volume di S R è l area di S. f X x )dx per ogi A B R. 4
17 Tale formula mette i evideza che, dato u qualsiasi isieme A B R, possiamo limitarci a cosiderare la sua traccia dell isieme A sulla retta S. Esempio..3 Esempio co margiali simmetriche co la stessa distribuzioe). Sia. Poiamo X gx ), dove gx) x se x x se x >. Allora X, X ) o può essere cotiua perché o è possibile trovare ua desità cotiua f X,X. Ifatti, se cosideriamo l isieme S x, x ) R : x gx )}, si ha P X, X ) S) per costruzioe e S ha area ulla el piao essedo l uioe di u segmeto e di due semirette). Poi osserviamo che, se X è simmetrica cioè X ha la stessa distribuzioe di X ), X e X hao la stessa distribuzioe. Questo si dimostra come segue. Per ogi t R si ha P X t) P X t} X }) + P X t} X > }) e, poiché per ipotesi di simmetria per la X si ha P X t} X }) + P X t} X > }) P X t} X > }) P X t} X > }) P X t} X > }), otteiamo che P X t) P X t} X }) + P X t} X > }) P X t). I coclusioe, se X è cotiua e per ipotesi di simmetria la sua desità cotiua deve essere ua fuzioe simmetrica), allora X è cotiua co la stessa desità. Esempio..4 Esempio co margiali simmetriche co la stessa distribuzioe). Sia. Poiamo X ZX, dove Z è ua variabile aleatoria idipedete da X e tale che P Z ) P Z ). Allora X, X ) o può essere cotiua perché o è possibile trovare ua desità cotiua f X,X. Ifatti, se cosideriamo l isieme S x, x ) R : x x }, si ha P X, X ) S) per costruzioe e S ha area ulla el piao essedo l uioe di due rette). Poi osserviamo che, se X è simmetrica cioè X ha la stessa distribuzioe di X ), X e X hao la stessa distribuzioe. Questo si dimostra come segue. Per ogi t R si ha P X t) P ZX t) P ZX t} Z }) + P ZX t} Z }) P X t} Z }) + P X t} Z }) e, poiché per le ipotesi si ha P X t} Z }) P X t)p Z ) P X t) P X t} Z }) P X t)p Z ) P X t) P X t), otteiamo che P X t) P X t) + P X t) P X t). Quidi possiamo cocludere come ell Esempio..3: se X è cotiua e per ipotesi di simmetria la sua desità cotiua deve essere ua fuzioe simmetrica), allora ache X è cotiua co la stessa desità. 5.)
18 ..6 Distribuzioe Normale -dimesioale I questo paragrafo viee utile cosiderare le variabili aleatorie -dimesioali come particolari vettori coloa. A tal fie scriveremo X X,..., X ) dove il simbolo viee usato per l operazioe di trasposta per matrici i tutto il paragrafo. I geerale la distribuzioe di ua variabile aleatoria -dimesioale X X,..., X ) per ; quidi possiamo ache cosiderare le variabili aleatorie reali) è idividuata dalla fuzioe caratteristica ϕ X : R C, la quale è defiita come segue: ϕ X t ) E[expit X )], dove i uità immagiaria complessa), t t,..., t ) R e t X i t ix i. Nel caso, la fuzioe caratteristica cosete di forire ua codizioe ecessaria e sufficiete per le variabili aleatorie X,..., X ; precisamete si ha idipedeza se e solo se ϕ X t ) ϕ Xi t i ) per ogi t t,..., t ) R. i La Defiizioe..5 riguarda l estesioe -dimesioale del caso uidimesioale stadardizzato dove stadardizzato sigifica co media e variaza ), metre la Defiizioe..6 riguarda l estesioe -dimesioale del caso geerale. Defiizioe..5. Si dice che X X,..., X ) ha distribuzioe Normale N, I ) se X,..., X soo variabili aleatorie reali idipedeti co distribuzioe N, ). I tal caso si ha ϕ X t ) e t, dove t t + + t ; ioltre possiamo dire che X X,..., X ) è cotiua co desità dove x x + + x. f X x ) e x e x e x π π π), Defiizioe..6. Sia Σ σ ij ) i,j,...,} R ua matrice co le segueti proprietà: simmetrica cioè σ ij σ ji per ogi i, j,..., }); semi-defiita positiva cioè t Σ t per ogi t t,..., t ) R, dove t Σ t i,j t iσ ij t j ). I tal caso esiste ua matrice Σ R simmetrica e semi-defiita positiva per cui si ha Σ Σ ). Allora, dato µ R, si dice che X X,..., X ) ha distribuzioe Normale N µ, Σ ) se ha la distribuzioe di µ + Σ Z dove Z Z,..., Z ) ha distribuzioe Normale N, I ) i accordo co la Defiizioe )..5. I corrispodeza la fuzioe caratteristica è ϕ X t ) exp it µ t Σ t. Spiegazioe dell esisteza della matrice Σ. Facedo riferimeto al Teorema Spettrale si veda [5], Capitolo ), per la simmetria di Σ esiste ua base di autovettori ortogoali di Σ ; i corrispodeza sia B la matrice otteuta co gli autovettori pesati come vettori coloa) ormalizzati. Allora si ha: B B I, che equivale a dire B B ; 6
19 B Σ B D dove D diagλ,..., λ ) è la matrice diagoale costituita dagli autovalori λ,..., λ di Σ, da cui segue Σ BDB BDB ; λ,..., λ perché la matrice Σ è semi-defiita positiva e, se cosideriamo la matrice D diag λ,..., λ ), la matrice richiesta è Σ BD B ifatti: Σ è simmetrica perché Σ BD B ) BD B Σ ; Σ è semi-defiita positiva perché, per ogi t R, posto B t a,..., a ), si ha t Σ t t BD B t Bt ) D B t i λi a i ; si ha Σ ) BD B )BD B ) BDB Σ ). Iterpretazioe dei parametri. Osserviamo che, se X X,..., X ) ha distribuzioe Normale N µ, Σ ), allora µ µ,..., µ ) è il vettore delle medie cioè µ i E[X i ] per i,..., }) e Σ è la matrice di covariaza cioè σ ij CovX i, X j ) per i, j,..., }). I particolare osserviamo ache che la matrice di covariaza deve essere simmetrica perché la covariaza tra due variabili aleatorie è simmetrica) e semi-defiita positiva perché, per ogi t R, si verifica che t Σ t Var[t X ] ). Combiazioi lieari di variabili Normali idipedeti. Siao X ),..., X h) variabili aleatorie -dimesioali idipedeti e, per ogi j,..., h}, X j) N µ j), Σ,j) ). Si osservi che e matrice di covariaza Σ,j) ulla. Nei qualcua tra queste potrebbe essere la costate µ j) calcoli co fuzioi caratteristiche che presetiamo di seguito le uguagliaze idicate co ) seguoo dall ipotesi di idipedeza, metre le uguagliaze idicate co ) seguoo dall ipotesi X j) N µ j), Σ,j) ) per ogi j,..., h}. Siao a,..., a h R; allora h j a jx j) N h j a jµ j), h j a j Σ,j) ). Questo si dimostra calcolado la sua fuzioe caratteristica come segue: h h t ) E exp it a j X j) E exp i a j t X j) ϕ h j a jx j) h E ) j j exp j ia j t X j) ) ) j h exp ia j t µ j) ) a jt Σ,j) t exp it h j a j µ j) t j h [ )] E exp ia j t X j) h a jσ,j) t. j Siao A,..., A h R m ; allora h j A jx j) N m h j A jµ j), h j A jσ,j) A j ). Que- 7
20 sto si dimostra calcolado la sua fuzioe caratteristica come segue: h h t m ) E exp it m A j X j) E exp i t ma j X j) ϕ h j A jx j) h E ) ) j j exp j it ma j X j) h [ )] E exp ia jt m ) X j) h j j ) h E j exp j ia jt m ) X j) exp ia jt m ) µ j) ) A jt m ) Σ,j) A jt m ) h exp it ma j µ j) ) t ma j Σ,j) A jt m exp it m h j A j µ j) t m h A j Σ,j) A jt m. j ) Classificazioe. []. Abbiamo due casi. Qui è presetata ua rielaborazioe dell Esercizio E.4 i. Σ ivertibile. I questo caso ache Σ è ivertibile. Allora, se cosideriamo il teorema del cambio di variabile Teorema..7) co la fuzioe ψ : R R defiita dalla trasformazioe affie ψz ) µ + Σ z, abbiamo ua fuzioe ivertibile co iversa ψ x ) Σ x µ ) e J ψ x ) Σ. I coclusioe X X,..., X ) ha desità f X x ) π) e Σ x µ ) detσ ) π) detσ )) e x µ ) Σ ) x µ ).. Σ o ivertibile. Abbiamo già visto che t Σ t Var[t X ]. Ioltre, se cosideriamo l isieme kerσ ) v R : Σ v } - dove R è il vettore ullo - detto ucleo di Σ, per t kerσ ) si ha che t X i t ix i è ua variabile aleatoria costate; quidi P i t ix i µ i ) ), cioè P X µ kerσ )) ), dove l isieme kerσ )) w R : w v per ogi v kerσ )} è detto ortogoale del ucleo di Σ. Ifie possiamo dimostrare che P X µ + ImΣ )),.) dove l isieme ImΣ ) Σ v : v R } è detto immagie di Σ ; a tal proposito si dovrà verificare che ImΣ ) kerσ ))..3) Prima di tutto iiziamo osservado che vale l iclusioe ImΣ ) kerσ )) perché, per ogi v R e w kerσ ) si ha w Σ v ) w Σ v ) v Σ w v 8
21 la prima uguagliaza segue dal fatto che la trasposta di u umero coicide co il umero stesso); ioltre, poiché abbiamo le due segueti uguagliaze ote i algebra lieare dim kerσ ) + dim ImΣ ) dim kerσ ) + dimkerσ )), si ha dim ImΣ ) dimkerσ )) ; i coclusioe ImΣ ) è u sottospazio vettoriale di kerσ )) co la stessa dimesioe di kerσ )), e questo dimostra l uguagliaza.3). Rivisitazioe degli Esempi..,..3 e..4. Per gli Esempi..3 e..4 si veda ache l Esercizio E.4 i [] e l Esercizio E.5 i [] dove, per semplicità, i etrambi i casi si assume σ ). Esempio... Cosideriamo l esempio i questioe assumedo che la variabile aleatoria X abbia distribuzioe Normale -dimesioale di media µ e variaza σ. È opportuo ricordare che le costati soo particolari distribuzioi Normali co variaza ulla. Quidi è cosetito cosiderare i segueti casi: σ e quidi X µ costate; a che porta ad avere X b costate. Questi casi verrao discussi alla fie di questo esempio rivisitato. I geerale è oto che ache la variabile aleatoria X ha distribuzioe Normale -dimesioale di media µ aµ +b e variaza σ a σ. I questo caso X, X ) ha distribuzioe Normale -dimesioale co vettore delle medie µ, µ ) µ, aµ + b) e matrice di covariaza ) ) Σ Var[X ] CovX, X ) σ aσ CovX, X ) Var[X ] aσ a σ ; gli elemeti extra-diagoali, coicideti per simmetria della matrice di covariaza, si ottegoo osservado che CovX, X ) CovX, ax + b) acovx, X ) + CovX, b) avar[x ] + aσ. Osserviamo che det Σ a σ ) a σ ) e quidi, i riferimeto alla classificazioe presetata sopra, siamo el secodo caso. A proposito della.), e i particolare dell isieme µ + ImΣ ) co, si ha ImΣ ) σ x + aσ x, aσ x + a σ x ) : x, x R} σ x + ax ), aσ x + ax )) : x, x R} σ y, ay) : y R}; quidi, se σ >, co probabilità la variabile aleatoria X, X ) assume valori ell isieme costituito dalla retta geerata dai multipli del vettore σ, a) e traslata co vettore delle medie µ µ, aµ + b). Si osservi che la matrice di covariaza che idividua la direzioe della retta dipede da a e o dipede da b; del resto le costati additive o hao iflueza el calcolo delle variaze e delle covariaze. Ora cocludiamo co i casi particolari. Se σ, la retta traslata citata sopra si riduce al sigolo puto µ e quidi si ha la variabile aleatoria costate X, X ) µ, aµ + b). Se a, la retta traslata citata sopra è del tipo x b i accordo co il fatto che si ha la variabile aleatoria costate X b. 9
22 Esempi..3 e..4. Cosideriamo gli esempi i questioe assumedo che la variabile aleatoria X abbia distribuzioe Normale -dimesioale di media perché vogliamo che X sia simmetrica) e variaza σ > escludiamo il caso che σ perché si avrebbe la variabile aleatoria costate X, da cui segue X ; quidi si avrebbe ua variabile aleatoria - dimesioale co distribuzioe Normale rappresetata dalla costate X, X ), ) ). Allora, per quato abbiamo visto i ciascuo dei due esempi i questioe, ache la variabile aleatoria X ha distribuzioe Normale di media e variaza σ >. Però i etrambi i casi la variabile aleatoria X, X ) o ha distribuzioe Normale -dimesioale perché: Nell Esempio..3, la variabile aleatoria X, X ) assume valori ell isieme S x, x ) R : x gx )} co probabilità ; Nell Esempio..4, la variabile aleatoria X, X ) assume valori ell isieme S x, x ) R : x x } co probabilità più precisamete egli isiemi x, x ) R : x x } e x, x ) R : x x } co probabilità e rispettivamete). Tali situazioi soo ovviamete i disaccordo co la.).
23 Capitolo Statistica Classica e Statistica Bayesiaa. Itroduzioe U modello statistico è ua famiglia di distribuzioi P θ : θ Ω} dove Ω R d per qualche d; le distribuzioi soo tutte dello stesso tipo, cioè soo tutte discrete o cotiue e, i corrispodeza, si fa riferimeto ad ua famiglia di desità discrete o cotiue) f θ) : θ Ω}. I geere si ha u isieme di riferimeto X detto spazio campioario) dove le desità soo positive almeo per u valore di θ. Peseremo sempre di avere ua situazioe di idetificabilità, cioè P θ P θ se θ θ. Si suppoe di avere delle variabili aleatorie osservabili dette osservazioi), la cui distribuzioe è ua tra quelle del modello statistico P θ, dove θ rappreseta il vero valore del parametro che idividua la vera distribuzioe delle osservazioi, e θ è icogito. Il problema dell Ifereza Statistica cosiste el dedurre iformazioi su θ a partire dai valori osservati. Abbiamo due possibili approcci di cui diamo subito ua breve descrizioe: Statistica Classica e Statistica Bayesiaa. Le defiizioi di stimatore e statistica sufficiete verrao presetati alla fie di questa sezioe. Statistica Classica. Si suppoe di avere variabili aleatorie X,..., X i.i.d. e co distribuzioe comue P θ, dove θ è u parametro icogito e determiistico. I tal caso si deve far riferimeto alla famiglia f X θ) : θ Ω} delle possibili desità cogiute discrete o cotiue) di X X,..., X ), cioè f X x θ) fx θ) fx θ). Talvolta, per x X fissato, questa espressioe viee cosiderata come la seguete fuzioe Ω θ L x θ) fx θ) fx θ),.) detta fuzioe di verosimigliaza. Statistica Bayesiaa. Si suppoe di avere variabili aleatorie X,..., X i.i.d. codizioatamete a Θ θ }, dove Θ è ua variabile aleatoria a valori i Ω; duque θ viee cosiderato u parametro icogito e aleatorio. I tal caso si deve far riferimeto alla desità cogiuta discreta,
24 cotiua o mista) di X,..., X, Θ), che è f X,Θx, θ) fx θ) fx θ)hθ), dove h è la desità margiale discreta o cotiua) di Θ. I quel che segue, ache alla luce degli esempi che verrao trattati el seguito, peseremo che h sia ua desità cotiua. Quidi vedremo spesso itegrali del tipo Ω dθ e o sommatorie del tipo θ Ω. Duque gli stati di iformazioe su θ i questo caso vegoo descritti da possibili desità su Ω discrete o cotiue) per la variabile aleatoria Θ. I particolare abbiamo lo stato di iformazioe iiziale prima delle osservazioi) e lo stato di iformazioe fiale dopo delle osservazioi); el primo caso si parla di desità iiziale o desità a priori) h che è la desità margiale di Θ, el secodo caso si parla di desità fiale o desità a posteriori) h x ) che è la desità margiale di Θ codizioata a X x. Statistiche: stimatori e statistiche sufficieti. u qualche isieme S ) viee detta statistica. Ua qualsiasi fuzioe S : X S per Ua statistica che forisce ua stima di ua certa fuzioe del parametro fθ) evetualmete il parametro stesso se f è la fuzioe idetità) viee detta stimatore di fθ). Ua statistica che cotiee tutte le iformazioi sul parametro date dalle osservazioi viee detta statistica sufficiete. Come vedremo il cocetto di statistica sufficiete i Statistica Classica e i Statistica Bayesiaa ha ua diversa formulazioe. Vedremo ache che i due cocetti coicidoo perché si ha ua stessa caratterizzazioe ota come Criterio di Fattorizzazioe delle desità per la statistica S : F): Esistoo due fuzioi H e K tali che fx θ) fx θ) H x )K S x ), θ). Vale la pea osservare che la scelta delle fuzioi H e K che appaioo ella codizioe F) o è uica; ad esempio si hao altre scelte H e K poedo H ch e K K c al variare di c.. Statistica Classica.. Sufficieza Ua statistica S x ) è ua statistica sufficiete classica) se e solo se vale la seguete codizioe: SC): La desità codizioata di X dato S X ) S x ) o dipede da θ. Come vedremo, SC) è equivalete alla codizioe F) presetata ella sezioe.. Teorema.. Criterio di fattorizzazioe classico)). Vale la codizioe SC) se e solo se vale la codizioe F). Dimostrazioe. Per fissare le idee facciamo riferimeto al caso i cui f θ) : θ Ω} siao desità discrete; i questo caso la desità codizioata di X dato S X ) S x ) è idividuata dal rapporto fx θ) fx θ) y X :Sy )Sx ) fy θ) fy θ) che i geerale dipede da x, θ). Suppoiamo che valga la codizioe SC). Allora, per u opportua fuzioe H x ), possiamo dire che fx θ) fx θ) y X :S y )S x ) fy θ) fy θ) H x ).
25 I corrispodeza abbiamo F) poedo K S x ), θ) y X :S y )S x ) fy θ) fy θ). Viceversa suppoiamo che valga la codizioe F). Allora si ha fx θ) fx θ) y X :S y )S x ) fy θ) fy θ) H x )K S x ), θ) y X :S y )S x ) H y )K S y ), θ) H x ) y X :S y )S x ) H y ), e quidi vale SC) perché.. Stimatori H x ) y X :Sy )Sx ) Hy ) ovviamete) o dipede da θ. I quel che segue useremo sempre la otazioe x per la media dei valori osservati, cioè x x + + x x i, da cui segue x i; i x i x )..) Iizieremo co lo stimatore co il metodo dei mometi e poi parleremo dello stimatore di massima verosimigliaza. Per molti modelli di uso comue, e i particolare per quelli presetati i queste ote, lo stimatore di massima verosimigliaza ha ottime proprietà e sarà quello a cui faremo pricipalmete riferimeto. Osservazioe... La Miscellaea alla fie del capitolo 7 i [3] illustra la coessioe tra questi due stimatori el caso di modelli statistici costituiti da ua famiglia espoeziale di desità), cioè se si ha fx θ) ax)bθ)e hx)kθ) per opportue fuzioi a, b, h, k. I modelli statistici presetati i queste ote soo espoeziali trae el caso delle osservazioi Uiformi. Stimatore co il metodo dei mometi. Nel caso i cui θ θ,..., θ k ) R k per qualche k, si tratta di cosiderare il seguete sistema di equazioi: E θ [X ] x E θ [X ] i x i. E θ [X k ] i xk i. Allora, se esiste ua soluzioe θ x ),..., θ k x )) del sistema, questa rappreseta lo stimatore di θ co il metodo dei mometi. Nel caso particolare di k abbiamo uo stimatore che dipede dalla media aritmetica x, ache quado questa o è ua statistica sufficiete. Cosideriamo il seguete esempio co k che è piuttosto aturale el caso di osservazioi ormali di media e variaza icogite: θ, θ ) E θ [X ], Var θ [X ]). Allora abbiamo il sistema θ x θ + θ i x i, da cui si ottiee θ x ) x θ x ) i x i x i x i x ). 3
26 Si osservi che l ultima uguagliaza si verifica come segue: x i x i x i x + x ) x i [ xi x ) + x + x x i x ) ] x i x i x ) + x + x x i x ) x i i x i x ). i Stimatore di massima verosimigliaza. come ua fuzioe se è possibile defiirla) ˆθ : X Ω tale che Lo stimatore di massima verosimigliaza è defiito L x ˆθx )) maxl x θ) : θ Ω}, dove L x θ) è la fuzioe di verosimigliaza defiita i.). È importate osservare che talvolta è utile fare riferimeto al logaritmo della fuzioe di verosimigliaza, cioè log L x ˆθx )) maxlog L x θ) : θ Ω}; ovviamete questo è lecito perché la fuzioe log ) è crescete. Ifie osserviamo che ˆθx ) è esprimibile come ua fuzioe di ua statistica sufficiete. Questo segue dal Criterio di Fattorizzazioe, cioè il Teorema.. perché, per la codizioe F), si ha L x ˆθx )) H x ) maxk S x ), θ) : θ Ω} e il puto di massimo i θ o cambia se si cosiderao due diverse scelte di puti di X che hao la stessa immagie tramite S. I altri termii possiamo dire che S x ) S y ) implica ˆθx ) ˆθy )..3 Statistica Bayesiaa Regole operative. Il legame tra desità iiziale e desità fiale è dato dalla formula hθ x ) fx θ) fx θ)hθ),.3) f X x ) dove f X x ) Ω fx η) fx η)hη)dη è la desità margiale di X discreta o cotiua, dello stesso tipo delle desità f θ) : θ Ω}; si osservi che la desità iiziale h e la desità fiale h x ) possoo essere dell altro tipo). È opportuo sottolieare che Ω hθ x )dθ e quidi il fattore f X x ), che o dipede da θ, è ua costate di ormalizzazioe. È utile cosiderare la seguete relazioe di proporzioalità: si dice che g è proporzioale a g, i simboli g g, se esiste c > tale che g θ) cg θ) per ogi θ Ω. Osserviamo che è ua relazioe di equivaleza: Riflessività: g g. Simmetria: g g implica g g. Trasitività: g g e g g 3 implicao g g 3. I alcui casi si potrebbe avere verosimigliaza ulla; i tal caso il logaritmo è uguale a, ma questo o ha essua iflueza ella ricerca dei puti di massimo. 4
27 U altra proprietà della relazioe di proporzioalità è la Chiusura rispetto al prodotto: g h e g h implicao g g h h. Ioltre, se g g, allora g g ; ifatti, se g g, si ha g θ) cg θ) per ogi θ Ω; allora itegrado si ha da cui segue c. g θ)dθ Ω } } I coclusioe la relazioe di proporzioalità c g θ)dθ, Ω } } hθ x ) fx θ) fx θ)hθ) è equivalete alla.3). La coveieza di usare la relazioe di proporzioalità cosiste el fatto che si evita di dover calcolare esattamete la desità e i particolare ua qualche costate moltiplicativa di ormalizzazioe) idividuado di fatto la desità a cui si è iteressati. Aggiorameto delle desità. iiziale quado arriva la + )-sima osservazioe; ifatti si ha La desità fiale dopo osservazioi diveta la uova desità fx + θ)hθ x ) fx θ) fx θ)fx + θ)hθ) hθ x + ). Quidi viee aturale pesare all aggiorameto delle desità e quidi degli stati di iformazioe sul parametro) co l acquisizioe di uove osservazioi. Famiglie coiugate. Ua famiglia di desità F h γ : γ I} è coiugata rispetto al modello statistico co desità f θ) : θ Ω} se esiste ua fuzioe ϕ : I X I tale che fx θ)h γ θ) h ϕγ,x) θ). L isieme I viee detto isieme degli iperparametri. Duque, se la desità iiziale appartiee alla famiglia F, ache la desità fiale appartiee alla famiglia F. L aggiorameto della desità cosiste ell aggiorameto dell iperparametro che idividua la desità; ifatti si passa da γ a ϕγ, x). Si ha la stessa cosa el caso di osservazioi e si passa da γ a ϕ γ, x ), dove ϕ : I X I coicide co ϕ per, metre per si ha la seguete defiizioe per ricorreza: ϕ γ, x ) ϕϕ γ, x ), x ). Il cocetto di famiglia coiugata ha iteresse el caso i cui l isieme I è sufficietemete maeggevole, cioè ad esempio I R d per qualche d, e i geerale γ rappreseta qualche gradezza caratteristica della distribuzioe co desità h γ..3. Sufficieza Ua statistica S x ) è ua statistica sufficiete Bayesiaa) se e solo se vale la seguete codizioe: SB): Per ogi desità iiziale h esiste ua fuzioe F h tale che hθ x ) F h S x ), θ). I altri termii la codizioe SB) coicide co la seguete: S x ) S y ) implica h x ) h y ). Ioltre, come vedremo, SB) è equivalete alla codizioe F) presetata ella sezioe.. 5
28 Teorema.3. Criterio di fattorizzazioe Bayesiao)). Vale la codizioe SB) se e solo se vale la codizioe F). Dimostrazioe. Suppoiamo che valga la codizioe SB). Allora si ha fx θ) fx θ)hθ) Ω fx η) fx η)hη)dη F hs x ), θ) per ua fuzioe F h opportua. Allora, se scegliamo ua desità iiziale h tale che hθ) > per ogi θ Ω, si verifica che vale la codizioe F) co ua opportua scelta delle fuzioi H e K idicata di seguito e che dipede dalla scelta della desità iiziale h): fx θ) fx θ) fx η) fx η)hη)dη FhS x ), θ). Ω hθ) } } } } H x ) K S x ),θ) Viceversa suppoiamo che valga la codizioe F). Allora si ha hθ x ) H x )K S x ), θ)hθ) Ω H x )K S x ), η)hη)dη, e quidi vale SB) co F h s, θ) Ks,θ)hθ) Ω Ks,η)hη)dη. Cocludiamo co u altro risultato che illustra u procedimeto per costruire ua famiglia coiugata el caso el caso i cui si abbiao statistiche sufficieti co opportue proprietà. Qui si preseta ua rielaborazioe di ua parte della sezioe 9.3 i [4]. Proposizioe.3. Costruzioe di ua famiglia coiugata). Sia f θ) : θ Ω} u modello statistico per ua sigola osservazioe. Suppoiamo che, per ogi, esiste ua statistica sufficiete Bayesiaa) S x ), dove S : X S per u isieme S che o dipede da. Quidi, per il Teorema.3., si ha la fattorizzazioe fx θ) fx θ) H x )K S x ), θ); ioltre suppoiamo che Ω K σ, θ)dθ, ) per ogi, σ) I N S dove N è l isieme dei umeri iteri positivi). Allora la famiglia di desità h α,σ) : α, σ) I} defiita dalla relazioe h α,σ) θ) K α σ, θ) è coiugata rispetto al modello statistico e la fuzioe ϕ : I X I è defiita come segue: ϕα, σ), x) + α, S +α x, S α σ))), dove S α σ) è u qualsiasi y α X α tale che S α y α ) σ. Dimostrazioe. Iiziamo osservado che, essedo fx θ) K S x), θ) e h α,σ) θ) K α σ, θ), si ha fx θ)h α,σ) θ) K S x), θ)k α σ, θ). Allora basta verificare che K S x), θ)k α σ, θ) K +α S +α x, S α σ)), θ),.4) perché i corrispodeza si avrebbe fx θ)h α,σ) θ) K +α S +α x, S α σ)), θ) h ϕα,σ),x). La relazioe di proporzioalità.4) si dimostra osservado che, per ogi m, m iteri, si ha fx θ) fx m θ) K m S m x m ), θ) fy θ) fy m θ) K m S m y m ), θ) fx θ) fx m θ)fy θ) fy m θ) K m +m S m +m x m, y m ), θ), da cui segue K m S m x m ), θ)k m S m y m ), θ) K m +m S m +m x m, y m ), θ); allora basterà porre m, x m x, m α e scegliere y m X m tale che S m y m ) σ. 6
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Probabilità 1, laurea triennale in Matematica II prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Algebra delle matrici
 Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Soluzioni quarta esercitazione
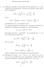 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
NUMERI REALI Mauro Saita Versione provvisoria. Settembre 2012.
 NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
NUMERI REALI Mauro Saita maurosaita@tiscaliet.it Versioe provvisoria. Settembre 2012. Idice 1 Numeri reali. 1 1.1 Numeri aturali, iteri, razioali......................... 1 1.2 La scoperta dei umeri irrazioali.........................
1 Congruenze. Definizione 1.1. Siano a, b, n Z con n 2, definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. Siao a, b, Z co 2, defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Geometria analitica: rette e piani
 Geometria aalitica: rette e piai Coordiate polari Cambiameti di riferimeto el piao Cambiameti di riferimeto i geerale Isometrie Simmetrie Isometrie el piao Isometrie ello spazio 2 2006 Politecico di Torio
Geometria aalitica: rette e piai Coordiate polari Cambiameti di riferimeto el piao Cambiameti di riferimeto i geerale Isometrie Simmetrie Isometrie el piao Isometrie ello spazio 2 2006 Politecico di Torio
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 Congruenze. Definizione 1.1. a, b, n Z n 2, allora definiamo a b (mod n) se n a b.
 1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
1 Cogrueze Defiizioe 1.1. a, b, Z 2, allora defiiamo a b (mod ) se a b. Proposizioe 1.2. 2 la cogrueza mod è ua relazioe di equivaleza su Z. a a () perché a a a b () b a () a b () b c () a b b c a c =
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
(A + B) ij = A ij + B ij, i = 1,..., m, j = 1,..., n.
 Algebra lieare Matematica CI) 263 Somma di matrici Siao m ed due iteri positivi fissati Date due matrici A, B di tipo m, sommado a ciascu elemeto di A il corrispodete elemeto di B, si ottiee ua uova matrice
Algebra lieare Matematica CI) 263 Somma di matrici Siao m ed due iteri positivi fissati Date due matrici A, B di tipo m, sommado a ciascu elemeto di A il corrispodete elemeto di B, si ottiee ua uova matrice
Precorso di Matematica, aa , (IV)
 Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
REGRESSIONE LINEARE E POLINOMIALE
 REGRESSIONE LINEARE E POLINOMIALE Nota ua tabella di dati relativi alle osservazioi di due gradezze X e Y, è aturale formulare ipotesi su quale possa essere ua ragioevole fuzioe che rappreseti o che approssimi
REGRESSIONE LINEARE E POLINOMIALE Nota ua tabella di dati relativi alle osservazioi di due gradezze X e Y, è aturale formulare ipotesi su quale possa essere ua ragioevole fuzioe che rappreseti o che approssimi
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
= = 32
 Algabra lieare (Matematica CI) - 9 Algebra delle matrici - Moltiplicazioe Euple, righe e coloe Notazioe I algebra lieare giocao u ruolo importate le coppie, tere,, ple ordiate di umeri reali; cosi come
Algabra lieare (Matematica CI) - 9 Algebra delle matrici - Moltiplicazioe Euple, righe e coloe Notazioe I algebra lieare giocao u ruolo importate le coppie, tere,, ple ordiate di umeri reali; cosi come
Lezione 2. . Gruppi isomorfi. Gruppi S n e A n. Sottogruppi normali. Gruppi quoziente. , ossia, equivalentemente, se x G Hx = xh.
 Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
Prerequisiti: Lezioe Gruppi Lezioe 2 Z Gruppi isomorfi Gruppi S e A Riferimeti ai testi: [FdG] Sezioe ; [H] Sezioe 26; [PC] Sezioe 58 Sottogruppi ormali Gruppi quoziete L Esempio 7 giustifica la seguete
v = ( v 1,..., v n ).
 Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE
 DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
a) la funzione costante k. Sia k un numero reale e consideriamo la funzione che ad ogni numero reale x associa k: x R k
 ALCUNE FUNZIONI ELEMENTARI ( E NON) E LORO GRAFICI (*) a) la fuzioe costate k. Sia k u umero reale e cosideriamo la fuzioe che ad ogi umero reale x associa k: x R k Tale fuzioe è detta fuzioe costate k;
ALCUNE FUNZIONI ELEMENTARI ( E NON) E LORO GRAFICI (*) a) la fuzioe costate k. Sia k u umero reale e cosideriamo la fuzioe che ad ogi umero reale x associa k: x R k Tale fuzioe è detta fuzioe costate k;
Esercizi sull estremo superiore ed inferiore
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
5. Derivate. Derivate. Derivate di funzioni elementari. Regole di derivazione. Derivate di funzioni composte e di funzioni inverse
 Di cosa parleremo Le derivate costituiscoo, per la maggioraza degli studeti, l argometo più semplice di questa parte dell aalisi matematica. I questo capitolo e daremo il cocetto assieme al sigificato
Di cosa parleremo Le derivate costituiscoo, per la maggioraza degli studeti, l argometo più semplice di questa parte dell aalisi matematica. I questo capitolo e daremo il cocetto assieme al sigificato
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Analisi e Geometria 1
 Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Unità Didattica N 33 L algebra dei vettori
 Uità Didattica N 33 Uità Didattica N 33 0) La ozioe di vettore 02) Immagie geometrica di u vettore umerico 03) Somma algebrica di vettori 04) Prodotto di u umero reale per u vettore 05) Prodotto scalare
Uità Didattica N 33 Uità Didattica N 33 0) La ozioe di vettore 02) Immagie geometrica di u vettore umerico 03) Somma algebrica di vettori 04) Prodotto di u umero reale per u vettore 05) Prodotto scalare
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Richiami sulle potenze
 Richiami sulle poteze Dopo le rette, le fuzioi più semplici soo le poteze: Distiguiamo tra: - poteze co espoete itero - poteze co espoete frazioario (razioale) - poteze co espoete reale = Domiio delle
Richiami sulle poteze Dopo le rette, le fuzioi più semplici soo le poteze: Distiguiamo tra: - poteze co espoete itero - poteze co espoete frazioario (razioale) - poteze co espoete reale = Domiio delle
Non presenta difficoltà concettuali il passaggio dalle equazioni lineari a coefficienti costanti del secondo ordine a quelle di ordine maggiore.
 Le equazioi differeziali lieari di ordie > a coefficieti costati. No preseta difficoltà cocettuali il passaggio dalle equazioi lieari a coefficieti costati del secodo ordie a quelle di ordie maggiore.
Le equazioi differeziali lieari di ordie > a coefficieti costati. No preseta difficoltà cocettuali il passaggio dalle equazioi lieari a coefficieti costati del secodo ordie a quelle di ordie maggiore.
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Appendice 2. Norme di vettori e matrici
 Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Congruenze in ; l insieme quoziente / n
 Cogrueze i ; l isieme quoziete / Per ogi, si cosideri i la relazioe, che per il mometo deoteremo co ( ), così defiita: a ( ) b divide a-b Esempio: 5 (7 ) 19, perché 7 5-19=-14, metre 4 o è ella relazioe
Cogrueze i ; l isieme quoziete / Per ogi, si cosideri i la relazioe, che per il mometo deoteremo co ( ), così defiita: a ( ) b divide a-b Esempio: 5 (7 ) 19, perché 7 5-19=-14, metre 4 o è ella relazioe
TEORIA DELLE MATRICI. dove aij K. = di ordine n, gli elementi aij con i = j (cioè gli elementi a 11
 1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Forme Bilineari 1 / 34
 Forme Bilieari 1 / 34 Defiizioe applicazioe Dicesi forma bilieare su uo spazio vettoriale V, ua ϕ : V V R che è lieare i etrambi gli argometi, ossìa tale che u,v,w V e a,b R si abbia: ϕ(au + bv,w) =aϕ(u,w)
Forme Bilieari 1 / 34 Defiizioe applicazioe Dicesi forma bilieare su uo spazio vettoriale V, ua ϕ : V V R che è lieare i etrambi gli argometi, ossìa tale che u,v,w V e a,b R si abbia: ϕ(au + bv,w) =aϕ(u,w)
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Cosa vogliamo imparare?
 Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Stima di somme: esercizio
 Stima di somme: esercizio Valutare l'ordie di gradezza della somma k l (1 + 3 k ) Quado x
Stima di somme: esercizio Valutare l'ordie di gradezza della somma k l (1 + 3 k ) Quado x
STUDIO DEL LANCIO DI 3 DADI
 Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Soluzione del Problema di Natale.
 Soluzioe del Problema di Natale. Idicheremo, per comodità, ua particella Mxyzptl co M(d, = (m + ; m 1,..., m, dove m+ è il puto di che rappreseta il suo ucleo mxyzptl +, e gli m i rappresetao le sue subparticelle
Soluzioe del Problema di Natale. Idicheremo, per comodità, ua particella Mxyzptl co M(d, = (m + ; m 1,..., m, dove m+ è il puto di che rappreseta il suo ucleo mxyzptl +, e gli m i rappresetao le sue subparticelle
Unità Didattica N 32 Grandezze geometriche omogenee e loro misura
 Uità Didattica N 3 Uità Didattica N 3 01) Classi di gradezze omogeee 0) Multipli e sottomultipli di ua gradezza geometrica 03) Gradezze commesurabili ed icommesurabili 04) Rapporto di due gradezze 05)
Uità Didattica N 3 Uità Didattica N 3 01) Classi di gradezze omogeee 0) Multipli e sottomultipli di ua gradezza geometrica 03) Gradezze commesurabili ed icommesurabili 04) Rapporto di due gradezze 05)
Y557 - ESAME DI STATO DI LICEO SCIENTIFICO. 3 lim
 Y557 - ESAME DI STATO DI LICEO SCIETIFICO PIAO AZIOALE DI IFORMATICA CORSO SPERIMETALE Tema di: MATEMATICA (Sessioe ordiaria 2002) QUESTIOARIO 1 Se a e b soo umeri positivi assegati quale è la loro media
Y557 - ESAME DI STATO DI LICEO SCIETIFICO PIAO AZIOALE DI IFORMATICA CORSO SPERIMETALE Tema di: MATEMATICA (Sessioe ordiaria 2002) QUESTIOARIO 1 Se a e b soo umeri positivi assegati quale è la loro media
DISTRIBUZIONE NORMALE MULTIVARIATA
 Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Congruenze in ; l insieme quoziente / n
 Cogrueze i ; l isieme quoziete / Per ogi, si cosideri i la relazioe così defiita: a b divide a-b. La relazioe biaria è detta cogrueza modulo. Se a b scriveremo pure a b (mod. ) e leggeremo a cogruo b (modulo
Cogrueze i ; l isieme quoziete / Per ogi, si cosideri i la relazioe così defiita: a b divide a-b. La relazioe biaria è detta cogrueza modulo. Se a b scriveremo pure a b (mod. ) e leggeremo a cogruo b (modulo
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Analisi Matematica I
 Aalisi Matematica I Isiemi di umeri Naturali, iteri, razioali I primi umeri che si icotrao soo gli iteri positivi, detti ache umeri aturali: 1, 2, 3,.... L isieme dei umeri aturali si idica co il simbolo
Aalisi Matematica I Isiemi di umeri Naturali, iteri, razioali I primi umeri che si icotrao soo gli iteri positivi, detti ache umeri aturali: 1, 2, 3,.... L isieme dei umeri aturali si idica co il simbolo
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
IV Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2011/12 Nome: 17 luglio
 IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
CAMBIAMENTO DI BASE IN UNO SPAZIO VETTORIALE
 CAMBIAMENTO DI BASE IN UNO SPAZIO VETTORIALE Sia V uo spazio vettoriale sul campo K. Siao v, v,..., v vettori dati apparteeti a V e siao, ioltre, assegati scalari k, k,..., k apparteeti a K. Si defiisce
CAMBIAMENTO DI BASE IN UNO SPAZIO VETTORIALE Sia V uo spazio vettoriale sul campo K. Siao v, v,..., v vettori dati apparteeti a V e siao, ioltre, assegati scalari k, k,..., k apparteeti a K. Si defiisce
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Esercitazione IV Complementi di Probabilità a.a. 2011/2012
 Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Esercitazioe IV Complemeti di Probabilità a.a. 2011/2012 Argometi: idipedeza, 2 lemma di Borel Catelli, σ-algebra coda. Esercizio 1. a) Dato (Ω, F, P), siao J 1, J 2,..., J m π-system su Ω tali che Ω J
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
