IL PROBLEMA CLASSICO DI GEOMETRIA
|
|
|
- Antonia Alfano
- 9 anni fa
- Просмотров:
Транскрипт
1 IL PROBLEMA CLASSICO DI GEOMETRIA Contenuto Questo lavoo contiene una pemessa metodologica geneale, e una seie di schemi isolutivi pe impostae alcuni poblemi fondamentali di geometia elementae su poligoni inscitti o cicoscitti a un cechio di aggio assegnato. In tutti i casi sono state poposte l impostazione geometica e quella tigonometica. Inolte è stata deteminata la figua di max/min peimeto o aea, dato l inteesse veso questo tipo di poblema da pate di docenti e studenti del Liceo Scientifico. Le figue notevoli studiate sono: Tiangolo ettangolo inscitto in un semicechio Tapezio isoscele inscitto in un semicechio Tiangolo isoscele inscitto in un cechio Cono cicolae etto inscitto in una sfea Rettangolo inscitto in un cechio Cilindo inscitto in una sfea Rettangolo inscitto in un semicechio Tiangolo isoscele cicoscitto a un cechio Cono cicolae etto cicoscitto a una sfea Tapezio isoscele cicoscitto a un cechio Tapezio isoscele cicoscitto a un semicechio Pemessa: l uso di schemi geneali nella isoluzione di poblemi di Geometia L impostazione dei poblemi di Geometia conduce genealmente all elaboazione di schemi geneali pe la isoluzione di classi di poblemi affini. Cosa significa classe di poblemi affini? Con ciò si intende un insieme di poblemi divesi come enunciato, ma la cui impostazione geometica è la stessa. Pe es., deteminae il tiangolo isoscele di peimeto massimo inscitto in un cechio e deteminae il tiangolo isoscele inscitto in un cechio tale che la somma della base e dell altezza è massima sono poblemi che hanno la stessa impostazione, peché in entambi i casi si tatta di calcolae le misue di segmenti in funzione di una incognita che può essee p.es. l altezza del tiangolo, o l angolo definito dal lato obliquo e dall altezza, ecc. Non solo, ma anche espimee l aea del tiangolo isoscele inscitto in un cechio di aggio R in funzione dell altezza ichiede la stessa impostazione. Cambia peò l obiettivo, peché in questo caso non si tatta di isolvee un equazione; ciò che impota è solo l impostazione cioè quella seie di passaggi che pemette di espimee gli elementi necessai alla isoluzione di un poblema in funzione di uno solo di essi, che saà una vaiabile. La isoluzione geneale di un poblema è una questione che non sempe viene affontata in modo efficace. Se si considea la capacità di appendee in modo poduttivo questa tecnica matematica (qui faccio ifeimento solo ai poblemi di Geometia), si può die che i isultati lasciano assai a desideae, tovandosi fequentemente il caso di studenti del liceo scientifico che non sanno neppue impostae un poblema (scivo nell anno 007), vale a die non sanno neppue come aivae all equazione isolvente. Le agioni di tale insuccesso sono vaie, e può essee che omai l oigine di questo poblema non sia neppue didattica nel senso stetto del temine. Pu ammettendo l impossibilità di definie con sicuezza l oigine ultima di cete difficoltà, una analisi della stuttua Ezio Foneo Il poblema classico di geometia 1/17
2 del poblema classico di Geometia può aiutae almeno a cecae stategie di insegnamentoappendimento efficaci. Il paee di chi scive è che una componente dell abilità nel isolvee i poblemi sta nella padonanza di schemi isolutivi nel senso sopa indicato. La questione non è il poblem solving, ma qualcosa di più specifico. Quando si pala di poblema di Geometia, si fa ifeimento a un insieme ben delimitato di ichieste. Un poblema di Geometia può ichiedee una dimostazione (che non è la esauiente giustificazione o simili che affliggono ceti temi dell esame di Stato) puamente sintetica, ma qui faccio ifeimento ad un alto tipo di poblema: quello nel quale si ichiede di convetie le gandezze geometiche in espessioni contenenti indeteminate, cioè vaiabili o incognite. Pe esempio, un poblema di massimo o minimo contiene questo passaggio. Si potebbeo definie come poblemi di applicazione dell algeba e/o della tigonometia alla Geometia, ma io li chiameei poblemi classici di Geometia, dato il uolo che hanno icopeto nella didattica della Matematica. In questo tipo di questioni non è ichiesta di solito una dimostazione sintetica, anche se può capitae talvolta di dove cecae delle elazioni di tipo sintetico. Il poblema classico sfutta dei teoemi, e ha una paticolaità: è classificabile secondo insiemi di poblemi affini, quindi pate della sua soluzione è uno schema fisso, che si può iapplicae a tutti i poblemi dello stesso genee. Ciò conduce alla fomulazione di schemi poblematici che sono i nuclei della soluzione; sulla soluzione dello schema si innesta poi la soluzione paticolae del quesito effettivamente fomulato. Questa classificabilità del poblema classico nel senso sopa esposto è ben nota, anzi è così nota che di fatto non vi facciamo caso. La cosa è più chiaa se consideiamo il modo in cui genealmente i testi espongono la isoluzione dei poblemi. Nella gande maggioanza dei casi, i testi pocedono pe esempi. Ciò dà la sgadevole impessione di un appoccio empiico, euistico alla questione, e diei suggeisce che si pocede in modo pefino occasionale, come se si potesse dedue un metodo geneale di isoluzione da una seie finita pe quanto numeosa di esempi poposti. Oa non intendo mettee in discussione l esistenza di un elemento euistico e quasi-speimentale nell appendimento della Matematica; ma la Matematica in sé non è né euistica né speimentale: è un insieme di elazioni logiche. La questione è: tali elazioni logiche, che sono quindi necessaiamente costitutive delle modalità di appendimento e ipso facto di insegnamento, non debbono fose essee chiaamente ese esplicite? Si badi che la questione di fondo non è l altenativa ta insegnamento dall alto o scopeta dal basso, ma iguada il contenuto dell appendimento. Peché si pendono in consideazione i poblemi classici di Geometia? Peché sevono a agionae, dià qualcuno. Ma peché sevono a agionae? Bene, qui possiamo tovae delle isposte; si può ispondee che, isolvendo un poblema, si impaa a concatenae i popi pensiei in modo sequenziale ecc, che si sviluppa l intuizione ecc ecc solo che si tascua quello che è, da Euclide anzi da molto pima, un aspetto fondamentale del agionamento matematico e poi anche scientifico: la iduzione di una molteplicità indeteminata (di egole, poposizioni, poblemi appunto) ad un insieme potenzialmente illimitato, ma concetamente finito, di infomazioni di base, peché sia i postulati di Euclide sia gli schemi isolutivi sia i teoemi più noti sono infomazione. La Matematica, sotto questo aspetto, è un pocesso di iodino/iduzione dell infomazione (Mach disse economia di pensieo ). L economia di pensieo o, se vogliamo, lo schematismo, ha un uolo essenziale nell oganizzazione delle stategie isolutive. Esso impedisce di dispedesi in una infinità Ezio Foneo Il poblema classico di geometia /17
3 potenziale di casi distinti da affontae sepaatamente. Ma quante sono le situazioni schematiche che si incontano nei poblemi classici? Si tova che il loo numeo è abbastanza idotto a meno di consideae poblemi un po fuoi dal comune. Inolte, fondamentalmente sono le stesse in Geometia piana e solida. Infine, gli schemi possono essee euclidei o tigonometici. Si può distinguee ta figue inscitte e cicoscitte. Di seguito ho poposto la soluzione di alcuni poblemi su figue inscitte in un cechio o in una sfea. FIGURE INSCRITTE IN UN CERCHIO O IN UNA SFERA La isoluzione di poblemi su poligoni inscitti in un cechio o in un semicechio e più in geneale in un segmento cicolae dipende essenzialmente dai teoemi sui tiangoli ettangoli e dal teoema della coda. L impostazione può essee elementae o algebica oppue tigonometica. Nel pimo caso, sono fondamentali i teoemi di Euclide e Pitagoa; nel secondo, le egole che espimono i cateti ispetto all ipotenusa e appunto il teoema della coda, insieme alle elazioni e popietà geneali degli angoli alla cf e al cento. I poblemi più semplici consistono in applicazioni delle popietà dei tiangoli ettangoli. A pate il Teoema di Pitagoa, questi semplici poblemi implicano i seguenti teoemi. Pimo teoema di Euclide: in un tiangolo ettangolo il quadato di un cateto è equivalente al podotto dell ipotenusa pe la poiezione del cateto sull ipotenusa Secondo teoema di Euclide: in un tiangolo ettangolo il quadato dell altezza elativa all ipotenusa è equivalente al podotto delle poiezioni dei cateti sull ipotenusa Pimo Teoema fondamentale dei tiangoli ettangoli: un cateto è dato dal podotto dell ipotenusa pe il seno dell angolo opposto a quel cateto Secondo Teoema fondamentale dei tiangoli ettangoli: un cateto è dato dal podotto dell ipotenusa pe il coseno dell angolo acuto adiacente al cateto 1. Tiangolo ettangolo inscitto in un semicechio (cioè di ipotenusa costante) Posto AB =, conviene espimee tutte le distanze in funzione di AH = x, con 0 x In base al pimo teoema di Euclide, pe cui AC = AH AB, si ottiene AC = x In base al secondo t. di Euclide si tova CH = AH HB e quindi, dato che HB = x, CH = x x Tigonometicamente si ha, pendendo x = H A C, Ezio Foneo Il poblema classico di geometia /17
4 AC = cosx BC = sinx CH = cosx sinx AH = cos x HB = sin x I poblemi sul tiangolo inscitto in un semicechio sono elementaissimi; il peimeto p è dato tigonometicamente da p = + sin x + cos x oppue algebicamente da p = + x + ( x) Pe l aea A abbiamo A (semipodotto dei cateti) = 1 sin x cos x = sin x cos x oppue (semipodotto dell ipotenusa pe l altezza ad essa elativa) A = 1 x x =. Tapezio isoscele inscitto in un semicechio Si iconduce al caso del tiangolo inscitto in un semicechio (vedi pima) x x Posto AH = x, con 0 x ( peché i casi limite della figua sono il tapezio di altezza nulla e il tiangolo isoscele inscitto nel semicechio, cioè il tapezio degenee di base minoe nulla), abbiamo AH = x AD = x DC = AB - AH = - x DH = x x Il peimeto è p = x + - x + = ( x + x ) 1 1 L aea A = ( AB + CD) DH = ( + x) x x = x( x) ( x x) x = Tigonometicamente si ha, pendendo x = D A H con 0 x 45 : p = AD + CD + AB = 4 cosx + ( 4 cos x) + (vedi le elazioni valide pe il tiangolo ettangolo inscitto nel semicechio) e quindi p = 4 4 cos x + 4 cosx = 4 (sin x + cosx ) 1 A = ( AB + CD) DH = 1 ( + 4 cos x) cos xsin x = 4 sin x cos x Ezio Foneo Il poblema classico di geometia 4/17
5 . Tiangolo isoscele inscitto in un cechio di aggio R. Supponiamo che AB sia la base, e CH l altezza ad essa elativa. Poniamo CH = x, con 0 x R Lo schema isolutivo consiste nel polungae l altezza CH fino al punto D, estemo opposto a C del diameto CD ; quindi costuiamo il tiangolo CAD ettangolo in A peché inscitto in un semicechio, cui possiamo applicae i teoemi di Euclide: applicando il pimo teoema di Euclide pe cui AC = CH CD calcoliamo il lato obliquo sostituendo CD = e CH = x abbiamo AC = x e quindi AC = BC = x Applicando il secondo di Euclide pe cui AH = CH HB otteniamo la base sostituendo CH = x e HB = - x abbiamo AH = x ( - x ) AH = AB = AH = x x Il peimeto del tiangolo è quindi p = x + x x L aea è data da A = x x x x x e quindi Il tiangolo isoscele di peimeto massimo si tova annullando la deivata di p : p = 1 x x x + ( x) x x( x + x) + = = x x x x x x x x x quindi annullando il numeatoe otteniamo la eq 4 x = x 4x -8x+4 = 0 4 x 4x 6x = 0 x = che coisponde al tiangolo equilateo. Ciò può essee confemato ossevando che in base ai due teoemi di Euclide il lato obliquo del tiangolo isoscele inscitto è = che è popio il Ezio Foneo Il poblema classico di geometia 5/17
6 lato del tiangolo equilateo, in base p.es. al teoema della coda, mente la base è = = come il lato obliquo. 4 Alcune ossevazioni impotanti. Anzitutto, benché il isultato ottenuto sia coetto, nella soluzione poposta mancano passaggi essenziali. In linea di pincipio, se si ceca il massimo o il minimo di una funzione continua il cui dominio è un intevallo chiuso limitato [ a ; b ] come in questo caso, è necessaio consideae la possibilità che i valoi estemi della funzione cadano negli estemi del dominio e non coispondano all annullasi della deivata pima. Nel poblema consideato e in genee nei poblemi in cui si cecano peimeto o aea o volume massimo questa eventualità è da escludee, peché genealmente gli estemi del dominio coispondono a valoi nulli della funzione di cui cechiamo il massimo o a minimi locali (nel poblema consideato pe x = 0 si tova p = 0, pe x = si ha p = p è la metà del peimeto p). Tuttavia, l analisi completa di un poblema in geneale ichiede che i valoi della funzione debbano essee confontati con la soluzione che annulla la deivata. In secondo luogo, nella iceca della soluzione ho tascuato x = 0 e di nuovo x = 0 quando si isolve l equazione di secondo gado ottenuta elevando al quadato. Ciò è localmente giustificato da quanto appena detto, e dall annullasi del denominatoe della deivata, ma le soluzioni algebiche ottenute vanno comunque pese in consideazione. L eq. di secondo gado è stata ottenuta elevando al quadato i membi di un eq. iazionale del tipo A = B, nella quale si suppone pe coeenza del segno che debba essee B > 0, cioè nel nosto caso x > 0 quindi x >. Una soluzione che non ispetti questa condizione sul segno di B non è una soluzione, e ciò va discusso. Infine, dal punto di vista analitico non abbiamo ancoa dimostato che x = è veamente un punto di massimo, anche se è geometicamente evidente. Possiamo consideae il sistema misto x( x + x) x x x > 0 0 x Dato che le adici sono positive, esta da isolvee la dis. 4 x > x. Pe quanto iguada il tiangolo di aea massima, abbiamo A = D ( x x x ) che è a de. di un podotto. Dato che x > 0, potiamo x sotto adice e 4 otteniamo A = x x - nel calcolo della deivata la adice si può tascuae (il massimo di una adice coincide col massimo del adicando) e quindi D (x x 4 ) = 6x 4x = 0 se x = 0 (che non inteessa) e x =, che coisponde al tiangolo di p max, cioè equilateo. In questo caso, la confema che si tatta di un massimo può essee ottenuta dal segno della de. seconda, che è A = 1x - 1x e che è negativa pe x =. Ezio Foneo Il poblema classico di geometia 6/17
7 Soluzioni tigonometiche specie pe il calcolo del peimeto, il metodo euclideo applicato semba essee complicato dal punto di vista del calcolo. Ciò induce a consideae la possibilità di cecae una soluzione tigonometica dello schema del tiangolo isoscele inscitto, nella quale l incognita x sia p.es. la metà dell angolo opposto alla base, cioè AC H = C B. E evidente che deve essee 0 x. Anche tigonometicamente la chiave di volta del poblema è la costuzione del tiangolo ettangolo CAD, nel quale AC = BC = cosx e AB = AH = ( AC sinx) = ( cosx sinx ) = 4 sinx cosx (a questo isultato possiamo anche giungee col teoema della coda pe cui AB = sin x = (sinx cosx). Pe l altezza si ha invece CH = cosx cosx = cos x. Abbiamo quindi le fomule tigonometiche p = 4 cosx + 4 sinxcosx = 4 cosx (1 + sinx) oppue ( cosx + sin x ), A = 4 sinxcos x. Lo studio dei massimi del peimeto e dell aea non pesenta paticolae difficoltà, a pate il fatto che nella deivata dell aea si ottiene un espessione di quato gado: cos 4 x sin x cos x che conduce all equazione cos x ( cos x sin x ) = 0 e alla disequazione associata (pe confemae che si tatta di un massimo). Dallo schema del tiangolo isoscele inscitto si passa al 4. Cono inscitto in una sfea La figua solida che coisponde a un poblema sul cono (cicolae etto) si ottiene uotando la figua piana (il tiangolo isoscele inscitto) intono al diameto contenente l altezza. Peciò le dimensioni lineai imangono le stesse, e lo schema isolutivo elaboato pe il tiangolo isoscele inscitto può essee applicato tale e quale, con la seguente intepetazione: h = altezza del cono = CH = x oppue cos x b = aggio di base del cono = AH = x x oppue sinx cosx a = apotema del cono = AC = x oppue cosx Possiamo quindi consideae: la supeficie lateale S l = π b a = π Rx Rx x = π 4R x Rx oppue π(r sinx cosx) (Rcosx ) = 4π R sin x cos x la supeficie totale S T = π b ( b + a) = π ( Rx x ) ( Rx x + Rx) oppue π(r sinx cosx) (R sinx cosx + Rcosx) = 4π R (sin x cos x + sin x cos x) π π π il volume V = b h = (Rx x ) x = (Rx x ) oppue π (R sinx cosx) (R cos 8π x ) = R sin x cos 4 x. Confontando la fomula tigonometica del volume con quella della supeficie lateale, si nota che V è popozionale al quadato di S l. Oa, se una gandezza è popozionale al quadato di un alta ed entambe sono positive nel loo dominio comune, cioè se F = k f, i max e i min di F coincidono con i max e i min di f oppue con le soluzioni dell equazione f = 0. Infatti la deivata di F ignoando la costante k, cioè D(f ) = f f = 0 implica f = 0 o f = 0. In patica, f = 0 coisponde a un minimo e quindi i massimi del quadato di una funzione positiva coincidono con i massimi della funzione. H Ezio Foneo Il poblema classico di geometia 7/17
8 Il cono di volume e di sup. lateale massimi si può tovae facilmente annullando la de. di Rx -x cioè 4Rx x 4R e si ottiene x = (valgono sempe le pecedenti ossevazioni sulla veifica che si tatti effettivamente di un massimo). Tigonometicamente coisponde all eq. 4R R cosx = cioè cosx =, cui coisponde l angolo di semiapetua 0, ad. 5. Rettangolo inscitto in un cechio E un poblema molto semplice. Algebicamente, detto il aggio, abbiamo che la metà dell altezza e la metà della base sono i cateti di un tiangolo ettangolo avente come ipotenusa. Quindi, se x è la metà della base, l altezza è x., con 0 x. Peciò p = 4x + 4 x A = 4x x Tigonometicamente, se indichiamo con x l angolo OC, con 0 x 90, avemo pe la base AB = cosx e BC = sinx pe cui abbiamo anche p = 4 sinx + 4 cosx e A = 4 sinx cosx. ettangolo inscitto in un cechio di peimeto massimo si ottiene il quadato. Ci sono molti modi pe giungee a questo isultato. Tigonometicamente, calcoliamo D(p) = 4 ( cosx - sinx ) = 0 x = 45. ettangolo inscitto in un cechio di aea massima si ottiene ancoa il quadato. Tigonometicamente, sinx cosx = 1 sin x che è massimo se x = 90 cioè x = 45. Ossevazione. Le due fomule algebiche del peimeto e dell aea sono invaianti ispetto alla sostituzione di x con x. Quindi, qualsiasi poblema avente pe agomento il peimeto o l aea è simmetico, vale a die: se ammette la soluzione x = s, deve ammettee anche x = s. Ciò significa che se la soluzione è unica alloa è fonita dall equazione x = H x x =, che definisce appunto il quadato. Tigonometicamente ciò si vede Ezio Foneo Il poblema classico di geometia 8/17
9 dall invaianza ispetto allo scambio sin x cos x. Nei poblemi sulle figue inscitte il punto di massimo è genealmente uno solo, e alloa si può concludee che la invaianza ispetto allo scambio di x con f(x) implica che la soluzione è data da x = f(x). Nelle figue cicoscitte è il minimo ad essee unico, e vale la stessa conclusione. 6. Cilindo inscitto in una sfea Supeficie lateale S l = π b h = π x ( R x ) = 4π x R x dove x è il aggio di base. Se x è l altezza, si avebbe π ( R x ) x che è la stessa fomula. Questa invaianza fomale della supeficie lateale ispetto allo scambio ta aggio e semialtezza come significato della x implica che la figua di supeficie lateale massima ha il diameto di base uguale all altezza (cilindo equilateo), cioè deve essee x = R R x che pota a x =. Tigonometicamente si avebbe S l = π R cosx R sinx (con lo stesso significato di x visto pima) cioè 4π R sinx cosx Pe la supeficie totale si ha S T = π b + π b h = π b ( b + h) = π x ( x + R x ), se x è il aggio di base. Tigonometicamente si avebbe π Rcosx ( Rcosx + Rsinx ) = πr ( cos x + sinx cosx ) Il volume è dato da V = π b h = π x R x = π x x R oppue πr cos x sinx 7. Rettangolo inscitto in un semicechio Può essee icondotto allo schema del ettangolo inscitto in un cechio, o a quello del tiangolo ettangolo inscitto nel semicechio. Nel pimo caso, applicando il t. di Pitagoa abbiamo, pendendo OB = x con 0 : BC = x e quindi p = 4x + x peimeto A = x x aea Tigonometicamente si avebbe OB = cos x e BC = sin x pe cui p = 4 cos x + sin x A = cosx sinx = sinx Ezio Foneo Il poblema classico di geometia 9/17
10 Se ne deduce che il ettangolo di A massima inscitto in un semicechio si ottiene pe sinx = 1 x = 90 e quindi x = 45, che coisponde al quadato, mente quello di p massimo è dato dall equazione D(p) = 0 - sin x + cos x = 0 tan x = 1. Questa soluzione può essee costuita gaficamente: 1 In base alla definizione di tangente di un angolo, si ha MF = tan x =. Quindi si può costuie la tangente al semicechio in uno degli estemi del diameto come F, e unie il cento del semicechio col punto sulla tangente che dista da F metà del aggio. L intesezione di OM con la semiciconfeenza è uno dei vetici del ettangolo. FIGURE CIRCOSCRITTE A UN CERCHIO O A UNA SFERA Questo tipo di poblemi è molto più inteessante (e difficile). Nel caso di figue cicoscitte, i teoemi fondamentali da tene pesenti sono: 1. il segmento che unisce il cento del cechio a un punto di tangenza del cechio con un lato è pependicolae al lato stesso. Quindi è possibile costuie tiangoli ettangoli unendo il cento del cechio, un vetice e un punto di tangenza ;. l aea di un poligono cicoscitto a un cechio è equivalente al podotto del semipeimeto pe il aggio del cechio, pe cui A = p ;. i segmenti di tangente condotti da un punto esteno a una ciconfeenza sono conguenti. Ezio Foneo Il poblema classico di geometia 10/17
11 Esaminiamo i seguenti casi: tiangolo isoscele cicoscitto a un cechio e cono cicoscitto a una sfea; tapezio isoscele cicoscitto a un cechio; tapezio isoscele cicoscitto a un semicechio. 1. Tiangolo isoscele cicoscitto a un cechio Costuzione della figua: con cento negli estemi A e B della base del tiangolo, tacciae due cf di aggio uguale a metà della base. Le intesezioni ta queste cf e la ciconfeenza inscitta nel tiangolo sono i punti di tangenza. Ovviamente i segmenti OT sono pependicolai ai lati obliqui. Algebicamente: un metodo consiste nel pendee come vaiabile indipendente x la distanza OC ta il vetice opposto alla base del tiangolo e il cento della cf inscitta. Limiti: x > 0 (se x = 0 la base AB diventa infinita, mente evidentemente non c è un limite supeioe). Noto HB, è possibile espimee sia il peimeto che l aea del tiangolo. Infatti l altezza è immediata essendo CH = x +, e il lato obliquo è calcolabile col teoema di Pitagoa. Quindi la chiave isolutiva è il calcolo di HB in funzione di CO = x. Ezio Foneo Il poblema classico di geometia 11/17
12 Si può sfuttae la similitudine ta i tiangoli CHB e CTO, pe cui OC : OT = BC : HB Posto il aggio della cf =, possiamo espimee HB in funzione di OC = x. Dobbiamo peò espimee il lato obliquo BC in funzione di x e di HB. Indichiamo HB con la lettea y ; abbiamo BC = HC + HB E quindi BC = ( x + ) + y BC = x + y + x + Ricaviamo HB = y dalla popozione: OC HB = OT BC. Elevando tutto al quadato si ha x y = ( x + y +x + ) [ icodae che y = HB, x = OC, = OT, x + y + x + = BC ]. icaviamo la y : y = ( x + x + ) ( x + ) ( x + ) = = x ( x + )( x ) x e infine y = HB = x + x Alto metodo In tutti i poligoni cicoscitti a un cechio, l aea è data dal podotto del semipeimeto pe il aggio del cechio: A = p. Nel nosto caso, l aea può essee calcolata anche come semipodotto della base pe l altezza. Quindi HB CH = (HB + BC) OT Da cui y (x + ) = ( y + ( x + ) + y ) x y = ( x + ) + y x y = ( x + x + + y ) (x ) y = ( x+ ) e si iottiene il isultato pecedente pe HB. Ancoa un alto metodo in base al teoema pe cui i segmenti di tangente condotti da un punto esteno a una ciconfeenza sono conguenti, si può ossevae che il lato obliquo può essee calcolato in due modi: in base al teoema di Pitagoa, pe cui BC = HB + HC e come somma di due segmenti di tangente BC = BT + TC. Indichiamo la metà della base, BH, con la lettea y, pe il teoema della conguenza dei segmenti di tangente, abbiamo pue BT = BH = y. Calcoliamo TC; applicando il t. di Pitagoa a COT, abbiamo TC = x Quindi BC = y + x = ( x + ) + y Quadando si ottiene y + x + y x = x + x + + y Ezio Foneo Il poblema classico di geometia 1/17
13 Riducendo abbiamo y x x + x = x + = ( x + ), da cui si ottiene HB = Inteessante è pue la isoluzione tigonometica. In questo caso, pendiamo come vaiabile l angolo x = ACH. Limiti: 0 < x < 90. La costante è il aggio ; da qui possiamo dedue OC = ( 1+ sin x) CH = + = sin x sin x sin x HB = CH HB = ( 1+ sin x) CH (1 + sin x) BC = = cos x cos x sin x cos x tan x Evidentemente l impostazione tigonometica è molto più semplice. Da notae l uso di fomule invese e la compasa di funzioni goniometiche al denominatoe, tipica dei poblemi su poligoni cicoscitti. Tiangolo isoscele di peimeto minimo e aea minima cicoscitto a un cechio Nel caso di figue cicoscitte, si possono solo cecae i minimi dell aea e del peimeto; infatti è evidente che queste gandezze in questo caso non possono ammettee massimo. Il poligono cicoscitto di aea minima coincide con quello di peimeto massimo, data la fomula A = p nella quale è costante. Se si adotta l impostazione algebica conviene cecae l aea massima, data la compasa di adicali che endono il calcolo della deivata piuttosto complicato quando vengono sommati. Come visto sopa, l aea è data da x + A = HB HC = ( x + ) x Ezio Foneo Il poblema classico di geometia 1/17
14 Poiché A 0, è massima quando lo è il suo quadato; peciò consideiamo ( è una ( x + ) costante moltiplicativa e si può ignoae annullando la deivata) =, la cui deivata è x ( x + ) ( x ) e si annulla pe x = (icodae che deve essee x > ). ( x ) Un esame immediato del segno confema che si tatta di un minimo. La figua coispondente ha altezza ( x + ) =, metà base ( x x + A ) = e quindi la tangente degli angoli alla base è = gli angoli alla base sono di 60 e il tiangolo è equilateo. ( 1+ sin x) Tigonometicamente, HB = cos x è la metà dell angolo opposto alla base. Si può cecae il minimo dell aea A = HB CH = e CH = ( 1+ sin x) sin x (vedi fig.) dove x (1 sin x) la cui deivata immediata è sin x cos x + (1 + sin x)cos xsin x + (sin x cos x)(1 + sin x) A = si sostituisce cos x con sin x cos x 1 sin x ; dopo iduzioni e accoglimenti il numeatoe si scompone in 1 (1 + sin x )(sin x + sin x 1) - a noi inteessa solo la soluzione sin x = cioè x = 0, essendo x la metà dell angolo opposto alla base si deduce il tiangolo equilateo.. Cono cicolae etto cicoscitto a una sfea I te poblemi fondamentali sono: il cono di volume minimo, di supeficie lateale minima e di supeficie totale minima. Pendiamo sempe x = OC, col limite x. Cono di volume minimo cicoscitto a una sfea Il volume è dato da V = 1 b h essendo b il aggio della cf di base, cioè HB, e h l altezza = CH. Con la soluzione algebica otteniamo V = 1 x + ( x + ) ( ) ( x + ) = x x la cui deivata = ( x + )( x ) ( x ) si annulla pe x =. Lo studio del segno confema che è un minimo. Ezio Foneo Il poblema classico di geometia 14/17
15 Cono di supeficie lateale minima cicoscitto a una sfea La supeficie lateale è il semipodotto della cf di base pe l apotema, cioè la distanza ta vetice e un punto della cf di base: S L = π b a. Anche in questo caso cechiamo la soluzione algebica, pe cui HB = x + x + e BC = a = HC + HB = ( x + ) + = x x x + x [ questo isultato si può dedue anche dalla similitudine ta COT e CHB, pe cui x BC : OC = HB : BC = pec. ] Quindi S L = OC HB x + x x π x. La deivata π x ( x ) x x + = x - vedi figua si annulla pe x = ± ; inteessa solo la soluzione maggioe +, dato il limite x. Lo studio del segno confema che si tatta di un minimo. Cono di supeficie totale minima cicoscitto a una sfea La sup. totale è data da S T = π + π a essendo al solito b b b e a il aggio di base e l apotema, ispettivamente. Indichiamo sempe con il aggio della sfea inscitta nel cono. In base alle fomule calcolate pima, pe cui HB = b e BC = a, abbiamo S T = x + x + π ( + x x x ) ( x + ) = π che, a pate una costante moltiplicativa, x coincide con quella del volume (vedi pima), pe cui il cono cicoscitto di volume minimo è anche quello di supeficie totale minima.. Tapezio isoscele cicoscitto a un cechio In base alla popietà di conguenza dei segmenti di tangente condotti da un punto esteno a una cf, ( AT AM e TD DK ) abbiamo che il lato obliquo è equivalente alla somma delle metà delle basi, pe cui la somma dei lati obliqui è equivalente alla somma delle basi. Quindi il peimeto equivale a 4 lati obliqui. Il tapezio cicoscitto di peimeto e aea minima (le due figue coincidono sempe quando sono cicoscitte) quindi è quello di lato obliquo minimo, che coisponde al caso del quadato (il lato obliquo è sempe maggioe dell altezza del tapezio, e il minimo si ha quando è conguente all altezza, cioè nel caso limite di otogonalità ispetto alle basi). Ezio Foneo Il poblema classico di geometia 15/17
16 Impostazione algebica. Pe calcolae gli elementi della figua, possiamo poe AM = x e DK = y, agionando su due incognite, con i limiti x e 0 y. Essendo il lato AD dato da AD = x + y e da AD = AH + HD, otteniamo ( x + y ) = ( x y ) + 4 x y = y = x [ a questa conclusione possiamo aivae anche applicando il secondo teoema di Euclide al tiangolo AOD, che è ettangolo. Infatti i lati AO e OD sono bisettici degli angoli in A e in D, pe cui la somma degli angoli OAT e ODT è equivalente alla semisomma degli angoli A e D, che è l angolo piatto essendo supplementai ] Quindi possiamo espimee tutti i lati in funzione della semibase maggioe x. Impostazione tigonometica. Possiamo poe x = BAD, con x 90. Patendo dalla costante DH =, otteniamo subito il lato obliquo: 8 AD = p = 4 AD =. Il peimeto è minimo se il denominatoe sin x sin x è massimo, cioè pe x = 90, come visto pima. x 1+ cos x La base maggioe può essee calcolata come cot g =, essendo AO bisettice sin x di BAD, il segmento AH = cotg x. 4. Tapezio isoscele cicoscitto a un semicechio Pe costuie la figua, tacciae la semiciconfeenza di diameto AO, pendendo A a piacee sul polungamento del diameto EF. L intesezione T ta questa semicf e la cf di diameto EF è il vetice etto di un tiangolo ettangolo ATO, quindi OT è al lato obliquo passante pe T. Pe Ezio Foneo Il poblema classico di geometia 16/17
17 completae la figua, costuie l asse del diameto EF, intesecae con la cf, condue pe l intesezione K la paallela al diameto, ecc. Il paameto costante della figua è il aggio = DH. Impostazione algebica - è basata sulla conguenza ta i due tiangoli ettangoli AHD e ATO ( ADH e AOT conguenti peché complementai di DAH che è in comune, AHD ATO, DH OT peché aggi della stessa cf ). Ne segue che il lato obliquo è conguente alla metà AO della base maggioe, mente la base minoe può essee calcolata come diffeenza ta la base maggioe e il doppio della poiezione AH del lato obliquo sulla stessa base maggioe. Ciò suggeisce di pendee come incognita x = AO, pe cui AD = x, AH = x, CD = ( x - x ), con il limite x. Il peimeto è quindi dato da p = 6x - x e l aea da A = ( x - x ) x Il peimeto minimo si ottiene dall equazione - = 0 x =. x 4 L aea minima coisponde invece a x =. Questo valoe numeo coisponde al lato del semiesagono egolae cicoscitto a un cechio, coeentemente con la egola geneale pe la quale il poligono cicoscitto di aea minima è quello egolae infatti, abbiamo visto che la metà 4 della base maggioe equivale al lato obliquo, mente CD = ( ) = ( ) = = AD. Ezio Foneo Il poblema classico di geometia 17/17
Unità Didattica N 27 Circonferenza e cerchio
 56 La ciconfeenza ed il cechio Ciconfeenza e cechio 01) Definizioni e popietà 02) Popietà delle code 03) Ciconfeenza passante pe te punti 04) Code e loo distanza dal cento 05) Angoli, achi e code 06) Mutua
56 La ciconfeenza ed il cechio Ciconfeenza e cechio 01) Definizioni e popietà 02) Popietà delle code 03) Ciconfeenza passante pe te punti 04) Code e loo distanza dal cento 05) Angoli, achi e code 06) Mutua
Equazioni e disequazioni irrazionali
 Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
IL VOLUME DEI SOLIDI Conoscenze
 IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal...e dalla...di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è... di quella sostanza c. Il peso specifico
IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal...e dalla...di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è... di quella sostanza c. Il peso specifico
Lo schema seguente spiega come passare da una equazione all altra e al grafico della circonferenza. Svolgere i calcoli.
 D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
GONIOMETRIA. MISURA DEGLI ANGOLI La misura di un angolo si può esprimere in diversi modi, a seconda dell unità di misura che si sceglie.
 of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
Geometria analitica in sintesi
 punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
AI VERTICI DI UN QUADRATO DI LATO 2L SONO POSTE 4 CARICHE UGUALI Q. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE.
 ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
ELEMENTI DI GEOMETRIA DELLO SPAZIO
 ELEMENTI DI GEOMETRIA DELLO SPAZIO ASSIOMI Lo spazio euclideo è un insieme infinito di elementi (i punti), contiene sottoinsiemi popi ed infiniti (i piani). In ogni piano valgono gli assiomi del piano
ELEMENTI DI GEOMETRIA DELLO SPAZIO ASSIOMI Lo spazio euclideo è un insieme infinito di elementi (i punti), contiene sottoinsiemi popi ed infiniti (i piani). In ogni piano valgono gli assiomi del piano
ELEMENTI DI GEOMETRIA SOLIDA
 POF. IN CEESO.S. EINSEIN EEMENI DI GEOMEI SOID Postulati: ) pe punti dello spazio, non allineati, passa uno e un solo piano; ) una etta passante pe due punti di un piano giace inteamente in quel piano;
POF. IN CEESO.S. EINSEIN EEMENI DI GEOMEI SOID Postulati: ) pe punti dello spazio, non allineati, passa uno e un solo piano; ) una etta passante pe due punti di un piano giace inteamente in quel piano;
Appunti su argomenti monografici per il corso di FM1 Prof. Pierluigi Contucci. Gravità e Teorema di Gauss
 1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
ESERCIZIO n.1. rispetto alle rette r e t indicate in Figura. h t. d b GA#1 1
 Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
Applicazioni della similitudine Unità 2
 OBIETTIVI INTERMEDI DI APPRENDIMENTO (I numei e le lettee indicate a fianco contassegnano le conoscenze, le abilità finali specifiche e quelle tasvesali coelate) Una volta completata l unità, gli allievi
OBIETTIVI INTERMEDI DI APPRENDIMENTO (I numei e le lettee indicate a fianco contassegnano le conoscenze, le abilità finali specifiche e quelle tasvesali coelate) Una volta completata l unità, gli allievi
C8. Teoremi di Euclide e di Pitagora
 8. Teoemi di uclide e di Pitagoa 8.1 igue equiscomponibili ue poligoni sono equiscomponibili se è possibile suddivideli nello stesso numeo di poligoni a due a due conguenti. Il ettangolo e il tiangolo
8. Teoemi di uclide e di Pitagoa 8.1 igue equiscomponibili ue poligoni sono equiscomponibili se è possibile suddivideli nello stesso numeo di poligoni a due a due conguenti. Il ettangolo e il tiangolo
Massimi e minimi con le linee di livello
 Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
Applicazioni della trigonometria alla geometria
 unti di matematica licazioni della tigonometia alla geometia. ea di un tiangolo, note le misue di due lati e quella dell'angolo da essi comeso. TEOREM L'aea di un qualsiasi tiangolo è eguale al semiodotto
unti di matematica licazioni della tigonometia alla geometia. ea di un tiangolo, note le misue di due lati e quella dell'angolo da essi comeso. TEOREM L'aea di un qualsiasi tiangolo è eguale al semiodotto
AUTOVALORI ED AUTOVETTORI DI UNA MATRICE
 AUTOVALORI ED AUTOVETTORI DI UNA MATRICE TEOREMA: Un elemento di K è un autovaloe pe una matice A, di odine n, se e solo se, indicata con I la matice identità di odine n, isulta: det( A I) Il deteminante
AUTOVALORI ED AUTOVETTORI DI UNA MATRICE TEOREMA: Un elemento di K è un autovaloe pe una matice A, di odine n, se e solo se, indicata con I la matice identità di odine n, isulta: det( A I) Il deteminante
MAPPA 8 FIGURE. Area dei poligoni e figure equivalenti. Misura dell estensione superficiale. Il metro quadrato. Figure equivalenti
 Misua de estensione supeficiae L aea è a misua de estensione supeficiae di una figua ispetto a unità di misua fissata. Indiciamo aea con a ettea. Esempio: R MPP 8 u 1 è aea de ettangoo R secondo unità
Misua de estensione supeficiae L aea è a misua de estensione supeficiae di una figua ispetto a unità di misua fissata. Indiciamo aea con a ettea. Esempio: R MPP 8 u 1 è aea de ettangoo R secondo unità
Origami: Geometria con la carta (I)
 Oigami: Geometia con la cata (I) La valenza atistica, ceativa ed estetica dell'oigami, è omai nota a tutti. Il pof. enedetto Scimemi in [ 1] ipota ta l'alto:...l'appoto educativo di giochi e passatempi
Oigami: Geometia con la cata (I) La valenza atistica, ceativa ed estetica dell'oigami, è omai nota a tutti. Il pof. enedetto Scimemi in [ 1] ipota ta l'alto:...l'appoto educativo di giochi e passatempi
Geometria analitica in sintesi
 geometia analitica Geometia analitica in sintesi punti istanza ta ue punti punto meio baicento ta ue punti i un tiangolo i vetici aea i un tiangolo i vetici C B A etta e foma implicita foma esplicita foma
geometia analitica Geometia analitica in sintesi punti istanza ta ue punti punto meio baicento ta ue punti i un tiangolo i vetici aea i un tiangolo i vetici C B A etta e foma implicita foma esplicita foma
Costruzioni di base. Enti geometrici fondamentali. unità 2. Definizioni. Costruzioni geometriche
 unità ostuzioni geometiche ostuzioni di ase nti geometici fondamentali efinizioni Punto nte geometico pivo di dimensioni; è definiile come isultato dell intesezione di due elementi lineai ettilinei o cuvilinei
unità ostuzioni geometiche ostuzioni di ase nti geometici fondamentali efinizioni Punto nte geometico pivo di dimensioni; è definiile come isultato dell intesezione di due elementi lineai ettilinei o cuvilinei
Momenti d'inerzia di figure geometriche semplici
 Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
LIBRO DI TESTO S.Melone, F.Rustichelli Introduzione alla Fisica Biomedica Libreria Scientifica Ragni Ancona, 1998
 LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
Regola di Ruffini - Wikipedia
 Pagina 1 di 7 Regola di Ruffini Da Wikipedia, l'enciclopedia libea. In matematica, la egola di Ruffini pemette la divisione veloce di un qualunque polinomio pe un binomio della foma x a. È stata descitta
Pagina 1 di 7 Regola di Ruffini Da Wikipedia, l'enciclopedia libea. In matematica, la egola di Ruffini pemette la divisione veloce di un qualunque polinomio pe un binomio della foma x a. È stata descitta
Gravitazione. Dati due corpi di massa m 1 e m 2, posti ad una distanza r, tra di essi si esercita una forza attrattiva data in modulo da
 Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Gilda Flaccavento Romano. Geometria e misura. R ealtà e RCS LIBRI EDUCATION SPA. modelli. corso di matematica per la scuola secondaria di primo grado
 Gilda Flaccavento Romano 3b Geometia e misua R ealtà e modelli coso di matematica pe la scuola secondaia di pimo gado RS LIRI EUTIN SP oodinamento editoiale: Giancalo Quadi oodinamento edazionale: Maia
Gilda Flaccavento Romano 3b Geometia e misua R ealtà e modelli coso di matematica pe la scuola secondaia di pimo gado RS LIRI EUTIN SP oodinamento editoiale: Giancalo Quadi oodinamento edazionale: Maia
INDICE. Unità 12 MISURA DELLA CIRCONFERENZA. Unità 13 LO SPAZIO TRIDIMENSIONALE, 51 E AREA DEL CERCHIO, 1 MISURA DELLA CIRCONFERENZA, 2
 INDIE Unità 1 MISUR DELL IRNFERENZ E RE DEL ERHI, 1 Il libo posegue nel D 1.1 MISUR DELL IRNFERENZ, Misua di p, Misua della ciconfeenza, ESERIZI da p. 15 1. MISUR DELL R DI IRNFERENZ, 4 ESERIZI da p. 1
INDIE Unità 1 MISUR DELL IRNFERENZ E RE DEL ERHI, 1 Il libo posegue nel D 1.1 MISUR DELL IRNFERENZ, Misua di p, Misua della ciconfeenza, ESERIZI da p. 15 1. MISUR DELL R DI IRNFERENZ, 4 ESERIZI da p. 1
BOOK IN PROGRESS GEOMETRIA STATISTICA DESCRITTIVA CALCOLO DELLE PROBABILITA INDICE GEOMETRIA
 ITE Enico Tosi OOK IN PROGRESS GEOMETRI STTISTI DESRITTIV LOLO DELLE PROILIT INDIE GEOMETRI PITOLO 1: L GEOMETRI DEL PINO 11 Genealità pag 1 12 ngoli paticolai pag 11 PITOLO 2: POLIGONI E TRINGOLI 21 I
ITE Enico Tosi OOK IN PROGRESS GEOMETRI STTISTI DESRITTIV LOLO DELLE PROILIT INDIE GEOMETRI PITOLO 1: L GEOMETRI DEL PINO 11 Genealità pag 1 12 ngoli paticolai pag 11 PITOLO 2: POLIGONI E TRINGOLI 21 I
Nicola De Rosa maturità 2015
 www.matematicamente.it Nicola De Rosa matuità 5 Esame di stato di istuzione secondaia supeioe Indiizzi: LI SCIENTIFICO LI - SCIENTIFICO - OPZIONE SCIENZE APPLICATE Tema di matematica (Testo valevole anche
www.matematicamente.it Nicola De Rosa matuità 5 Esame di stato di istuzione secondaia supeioe Indiizzi: LI SCIENTIFICO LI - SCIENTIFICO - OPZIONE SCIENZE APPLICATE Tema di matematica (Testo valevole anche
Complementi. 1) Come raggruppare oggetti.
 Complementi. ) Come agguppae oggetti. Quando consideiamo il poblema di agguppae oggetti, in ealtà affontiamo poblemi di tipo assai diveso. A volte dobbiamo distibuie degli oggetti in cete posizioni, tenendo
Complementi. ) Come agguppae oggetti. Quando consideiamo il poblema di agguppae oggetti, in ealtà affontiamo poblemi di tipo assai diveso. A volte dobbiamo distibuie degli oggetti in cete posizioni, tenendo
Geometria analitica: assi e punti
 Geometia analitica: ai e punti itema di ai cateiani monometico otogonale è l oigine degli ai cateiani è l ae delle acie : è l ae delle odinate ditanza ta due punti O(0,0): oigine degli ai cateiani : punto
Geometia analitica: ai e punti itema di ai cateiani monometico otogonale è l oigine degli ai cateiani è l ae delle acie : è l ae delle odinate ditanza ta due punti O(0,0): oigine degli ai cateiani : punto
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA
 Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
Indice. UNITÀ 12 Misura della circonferenza e area del cerchio, 1
 Indice IDEO UNITÀ 1 Misua della ciconfeenza e aea del cechio, 1 1.1 MAPPA 1. 1.3 1.4 1.5 MISURA DELLA IRONERENZA, MISURA DELL ARO DI IRONERENZA, 4 AREA DEI POLIGONI IROSRITTI A UNA IRONERENZA, 5 AREA DEL
Indice IDEO UNITÀ 1 Misua della ciconfeenza e aea del cechio, 1 1.1 MAPPA 1. 1.3 1.4 1.5 MISURA DELLA IRONERENZA, MISURA DELL ARO DI IRONERENZA, 4 AREA DEI POLIGONI IROSRITTI A UNA IRONERENZA, 5 AREA DEL
Campo elettrico e potenziale di un disco uniformemente carico
 Campo elettico e poteniale di un disco unifomemente caico q S densità supeficiale di caica Consideo l anello di aggio e spessoe d calcolo l anello sommo sugli anelli ho due integaioni dq da πd d Σ anello
Campo elettico e poteniale di un disco unifomemente caico q S densità supeficiale di caica Consideo l anello di aggio e spessoe d calcolo l anello sommo sugli anelli ho due integaioni dq da πd d Σ anello
216 Luciano De Menna Corso di Elettrotecnica
 216 Luciano De Menna Coso di Elettotecnica Sulla base delle nozioni intodotte possiamo a questo punto mostae un alto motivo di convenienza dell'uso di sistemi tifasi. Confontiamo due sistemi di alimentazione,
216 Luciano De Menna Coso di Elettotecnica Sulla base delle nozioni intodotte possiamo a questo punto mostae un alto motivo di convenienza dell'uso di sistemi tifasi. Confontiamo due sistemi di alimentazione,
LA CIRCONFERENZA e IL CERCHIO
 LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
Verifica di Matematica sommativa durata della prova : 2 ore. Punt. attr. Problema
 Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
Esercizio 1. Date le rette
 Date le ette Eseciio y : : y a) Scivee le equaioni paametiche delle ette e. b) Dopo ave veificato che le ette ed sono sghembe, tovae l equaione di un piano σ contenente e paallelo a. c) Deteminae le equaioni
Date le ette Eseciio y : : y a) Scivee le equaioni paametiche delle ette e. b) Dopo ave veificato che le ette ed sono sghembe, tovae l equaione di un piano σ contenente e paallelo a. c) Deteminae le equaioni
Circuiti RLC RIASSUNTO: L(r)C serie: impedenza Z(ω) Q valore risposta in frequenza L(r)C parallelo Circuiti risonanti Circuiti anti-risonanti
 icuiti R RIASSUNTO: () seie: impedenza () valoe isposta in fequenza () paallelo icuiti isonanti icuiti anti-isonanti icuito in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un
icuiti R RIASSUNTO: () seie: impedenza () valoe isposta in fequenza () paallelo icuiti isonanti icuiti anti-isonanti icuito in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un
Idraulica Scale di deflusso
 Idaulica Scale di deflusso amando caavetta 31/05/007 1 efinizione La scala di deflusso esplicita il legame che, in un alveo di assegnata pendenza, si istituisce ta potata e tiante idico Questo legame è
Idaulica Scale di deflusso amando caavetta 31/05/007 1 efinizione La scala di deflusso esplicita il legame che, in un alveo di assegnata pendenza, si istituisce ta potata e tiante idico Questo legame è
ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI
 ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI LE RELAZIONI FRA GLI ELEMENTI DI UN TRIANGOLO 1) La somma degli angoli interni di un triangolo è 180 γ Consideriamo il triangolo ABC. Tracciamo la parallela
ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI LE RELAZIONI FRA GLI ELEMENTI DI UN TRIANGOLO 1) La somma degli angoli interni di un triangolo è 180 γ Consideriamo il triangolo ABC. Tracciamo la parallela
Disequazioni. 21.1 Intervalli sulla retta reale
 Disequazioni 1 11 Intevalli sulla etta eale Definizione 11 Dati due numei eali a e b, con a < b, si chiamano intevalli, i seguenti sottoinsiemi di R: a, b) = {x R/a < x < b} intevallo limitato apeto, a
Disequazioni 1 11 Intevalli sulla etta eale Definizione 11 Dati due numei eali a e b, con a < b, si chiamano intevalli, i seguenti sottoinsiemi di R: a, b) = {x R/a < x < b} intevallo limitato apeto, a
ESAME DI STATO LICEO SCIENTIFICO MATEMATICA 2011
 ESAME DI STATO LICEO SCIENTIFICO MATEMATICA PROBLEMA La funzione f ( ) ( )( ) è una funzione dispari di terzo grado Intercetta l asse nei punti ;, ; e ; Risulta f per e per è invece f per e per f ' risulta
ESAME DI STATO LICEO SCIENTIFICO MATEMATICA PROBLEMA La funzione f ( ) ( )( ) è una funzione dispari di terzo grado Intercetta l asse nei punti ;, ; e ; Risulta f per e per è invece f per e per f ' risulta
La legge di Lenz - Faraday Neumann
 1 La legge di Lenz - Faaday Neumann Il flusso del campo magnetico B Pe dae una veste matematica alle conclusioni delle espeienze viste nella lezione pecedente, abbiamo bisogno di definie una nuova gandezza
1 La legge di Lenz - Faaday Neumann Il flusso del campo magnetico B Pe dae una veste matematica alle conclusioni delle espeienze viste nella lezione pecedente, abbiamo bisogno di definie una nuova gandezza
1 I solidi a superficie curva
 1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI
 1 DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI I copi conduttoi sono caatteizzati dal fatto di avee moltissimi elettoni libei di muovesi (elettoni di conduzione). Cosa accade se un copo conduttoe viene caicato
1 DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI I copi conduttoi sono caatteizzati dal fatto di avee moltissimi elettoni libei di muovesi (elettoni di conduzione). Cosa accade se un copo conduttoe viene caicato
BOOK IN PROGRESS MATEMATICA GEOMETRIA PRIMO ANNO TOMO NR. 1
 OOK IN PROGRESS MTEMTI GEOMETRI PRIMO NNO TOMO NR 1 ITIS Majoana indisi (R) IT Tosi usto sizio (V) IT alabetta Soveao (Z) ISISS Scaambine Lecce (LE) ITIS uzzi Pato (PO) ITIS Feais Napoli (N) IT Pacioli
OOK IN PROGRESS MTEMTI GEOMETRI PRIMO NNO TOMO NR 1 ITIS Majoana indisi (R) IT Tosi usto sizio (V) IT alabetta Soveao (Z) ISISS Scaambine Lecce (LE) ITIS uzzi Pato (PO) ITIS Feais Napoli (N) IT Pacioli
SIMULAZIONE - 22 APRILE 2015 - QUESITI
 www.matefilia.it Assegnata la funzione y = f(x) = e x 8 SIMULAZIONE - APRILE 5 - QUESITI ) veificae che è invetibile; ) stabilie se la funzione invesa f è deivabile in ogni punto del suo dominio di definizione,
www.matefilia.it Assegnata la funzione y = f(x) = e x 8 SIMULAZIONE - APRILE 5 - QUESITI ) veificae che è invetibile; ) stabilie se la funzione invesa f è deivabile in ogni punto del suo dominio di definizione,
Problemi di massimo e minimo
 Problemi di massimo e minimo Supponiamo di avere una funzione continua in Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m I problemi di massimo e minimo sono problemi
Problemi di massimo e minimo Supponiamo di avere una funzione continua in Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m I problemi di massimo e minimo sono problemi
Problema Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo.
 SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MODELLI SCHEDA DI LAVORO 1 La siepe Sul eto di una villetta deve essee ealizzato un piccolo giadino ettangolae di m, ipaato da una siepe posta lungo il bodo Dato che un lato del giadino è occupato
REALTÀ E MODELLI SCHEDA DI LAVORO 1 La siepe Sul eto di una villetta deve essee ealizzato un piccolo giadino ettangolae di m, ipaato da una siepe posta lungo il bodo Dato che un lato del giadino è occupato
Il rischio della embolia gassosa. Fsica Medica
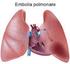 Il ischio della embolia gassosa La espiazione nei subacquei h 1atm 1atm +ρgh Il subacqueo che si tova alla pofondità h deve espiae aia ad una pessione maggioe ispetto a quella atmosfeica ate dell aia espiata
Il ischio della embolia gassosa La espiazione nei subacquei h 1atm 1atm +ρgh Il subacqueo che si tova alla pofondità h deve espiae aia ad una pessione maggioe ispetto a quella atmosfeica ate dell aia espiata
Manuela Zarattini. Matematica. &Realtà. Figure 3. Pearson Italia spa. Edizioni Scolastiche Bruno Mondadori
 Manuela Zaattini M MR Matematica &Realtà & Figue 3 Edizioni Scolastiche Buno Mondadoi Manuela Zaattini MR Matematica & Realtà EN 9788844475 84m-lfgx-llo Figue 3 Edizioni Scolastiche Buno Mondadoi Pogetto
Manuela Zaattini M MR Matematica &Realtà & Figue 3 Edizioni Scolastiche Buno Mondadoi Manuela Zaattini MR Matematica & Realtà EN 9788844475 84m-lfgx-llo Figue 3 Edizioni Scolastiche Buno Mondadoi Pogetto
Lezione 27 - Torsione nelle sezioni circolari ed ellittiche
 Lezione 7 - Tosione nelle sezioni cicolai ed ellittiche ü [A.a. 11-1 : ultima evisione 7 agosto 11] In questa lezione si applicano i isultati della lezione pecedente allo studio di alcune sezione di foma
Lezione 7 - Tosione nelle sezioni cicolai ed ellittiche ü [A.a. 11-1 : ultima evisione 7 agosto 11] In questa lezione si applicano i isultati della lezione pecedente allo studio di alcune sezione di foma
