Compositi: teoria dei laminati
|
|
|
- Fabiana Pieri
- 8 anni fa
- Visualizzazioni
Transcript
1 Compositi: teoria dei laminati Introduzione Il laminato singolo Equazioni costitutive e proprietà Criteri di rottura Fibre fuori asse
2 Introduzione: progettazione Materiali e frazione fibre Spessore laminato Design laminato singolo Dimensione sublaminato Angoli possibili Ranking method Carichi massimi ammissibili Ranking rottura Verifica deformazioni Massime deformazioni Ranking per rigidezza Verifica a rottura Disposizione laminati Specifiche multilaminato
3 Introduzione: design multilaminato Design laminato: Materiali e proprietà (lezioni precedenti Equazioni costitutive (progettazione a rigidezza Criteri di rottura (progettazione a rottura Laminato con fibre fuori asse Multilaminato Equazioni costitutive multilaminato Criteri di rottura Il sublaminato The ranking method Disposizione laminati e regole per un buon design
4 Il laminato singolo: ipotesi di base Lavoriamo in regime lineare elastico: frazione fibre elevata => rottura quando abbiamo rottura delle fibre Sforzo piano: si considera il laminato sottile per cui lo sforzo nella direzione perpendicolare al laminato è trascurabile e il laminato è libero di deformarsi nella direzione perpendicolare Laminato a fibre unidirezionali: le proprietà di base possono essere calcolate o misurate sperimentalmente Regime di piccole deformazioni.
5 Equazioni costitutive laminato Sforzo piano: " z = 0 " = Q# dove: # " = $ " x " y " s ' ( Q = e in maniera esplicita: $ E x ' # x Q yy 0 1"# x # y E # y Q y xx 0 1"# x # y 0 0 E s ( " y = " x E y E x # " = $ $ E x # y E x ' 0 1"# x # y 1"# x # y # Q = x E y E y 0 1"# x # y 1"# x # y 0 0 E s ( " x " y " s ' (
6 Equazioni costitutive laminato Nel caso isotropo otteniamo: $ E #E 0 1"# 2 1"# 2 #E E Q = 0 1"# 2 1"# E 2 1+ # ( esplicitando otteniamo le equazioni per sforzo piano: " x = E ( 1#$ + $ 2 x y " y = E 1#$ 2 y + $ x " s = = G' = ( E 2( 1+ $ s ' (
7 Proprietà per alcuni laminati
8 Resistenze e deformazioni a rottura X = Resistenza longitudinale a trazione X = Resistenza longitudinale a compressione Y = Resistenza trasversale a trazione Y = Resistenza trasversale a compressione S = Resistenza a taglio longitudinale
9 Criterio di rottura lineare Per un laminato ortotropico soggetto a sforzi o deformazioni combinati il criterio di rottura 2- dimensionale lineare si scrive come: " max = R" appl " max = R" appl R viene definito come il rapporto tra lo sforzo (o deformazione a rottura e quello applicato (applicata. Di conseguenza abbiamo: se R=1, si ha rottura se R>1, ad esempio R=2, il fattore di sicurezza è 2, cioè possiamo avere un incremento dello sforzo quasi doppio senza rottura. se R<1 lo sforzo eccede quello a rottura e indica che il laminato è sottodimensionato di 1/R
10 Criterio di rottura quadratico Il criterio lineare non funziona bene nel caso di carichi biassiali. F ij " j + F i #1, i, j = x, y,s dove: F xx = 1 XX', F yy = 1 YY', F ss = 1 S 2 F x = 1 X " 1 X', F y = 1 Y " 1 Y', F s = 0 F xy = F xy * F xx F yy, "1< F xy * <1 F xy * è il termine normalizzato di interazione e deve essere determinato sperimentalmente tramite un test biassiale. Altrimenti va preso con buona approssimazione come -0.5.
11 Caso isotropo Nel caso isotropo si può dimostrare che il criterio equivale a Von Mises. In tal caso abbiamo: X = X'= Y = Y' S = X 3 inoltre poniamo: otteniamo allora: F xy * = "0.5 (" x #" 2 y + 3" 2 s $ X 2 che corrisponde a Von Mises nel caso generale (con x e y assi principali di sforzo, il taglio diventa 0.
12 Elissoidi di rottura nello spazio degli sforzi
13 Criterio di rottura quadratico per gli sforzi Si ha rottura per combinazione di sforzi che escono dagli elissoidi, utilizzando il rapporto R come per il criterio lineare possiamo scrivere: F ij " j R 2 + F i R #1= 0, R $1 Risolviamo l equazione in R: ar 2 + br "1= 0 a = F ij " j, b = F i solo la soluzione positiva è quella corretta: R = " b 2a + # b ( $ 2a' a
14 Criterio quadratico nello spazio delle deformazioni Analogamente agli sforzi: G ij " j + G i #1, i, j = x, y,s dove: G xx = F xx Q 2 2 xx + 2F xy Q xx Q xy + F yy Q xy G yy = F xy Q 2 2 xy + 2F xy Q yy Q xy + F yy Q yy ( + F yy Q yy Q xy 2 G xy = F xx Q xx Q xy + F xy Q xx Q yy + Q xy 2 G ss = 4F ss Q ss G x = F x Q xx + F y Q xy G y = F x Q xy + F y Q yy risolvendo l equazione in R: G ij " j R 2 + G i R #1= 0, R $1 ar 2 + br "1= 0 a = G ij " j, b = G i R = " b 2a + # b ( $ 2a' a
15 Elissoidi di rottura nello spazio delle deformazioni
16 Caso con fibre di Kevlar
17 Laminato con fibre fuori asse Le proprietà, equazioni costitutive etc. si ottengono tramite trasformazione d assi rispetto alle equazioni già viste. Per un laminato con fibre ruotate di un angolo! basta analizzare il laminato uniassiale ruotato di un angolo!. La trasformazione d assi si ottiene dalle relazioni geometriche usuali: " = Q# "' = T" = TQ# "' = TQT T #' "' = Q'#' Q' = TQT T
18 Le matrici di trasformazione La matrice T si scrive in termini dell angolo di rotazione! # m 2 n 2 "2mn ( m = cos" T = n 2 m 2 2mn ( $ mn "mn m 2 " n 2 ' ( n = sin" e la matrice Q in funzione di Q diventa: Q xx Q yy Q xy Q ss Q xx m 4 n 4 2m 2 n 2 4m 2 n 2 Q yy n 4 m 4 2m 2 n 2 4m 2 n 2 Q xy =Q yx m 2 n 2 m 2 n 2 m 4 +n 4-4m 2 n 2 Q ss m 2 n 2 m 2 n 2-2m 2 n 2 (m 2 -n 2 2 Q sx =Q xs m 3 n -mn 3 mn 3 -m 3 n 2(mn 3 -m 3 n Q sy =Q ys mn 3 -m 3 n m 3 n- 2(m 3 n-mn 3
Progettazione laminati
 Progettazione laminati Equazioni costitutive laminato Criteri di rottura Il sublaminato The ranking method Disposizione strati e regole per un buon design Laminated plate theory L ipotesi base della teoria
Progettazione laminati Equazioni costitutive laminato Criteri di rottura Il sublaminato The ranking method Disposizione strati e regole per un buon design Laminated plate theory L ipotesi base della teoria
Micromeccanica e Macromeccanica dei MaterialiCompositi
 Micromeccanica e Macromeccanica dei Materialiompositi orso di Tecnologie dei Materiali non onvenzionali - Prof. Luigi arrino Micromeccanica Micromeccanica La micromeccanica studia le proprietà della singola
Micromeccanica e Macromeccanica dei Materialiompositi orso di Tecnologie dei Materiali non onvenzionali - Prof. Luigi arrino Micromeccanica Micromeccanica La micromeccanica studia le proprietà della singola
17/03/2014. Le prove meccaniche distruttive. Tipologie di deformazione. Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T.
 Le prove meccaniche distruttive Le prove meccaniche distruttive Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T. Editrice, 2008 capitolo 3 Tecnologia meccanica S. Kalpakjian, S. R. Schmid Pearson
Le prove meccaniche distruttive Le prove meccaniche distruttive Sistemi di Produzione D. Antonelli, G. Murari C.L.U.T. Editrice, 2008 capitolo 3 Tecnologia meccanica S. Kalpakjian, S. R. Schmid Pearson
REGOLA DELLE MISCELE, TEORIA DELLA LAMINAZIONE
 REGOLA DELLE MISCELE, TEORIA DELLA LAMINAZIONE Si va ad analizzare la matrice di legame costitutivo che lega le σ con le ε. Si va a considerare il materiale da isotropo a ortotropo ovvero una lamina che
REGOLA DELLE MISCELE, TEORIA DELLA LAMINAZIONE Si va ad analizzare la matrice di legame costitutivo che lega le σ con le ε. Si va a considerare il materiale da isotropo a ortotropo ovvero una lamina che
Proprietà meccaniche dei compositi. Calcolo moduli elastici Caso inclusioni random Fibre unidirezionali Resistenze a rottura Effetto orientazione
 Proprietà meccaniche dei compositi Calcolo moduli elastici Caso inclusioni random Fibre unidirezionali Resistenze a rottura Effetto orientazione Calcolo modulo elastico: inclusioni random Deformazione
Proprietà meccaniche dei compositi Calcolo moduli elastici Caso inclusioni random Fibre unidirezionali Resistenze a rottura Effetto orientazione Calcolo modulo elastico: inclusioni random Deformazione
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
Criteri di Resistenza e Sicurezza
 Criteri di Resistenza e Sicurezza Per uno stato di tensione monoassiale sono sufficienti le due tensioni limiti t e c per delimitare il dominio di crisi. z F z z z t y z x ε z F Teorie di rottura Carichi
Criteri di Resistenza e Sicurezza Per uno stato di tensione monoassiale sono sufficienti le due tensioni limiti t e c per delimitare il dominio di crisi. z F z z z t y z x ε z F Teorie di rottura Carichi
MATERIALI COMPOSITI: comportamento meccanico
 MATERIALI COMPOSITI: comportamento meccanico Materiali tradizionali Proprietà Metalli Ceramiche Polimeri in massa in fibre Resistenza a trazione Rigidezza Tenacità Resistenza all'impatto Limite di fatica
MATERIALI COMPOSITI: comportamento meccanico Materiali tradizionali Proprietà Metalli Ceramiche Polimeri in massa in fibre Resistenza a trazione Rigidezza Tenacità Resistenza all'impatto Limite di fatica
Elementi Costruttivi delle Macchine. Esercizi Resistenza statica -Effetto di intaglio. Politecnico di Torino CeTeM
 E. E. E.3 E.4 E.5 E.6 Un punto di un componente in acciaio 4Cr4 bonificato (R p0, 800 Ma, R m 000-00 Ma) è soggetto allo stato di tensione: xx xy xz 0 0 0 yx yy yz 0 0 0 Ma 0 0 360 zx zy zz Calcolare il
E. E. E.3 E.4 E.5 E.6 Un punto di un componente in acciaio 4Cr4 bonificato (R p0, 800 Ma, R m 000-00 Ma) è soggetto allo stato di tensione: xx xy xz 0 0 0 yx yy yz 0 0 0 Ma 0 0 360 zx zy zz Calcolare il
REGISTRO DELLE LEZIONI 2006/2007. Tipologia. Addì Tipologia. Addì Tipologia
 Introduzione ai contenuti del corso. Descrizione dell'organizzazione del corso e delle modalità di svolgimento delle lezioni e degli esami. Teoria lineare della trave. Ipotesi di base. Problema assiale:
Introduzione ai contenuti del corso. Descrizione dell'organizzazione del corso e delle modalità di svolgimento delle lezioni e degli esami. Teoria lineare della trave. Ipotesi di base. Problema assiale:
Giacomo Sacco Appunti di Costruzioni Edili
 Giacomo Sacco Appunti di Costruzioni Edili Le tensioni dovute a sforzo normale, momento, taglio e a pressoflessione. 1 Le tensioni. Il momento, il taglio e lo sforzo normale sono le azioni che agiscono
Giacomo Sacco Appunti di Costruzioni Edili Le tensioni dovute a sforzo normale, momento, taglio e a pressoflessione. 1 Le tensioni. Il momento, il taglio e lo sforzo normale sono le azioni che agiscono
Comportamento meccanico dei materiali
 Comportamento meccanico dei materiali Riferimento: capitolo 2 del Kalpakjian Importante per comprendere il comportamento dei materiali durante le lavorazioni Introduzione Tensione e compressione Torsione
Comportamento meccanico dei materiali Riferimento: capitolo 2 del Kalpakjian Importante per comprendere il comportamento dei materiali durante le lavorazioni Introduzione Tensione e compressione Torsione
Flessione deviata. A B t mm A 1. x 50 mm y mm x mm y mm
 Esercizio N.1 (pag. 81) La coppia M agisce in un piano verticale passante per l asse baricentrico di una trave la cui sezione trasversale è mostrata in figura. Determinare la tensione nel punto A. Soluzione
Esercizio N.1 (pag. 81) La coppia M agisce in un piano verticale passante per l asse baricentrico di una trave la cui sezione trasversale è mostrata in figura. Determinare la tensione nel punto A. Soluzione
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Calcolo di una trave a C
 Calcolo di una trave a C Analisi matematica e FEM con Abaqus Giacomo Barile 26/01/2015 Calcolo analitico e simulato di una trave a C di differenti materiali (ERGAL e Graphite/Epoxy) sottoposta ad uno sforzo
Calcolo di una trave a C Analisi matematica e FEM con Abaqus Giacomo Barile 26/01/2015 Calcolo analitico e simulato di una trave a C di differenti materiali (ERGAL e Graphite/Epoxy) sottoposta ad uno sforzo
Le piastre:classificazione
 Le piastre 1. piastre sottili h/l= 1/50-1/10 : piastre sottili con rigidezza flessionale che portano distribuzioni di carico bidimensionale prevalentemente attraverso momenti flettenti, momenti torcenti
Le piastre 1. piastre sottili h/l= 1/50-1/10 : piastre sottili con rigidezza flessionale che portano distribuzioni di carico bidimensionale prevalentemente attraverso momenti flettenti, momenti torcenti
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 05/12/2011 Esercizio n 1
 PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 05/1/011 Esercizio n 1 Sia data una sezione di c.a. avente dimensioni 40 x 60 cm. I materiali impiegati sono: a) calcestruzzo Rck=0 N/, b) acciaio tipo B450C.
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 05/1/011 Esercizio n 1 Sia data una sezione di c.a. avente dimensioni 40 x 60 cm. I materiali impiegati sono: a) calcestruzzo Rck=0 N/, b) acciaio tipo B450C.
Teoria Classica della Laminazione
 Teoria Classica della Laminazione Classical Lamination Theor - CLT - Calcolo matrici di rigidezza dei laminati in base alla teoria delle piastre th σ dz { } { } { } κ z + eformazione: [ ] piastra th th
Teoria Classica della Laminazione Classical Lamination Theor - CLT - Calcolo matrici di rigidezza dei laminati in base alla teoria delle piastre th σ dz { } { } { } κ z + eformazione: [ ] piastra th th
Strutture Elastoplastiche sotto carichi ripetuti
 Strutture Elastoplastiche sotto carichi ripetuti Si possono verificare i seguenti casi: -adattamento in campo elastico o shakedown -collasso incrementale o ratchetting - Plasticità alternata, o fatica
Strutture Elastoplastiche sotto carichi ripetuti Si possono verificare i seguenti casi: -adattamento in campo elastico o shakedown -collasso incrementale o ratchetting - Plasticità alternata, o fatica
1 Cambiamenti di riferimento nel piano
 1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
CRITERI DI RESISTENZA DEI MATERIALI
 CRITERI DI RESISTENZA DEI MATERIALI Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
CRITERI DI RESISTENZA DEI MATERIALI Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
LEZIONE 2. MATERIALI E CARICHI DELLA COSTRUZIONE Parte I. I materiali della costruzione
 Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà di Architettura Università degli Studi di Genova LEZIONE 2 MATERIALI E CARICHI DELLA COSTRUZIONE Parte I. I materiali della costruzione
Corso di TECNICA DELLE COSTRUZIONI Chiara CALDERINI A.A. 2007-2008 Facoltà di Architettura Università degli Studi di Genova LEZIONE 2 MATERIALI E CARICHI DELLA COSTRUZIONE Parte I. I materiali della costruzione
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Tipi di flusso e funzioni materiali Caratterizzazione reologica. Romano Lapasin
 Tipi di flusso e funzioni materiali Caratterizzazione reologica Romano Lapasin DICAMP - Università di Trieste Tipi di flusso classificazione in base alle componenti del tensore velocità di deformazione
Tipi di flusso e funzioni materiali Caratterizzazione reologica Romano Lapasin DICAMP - Università di Trieste Tipi di flusso classificazione in base alle componenti del tensore velocità di deformazione
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
CRITERI DI RESISTENZA DEI MATERIALI
 CRTER D RESSTENZA DE MATERAL Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
CRTER D RESSTENZA DE MATERAL Tutti i materiali da costruzione rimangono in campo elastico sino ad una certa entità delle sollecitazioni su di essi agenti. Successivamente, all incrementare dei carichi,
Ricordiamo. 1. Tra le equazioni delle seguenti rette individua e disegna quelle parallele all asse delle ascisse:
 La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
Lezione 17 - Il solido isotropo
 Lezione 17 - Il solido isotropo ü [A.a. 2011-2012 : ultima revisione 23 agosto 2011] Si e' visto che le costanti elastiche previste dalla teoria di Green sono, in generale, 21. Non sembra possibile ridurre
Lezione 17 - Il solido isotropo ü [A.a. 2011-2012 : ultima revisione 23 agosto 2011] Si e' visto che le costanti elastiche previste dalla teoria di Green sono, in generale, 21. Non sembra possibile ridurre
6 Stato Limite Ultimo per tensioni normali
 6 Stato Limite Ultimo per tensioni normali Legami costitutivi non lineari Si considerano i seguenti legami costitutivi non lineari del calcestruzzo e dell acciaio Legame parabola - rettangolo Legame stress
6 Stato Limite Ultimo per tensioni normali Legami costitutivi non lineari Si considerano i seguenti legami costitutivi non lineari del calcestruzzo e dell acciaio Legame parabola - rettangolo Legame stress
PROPRIETÀ MECCANICHE DEI POLIMERI. Proprietà meccaniche
 PROPRIETÀ MECCANICHE DEI POLIMERI Informazioni necessarie per la progettazione di componenti in materiale polimerico: MODULO DI YOUNG (RIGIDEZZA) RESISTENZA ULTIMA DUTTILITÀ / FRAGILITÀ Ricavate da curve
PROPRIETÀ MECCANICHE DEI POLIMERI Informazioni necessarie per la progettazione di componenti in materiale polimerico: MODULO DI YOUNG (RIGIDEZZA) RESISTENZA ULTIMA DUTTILITÀ / FRAGILITÀ Ricavate da curve
3x + x 5x = x = = 4 + 3x ; che equivale, moltiplicando entrambi i membri per 2, a risolvere. 4x + 6 x = 4 + 3x.
 1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
Classificazione sezioni di acciaio e metodi di analisi
 di acciaio e metodi di analisi Maurizio Orlando Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Firenze www.dicea.unifi.it/maurizio.orlando Analisi elasto-plastica Legame costitutivo
di acciaio e metodi di analisi Maurizio Orlando Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Firenze www.dicea.unifi.it/maurizio.orlando Analisi elasto-plastica Legame costitutivo
FINALE: PROVA 1: + = PROVA 2: + =
 SCIENZA DELLE COSTRUZIONI: GES L - Z 2 a PROVA 29/06/2006 Tema C : allievo PROVA 1: + = PROVA 2: + = FINALE: ESERCIZIO 1 (punti 12) La struttura una volta iperstatica di figura è soggetta al carico q,
SCIENZA DELLE COSTRUZIONI: GES L - Z 2 a PROVA 29/06/2006 Tema C : allievo PROVA 1: + = PROVA 2: + = FINALE: ESERCIZIO 1 (punti 12) La struttura una volta iperstatica di figura è soggetta al carico q,
-gdl>gdv il sistema è staticamente labile (trave labile, cioè in grado di muoversi);
 Meccanica a trave Trave in equilibrio con due vincoli I gradi di libertà per un corpo sul piano sono 3, mentre quelli di un corpo nello spazio sono 6. Consideriamo un sistema di riferimento formato da:
Meccanica a trave Trave in equilibrio con due vincoli I gradi di libertà per un corpo sul piano sono 3, mentre quelli di un corpo nello spazio sono 6. Consideriamo un sistema di riferimento formato da:
Resistenza dei materiali
 Scheda riassuntiva capitoli 8-1 Resistenza dei materiali a resistenza dei materiali mette in relazione tra loro i seguenti elementi: Trazione/ Carichi compressione Taglio Flessione Torsione Deformazioni
Scheda riassuntiva capitoli 8-1 Resistenza dei materiali a resistenza dei materiali mette in relazione tra loro i seguenti elementi: Trazione/ Carichi compressione Taglio Flessione Torsione Deformazioni
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta
 Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
Analisi sismica di un sistema lineare viscoso a più gradi di libertà con il metodo dello Spettro di Risposta Prof. Adolfo Santini - Dinamica delle Strutture 1 Analisi sismica con lo spettro di risposta
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
GEOMETRIA ANALITICA 1 IL PIANO CARTESIANO
 GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
Lezione. Tecnica delle Costruzioni
 Lezione Tecnica delle Costruzioni 1 Comportamento e modellazione del cemento armato 2 Modellazione del cemento armato Comportamento del cemento armato Il comportamento del cemento armato dipende dalle
Lezione Tecnica delle Costruzioni 1 Comportamento e modellazione del cemento armato 2 Modellazione del cemento armato Comportamento del cemento armato Il comportamento del cemento armato dipende dalle
Sollecitazioni delle strutture
 Sollecitazioni delle strutture I pilastri e i muri portanti sono tipicamente sollecitati a compressione Le travi e i solai sono sollecitati a flessione L indeformabilità di questi elementi costruttivi
Sollecitazioni delle strutture I pilastri e i muri portanti sono tipicamente sollecitati a compressione Le travi e i solai sono sollecitati a flessione L indeformabilità di questi elementi costruttivi
Tipologie di murature portanti
 Tipologie di murature portanti Le murature costituite dall assemblaggio organizzato ed efficace di elementi e malta possono essere a singolo paramento, se la parete è senza cavità o giunti verticali continui
Tipologie di murature portanti Le murature costituite dall assemblaggio organizzato ed efficace di elementi e malta possono essere a singolo paramento, se la parete è senza cavità o giunti verticali continui
INDICE. Pag. STRUTTURA IN ELEVAZIONE
 INDICE STRUTTURA IN ELEVAZIONE Pag. 1. Considerazioni preliminari 9 1.1. Descrizione generale dell opera 9 1.2. Schema strutturale 9 1.3. Durabilità strutturale 10 1.4. Criteri di calcolo 11 1.4.1. Combinazione
INDICE STRUTTURA IN ELEVAZIONE Pag. 1. Considerazioni preliminari 9 1.1. Descrizione generale dell opera 9 1.2. Schema strutturale 9 1.3. Durabilità strutturale 10 1.4. Criteri di calcolo 11 1.4.1. Combinazione
1 Equilibrio statico nei corpi deformabili
 Equilibrio statico nei corpi deformabili Poiché i materiali reali non possono considerarsi rigidi, dobbiamo immaginare che le forze esterne creino altre forze interne che tendono ad allungare (comprimere)
Equilibrio statico nei corpi deformabili Poiché i materiali reali non possono considerarsi rigidi, dobbiamo immaginare che le forze esterne creino altre forze interne che tendono ad allungare (comprimere)
Risoluzioni di alcuni esercizi
 Risoluzioni di alcuni esercizi Reti topografiche, trasformazioni di coordinate piane In una poligonale piana il punto è nell origine delle coordinate, l angolo (in verso orario fra il semiasse positivo
Risoluzioni di alcuni esercizi Reti topografiche, trasformazioni di coordinate piane In una poligonale piana il punto è nell origine delle coordinate, l angolo (in verso orario fra il semiasse positivo
Statica delle murature
 Statica delle murature Corso di Laurea Specialistica in Ingegneria Edile - A.A. 2006-2007 Università degli Studi di Cagliari Prof. ing. Antonio Cazzani [email protected] http://www.ing.unitn.it/~cazzani/didattica/sdm
Statica delle murature Corso di Laurea Specialistica in Ingegneria Edile - A.A. 2006-2007 Università degli Studi di Cagliari Prof. ing. Antonio Cazzani [email protected] http://www.ing.unitn.it/~cazzani/didattica/sdm
X = x + 1. X = x + 1
 CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
Teoria Classica della Laminazione
 Teoria Classica della Laminazione Classical Lamination Theor - CLT { } { k } Procedura Inversa : Analisi del Laminato 1) Noto il vettore delle forze applicate si possono calcolare le deformazioni generalizzate
Teoria Classica della Laminazione Classical Lamination Theor - CLT { } { k } Procedura Inversa : Analisi del Laminato 1) Noto il vettore delle forze applicate si possono calcolare le deformazioni generalizzate
La deformazione plastica. La deformazione plastica. Lavorazioni per deformazione. Il processo di laminazione. Estrusione e trafilatura La forgiatura
 a deformazione plastica a deformazione plastica avorazioni per deformazione Estrusione e trafilatura a forgiatura a formatura della lamiera 006 Politecnico di Torino 1 Obiettivi della lezione Evidenziare
a deformazione plastica a deformazione plastica avorazioni per deformazione Estrusione e trafilatura a forgiatura a formatura della lamiera 006 Politecnico di Torino 1 Obiettivi della lezione Evidenziare
ESERCITAZIONE SUL CRITERIO
 TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE SUL CRITERIO DI JUVINALL Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 IL CRITERIO DI JUVINALL La formulazione del criterio
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CLASSE 3 A APPUNTI DAL CORSO DI COSTRUZIONI. Diagrammi delle sollecitazioni ESERCIZI SVOLTI IN AULA
 the design of he Forth Bridge (Scotland) 1883-1890 by Sir John Fowler and Sir Benjamin Baker Nessun effetto è in natura sanza ragione; intendi la ragione e non ti bisogna sperienzia. Leonardo da Vinci
the design of he Forth Bridge (Scotland) 1883-1890 by Sir John Fowler and Sir Benjamin Baker Nessun effetto è in natura sanza ragione; intendi la ragione e non ti bisogna sperienzia. Leonardo da Vinci
Francesco Zumbo
 La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
~ E 2 (R) si determini l equazione cartesiana del
 In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO
 Parte da stralciare portandola a me tematica Parte da stralciare portandola a me tematica COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO LEZIONE ARGOMENTI note 1. Introduzione Presentazione del corso 2. Cenni
Parte da stralciare portandola a me tematica Parte da stralciare portandola a me tematica COSTRUZIONI IN CEMENTO ARMATO PROF.RIZZO LEZIONE ARGOMENTI note 1. Introduzione Presentazione del corso 2. Cenni
Teoria generale delle coniche 1 / 17
 Teoria generale delle coniche 1 / 17 Introduzione 2 / 17 Una conica in R 2 è il luogo di punti γ definito da un equazione di secondo grado in x,y, cioè γ : a 11 x 2 + 2a 12 xy+a 22 y 2 + 2a 13 x+2a 23
Teoria generale delle coniche 1 / 17 Introduzione 2 / 17 Una conica in R 2 è il luogo di punti γ definito da un equazione di secondo grado in x,y, cioè γ : a 11 x 2 + 2a 12 xy+a 22 y 2 + 2a 13 x+2a 23
4.11 Massimi e minimi relativi per funzioni di più variabili
 5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
Le unioni. 5 L acciaio 5.3 Strutture in acciaio. Unioni con chiodi. Unioni con perni. Unioni con bulloni
 1 Le unioni Unioni con chiodi È il sistema di collegamento più antico, ma è in disuso in quanto sostituito dalle unioni bullonate o saldate, per cui si può ritrovare solo su vecchie strutture in acciaio.
1 Le unioni Unioni con chiodi È il sistema di collegamento più antico, ma è in disuso in quanto sostituito dalle unioni bullonate o saldate, per cui si può ritrovare solo su vecchie strutture in acciaio.
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
PROPRIETÀ MECCANICHE DEI MATERIALI
 PROPRIETÀ MECCANICHE DEI MATERIALI Il comportamento meccanico di un materiale rappresenta la risposta ad una forza o ad un carico applicato 1. Comportamento elastico 2. Comportamento plastico 3. Comportamento
PROPRIETÀ MECCANICHE DEI MATERIALI Il comportamento meccanico di un materiale rappresenta la risposta ad una forza o ad un carico applicato 1. Comportamento elastico 2. Comportamento plastico 3. Comportamento
Coniche - risposte 1.9
 Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Problema. caso uniassiale prova di trazione. caso multiassiale (carico generico)
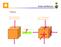 Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Unità Didattica N 9 : La parabola
 0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
MOMENTI DI INERZIA PER CORPI CONTINUI
 MOMENTI D INERZIA E PENDOLO COMPOSTO PROF. FRANCESCO DE PALMA Indice 1 INTRODUZIONE -------------------------------------------------------------------------------------------------------------- 3 2 MOMENTI
MOMENTI D INERZIA E PENDOLO COMPOSTO PROF. FRANCESCO DE PALMA Indice 1 INTRODUZIONE -------------------------------------------------------------------------------------------------------------- 3 2 MOMENTI
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI
 LEZIONI N 32 E 33 COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI Prima di addentrarci nei dettagli della teoria tecnica delle costruzioni di cemento armato, è utile richiamare
LEZIONI N 32 E 33 COMPORTAMENTO SPERIMENTALE DI TRAVI DI C.A. E RELATIVI METODI DI ANALISI Prima di addentrarci nei dettagli della teoria tecnica delle costruzioni di cemento armato, è utile richiamare
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Indice I vettori Geometria delle masse
 Indice 1 I vettori 1 1.1 Vettori: definizioni................................ 1 1.2 Componenti scalare e vettoriale di un vettore secondo una retta orientata. 2 1.3 Operazioni di somma, differenza tra
Indice 1 I vettori 1 1.1 Vettori: definizioni................................ 1 1.2 Componenti scalare e vettoriale di un vettore secondo una retta orientata. 2 1.3 Operazioni di somma, differenza tra
ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI. (Visione 3D)
 ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI () Structure From Motion Date m immagini di n punti 3D (fissi) Stimare le m matrici di proiezione P i e gli n vettori X j date le mn corrispondenze x ij SFM
ESTRAZIONE DI DATI 3D DA IMMAGINI DIGITALI () Structure From Motion Date m immagini di n punti 3D (fissi) Stimare le m matrici di proiezione P i e gli n vettori X j date le mn corrispondenze x ij SFM
LA PARABOLA E LA SUA EQUAZIONE
 LA PARABOLA E LA SUA EQUAZIONE Prof. Giovanni Ianne CHE COS È LA PARABOLA DEFINIZIONE Parabola Scegliamo sul piano un punto F e una retta d. Possiamo tracciare sul piano i punti equidistanti da F e da
LA PARABOLA E LA SUA EQUAZIONE Prof. Giovanni Ianne CHE COS È LA PARABOLA DEFINIZIONE Parabola Scegliamo sul piano un punto F e una retta d. Possiamo tracciare sul piano i punti equidistanti da F e da
CONTROLLI AUTOMATICI Ingegneria Gestionale ANALISI ARMONICA
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANALISI ARMONICA Ing. Federica Grossi Tel. 059 2056333 e-mail: [email protected]
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANALISI ARMONICA Ing. Federica Grossi Tel. 059 2056333 e-mail: [email protected]
Risoluzione di sistemi lineari sparsi e di grandi dimensioni
 Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
LEZIONE N 13 LA VERIFICA ALLO SLU DELLE TRAVI DI ACCIAIO
 LEZIOE 13 LA ERIFICA ALLO SLU DELLE TRAI DI ACCIAIO Identificata la classe cui appartiene l asta, la modalità di verifica dell asta dipende dalla classe del profilato. Se il profilato appartiene alle classi
LEZIOE 13 LA ERIFICA ALLO SLU DELLE TRAI DI ACCIAIO Identificata la classe cui appartiene l asta, la modalità di verifica dell asta dipende dalla classe del profilato. Se il profilato appartiene alle classi
per i tuoi acquisti di libri, banche dati, riviste e software specializzati
 1. STRUTTURA DELL'EC2 - Introduzione - Scopo dell'ec2 - "Struttura" dell'ec2 - Presupposti fondamentali 2. BASI DEL PROGETTO - Requisiti fondamentali - Stati limite - definizioni - Valori caratteristici
1. STRUTTURA DELL'EC2 - Introduzione - Scopo dell'ec2 - "Struttura" dell'ec2 - Presupposti fondamentali 2. BASI DEL PROGETTO - Requisiti fondamentali - Stati limite - definizioni - Valori caratteristici
Risoluzione delle Piastre Le piastre sottili in regime elastico
 Corso di rogetto di Strutture OTENZA, a.a. 1 13 Risoluione delle iastre Le piastre sottili in regime elastico Dott. arco VONA DiSGG, Università di Basilicata [email protected] http://www.unibas.it/utenti/vona/
Corso di rogetto di Strutture OTENZA, a.a. 1 13 Risoluione delle iastre Le piastre sottili in regime elastico Dott. arco VONA DiSGG, Università di Basilicata [email protected] http://www.unibas.it/utenti/vona/
Elementi finiti solidi
 Esercitazioni del corso di Costruzione di Macchine 2 e Progettazione FEM a cura dell ing. Francesco Villa Elementi finiti solidi Costruzione di Macchine 2 e Progettazione FEM Prof. Sergio Baragetti Dalmine
Esercitazioni del corso di Costruzione di Macchine 2 e Progettazione FEM a cura dell ing. Francesco Villa Elementi finiti solidi Costruzione di Macchine 2 e Progettazione FEM Prof. Sergio Baragetti Dalmine
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Il modello di trave adottato dal Saint-Venant si basa sulle seguenti ipotesi:
 IL PROBLEM DEL DE SINT-VENNT Il problema del De Saint-Venant è un particolare problema di equilibrio elastico di notevole interesse applicativo, potendosi considerare alla base della teoria tecnica delle
IL PROBLEM DEL DE SINT-VENNT Il problema del De Saint-Venant è un particolare problema di equilibrio elastico di notevole interesse applicativo, potendosi considerare alla base della teoria tecnica delle
Lezione Il calcestruzzo armato I
 Lezione Il calcestruzzo armato I Sommario Il calcestruzzo armato Il comportamento a compressione Il comportamento a trazione Il calcestruzzo armato Il cemento armato Il calcestruzzo armato Il calcestruzzo
Lezione Il calcestruzzo armato I Sommario Il calcestruzzo armato Il comportamento a compressione Il comportamento a trazione Il calcestruzzo armato Il cemento armato Il calcestruzzo armato Il calcestruzzo
NYLON-CARBON DUREZZA & TRAZIONE
 NYLON-CARBON DUREZZA & TRAZIONE D R. F L A V I A N A C A L I G N A NO D R. M A S S I M O L O R U S S O D R. I G N A Z I O R O P P O L O N Y LO N - C A R BON PROVE DI DUREZZA E DI TRAZIONE INTRODUZIONE
NYLON-CARBON DUREZZA & TRAZIONE D R. F L A V I A N A C A L I G N A NO D R. M A S S I M O L O R U S S O D R. I G N A Z I O R O P P O L O N Y LO N - C A R BON PROVE DI DUREZZA E DI TRAZIONE INTRODUZIONE
NUMERI COMPLESSI Esercizi svolti. d) (1 i) 3. b) (1 + i)(1 i)(1 + 3 i) c) 1 i 1
 Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
Calcolare le seguenti potenze di i: NUMERI COMPLESSI Esercizi svolti a) i b) i 7 c) i d) i e) i f) i 9 Semplificare le seguenti espressioni: a) i) i i) b) + i) i) + ) 0 i c) i) i) i) d) i) Verificare che
4 SOLLECITAZIONI INDOTTE. 4.1 Generalità
 4 SOLLECITAZIONI INDOTTE 4.1 Generalità Le azioni viste inducono uno stato pensionale interno alla struttura e all edificio che dipende dalla modalità con cui le azioni si esplicano. Le sollecitazioni
4 SOLLECITAZIONI INDOTTE 4.1 Generalità Le azioni viste inducono uno stato pensionale interno alla struttura e all edificio che dipende dalla modalità con cui le azioni si esplicano. Le sollecitazioni
TRASFORMAZIONI GEOMETRICHE
 TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
TRASFORMAZIONI GEOMETRICHE Def. Una trasformazione geometrica T tra i punti di un piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e un solo punto P' appartenente al piano
ẋ 1 = 2x 1 + (sen 2 (x 1 ) + 1)x 2 + 2u (1) y = x 1
 Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
29. Mezzi elastici RELAZIONE SFORZO-DEFORMAZIONE
 29. Mezzi elastici I mezzi continui solidi sono caratterizzati da piccole deformazioni, che consentono di stabilire una relazione lineare tra sforzo e deformazione nota come legge di Hook. Linearizzando
29. Mezzi elastici I mezzi continui solidi sono caratterizzati da piccole deformazioni, che consentono di stabilire una relazione lineare tra sforzo e deformazione nota come legge di Hook. Linearizzando
SCIENZA DELLE COSTRUZIONI: GES L - Z 2 a PROVA 27/06/2005 Tema G : allievo
 SCIENZA DELLE COSTRUZIONI: GES L - Z 2 a PROVA 27/06/2005 Tema G : allievo EI, ma deformabile termicamente; le variazioni termiche nei 2 tratti sono opposte di segno, nulle entrambe lungo la linea d'assi.
SCIENZA DELLE COSTRUZIONI: GES L - Z 2 a PROVA 27/06/2005 Tema G : allievo EI, ma deformabile termicamente; le variazioni termiche nei 2 tratti sono opposte di segno, nulle entrambe lungo la linea d'assi.
