Meccanica. 3. Elementi di Analisi Vettoriale. Domenico Galli. Dipartimento di Fisica e Astronomia.
|
|
|
- Leopoldo Corsi
- 6 anni fa
- Visualizzazioni
Transcript
1 Meccanica 3. Elementi di Analisi Vettoriale Domenico Galli Dipartimento di Fisica e Astronomia 5 maggio 2017
2 Traccia 1. Vettori Variabili 2. Derivate e Integrali 3. Derivate dei Versori 4. Spostamento Elementare 5. Aree e Volumi Elementari 6. Operatori Differenziali 2
3 Vettori Dipendenti da un Parametro Uno scalare fisico (p. es. la temperatura) può dipendere da un parametro s (per esempio il tempo o la coordinata intrinseca). In tal caso la variazione è descritta da una funzione scalare del parametro: f : s [ R] f (s) R Analogamente un vettore fisico (p. es. la velocità) può dipendere da un parametro s (per esempio il tempo o la coordinata intrinseca). In questo caso la variazione è descritta da una funzione vettoriale del parametro: v : s [ R] v (s) V 3
4 Vettori Dipendenti dal Punto di Applicazione e Campi Vettoriali Uno scalare fisico (p. es. la temperatura) può variare con la posizione P (x, y, z) nello spazio. In tal caso la variazione è descritta da un campo scalare (ovvero da una funzione scalare delle 3 coordinate spaziali): f : P î R 3ó f (P ) R Analogamente un vettore fisico (p. es. la velocità) può variare con la posizione P (x, y, z) nello spazio. In questo caso la variazione è descritta da un campo vettoriale (ovvero da una funzione vettoriale delle 3 coordinate spaziali): v : P î R 3ó v (P ) V campo vettoriale della velocità del vento 4
5 Derivata di un Vettore Dato un vettore v(s) dipendente in modo continuo da un parametro s (p. es. il tempo), si definisce derivata del vettore v(s) rispetto alla variabile s il limite del rapporto incrementale: d v(s) ds v = lim s 0 1 s = lim s 0 v(s + s) v(s) s = lim s 0 s [ v(s + s) v(s)] Essendo una moltiplicazione scalare tra la differenza v(s + s) v(s) di due vettori (che è un vettore) e lo scalare 1 s, la derivata di un vettore è un vettore. La direzione della derivata d v(s) ds, in generale, è diversa dalla direzione di v(s). = 5
6 Regole di Derivazione dei Vettori Per i vettori valgono le seguenti regole di derivazione: d Ä ä a ± d a b = dt dt ± d b dt d dα (α a) = a + αd a dt dt dt d Ä ä d a a b = dt dt b + a d b dt d Ä ä a d a b = dt dt b + a d b dt Le derivate dei vettori possono essere effettuate mediante le espressioni cartesiane: d v dt = dv x dt î + dv y dt ĵ + dv z dt ˆk essendo i versori cartesiani {î, ĵ, ˆk} costanti. { α R a, b V 6
7 Funzione Primitiva o Integrale Indefinito Data una funzione scalare: f s [ R] f (s) R si definisce funzione primitiva o integrale indefinito della funzione f la funzione F tale che f sia la derivata di F : F = f (s) ds f = df ds Analogamente, data una funzione vettoriale: s [ R] v v (s) V si definisce funzione primitiva o integrale indefinito della funzione v la funzione w tale che v sia la derivata di w: w = v (s) ds v = d w ds 7
8 Funzione Primitiva o Integrale Indefinito (II) La funzione primitiva (o integrale indefinito) si può calcolare mediante le espressioni cartesiane: v (s) = v x (s) î + v y (s) ĵ + v z (s) ˆk v (s) ds = î v x (s) ds + ĵ v y (s) ds + ˆk v z (s) ds 8
9 Derivate Parziali Data una funzione scalare di più variabili f (x, y, z), si definiscono derivate parziali i limiti (se esistono): f f (x + x, y, z) f (x, y, z) (x, y, z) = lim x x 0 x f f (x, y + y, z) f (x, y, z) (x, y, z) = lim y y 0 y f f (x, y, z + z) f (x, y, z) (x, y, z) = lim z z 0 z Esempio: f (x, y, z) = xy 2 sin z f x (x, y, z) = y2 sin z f (x, y, z) = 2xy sin z y f z (x, y, z) = xy2 cos z 9
10 Derivata Parziale e Derivata Totale La derivata totale è diversa dalla derivata parziale se esiste una dipendenza funzionale tra le variabili. Esempio: Funzione di 2 variabili; una delle due variabili è funzione dell altra: f (x, y) = x 2 y 2 y = 2x Le derivate parziali rispetto a una variabile sono effettuate considerando le altre variabili come se fossero costanti: f x = f 2xy2, y = 2x2 y La derivata totale rispetto a x si effettua considerando la dipendenza funzionale di y da x: f (x, y (x)) = x 2 y 2 (x) = x 2 (2x) 2 = 4x 4 df dx = 16x3 f x 10
11 Derivata Parziale e Derivata Totale (II) Esempio: Si osservi che in questo esempio: f (x, y) = x 2 y 2 y = 2x vale la relazione: df dx = f x + f y Infatti: f x + f y dy dx dy dx = 2xy2 + ( 2x 2 y ) 2 = 2xy 2 + 4x 2 y = 2x (2x) 2 + 4x 2 (2x) = = 8x 3 + 8x 3 = 16x 3 = df dx 11
12 Derivate dei Versori della Base Cartesiana Rispetto alle Coordinate Cartesiane La base cartesiana è globale: I versori non dipendono dalle coordinate: î x = 0, ĵ x = 0, ˆk x = 0, î y = 0, ĵ y = 0, ˆk y = 0, î z = 0, ĵ z = 0, ˆk z = 0. 12
13 Derivate dei Versori della Base Cilindrica Rispetto alle Coordinate Cilindriche La base cilindrica è locale: Alcuni versori dipendono dalle coordinate: î r (ϕ) = 0, r î ϕ (ϕ) = 0, r ˆk r = 0, î r (ϕ) ϕ = î ϕ, î ϕ (ϕ) ϕ = î r, ˆk ϕ = 0, î r (ϕ) = 0, z î ϕ (ϕ) = 0, z ˆk z = 0. parallelo 13
14 Derivate dei Versori della Base Cilindrica Rispetto alle Coordinate Cilindriche (II) Infatti: î r (ϕ) = (cos ϕ) î + (sin ϕ) ĵ î ϕ (ϕ) = (sin ϕ) î + (cos ϕ) ĵ ˆk = ˆk Quindi: î r ϕ = (sin ϕ) î + (cos ϕ) ĵ = î ϕ î ϕ ϕ = (cos ϕ) î (sin ϕ) ĵ = î r parallelo 14
15 Derivate dei Versori della Base Intrinseca Rispetto alla Coordinata Intrinseca La base intrinseca è locale: In generale i versori dipendono dalla coordinata s: dˆt(s) = κ ˆn ds dˆn(s) = κ ˆt + τ ds ˆb dˆb(s) = τ ˆn ds (formule di Frenet-Serret). Infatti, per quanto riguarda la I si ha: ˆn = ρ dˆt ds dˆt ds = 1 ˆn = κ ˆn ρ ˆb 15
16 Derivate dei Versori della Base Intrinseca Rispetto alla Coordinata Intrinseca (II) Per dimostrare la III, utilizziamo la scomposizione di un generico vettore in coordinate intrinseche: v = Ä v ˆt ä ˆt + Ä v ˆn ä ˆn + Ä v ˆb ä ˆb applicandola a v = dˆb ds ( ) ( : ) dˆb dˆb dˆb ds = ds ˆt ˆt + ds ˆn ˆn + ( ) dˆb ds ˆb ˆb Calcoliamo i 3 termini tra parentesi. Il 1 o si scrive: ï dˆb d ds ˆt = Ĉt ˆn äò ñ dˆt ˆt = ds ds ˆn + ˆt dˆn ô ˆt = ds ï = (κˆn) ˆn + ˆt dˆn ò ï ˆt = κ (ˆn ˆn) + ˆt dˆn ò ˆt = ds ds Å = ˆt dˆn ã ˆt = Ĉt ˆt ä dˆn ds ds = 0 ˆb 16
17 Derivate dei Versori della Base Intrinseca Rispetto alla Coordinata Intrinseca (III) Il 2 o termine tra parentesi si ricava dalla definizione di torsione: τ = ˆn dˆb dˆb ˆn = τ ds ds Il 3 o termine tra parentesi si ricava dalla relazione di ortonormalità: ˆb ˆb = 1 d Ĉb ˆbä = 0 ds dˆb ds ˆb + ˆb dˆb ds = 0 2 dˆb ds ˆb = 0 dˆb ds ˆb = 0 ˆb 17
18 Derivate dei Versori della Base Intrinseca Rispetto alla Coordinata Intrinseca (IV) Mettendo insieme i 3 termini della III avremo quindi: ( ) ( ) ( ) dˆb dˆb dˆb dˆb ds = ds ˆt ˆt + ds ˆn ˆn + ds ˆb ˆb = = 0 ˆt τ ˆn + 0 ˆb = τ ˆn Dimostriamo infine la II: dˆn ds = d Ĉb ˆt ä = dˆb ds ds ˆt + ˆb dˆt ds = = ( τ ˆn) ˆt + ˆb (κ ˆn) = = τ Ĉn ˆt ä + κ Ĉb ˆn ä = = τ Ä ˆb ä + κ Ä ˆt ä = κ ˆt + τ ˆb ˆb 18
19 Il Vettore Spostamento Elementare Il vettore spostamento elementare o spostamento infinitesimo d r: È la variazione elementare o infinitesima del vettore posizionale, Ovvero è il differenziale del vettore posizionale. Le sue componenti, rispetto a una prefissata base di versori: Sono gli spostamenti infinitesimi nelle direzioni orientate dei versori della base. 19
20 Il Vettore Spostamento Elementare nella Base Cartesiana Nella base cartesiana si ha: d r = dx î + dy ĵ + dz ˆk,» d r = (dx) 2 + (dy) 2 + (dz) 2 20
21 Il Vettore Spostamento Elementare nella Base Cilindrica Nella base cilindrica si ha: d r = dr î r + r dϕ î ϕ + dz ˆk» d r = (dr) 2 + r 2 (dϕ) 2 + (dz) 2 d r a primo membro è il vettore spostamento elementare; dr a secondo membro è la variazione della coordinata cilindrica r. 21
22 Il Vettore Spostamento Elementare nella Base Sferica Nella base sferica si ha: d r = dρ î ρ + ρ dθ î θ + ρ (sin θ) dϕ î ϕ d r = (dρ) 2 + ρ 2 (dθ) 2 + ρ Ä 2 sin 2 θ ä (dϕ) 2 22
23 Il Vettore Spostamento Elementare nella Base Intrinseca Nella base intrinseca si ha: d r = ds ˆt d r = ds ˆb 23
24 Aree Elementari in Coordinate Cartesiane Dalle componenti dello spostamento elementare nella base cartesiana possiamo costruire le seguenti tre aree elementari giacenti sui piani perpendicolari ai versori cartesiani î, ĵ e ˆk: d r = dx î + dy ĵ + dz ˆk quindi: ds x = dy dz ds y = dz dx ds z = dx dy 24
25 Aree Elementari in Coordinate Cilindriche Dalle componenti dello spostamento elementare nella base cilindrica possiamo costruire le seguenti tre aree elementari giacenti sui piani perpendicolari ai versori cilindrici î r, î ϕ e ˆk: d r = dr î r + r dϕ î ϕ + dz ˆk quindi: ds r = r dϕ dz ds ϕ = dr dz ds z = r dr dϕ 25
26 Aree Elementari in Coordinate Sferiche Dalle componenti dello spostamento elementare nella base sferica possiamo costruire le seguenti tre aree elementari giacenti sui piani perpendicolari ai versori sferici î ρ, î θ e î ϕ : d r = dρ î ρ + ρ dθ î θ + ρ (sin θ) dϕ î ϕ quindi: ds ρ = ρ 2 (sin θ) dθ dϕ ds θ = ρ (sin θ) dρ dϕ ds ϕ = ρ dρ dθ 26
27 Volume Elementare in Coordinate Cartesiane Dalle componenti dello spostamento elementare nella base cartesiana possiamo costruire il volume elementare espresso in coordinate cartesiane: d r = dx î + dy ĵ + dz ˆk quindi: dv = dx dy dz 27
28 Volume Elementare in Coordinate Cilindriche Dalle componenti dello spostamento elementare nella base cilindrica possiamo costruire il volume elementare espresso in coordinate cilindriche: d r = dr î r + r dϕ î ϕ + dz ˆk quindi: dv = r dr dϕ dz 28
29 Volume Elementare in Coordinate Sferiche Dalle componenti dello spostamento elementare nella base sferica possiamo costruire il volume elementare espresso in coordinate sferiche: d r = dρ î ρ + ρ dθ î θ + ρ (sin θ) dϕ î ϕ quindi: dv = ρ 2 (sin θ) dρ dθ dϕ 29
30 Il Simbolo Nabla Il simbolo nabla, che si indica con il simbolo, è un operatore differenziale vettoriale formale che in una base di versori cartesiana {î, ĵ, ˆk} si rappresenta simbolicamente come: = î x + ĵ y + ˆk z L applicazione del simbolo nabla a campi scalari e vettoriali produce gli operatori gradiente, divergenza e rotore : f gradiente v divergenza v rotore 30
31 L Operatore Gradiente Consideriamo una funzione scalare della posizione P : f = f (P ) = f (x, y, z) Si definisce l operatore gradiente come: f = î x + ĵ y + ˆk z f = î f x + ĵ f f + ˆk y z f = grad f = î f x + ĵ f f + ˆk y z L operatore gradiente si applica a una funzione scalare; il risultato è un vettore: P î R 3ó f f (P ) R P î R 3ó f Ä ä f (P ) V 31
32 L Operatore Gradiente (II) Esempio: Data la funzione scalare: f (x, y, z) = x 2 + y 2 + z 2 + 2xy R il gradiente è la funzione vettoriale: Ä ä f f (x, y, z) = î x + ĵ f f + ˆk y z = = 2 (x + y) î + 2 (x + y) ĵ + 2z ˆk V 32
33 L Operatore Divergenza Consideriamo una funzione vettoriale della posizione P : v = v (P ) = v (x, y, z) = v x (x, y, z) î + v y (x, y, z) ĵ + v z (x, y, z) ˆk Si definisce l operatore divergenza come: v = î x + ĵ y + ˆk z Äv v x x î + v y ĵ + v z ˆkä = x + v y y + v z z v = div v = v x x + v y y + v z z L operatore divergenza si applica a una funzione vettoriale; il risultato è uno scalare: P î R 3ó v v (P ) V P î R 3ó v Ä v ä (P ) R 33
34 L Operatore Divergenza (II) Esempio: Data la funzione vettoriale: v (x, y, z) = ( x 2 + y 2) î + ( x 2 + z 2) ĵ + z ˆk V la divergenza è la funzione scalare: Ä ä v x v (x, y, z) = x + v y y + v z z = = 2x + 1 R 34
35 L Operatore Rotore Consideriamo una funzione vettoriale della posizione P : v = v (P ) = v (x, y, z) = v x (x, y, z) î + v y (x, y, z) ĵ + v z (x, y, z) ˆk Si definisce l operatore rotore come: v = î x + ĵ y + ˆk z Ä v x î + v y ĵ + v z ˆkä î ĵ ˆk v = rot v = det x y z = v x v y v z ï vz = y v ò ï y vx î + z z v ò ï z vy ĵ + x x v ò x ˆk y 35
36 L Operatore Rotore (II) L operatore rotore si applica a una funzione vettoriale; il risultato è un vettore: P î R 3ó v v (P ) V P î R 3ó v Ä v ä (P ) V 36
37 L Operatore Rotore (III) Esempio: Data la funzione vettoriale: v (x, y, z) = 2y î + 2x ĵ + 2z ˆk V il rotore è la funzione vettoriale: î ĵ ˆk î ĵ ˆk Ä ä v (x, y, z) = det x y z = det x y z = v x v y v z 2y 2x 2z ï (2z) = (2x) ò ï ( 2y) î + (2z) ò ĵ + y z z ï x (2x) + x ( 2y) ò ˆk = y = 4 ˆk V 37
38 Operatori Differenziali Riassumendo, definite le funzioni: R 3 f R (funzione scalare) R 3 si ha: R 3 R 3 R 3 v V f V v R v V (funzione vettoriale) (gradiente) (divergenza) (rotore) 38
39 Domenico Galli Dipartimento di Fisica e Astronomia domenico.galli@unibo.it
Meccanica. 5. Moti Relativi. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
Meccanica. 5. Cinematica del Corpo Rigido. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 5. Cinematica del Corpo Rigido http://campus.cib.unibo.it/252232/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. 2. 2 Si chiama numero dei gradi di libertà (GdL)
Meccanica 5. Cinematica del Corpo Rigido http://campus.cib.unibo.it/252232/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. 2. 2 Si chiama numero dei gradi di libertà (GdL)
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Funzioni di più variabili a valori vettoriali n t m
 Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Forme differenziali e campi vettoriali: esercizi svolti
 Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Meccanica. 4. Cinematica del Punto Materiale. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 4. Cinematica del Punto Materiale http://campus.cib.unibo.it/2422/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Definizioni 2. Tempo e Spazio 3. La Legge Vettoriale
Meccanica 4. Cinematica del Punto Materiale http://campus.cib.unibo.it/2422/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Definizioni 2. Tempo e Spazio 3. La Legge Vettoriale
1 Sistemi di riferimento
 Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Teoremi di Stokes, della divergenza e di Gauss Green.
 Matematica 3 Esercitazioni eoremi di tokes, della divergenza e di Gauss Green. Esercizio 1 : Calcolare l area del dominio avente per frontiera la linea chiusa γ di equazioni parametriche x (1 t) t γ :,
Matematica 3 Esercitazioni eoremi di tokes, della divergenza e di Gauss Green. Esercizio 1 : Calcolare l area del dominio avente per frontiera la linea chiusa γ di equazioni parametriche x (1 t) t γ :,
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
Sistemi di coordinate
 Sistemi di coordinate Servono a descrivere la posizione di una punto nello spazio. Un sistema di coordinate consiste in Un punto fisso di riferimento chiamato origine Degli assi specifici con scale ed
Sistemi di coordinate Servono a descrivere la posizione di una punto nello spazio. Un sistema di coordinate consiste in Un punto fisso di riferimento chiamato origine Degli assi specifici con scale ed
Derivata materiale (Lagrangiana) e locale (Euleriana)
 ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
Calcolo vettoriale. Versore: vettore u adimensionale di modulo unitario (rapporto tra un vettore e il suo modulo)
 Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Calcolo vettoriale. Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc)
 Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Forme differenziali lineari
 Forme differenziali lineari Sia Ω R 3 un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A x, y, z dx + B x, y, z dy + C x, y, z dz
Forme differenziali lineari Sia Ω R 3 un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A x, y, z dx + B x, y, z dy + C x, y, z dz
Meccanica. 10. Pseudo-Forze. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 10. Pseudo-Forze http://campus.cib.unibo.it/2429/ Domenico Galli Dipartimento di Fisica e Astronomia 17 febbraio 2017 Traccia 1. Le Pseudo-Forze 2. Esempi 3. Pseudo-Forze nel Riferimento Terrestre
Meccanica 10. Pseudo-Forze http://campus.cib.unibo.it/2429/ Domenico Galli Dipartimento di Fisica e Astronomia 17 febbraio 2017 Traccia 1. Le Pseudo-Forze 2. Esempi 3. Pseudo-Forze nel Riferimento Terrestre
Cap 3- Legge di Gauss. 3.1-Concetto di flusso Flusso del campo elettrico. Cap 3- Legge di Gauss
 Cap 3- Legge di Gauss Cap 3- Legge di Gauss Una formulazione equivalente alla legge di Coulomb è quella stabilita dal teorema di Gauss, che trae vantaggio dalle situazioni nelle quali vi è una simmetria
Cap 3- Legge di Gauss Cap 3- Legge di Gauss Una formulazione equivalente alla legge di Coulomb è quella stabilita dal teorema di Gauss, che trae vantaggio dalle situazioni nelle quali vi è una simmetria
Gradiente, divergenza e rotore
 Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
Elettromagnetismo Formulazione differenziale
 Elettromagnetismo Formulazione differenziale 1. Legge di Gauss 2. Legge di Ampere 3. Equazioni di Maxwell statiche V - 0 Legge di Gauss Campo elettrico Carica contenuta all interno della superficie A Flusso
Elettromagnetismo Formulazione differenziale 1. Legge di Gauss 2. Legge di Ampere 3. Equazioni di Maxwell statiche V - 0 Legge di Gauss Campo elettrico Carica contenuta all interno della superficie A Flusso
Elettronica II Grandezze elettriche microscopiche (parte 1) p. 2
 Elettronica II Grandezze elettriche microscopiche (parte 1) Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it http://www.dti.unimi.it/
Elettronica II Grandezze elettriche microscopiche (parte 1) Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: liberali@dti.unimi.it http://www.dti.unimi.it/
Cinematica: considerazioni generali
 Cinematica: considerazioni generali La cinematica studia la descrizione del moto dei corpi (cioè la posizione di un oggetto nello spazio e nel tempo) senza considerare le cause che hanno prodotto il moto.
Cinematica: considerazioni generali La cinematica studia la descrizione del moto dei corpi (cioè la posizione di un oggetto nello spazio e nel tempo) senza considerare le cause che hanno prodotto il moto.
Geometria Analitica nello Spazio
 Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
Esercizi di Analisi Matematica 3. Prima parte
 Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
COMPLEMENTI SUI DIFFERENZIALI ESATTI E L INTEGRAZIONE DI FORME DIFFERENZIALI
 COMPLEMENTI SUI DIFFERENZIALI ESATTI E L INTEGRAZIONE DI FORME DIFFERENZIALI Sergio Console Derivate parziali (notazione) Data una funzione z = f(x, y), si può pensare di tener fissa la variabile y (considerandola
COMPLEMENTI SUI DIFFERENZIALI ESATTI E L INTEGRAZIONE DI FORME DIFFERENZIALI Sergio Console Derivate parziali (notazione) Data una funzione z = f(x, y), si può pensare di tener fissa la variabile y (considerandola
Elettrostatica nel vuoto
 Elettrostatica nel vuoto Come abbiamo visto nella parte di meccanica le forze sono o di contatto (attrito, pressione, forza elastica) o a distanza (gravitazione): osservazioni sperimentali hanno mostrato
Elettrostatica nel vuoto Come abbiamo visto nella parte di meccanica le forze sono o di contatto (attrito, pressione, forza elastica) o a distanza (gravitazione): osservazioni sperimentali hanno mostrato
I tensori ed il calcolo tensoriale... 1
 Appunti di Campi lettromagnetici Capitolo Richiami di calcolo vettoriale e tensoriale I tensori ed il calcolo tensoriale... IL CALCOLO VTTORIAL... Introduzione... Operatore immaginario j... 4 Operatore
Appunti di Campi lettromagnetici Capitolo Richiami di calcolo vettoriale e tensoriale I tensori ed il calcolo tensoriale... IL CALCOLO VTTORIAL... Introduzione... Operatore immaginario j... 4 Operatore
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Esercitazioni di Meccanica Razionale
 Esercitazioni di Meccanica Razionale a.a. 2002/2003 Esempi di forze conservative Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Esercitazioni di Meccanica Razionale a.a. 2002/2003 Esempi di forze conservative Maria Grazia Naso naso@ing.unibs.it Dipartimento di Matematica Università degli Studi di Brescia Esercitazioni di Meccanica
Calcolare l area di una superficie. 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al cilindro x 2 + y 2 = 1.
 Calcolare l area di una superficie. Calcolare l area della porzione del piano x + 2y + z = 5 sopra il cono z = 3(x 2 + y 2 ). 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al
Calcolare l area di una superficie. Calcolare l area della porzione del piano x + 2y + z = 5 sopra il cono z = 3(x 2 + y 2 ). 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al
Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F (x) = x i. i=1. x 2 + y 2
 Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
Capitolo 4 Campi vettoriali Ultimo aggiornamento: 3 maggio 2017 Ricordiamo che l operatore divergenza agisce su un campo vettoriale F ed è definito come segue: div F x = n F i x. x i i=1 Esercizio 4.1
Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3
![Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3](/thumbs/69/60553365.jpg) 1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
Formulario di Matematica. Salvatore di Maggio
 Formulario di Matematica Salvatore di Maggio Indice 1 Disequazioni 5 Calcolo Combinatorio 7 3 Logaritmi 9 4 Trigonometria 11 5 Geometria Analitica 1 5.1 Punti e rette..........................................
Formulario di Matematica Salvatore di Maggio Indice 1 Disequazioni 5 Calcolo Combinatorio 7 3 Logaritmi 9 4 Trigonometria 11 5 Geometria Analitica 1 5.1 Punti e rette..........................................
Dinamica Rotazionale
 Dinamica Rotazionale Richiamo: cinematica rotazionale, velocità e accelerazione angolare Energia cinetica rotazionale: momento d inerzia Equazione del moto rotatorio: momento delle forze Leggi di conservazione
Dinamica Rotazionale Richiamo: cinematica rotazionale, velocità e accelerazione angolare Energia cinetica rotazionale: momento d inerzia Equazione del moto rotatorio: momento delle forze Leggi di conservazione
Cap 7 - Lavoro ed energia Lavoro di una forza costante
 N.Giglietto A.A. 2005/06-7.3 - Lavoro di una forza costante - 1 Cap 7 - Lavoro ed energia Abbiamo visto come applicare le leggi della dinamica in varie situazioni. Spesso però l analisi del moto spesso
N.Giglietto A.A. 2005/06-7.3 - Lavoro di una forza costante - 1 Cap 7 - Lavoro ed energia Abbiamo visto come applicare le leggi della dinamica in varie situazioni. Spesso però l analisi del moto spesso
Corso di FISICA II Prof. Umberto del Pennino
 Contenuti del Corso: Elettricità Magnetismo Ottica Corso di FISICA II Prof. Umberto del Pennino Elettromagnetismo Testo: Mazzoldi, Nigro, Voci:" Elementi di Fisica: Elettromagnetismo e Onde EdiSES Operatori
Contenuti del Corso: Elettricità Magnetismo Ottica Corso di FISICA II Prof. Umberto del Pennino Elettromagnetismo Testo: Mazzoldi, Nigro, Voci:" Elementi di Fisica: Elettromagnetismo e Onde EdiSES Operatori
Le soluzioni del foglio 3
 Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
VETTORI E SCALARI DEFINIZIONI. Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura.
 VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
Cinematica in due o più dimensioni
 Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
LEZIONE DEL 23 SETTEMBRE
 INGEGNERI GESTIONLE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 23 SETTEMRE 2008 Introduzione Sistemi di coordinate y y (x,y) Q( 3,4) (x,y) r P (7,2) O x Coordinate cartesiane. Ogni punto è individuato
INGEGNERI GESTIONLE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 23 SETTEMRE 2008 Introduzione Sistemi di coordinate y y (x,y) Q( 3,4) (x,y) r P (7,2) O x Coordinate cartesiane. Ogni punto è individuato
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
7. Integrazione delle funzioni di più variabili (II)
 7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
CAMPI VETTORIALI (Note)
 CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 17.XI.17 1. Le curve hanno tutte parametrizzazioni di classe C. Per studiare
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 17.XI.17 1. Le curve hanno tutte parametrizzazioni di classe C. Per studiare
OPERAZIONI SU SPAZI DI HILBERT. Nel seguito introdurremo i concetti di prodotto diretto e somma diretta di due spazi di Hilbert.
 2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
2/7 OPERAZIONI SU SPAZI DI HILBERT 11/12 1 OPERAZIONI SU SPAZI DI HILBERT Dati due spazi di Hilbert H (1) e H (2) si possono definire su di essi operazioni il cui risultato è un nuovo spazio di Hilbert
ELETTROLOGIA Cap II. Calcolo del Campo Elettrico dovuto ad alcune distribuzioni di carica. Elettrologia II
 ELETTROLOGIA Cap II Calcolo del Campo Elettrico dovuto ad alcune distribuzioni di carica 1 Anello di raggio R uniformemente carco con carica Q. Anello di dimensioni trasversali trascurabili rispetto al
ELETTROLOGIA Cap II Calcolo del Campo Elettrico dovuto ad alcune distribuzioni di carica 1 Anello di raggio R uniformemente carco con carica Q. Anello di dimensioni trasversali trascurabili rispetto al
Integrali di superficie: esercizi svolti
 Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
4. Calcolare il baricentro delle seguenti regioni del piano dotate di densità unitaria:
 INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
INTEGRLI OPPI e TRIPLI Esercii risolti. Calcolare i seguenti integrali doppi: a b c d e f g h i j k y d dy,, y :, y }; d dy,, y :, y }; + y + y d dy,, y :, y }; y d dy,, y :, y }; y d dy,, y :, y + };
Esercizi di Analisi Matematica L-B
 Esercii di Analisi Matematica L-B Marco Alessandrini Gennaio-Maro 7 Indice Funioni di più variabili reali. Calcolo differeniale........................................... Ricerca di massimi e minimi.......................................
Esercii di Analisi Matematica L-B Marco Alessandrini Gennaio-Maro 7 Indice Funioni di più variabili reali. Calcolo differeniale........................................... Ricerca di massimi e minimi.......................................
Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza I S. J ds. dj y. div J dv S.
 estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza Ricordiamo che,
estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza Ricordiamo che,
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
dλ + Γµ ναu ν V α = 0 (3)
 SESTA ESERCITAZIONE Trasporto parallelo Lungo una curva di parametro λ, di vettore tangente U µ = dxµ dλ, (1) il vettore V µ è trasportato parallelamente se soddisfa le equazioni del trasporto parallelo
SESTA ESERCITAZIONE Trasporto parallelo Lungo una curva di parametro λ, di vettore tangente U µ = dxµ dλ, (1) il vettore V µ è trasportato parallelamente se soddisfa le equazioni del trasporto parallelo
Derivate parziali, derivate direzionali, differenziabilità. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) =
 Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Meccanica dei Fluidi
 POLITECNICO DI MILANO Meccanica dei Fluidi 4. Dinamica dei Fluidi A cura di: Diego Berzi v1.2 Indice 1 Bilancio di massa 3 1.1 Forma indefinita......................... 3 1.2 Forma globale...........................
POLITECNICO DI MILANO Meccanica dei Fluidi 4. Dinamica dei Fluidi A cura di: Diego Berzi v1.2 Indice 1 Bilancio di massa 3 1.1 Forma indefinita......................... 3 1.2 Forma globale...........................
Esercizi svolti e assegnati su integrali doppi e tripli
 Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove Calcolare R = R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x =, C :
P = r. o + r. O + ω r (1)
 1 5.1-MOTI RELATIVI Parte I 5.1-Moti relativi-cap5 1 5.1-Moti relativi Teorema delle velocità relative Riprendiamo l impostazione tracciata nel paragrafo 2.6 (moti relativi 2-D) e consideriamo un sistema
1 5.1-MOTI RELATIVI Parte I 5.1-Moti relativi-cap5 1 5.1-Moti relativi Teorema delle velocità relative Riprendiamo l impostazione tracciata nel paragrafo 2.6 (moti relativi 2-D) e consideriamo un sistema
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
RISOLUZIONE DI PROBLEMI DI FISICA
 RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Forme differenziali lineari e loro integrazione
 Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Potenziale vettore F i s i c a s p e r i m e n t a l e C. d. l. C h i m i c a
 Potenziale vettore F i s i c a s p e r i m e n t a l e C. d. l. C h i m i c a I I Per risolvere semplici problemi basta la legge di Ampere In generale occorrerà seguire la stessa linea usata nel caso elettrostatico
Potenziale vettore F i s i c a s p e r i m e n t a l e C. d. l. C h i m i c a I I Per risolvere semplici problemi basta la legge di Ampere In generale occorrerà seguire la stessa linea usata nel caso elettrostatico
Meccanica. 1. Vettori. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 1. Vettori http://campus.cib.unibo.it/2421/ Domenico Galli Dipartimento di Fisica e Astronomia 3 febbraio 2017 Traccia 1. Grandezze Fisiche 2. Vettori 3. Calcolo Vettoriale 4. Somma e Differenza
Meccanica 1. Vettori http://campus.cib.unibo.it/2421/ Domenico Galli Dipartimento di Fisica e Astronomia 3 febbraio 2017 Traccia 1. Grandezze Fisiche 2. Vettori 3. Calcolo Vettoriale 4. Somma e Differenza
Il Corso di Fisica per Scienze Biologiche
 Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 2708 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://cms.pg.infn.it/santocchia/
Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 2708 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://cms.pg.infn.it/santocchia/
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 2. Giugno Docenti: F. Lastaria, M. Citterio, M.
 POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Gradiente, Divergenza, Rotore. Plinio Gatto
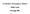 Gradiente, Divergenza, Rotore Plinio Gatto 06 maggio 2006 Indice generale Licenza... 3 Introduzione...4 Gradiente... 5 Gradiente di temperatura... 5 Proprietà del campo Coulombiano... 6 Osservazioni sul
Gradiente, Divergenza, Rotore Plinio Gatto 06 maggio 2006 Indice generale Licenza... 3 Introduzione...4 Gradiente... 5 Gradiente di temperatura... 5 Proprietà del campo Coulombiano... 6 Osservazioni sul
Unità di misura. Grandezza Unità Simbolo
 Grandezze Fisiche Sono grandezze in base alle quali descriviamo i fenomeni fisici; ad esempio la velocità, la temperatura, la pressione, la resistenza elettrica, etc. Per le grandezze fisiche è possibile
Grandezze Fisiche Sono grandezze in base alle quali descriviamo i fenomeni fisici; ad esempio la velocità, la temperatura, la pressione, la resistenza elettrica, etc. Per le grandezze fisiche è possibile
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
1. Calcolare, giustificandone l esistenza, il seguente integrale: y (1 + x) 2 dxdy, ydxdy. x 2 dxdy,
 . Calcolare, giustificandone l esistenza, il seguente integrale: ( + x dxd, = {(x, R :, x }.. isegnare il dominio = {(x, R : x, + x } e calcolare dxd. 3. Calcolare x dxd, è il triangolo di vertici ( 3,,
. Calcolare, giustificandone l esistenza, il seguente integrale: ( + x dxd, = {(x, R :, x }.. isegnare il dominio = {(x, R : x, + x } e calcolare dxd. 3. Calcolare x dxd, è il triangolo di vertici ( 3,,
1 Trasformazione di vettori e 1-forme per cambiamenti
 PRIMA ESERCITAZIONE Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx
PRIMA ESERCITAZIONE Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx
Corso di laurea in Ingegneria civile - ambientale - edile Prova scritta del 3 febbraio Regole per lo svolgimento
 Corso di laurea in Ingegneria civile - ambientale - edile Prova scritta del febbraio 6 Regole per lo svolgimento (a) Gli studenti di ingegneria civile e edile -5 faranno gli esercizi,,. (b) Gli studenti
Corso di laurea in Ingegneria civile - ambientale - edile Prova scritta del febbraio 6 Regole per lo svolgimento (a) Gli studenti di ingegneria civile e edile -5 faranno gli esercizi,,. (b) Gli studenti
Prodotto Scalare e Prodotto Vettore I
 Prodotto Scalare e Prodotto Vettore I Prodotto Scalare: pplicaione che va dallo spaio prodotto R 3 R 3 in R tale che: 3 B B B, = j = 1 j j Norma di un Vettore: pplicaione che va dallo spaio dei vettori
Prodotto Scalare e Prodotto Vettore I Prodotto Scalare: pplicaione che va dallo spaio prodotto R 3 R 3 in R tale che: 3 B B B, = j = 1 j j Norma di un Vettore: pplicaione che va dallo spaio dei vettori
Il calcolo vettoriale. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Il calcolo vettoriale Universita' di Udine 1 I vettori: definizione Attenzione a definizioni superficiali Del tipo: Definito da modulo, direzione, verso Sono valide a senso, e solo in coordinate cartesiane!
Il calcolo vettoriale Universita' di Udine 1 I vettori: definizione Attenzione a definizioni superficiali Del tipo: Definito da modulo, direzione, verso Sono valide a senso, e solo in coordinate cartesiane!
Capitolo 10. Appendice GlioperatoriGRAD,DIV,ROT Significato del Gradiente
 Capitolo 10 Appendice 1 10.1 GlioperatoriGRAD,DIV,ROT 10.1.1 ignificato del Gradiente iadatalafunzionef : D R 3 R, D insieme aperto, f C 2 (D). Tale funzione è anche detta campo scalare. celto un sistema
Capitolo 10 Appendice 1 10.1 GlioperatoriGRAD,DIV,ROT 10.1.1 ignificato del Gradiente iadatalafunzionef : D R 3 R, D insieme aperto, f C 2 (D). Tale funzione è anche detta campo scalare. celto un sistema
L OPERATORE NABLA spiegato da un vil meccanico
 Pier Maria Boria Agg. 10/2009 L OPERATORE NABLA spiegato da un vil meccanico 1 PREMESSA Ad uso dei giovani studenti che si accingono ad attrezzare il loro bagaglio culturale per divenire dei professionisti
Pier Maria Boria Agg. 10/2009 L OPERATORE NABLA spiegato da un vil meccanico 1 PREMESSA Ad uso dei giovani studenti che si accingono ad attrezzare il loro bagaglio culturale per divenire dei professionisti
Anna Pandolfi Analisi Strutturale e Termica 4.1
 Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Dipolo Elettrico: due cariche (puntiformi) +q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo
 Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
Superfici. V. Tibullo, rev.1, 04/04/2006.
 uperfici. Tibullo, rev.1, 04/04/2006. 1 Integrali di superficie Consideriamo una superficie nello spazio tridimensionale R 3. Il concetto di superficie è noto dalla geometria elementare e non se ne darà
uperfici. Tibullo, rev.1, 04/04/2006. 1 Integrali di superficie Consideriamo una superficie nello spazio tridimensionale R 3. Il concetto di superficie è noto dalla geometria elementare e non se ne darà
Introduzione alla Meccanica: Cinematica
 Introduzione alla Meccanica: Cinematica La Cinematica si occupa della descrizione geometrica del moto, senza riferimento alle sue cause. E invece compito della Dinamica mettere in relazione il moto con
Introduzione alla Meccanica: Cinematica La Cinematica si occupa della descrizione geometrica del moto, senza riferimento alle sue cause. E invece compito della Dinamica mettere in relazione il moto con
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Analisi Matematica II Integrali curvilinei (svolgimenti) 1 t 9t dt (a) = dt t 1 t 2 = 1 2. x dx (b) log y 1. dy.
 Analisi Matematica II Integrali curvilinei svolgimenti Svolgimento esercizio Si ha, successivamente, t t, t, t 9t 4 + 4t t 9t + 4, l t dt t 9t + 4 dt a 8 dove in a si è usata la sostituzione 9t + 4 8t
Analisi Matematica II Integrali curvilinei svolgimenti Svolgimento esercizio Si ha, successivamente, t t, t, t 9t 4 + 4t t 9t + 4, l t dt t 9t + 4 dt a 8 dove in a si è usata la sostituzione 9t + 4 8t
Esercizi sul Calcolo Vettoriale 10/10/2014
 Esercizi sul Calcolo Vettoriale 10/10/2014 Problema 1. Fissata una terna cartesiana eortogonale e dati due vettori a=11 î 7 ĵ +9 k, b=14 î+5 ĵ k determinare modulo, direzione e verso sia della somma a+
Esercizi sul Calcolo Vettoriale 10/10/2014 Problema 1. Fissata una terna cartesiana eortogonale e dati due vettori a=11 î 7 ĵ +9 k, b=14 î+5 ĵ k determinare modulo, direzione e verso sia della somma a+
Coordinate e Sistemi di Riferimento
 Coordinate e Sistemi di Riferimento Sistemi di riferimento Quando vogliamo approcciare un problema per risolverlo quantitativamente, dobbiamo per prima cosa stabilire in che sistema di riferimento vogliamo
Coordinate e Sistemi di Riferimento Sistemi di riferimento Quando vogliamo approcciare un problema per risolverlo quantitativamente, dobbiamo per prima cosa stabilire in che sistema di riferimento vogliamo
Energia meccanica. Lavoro Energia meccanica Concetto di campo in Fisica. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_)
 Energia meccanica Lavoro Energia meccanica Concetto di campo in Fisica Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro potete
Energia meccanica Lavoro Energia meccanica Concetto di campo in Fisica Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro potete
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Fisica Generale 1 per Chimica Formulario di Meccanica
 Fisica Generale 1 per Chimica Formulario di Meccanica Vettori : operazioni elementari: Nota: un vettore verra' qui rappresentato in grassetto es: A = ( A x, A y, A z ) Prodotto scalare A. B = A B cos θ,
Fisica Generale 1 per Chimica Formulario di Meccanica Vettori : operazioni elementari: Nota: un vettore verra' qui rappresentato in grassetto es: A = ( A x, A y, A z ) Prodotto scalare A. B = A B cos θ,
Momento angolare L. P. Maggio Prodotto vettoriale
 Momento angolare L. P. Maggio 2007 1. Prodotto vettoriale 1.1. Definizione Il prodotto vettoriale di due vettori tridimensionali a e b è un vettore c così definito: a) Il modulo di c è pari all area del
Momento angolare L. P. Maggio 2007 1. Prodotto vettoriale 1.1. Definizione Il prodotto vettoriale di due vettori tridimensionali a e b è un vettore c così definito: a) Il modulo di c è pari all area del
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
ESERCIZI SUI VETTORI CON SOLUZIONE di Mauro Morganti e Juri Riccardi
 ESERCIZI SUI VETTORI CON SOLUZIONE di Mauro Morganti e Juri Riccardi Esercizio 1 Rispetto ad una terna cartesiana ortogonale di origine O e versori i ˆ, ĵ, ˆk due vettori spostamento a e b hanno componenti
ESERCIZI SUI VETTORI CON SOLUZIONE di Mauro Morganti e Juri Riccardi Esercizio 1 Rispetto ad una terna cartesiana ortogonale di origine O e versori i ˆ, ĵ, ˆk due vettori spostamento a e b hanno componenti
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Divergenza. ato una superficie chiusa S che racchiude il volume V, lo dividiamo in due rti con la superficie D mostrata in figura
 Divergenza Deriva dal concetto di flusso attraverso una superficie di una proprietà fisica ed è stato introdotto nei corsi di elettromagnetismo elementare (Legge di Gauss per il campo elettrico). ato una
Divergenza Deriva dal concetto di flusso attraverso una superficie di una proprietà fisica ed è stato introdotto nei corsi di elettromagnetismo elementare (Legge di Gauss per il campo elettrico). ato una
CP. Cinematica del punto
 Cinematica CP. Cinematica del punto Per iniziare a trattare la cinematica presupponiamo come primitive le nozioni di spazio e di tempo che assumiamo come note dalla fisica ed iniziamo subito ad esaminare
Cinematica CP. Cinematica del punto Per iniziare a trattare la cinematica presupponiamo come primitive le nozioni di spazio e di tempo che assumiamo come note dalla fisica ed iniziamo subito ad esaminare
S.Barbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie. Cap. 2. Cinematica del punto
 SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
SBarbarino - Appunti di Fisica - Scienze e Tecnologie Agrarie Cap 2 Cinematica del punto 21 - Posizione, velocitá e accelerazione di una particella La posizione di una particella puó essere definita, ad
Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico
 5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
