Metodi Stocastici per la Finanza
|
|
|
- Romolo Pavone
- 5 anni fa
- Visualizzazioni
Transcript
1 Metodi Stocastici per la Finanza Tiziano Vargiolu 1 1 Università degli Studi di Padova Anno Accademico Lezione 8
2 Indice 1 Modello di Vasicek 2 Calibrazione e ottimizzazione numerica 3 Implementazione
3 Indice 1 Modello di Vasicek 2 Calibrazione e ottimizzazione numerica 3 Implementazione
4 Indice 1 Modello di Vasicek 2 Calibrazione e ottimizzazione numerica 3 Implementazione
5 Modelli affini Un modello affine è un modello per il tasso corto r tale che i prezzi degli zero-coupon bonds p(t, T ) al tempo t con maturità T possono essere espressi mediante p(t, T ) = exp(a(t, T ) B(t, T )r t ) Se il tasso corto r è un processo di Itô, questo accade se r ha dinamica dr t = (α(t)r t + β(t)) dt + γ(t)r t + δ(t) dw t dove (α, β, γ, δ) sono opportune funzioni deterministiche di t. Il legame tra queste e le funzioni A e B che compaiono nel prezzo dei bonds è dato dal fatto che A e B sono soluzioni delle seguenti equazioni differenziali ordinarie { Bt (t, T ) + α(t)b(t, T ) 1 2 γ(t)b2 (t, T ) = 1, B(T, T ) = 0, A t (t, T ) = β(t)b(t, T ) 1 2 δ(t)b2 (t, T ), A(T, T ) = 0
6 Modelli affini Un modello affine è un modello per il tasso corto r tale che i prezzi degli zero-coupon bonds p(t, T ) al tempo t con maturità T possono essere espressi mediante p(t, T ) = exp(a(t, T ) B(t, T )r t ) Se il tasso corto r è un processo di Itô, questo accade se r ha dinamica dr t = (α(t)r t + β(t)) dt + γ(t)r t + δ(t) dw t dove (α, β, γ, δ) sono opportune funzioni deterministiche di t. Il legame tra queste e le funzioni A e B che compaiono nel prezzo dei bonds è dato dal fatto che A e B sono soluzioni delle seguenti equazioni differenziali ordinarie { Bt (t, T ) + α(t)b(t, T ) 1 2 γ(t)b2 (t, T ) = 1, B(T, T ) = 0, A t (t, T ) = β(t)b(t, T ) 1 2 δ(t)b2 (t, T ), A(T, T ) = 0
7 Modelli affini Un modello affine è un modello per il tasso corto r tale che i prezzi degli zero-coupon bonds p(t, T ) al tempo t con maturità T possono essere espressi mediante p(t, T ) = exp(a(t, T ) B(t, T )r t ) Se il tasso corto r è un processo di Itô, questo accade se r ha dinamica dr t = (α(t)r t + β(t)) dt + γ(t)r t + δ(t) dw t dove (α, β, γ, δ) sono opportune funzioni deterministiche di t. Il legame tra queste e le funzioni A e B che compaiono nel prezzo dei bonds è dato dal fatto che A e B sono soluzioni delle seguenti equazioni differenziali ordinarie { Bt (t, T ) + α(t)b(t, T ) 1 2 γ(t)b2 (t, T ) = 1, B(T, T ) = 0, A t (t, T ) = β(t)b(t, T ) 1 2 δ(t)b2 (t, T ), A(T, T ) = 0
8 Modello di Vasicek Nel modello di Vasicek (1978), il tasso corto è soluzione di dr t = a(b r t ) dt + σ dw t e si può scrivere direttamente la soluzione esplicita r t = e at r 0 + b t 0 e a(t u) du + σ t 0 e a(t u) dw u e si possono calcolare esplicitamente molte quantità mediante questa formula esplicita. In particolare, r è un processo gaussiano con media e varianza E[r t ] = e at r 0 + b t 0 e a(t u) du t Var[r t ] = σ 2 e 2a(t u) du 0
9 Modello di Vasicek Nel modello di Vasicek (1978), il tasso corto è soluzione di dr t = a(b r t ) dt + σ dw t e si può scrivere direttamente la soluzione esplicita r t = e at r 0 + b t 0 e a(t u) du + σ t 0 e a(t u) dw u e si possono calcolare esplicitamente molte quantità mediante questa formula esplicita. In particolare, r è un processo gaussiano con media e varianza E[r t ] = e at r 0 + b t 0 e a(t u) du t Var[r t ] = σ 2 e 2a(t u) du 0
10 Modello di Vasicek come modello affine In alternativa, seguendo la teoria generale dei modelli affini, poniamo α(t) a, β(t) ab, γ(t) 0, δ t σ 2 e quindi i due sistemi di equazioni ordinarie diventano { Bt (t, T ) = ab(t, T ) 1, B(T, T ) = 0, A t (t, T ) = abb(t, T ) 1 2 σ2 B 2 (t, T ), A(T, T ) = 0 che hanno soluzioni esplicite 1 e a(t t) B(t, T ) =, a 1 e a(t t) A(t, T ) = b(t t) + b σ2 a 4a 3 (1 e a(t t) ) 2 + ( ) + σ2 1 e a(t t) 2a 2 T t a
11 Tasso yield sotto il modello di Vasicek Calcoliamo ora il tasso continuo R(t, T ): siccome questo tasso soddisfa p(t, T ) = exp( (T t)r(t, T )), allora dobbiamo avere R(t, T ) = = 1 T t (B(t, T )r t A(t, T )) = ( 1 e a(t t) r t + R 1 a(t t) + σ2 (1 e a(t t) ) 2 4a 3 T t 1 e a(t t) a(t t) dove R := b σ2 è il tasso lungo : difatti, fissati t e r 2a 2 t, si ha che lim R(t, T ) = 0 r t + R (1 0) + 0 = R T La variabile r t continua a conservare la sua interpretazione di tasso a breve: difatti fissati t e r t, si ha che lim T t + R(t, T ) = 1 r t + R (1 1) + 0 = r t ) +
12 Tasso yield sotto il modello di Vasicek Calcoliamo ora il tasso continuo R(t, T ): siccome questo tasso soddisfa p(t, T ) = exp( (T t)r(t, T )), allora dobbiamo avere R(t, T ) = = 1 T t (B(t, T )r t A(t, T )) = ( 1 e a(t t) r t + R 1 a(t t) + σ2 (1 e a(t t) ) 2 4a 3 T t 1 e a(t t) a(t t) dove R := b σ2 è il tasso lungo : difatti, fissati t e r 2a 2 t, si ha che lim R(t, T ) = 0 r t + R (1 0) + 0 = R T La variabile r t continua a conservare la sua interpretazione di tasso a breve: difatti fissati t e r t, si ha che lim T t + R(t, T ) = 1 r t + R (1 1) + 0 = r t ) +
13 Calibrazione con il modello di Vasicek La calibrazione con un modello come quello di Vasicek, in cui il modello cioè prevede una specifica forma funzionale per i tassi di interesse in funzione della maturità, procede in questo modo. Date determinate maturità T 1,..., T n per cui si possano ricavare i tassi R(t, T i ), i = 1,..., n dal mercato, per ogni a, b, σ si possono calcolare i tassi teorici R(t, T ) = R(t, T ; a, b, σ) in base alle formule viste sopra. Il metodo più usato per calibrare il modello è allora quello di minimizzare la somma degli scarti quadratici, cioè risolvere il problema min a,b,σ n ( R(t, T i ) R(t, T i ; a, b, σ)) 2 (1) i=1 che in effetti è un caso particolare di calibrazione parametrica.
14 Calibrazione con il modello di Vasicek La calibrazione con un modello come quello di Vasicek, in cui il modello cioè prevede una specifica forma funzionale per i tassi di interesse in funzione della maturità, procede in questo modo. Date determinate maturità T 1,..., T n per cui si possano ricavare i tassi R(t, T i ), i = 1,..., n dal mercato, per ogni a, b, σ si possono calcolare i tassi teorici R(t, T ) = R(t, T ; a, b, σ) in base alle formule viste sopra. Il metodo più usato per calibrare il modello è allora quello di minimizzare la somma degli scarti quadratici, cioè risolvere il problema min a,b,σ n ( R(t, T i ) R(t, T i ; a, b, σ)) 2 (1) i=1 che in effetti è un caso particolare di calibrazione parametrica.
15 Calibrazione con il modello di Vasicek La calibrazione con un modello come quello di Vasicek, in cui il modello cioè prevede una specifica forma funzionale per i tassi di interesse in funzione della maturità, procede in questo modo. Date determinate maturità T 1,..., T n per cui si possano ricavare i tassi R(t, T i ), i = 1,..., n dal mercato, per ogni a, b, σ si possono calcolare i tassi teorici R(t, T ) = R(t, T ; a, b, σ) in base alle formule viste sopra. Il metodo più usato per calibrare il modello è allora quello di minimizzare la somma degli scarti quadratici, cioè risolvere il problema min a,b,σ n ( R(t, T i ) R(t, T i ; a, b, σ)) 2 (1) i=1 che in effetti è un caso particolare di calibrazione parametrica.
16 Ottimizzazione non lineare Per risolvere il problema min φ(x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@phi,@g,@h) L input consiste in: x0: @h: funzioni possono essere sostituite da []. Output: x: ottimo; obj: valore ottimo; info: codice di funzionamento della routine; iter: n. iterazioni occorse; lambda: valore dei moltiplicatori di Lagrange.
17 Ottimizzazione non lineare Per risolvere il problema min φ(x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@phi,@g,@h) L input consiste in: x0: @h: funzioni possono essere sostituite da []. Output: x: ottimo; obj: valore ottimo; info: codice di funzionamento della routine; iter: n. iterazioni occorse; lambda: valore dei moltiplicatori di Lagrange.
18 Ottimizzazione non lineare Per risolvere il problema min φ(x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@phi,@g,@h) L input consiste in: x0: @h: funzioni possono essere sostituite da []. Output: x: ottimo; obj: valore ottimo; info: codice di funzionamento della routine; iter: n. iterazioni occorse; lambda: valore dei moltiplicatori di Lagrange.
19 Ottimizzazione non lineare Per risolvere il problema min φ(x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@phi,@g,@h) L input consiste in: x0: @h: funzioni possono essere sostituite da []. Output: x: ottimo; obj: valore ottimo; info: codice di funzionamento della routine; iter: n. iterazioni occorse; lambda: valore dei moltiplicatori di Lagrange.
20 Ottimizzazione parametrica Per risolvere il problema, dipendente dal parametro a, min φ a (x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@(x) phi(x,a),@g,@h) in questo modo: > z0 = [0.03;-0.03;-0.02;0.5] > [x, obj, info, iter, nf, lambda] = sqp(z0,@(z) phivasicek(t,r,z),[],[])
21 Ottimizzazione parametrica Per risolvere il problema, dipendente dal parametro a, min φ a (x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@(x) phi(x,a),@g,@h) in questo modo: > z0 = [0.03;-0.03;-0.02;0.5] > [x, obj, info, iter, nf, lambda] = sqp(z0,@(z) phivasicek(t,r,z),[],[])
22 Ottimizzazione parametrica Per risolvere il problema, dipendente dal parametro a, min φ a (x) g(x) = 0, h(x) 0, si usa l istruzione [x, obj, info, iter, nf, lambda] = sqp(x0,@(x) phi(x,a),@g,@h) in questo modo: > z0 = [0.03;-0.03;-0.02;0.5] > [x, obj, info, iter, nf, lambda] = sqp(z0,@(z) phivasicek(t,r,z),[],[])
23 File Vasicek.m function obj = Vasicek(T,a,b,sigma,r0) e = exp(-a*t); Rinf = b - sigma^2/(2*a^2); obj = (1 - e)*r0/(a*t) + Rinf * (1 - (1 - e)/(a*t)) +... sigma^2/(4*a^3) * (1 - e)^2/t; endfunction
24 File plotvasicek.m function plotvasicek(a,b,sigma,r0,t,delta) N = T/delta; for u = 1:N g(u) = Vasicek(u*delta,a,b,sigma,r0); v(u) = u*delta; end plot(v,g,0) endfunction
25 File phivasicek.m function obj = phivasicek(t,r,z,r0) obj = 0; [n m] = size(r); a = z(1); b = z(2); sigma = z(3); for i = 2:n obj = obj + (R(i) - Vasicek(T(i) - T(1),a,b,sigma,r0))^2; end endfunction
26 Calibrazione globale Siamo ora pronti per calibrare la curva zero-coupon. Per fare questo, si usa la funzione di minimizzazione sqp, e in particolare le seguenti istruzioni Octave: > z0 = [a;b;sigma] inizializziamo il vettore di parametri poichè sqp ha bisogno di un punto di partenza; > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t,r,z,r(2)),[],[]) minimizza la funzione z phivasicek(t, R, z) partendo da z0 e senza vincoli Disegnamo questa curva contro la curva originale: > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Sono molto diverse: il modello di Vasicek riesce a catturare solo alcune curve di tassi tipiche, ma ci possono essere particolari curve che non sono di quella forma.
27 Calibrazione globale Siamo ora pronti per calibrare la curva zero-coupon. Per fare questo, si usa la funzione di minimizzazione sqp, e in particolare le seguenti istruzioni Octave: > z0 = [a;b;sigma] inizializziamo il vettore di parametri poichè sqp ha bisogno di un punto di partenza; > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t,r,z,r(2)),[],[]) minimizza la funzione z phivasicek(t, R, z) partendo da z0 e senza vincoli Disegnamo questa curva contro la curva originale: > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Sono molto diverse: il modello di Vasicek riesce a catturare solo alcune curve di tassi tipiche, ma ci possono essere particolari curve che non sono di quella forma.
28 Calibrazione globale Siamo ora pronti per calibrare la curva zero-coupon. Per fare questo, si usa la funzione di minimizzazione sqp, e in particolare le seguenti istruzioni Octave: > z0 = [a;b;sigma] inizializziamo il vettore di parametri poichè sqp ha bisogno di un punto di partenza; > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t,r,z,r(2)),[],[]) minimizza la funzione z phivasicek(t, R, z) partendo da z0 e senza vincoli Disegnamo questa curva contro la curva originale: > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Sono molto diverse: il modello di Vasicek riesce a catturare solo alcune curve di tassi tipiche, ma ci possono essere particolari curve che non sono di quella forma.
29 Calibrazione globale Siamo ora pronti per calibrare la curva zero-coupon. Per fare questo, si usa la funzione di minimizzazione sqp, e in particolare le seguenti istruzioni Octave: > z0 = [a;b;sigma] inizializziamo il vettore di parametri poichè sqp ha bisogno di un punto di partenza; > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t,r,z,r(2)),[],[]) minimizza la funzione z phivasicek(t, R, z) partendo da z0 e senza vincoli Disegnamo questa curva contro la curva originale: > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Sono molto diverse: il modello di Vasicek riesce a catturare solo alcune curve di tassi tipiche, ma ci possono essere particolari curve che non sono di quella forma.
30 Calibrazione globale Siamo ora pronti per calibrare la curva zero-coupon. Per fare questo, si usa la funzione di minimizzazione sqp, e in particolare le seguenti istruzioni Octave: > z0 = [a;b;sigma] inizializziamo il vettore di parametri poichè sqp ha bisogno di un punto di partenza; > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t,r,z,r(2)),[],[]) minimizza la funzione z phivasicek(t, R, z) partendo da z0 e senza vincoli Disegnamo questa curva contro la curva originale: > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Sono molto diverse: il modello di Vasicek riesce a catturare solo alcune curve di tassi tipiche, ma ci possono essere particolari curve che non sono di quella forma.
31 Calibrazione per comparti : maturità corte Si può però tentare una calibrazione per comparti : ci si accontenta cioè di calibrare la curva solo su un sottointervallo (a, b) (0, 50). Questo può essere fatto fornendo come input alla funzione phivasicek non tutti i vettori T ed R, ma solo alcune componenti. Proviamo all inizio con il comparto (0, 6) (maturità fino a 6 anni): dato che 6 = T 14, la sintassi è la seguente > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t(1:14),r(1:14),z,r(2)),[],[]) > plotvasicek(x(1),x(2),x(3),r(2),6,0.1) > plot(t(1:14),r(1:14),0) Da qui si vede che la calibrazione è molto migliore di prima, ma ovviamente limitata alle maturità fino a 6 anni: in particolare, il vettore ottimale dei coefficienti è x = [ ; ; ].
32 Calibrazione per comparti : maturità corte Si può però tentare una calibrazione per comparti : ci si accontenta cioè di calibrare la curva solo su un sottointervallo (a, b) (0, 50). Questo può essere fatto fornendo come input alla funzione phivasicek non tutti i vettori T ed R, ma solo alcune componenti. Proviamo all inizio con il comparto (0, 6) (maturità fino a 6 anni): dato che 6 = T 14, la sintassi è la seguente > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t(1:14),r(1:14),z,r(2)),[],[]) > plotvasicek(x(1),x(2),x(3),r(2),6,0.1) > plot(t(1:14),r(1:14),0) Da qui si vede che la calibrazione è molto migliore di prima, ma ovviamente limitata alle maturità fino a 6 anni: in particolare, il vettore ottimale dei coefficienti è x = [ ; ; ].
33 Calibrazione per comparti : maturità corte Si può però tentare una calibrazione per comparti : ci si accontenta cioè di calibrare la curva solo su un sottointervallo (a, b) (0, 50). Questo può essere fatto fornendo come input alla funzione phivasicek non tutti i vettori T ed R, ma solo alcune componenti. Proviamo all inizio con il comparto (0, 6) (maturità fino a 6 anni): dato che 6 = T 14, la sintassi è la seguente > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t(1:14),r(1:14),z,r(2)),[],[]) > plotvasicek(x(1),x(2),x(3),r(2),6,0.1) > plot(t(1:14),r(1:14),0) Da qui si vede che la calibrazione è molto migliore di prima, ma ovviamente limitata alle maturità fino a 6 anni: in particolare, il vettore ottimale dei coefficienti è x = [ ; ; ].
34 Calibrazione per comparti : maturità lunghe Vediamo un altro esempio, con il comparto (1, 50) (tutte le maturità tranne quelle fino a 1 anno). Dato che 1 = T 9 e 50 = T 42, la sintassi è la seguente: > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t(9:42),r(9:42),z,r(2)),[],[]) > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Anche qui si osserva una calibrazione molto migliore della precedente, ma solo per periodi più lunghi di 1 anno: stavolta il vettore ottimale è x = [ ; ; ].
35 Calibrazione per comparti : maturità lunghe Vediamo un altro esempio, con il comparto (1, 50) (tutte le maturità tranne quelle fino a 1 anno). Dato che 1 = T 9 e 50 = T 42, la sintassi è la seguente: > [x,obj,info,iter,nf,lambda] = sqp(z0,@(z) phivasicek(t(9:42),r(9:42),z,r(2)),[],[]) > plotvasicek(x(1),x(2),x(3),r(2),50,0.1) > plot(t,r,0) Anche qui si osserva una calibrazione molto migliore della precedente, ma solo per periodi più lunghi di 1 anno: stavolta il vettore ottimale è x = [ ; ; ].
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2012-2013 Lezione 9 Indice 1 Opzioni su obbligazioni con modelli ad un fattore
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2012-2013 Lezione 9 Indice 1 Opzioni su obbligazioni con modelli ad un fattore
Zero-coupon bond e tassi di interesse a breve termine
 Zero-coupon bond e tassi di interesse a breve termine Definizione. Uno zero-coupon bond con data di maturità T > 0, detto anche T -bond, è un contratto che prevede il pagamento alla scadenza T del suo
Zero-coupon bond e tassi di interesse a breve termine Definizione. Uno zero-coupon bond con data di maturità T > 0, detto anche T -bond, è un contratto che prevede il pagamento alla scadenza T del suo
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2012-2013 Lezione 2 Indice 1 Dal modello alla formula di Black-Scholes 2 Calibrazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2012-2013 Lezione 2 Indice 1 Dal modello alla formula di Black-Scholes 2 Calibrazione
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2013-2014 Lezione 5 Indice 1 Riduzione della varianza nei metodi Monte Carlo
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2013-2014 Lezione 5 Indice 1 Riduzione della varianza nei metodi Monte Carlo
Metodi Numerici Prova di Laboratorio Esami del Stefano Gualandi
 Metodi Numerici Prova di Laboratorio Esami del 2018 Stefano Gualandi October 11, 2018 ii Premessa Questo documento presenta la raccolta dei testi di esame degli appelli del corso di Metodi Numerici, Prova
Metodi Numerici Prova di Laboratorio Esami del 2018 Stefano Gualandi October 11, 2018 ii Premessa Questo documento presenta la raccolta dei testi di esame degli appelli del corso di Metodi Numerici, Prova
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2014-2015 Lezione 5 Indice 1 Errori nella simulazione Monte Carlo di processi
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2014-2015 Lezione 5 Indice 1 Errori nella simulazione Monte Carlo di processi
Ottimizzazione Statica con Octave
 Ottimizzazione Statica con Octave Domenico Suppa 29 luglio 2013 I punti critici delle funzioni di più variabili possono essere caratterizzati attraverso l esame della matrice hessiana calcolata, appunto,
Ottimizzazione Statica con Octave Domenico Suppa 29 luglio 2013 I punti critici delle funzioni di più variabili possono essere caratterizzati attraverso l esame della matrice hessiana calcolata, appunto,
AM2: Tracce delle lezioni- X Settimana
 AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
x 1 x 2 x 3 x 5 La base iniziale è B 0 = I e risulta x B 0 = , x N 0 = Iterazione 0. Calcolo dei costi ridotti. γ 0 = c N 0 (N 0 ) T c B 0 =
 56 IL METODO DEL SIMPLESSO 7.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
56 IL METODO DEL SIMPLESSO 7.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Integrali doppi. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Discretizzazione equazione del calore Per l equazione usiamo lo schema esplicito p tk+1 (x i ) p tk (x i ) h t p t = σ2 2 p 2 x 2 = σ2 2 p tk (x i+1 ) p tk
Probablità, Statistica e Processi Stocastici Discretizzazione equazione del calore Per l equazione usiamo lo schema esplicito p tk+1 (x i ) p tk (x i ) h t p t = σ2 2 p 2 x 2 = σ2 2 p tk (x i+1 ) p tk
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 6 punti.
 Es. 1 Es. 2 Es. 3 Es. Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 0 Febbraio 2013 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Es. 1 Es. 2 Es. 3 Es. Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 0 Febbraio 2013 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1 Esercizi sulla teoria del portafoglio
 1 Esercizi sulla teoria del portafoglio 1. Sia dato un mercato uniperiodale in cui siano disponibili soltanto due titoli rischiosi A e B caratterizzati da scarto quadratico medio e coefficiente di correlazione
1 Esercizi sulla teoria del portafoglio 1. Sia dato un mercato uniperiodale in cui siano disponibili soltanto due titoli rischiosi A e B caratterizzati da scarto quadratico medio e coefficiente di correlazione
ESAME SCRITTO DI FISICA MODERNA. 22 giugno Traccia di soluzione
 ESAME SCRITTO DI FISICA MODERNA giugno 08 Traccia di soluzione ) Ponendo α = /σ ), il valore medio della posizione è + ψ ˆx ψ = dx ψ ˆx x x ψ = dx ψ x)xψx) = α + dx x e αx x 0), ) e con un semplice cambio
ESAME SCRITTO DI FISICA MODERNA giugno 08 Traccia di soluzione ) Ponendo α = /σ ), il valore medio della posizione è + ψ ˆx ψ = dx ψ ˆx x x ψ = dx ψ x)xψx) = α + dx x e αx x 0), ) e con un semplice cambio
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2013-2014 Lezione 4 Indice 1 Convergenza in legge di processi stocastici 2
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2013-2014 Lezione 4 Indice 1 Convergenza in legge di processi stocastici 2
Serie di Fourier - Esercizi svolti
 Serie di Fourier - Esercizi svolti Esercizio 1 È data la funzione f con domf) = R, periodica di periodo, tale che onda quadra) 1 se < x < fx) = se x = e x = 1 se < x < 1) 1 Calcolare i coefficienti di
Serie di Fourier - Esercizi svolti Esercizio 1 È data la funzione f con domf) = R, periodica di periodo, tale che onda quadra) 1 se < x < fx) = se x = e x = 1 se < x < 1) 1 Calcolare i coefficienti di
Analisi Vettoriale A.A Soluzioni del Foglio 2
 Analisi Vettoriale A.A. 2006-2007 - Soluzioni del Foglio 2 2.1 Esercizio Assegnato il sistema e y + z + x 2 = 0 x 2 + y 2 + z 2 + y 1 = 0 dimostrare che in un intorno del punto (0,0,1) il sistema definisce
Analisi Vettoriale A.A. 2006-2007 - Soluzioni del Foglio 2 2.1 Esercizio Assegnato il sistema e y + z + x 2 = 0 x 2 + y 2 + z 2 + y 1 = 0 dimostrare che in un intorno del punto (0,0,1) il sistema definisce
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
5.7 Esercizi (V Settimana)
 5.7 Esercizi (V Settimana) 7 5.7 Esercizi (V Settimana) 5.7. Sia data f :(R 3 ) (R 3 ) da f(a,b,c) =(a + b, b, a + b + c). Si scriva la f sotto forma del prodotto di un vettore riga per una matrice A;.
5.7 Esercizi (V Settimana) 7 5.7 Esercizi (V Settimana) 5.7. Sia data f :(R 3 ) (R 3 ) da f(a,b,c) =(a + b, b, a + b + c). Si scriva la f sotto forma del prodotto di un vettore riga per una matrice A;.
ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f:
![ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f: ANALISI MATEMATICA 2 Prova scritta 02/07/2012. log(x 2 + 3y 2 ) ) [15 pt] Data la funzione f : dom f R 2 R, f(x, y) = 1 4. [1 pt] calcolare f:](/thumbs/103/158892828.jpg) ANALISI MATEMATICA Prova scritta /7/1 COGNOME e Nome firma 1. [15 pt] Data la funzione f : dom f R R, fx, y) 1 4 logx + 3y ) ) [1 pt] calcolare f: [ pt] Disegnare l insieme dei punti stazionari di f [
ANALISI MATEMATICA Prova scritta /7/1 COGNOME e Nome firma 1. [15 pt] Data la funzione f : dom f R R, fx, y) 1 4 logx + 3y ) ) [1 pt] calcolare f: [ pt] Disegnare l insieme dei punti stazionari di f [
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec. Altro.
 Controlli Automatici A 22 Giugno 11 - Esercizi Si risolvano i seguenti esercizi. Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec. Altro. a.1) Calcolare la trasformata di Laplace X(s) dei seguenti segnali
Controlli Automatici A 22 Giugno 11 - Esercizi Si risolvano i seguenti esercizi. Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec. Altro. a.1) Calcolare la trasformata di Laplace X(s) dei seguenti segnali
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = x 2 + y 3 4y. 4 1, y 2 2(1 + }
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
Probablità, Statistica e Processi Stocastici Riassunto Abbiamo introdotto le equazioni differenziali stocastiche, equazioni del tipo dx t = b (t, X t ) dt + σdb t (o un po più generali) dove B t è il moto
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
4.8 Metodi quasi-newton
 4.8 Metodi quasi-newton Varianti del metodo di Newton in cui invece di usare/invertire la matrice Hessiana di f (x) si estraggono informazioni relative alle derivate seconde dalle variazioni di f (x).
4.8 Metodi quasi-newton Varianti del metodo di Newton in cui invece di usare/invertire la matrice Hessiana di f (x) si estraggono informazioni relative alle derivate seconde dalle variazioni di f (x).
F x 1 = x 1 + x 2. 2x 1 x 2 Determinare la matrice C associata a F rispetto alla base canonica (equivalentemente,
 Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
Corso di Laurea in Fisica. Geometria 1. a.a. 2006-07. Gruppo B. Prof. P. Piazza Esonero del 1/12/06 con soluzione Esercizio. Spazio vettoriale R 2 con base canonica fissata e coordinate associate (x 1,
METODI DI PUNTO FISSO
 METODI DI PUNTO FISSO Sia ϕ : [a, b] R [a, b] continua. Def. α è punto fisso per ϕ se ϕ(α) = α Il metodo di punto fisso è: { x (0) dato x (k+1) = ϕ(x (k) ), per k 0 Scrivere una function per l approssimazione
METODI DI PUNTO FISSO Sia ϕ : [a, b] R [a, b] continua. Def. α è punto fisso per ϕ se ϕ(α) = α Il metodo di punto fisso è: { x (0) dato x (k+1) = ϕ(x (k) ), per k 0 Scrivere una function per l approssimazione
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Minimi quadrati e massima verosimiglianza
 Minimi quadrati e massima verosimiglianza 1 Introduzione Nella scorsa lezione abbiamo assunto che la forma delle probilità sottostanti al problema fosse nota e abbiamo usato gli esempi per stimare i parametri
Minimi quadrati e massima verosimiglianza 1 Introduzione Nella scorsa lezione abbiamo assunto che la forma delle probilità sottostanti al problema fosse nota e abbiamo usato gli esempi per stimare i parametri
Geometria Differenziale 2017/18 Esercizi 3
 Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
PDE lineari primo ordine
 PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
MODELLO DI REGRESSIONE LINEARE. le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza,
 MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
Laboratorio di Calcolo Numerico A.A Laboratorio 4 Risoluzione di sistemi non lineari Metodo di punto fisso
 Laboratorio di Calcolo Numerico A.A. 2007-2008 Laboratorio 4 Risoluzione di sistemi non lineari Metodo di punto fisso Esercizio 1. Risoluzione di sistemi non lineari Si consideri il seguente sistema non
Laboratorio di Calcolo Numerico A.A. 2007-2008 Laboratorio 4 Risoluzione di sistemi non lineari Metodo di punto fisso Esercizio 1. Risoluzione di sistemi non lineari Si consideri il seguente sistema non
LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE. L'ipotesi di razionalità implica che un decisore cerchi di
 LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE L'ipotesi di razionalità implica che un decisore cerchi di individuare la migliore tra tutte le alternative a sua disposizione. Problemi di ottimizzazione =
LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE L'ipotesi di razionalità implica che un decisore cerchi di individuare la migliore tra tutte le alternative a sua disposizione. Problemi di ottimizzazione =
CMP-II Equazioni di Hartree-Fock
 CMP-II Equazioni di Hartree-Fock Dipartimento di Fisica, UniTS 9 marzo 019 1 Equazioni di Hartree-Fock 1.1 Funzioni d onda a singolo determinante di Slater (Fermioni) Consideriamo un Hamiltoniana di Fermioni
CMP-II Equazioni di Hartree-Fock Dipartimento di Fisica, UniTS 9 marzo 019 1 Equazioni di Hartree-Fock 1.1 Funzioni d onda a singolo determinante di Slater (Fermioni) Consideriamo un Hamiltoniana di Fermioni
Esercizi su formula di Itô
 Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
Esercizi su formula di Itô 1. Scrivere il differenziale stocastico dei seguenti processi: (i) X t = B t (ii) X t = t + e B t (iii) X t = B 3 t 3tB t (iv) X t = 1 + t + e B t (v) X t = [B 1 (t)] + [B (t)]
5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate. min f(x) s.v. c i (x) 0 i I c i (x) = 0 i E (1) x R n
 5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate Consideriamo il generico problema di PNL min f(x) s.v. c i (x) 0 i I c i (x) = 0 i E (1) x R n dove f e le c i sono di classe
5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate Consideriamo il generico problema di PNL min f(x) s.v. c i (x) 0 i I c i (x) = 0 i E (1) x R n dove f e le c i sono di classe
3.7 Metodi quasi-newton
 3.7 Metodi quasi-newton Varianti del metodo di Newton in cui invece di usare/invertire la matrice Hessiana di f si estraggono informazioni relative alle derivate seconde dalle variazioni di f. Si genera
3.7 Metodi quasi-newton Varianti del metodo di Newton in cui invece di usare/invertire la matrice Hessiana di f si estraggono informazioni relative alle derivate seconde dalle variazioni di f. Si genera
La miglior approssimazione esiste se le funzioni descrivono un chiuso
 NON SMOOTH Funzione non C 1 tipico esempio massimo numero finito funzioni Φ(x) = max { f i (x), i I, f i C 1 } e anche massimo(sup) puntuale Φ(x) = sup { f t (x), t I, f t C 1 } Esempi a) Max numero finito
NON SMOOTH Funzione non C 1 tipico esempio massimo numero finito funzioni Φ(x) = max { f i (x), i I, f i C 1 } e anche massimo(sup) puntuale Φ(x) = sup { f t (x), t I, f t C 1 } Esempi a) Max numero finito
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Metodi di Ricerca Lineare
 Metodi di Ricerca Lineare Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com Metodi di Ottimizzazione
Metodi di Ricerca Lineare Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com Metodi di Ottimizzazione
FM1 - Equazioni differenziali e meccanica. Il metodo di variazione delle costanti (Livia Corsi)
 Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
NLP KKT 1. Le condizioni necessarie di ottimo per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J
 NLP KKT 1 Le condizioni necessarie di ottimo per il problema min f o (x) g i (x) 0 i I h j (x) = 0 j J sono, riferite ad un punto ammissibile x*, μ 0 f o (x*) + i I μ i g i (x*) + j J λ j h j (x*) = 0
NLP KKT 1 Le condizioni necessarie di ottimo per il problema min f o (x) g i (x) 0 i I h j (x) = 0 j J sono, riferite ad un punto ammissibile x*, μ 0 f o (x*) + i I μ i g i (x*) + j J λ j h j (x*) = 0
Complementi di Matematica e Calcolo Numerico A.A Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie
 Complementi di Matematica e Calcolo Numerico A.A. 2014-2015 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il Problema di Cauchy: { y (t) = f(t, y(t)) t I, y(t 0 ) =
Complementi di Matematica e Calcolo Numerico A.A. 2014-2015 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il Problema di Cauchy: { y (t) = f(t, y(t)) t I, y(t 0 ) =
Analisi Matematica 2. Ottimizzazione in due variabili. Ottimizzazione in due variabili 1 / 31
 Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
Analisi Matematica 2 Ottimizzazione in due variabili Ottimizzazione in due variabili 1 / 31 Ottimizzazione. Figure: Massimi e minimi relativi (o locali), Massimi e minimi assoluti (o globali) Ottimizzazione
DEFINIZIONE. u (u; v); α 3. v (u; v); α 3. ha rango 2 in ogni punto della parametrizzazione. DEFINIZIONE
 DEFINIZIONE Una superficie in R 3 è un applicazione α : U R 3, di classe almeno C. In realtà, tratteremo solamente superfici di classe C. Inoltre, U R deve essere un aperto, e α deve essere iniettiva.
DEFINIZIONE Una superficie in R 3 è un applicazione α : U R 3, di classe almeno C. In realtà, tratteremo solamente superfici di classe C. Inoltre, U R deve essere un aperto, e α deve essere iniettiva.
min 2x 1 +4x 2 2x 3 +2x 4 x 1 +4x 2 +2x 3 + x 4 =6 2x 1 + x 2 +2x 3 + x 5 =3 x 0.
 5 IL METODO DEL SIMPLESSO 6.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
5 IL METODO DEL SIMPLESSO 6.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
ẋ + a 0 x = 0 (1) Dimostrazione. Risolvendo la (1) per separazione di variabili, troviamo x(t) = c 0 e a0t (2) φ :R S 1 ẍ + a 1 ẋ + a 0 x = 0 (3)
 Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 30 gennaio 2017
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 30 gennaio 2017 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. I soli risultati,
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 30 gennaio 2017 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. I soli risultati,
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Risoluzione di sistemi lineari sparsi e di grandi dimensioni
 Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Metodi Matematici per l Ingegneria - 08/07/ Parte A
 Metodi Matematici per l Ingegneria - 08/07/2013 - Parte A Esercizio: 1-OT Si consideri la funzione f(x = (x, y)) = a x 2 + b y 2 + c x y + d y, con a, b, c, d R: 1. trovare i punti stazionari; 2. scrivere
Metodi Matematici per l Ingegneria - 08/07/2013 - Parte A Esercizio: 1-OT Si consideri la funzione f(x = (x, y)) = a x 2 + b y 2 + c x y + d y, con a, b, c, d R: 1. trovare i punti stazionari; 2. scrivere
5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate
 5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate Consideriamo il generico problema di PNL min f (x) s.v. c i (x) 0 i I c i (x) = 0 i E (1) x R n dove f e le c i sono di classe
5.6 Metodo di penalità e metodo basato sulle funzioni lagrangiane aumentate Consideriamo il generico problema di PNL min f (x) s.v. c i (x) 0 i I c i (x) = 0 i E (1) x R n dove f e le c i sono di classe
Esercizio 1. Esercizio 2
 Sia data la matrice A A(α) = Esercizio α 2 2α 2 2, α R.) determinare per quali valori del parametro reale α é verificata la condizione necessaria e sufficiente di convergenza per il metodo di Jacobi;.2)
Sia data la matrice A A(α) = Esercizio α 2 2α 2 2, α R.) determinare per quali valori del parametro reale α é verificata la condizione necessaria e sufficiente di convergenza per il metodo di Jacobi;.2)
Matematica con elementi di Informatica
 Funzioni a più variabili Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Funzioni
Funzioni a più variabili Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche. () Funzioni
MATEMATICA GENERALE APPLICAZIONI DI MATEMATICA PER L ECONOMIA 1/6/2011 A. NOME e COGNOME Matricola. x = x 3 + 1
 1/6/2011 A NOME e COGNOME Matricola I parte: quesiti preliminari (riportare le soluzioni su questo foglio, giusti cando la risposta) i) Si risolva l equazione: x + 5 7 = x 3 + 1 ii) Si risolva la disequazione:
1/6/2011 A NOME e COGNOME Matricola I parte: quesiti preliminari (riportare le soluzioni su questo foglio, giusti cando la risposta) i) Si risolva l equazione: x + 5 7 = x 3 + 1 ii) Si risolva la disequazione:
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
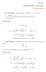 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Teoria dei Fenomeni Aleatori AA 2012/13. Il Concetto di Distribuzione Condizionata ( )
 Il Concetto di Distribuzione Condizionata Se B è un evento, la probabilità di un evento A condizionata a B vale: ponendo: P A B = ( ) P A B P B A = { x} si giunge al concetto di distribuzione condizionata
Il Concetto di Distribuzione Condizionata Se B è un evento, la probabilità di un evento A condizionata a B vale: ponendo: P A B = ( ) P A B P B A = { x} si giunge al concetto di distribuzione condizionata
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Equazioni e sistemi non lineari
 Equazioni e sistemi non lineari Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 4 novembre 2007 Outline 1 Ricerca degli zeri di una funzione Problema e definizioni Metodo di
Equazioni e sistemi non lineari Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 4 novembre 2007 Outline 1 Ricerca degli zeri di una funzione Problema e definizioni Metodo di
Complementi di Matematica e Calcolo Numerico A.A Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie
 Complementi di Matematica e Calcolo Numerico A.A. 2010-2011 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il seguente Problema di Cauchy: Trovare una funzione y : I
Complementi di Matematica e Calcolo Numerico A.A. 2010-2011 Laboratorio 11 - Metodi numerici per equazioni differenziali ordinarie Cosideriamo il seguente Problema di Cauchy: Trovare una funzione y : I
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Energia immessa da un white noise Ricordiamo la motivazione applicativa della volta scorsa: un white noise additivo, messo in un equazione che nel caso deterministico
Probablità, Statistica e Processi Stocastici Energia immessa da un white noise Ricordiamo la motivazione applicativa della volta scorsa: un white noise additivo, messo in un equazione che nel caso deterministico
Esercizi 2: Curve dello spazio Soluzioni
 Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
LEZIONE ICO
 LEZIONE ICO 9-10-2009 Argomento. Rassegna dei metodi numerici utilizzabili per la soluzione di problemi di ottimizzazione statica. Metodi del gradiente e di Newton e loro derivati. Metodi di penalita e
LEZIONE ICO 9-10-2009 Argomento. Rassegna dei metodi numerici utilizzabili per la soluzione di problemi di ottimizzazione statica. Metodi del gradiente e di Newton e loro derivati. Metodi di penalita e
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche I 15 gennaio 2004
 Esame di Istituzioni di Matematiche I 5 gennaio 2004 Monaco 02BJVa W0034 60 De ngelis 02BJVb W003 630 Pieraccini 0BJU Biglio 03BJV Esame completo Prova intermedia Teoria: teoremi sulle funzioni continue.
Esame di Istituzioni di Matematiche I 5 gennaio 2004 Monaco 02BJVa W0034 60 De ngelis 02BJVb W003 630 Pieraccini 0BJU Biglio 03BJV Esame completo Prova intermedia Teoria: teoremi sulle funzioni continue.
Esame di Calcolo delle Probabilità del 4 luglio 2006 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esame di Calcolo delle Probabilità del 4 luglio 26 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione:
Esame di Calcolo delle Probabilità del 4 luglio 26 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione:
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
(a) E è convesso; (b) (1, 0) non è punto interno; (c) E non è misurabile.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 3 4 5 6 A Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni A.A.
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 3 4 5 6 A Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni A.A.
7 febbraio 2019, es.1) Programmazione lineare
 7 febbraio 09, es.) Programmazione lineare Discutere il seguente problema di Programmazione lineare: trovare, se esiste, il massimo di p(x, x, x 3 ) = x - x + 6 x 3 con i vincoli x k 0 ( k 3) e x - 3 x
7 febbraio 09, es.) Programmazione lineare Discutere il seguente problema di Programmazione lineare: trovare, se esiste, il massimo di p(x, x, x 3 ) = x - x + 6 x 3 con i vincoli x k 0 ( k 3) e x - 3 x
9.3 Il metodo dei minimi quadrati in formalismo matriciale
 9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
Cenni di ottimizzazione dinamica
 Cenni di ottimizzazione dinamica Testi di riferimento: K. Dixit Optimization in Economic Theory. Second Edition, 1990, Oxford: Oxford University Press. A. C. Chiang Elements of Dynamic Optimization, 1992,
Cenni di ottimizzazione dinamica Testi di riferimento: K. Dixit Optimization in Economic Theory. Second Edition, 1990, Oxford: Oxford University Press. A. C. Chiang Elements of Dynamic Optimization, 1992,
Progr. Non Lineare: algoritmi
 Progr. Non Lineare: algoritmi Fabio Schoen schoen@ing.unifi.it http://globopt.dsi.unifi.it/users/schoen A.A. 22-23 Programmazione Non Lineare: Cenni sugli algoritmi di ottimizzazione locale Schema generale
Progr. Non Lineare: algoritmi Fabio Schoen schoen@ing.unifi.it http://globopt.dsi.unifi.it/users/schoen A.A. 22-23 Programmazione Non Lineare: Cenni sugli algoritmi di ottimizzazione locale Schema generale
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Capitolo 3: Ottimizzazione non vincolata parte III. E. Amaldi DEI, Politecnico di Milano
 Capitolo 3: Ottimizzazione non vincolata parte III E. Amaldi DEI, Politecnico di Milano 3.4 Metodi di ricerca unidimensionale In genere si cerca una soluzione approssimata α k di min g(α) = f(x k +αd k
Capitolo 3: Ottimizzazione non vincolata parte III E. Amaldi DEI, Politecnico di Milano 3.4 Metodi di ricerca unidimensionale In genere si cerca una soluzione approssimata α k di min g(α) = f(x k +αd k
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Introduzione al Metodo agli Elementi Finiti (FEM) (x, y) Γ Tale formulazione viene detta Formulazione forte del problema.
 Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese
 Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese Università degli Studi di Milano Laboratory of Applied Intelligent Systems (AIS-Lab) Dipartimento di Informatica borghese@di.unimi.it
Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese Università degli Studi di Milano Laboratory of Applied Intelligent Systems (AIS-Lab) Dipartimento di Informatica borghese@di.unimi.it
Statistica Matematica e Trattamento Informatico dei Dati. Analisi Matematica 3. Esercizi svolti nelle lezioni. V. Del Prete
 Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
Statistica Matematica e Trattamento Informatico dei Dati A.A.00-0 Analisi Matematica 3 Esercizi svolti nelle lezioni V. Del Prete Numeri complessi Argomenti ed esercizi svolti nelle lezioni 30.09.00 e
DERIVATE E LORO APPLICAZIONE
 DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
Esercitazione 7: Aggiornamento minimi quadrati.
 Esercitazione 7: Aggiornamento minimi quadrati. Esercizio 1 Per calcolare il piano di equazione p(x) = a+b xc y che minimizza gli scarti quadratici relativi alle misure (x i, y i, z i ) è necessario risolvere
Esercitazione 7: Aggiornamento minimi quadrati. Esercizio 1 Per calcolare il piano di equazione p(x) = a+b xc y che minimizza gli scarti quadratici relativi alle misure (x i, y i, z i ) è necessario risolvere
Rischi di mercato. Francesco Menoncin
 Rischi di mercato Francesco Menoncin 6-0-0 Sommario Le risposte devono essere C.C.C (Chiare, Concise e Corrette). Il tempo a disposizione è di (due) ore. Esercizi. Su un mercato completo con tre stati
Rischi di mercato Francesco Menoncin 6-0-0 Sommario Le risposte devono essere C.C.C (Chiare, Concise e Corrette). Il tempo a disposizione è di (due) ore. Esercizi. Su un mercato completo con tre stati
Analisi Matematica II per il corso di Laurea Triennale in Matematica. Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca
 Analisi Matematica II per il corso di Laurea Triennale in Matematica Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca Esercizi: estremi liberi e vincolati per funzioni in piú variabili.
Analisi Matematica II per il corso di Laurea Triennale in Matematica Dipartimento di Matematica e Applicazioni, Università di Milano Bicocca Esercizi: estremi liberi e vincolati per funzioni in piú variabili.
Kernel Methods. Corso di Intelligenza Artificiale, a.a Prof. Francesco Trovò
 Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 settembre 2007 Outline 1 M-file di tipo Script e Function Script Function 2 Elementi di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 settembre 2007 Outline 1 M-file di tipo Script e Function Script Function 2 Elementi di programmazione
Fondamenti di Automatica
 Fondamenti di Automatica Introduzione e modellistica dei sistemi Introduzione allo studio dei sistemi Modellistica dei sistemi dinamici elettrici Modellistica dei sistemi dinamici meccanici Modellistica
Fondamenti di Automatica Introduzione e modellistica dei sistemi Introduzione allo studio dei sistemi Modellistica dei sistemi dinamici elettrici Modellistica dei sistemi dinamici meccanici Modellistica
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Esercizi Di Geometria 1 (BAER) Canale 1
 Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Metodi e Modelli dei Mercati Finanziari
 Diario delle lezioni di Metodi e Modelli dei Mercati Finanziari a.a. 2018/2019 www.mat.uniroma2.it/~caramell/did 1819/mmmf.htm Parte I: Opzioni Europee e Metodi Monte Carlo Lezioni 1, 2-02/10/2018 Breve
Diario delle lezioni di Metodi e Modelli dei Mercati Finanziari a.a. 2018/2019 www.mat.uniroma2.it/~caramell/did 1819/mmmf.htm Parte I: Opzioni Europee e Metodi Monte Carlo Lezioni 1, 2-02/10/2018 Breve
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
