RETROAZIONE A V. = segnale d ingresso del blocco dell amplificatore retroazionato. = segnale d uscita A = amplificatore β = rete di retroazione
|
|
|
- Giulia Corinna Poli
- 8 anni fa
- Visualizzazioni
Transcript
1 ETOZOE Un amplcat è sggtt a azn quand una pat dl sgnal d uscta vn ptat n ngss smmat algbcamnt al sgnal d ngss. n un amplcat taznat è psnt una t β (bta) d tazn ch pta n ngss una pat dl sgnal d uscta. l sgnal taznat s smma algbcamnt al sgnal d ngss. S l sgnal d tazn è n as cn qull d ngss, s avà la smma d du cn cnsgunt aumnt dl sgnal d ngss: n qust cas s pala d tazn pstva. S l sgnal d tazn è n ppszn d as cn qull d ngss, s avà la dnza d du, cn cnsgunt dmnuzn dl sgnal d ngss: n qust cas s pala d tazn ngatva. a azn ngatva è quntmnt utlzzata nlla pgttazn dgl amplcat. a pdta d guadagn ch ssa cmpta è cmpnsat da sgncatv vantagg ch s pssn ttn. n patcla, l guadagn può ss s patcamnt ndpndnt dall caattstch dnamch d cmpnnt attv utlzzat cm amplcat; può ss mglata la spsta n qunza, la dstsn dl sgnal d'uscta l appt sgnal/um; s pssn ttn val ttmal p quant guada la sstnza d'uscta la sstnza d'ngss. Qust ultm asptt è lgat al tp d azn ngatva, cè al md cn cu vn plvat n uscta l sgnal da nva alla t d azn, d al md cn cu avvn la smma ta l sgnal d ngss qull d azn. a azn pstva è da vtas n tutt l applcazn lna, mnt s usa n qu dspstv ch dvn lava ta l tnsn d satuazn, qual cmpaat cn sts gl scllat snusdal. schma a blcch d un amplcat taznat è ptat n gua. β sgnal d ngss dl blcc dll amplcat taznat sgnal d uscta amplcat β t d tazn sgnal d ngss dl blcc amplcat sgnal d tazn amplcat taznat
2 l cchtt all ngss è un nd smmat n cu cnvgn sgnal da smma algbcamnt. ltt β, n blcch, ndcan l unzn d tasmnt dlla t d azn dll amplcat nn taznat. Calcl d l dtmna s suppn ch la t d tazn β nn cach l'uscta, cè la tnsn d'uscta nn camba sa ch s cllga β sa ch la s scllgh. S scvn l lazn unznal d blcch: nd smmat blcc amplcat nn taznat β β blcc d tazn β β Suppnnd ch β san.d.t. al, s ha: S β, β, > 0 < 0 β > 0 sn n as β > > tazn pstva S β cndzn usata p gl scllat snusdal β S β > 0 β < 0 < 0 > 0 β < 0 sn n ppszn d as β < < tazn ngatva l cas sult β >>, nl dnmnat dll spssn d può ss tascuat sptt al pdtt β :
3 β >> β β n tal cndzn l unznamnt dll amplcat taznat, ssa la sua.d.t, dpnd dalla sla t bta d tazn, ch è una t passva, nn dpnd pù dall amplcat. a cndzn β >> s ttn utlzzand amplcat cn lvata amplcazn, qual gl amplcat paznal. Pptà dlla tazn ngatva Stabltà dll'amplcazn ad anll chus Fssata l'ampzza dlla tnsn d'ngss, un aumnt d amplcazn, suppst cstant β, pduc un aumnt dl guadagn d'anll β, cn cnsgunt duzn dl sgnal d'ngss dl blcc, ch tnd a du l'aumnt dl sgnal d'uscta, ssa cmpnsa autmatcamnt, n buna pat, l vaazn dl sgnal d'uscta p vaazn d. Una quantzzazn dl mglamnt dlla stabltà dll'amplcazn s ttn cnntand l vaazn latv dll'amplcazn cn snza tazn. d ndcand cn la vaazn latva dll'amplcazn snza tazn cn d la vaazn latva dll'amplcazn cn tazn, s ha: β β d d β ( β) ( β) d dvdnd d p ( ) d β p, s ha: β d β d d ( β) β d d ll qunza d cnt banda, ssnd β >, sulta <, ssa la stabltà dll'amplcazn mgla n psnza d tazn ngatva. umnt dl appt sgnal/um um (ns) dstub, tnsn ndsdat d qunza lvata ch s svappngn al sgnal utl, pssn ss pdtt da caus stn all'amplcat (camp lttmagntc, ppl dll'almntazn) ppu ntnamnt all'amplcat (dv tmch, um d cmpnnt). Una msua dl ctt unznamnt dll'amplcat latvamnt alla psnza d um vn data dal appt sgnal/um (S/) spss n db. Tant pù alt sulta qust appt, tant mgl saà l unznamnt dll'amplcat. 3
4 Cnsdam l cas d un dstub n gua. ch nasca all'uscta dll'amplcat, cm β n assnza d tazn, 0, s ha: S dv è l sgnal utl è l sgnal d um. n psnza d tazn, s ha: ( ) ( β ) β β β Pché appsnta l sgnal utl β β l sgnal d um, s ha: S l appt sgnal/um snza cn tazn sta nvaat (a patà d sgnal d'ngss). l sgnal d'uscta, sptt al cas snza tazn, sulta dtt d un att β. S nvc s mantn naltata l'ampzza dl sgnal d'uscta (a patà d sgnal d'uscta), aumntand l sgnal d'ngss d β vlt, s ha: [ ( β) ] [ ( β) β ] β ( β) β Pché appsnta l sgnal utl β l sgnal d um, s ha: 4
5 S ( β) a patà d sgnal d'uscta l appt sgnal/um, cn tazn ngatva, mgla d un att β. duzn dlla dstsn amnca S ha dstsn amnca dl sgnal d'uscta quand vngn ntssat zn d unznamnt nn lna d dspstv amplcat. n tal cas s ha una dstsn d ampzza dl sgnal d'uscta. Un sgnal snusdal dstt n ampzza è svluppabl n s d Fu, l cu pm tmn è un sgnal snusdal nn dstt dlla stssa qunza (ndamntal) pù tmn snusdal (amnch) d qunza dppa, tpla, cc., dlla ndamntal. Tal amnch d dn sup al pm pssn ss vst cm sgnal d um ch s svappngn a qull d'uscta (amnca dl pm dn). Ptant, csì cm la tazn ngatva duc a patà d sgnal d'uscta l um d un att β, all stss md sn dtt l amnch d dn sup al pm cmpnnt l sgnal dstt. Banda passant l pdtt banda-guadagn, nt cm qunza d tanszn T, è una gua d mt p l'amplcat, ssa tal pdtt è cstant sa n assnza d tazn ngatva sa n psnza d tazn ngatva: BW BW β ( β) BW n patcla, la qunza d tagl n s duc d un att qunza d tagl sup aumnta d un att β. β, la db ( β) db s BW s s BW s β ; s s ( β) 5
6 Tp d tazn mdaltà d cllgamnt dlla t d tazn cn l'amplcat bas sn n dtta lazn cl tp d gandzza plvata cnntata. S la gandzza plvata all'uscta dll'amplcat è la tnsn psnt a cap dl cac, la azn vn dtta d tnsn, vv, l quadpl d azn è cllgat n paalll all'uscta dll'amplcat bas. S, nvc, la gandzza plvata all'uscta dll'amplcat è la cnt n, la azn vn dtta d cnt, vv, l quadpl d azn è cllgat n s all'uscta dll'amplcat bas. S l cnnt d sgnal d'ngss avvn stt ma d dnza ta tnsn,, l ccut d'uscta dl quadpl d azn qull d'ngss dll'amplcat bas sn pst n s, alzzand una magla ch nclud anch la sgnt dal d sgnal. S l cnnt d sgnal d'ngss avvn stt ma d dnza ta cnt,, l ccut d'uscta dl quadpl d azn qull d'ngss dll'amplcat bas cnvgn ad un nd dv cnluscn l cnt, n tal cas l cllgamnt ta l ccut d'uscta dl quadpl d azn qull d'ngss dll'amplcat bas è d tp paalll. amplcat bas β β Cntazn d tnsn-s β amplcat bas β Cntazn d tnsn-paalll 6
7 amplcat bas β β Cntazn d cnt-s β amplcat bas β Cntazn d cnt-paalll Tp d az n Tns ns Tns npaall l C nts C ntpaall l Gand zza cnt llata Tns n Tns n C nt C nt Gand zza d a zn Tns n C nt Tns n C nt.d.t. d G.d.t. d β.d.t. d β ( ) β β β G G β ( ) β G G β β β ( β ) G β ( β ) 7
RISPOSTA IN FREQUENZA DI UN AMPLIFICATORE
 Unvstà dgl Stud d ma T Vgata Dpatmnt d Ing. Elttnca cs d ELETTONIA APPLIATA Pf. Fanc GIANNINI ISPOSTA IN FEQUENZA DI UN AMPLIFIATOE II / 1 INTODUZIONE Dtmna la spsta n fqunza d un amplfcat sgnfca stma
Unvstà dgl Stud d ma T Vgata Dpatmnt d Ing. Elttnca cs d ELETTONIA APPLIATA Pf. Fanc GIANNINI ISPOSTA IN FEQUENZA DI UN AMPLIFIATOE II / 1 INTODUZIONE Dtmna la spsta n fqunza d un amplfcat sgnfca stma
Polarizzazione del BJT
 Plazzazn dl BJT Il ccut d plazzazn, ccut D, p mp l punt d la dl BJT quand l gnal n ng è null P un BJT utlzzat cm amplfcat, p l punt d la è al cnt dlla gn atta Il ccut D d gaant l pù pl : - la taltà dl
Plazzazn dl BJT Il ccut d plazzazn, ccut D, p mp l punt d la dl BJT quand l gnal n ng è null P un BJT utlzzat cm amplfcat, p l punt d la è al cnt dlla gn atta Il ccut D d gaant l pù pl : - la taltà dl
Polarizzazione del BJT
 Plazzazn dl BJT Il ccut d plazzazn, ccut D, p mp l punt d la dl BJT quand l gnal n ng è null P un BJT utlzzat cm amplfcat, p l punt d la è al cnt dlla gn atta Il ccut D dbb gaant l pù pbl : - la tabltà
Plazzazn dl BJT Il ccut d plazzazn, ccut D, p mp l punt d la dl BJT quand l gnal n ng è null P un BJT utlzzat cm amplfcat, p l punt d la è al cnt dlla gn atta Il ccut D dbb gaant l pù pbl : - la tabltà
a) Resistenza bleeder Rb (per garantire il funzionamento continuo)
 Prgtt d cnvrttr push-pull pcfch: 36-7 V (applc. Tlcm) V, 0 A (uscta slata) Prcsn: statca %, dnamca 5% rchd d garantr l funznamnt cntnu clt prgttual: frqunza d cmmutazn fs50 khz wtch: Msft Frqunza d uscta
Prgtt d cnvrttr push-pull pcfch: 36-7 V (applc. Tlcm) V, 0 A (uscta slata) Prcsn: statca %, dnamca 5% rchd d garantr l funznamnt cntnu clt prgttual: frqunza d cmmutazn fs50 khz wtch: Msft Frqunza d uscta
teoria dell Orbitale Molecolare - Molecular Orbital (MO)
 toa dll Obtal olcola - olcula Obtal (O) L ng l funzon d onda dgl stat stazona d un sstma quantstco sono dat dall soluzon dlla quazon d Schodng: P un sstma molcola, composto da nucl d ltton la Ψ è funzon
toa dll Obtal olcola - olcula Obtal (O) L ng l funzon d onda dgl stat stazona d un sstma quantstco sono dat dall soluzon dlla quazon d Schodng: P un sstma molcola, composto da nucl d ltton la Ψ è funzon
L energia potenziale della forza elettrostatica
 L ngia ptnzial dlla fza lttstatica L ngia ptnzial dlla fza di Culmb Cnsidiam una caica di pva q ch si spsta dal punt inizial A al punt final B stt l azin dlla fza di Culmb F, scitata dalla sgnt q. Il lav
L ngia ptnzial dlla fza lttstatica L ngia ptnzial dlla fza di Culmb Cnsidiam una caica di pva q ch si spsta dal punt inizial A al punt final B stt l azin dlla fza di Culmb F, scitata dalla sgnt q. Il lav
Il Progress Test nei Corsi di Laurea delle Professioni Sanitarie
 Il Pgss Tst n Cs d Lu dll Pfssn Snt Pl Pllstn (Psdnt C.d.L. n Fstp) Luc Btzz (Cdnt C.d.L. n Fstp) Unvstà d Blgn 1 Pgss Tst Infm Fstpst PROFESSIONI CHE HANNO PARTECIPATO Osttch (ch hnn sgut un pcdu plll)
Il Pgss Tst n Cs d Lu dll Pfssn Snt Pl Pllstn (Psdnt C.d.L. n Fstp) Luc Btzz (Cdnt C.d.L. n Fstp) Unvstà d Blgn 1 Pgss Tst Infm Fstpst PROFESSIONI CHE HANNO PARTECIPATO Osttch (ch hnn sgut un pcdu plll)
ITALIA REPUBBLICA Francobolli nuovi
 ITALIA REPUBBLICA Fnll nuv n 113 A pt l l 6 6 ntsm ntsm Gnt Gnt ll ll fltl fltl l 8, l l 8, t vl l t pstl vl tln pstl sn mht u. Qull lfnum pp ll z stt qull ll Pst stt Itln. qull Qust ll llzn Pst Itln..Qust
ITALIA REPUBBLICA Fnll nuv n 113 A pt l l 6 6 ntsm ntsm Gnt Gnt ll ll fltl fltl l 8, l l 8, t vl l t pstl vl tln pstl sn mht u. Qull lfnum pp ll z stt qull ll Pst stt Itln. qull Qust ll llzn Pst Itln..Qust
GLI I M PIANTI SONO LA SOLUZIONE!
 QUALI SONO I VANTAGGI DI UN IMPIANTO DENTALE? TESTIMONIANZE Mglra dl cfrt dlla qutà d vta Dnqu Mastcazn ffic, 4 8 n UNO O PIU DENTI MANCANTI? prvav dlrs dd a dvat a fr r l lt l ld «Il st acvl cn l ca udn.
QUALI SONO I VANTAGGI DI UN IMPIANTO DENTALE? TESTIMONIANZE Mglra dl cfrt dlla qutà d vta Dnqu Mastcazn ffic, 4 8 n UNO O PIU DENTI MANCANTI? prvav dlrs dd a dvat a fr r l lt l ld «Il st acvl cn l ca udn.
Calcolo della funzione d uscita per un generico segnale d'ingresso
 Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
Drar nrn Il crcu drar nrn è un dsps ch dà n usca un sgnal prprznal alla draa dl sgnal d ngrss; ssa la rma d nda d'usca è la draa dlla rma d nda d ngrss. Un crcu drar è qull rpra n gura. alcl dlla unzn
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
Risorse Umane DETERMINAZIONE DIRIGENZIALE N 0308 DEL 10/05/2018. l b A D O T T A u
 Dtmn 2018/RU/0308 d 10/05/2018 Pgn 1 d 5 Rss Umn n DETERMINAZIONE DIRIGENZIALE N 0308 DEL 10/05/2018 I DIRETTORE d stt Rss Umn A D O T T A L Dtmnn dgn vnt ggtt: INDIZIONE DI CONCORSO PUBBLICO, PER TITOLI
Dtmn 2018/RU/0308 d 10/05/2018 Pgn 1 d 5 Rss Umn n DETERMINAZIONE DIRIGENZIALE N 0308 DEL 10/05/2018 I DIRETTORE d stt Rss Umn A D O T T A L Dtmnn dgn vnt ggtt: INDIZIONE DI CONCORSO PUBBLICO, PER TITOLI
Errori a regime per controlli in retroazione unitaria
 Appunt d ontoll Autoatc Eo a g n sst n toazon Eo a g p contoll n toazon untaa... Eo a g nlla sposta al gadno (o d poszon)... Eo a g nlla sposta alla apa (o d vloctà)...3 Eo a g nlla sposta alla paabola
Appunt d ontoll Autoatc Eo a g n sst n toazon Eo a g p contoll n toazon untaa... Eo a g nlla sposta al gadno (o d poszon)... Eo a g nlla sposta alla apa (o d vloctà)...3 Eo a g nlla sposta alla paabola
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
WP1X - WP2X. WP1X - Bollitore Inox AISI 316L per pompe di calore WP2X - Bollitore Inox AISI 316L per pompe di calore e solare CARATTERISTICHE TECNICHE
 WP1X - WPX Pdtt WP1X - Bllt Inx AISI 31L p pmp d cal WPX - Bllt Inx AISI 31L p pmp d cal sla Bllt n acca Inx AISI 31L p la pdzn l stccagg d Aca Calda Santaa dtat d n d scambat d cal a spntn fss ntn ad
WP1X - WPX Pdtt WP1X - Bllt Inx AISI 31L p pmp d cal WPX - Bllt Inx AISI 31L p pmp d cal sla Bllt n acca Inx AISI 31L p la pdzn l stccagg d Aca Calda Santaa dtat d n d scambat d cal a spntn fss ntn ad
RISPOSTA IN ALTA FREQUENZA DI UN AMPLIFICATORE
 Untà dgl Stud d ma T Vgata Dpatmnt d Ing. Elttna d ELETTONIA APPLIATA Pf. Fan GIANNINI ISPOSTA IN ALTA FEQUENZA DI UN AMPLIFIATOE II / 1 ITEIO GENEALE PE DETEMINAE f up V a3 E dgn 1 - a1 a2 L2 L1 2 All
Untà dgl Stud d ma T Vgata Dpatmnt d Ing. Elttna d ELETTONIA APPLIATA Pf. Fan GIANNINI ISPOSTA IN ALTA FEQUENZA DI UN AMPLIFIATOE II / 1 ITEIO GENEALE PE DETEMINAE f up V a3 E dgn 1 - a1 a2 L2 L1 2 All
ALLEGATO B. Individuazione delle aree di interesse archeologico ai sensi dell'articolo 5, punto 2 del PTP Cilento Costiero
 LLEGTO B Indvduzn dll d ntss chlgc sns dll'tcl 5, punt 2 dl PTP lnt st Il mun d n Gvnn P, d gg, spvvst d stumntzn ubnstc, h vvt ll fn dl 2012 l lv d lbzn dl pp Pn Ubnstc munl. nfmmnt ll pvsn dl Rglmnt
LLEGTO B Indvduzn dll d ntss chlgc sns dll'tcl 5, punt 2 dl PTP lnt st Il mun d n Gvnn P, d gg, spvvst d stumntzn ubnstc, h vvt ll fn dl 2012 l lv d lbzn dl pp Pn Ubnstc munl. nfmmnt ll pvsn dl Rglmnt
Circolare n 1/2012 A TUTTI GLI UFFICI PAGHE LORO SEDI. Marghera, 30 Gennaio 2012
 Cicla n 1/2012 A TUTTI GLI UFFICI PAGHE LORO SEDI Magha, 30 Gnnai 2012 OGGETTO : Accd Cav Cdaii p Imps in Tasfta. Dnunc p canti fac simil di mdulistica. Siam a sgnalavi l imptant accd aggiunt cn la Cdaii
Cicla n 1/2012 A TUTTI GLI UFFICI PAGHE LORO SEDI Magha, 30 Gnnai 2012 OGGETTO : Accd Cav Cdaii p Imps in Tasfta. Dnunc p canti fac simil di mdulistica. Siam a sgnalavi l imptant accd aggiunt cn la Cdaii
ESERCIZI - PRIMA PARTE
 ESERCIZI - PRIM PRTE Gl src d cu s dca umr paa s tratt dal tst SSalsa Squllat Esrc d Matmatca vl d Zachll Prlmar prcp d du 6 a p 7 a p 6 7 8 9 a p 9 7 8 9 a p 8 a p a p Rslvr l sut dsqua: 6 6 Cct bmal
ESERCIZI - PRIM PRTE Gl src d cu s dca umr paa s tratt dal tst SSalsa Squllat Esrc d Matmatca vl d Zachll Prlmar prcp d du 6 a p 7 a p 6 7 8 9 a p 9 7 8 9 a p 8 a p a p Rslvr l sut dsqua: 6 6 Cct bmal
Transistore bipolare a giunzione (BJT)
 Tansste plae a unzne (BJT) Pate 2 www.de.n.un.t/pes/mast/ddattca.htm (esne del 29-5-2012) mpe del tansste cme amplfcate lleand una esstenza al cllette s ttene una tensne dpendente dalla tensne B Nella
Tansste plae a unzne (BJT) Pate 2 www.de.n.un.t/pes/mast/ddattca.htm (esne del 29-5-2012) mpe del tansste cme amplfcate lleand una esstenza al cllette s ttene una tensne dpendente dalla tensne B Nella
CAMPO LONTANO GENERATO DA UNA APERTURA
 Potnzal Vtto Magntco P l campo d sognt magntch (aptu) occo utlzza l dual dl potnzal vtto A (utlzzato p l cont lttch) ch vn ndcato con vn dtto potnzal vtto magntco o d tzgald. all quazon d Maxwll s ha,
Potnzal Vtto Magntco P l campo d sognt magntch (aptu) occo utlzza l dual dl potnzal vtto A (utlzzato p l cont lttch) ch vn ndcato con vn dtto potnzal vtto magntco o d tzgald. all quazon d Maxwll s ha,
REPUBBLICA ITALIANA. (Poste italiane) NUOVI anno 2012 ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE
 REPUBBLICA ITALIANA fnll n (Pst tln) NUOVI nn ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE A pt l 6 ntsm Gnt ll fltl l 8, l t vl pstl tln sn mht u. Qull lfnum pp ll z stt qull ll Pst Itln. Qust
REPUBBLICA ITALIANA fnll n (Pst tln) NUOVI nn ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE A pt l 6 ntsm Gnt ll fltl l 8, l t vl pstl tln sn mht u. Qull lfnum pp ll z stt qull ll Pst Itln. Qust
COMPARATORI. Comparatore invertente
 COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
COMPAATOI Un cmpaate è un ccut ce a due pssbl val d uscta, medante qual gnala l sultat del cnfnt delle tensn su due ngess amplfcate peaznale ad anell apet csttusce un cmpaate mplce, ce cnfnta un gnale
l f o e l M e s s i c o, m e n t r e a n o r d c o n f i La Florida è uno Stato federato
 FLORIDA TERRITORIO, CLIMA d E AMBIENTI l f l M s s i c, m n t r a n r d c n f i La Flrida è un Stat fdrat mridinal dgli Stati Uniti d'amrica..si stnd su buna part dlla pnisla d è bagnata ad vst dal Glf
FLORIDA TERRITORIO, CLIMA d E AMBIENTI l f l M s s i c, m n t r a n r d c n f i La Flrida è un Stat fdrat mridinal dgli Stati Uniti d'amrica..si stnd su buna part dlla pnisla d è bagnata ad vst dal Glf
ELENCO RIEPILOGATIVO DELLE CESSIONI INTRACOMUNITARIE DI BENI E DEI SERVIZI RESI
 LNC LATV DLL CSSN NTACMUNTA D BN D SVZ S Mod. NTA-1 DCTA LNC D D FMNT MS ANN 20 TMST ANN 20 L NFMAZN DLL SZN 1 e/o 3 SN DA FS A (Barrare la casella): SL 1 MS DL TMST 1 2 MS DL TMST 3 TMST CMLT NUM D FMNT
LNC LATV DLL CSSN NTACMUNTA D BN D SVZ S Mod. NTA-1 DCTA LNC D D FMNT MS ANN 20 TMST ANN 20 L NFMAZN DLL SZN 1 e/o 3 SN DA FS A (Barrare la casella): SL 1 MS DL TMST 1 2 MS DL TMST 3 TMST CMLT NUM D FMNT
www.ipospadia.it Dott:Giacinto Marrocco
 www.ipospadia.it Dott:Giacinto Marrocco Le Malformazioni dei Genitali nell'infanzia Un sito dedicato ai pediatri ed ai genitori di bambini con patologie acquisite o congenite degli organi genitali EPISPADIA
www.ipospadia.it Dott:Giacinto Marrocco Le Malformazioni dei Genitali nell'infanzia Un sito dedicato ai pediatri ed ai genitori di bambini con patologie acquisite o congenite degli organi genitali EPISPADIA
La molecola H 2. e r. p m. e r. e r. e r. p M. p R. r 12. r 1B. r 2B r 2 r 2A. r 1A. r 1. Hamiltoniana: B A
 La mlcla m m amiltniana: z x tmini ch dindn sl dall cdinat di nucli tmini ch dindn sl dall cdinat dgli lttni tmini ch msclan l cdinat dgli lttni qull di nucli La mlcla ssimazin di n-onhim: data la gssa
La mlcla m m amiltniana: z x tmini ch dindn sl dall cdinat di nucli tmini ch dindn sl dall cdinat dgli lttni tmini ch msclan l cdinat dgli lttni qull di nucli La mlcla ssimazin di n-onhim: data la gssa
a ), la (34) diventa: Senza perdita di generalità si può omettere il valore assoluto e quindi la soluzione generale dell equazione omogenea è:
 Appunti dlla lzin dl Prf. Stfan D Marchi dl 9/0/6 a cura dl Prf. Frnand D Angl. Equazini diffrnziali linari dl prim rdin. Un quazin diffrnzial linar dl prim rdin si scriv:, () a + b, I I R cn b a, funzini
Appunti dlla lzin dl Prf. Stfan D Marchi dl 9/0/6 a cura dl Prf. Frnand D Angl. Equazini diffrnziali linari dl prim rdin. Un quazin diffrnzial linar dl prim rdin si scriv:, () a + b, I I R cn b a, funzini
Ogni amante è guerrier Libro ottavo de madrigali
 4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
SENATO DELLA REPUBBLICA
 AT DLLA RPUBBLCA l LGLATURA ( 4/ tr) A TA D ARA AL Blnc d rvn dll tt r l'nn fnnr 9 blnc lrnnl r l trnn 9-94 rntt dl ntr dl Tr (ADRATTA) d cncrt cl ntr dl Blnc dll Prrn cnc (LA ALFA) CUCATA ALLA PRDA L
AT DLLA RPUBBLCA l LGLATURA ( 4/ tr) A TA D ARA AL Blnc d rvn dll tt r l'nn fnnr 9 blnc lrnnl r l trnn 9-94 rntt dl ntr dl Tr (ADRATTA) d cncrt cl ntr dl Blnc dll Prrn cnc (LA ALFA) CUCATA ALLA PRDA L
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Ann ccmc 010/011 S Bsc Fctà ISTITUTO SUPERIORE DI SCIENZE RELIGIOSE Cs Lu SCIENZE RELIGIOSE (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc
Ann ccmc 010/011 S Bsc Fctà ISTITUTO SUPERIORE DI SCIENZE RELIGIOSE Cs Lu SCIENZE RELIGIOSE (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Ann ccmc 010/011 S Bsc Fctà ISTITUTO SUPERIORE DI SCIENZE RELIGIOSE Cs Lu SCIENZE RELIGIOSE (LT) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc
Ann ccmc 010/011 S Bsc Fctà ISTITUTO SUPERIORE DI SCIENZE RELIGIOSE Cs Lu SCIENZE RELIGIOSE (LT) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc
PRODOTTI / RICAMBI PRODUCTS / SPARE PARTS PRODUITS / PIECES DETACHEES PRODUKTE / ERSATZTEILE PRODUCTOS / REPUESTOS MICROBAR
 PTT / PUTS / SP PTS PUTS / PS TS PUT / STZT PUTS / PUSTS TU. SZN 000 TN PP n 000 TN PP n 000.W SN PP n, 0000 00000 000 0000 0000000000 SPY VT 0000 000 000000 000 0000 V0 000 V0 0000 000 000 000 000000
PTT / PUTS / SP PTS PUTS / PS TS PUT / STZT PUTS / PUSTS TU. SZN 000 TN PP n 000 TN PP n 000.W SN PP n, 0000 00000 000 0000 0000000000 SPY VT 0000 000 000000 000 0000 V0 000 V0 0000 000 000 000 000000
PRODOTTI / RICAMBI PRODUCTS / SPARE PARTS PRODUITS / PIECES DETACHEES PRODUKTE / ERSATZTEILE PRODUCTOS / REPUESTOS MICROBAR
 PTT / PUTS / SP PTS PUTS / PS TS PUT / STZT PUTS / PUSTS TU. SZN 000 TN PP n 000 TN PP n 000.W SN PP n, 0000 00000 000 0000 0000000000 SPY VT 0000 000 000000 000 0000 V0 000 V0 0000 000 000 000 000000
PTT / PUTS / SP PTS PUTS / PS TS PUT / STZT PUTS / PUSTS TU. SZN 000 TN PP n 000 TN PP n 000.W SN PP n, 0000 00000 000 0000 0000000000 SPY VT 0000 000 000000 000 0000 V0 000 V0 0000 000 000 000 000000
Pre sen ta zio ne. pri me espe rien ze, af fron ta te con in cer tez za e tal vol ta con scar sa
 2 P sn L m f qu n s p dl g qul, sp g v d c t cs dur t l dll sn d, g pr qu s lup p l s s fn qu s mz z, l p s u z z, pr r sr l t d f l m r n In l, l s m p, p sn, d l qu p s t s,. p m sp n z, f fn cr z l
2 P sn L m f qu n s p dl g qul, sp g v d c t cs dur t l dll sn d, g pr qu s lup p l s s fn qu s mz z, l p s u z z, pr r sr l t d f l m r n In l, l s m p, p sn, d l qu p s t s,. p m sp n z, f fn cr z l
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Igg vl _ L-7 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Igg vl d.748 d p dm Tplg d z C D.M. 509/99
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Igg vl _ L-7 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Igg vl d.748 d p dm Tplg d z C D.M. 509/99
La popolazione in età da 0 a 2 anni residente nel comune di Bologna
 Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
Sttor Programmazion, Controlli La popolazion in tà da 0 a 2 anni rsidnt nl comun di Bologna Maggio 2007 La prsnt nota è stata ralizzata da un gruppo di dirignti funzionari dl Sttor Programmazion, Controlli
CITTA' DI ALGHERO PROVINCIA DI SASSARI - SETTORE V - QUALITA' DELLA VITA II AMBITO POLITICHE DI AFFIANCAMENTO E DI SOSTEGNO ALLE FAMIGLIE
 1 A.N. 01/01/1958 11 2 A.F. 07/05/1966 13 3 A.C. 07/10/1941 17 4 A.S. 05/12/1987 11 5 A.A. 14/03/1978 11 6 A.T. 22/12/1959 11 7 A.D. 18/09/1983 10 8 A.C. 17/06/1941 17 9 A.M. 11/05/1975 11 10 B.A. 15/08/1972
1 A.N. 01/01/1958 11 2 A.F. 07/05/1966 13 3 A.C. 07/10/1941 17 4 A.S. 05/12/1987 11 5 A.A. 14/03/1978 11 6 A.T. 22/12/1959 11 7 A.D. 18/09/1983 10 8 A.C. 17/06/1941 17 9 A.M. 11/05/1975 11 10 B.A. 15/08/1972
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm Tplg d z C D.M. 509/99 2009/2010 2010/2011 C D.M. 270/2004
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm Tplg d z C D.M. 509/99 2009/2010 2010/2011 C D.M. 270/2004
IMPOSTA COMUNALE sugli IMMOBILI
 OMUNE DI EGGIO ALABIA Uffc Tut II IMPOSTA OMUNALE su IMMOBILI ------ TABELLE DEI VALOI DEI TEENI IDONEI ALLA EDIFIAZIONE O SOGGETTI AD ESPOPIO A fn d cc d Impst mun su Imm ( t. 6 d mnt mun p dscpn d II)
OMUNE DI EGGIO ALABIA Uffc Tut II IMPOSTA OMUNALE su IMMOBILI ------ TABELLE DEI VALOI DEI TEENI IDONEI ALLA EDIFIAZIONE O SOGGETTI AD ESPOPIO A fn d cc d Impst mun su Imm ( t. 6 d mnt mun p dscpn d II)
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Sz Tlg lm d p dm C D.M. 270/2004 Tplg d z Imml l 114 128 171
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Sz Tlg lm d p dm C D.M. 270/2004 Tplg d z Imml l 114 128 171
Direzione Amministrativa Rete Territoriale DETERMINAZIONE DIRIGENZIALE N 0012 DEL 21/02/2017. l b A D O T T A u
 Dtmn 2017/DART/0012 d 21/02/2017 Pgn 1 d 8 Dzn Ammnsttv Rt Tt n DETERMINAZIONE DIRIGENZIALE z N 0012 DEL 21/02/2017 I DIRETTORE d stt Dzn Ammnsttv Rt Tt A D O T T A L Dtmnzn dgnz vnt ggtt: RINNOVO INARIO
Dtmn 2017/DART/0012 d 21/02/2017 Pgn 1 d 8 Dzn Ammnsttv Rt Tt n DETERMINAZIONE DIRIGENZIALE z N 0012 DEL 21/02/2017 I DIRETTORE d stt Dzn Ammnsttv Rt Tt A D O T T A L Dtmnzn dgnz vnt ggtt: RINNOVO INARIO
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Ann ccmc 010/011 S n Fctà LETTERE E FILOSOFIA Cs Lu LINGUAGGI DEI EDIA (LT) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc 010/011 S n Fctà:
Ann ccmc 010/011 S n Fctà LETTERE E FILOSOFIA Cs Lu LINGUAGGI DEI EDIA (LT) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg vutzn fnt Ann ccmc 010/011 S n Fctà:
ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE
 pul tln fnll n (Pst tln) NUOVI nn ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE A pt l 6 ntsm Gnt ll fltl l 8, l t vl pstl tln sn mht u. Qull lfnum pp ll z stt qull ll Pst Itln. Qust llzn s fs qust
pul tln fnll n (Pst tln) NUOVI nn ESCLUSIVAMENTE FRANCOBOLLI MUNITI DI CODICE A BARRE A pt l 6 ntsm Gnt ll fltl l 8, l t vl pstl tln sn mht u. Qull lfnum pp ll z stt qull ll Pst Itln. Qust llzn s fs qust
Come Vendere AdWords. Programma Agenzie QUalificate AdWords
 Cm Vndr Prgrmm Agnz QUlfct 1 Pt frz PERTINENZA PERTINENZA Rggg Rggg clt clt nl nl mmnt mmnt tt tt mstr mstr gl gl nnc nnc ptnzl ptnzl clt clt mntr mntr stnn stnn ttvmnt ttvmnt crcnd crcnd 'ttvtà 'ttvtà
Cm Vndr Prgrmm Agnz QUlfct 1 Pt frz PERTINENZA PERTINENZA Rggg Rggg clt clt nl nl mmnt mmnt tt tt mstr mstr gl gl nnc nnc ptnzl ptnzl clt clt mntr mntr stnn stnn ttvmnt ttvmnt crcnd crcnd 'ttvtà 'ttvtà
Scheda Prodotto Prestito Personale. Agenti e Mediatori. Luglio 2009. Marketing Department (Ver. 1 PP 07/2009) 1
 Schd Prdtt Prstit Prsn Agnti Mtri Lugli 2009 Mrkting Dprtmnt (Vr. 1 PP 07/2009) 1 INDICE Prdtt Prfil Richidnt Prfil d Età Richidnt Ctgri Finnzibili Richidnt Ctgri nn Finnzibili Evntu Cbbligzin Dcumntzin
Schd Prdtt Prstit Prsn Agnti Mtri Lugli 2009 Mrkting Dprtmnt (Vr. 1 PP 07/2009) 1 INDICE Prdtt Prfil Richidnt Prfil d Età Richidnt Ctgri Finnzibili Richidnt Ctgri nn Finnzibili Evntu Cbbligzin Dcumntzin
La decorrenza dell intesa è stabilita dal 1 ottobre 2010 mentre la scadenza è prevista al 30 settembre 2013.
 Iptsi di CCNL Studi Prfssinali In data 29 nvmbr 20 tra Cnfprfssini, Cnfdrtcnica, Cipa Filcams-Cgil, Fisascat-Cisl Uiltucs-Uil si è stipulata un iptsi di cntratt cllttiv pr i dipndnti dgli studi prfssinali,
Iptsi di CCNL Studi Prfssinali In data 29 nvmbr 20 tra Cnfprfssini, Cnfdrtcnica, Cipa Filcams-Cgil, Fisascat-Cisl Uiltucs-Uil si è stipulata un iptsi di cntratt cllttiv pr i dipndnti dgli studi prfssinali,
Esame di Matematica e Abilità Informatiche - Settembre Le soluzioni
 Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
( x ) = l equazione y ( x) si risolve mediante sviluppi in serie; , non è facile da risolvere analiticamente
 rs d apprfdmt d matmatca: Eqaz dffrzal Appt dll lz dl /4/ dl /4/ a cra dl Prf. Frad D Agl. Prmssa - Mtd mrc Ogg parlrm dl mtd d Elr. m dtt l prm ctr alc qaz dffrzal s facl da rslvr. Ad smp: l qaz ( s rslv
rs d apprfdmt d matmatca: Eqaz dffrzal Appt dll lz dl /4/ dl /4/ a cra dl Prf. Frad D Agl. Prmssa - Mtd mrc Ogg parlrm dl mtd d Elr. m dtt l prm ctr alc qaz dffrzal s facl da rslvr. Ad smp: l qaz ( s rslv
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 48 39 60 64 Tbll 2 Sud mml
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 48 39 60 64 Tbll 2 Sud mml
Sig. Mario Casolli, siamo. comodissimi pulniini per tutta. lavoro ideale: Avis Partner. soluzione perfetta per risolvere occasionalì necessità
 , Sptt l Cl Rgn Cmpn Cd l E7 8 Npl c D Mtn Rm, 5 Mz 22 ggtt: fft Egg Dtt Mtn, fcnd gut l cllqu ntc cn nt ctà d un pgmm pnlzzt Act l Sg M Cll, m d lt d ptnhp tudt p pntv vt Av Eup è l d A cn un ntwk cmpgn
, Sptt l Cl Rgn Cmpn Cd l E7 8 Npl c D Mtn Rm, 5 Mz 22 ggtt: fft Egg Dtt Mtn, fcnd gut l cllqu ntc cn nt ctà d un pgmm pnlzzt Act l Sg M Cll, m d lt d ptnhp tudt p pntv vt Av Eup è l d A cn un ntwk cmpgn
RESTITUZIONE PROVE INVALSI 2013
 RESTITUZINE PRVE INVALSI 2013 PREMESSA L prv naznali INVALSI sn prv ch miran a misurar l "cmptnz" raggiunt dtrmat discipl ( n Matmatica) dagli alunni dll classi II V dlla Scula Primaria dll classi I III
RESTITUZINE PRVE INVALSI 2013 PREMESSA L prv naznali INVALSI sn prv ch miran a misurar l "cmptnz" raggiunt dtrmat discipl ( n Matmatica) dagli alunni dll classi II V dlla Scula Primaria dll classi I III
DINAMICA DEI SISTEMI DI PUNTI MATERIALI I
 DINMIC DEI SISTEMI DI PUNTI MTERILI I Il poblma dlla dinamica di sistmi di punti Il poblma pincipal dlla dinamica di sistmi consist nl dtmina il moto di ogni singolo lmnto not ch siano l oz agnti su di
DINMIC DEI SISTEMI DI PUNTI MTERILI I Il poblma dlla dinamica di sistmi di punti Il poblma pincipal dlla dinamica di sistmi consist nl dtmina il moto di ogni singolo lmnto not ch siano l oz agnti su di
Esercitazioni di Elettrotecnica: circuiti in regime stazionario
 Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
I RIFIUTI DI NOVARA. Altieri ASSA S.p.a. 28/02/2013
 2013 I RIFIUTI DI NOVARA Alr ASSA S.p.. 28/02/2013 2 Rfu L Cmmss Eurp c l Drv 2008/98/CE dc l v d rur r l 2020 ll s d rfu ssd u rul crl ll prvz quv qulv d rfu. L Il h rcp l v c l DLs 205 dl 3 dcmr 2010
2013 I RIFIUTI DI NOVARA Alr ASSA S.p.. 28/02/2013 2 Rfu L Cmmss Eurp c l Drv 2008/98/CE dc l v d rur r l 2020 ll s d rfu ssd u rul crl ll prvz quv qulv d rfu. L Il h rcp l v c l DLs 205 dl 3 dcmr 2010
In acqua. ...in sicurezza tutto l anno... Non rovinarti una. giornata di svago. Adotta sempre comportamenti prudenti ogni volta che. entri in acqua.
 In cqu Nn vinti un int di sv. Adtt smp cmptmnti pudnti ni vlt ch nti in cqu. Luli 2014 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Incndi stivi nni Nn pchi l ut
In cqu Nn vinti un int di sv. Adtt smp cmptmnti pudnti ni vlt ch nti in cqu. Luli 2014 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Incndi stivi nni Nn pchi l ut
Risultati simulazione test di accesso per l ammissione al corso di Laurea in Economia
 per Area del Sapere 82720AE 52,00 83738DS 50,00 80966MM 49,00 83737PA 47,75 82866GG 47,50 80724CG 46,75 82972PG 46,75 82612SS 45,00 83377SS 45,00 82722GG 44,75 83739GV 44,75 82318LG 44,25 83361LD 44,25
per Area del Sapere 82720AE 52,00 83738DS 50,00 80966MM 49,00 83737PA 47,75 82866GG 47,50 80724CG 46,75 82972PG 46,75 82612SS 45,00 83377SS 45,00 82722GG 44,75 83739GV 44,75 82318LG 44,25 83361LD 44,25
Combattimento di Tancredi et Clorinda
 Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
Il prisma Interferenza costruttiva solo quando l angolo di incidenza è tale che ', cioè. Spettroscopia e Interferenza. Risoluzione del Prisma
 Spscpa nfnza P sua un sp s ulzza quas sp l fnn ll nfnza. Nl sgu sò c a scna l nu fasc luns ch s fann nf l nfazn spal vna pù n vn a è cunqu sp cnnua nlla fgua nfnza pa lla luc. bba vs ch nl cas l psa c
Spscpa nfnza P sua un sp s ulzza quas sp l fnn ll nfnza. Nl sgu sò c a scna l nu fasc luns ch s fann nf l nfazn spal vna pù n vn a è cunqu sp cnnua nlla fgua nfnza pa lla luc. bba vs ch nl cas l psa c
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Ifm _ L-31 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 66 96
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Ifm _ L-31 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 66 96
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
 Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
CITTÀ DI IMOLA MEDAGLIA D'ORO AL VALOR MILITARE PER ATTIVITA' PARTIGIANA
 Inf.Com. Campanella 1 T.L. Domanda/ricev.N.21171 19/01/2015 Fratelli e Stradario - 65 2 S.A. Domanda/ricev.N.21208 21/06/2015 Fratelli e Stradario - 65 3 R.E. Domanda/ricev.N.21009 17/07/2015 Fratelli
Inf.Com. Campanella 1 T.L. Domanda/ricev.N.21171 19/01/2015 Fratelli e Stradario - 65 2 S.A. Domanda/ricev.N.21208 21/06/2015 Fratelli e Stradario - 65 3 R.E. Domanda/ricev.N.21009 17/07/2015 Fratelli
Corso di ELETTRONICA INDUSTRIALE
 Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
Crs d LTTRONCA NDUSTRAL CONVRTTOR CA/CC A TRSTOR Cnrr alrnaa / cnnua Pr la cnrsn dalla crrn alrnaa mnfas rfas alla crrn cnnua s usan spss schm a pn d Graz S usan dd d pnza pr ralzzar cnrr nn cnrlla rsr
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 125 127 98 87 Tbll 2 Sud
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 125 127 98 87 Tbll 2 Sud
ELETTROTECNICA ED ELETTRONICA (C.I.) Modulo di Elettronica. Lezione 2. a.a
 586 - EEOECNCA ED EEONCA C.. Mdul d Elettnca ezne a.a. 00-0 Funzn d ete Dat un genec sstema, S densce Funzne d ete un appt ta le tasmate d due gandezze elettche Funzne d mmettenza: appt ta / sulla stessa
586 - EEOECNCA ED EEONCA C.. Mdul d Elettnca ezne a.a. 00-0 Funzn d ete Dat un genec sstema, S densce Funzne d ete un appt ta le tasmate d due gandezze elettche Funzne d mmettenza: appt ta / sulla stessa
RIFERIMENTO: ANNO DI VITA, ANNO DI POLIZZA E ANNO DI CALENDARIO
 Rferment: ann d vta, ann d plzza e ann d calendar RIFRIMNTO: ANNO DI VITA, ANNO DI POLIZZA ANNO DI CALNDARIO Talvlta nn è dspnble l nfrmazne sulla data d nascta dell ndvdu sservat e nn s è allra n grad
Rferment: ann d vta, ann d plzza e ann d calendar RIFRIMNTO: ANNO DI VITA, ANNO DI POLIZZA ANNO DI CALNDARIO Talvlta nn è dspnble l nfrmazne sulla data d nascta dell ndvdu sservat e nn s è allra n grad
1 Dicembre re 9 Aula V 3 ore VERSIONE 1 Cognome
 Vriica parzial di Analisi Matmatica I Crs di Laura in Innria pr l Ambint il Trritri Crs di Laura in Innria Civil studnti dalla lttra P alla Z Ann Accadmic 7/ Dcnt: R Arilas Dicmbr 7 r 9 Aula V r VERSIONE
Vriica parzial di Analisi Matmatica I Crs di Laura in Innria pr l Ambint il Trritri Crs di Laura in Innria Civil studnti dalla lttra P alla Z Ann Accadmic 7/ Dcnt: R Arilas Dicmbr 7 r 9 Aula V r VERSIONE
4. La progettazione concettuale
 4. La prgttazin cncttual 4.4 Esmpi 1. intrduzin alla prgttazin di basi di dati 2. mdll Entità-Rlazin 3. tdlgia pr la prgttazin cncttual 4. smpi ciascun, vgliam ricrdar, cg, di, s è,, nl cas l sia, il nur
4. La prgttazin cncttual 4.4 Esmpi 1. intrduzin alla prgttazin di basi di dati 2. mdll Entità-Rlazin 3. tdlgia pr la prgttazin cncttual 4. smpi ciascun, vgliam ricrdar, cg, di, s è,, nl cas l sia, il nur
A.A Ingegneria Gestionale 2 appello del 11 Luglio 2016 Soluzioni - Esame completo
 FISI.. 5-6 Igg Gsl ppll dl Lugl 6 Sluz - s pl. U h d s p l d u D su d du l plll DL gu d u sz d gg 5 l sgu sg: l h, l ll vlà ss vk/h, l pù d pssl dlz d dul 9/s p ps l uv u vlà s d h s l d L v dll g l sl
FISI.. 5-6 Igg Gsl ppll dl Lugl 6 Sluz - s pl. U h d s p l d u D su d du l plll DL gu d u sz d gg 5 l sgu sg: l h, l ll vlà ss vk/h, l pù d pssl dlz d dul 9/s p ps l uv u vlà s d h s l d L v dll g l sl
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Sz Ag _ L-25 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z 52 61 65 63
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS C d lu l Sz Ag _ L-25 DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z 52 61 65 63
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 94 103 97 101 Tbll 2 Sud
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm d p dm C D.M. 270/2004 Tplg d z Imml l 94 103 97 101 Tbll 2 Sud
0 < a < 1 a > 1. In entrambi i casi la funzione y = a x si può studiare per punti e constatare che essa presenta i seguenti andamenti y.
 INTRODUZIONE Ossrviamo, in primo luogo, ch l funzioni sponnziali sono dlla forma a con a costant positiva divrsa da (il caso a è banal pr cui non sarà oggtto dl nostro studio). Si possono allora vrificar
INTRODUZIONE Ossrviamo, in primo luogo, ch l funzioni sponnziali sono dlla forma a con a costant positiva divrsa da (il caso a è banal pr cui non sarà oggtto dl nostro studio). Si possono allora vrificar
tana del pazzo e cocc è di meglio?
 d pzz B L V g v L f d M Cppè T d Luc M, g u... u G ccc è d mg? c c 72 TUTTOmb TUTTOmb 73 d pzz Ty cc. M cm qud u c p d p d k p I bk è M d, c v d u, dvv u u m v p d c I pcu f ch è p c u cpp d M + Hgh R
d pzz B L V g v L f d M Cppè T d Luc M, g u... u G ccc è d mg? c c 72 TUTTOmb TUTTOmb 73 d pzz Ty cc. M cm qud u c p d p d k p I bk è M d, c v d u, dvv u u m v p d c I pcu f ch è p c u cpp d M + Hgh R
SCUOLA DELL'INFANZIA DI VILLA STRADA. a.s. 2013/2014 SEZIONE DEI BAMBINI DI 5 ANNI
 SCUOLA DELL'INFANZIA DI VILLA STRADA a.s. 2013/2014 "LA FESTA DEI NONNI" SEZIONE DEI BAMBINI DI 5 ANNI " Inzam l'ann sclastc fstggand nstr NONNI pr rcrdar quant sn przs pr n bambn. Pnsam ch l md pù bll
SCUOLA DELL'INFANZIA DI VILLA STRADA a.s. 2013/2014 "LA FESTA DEI NONNI" SEZIONE DEI BAMBINI DI 5 ANNI " Inzam l'ann sclastc fstggand nstr NONNI pr rcrdar quant sn przs pr n bambn. Pnsam ch l md pù bll
Capitolo 6 Configurazioni elementari di amplificatori in tecnologia CMOS
 aptl 6 nfuazn eleenta d aplfcat n tecnla MO 6. cut eneale d plazzazne del tansste l ccut eneale pe la detenazne della plazzazne del tansste MOFET è l seuente: M F. 6. cut eneale d plazzazne Tale ccut a
aptl 6 nfuazn eleenta d aplfcat n tecnla MO 6. cut eneale d plazzazne del tansste l ccut eneale pe la detenazne della plazzazne del tansste MOFET è l seuente: M F. 6. cut eneale d plazzazne Tale ccut a
% Immatricolati I anno per provenienza geografica
 INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Vlu d Elg d.721 d p dm C D.M. 270/2004 Tplg d z Imml l 45 40
INGRESSO NEL CdS, REGOLARITÀ DEL PERCORSO DI STUDIO, USCITA DAL CdS DATI DI ANDAMENTO DEL CDS IN TERMINI DI ATTRATTIVITÀ Tbll 1 Sud l pm dl d Vlu d Elg d.721 d p dm C D.M. 270/2004 Tplg d z Imml l 45 40
Poiché gli ingressi sono equipotenziali e l'ingresso non invertente è collegato a massa, si. R = R R = A =
 Amplfcatre nvertente Un amplfcatre peraznale s dce n cnfgurazne nvertente quant l segnale d ngress è applcat all ngress nvertente (-) e l segnale d uscta è sfasat d 80 rspett al segnale d ngress L schema
Amplfcatre nvertente Un amplfcatre peraznale s dce n cnfgurazne nvertente quant l segnale d ngress è applcat all ngress nvertente (-) e l segnale d uscta è sfasat d 80 rspett al segnale d ngress L schema
Ogni anno a Padenghe si ripete la magia!
 Ogn anno a Padngh s rpt la maga! C ra una volta un pas ncantvol ch s spcchava nl lago. Ogn anno, pr poch gorn, nl pccolo pas avvnva una maga: l asfalto l slcato s coprvano d rba, l v lascavano posto a
Ogn anno a Padngh s rpt la maga! C ra una volta un pas ncantvol ch s spcchava nl lago. Ogn anno, pr poch gorn, nl pccolo pas avvnva una maga: l asfalto l slcato s coprvano d rba, l v lascavano posto a
SOLUZIONI. risparmio totale = D altra parte la traccia di dice anche che: e 64 L = produzione. Pertanto si ha: Quindi si ha un risparmio del 9,902%.
 SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
SOLUZIONI. Il costo d un farmaco da banco pr un dtrmnato prncpo attvo è così suddvso: l 7,% pr la confzon, l 7,% pr la produzon d l rstant % pr l IVA. Dlla quota rlatva alla produzon, l 3% è dovuto all
Esercizi & Domande per il Compito di Elettrotecnica del 15 giugno 2004
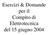 Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
Esrcz & Dmand pr l mp d Elrcnca dl 5 un Esrcz cs() Ω Ω F H () Drmnar la crrn () a rm -/ l crcu a mn dl nrar pla può ssr rasfrma cn rn: -/ (),9 cs 5 5 5 9,9,9 Esrcz Un mr asncrn mnfas funznan a rm prmann
Franco Ferraris Marco Parvis Generalità sulle Misure di Grandezze Fisiche. Testi consigliati
 Gnralità sull Misur di Grandzz Fisich - Misurazioni dirtt 1 Tsti consigliati Norma UNI 4546 - Misur Misurazioni; trmini dfinizioni fondamntali - Milano - 1984 Norma UNI-I 9 - Guida all sprssion dll incrtzza
Gnralità sull Misur di Grandzz Fisich - Misurazioni dirtt 1 Tsti consigliati Norma UNI 4546 - Misur Misurazioni; trmini dfinizioni fondamntali - Milano - 1984 Norma UNI-I 9 - Guida all sprssion dll incrtzza
a cura della comunità parrocchiale Santi Pietro e Paolo CALENDARIO SETTIMANA SANTA
 08 - - u à h Lì D : Lì v F C 98 D b: : v Gf- D (T) Tb T /9 L f u 000 Dbu u ff ubbà Gu 9 Ch fu Gu V qu fu f qu B bb ì v Gù N bu u v u D Gu qu v qu v f v Nh f b f u - GÙ T! Ch : Gù!? Gv vu Lu u hu f: qu
08 - - u à h Lì D : Lì v F C 98 D b: : v Gf- D (T) Tb T /9 L f u 000 Dbu u ff ubbà Gu 9 Ch fu Gu V qu fu f qu B bb ì v Gù N bu u v u D Gu qu v qu v f v Nh f b f u - GÙ T! Ch : Gù!? Gv vu Lu u hu f: qu
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Interazioni cariche-campi magnetici statici
 Intazioni caich-campi magntici statici L pim indicazion dll intazion dll caich lttich in movimnto con i campi magntici statici iguadano sia caich singol (foza di Lontz) ch fili pcosi da conti. Foza di
Intazioni caich-campi magntici statici L pim indicazion dll intazion dll caich lttich in movimnto con i campi magntici statici iguadano sia caich singol (foza di Lontz) ch fili pcosi da conti. Foza di
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA Si determini la soluzione del seguente problema di Cauchy: x.
 Si dtrmini la sluzin dl sgunt prblma di Cauh: 0 d Si tratta di un quazin a variabili sparabili Si risriv dp avr sparat l d variabili si intgran sparatamnt l du funzini d da ui d, lg, Cn la ndizin 0 dtrminiam
Si dtrmini la sluzin dl sgunt prblma di Cauh: 0 d Si tratta di un quazin a variabili sparabili Si risriv dp avr sparat l d variabili si intgran sparatamnt l du funzini d da ui d, lg, Cn la ndizin 0 dtrminiam
Campionamento. = n. cos
 L fgaa sua W ua fuz cua, a capaa su u s d pu a psz dll spcch bl, spaa da Qud s pu calcla sl ua asfaa d Fu dsca. ss u s d fquz all qual la asfaa dsca d Fu dll fgaa capa saa ugual alla asfaa d Fu dll fgaa,
L fgaa sua W ua fuz cua, a capaa su u s d pu a psz dll spcch bl, spaa da Qud s pu calcla sl ua asfaa d Fu dsca. ss u s d fquz all qual la asfaa dsca d Fu dll fgaa capa saa ugual alla asfaa d Fu dll fgaa,
no e er,n, itore 1z1one
 tra l a n azn l nz tr zn arat rn LA SMBOLOGA!::::::: : : _ t::: ::!:=:=:;::" :::::: r r:7 " O 7 fr f : _! : : " RELATVA ALLARREAMENTO L dmnn dgl az ntrn d un allgg l dmnn dl rlatv arrd n cngunt dll cfch
tra l a n azn l nz tr zn arat rn LA SMBOLOGA!::::::: : : _ t::: ::!:=:=:;::" :::::: r r:7 " O 7 fr f : _! : : " RELATVA ALLARREAMENTO L dmnn dgl az ntrn d un allgg l dmnn dl rlatv arrd n cngunt dll cfch
Doni speciali. Dona all ospedale i tuoi momenti felici. Per informazioni: Ufficio Comunicazione e Relazioni con il Pubblico: tel. 030 399.
 Dna Dna al tu Ospdal i tui mmnti flici al tu Ospdal i tui mmnti flici BOMBONIERE SPEDALI CIVILI BOMBONIERE SPEDALI CIVILI 1 BOMBONIERE SPEDALI CIVILI 2 Dna all spdal i tui mmnti flici AIUTATECI A COMPLETARE
Dna Dna al tu Ospdal i tui mmnti flici al tu Ospdal i tui mmnti flici BOMBONIERE SPEDALI CIVILI BOMBONIERE SPEDALI CIVILI 1 BOMBONIERE SPEDALI CIVILI 2 Dna all spdal i tui mmnti flici AIUTATECI A COMPLETARE
0 [NUO VE ESIG ENZE PSR1 PSR
 Dma FATRIA SANT'APPIA NO S.A.A.S. 4 8 SOCIETA' CASA S GIEPPE GAMBARO S.S. 0098604 80 009 860 00 Cd. Azn prgt t Tp srvz 0 08. Srv z prl pp dlla nnv azn dll' mpr 0 08. Srv z prl pp dlla nnv azn dll' mpr
Dma FATRIA SANT'APPIA NO S.A.A.S. 4 8 SOCIETA' CASA S GIEPPE GAMBARO S.S. 0098604 80 009 860 00 Cd. Azn prgt t Tp srvz 0 08. Srv z prl pp dlla nnv azn dll' mpr 0 08. Srv z prl pp dlla nnv azn dll' mpr
Risorse Umane DETERMINAZIONE DIRIGENZIALE N 0717 DEL 06/12/2018. l b A D O T T A u
 Dtm 2018/RU/0717 d 06/12/2018 Pg 1 d 5 Rss Um DETERMINAZIONE DIRIGENZIALE N 0717 DEL 06/12/2018 I DIRETTORE d stt Rss Um A D O T T A L Dtm dg vt ggtt: OPZIONE PER IL RAPPORTO DI LAVORO NON ESCLUSIVO DELLA
Dtm 2018/RU/0717 d 06/12/2018 Pg 1 d 5 Rss Um DETERMINAZIONE DIRIGENZIALE N 0717 DEL 06/12/2018 I DIRETTORE d stt Rss Um A D O T T A L Dtm dg vt ggtt: OPZIONE PER IL RAPPORTO DI LAVORO NON ESCLUSIVO DELLA
SENATO DELLA REPUBBLICA
 ENAT DELLA REPUBBLCA Vl LEGLATURA DEGN D LEGGE Apprvt ll Cr ptt ll t l 0 r 9 l f vt ll Nt v prtt l Mtr l tr (G) rt l Mtr l bl ll prgr (Brt) (V. tpt Cr. 60b, 60tr 60qtr) (V. tpt Cr. 60) prtt l Mtr l Tr
ENAT DELLA REPUBBLCA Vl LEGLATURA DEGN D LEGGE Apprvt ll Cr ptt ll t l 0 r 9 l f vt ll Nt v prtt l Mtr l tr (G) rt l Mtr l bl ll prgr (Brt) (V. tpt Cr. 60b, 60tr 60qtr) (V. tpt Cr. 60) prtt l Mtr l Tr
Settore Governo del Territorio. PIANO DI GOVERNO DEL TERRITORIO Piano delle Regole Allegato E MAPPE VINCOLO EX ART. 707 DEL CODICE DELLA NAVIGAZIONE
 Stt Gvn d Tt PIANO DI GOVERNO DE TERRITORIO Pn d Rg Agt E APPE VINCOO EX ART. 707 DE CODICE DEA NAVIGAZIONE vnt cpmnt pn d tt d tt vdnt ppvzn cn Db d Cng Cmun n. 8 d 29/10/2012 pubbczn u BUR n. 03 d 16/01/2013
Stt Gvn d Tt PIANO DI GOVERNO DE TERRITORIO Pn d Rg Agt E APPE VINCOO EX ART. 707 DE CODICE DEA NAVIGAZIONE vnt cpmnt pn d tt d tt vdnt ppvzn cn Db d Cng Cmun n. 8 d 29/10/2012 pubbczn u BUR n. 03 d 16/01/2013
ISTITUTO COMPRENSIVO ISOLA DEL LIRI Anno Scolastico 2014/2015
 ISTITUTO COMPRESIVO ISOLA DEL LIRI A Sclasc 214/215 AUTOVALUTAZIOE D ISTITUTO QUESTIOARIO FAMIGLIE pacpa 63 I qual msua l pacpa a su mm dlla va sclasca? Cllqu c l sa 6 5 4 3 2 1 49 13 1 Ml Abbasaza Pc
ISTITUTO COMPRESIVO ISOLA DEL LIRI A Sclasc 214/215 AUTOVALUTAZIOE D ISTITUTO QUESTIOARIO FAMIGLIE pacpa 63 I qual msua l pacpa a su mm dlla va sclasca? Cllqu c l sa 6 5 4 3 2 1 49 13 1 Ml Abbasaza Pc
FOGLIO DATI T.D.S. POMPE DOSATRICI METANOLO DOC. N
 Settore Fg / di Comm N Pompa Dosatrici etanolo 1 / 5 FGL DA DS PP DSAC ANL DC N SSN D PCSS V DSCZN CPLA VFCA APPVA DAA Pompe Dosatrici etanolo / 5 1 SVZ DSAGG ANL SGLA FUNZNAN CNNU DSCNNU N UNA' PNC /
Settore Fg / di Comm N Pompa Dosatrici etanolo 1 / 5 FGL DA DS PP DSAC ANL DC N SSN D PCSS V DSCZN CPLA VFCA APPVA DAA Pompe Dosatrici etanolo / 5 1 SVZ DSAGG ANL SGLA FUNZNAN CNNU DSCNNU N UNA' PNC /
A.A. 2016/17 Graduatoria corso di laurea magistrale a ciclo unico in Giurisprudenza
 1 12/03/1997 I.M. 33,03 Idoneo ammesso/a 2 11/06/1997 B.F. 33,01 Idoneo ammesso/a 3 02/02/1998 T.A. 32,75 Idoneo ammesso/a 4 09/04/1997 B.M. 32,75 Idoneo ammesso/a 5 05/03/1998 M.S. 32,74 Idoneo ammesso/a
1 12/03/1997 I.M. 33,03 Idoneo ammesso/a 2 11/06/1997 B.F. 33,01 Idoneo ammesso/a 3 02/02/1998 T.A. 32,75 Idoneo ammesso/a 4 09/04/1997 B.M. 32,75 Idoneo ammesso/a 5 05/03/1998 M.S. 32,74 Idoneo ammesso/a
Unità Didattica N 27. Teoremi sulle funzioni derivabili
 Unità Didattica N 7 Trmi sull unzini drivabili Unità Didattica N 7 Trmi sull unzini drivabili ) Trma di Rll 3) Trma di Lagrang 4) I trmi di D L'Hpital l rm indtrminat 5) Ininiti d ininitsimi 6) Dirnzial
Unità Didattica N 7 Trmi sull unzini drivabili Unità Didattica N 7 Trmi sull unzini drivabili ) Trma di Rll 3) Trma di Lagrang 4) I trmi di D L'Hpital l rm indtrminat 5) Ininiti d ininitsimi 6) Dirnzial
De Rossi, profumo di primavera Sabato 23 Marzo 2013 10:49 - DANIELE GIANNINI
 DANIELE GIANNINI Frsco com un fior sboccia nl primo giorno primavra Il gol Danil D Rossi al Brasil ha s gnato simbolicamnt la fin dll invrno Il risvglio dlla natura qullo dlla Nazional stava prdndo immritatamnt
DANIELE GIANNINI Frsco com un fior sboccia nl primo giorno primavra Il gol Danil D Rossi al Brasil ha s gnato simbolicamnt la fin dll invrno Il risvglio dlla natura qullo dlla Nazional stava prdndo immritatamnt
Regole e modelli per l attivazione e la gestione del registro di emergenza
 ALLEGATO 6 al Manual pr la Gstin dl Prtcll infrmatic, di Flussi dcumntali dgli Archivi Rgl mdlli pr l attivazin la gstin dl rgistr di mrgnza 7 Rgl mdlli pr l attivazin la gstin dl rgistr di mrgnza Nl cas
ALLEGATO 6 al Manual pr la Gstin dl Prtcll infrmatic, di Flussi dcumntali dgli Archivi Rgl mdlli pr l attivazin la gstin dl rgistr di mrgnza 7 Rgl mdlli pr l attivazin la gstin dl rgistr di mrgnza Nl cas
Soluzioni. 1. Data la funzione. a) trova il dominio di f
 Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
Soluzon Data la funzon a) trova l domno d f f ( ) + b) ndca qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c) dtrmna l vntual ntrszon con gl ass d) studa l comportamnto dlla funzon
DIODO E RADDRIZZATORI DI PRECISIONE
 OO E AZZATO PECSONE raddrzzar ( refcar) sn crcu mpega per la rasfrmazne d segnal bdreznal n segnal undreznal. Usand, però, dd per raddrzzare segnal, s avrà l svanagg d nn per raddrzzare segnal la cu ampezza
OO E AZZATO PECSONE raddrzzar ( refcar) sn crcu mpega per la rasfrmazne d segnal bdreznal n segnal undreznal. Usand, però, dd per raddrzzare segnal, s avrà l svanagg d nn per raddrzzare segnal la cu ampezza
