Quotatura (UNI ISO 129-1)
|
|
|
- Fortunato Napolitano
- 8 anni fa
- Visualizzazioni
Transcript
1 SCHED DI GGIRNMENT Quotatura (UNI IS 129-1) MENCLTUR Quotatura è l'insieme delle quote e delle informazioni alfanumeriche necessarie a determinare le dimensioni di un oggetto in tutti i suoi elementi. Quota è l'insieme della linea di misura, delle linee di riferimento e del valore numerico che definisce una dimensione nel disegno. valore numerico PRINCÌPI GENERLI DI QUTTUR Le quote di un disegno devono essere espresse nella stessa unità di misura. In genere le quote sono espresse in mm; altre unità di misura devono essere indicate esplicitamente Un eccezione è costituita dalle quote ausiliarie, aggiuntive per comodità di lettura. Ø2 Ciascun elemento dell'oggetto deve essere quotato non più di una volta. Quotatura ripetuta, quindi errata. Ø2 linea di riferimento 3 Ø2 Le quote (UNI IS 129-1) sono distinte in: quote funzionali, essenziali alla funzione dell'oggetto; quote non funzionali, non essenziali alla funzione dell'oggetto; quote ausiliarie, già deducibili da altre quote, ma utili per evitare calcoli. Esse si indicano tra parentesi. F linea di misura F Le quote non si devono rilevare dal disegno mediante scala Quotatura incompleta, quindi errata. 1 Le quote devono essere disposte sulle viste che mostrano l'elemento da quotare nel modo più chiaro. La quota è molto più chiara della quota, quindi è da preferire. NF NF Una quota funzionale non si deve dedurre da altre quote. NF F = Funzionale NF = Non Funzionale ux = usiliaria nota bene In una quotatura geometrica, che descrive cioè solo la forma e le dimensioni dell'oggetto, non vi è distinzione tra quote funzionali e non funzionali; questa distinzione è invece essenziale in una quotatura funzionale. Copyright 212 Zanichelli Editore Sp, ologna [23] La lunghezza del gambo della vite è una quota funzionale e quindi non si deve ricavare da altre quote; pertanto la quotatura è errata. 3 Gli elementi normalizzati (viti, chiodi, ecc.) possono non essere quotati, ma individuati mediante designazione normalizzata o altro codice. Chiodi 4 x 2 UNI 134 1
2 CRTTERISTICHE DELLE LINEE DI MISUR La linea di misura individua una dimensione dell'oggetto; in generale è provvista di frecce terminali alle estremità ed è delimitata da linee di riferimento. Frecce e tratti obliqui devono essere dimensionati in proporzione alla grandezza del disegno e in funzione delle esigenze di chiarezza. SCHED DI GGIRNMENT nelle quote di diametri. Ø32 Ø32 Le linee di misura si eseguono con linea continua fine (tipo 1.1). Non si possono utilizzare altri tipi di linee (mista fine, a tratti, ecc.). Le estremità delle linee di misura sono provviste di: frecce terminali, delle forme riportate in figura, con angoli di 3 oppure 9 ; le frecce chiuse possono essere annerite; perta a 3 perta a 9 Chiusa a 3 Piena a a 3 tratti obliqui, inclinati di 45 rispetto alla linea di misura; punto, quando non vi è spazio sufficiente per frecce terminali; circonferenza, con diametro di circa 3 mm, quando l'estremità è origine di un sistema di riferimento. Frecce proporzionate alla grandezza del disegno In un disegno si deve usare lo stesso tipo di freccia terminale. Normalmente le frecce si dispongono all'interno delle linee di riferimento; in caso di mancanza di spazio si possono disegnare all'esterno. In alcuni casi si possono disegnare linee di misura incomplete: nelle semiviste o semisezioni di parti simmetriche; in questi casi la linea di misura oltrepassa l asse di simmetria; nella quotatura riferita a una origine; 1 Ø2 Ø2 Ø32 Ø3 Ø2 Ø22 CRTTERISTICHE DELLE LINEE DI RIFERIMENT Le linee di riferimento collegano punti dell'oggetto con le estremità delle linee di misura, sporgendo di poco da esse. Vengono disegnate con linea continua fine (tipo 1.1). La linea di riferimento sopravanza la linea di misura, mentre questa si arresta sull'altra. Le linee di riferimento hanno inizio nell estremo dell elemento da quotare. È anche possibile distaccarle di una piccola misura (circa 8 volte lo spessore della linea usata). Qualora le linee di riferimento avessero origine in un punto su linee di costruzione, queste ultime proseguono di poco oltre il punto stesso. Come linee di riferimento si possono usare assi di simmetria, linee di contorno, ecc. nota bene In un disegno devono apparire frecce disegnate tutte nella stessa modalità Copyright 212 Zanichelli Editore Sp, ologna [23] 2
3 DISPSIZINE DELLE LINEE DI RIFERIMENT Per quanto possibile le linee di riferimento devono essere disposte secondo i seguenti criteri. DISPSIZINE DELLE LINEE DI MISUR Le linee di misura devono essere disposte secondo i seguenti criteri. SCHED DI GGIRNMENT minori alle maggiori, allontanandosi dal contorno delle figure. 1. Non devono intersecare altre linee del disegno. 1. Non devono coincidere con assi di simmetria, linee di contorno o di riferimento.. Devono riferirsi ad elementi paralleli al piano del disegno. Le linee di misura, quindi, non possono riferirsi a dimensioni viste di scorcio. 2. Non devono intersecare le inee di misura. 2. Devono, per quanto possibile, essere disposte all'esterno delle figure. 3. Devono essere opportunamente distanziate tra loro e dal contorno delle figure.. Devono essere tracciate interamente anche se riferite a elementi rappresentati con interruzioni. 3. Sono perpendicolari alle linee di misura. SCRITTUR DEI VLRI NUMERICI 1. Devono essere ben leggibili Devono essere parallele alla dimensione a cui si riferiscono. 9 Eccezionalmente le linee di riferimento possono essere oblique rispetto alle linee di misura, come in figura. 5. Non devono, per quanto possibile, intersecare le linee di riferimento. 2. Non devono sovrapporsi alle linee del disegno. Copyright 212 Zanichelli Editore Sp, ologna [23] Le linee di misura andranno quindi disegnate in ordine progressivo, dalle 8 8 3
4 SCHED DI GGIRNMENT 3. Le cifre devono essere disposte parallelamente alle linee di misura, al di sopra e staccate da esse. I valori devono essere letti dalla base o dal lato destro del disegno QUTTUR DI NGLI La linea di misura di un angolo è costituita da un arco con centro nel vertice dell'angolo. Le linee di riferimento si trovano sui lati dell'angolo. 9 QUTTUR DI FRI I fori si quotano con i loro diametri e gli interassi (posizione degli assi) I valori di quote oblique vanno orientati come in figura. QUTTUR DI RGGI QUTTUR DI DIMETRI Le linee di misura possono essere costituite da segmenti diametrali oppure da segmenti esterni paralleli a un asse. Il valore numerico è preceduto dal simbolo Ø. Ø Ø Quando la linea di misura è parziale, essa prosegue oltre il centro. Ø8 Ø Ø9 Le linee di misura sono segmenti radiali, interni o esterni; la linea di misura presenta una sola freccia terminale con la punta rivolta verso la circonferenza. Il valore numerico è preceduto dal simbolo R. R5 R5 Il valore dell'angolo viene disposto come indicato nella figura. QUTTUR DI RCHI 3 3 La linea di misura è un arco concentrico con quello da quotare, mentre le linee di riferimento si trovano sui raggi passanti per gli estremi dell'arco stesso. Il valore numerico è preceduto 2 dal simbolo. QUTTUR DI PRTI SFERICHE Le parti sferiche si quotano mediante il diametro o il raggio, preceduti dai simboli rispettivamente SØ e SR. SØ1 QUTTUR DI QUDRI SR8 I quadri (barre a sezione quadrata) vengono quotati con il lato preceduto dal simbolo. QUTTUR DI ELEMENTI FURI SCL Elementi rappresentati fuori scala (per essempio quelli troppo lunghi e ingombranti) vengono quotati con cifre sottolineate QUTTUR DI ELEMENTI RIPETUTI La quotatura di elementi ripetuti a distanze costanti può essere semplificata come in figura. La misura complessiva si indica tra parentesi. 3 x 1 = (48) Qualora vi sia possibilità di confondere il valore del passo e il numero dei passi, si quota anche un singolo passo. 5 x = (3) Copyright 212 Zanichelli Editore Sp, ologna [23] 4
5 QUTTUR DI SMUSSI Gli smussi si quotano con l'altezza della superficie smussata e il semiangolo al vertice. Se il semiangolo al vertice è di 45, la quota può essere eseguita come in figura. 3 x 45 2 SISTEM DI QUTTUR IN SERIE In questo sistema ogni quota è determinata rispetto a quella contigua. Esso è particolarmente vantaggioso quando l'accumulo di errori costruttivi dalla misura indicata non compromette la funzionalità dell'oggetto. Le quote ausiliarie, indicate tra parentesi, possono facilitare la lettura di misure ricavabili solo con calcoli talora complessi. SCHED DI GGIRNMENT Quotatura a quote sovrapposte (o progressiva) È una quotatura in parallelo semplificata con l'adozione di una unica linea di misura e con l'elemento di origine che assume la quota. L'origine deve essere contrassegnata da un cerchietto; dalla parte opposta all'origine ogni quota porta una sola freccia terminale. QUTTUR DI INFISSI IN PINT La quotatura di infissi (porte, finestre) in pianta si esegue mediante: il valore della larghezza del vano, sopra l'asse; il valore dell'altezza del vano, sotto l'asse. Il valore numerico deve essere apposto in prossimità della freccia in uno dei due modi seguenti: sul prolungamento della linea di riferimento (fig. ); al di sopra della linea di misura e un po' staccata da essa (fig. ) Porta Finestra SISTEMI DI QUTE CN RIGINE CMUNE QUTTUR DI LIVELLI LTIMETRICI I livelli altimetrici si indicano con frecce come quelle usate in figura. + 8,2 Quotatura in parallelo Le quote in questo sistema sono riferite a una stessa origine. Si evita in questo modo la possibilità di accumulare errori costruttivi; è un sistema particolarmente indicato per lavorazioni con macchine a spostamento progressivo. SISTEM DI QUTTUR CMINT Dalla combinazione dei due precedenti sistemi si ottiene una quotatura che soddisfa tutte le esigenze del disegno costruttivo. +,4 + 5, SISTEMI DI QUTTUR I sistemi di quotatura servono a organizzare le singole quote secondo criteri funzionali alle esigenze descrittive e operative. lcuni sistemi rendono il disegno più semplice e meno ingombro di quote, altri aiutano l'operatore a trovare riferimenti fissi e funzionali ad alcune lavorazioni (ad esempio i sistemi con origine comune e quello per coordinate). Copyright 212 Zanichelli Editore Sp, ologna [23] nota bene Le linee di misura devono essere disposte a distanza costante; in disegni su formati 4 oppure 3 questa distanza può essere compresa tra e 12 mm. 5
6 SCHED DI GGIRNMENT SISTEM DI QUTTUR IN CRDINTE Coordinate cartesiane In una tabella sono riportati i valori delle coordinate cartesiane di elementi connotati da sigle o numeri. QUTTUR DI SSMETRIE Nel caso di quotatura di assonometrie si applicano tutte le norme viste finora. Le linee di misura e di riferimento sono però parallele agli assi dell'assonometria utilizzata. lcuni esempi sono riportati di seguito. C y D E 2, 15, 4, x Nella tabella sono indicate con x e y le coordinate del centro del foro, con Ø il diametro e con z la sua profondità. C D E x y Ø z , In alternativa all'uso della tabella si possono indicare le coordinate a fianco di ciascun punto. x = 2 x = y = 21 y y = 1 Quote in m 3, 2, 1, x x = 33 y = 4 8, 8, Coordinate polari In una tabella si possono anche riportare i valori delle coordinate polari, rispetto a riferimenti costituiti da un'origine e da un asse orientato. 5, 5, M ϑ 3,2 4, Quote in m 3,2 4, ϑ M 4, ϑ M 9 22, 15 3, ,5 3 31, 12 24,1 45 2, ,8 24,1 15 3,3 5 22, , 18 35, Nella tabella sono indicate con M il modulo del singolo punto e con ϑ l'anomalia dello stesso x3 = (2) memo 3 Le coordinate polari sono: modulo, cioè la distanza di un punto dall'origine; anomalia, cioè l'angolo formato dall'asse con la semiretta condotta dall'origine al punto x = () Copyright 212 Zanichelli Editore Sp, ologna [23]
7 SCHED DI GGIRNMENT ESEMPI DI DISEG QUTT ESEMPI 1 ESEMPI 2 Sezione di conduttura fognaria in calcestruzzo Prospetto di edificio (535) R 145 R Ø4 44 R ESEMPI 3 Pianta di alloggio () Copyright 212 Zanichelli Editore Sp, ologna [23]
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico
 La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
Unificazione nel disegno. Enti di unificazione
 Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
Quotatura (UNI ISO 129-1)
 Quotatura (UNI IS 19-1) MENCLATURA Quotatura è l'insieme delle quote e delle informazioni alfanumeriche necessarie a determinare le dimensioni di un oggetto in tutti i suoi elementi. Quota è l'insieme
Quotatura (UNI IS 19-1) MENCLATURA Quotatura è l'insieme delle quote e delle informazioni alfanumeriche necessarie a determinare le dimensioni di un oggetto in tutti i suoi elementi. Quota è l'insieme
QUOTATURA. Introduzione
 QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
QUOTATURA DISEGNO TECNICO
 QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
LE SCALE DI RAPPRESENTAZIONE
 IL SUPPORTO La CARTA DA DISEGNO è raggruppabile in due tipi fondamentali: - carta opaca o bianca - carta trasparente o da lucido, usata per disegni a china. GLI STRUMENTI Il gruppo di linee da usare per
IL SUPPORTO La CARTA DA DISEGNO è raggruppabile in due tipi fondamentali: - carta opaca o bianca - carta trasparente o da lucido, usata per disegni a china. GLI STRUMENTI Il gruppo di linee da usare per
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
 6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
4. Proiezioni del piano e dello spazio
 4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Fig. 23. Viste assonometriche di un cubo
 4. L ASSONOMETRIA Marco Cardini L'assonometria, come metodo grafico di rappresentazione degli oggetti nello spazio tridimensionale, viene descritta da MONGE nel trattato di "GEOMETRIE DESCRIPTIVE" edito
4. L ASSONOMETRIA Marco Cardini L'assonometria, come metodo grafico di rappresentazione degli oggetti nello spazio tridimensionale, viene descritta da MONGE nel trattato di "GEOMETRIE DESCRIPTIVE" edito
Sistema di diagnosi CAR TEST
 Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON
 PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
Rappresentazione delle saldature
 TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
Corso di Automazione industriale
 Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni
 Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
Prodotti Siderurgici. 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate
 Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
IL CALIBRO A CORSOIO
 di Tecnologia Meccanica IL CALIBRO A CORSOIO A cura dei proff. Morotti Giovanni e Santoriello Sergio IL CALIBRO A CORSOIO Il calibro a corsoio è lo strumento di misura lineare più impiegato in officina.
di Tecnologia Meccanica IL CALIBRO A CORSOIO A cura dei proff. Morotti Giovanni e Santoriello Sergio IL CALIBRO A CORSOIO Il calibro a corsoio è lo strumento di misura lineare più impiegato in officina.
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Sezioni e Norme di rappresentazione
 Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
LA MISURAZIONE DEL CARATTERE
 TPO PROGETTAZIONE UD 03 GESTIONE DEL CARATTERE IL TIPOMETRO LA MISURAZIONE DEL CARATTERE A.F. 2011/2012 MASSIMO FRANCESCHINI - SILVIA CAVARZERE 1 IL TIPOMETRO: PARTI FONDAMENTALI Il tipometro è uno strumento
TPO PROGETTAZIONE UD 03 GESTIONE DEL CARATTERE IL TIPOMETRO LA MISURAZIONE DEL CARATTERE A.F. 2011/2012 MASSIMO FRANCESCHINI - SILVIA CAVARZERE 1 IL TIPOMETRO: PARTI FONDAMENTALI Il tipometro è uno strumento
LA PROGRAMMAZIONE N10 G0 X5 Y5
 LA PROGRAMMAZIONE Un programma per una Macchina Utensile CNC è costituito da una sequenza logica di informazioni geometriche, tecnologiche ed ausiliarie (fasi di lavoro). Le informazioni geometriche riguardano
LA PROGRAMMAZIONE Un programma per una Macchina Utensile CNC è costituito da una sequenza logica di informazioni geometriche, tecnologiche ed ausiliarie (fasi di lavoro). Le informazioni geometriche riguardano
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Punti notevoli di un triangolo
 Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
r.berardi COSTRUZIONI GEOMETRICHE
 r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
ISTITUTO SUPERIORE D. MILANI MONTICHIARI CORSO DI AUTOCAD 2014/15 DOCENTE :GIOACCHINO IANNELLO
 ISTITUTO SUPERIORE D. MILANI MONTICHIARI CORSO DI AUTOCAD 2014/15 DOCENTE :GIOACCHINO IANNELLO AutoCAD (prodotto dall'autodesk) è, senza dubbio, il programma più diffuso nel campo del disegno tecnico assistito
ISTITUTO SUPERIORE D. MILANI MONTICHIARI CORSO DI AUTOCAD 2014/15 DOCENTE :GIOACCHINO IANNELLO AutoCAD (prodotto dall'autodesk) è, senza dubbio, il programma più diffuso nel campo del disegno tecnico assistito
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
DALLE CARTE ALLE SEZIONI GEOLOGICHE
 DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
f : A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che si può invertire.
 Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
Norme. Norme. Università degli Studi di Brescia DIMI
 - UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
- UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
Principi generali di normativa per il Disegno Tecnico e introduzione alle Proiezioni Ortogonali
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
Eurocodici Strutturali
 Eurocodici Strutturali 5 Capitolo Strutture in acciaio Rappresentazione saldature Unificazione viti/bulloni Indicazioni pratiche collegamenti bullonati Rappresentazione bullonature Caratteristiche dimensionali
Eurocodici Strutturali 5 Capitolo Strutture in acciaio Rappresentazione saldature Unificazione viti/bulloni Indicazioni pratiche collegamenti bullonati Rappresentazione bullonature Caratteristiche dimensionali
PROGRAMMAZIONE della M.U. CNC
 PROGRAMMAZIONE della M.U. CNC 1 La programmazione delle M.U. CNC 1 Generalità 2 Geometrie di riferimento 3 Grammatica 4 Lessico 5 Sintassi 6 Esempi 7 Linguaggio APT 2 La programmazione delle M.U. CNC Le
PROGRAMMAZIONE della M.U. CNC 1 La programmazione delle M.U. CNC 1 Generalità 2 Geometrie di riferimento 3 Grammatica 4 Lessico 5 Sintassi 6 Esempi 7 Linguaggio APT 2 La programmazione delle M.U. CNC Le
Minicorso Regole di Disegno Meccanico
 Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
www.rodacciai.it PROVA DI TRAZIONE L 0 = 5.65 S 0 PROVE MECCANICHE
 PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
AddCAD per ZWCad. Passa alla progettazione 3D rimanendo sul tuo Cad famigliare
 AddCAD per ZWCad Passa alla progettazione 3D rimanendo sul tuo Cad famigliare Passare alla progettazione 3D è un salto di qualità che molti Professionisti tentano di compiere, ma in tanti casi senza successo.
AddCAD per ZWCad Passa alla progettazione 3D rimanendo sul tuo Cad famigliare Passare alla progettazione 3D è un salto di qualità che molti Professionisti tentano di compiere, ma in tanti casi senza successo.
ALLEGATO II Dispositivi di attacco
 ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
Il disegno dei materiali
 materiali per l architettura TDM 4 Il disegno dei materiali Il disegno tecnico è quel particolare tipo di disegno in grado di rappresentare un oggetto attraverso i metodi di rappresentazione di trasferire
materiali per l architettura TDM 4 Il disegno dei materiali Il disegno tecnico è quel particolare tipo di disegno in grado di rappresentare un oggetto attraverso i metodi di rappresentazione di trasferire
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Ministero delle Infrastrutture e dei Trasporti
 Ministero delle Infrastrutture e dei Trasporti Direzione generale per i porti S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO Guida alla compilazione del Modello Domanda D3 (Parte Tecnica: cartelloni, insegne
Ministero delle Infrastrutture e dei Trasporti Direzione generale per i porti S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO Guida alla compilazione del Modello Domanda D3 (Parte Tecnica: cartelloni, insegne
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
COMANDI AUTOCAD. 2.Copia. 1.Cancella STRUMENTI FONDAMENTALI. dfh. Lo strumento cancella elimina gli oggetti dal disegno
 Istituto «25 Aprile» Corso CAT a.s. 2013/14 Barra degli strumenti Edita COMANDI AUTOCAD Concetti fondamentali dei comandi AUTOCAD STRUMENTI FONDAMENTALI 1. Cancella 2. Copia 3. Specchio 4. Offset 5. Sposta
Istituto «25 Aprile» Corso CAT a.s. 2013/14 Barra degli strumenti Edita COMANDI AUTOCAD Concetti fondamentali dei comandi AUTOCAD STRUMENTI FONDAMENTALI 1. Cancella 2. Copia 3. Specchio 4. Offset 5. Sposta
Fig. 2. Proiezioni ortogonali di un parallelepipedo su piani esterni alla figura
 3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE
 ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
 Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
IMPOSTAZIONE DELLE TAVOLE GRAFICHE
 IMPOSTAZIONE DELLE TAVOLE GRAFICHE Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
IMPOSTAZIONE DELLE TAVOLE GRAFICHE Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
Il programma CONFELMOD CAD creazione e modifica
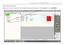 CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
CREAZIONE DEI PEZZI DEL MODELLO Dopo aver fatto la lista di tutti i componenti nella scheda modello si passa alla creazione dei pezzi. Si seleziona il modello e si clicca su Apri Modello 1 Con questa operazione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
LE SCALE: TIPOLOGIE COSTRUTTIVE ED ELEMENTI PER IL PROGETTO
 LE SCALE: TIPOLOGIE COSTRUTTIVE ED ELEMENTI PER IL PROGETTO Le scale L'insieme di tutte le strutture portanti che individuano lo spazio della scala si chiama gabbia. L'insieme delle strutture portanti
LE SCALE: TIPOLOGIE COSTRUTTIVE ED ELEMENTI PER IL PROGETTO Le scale L'insieme di tutte le strutture portanti che individuano lo spazio della scala si chiama gabbia. L'insieme delle strutture portanti
Fondazioni a platea e su cordolo
 Fondazioni a platea e su cordolo Fondazione a platea massiccia Una volta normalmente impiegata per svariate tipologie di edifici, oggi la fondazione a platea massiccia viene quasi esclusivamente adottata
Fondazioni a platea e su cordolo Fondazione a platea massiccia Una volta normalmente impiegata per svariate tipologie di edifici, oggi la fondazione a platea massiccia viene quasi esclusivamente adottata
Tabella A.1 Classificazione generale degli edifici per categorie
 Appendice A Modalità di installazione degli impianti fotovoltaici sugli edifici Ai fini dell applicabilità della tariffa incentivante competente agli impianti fotovoltaici realizzati sugli edifici si adotta
Appendice A Modalità di installazione degli impianti fotovoltaici sugli edifici Ai fini dell applicabilità della tariffa incentivante competente agli impianti fotovoltaici realizzati sugli edifici si adotta
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Proiezioni Grafica 3d
 Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Introduzione. 001_007_pagine_iniziali.indd 7 22/01/14 11.21
 7 Introduzione Questo volume si propone di riorganizzare i percorsi di aritmetica e di geometria del corso principale adattandoli a studenti con esigenze specifiche. Il progetto grafico originale del corso
7 Introduzione Questo volume si propone di riorganizzare i percorsi di aritmetica e di geometria del corso principale adattandoli a studenti con esigenze specifiche. Il progetto grafico originale del corso
Corso di Disegno di Macchine + Abilità Informatiche. Test di autovalutazione 14 marzo 2012 / A
 Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Esercizio Decorazioni
 Nome Cognome Classe Data La riproduzione di questa pagina tramite fotocopie è autorizzata ai soli fini dell utilizzo nell attività didattica degli alunni delle classi che hanno adottato il testo. Esercizio
Nome Cognome Classe Data La riproduzione di questa pagina tramite fotocopie è autorizzata ai soli fini dell utilizzo nell attività didattica degli alunni delle classi che hanno adottato il testo. Esercizio
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
Tutorial 3DRoom. 3DRoom
 Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Esercizi complementari al corso di DISEGNO TECNICO INDUSTRIALE (MECL, AUTL, MATL), a.a. 2005/06.
 UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
Capitolo 3. L applicazione Java Diagrammi ER. 3.1 La finestra iniziale, il menu e la barra pulsanti
 Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RUOTE DENTATE. Introduzione
 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
Trasformazioni 2D. Grande differenza rispetto alla grafica raster!
 Trasformazioni 2D Il grande vantaggio della grafica vettoriale è che le immagini vettoriali descrivono entità matematiche È immediato manipolare matematicamente tali entità In quasi tutte le manipolazioni
Trasformazioni 2D Il grande vantaggio della grafica vettoriale è che le immagini vettoriali descrivono entità matematiche È immediato manipolare matematicamente tali entità In quasi tutte le manipolazioni
Capitolo 11. Il disegno in 3D
 Capitolo 11 Il disegno in 3D o 11.1 Uso delle coordinate nello spazio o 11.2 Creazione di oggetti in 3D o 11.3 Uso dei piani di disegno in 3D (UCS) o 11.4 Creazione delle finestre di vista o 11.5 Definizione
Capitolo 11 Il disegno in 3D o 11.1 Uso delle coordinate nello spazio o 11.2 Creazione di oggetti in 3D o 11.3 Uso dei piani di disegno in 3D (UCS) o 11.4 Creazione delle finestre di vista o 11.5 Definizione
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Disegno di Macchine. corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
di sfere a contatto radiale 262
 Cuscinetti a due corone di sfere Cuscinetti a due corone di sfere a contatto radiale 262 Definizione ed attitudini 262 Serie 262 Tolleranze e giochi 262 Elementi di calcolo 263 Suffissi 263 Caratteristiche
Cuscinetti a due corone di sfere Cuscinetti a due corone di sfere a contatto radiale 262 Definizione ed attitudini 262 Serie 262 Tolleranze e giochi 262 Elementi di calcolo 263 Suffissi 263 Caratteristiche
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
0. Piano cartesiano 1
 0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
Dispositivi di rete. Ripetitori. Hub
 Ripetitori Dispositivi di rete I ripetitori aumentano la distanza che può essere ragginta dai dispositivi Ethernet per trasmettere dati l'uno rispetto all'altro. Le distanze coperte dai cavi sono limitate
Ripetitori Dispositivi di rete I ripetitori aumentano la distanza che può essere ragginta dai dispositivi Ethernet per trasmettere dati l'uno rispetto all'altro. Le distanze coperte dai cavi sono limitate
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Ministero delle Infrastrutture e dei Trasporti
 Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
2012 Alberto Broggian albertobroggian.it 1 Page. Buongiorno a tutti. Oggi andremo a eseguire un cerchio in lega della nostra Bugatti.
 Buongiorno a tutti Oggi andremo a eseguire un cerchio in lega della nostra Bugatti. Questo è il primo tutorial Iniziamo con il definire le Unità all interno di proprietà del documento : Unità di sistema:
Buongiorno a tutti Oggi andremo a eseguire un cerchio in lega della nostra Bugatti. Questo è il primo tutorial Iniziamo con il definire le Unità all interno di proprietà del documento : Unità di sistema:
METODO PER LA STESURA DI PROGRAMMI PER IL CENTRO DI LAVORO CNC
 METODO PER LA STESURA DI PROGRAMMI PER IL CENTRO DI LAVORO CNC Riferimento al linguaggio di programmazione STANDARD ISO 6983 con integrazioni specifiche per il Controllo FANUC M21. RG - Settembre 2008
METODO PER LA STESURA DI PROGRAMMI PER IL CENTRO DI LAVORO CNC Riferimento al linguaggio di programmazione STANDARD ISO 6983 con integrazioni specifiche per il Controllo FANUC M21. RG - Settembre 2008
2 - Modifica. 2.1 - Annulla. 2.2 - Selezione finestra. S.C.S. - survey CAD system FIGURA 2.1
 2 - Modifica FIGURA 2.1 Il menu a tendina Modifica contiene il gruppo di comandi relativi alla selezione delle entità del disegno, alla gestione dei layer, alla gestione delle proprietà delle varie entità
2 - Modifica FIGURA 2.1 Il menu a tendina Modifica contiene il gruppo di comandi relativi alla selezione delle entità del disegno, alla gestione dei layer, alla gestione delle proprietà delle varie entità
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
2.2.4 Distanze di sicurezza UNI EN ISO 13857:2008, UNI EN 349:1994
 2.2.4 Distanze di sicurezza UNI EN ISO 13857:2008, UNI EN 349:1994 2.2.4.1 Descrizione L uso delle distanze di sicurezza rappresenta un modo per garantire l integrità fisica dei lavoratori in presenza
2.2.4 Distanze di sicurezza UNI EN ISO 13857:2008, UNI EN 349:1994 2.2.4.1 Descrizione L uso delle distanze di sicurezza rappresenta un modo per garantire l integrità fisica dei lavoratori in presenza
REP 050 MISURATORE DI ECCENTRICITA PER RUOTE VEICOLI INDUSTRIALI.
 Cod. 024.042 REP 050 MISURATORE DI ECCENTRICITA PER RUOTE VEICOLI INDUSTRIALI. REP 050 è un nuovo strumento per la misurazione dell eccentricità radiale e laterale dei pneumatici di ruote per veicoli industriali.
Cod. 024.042 REP 050 MISURATORE DI ECCENTRICITA PER RUOTE VEICOLI INDUSTRIALI. REP 050 è un nuovo strumento per la misurazione dell eccentricità radiale e laterale dei pneumatici di ruote per veicoli industriali.
