TRANSIZIONI DI FASE NEL MODELLO XY. dott. Emanuele Francesco Pecora matricola n. Docente:
|
|
|
- Michelina Biondi
- 6 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITÀ DEGLI STUDI DI CATANIA Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Specialistica in Fisica Transizioni di fase nei materiali TRANSIZIONI DI FASE NEL MODELLO XY dott. Emanuele Francesco Pecora matricola n. Docente:
2 INDICE Indice 1 Introduzione 2 2 Rassegna sperimentale: fluidi e sistemi magnetici 4 3 Proprietà generali Esponenti di punto critico Funzione di correlazione Modelli teorici per le transizioni di fase La transizione Berezinskii-Kosterlitz-Thouless Il modello XY Riferimenti bibliografici 23 Elenco delle figure 24 In copertina: esempio di vortici ed antivortici nel modello XY. Ulteriori informazioni a pag. 15, fig. 8. 1
3 1 Introduzione 1 Introduzione Le transizioni di fase sono tra i fenomeni più importanti e trasversali in natura. Consistono in cambiamenti improvvisi di quantità misurabili a livello macroscopico al variare di parametri come pressione o temperatura; questi cambiamenti riflettono delle modifiche a livello microscopico che matematicamente sono descritte dal comportamento non analitico di opportune funzioni termodinamiche (vd. fig. 1). Tipicamente, ma non necessariamente, avvengono in condizioni alle quali il sistema non è in equilibrio termodinamico [1]. Figura 1: Calore specifico di un sistema di 4 He in prossimità del punto critico della transizione alla fase superfluida. Si nota immediatamente l andamento della curva, che ricorda la lettera greca λ (da cui il nome transizione λ, paramentro che in questo caso assume un valore molto piccolo, prossimo allo zero). La forma è dovuta ad una discontinuità della derivata prima dell energia libera del sistema. Si noti inoltre che nei tre grafici la scala delle temperature è ingrandita progressivemante di un fattore 1000, cosa da ricollegare alle proprietà di scaling tipiche delle transizioni. 2
4 1 Introduzione Esempi familiari di questo tipo di trasformazioni sono la transizione acqua/ghiaccio, la demagnetizzazione di certi materiali ad alte temperature, lo studio dei solidi sottoposti ad alte pressioni, la transizione ad uno stato superconduttore. Ma in realtà i fenomeni interpretati come transizioni di fase sono molto vari, e sono alla base della scienza dei materiali, della cosmologia, della fisica delle particelle, di chimica, biologia, sociologia etc. Ma non solo: questi modelli sono utilizzati anche per interpretare alcuni fenomeni estranei alla fisica, come il traffico, in particolare nel passaggio dallo stato di libera circolazione allo stato di imbottigliamento, oppure i fenomeni di crescita o di accumulazione di peso. L importanza dello studio delle transizioni di fase è legato alla comprensione del sistema in cui queste avvengono; potremmo dire che la fisica di un sistema si ottiene studiando le sue fasi e le transizioni da una fase all altra. Una caratteristica propria delle transizioni di fase è l esistenza di un parametro d ordine, cioè di una variabile che assume valori non nulli in una fase, e vale zero dopo la transizione. Si vede che questa è legato non al singolo sistema fisico, ma alla transizione nella sua essenza, ovvero è un parametro universale che ci permette di studiare proprietà globali dei sistemi fisici. Ed è per questo che ad esempio Wilson ha dimostrato che esiste un parallelismo impressionante tra la fisica dei superconduttori e la fisica delle particelle elementari [2]. Ma la fisica delle transizioni di fase è legata anche ad un altro aspetto che caratterizza in modo sostanziale un sistema fisico: le simmetrie di cui esso gode. Infatti ad una transizione di fase è legata spesso la rottura di una simmetria che il sistema possiede in un suo determinato stato. Ad esempio oggi si pensa che lo stato primordiale dell universo fosse fortemente simmetrico e che la sua evoluzione sia stata contraddistinta da una serie di transizioni di fase attraverso le quali si sono formate le particelle di materia oggi note (elettroni, protoni, bosoni...). Inoltre durante 3
5 2 Rassegna sperimentale: fluidi e sistemi magnetici la transizione il sistema assume la notevole proprietà di scala, per cui ci appare lo stesso qualunque scala adoperiamo per osservarlo. In questa tesina, dopo una rassegna in cui sono evidenziate le proprietà delle transizioni di fase prendendo in esame due sistemi particolari (i fluidi e i sistemi magnetici), si discuterà delle principali proprietà matematiche utilizzate per descrivere questi fenomeni. Quindi si entrerà nel dettaglio di una particolare transizione - transizione di Berezinskii- Kosterlitz-Thouless - e di un modello, il modello XY in cui si verifica questa transizione. 2 Rassegna sperimentale: fluidi e sistemi magnetici Come detto una grande varietà di sistemi fisici mostrano delle transizioni di fase, che sono caratterizzate da proprietà del tutto generali. Per illustrarle ci riferiremo per semplicità alle transizioni liquido/gas e magnetiche. Già a partire da questi due esempi, che coinvolgono sistemi totalmente diversi, si possono apprezzare molte proprietà generali [3]. E noto studiando il diagramma di fase di un fluido reale (ovvero rappresentando il sistema al variare dei parametri pressione e temperatura, cfr. fig. 2) che questo divide il piano in diverse regioni: in ognuna si ha la stabilità per una sola fase (liquida, solida o gassosa); le diverse regioni sono delimitate da curve che segnano il passaggio del sistema da una fase all altra. Il luogo dei punti appartenente a queste curve rappresenta una condizione di equilibrio tra due fasi. Spesso si osserva pure l esistenza di un punto del diagramma, che prende il nome di punto triplo, in cui si ha l equilibrio tra le tre fasi. Per descrivere questi comportamenti è utile introdurre un parametro d ordine ρ L ρ G 4
6 2 Rassegna sperimentale: fluidi e sistemi magnetici Figura 2: A sinistra, proiezione nel piano P T del diagramma di fase P V T di un fluido reale. Si notano le tre diverse regioni, corrispondenti alla stabilità delle tre fasi della materia, separate dalle curve di equilibrio tra due fasi. Da osservare che la curva di evaporazione non si estende all infinito, ma si interrompe nel punto triplo. Il percorso tratteggiato indica la possibilità di effettuare una transizione da liquido a gas senza attraversare l equilibrio tra le due fasi. A destra, proiezione dello stesso diagramma sul piano ρt al variare della temperatura. In questo grafico si mette in luce l esistenza del parametro d ordine ρ L ρ G. Si osservi che ad alte temperature le isoterme tendono ad una retta, che rappresenta il limite per un sistema non interagente. dove ρ indica la densità di materia, e con i pedici L e G si indica la fase liquida e gassosa rispettivamente. Si vede che questa quantità è non nulla sotto la temperatura del punto critico T c, e vale zero al di sopra. Consideriamo ora invece un sistema ferromagnetico e lo studiamo rappresentando in un diagramma il suo stato al variare del campo magnetico applicato H e della sua magnetizzazione M (vd. fig. 2). Ritroviamo una analogia sorprendente tra questo sistema e il fluido discusso prima, non solo a livello qualitativo guardando i due diagrammi, ma anche a livello quantitativo: si ritrova una analogia formale tra i paramentri utilizzati per descrivere i due sistemi, come ad esempio suscettività magnetica e coefficiente di compressibilità. Anche in questo caso è possibile definire un parametro d ordine che ha le stesse caratteristiche dette prima, ma che ora è rappresentato dalla magnetizzazione M 0 presente in assenza di 5
7 2 Rassegna sperimentale: fluidi e sistemi magnetici Figura 3: A sinistra proiezione nel piano HM al variare della temperatura del diagramma di fase HMT per un sistema magnetico. Si osservi che ad alte temperature le isoterme tendono ad una retta, che rappresenta ancora una volta il limite per un sistema non interagente. A destra proiezione dello stesso nel piano HT. Figura 4: A sinistra, proiezione del diagramma di fase di un fluido nel piano T ρ: si osservi l andamento del parametro d ordine ρ L ρ G ɛ λ. A destra, proiezione del diagramma di un sistema magnetico sul piano M T. Dal confronto di questi due grafici è evidente il comportamento simile dei due sistemi, e il fatto che le grandezze M 0 e ρ L ρ G svolgono lo stesso ruolo. campo magnetico esterno (vd. fig. 2). In particolare è di rilevante interesse il comportamento dei due sistemi in prossimità dei punti critici in cui si ha l equilibrio tra due stati diversi del 6
8 3 Proprietà generali sistema. E stato sviluppato a tal proposito un modello microscopico che descrive in modo simile i due sistemi: si consideri un volume V costituito da celle microscopiche di fluido, ovvero dalle celle elementari contenenti il momento magnetico. La situazione in cui T > T c corrisponde ad una rapida e casuale orientazione del momento magnetico di ogni cella, ovvero del moto del fluido. Non appena ci si avvicina alla temperatura critica si osserva una interazione tra le varie celle, per cui si formano dei piccoli agglomerati in cui tutte le celle hanno lo stesso momento magnetico, ovvero si ha la nucleazione della nuova fase. Questo fenomeno, che prende il nome di opalescenza critica, è stato osservato sperimentalmente: infatti non appena agglomerati assumono dimensioni laterali paragonabili alla lunghezza d onda della luce, questa viene scatterata con un effetto osservabile. Raggiunta poi la temperatura critica, l ordine che si stava formando negli agglomerati si estende a lungo range in tutto il sistema (cfr. fig. 2). 3 Proprietà generali Entrando più nel dettaglio della trattazione matematica [4], la fisica delle transizioni di fase si basa sulle seguenti premesse: la probabilità di trovare un sistema in un certo stato S con energia E e alla temperatura T è P (S) = e βe(s) Z L (β) essendo β = 1 e Z k B T L un fattore di normalizzazione noto come funzione di partizione nell approssimazione lineare: Z L (t) = S e βe(s). Altro parametro importante è l energia libera f L (β) = 1 L d ln Z L(β) 7
9 3.1 Esponenti di punto critico Figura 5: Rappresentazione pittorica del modello microscopico di un sistema durante una transizione di fase. Una quadrato colorato indica una cella occupata, ovvero uno spin up. Si nota al tendere di T T c la formazione di aggregati ordinati di celle, fino al raggiungimento di un ordine a lungo range. Con ξ viene indicata la lunghezza di correlazione del sistema. dove d è la dimensionalità del sistema in considerazione. Una transizione di fase può avvenire solo se il sistema sotto determinate condizioni può esistere in un infinito numero di stati (nel limite termodinamico L ). Vediamo ora più in dettaglio due grandezze importanti per il nostro studio: gli esponenti di punto critico e la funzione di correlazione. 3.1 Esponenti di punto critico In tutti i sistemi in cui si presentano transizioni di fase sono stati ritrovati elementi comuni come un diagramma di fase, un punto critico, un parametro d ordine. E chiaro allora che sono stati fatti molti sforzi per 8
10 3.1 Esponenti di punto critico trovare un modello teorico unitario che potesse descrivere questi fenomeni. L attenzione è stata puntata in modo particolare sul poter esprimere i parametri d ordine in funzione di una grandezza tipica del sistema elevata ad un esponente, che prende il nome di esponente di punto critico λ, con la speranza che questo possa assumere lo stesso valore per tutti i sistemi. Ad esempio nel caso della magnetizzazione residua di un materiale ferromagnetico, questa si può esprimere come [5]: M ( T T ) λ c = ( ɛ) λ T c Il fatto che sia stata riposta maggiore attenzione non sul trovare una teoria per fittare l intero range di dati sperimentali, ma per spiegare il comportamento solo in prossimità del punto critico, si spiega con l osservazione che solo in questa regione si ha un comportamento indipendente dal particolare sistema fisico, e che può essere spiegato ricorrendo a considerazioni di base di meccanica statistica e termodinamica. Diamo allora una definizione rigorosa e generale dell esponente di punto critico [3]: si consideri una generica funzione positiva e continua f(ɛ), funzione della variabile ɛ = T T C T C ed esista il limite ln f(ɛ) λ = lim ɛ 0 ln ɛ Si definisce esponente di punto critico da associare alla funzione f(ɛ) la quantità λ. Questo concetto si indica con la scrittura f(ɛ) ɛ λ Da questa definizione segue che valori negativi di λ corrispondono a funzioni che divergono in prossimità del punto critico, mentre esponenti positivi sono da associare a funzioni che ivi tendono a zero. Per λ = 0 il 9
11 3.1 Esponenti di punto critico Figura 6: Esempi di varie tipologie di comportamento per ɛ = 0. In a) si ha il caso λ < 0; in b) si ha λ > 0; in c) λ = 0, ma si ha una divergenza logaritmica (f(ɛ) ln f(ɛ) ); in d) si ha ancora λ = 0, ma stavolta λ s = 1 2, e dunque f(ɛ) const. comportamento della f(0) può essere una divergenza logaritmica, o una singolarità di cuspide, o una discontinuità eliminabile (vd. fig. 3.1). Per distinguere tra queste tre possibilità si introduce un secondo parametro che separa le singolarità logaritmiche da quelle di cuspide; per far questo è necessario trovare la prima derivata che diverge ad ɛ 0: si definisce allora: λ s = j + lim ɛ 0 ln f (j) (ɛ) ln ɛ 10
12 3.2 Funzione di correlazione Queste definizioni del tutto generali andranno poi applicate al singolo sistema fisico e alle grandezze termodinamiche rilevanti per la transizione di fase, per cui si definiscono nei vari casi opportuni parametri. In generale diremo che una transizione è del primo ordine se si ha un comportamento non analitico della derivata prima di una opportuna funzione termodinamica; si parla di transizioni di ordine superiore o continue se in prossimità del punto critico tale derivata prima risulta continua, mentre la derivata seconda è o discontinua o divergente. Come detto la cosa più interessante è che nonostante ogni sistema fisico abbia le sue peculiarità, per cui ad esempio nel caso dei fluidi la temperatura critica vari di molto da caso a caso, ciò che si trova sperimentalmente è che il rispettivo esponente assume in tutti i casi sostanzialmente lo stesso valore. Un tempo si pensava che esistesse addirittura un solo esponente universale, per tutti i materiali; questa speranza non è stata supportata dai dati sperimentali, ma non modifica l essenza del discorso, e cioè che il valore dell esponente è legato alla transizione in quanto tale e non al sistema particolare. 3.2 Funzione di correlazione Un altra grandezza che svolge un ruolo molto importante nella trattazione matematica dei sistemi fisici è la funzione di correlazione [6], definita, nel caso di un sistema spazialmente uniforme, ovvero invariante per traslazione, con la seguente equazione: G( r r ) =< n( r)n( r ) > n 2 essendo n( r) la densità di particelle nella posizione indicata dal vettore r. Questa funzione è una misura delle correlazioni delle fluttuazioni della densità rispetto al valore medio, e fisicamente indica una misura di 11
13 3.2 Funzione di correlazione probabilità condizionata, ovvero la probabilità di trovare una particella nella posizione r se è presente una particella nella posizione r (infatti per r r si ha G 0). Ovviamente la dipendenza esplicita della funzione di correlazione dipende direttamente dal potenziale che agisce tra le particelle del particolare sistema in considerazione. La cosa interessante è che a partire da questa funzione così definita possono essere ricavate molte grandezze fisiche di rilevanza anche sperimentale. Ad esempio si può vedere [3] che per un fluido, in cui agisce un potenziale tra le particelle del tipo di Lennard-Jones (potenziale 6:12), a partire dalla G( r r ) si può ricavare il parametro di compressibilità isotermica: K T = n 1 G( r)d r KT 0 Una relazione analoga si ricava per la suscettività di un sistema di spin. In entrambi i casi si vede che in prossimità del punto critico si ha un aumento del valore della funzione di correlazione. Altro significato molto importante della funzione di correlazione è che la sua trasformata di Fourier spaziale è definita come il fattore di struttura tipico di un sistema. Questo fattore entra in gioco ad esempio nel calcolo della distribuzione di intensità di una radiazione e.m. scatterata elettronicamente I( q), essendo q il vettore d onda della radiazione incidente. Si prova ad esempio che il rapporto tra la I( q) e la distribuzione I 0 ( q) relativa ad un sistema non interagente vale I( q) I 0 ( q) = n 1 G( r)e i q rd r = n 1 S( q). Si vede che in vicinanza del punto critico si osserva S( q 0), ovvero abbiamo ritrovato analiticamente il fenomeno dell opalescenza critica di cui avevamo già discusso qualitativamente (cfr. fig. 2). 12
14 4 Modelli teorici per le transizioni di fase 4 Modelli teorici per le transizioni di fase Nel corso degli anni sono state presentate molte teorie e modelli aventi lo scopo di bene interpretare i dati sperimentali relativi alle varie transizioni di fase, tentando di dare ad esse una chiara interpretazione a livello microscopico [3]. La prima teoria risale alla tesi di dottorato di van der Waals, che segue di tre anni i primi risultati sperimentali sul punto critico dell anidride carbonica (Andrews, 1869), e in cui si tenta di dare una descrizione di questi dati. La teoria parte dall equazione di stato dei gas reali per ottenere utili equazioni verificate sperimentalmente. Circa invece il magnetismo, la prima teoria, ancora oggi valida, è risalente al 1907, dovuta a Weiss, ed è la nota teoria del campo molecolare [5]. Questa consiste essenzialmente nella (brutale) assunzione che in un materiale ferromagnetico gli spin interagiscano l uno con l altro attraverso un campo magnetico molecolare che è proporzionale alla magnetizzazione residua misurata sperimentalmente. Una terza teoria classica è la teoria di Ornstein-Zernike, in cui si ha la novità dell introduzione della funzione di correlazione. Si tratta in tutti i casi comunque di teorie fenomenologiche che partendo dai dati sperimentali trovano delle equazioni in grado di spiegarli. Nel seguito degli anni sono stati sviluppati dei modelli che a partire da principi primi tentano una spiegazione più generale. Si tratta del modello di Ising, del modello di Vaks-Larkin, del modello di Heisemberg classico e del modello sferico. Tutti descrivono il generico sistema fisico con una hamiltoniana modello che si scrive nella forma H D = J <ij> S D i S D j dove Si D è il vettore D-dim degli spin, J è l energia tra la coppia di spin < ij > paralleli e vicini. Questa hamiltoniana è stata risolta in vari 13
15 4.1 La transizione Berezinskii-Kosterlitz-Thouless casi, ma poche volte in maniera analitica; la maggior parte delle volte è necessario ricorrere a delle approssimazioni numeriche per poter avere dei risultati. Il modello attualmente più completo è certamente il modello di Ising, che è risolvibile analiticamente nel caso 1D (e già questo è un buon risultato), mentre nel caso 3D alcuni pensano sia proprio impossibile da risolvere esattamente. In questa tesina riporto alcuni risultati relativi al modello XY, un modello 2D che rappresenta un tipico esempio di transizione di fase di ordine infinito mediata tramite difetti topologici (vortici) del reticolo in cui sono inseriti gli spin e che avviene in un sistema che rimane in equilibrio termodinamico. Una transizione di questo tipo prende il nome di transizione di Berezinskii-Kosterlitz-Thouless. Questo tipo di transizioni non sono esclusive di questo modello, ma si ritrovano ad esempio in sistemi antiferromagnetici, modelli ice-type F, nella teoria delle stringhe e in generale nei modelli in cui si ha interazione a lungo range. 4.1 La transizione Berezinskii-Kosterlitz-Thouless Per la prima volta nel 1971 Berezinskii [7] e poi nel dettaglio Kosterlitz e Thouless nel 1973 [8], identificarono, proprio nel modello XY di cui parlerò in questa tesina, l esistenza di configurazioni vorticose in cui il campo dovuto agli spin risulta ovunque smooth, eccetto che in piccole regioni. La situazione è molto simile alla struttura del campo di velocità che si crea in un fluido turbolento (vd. fig. 4.1, [9]), quando, anche nella trattazione matematica, il vortice viene sovrapposto ad un fondo continuo e morbido. Considerando un persorso chiuso che racchiuda al suo interno questa regione, poichè tutte le grandezze fisiche sono funzioni di periodo 2π, si ricava che la carica topologica contenuta in queste regioni non può che essere un valore intero (cfr. fig. 8). Questi difetti topologici hanno la propietà che una volta formatisi nel sistema, immediatamente 14
16 4.1 La transizione Berezinskii-Kosterlitz-Thouless Figura 7: Esempi di vortici: a sinistra vortici creati dalla turbolenza di un jet; a destra il Big Red Spot su Giove, un vortice gigante, più grande dell intero pianeta terra e che permane per secoli. Figura 8: Configurazione di vortici, caratterizzati da una carica topologica di n = +1 (quello a sinistra, vortice propriamente detto) e n = 1 (a destra, antivortice). In entrambi i casi gli spin ruotano di 2π e 4π attorno ai due punti evidenziati. eliminano la correlazione tra la fase degli spin; dunque un numero elevato di vortici disposti casualmente nel reticolo hanno l effetto di disordinare 15
17 4.1 La transizione Berezinskii-Kosterlitz-Thouless il sistema, costringendolo ad un ordine a corto range. Il loro effetto si annulla solo se si dispongono in coppie di vortici ed antivortici. Per poter fare delle valutazioni qualitative, è necessario poter calcorare il numero di vortici presenti in un reticolo ad una data temperatura; per far questo bisogna confrontare l energia per creare un vortice con il guadagno di entropia associato al numero di configurazioni in cui questo può disporsi, il che vuol dire calcolare l energia libera necessaria per creare un vortice. La trattazione è simile a quella che si adotta per descrivere i vortici nei fluidi: in tal caso il campo di velocità associato al sistema si scompone nella forma v(x) = E(x) + θ v (x) essendo il primo termine il potenziale di fondo, che non gioca nessun ruolo nella creazione dei vortici e che dunque trascureremo subito, mentre il secondo termine descrive la configurazione vorticosa. Questo termine, come tutti i termini che rappresentano sorgenti in un campo vettoriale, si può scrivere nella forma θ v (x) = A(x) La funzione A(x) formalmente è soluzione del problema A(x) = G(x x )J(x )d 2 x essendo J(x) la sorgente del campo, collegata alla posizione dei vortici. Ricordando la condizione per cui effettuando un giro attorno ad un vortice la variazione di fase deve essere una quantità intera, si impone la condizione N i=1 2πn i = 2 A(x)dS C 16
18 4.1 La transizione Berezinskii-Kosterlitz-Thouless da cui segue che A(x) = N n i ln x x i A questo punto calcolare l energia del singolo vortice è semplice: βe vort = 1 ( v (x)) 2 dx 2g i=1 e da questa è possibile calcolare l energia libera del vortice, che si dimostra vale E n = E 0 n + n2 π g ln L a 2 ln L a essendo n il valore di carica del vortice, E 0 n una costante che tiene conto dell energia della carica del difetto che rompe la continuità del reticolo, g una costante di accoppiamento tra i vortici. Chiaramente i vortici con n = ±1 sono quelli che hanno un minor costo energetico e dunque sono i più numerosi. Il primo termine di questa espressione è un valore finito, mentre gli altri due divergono come il logaritmo nel limite termodinamico (L, reticolo di dimensioni infinite). Il termine entropico prevarrà, e dunque si avrà comunque un numero finito di vortici, quando g > g c = π 2 Invece il numero di vortici invece diverge, con la conseguente distruzione totale dell ordine del sistema, se la temperatura del sistema è tale che T BKT g c. (1) Peraltro a temperature inferiori a queste si prova che la coppia vorticeantivortice tende a legarsi, annullando come sappiamo ogni suo effetto. In conclusione, le transioni Berezinskii-Kosterlitz-Thouless sono transizioni mediate da difetti topologici, la loro peculiarità sta nel termine logaritmico che compare nel calcolo dell energia del sistema, e sono state 17
19 4.2 Il modello XY osservate in molti sistemi. Il più importante di questi è senz altro il modello XY, e nella prossima sezione specificheremo la trattazione di questa transizione per questo modello. 4.2 Il modello XY Il modello XY [4] viene adottato per studiare sistemi come film di He superfluido, materiali superconduttori, superfici fluttuanti e particolari sistemi magnetici, gassosi o liquido-cristallini; una delle migliori applicazioni di questo modello, e che ha ricevuto una notevole spinta nella ricerca sia teorica che sperimentale, è un sistema 2D di giunzioni Josephson. Questo sistema si realizza sperimentalmente a partire dalla condensazione di atomi bosonici in un reticolo ottico bidimensionale, e studiandone le loro oscillazioni. In questo sistema è stata osservata una transizione di fase mediata da vortici, che però scompare sotto certe condizioni, riconducibili probabilmente alle fluttuazioni quantistiche del sistema (cfr. per es. [10, 11]). Nel corso degli anni sono stati sviluppati molti metodi analitici e numerici nel tentativo di capire la natura delle transizioni in questo sistema. I successi furono pochi fin quando non si compresero gli effetti di correzioni logaritmiche che modificano la trattazione matematica del modello. Il modello è definito in un reticolo regolare 2D di spin, in cui con l indice i si indica il singolo sito, che è occupato dallo spin s i. L energia del sistema è data dunque da H = s i s j <i,j> con la sommatoria su tutti i siti primi vicini. La caratteristica di questo sistema è che sono presenti vortici e antivortici che sopra la temperatura critica sono slegati e disordinati; sotto la temperatura critica si legano insieme e sono importanti come gradi di libertà dinamici per il sistema. 18
20 4.2 Il modello XY Questi vortici consistono in rotazioni coordinate degli spin di un angolo pari a 2π o 4π attorno ad un punto. L esistenza di questi vortici implica l esistenza di correlazioni a lungo-range tra i due spin generici che occupano le posizioni i e j e si trovano a distanza r. Queste correlazioni sono descritte da una funzione che nel limite termodinamico di un volume infinito si esprime come G (r) r η(β) In questo regime la lunghezza di correlazione caratteristica nel punto critico risulta essere divergente. Invece al di sopra di questo punto decade esponenzialmente con un andamento del tipo G (r) r r ξ (ɛ) essendo ξ (ɛ) la lunghezza di correlazione per ɛ > 0. Non appena si raggiunge il punto critico, il comportamento della lunghezza di correlazione 1, del calore specifico e della suscettività del sistema diventano essendo b una costante universale di scala. ξ (ɛ) e bɛ ν (2) C (ɛ) ξ 2 (3) χ (ɛ) ξ 2 ηc (4) Per lungo tempo il modello è stato trattato numericamente fissando ν = 1 2 (condizione questa che si può ricavare in modo analitico a partire dall eq. 1) e poi determinando il valore di β c. Ma i valori ricavati con questi parametri per la η c erano incompatibili con i dati sperimentali, al punto da supporre che il modello non fosse del tutto corretto. 1 La lunghezza di correlazione, così come indicato in fig. 2, è una misura della distanza alla quale due spin posti in siti differenti sono in grado di interagire. 19
21 4.2 Il modello XY Il problema fu risolto quando si capì che le eqq. 2, 3, 4 risultavano inconsistenti in questa forma, e che dovevano essere modificate introducendo delle correzioni logaritmiche in modo che C (ɛ) ξ 2 (ln ξ ) eq (5) χ (ɛ) ξ 2 ηc (ln ξ ) 2r (6) con q = 6 e r = In particolare l eq. 5 è imposta, mente l eq. 6 è una prediziona analitica basata sulla teoria perturbativa e che deve essere confermata tramite approcci non perturbativi. Per far questo è stata fatta una simulazione numerica su un sistema di dimensioni finite L (predizione FSS - finite-size scaling) e si è trovato χ L (0) L 2 ηc (ln L) 2r (7) Simulazioni numeriche sono state svolte per confermare le due predizioni, ed è stato trovato r = 0.02, in contrasto con la previsione teorica. Dunque l introduzione di correzioni logaritmiche ha portato a questi problemi. Si pensò dunque che così come le correzioni logaritmiche hanno generato il corretto comportamento di scala, una attendibile misura di r potesse venire da correzioni del secondo ordine. In particolare è stata scelta l espressione χ L (0) L 2 ηc (ln L) 2r {1 + O ( )} ln ln L ln L Questa equazione è stata risolta numericamente su un reticolo finito (L = 256) utilizzando l ansatz (8) χ L (0) L 2 ηc (C + ln L) 2r (9) trovando il valore di r = 0.056, compatibile con la predizione analitica. Ma il passaggio cruciale nella transizione di fase del tipo Berezinskii- Kosterlitz-Thouless è la correlazione tra i vortici. Una conseguenza del 20
22 4.2 Il modello XY termine logaritmico nella funzione di correlazione è che l energia del singolo vortice cresce con la dimensione del sistema, e dunque a bassa temperatura, per sistemi molto grandi, possono solo crearsi delle coppie vorticeantivortice. Ma in questa coppia si ha chiaramente la mutua cancellazione dell effetto di ordine del singolo vortice, per cui questa coppia non ha la capacità di disordinare il sistema. Dunque a bassa temperatura esiste un ordine topologico a lungo range. Al contrario, ad alta temperatura il numero dei vortici aumenta e la distanza tra una coppia diventa così grande che questi si possono considerare liberi, al punto da essere in grado di disordinare il sistema. A lungo si è creduto che modificando l hamiltoniana del sistema si dovesse ottenere una transizione non del tipo di Berezinskii-Kosterlitz-Thouless. In particolare a partire dal modello XY si ottiene il modello a step adottando l hamiltoniana H = sgn ( s i s j ) <i,j> in cui l energia associata al singolo vortice è indipendente dalla dimensione del reticolo, e dunque i vortici possono esistere a tutte le temperature: non ci dovrebbe essere una transizione mediata dai vortici. Sorprendentemente con analisi numeriche si è visto che anche in questo sistema si ha una transizione mediata dai vortici, proprio del tipo Berezinskii- Kosterlitz-Thouless. In questo caso probabilmente mentre in effetti l energia associata al singolo vortice rimane finita, l energia libera del sistema cresce comunque come ln L, cosa che inibisce la proliferazione di vortici liberi nella fase a bassa temperatura. In conclusione, di seguito sono presentate alcune delle possibili linee di ricerca da seguire per migliorare, estendere, chiarire questo modello. Il modello XY di cui abbiamo discusso gode di una simmetria di gruppo O(2). Da considerazioni teoriche si vede che modelli che godono di 21
23 4.2 Il modello XY simmetrie del tipo O(N), con N > 2 non dovrebbero supportare l esistenza di difetti topologici come i vortici, e dunque in questi sistemi non si dovrebbe avere alcuna transizione di fase. E invece sembrano esserci delle evidenze per cui in questi sistemi si ha una transizione del tipo Berezinskii-Kosterlitz-Thouless. La questione è ancora aperta. Un altro argomento interessante di ricerca è il ruolo delle impurezze nel modello XY, ovvero l introduzione nel reticolo bidimensionale in modo casuale di difetti che rendano il modello più realistico. L introduzione di impurezze dovrebbe diminuire il valore della temperatura critica. Si vede infatti che i vortici sono attratti, e in un certo senso ancorati alle impurezze, al punto che l energia del vortice si riduce a quella tipica di una vacanza: all aumentare delle impurezze, è possibile formare un maggior numero di vortici, cosa che aumenta il disordine del sistema e dunque abbassa la temperatura critica. Il limite di impurezze è stabilito dal fatto che oltre una certa densità viene inibita la percolazione degli spin attraverso il reticolo (che ormai appare rotto in una serie di siti interconnessi) e dunque non ha senso più parlare di transizione di fase. E ancora da capire però il ruolo delle impurezze sul valore delle grandezze di scala, come l esponente critico delle transizioni. Infine un altra linea di ricerca riguarda le correzioni logaritmiche e sub-logaritmiche che sono necessarie nel modello XY, ma che si ritrovano anche in altri modelli: va capito perché è necessario introdurre queste variazioni e il ruolo di queste correzioni nei vari modelli. 22
24 RIFERIMENTI BIBLIOGRAFICI Riferimenti bibliografici [1] R. Pucci, appunti del corso Transizioni di fase nei materiali, A. A. 2005/2006. [2] R. Pucci, Le simmetrie e la Fisica, inaugurazione A. A. 2002/2003 dell Università degli Studi di Catania. [3] H. E. Stanley, Introduction to Phase Transition and Critical Phenomena (Oxford University Press, Oxford, 1971). [4] R. Kenna, cond-mat/ [5] C. Kittel, Introduzione alla fisica dello stato solido (Bollati Boringhieri, Torino, 2001). [6] R. Pucci, appunti del corso Struttura della materia II, A. A. 2004/2005. [7] V. Berezinskii, Soviet Phys. 32, 493 (1971). [8] J. M. Kosterlitz and D. J. Thouless, J. Phys. C6, 1181 (1973). [9] V. Dobrosavljevic, lectures on Phase Transitions and Critical Phenomena, Florida State University. [10] L. Capriotti, A. Cuccoli, A. Fubini, V. Tognetti, and R. Vaia, condmat/ [11] A. Trombettoni, A. Smerzi, and P. Sodano, New J. Phys. 7, 57 (2005). 23
25 ELENCO DELLE FIGURE Elenco delle figure 1 Calore specifico di un sistema di 4 He in prossimità del punto critico della transizione alla fase superfluida. Si nota immediatamente l andamento della curva, che ricorda la lettera greca λ (da cui il nome transizione λ, paramentro che in questo caso assume un valore molto piccolo, prossimo allo zero). La forma è dovuta ad una discontinuità della derivata prima dell energia libera del sistema. Si noti inoltre che nei tre grafici la scala delle temperature è ingrandita progressivemante di un fattore 1000, cosa da ricollegare alle proprietà di scaling tipiche delle transizioni. 2 2 A sinistra, proiezione nel piano P T del diagramma di fase P V T di un fluido reale. Si notano le tre diverse regioni, corrispondenti alla stabilità delle tre fasi della materia, separate dalle curve di equilibrio tra due fasi. Da osservare che la curva di evaporazione non si estende all infinito, ma si interrompe nel punto triplo. Il percorso tratteggiato indica la possibilità di effettuare una transizione da liquido a gas senza attraversare l equilibrio tra le due fasi. A destra, proiezione dello stesso diagramma sul piano ρt al variare della temperatura. In questo grafico si mette in luce l esistenza del parametro d ordine ρ L ρ G. Si osservi che ad alte temperature le isoterme tendono ad una retta, che rappresenta il limite per un sistema non interagente. 5 24
26 ELENCO DELLE FIGURE 3 A sinistra proiezione nel piano HM al variare della temperatura del diagramma di fase HMT per un sistema magnetico. Si osservi che ad alte temperature le isoterme tendono ad una retta, che rappresenta ancora una volta il limite per un sistema non interagente. A destra proiezione dello stesso nel piano HT A sinistra, proiezione del diagramma di fase di un fluido nel piano T ρ: si osservi l andamento del parametro d ordine ρ L ρ G ɛ λ. A destra, proiezione del diagramma di un sistema magnetico sul piano MT. Dal confronto di questi due grafici è evidente il comportamento simile dei due sistemi, e il fatto che le grandezze M 0 e ρ L ρ G svolgono lo stesso ruolo Rappresentazione pittorica del modello microscopico di un sistema durante una transizione di fase. Una quadrato colorato indica una cella occupata, ovvero uno spin up. Si nota al tendere di T T c la formazione di aggregati ordinati di celle, fino al raggiungimento di un ordine a lungo range. Con ξ viene indicata la lunghezza di correlazione del sistema Esempi di varie tipologie di comportamento per ɛ = 0. In a) si ha il caso λ < 0; in b) si ha λ > 0; in c) λ = 0, ma si ha una divergenza logaritmica (f(ɛ) ln f(ɛ) ); in d) si ha ancora λ = 0, ma stavolta λ s = 1, e dunque f(ɛ) const Esempi di vortici: a sinistra vortici creati dalla turbolenza di un jet; a destra il Big Red Spot su Giove, un vortice gigante, più grande dell intero pianeta terra e che permane per secoli
27 ELENCO DELLE FIGURE 8 Configurazione di vortici, caratterizzati da una carica topologica di n = +1 (quello a sinistra, vortice propriamente detto) e n = 1 (a destra, antivortice). In entrambi i casi gli spin ruotano di 2π e 4π attorno ai due punti evidenziati
delle curve isoterme dell anidride carbonica
 COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
COMPORTAMENTO DEI GAS REALI l andamento delle curve isoterme dell anidride carbonica mostra che: a temperature elevate le isoterme assomigliano a quelle di un gas perfetto Diagramma di Andrews a temperature
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Transizioni liquido-solido: Aspetti cinetici
 Transizioni liquido-solido: Aspetti cinetici Prof.G.Marletta Chimica Fisica dei Materiali II e Laboratorio Laurea Magistrale in Chimica dei Materiali Università di Catania A.A. 2011/2012 1- Caratteri generali
Transizioni liquido-solido: Aspetti cinetici Prof.G.Marletta Chimica Fisica dei Materiali II e Laboratorio Laurea Magistrale in Chimica dei Materiali Università di Catania A.A. 2011/2012 1- Caratteri generali
Struttura dell atomo atomo particelle sub-atomiche - protoni positiva - neutroni } nucleoni - elettroni negativa elemento
 Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Grandezze fisiche e loro misura
 Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e che implicano grandezze misurabili. - Sono
Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e che implicano grandezze misurabili. - Sono
Esploriamo la chimica
 1 Valitutti, Tifi, Gentile Esploriamo la chimica Seconda edizione di Chimica: molecole in movimento Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. L atomo di Bohr 3. Il modello atomico
1 Valitutti, Tifi, Gentile Esploriamo la chimica Seconda edizione di Chimica: molecole in movimento Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. L atomo di Bohr 3. Il modello atomico
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Analisi delle corrispondenze
 Capitolo 11 Analisi delle corrispondenze L obiettivo dell analisi delle corrispondenze, i cui primi sviluppi risalgono alla metà degli anni 60 in Francia ad opera di JP Benzécri e la sua equipe, è quello
Capitolo 11 Analisi delle corrispondenze L obiettivo dell analisi delle corrispondenze, i cui primi sviluppi risalgono alla metà degli anni 60 in Francia ad opera di JP Benzécri e la sua equipe, è quello
laboratorio di fisica moderna magnetismo e nanostrutture
 laboratorio di fisica moderna magnetismo e nanostrutture il comportamento magnetico dei materiali La materia contiene elettroni, che hanno la caratteristica di possedere un momento magnetico: ogni elettrone
laboratorio di fisica moderna magnetismo e nanostrutture il comportamento magnetico dei materiali La materia contiene elettroni, che hanno la caratteristica di possedere un momento magnetico: ogni elettrone
RISOLUZIONE DI PROBLEMI DI FISICA
 RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
RISOUZIONE DI PROBEMI DI FISICA Problema 1 Una massa puntiforme m = 2 kg è soggetta ad una forza centrale con associata energia potenziale radiale U( r) 6 A =, dove A = 2 J m 6. Il momento angolare della
Misura del momento magnetico dell elettrone
 FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
(1;1) y=2x-1. Fig. G4.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
TERMODINAMICA. Studia le trasformazioni dei sistemi in relazione agli scambi di calore e lavoro. GENERALITÀ SUI SISTEMI TERMODINAMICI
 TERMODINAMICA Termodinamica: scienza che studia le proprietà e il comportamento dei sistemi, la loro evoluzione e interazione con l'ambiente esterno che li circonda. Studia le trasformazioni dei sistemi
TERMODINAMICA Termodinamica: scienza che studia le proprietà e il comportamento dei sistemi, la loro evoluzione e interazione con l'ambiente esterno che li circonda. Studia le trasformazioni dei sistemi
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Istituto Professionale di Stato Maffeo Pantaleoni di Frascati SCHEDA PROGRAMMAZIONE DIDATTICA DISCIPLINARE
 Istituto Professionale di Stato Maffeo Pantaleoni di Frascati SCHEDA PROGRAMMAZIONE DIDATTICA DISCIPLINARE ANNO SCOLASTICO 2013/2014 CLASSI 1 sez, A B C D E F G H MATERIA DOCENTEScienze Integrate: FISICA
Istituto Professionale di Stato Maffeo Pantaleoni di Frascati SCHEDA PROGRAMMAZIONE DIDATTICA DISCIPLINARE ANNO SCOLASTICO 2013/2014 CLASSI 1 sez, A B C D E F G H MATERIA DOCENTEScienze Integrate: FISICA
INTRODUZIONE ALLA TERMODINAMICA. Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta
 INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
INTRODUZIONE ALLA TERMODINAMICA Supponiamo di voler studiare il comportamento di una determinata quantità di gas contenuta in un recipiente, ad esempio 5g di ossigeno. Dato l elevato numero di molecole
Elementi di Teoria dei Sistemi. Definizione di sistema dinamico. Cosa significa Dinamico? Sistema dinamico a tempo continuo
 Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
La Termodinamica è la disciplina che si occupa dello studio degli scambi di energia e di materia nei processi fisici e chimici
 La Termodinamica è la disciplina che si occupa dello studio degli scambi di energia e di materia nei processi fisici e chimici Materia = tutto ciò che possiede una massa ed occupa uno spazio Energia =
La Termodinamica è la disciplina che si occupa dello studio degli scambi di energia e di materia nei processi fisici e chimici Materia = tutto ciò che possiede una massa ed occupa uno spazio Energia =
Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per
 Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per molti versi al problema del commesso viaggiatore lasciano
Simulazioni e Metodi Montecarlo Cercano gli stati fondamentali di sistemi complessi non risolubili analiticamente e le loro proprietà analoghi per molti versi al problema del commesso viaggiatore lasciano
LA DISTRIBUZIONE NORMALE
 LA DISTRIBUZIONE NORMALE Italo Nofroni Statistica medica - Facoltà di Medicina Sapienza - Roma La più nota ed importante distribuzione di probabilità è, senza alcun dubbio, la Distribuzione normale, anche
LA DISTRIBUZIONE NORMALE Italo Nofroni Statistica medica - Facoltà di Medicina Sapienza - Roma La più nota ed importante distribuzione di probabilità è, senza alcun dubbio, la Distribuzione normale, anche
LOGARITMI. Corso di laurea: BIOLOGIA Tutor: Floris Marta; Max Artizzu PRECORSI DI MATEMATICA. L uguaglianza: a x = b
 Corso di laurea: BIOLOGIA Tutor: Floris Marta; Max Artizzu PRECORSI DI MATEMATICA LOGARITMI L uguaglianza: a x = b nella quale a e b rappresentano due numeri reali noti ed x un incognita, è un equazione
Corso di laurea: BIOLOGIA Tutor: Floris Marta; Max Artizzu PRECORSI DI MATEMATICA LOGARITMI L uguaglianza: a x = b nella quale a e b rappresentano due numeri reali noti ed x un incognita, è un equazione
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5.
 Unità n 6 Le leggi dei gas 1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5. La legge di Gay-Lussac o legge
Unità n 6 Le leggi dei gas 1. Lo studio dei gas nella storia 2. I gas ideali e la teoria cinetico-molecolare 3. La pressione dei gas 4. La legge di Boyle o legge isoterma 5. La legge di Gay-Lussac o legge
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Capitolo 8 La struttura dell atomo
 Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
Capitolo 8 La struttura dell atomo 1. La doppia natura della luce 2. La «luce» degli atomi 3. L atomo di Bohr 4. La doppia natura dell elettrone 5. L elettrone e la meccanica quantistica 6. L equazione
Teoria cinetica di un sistema di particelle
 Teoria cinetica di un sistema di particelle La meccanica dei fluidi modellati come sistemi continui, sviluppata dal XII e XIII secolo e in grado di descrivere fenomeni dinamici macroscopici con buona approssimazione
Teoria cinetica di un sistema di particelle La meccanica dei fluidi modellati come sistemi continui, sviluppata dal XII e XIII secolo e in grado di descrivere fenomeni dinamici macroscopici con buona approssimazione
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
CALORIMETRO DELLE mescolanze
 CALORIMETRO DELLE mescolanze Scopo dell esperienza è la misurazione del calore specifico di un corpo solido. Il funzionamento del calorimetro si basa sugli scambi di energia, sotto forma di calore, che
CALORIMETRO DELLE mescolanze Scopo dell esperienza è la misurazione del calore specifico di un corpo solido. Il funzionamento del calorimetro si basa sugli scambi di energia, sotto forma di calore, che
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
Note sulla probabilità
 Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Capitolo 6. Variabili casuali continue. 6.1 La densità di probabilità
 Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
Capitolo 6 Variabili casuali continue Le definizioni di probabilità che abbiamo finora usato sono adatte solo per una variabile casuale che possa assumere solo valori discreti; vediamo innanzi tutto come
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Lecture 18. Text: Motori Aeronautici Mar. 26, Mauro Valorani Università La Sapienza. Analisi dimensionale delle turbomacchine
 Lecture 18 Analisi Text: Motori Aeronautici Mar. 26, 2015 Analisi Mauro Valorani Università La Sapienza 18.331 Agenda Analisi 1 Numero di giri e 18.332 Analisi L analisi e il confronto tra le turbomacchine
Lecture 18 Analisi Text: Motori Aeronautici Mar. 26, 2015 Analisi Mauro Valorani Università La Sapienza 18.331 Agenda Analisi 1 Numero di giri e 18.332 Analisi L analisi e il confronto tra le turbomacchine
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale
 4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
4. Esercitazione 4: Dimensionamento del primo stadio di un compressore assiale Lo scopo della presente esercitazione è il dimensionamento del primo stadio di un compressore assiale. Con riferimento alla
ESPONENZIALI. n volte
 Corso di laurea: BIOLOGIA Tutor: Floris Marta; Max Artizzu PRECORSI DI MATEMATICA ESPONENZIALI IL CONCETTO DI POTENZA E LA SUA GENERALIZZAZIONE L elevamento a potenza è un operazione aritmetica che associa
Corso di laurea: BIOLOGIA Tutor: Floris Marta; Max Artizzu PRECORSI DI MATEMATICA ESPONENZIALI IL CONCETTO DI POTENZA E LA SUA GENERALIZZAZIONE L elevamento a potenza è un operazione aritmetica che associa
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
il ciclo di Ericsson (1853) caratterizzato da due isoterme e due isobare; il ciclo di Reitlinger (1873) con due isoterme e due politropiche.
 16 Il ciclo di Stirling Il coefficiente di effetto utile per il ciclo frigorifero di Carnot è, in base alla (2.9): T min ɛ =. (2.31) T max T min Il ciclo di Carnot è il ciclo termodinamico che dà il maggior
16 Il ciclo di Stirling Il coefficiente di effetto utile per il ciclo frigorifero di Carnot è, in base alla (2.9): T min ɛ =. (2.31) T max T min Il ciclo di Carnot è il ciclo termodinamico che dà il maggior
LA MATERIA ED I SUOI STATI
 LA MATERIA ED I SUOI STATI GAS COMPOSIZIONE DELL ARIA 1. I gas ideali e la teoria cineticomolecolare Nel modello del gas ideale le particelle 1. l energia cinetica media delle particelle è proporzionale
LA MATERIA ED I SUOI STATI GAS COMPOSIZIONE DELL ARIA 1. I gas ideali e la teoria cineticomolecolare Nel modello del gas ideale le particelle 1. l energia cinetica media delle particelle è proporzionale
Chimica. La Chimica è la scienza che cerca di comprendere il comportamento della materia studiando il comportamento di atomi e molecole
 Chimica La Chimica è la scienza che descrive la materia, le sue proprietà e le trasformazioni che essa subisce, insieme alle variazioni energetiche che accompagnano questi processi La Chimica è la scienza
Chimica La Chimica è la scienza che descrive la materia, le sue proprietà e le trasformazioni che essa subisce, insieme alle variazioni energetiche che accompagnano questi processi La Chimica è la scienza
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
1.Pressione di un Gas
 1.Pressione di un Gas Un gas è formato da molecole che si muovono in modo disordinato, urtandosi fra loro e urtando contro le pareti del recipiente che le contiene. Durante gli urti, le molecole esercitano
1.Pressione di un Gas Un gas è formato da molecole che si muovono in modo disordinato, urtandosi fra loro e urtando contro le pareti del recipiente che le contiene. Durante gli urti, le molecole esercitano
Grandezze fisiche e loro misura
 Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e caratterizzati da grandezze misurabili.
Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e caratterizzati da grandezze misurabili.
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Corso di Matematica per la Chimica
 Corso di Matematica per la Chimica Dott.ssa Maria Carmela De Bonis Dipartimento di Matematica, Informatica e Economia Università della Basilicata a.a. 2014-15 Introduzione La MATEMATICA è uno strumento
Corso di Matematica per la Chimica Dott.ssa Maria Carmela De Bonis Dipartimento di Matematica, Informatica e Economia Università della Basilicata a.a. 2014-15 Introduzione La MATEMATICA è uno strumento
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Funzioni elementari: funzioni potenza
 Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
Funzioni elementari: funzioni potenza Lezione per Studenti di Agraria Università di Bologna (Università di Bologna) Funzioni elementari: funzioni potenza 1 / 36 Funzioni lineari Come abbiamo già visto,
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Lezione 1: Introduzione alle grandezze magnetiche
 Lezione 1: Introduzione alle grandezze magnetiche 1 Campi Magnetici Il campo magnetico è un campo vettoriale: associa, cioè, ad ogni punto nello spazio un vettore. Un campo magnetico si puo misurare per
Lezione 1: Introduzione alle grandezze magnetiche 1 Campi Magnetici Il campo magnetico è un campo vettoriale: associa, cioè, ad ogni punto nello spazio un vettore. Un campo magnetico si puo misurare per
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari)
 Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
ISTOGRAMMI E DISTRIBUZIONI:
 ISTOGRAMMI E DISTRIBUZIONI: i 3 4 5 6 7 8 9 0 i 0. 8.5 3 0 9.5 7 9.8 8.6 8. bin (=.) 5-7. 7.-9.4 n k 3 n k 6 5 n=0 =. 9.4-.6 5 4.6-3.8 3 Numero di misure nell intervallo 0 0 4 6 8 0 4 6 8 30 ISTOGRAMMI
ISTOGRAMMI E DISTRIBUZIONI: i 3 4 5 6 7 8 9 0 i 0. 8.5 3 0 9.5 7 9.8 8.6 8. bin (=.) 5-7. 7.-9.4 n k 3 n k 6 5 n=0 =. 9.4-.6 5 4.6-3.8 3 Numero di misure nell intervallo 0 0 4 6 8 0 4 6 8 30 ISTOGRAMMI
5. Applicazione ai dati sperimentali, un modello di previsione delle temperature
 5. Applicazione ai dati sperimentali, un modello di previsione delle temperature 5.1 Ricostruzione dello spazio delle fasi L utilizzo del teorema di embedding per ricostruire lo spazio delle fasi relativo
5. Applicazione ai dati sperimentali, un modello di previsione delle temperature 5.1 Ricostruzione dello spazio delle fasi L utilizzo del teorema di embedding per ricostruire lo spazio delle fasi relativo
Diffrazione di Raggi-X da Monocristalli A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 Diffrazione di Raggi-X da Monocristalli A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Raccolta Dati di Diffrazione: Diffrazione di Raggi X Raccolta
Diffrazione di Raggi-X da Monocristalli A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Raccolta Dati di Diffrazione: Diffrazione di Raggi X Raccolta
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
GIUSTIFICAZIONE TEORICA DELLA FORMULA DI PETRY MEDIANTE L ANALISI DIMENSIONALE
 M. G. BUSATO GIUSTIFICAZIONE TEORICA DELLA FORMULA DI PETRY MEDIANTE L ANALISI DIMENSIONALE NOTA TECNICA MGBSTUDIO.NET SOMMARIO La formula di Petry è una formula semiempirica che consente di stimare,
M. G. BUSATO GIUSTIFICAZIONE TEORICA DELLA FORMULA DI PETRY MEDIANTE L ANALISI DIMENSIONALE NOTA TECNICA MGBSTUDIO.NET SOMMARIO La formula di Petry è una formula semiempirica che consente di stimare,
TERMODINAMICA Per lo studio scientifico di un problema occorre separare idealmente una regione di spazio limitata ( sistema ) da tutto ciò che la
 ERMODINAMICA Per lo studio scientifico di un problema occorre separare idealmente una regione di spazio limitata ( sistema ) da tutto ciò che la circonda e può influenzarne il comportamento ( ambiente
ERMODINAMICA Per lo studio scientifico di un problema occorre separare idealmente una regione di spazio limitata ( sistema ) da tutto ciò che la circonda e può influenzarne il comportamento ( ambiente
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
FUNZIONI. }, oppure la
 FUNZIONI 1. Definizioni e prime proprietà Il concetto di funzione è di uso comune per esprimere la seguente situazione: due grandezze variano l una al variare dell altra secondo una certa legge. Ad esempio,
FUNZIONI 1. Definizioni e prime proprietà Il concetto di funzione è di uso comune per esprimere la seguente situazione: due grandezze variano l una al variare dell altra secondo una certa legge. Ad esempio,
ESERCITAZIONE: ESPONENZIALI E LOGARITMI
 ESERCITAZIONE: ESPONENZIALI E LOGARITMI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Esercizio 1 In una coltura batterica, il numero di batteri triplica ogni ora. Se all inizio dell osservazione
ESERCITAZIONE: ESPONENZIALI E LOGARITMI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Esercizio 1 In una coltura batterica, il numero di batteri triplica ogni ora. Se all inizio dell osservazione
Esercitazione 2 Ciclo a vapore a recupero
 Esercitazione 2 Ciclo a vapore a recupero Lo scopo di questa esercitazione è la progettazione di un ciclo a recupero: l impianto è composto da un ciclo a vapore ad un livello di pressione che utilizza
Esercitazione 2 Ciclo a vapore a recupero Lo scopo di questa esercitazione è la progettazione di un ciclo a recupero: l impianto è composto da un ciclo a vapore ad un livello di pressione che utilizza
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Distribuzione Gaussiana - Facciamo un riassunto -
 Distribuzione Gaussiana - Facciamo un riassunto - Nell ipotesi che i dati si distribuiscano seguendo una curva Gaussiana è possibile dare un carattere predittivo alla deviazione standard La prossima misura
Distribuzione Gaussiana - Facciamo un riassunto - Nell ipotesi che i dati si distribuiscano seguendo una curva Gaussiana è possibile dare un carattere predittivo alla deviazione standard La prossima misura
6. LIMITI. Definizione - Funzioni continue - Calcolo dei limiti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 6. LIMITI Definizione - Funzioni continue - Calcolo dei limiti A. A. 2014-2015 L.Doretti 1 IDEA INTUITIVA DI LIMITE I Caso: comportamento di una
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 6. LIMITI Definizione - Funzioni continue - Calcolo dei limiti A. A. 2014-2015 L.Doretti 1 IDEA INTUITIVA DI LIMITE I Caso: comportamento di una
LE EQUAZIONI DIFFERENZIALI. che, insieme alle loro derivate, soddisfano un equazione differenziale.
 LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
n(z) = n(0) e m gz/k B T ; (1)
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Lezione 3. Principi generali della Meccanica Cinematica, Statica e Dinamica
 Lezione 3 Principi generali della Meccanica Cinematica, Statica e Dinamica Premessa L Universo in cui viviamo costituisce un sistema dinamico, cioè un sistema in evoluzione nel tempo secondo opportune
Lezione 3 Principi generali della Meccanica Cinematica, Statica e Dinamica Premessa L Universo in cui viviamo costituisce un sistema dinamico, cioè un sistema in evoluzione nel tempo secondo opportune
Fenomeni quantistici
 Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
Fenomeni quantistici 1. Radiazione di corpo nero Leggi di Wien e di Stefan-Boltzman Equipartizione dell energia classica Correzione quantistica di Planck 2. Effetto fotoelettrico XIII - 0 Radiazione da
Filtri passivi Risposta in frequenza dei circuiti RC-RL-RLC
 23. Guadagno di un quadripolo Filtri passivi isposta in frequenza dei circuiti C-L-LC In un quadripolo generico (fig. ) si definisce guadagno G il rapporto tra il valore d uscita e quello d ingresso della
23. Guadagno di un quadripolo Filtri passivi isposta in frequenza dei circuiti C-L-LC In un quadripolo generico (fig. ) si definisce guadagno G il rapporto tra il valore d uscita e quello d ingresso della
Liberamente tratto da Prima Legge di Ohm
 Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica
 Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica Regressione Lineare e Correlazione Argomenti della lezione Determinismo e variabilità Correlazione Regressione Lineare
Università del Piemonte Orientale Specializzazioni di area sanitaria Statistica Medica Regressione Lineare e Correlazione Argomenti della lezione Determinismo e variabilità Correlazione Regressione Lineare
ATOMO POLIELETTRONICO. Numero quantico di spin m s
 ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Modelli e Metodi per la Simulazione (MMS)
 Modelli e Metodi per la Simulazione (MMS) adacher@dia.uniroma3.it Programma La simulazione ad eventi discreti, è una metodologia fondamentale per la valutazione delle prestazioni di sistemi complessi (di
Modelli e Metodi per la Simulazione (MMS) adacher@dia.uniroma3.it Programma La simulazione ad eventi discreti, è una metodologia fondamentale per la valutazione delle prestazioni di sistemi complessi (di
Università degli studi di Trento Corso di Laurea in Enologia e Viticoltura. Prof. Dino Zardi Dipartimento di Ingegneria Civile, Ambientale e Meccanica
 Università degli studi di Trento Corso di Laurea in Enologia e Viticoltura Prof. Dino Zardi Dipartimento di Ingegneria Civile, Ambientale e Meccanica Agrometeorologia 5. Caratteristiche dei moti atmosferici
Università degli studi di Trento Corso di Laurea in Enologia e Viticoltura Prof. Dino Zardi Dipartimento di Ingegneria Civile, Ambientale e Meccanica Agrometeorologia 5. Caratteristiche dei moti atmosferici
Risonanza magnetica nucleare
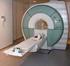 Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
Risonanza magnetica nucleare Università di Firenze Corso di Tecnologie Biomediche Lezione del 31 ottobre 2003 Leonardo Bocchi Principi fisici Premessa Modello classico Visualizzazione semplificata Equazione
LEZIONE 9. k, tenendo conto delle formule che permettono di calcolare il prodotto scalare ed il prodotto vettoriale, otteniamo
 LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
Se la funzione è analiticamente invertibile, estratto q, si può ricavare x = x(q).
 La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
La tecnica Monte Carlo Il metodo Monte Carlo è basato sulla scelta di eventi fisici con una probabilità di accadimento nota a priori. sia p(x) la distribuzione di probabilità con la quale si manifesta
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Appello di Meccanica Quantistica I
 Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Il calcolo vettoriale: ripasso della somma e delle differenza tra vettori; prodotto scalare; prodotto vettoriale.
 Anno scolastico: 2012-2013 Docente: Paola Carcano FISICA 2D Il calcolo vettoriale: ripasso della somma e delle differenza tra vettori; prodotto scalare; prodotto vettoriale. Le forze: le interazioni fondamentali;
Anno scolastico: 2012-2013 Docente: Paola Carcano FISICA 2D Il calcolo vettoriale: ripasso della somma e delle differenza tra vettori; prodotto scalare; prodotto vettoriale. Le forze: le interazioni fondamentali;
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Grandezze fisiche e loro misura
 Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e caratterizzati da entità o grandezze misurabili.
Grandezze fisiche e loro misura Cos è la fisica? e di che cosa si occupa? - Scienza sperimentale che studia i fenomeni naturali suscettibili di sperimentazione e caratterizzati da entità o grandezze misurabili.
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
